Application of the Method of Continued Boundary Conditions to the Solution of the Problem of Wave Diffraction on Scatterers of Complex Geometry Located in Homogeneous and Heterogeneous Media

Abstract

A method that allows modeling the scattering characteristics of bodies of arbitrary geometry has been proposed on the basis of the method of continued boundary conditions. The paper considers a two-dimensional problem of plane wave diffraction on dielectric bodies with complex cross-section geometry—in particular, on fractal-like bodies. Numerical algorithms for solving the diffraction problem based on systems of integral equations of the first and second kind have been compared. The method has been generalized to the problem of diffraction on a cylindrical body located in a homogeneous magnetodielectric half-space. The correctness of the method was confirmed by checking the fulfillment of the optical theorem for different bodies and by comparing with the results of calculations obtained by a modified method of discrete sources.

INTRODUCTION

The problem of wave diffraction on a dielectric body of complex geometry is very relevant and remains relatively poorly investigated because of the complexity of its solution. The results of modeling the characteristics of wave scattering by dielectric bodies are of great interest in such areas as optics of inhomogeneous media, laser flaw detection, and design of absorbing coatings [1–3]. Despite the fact that a number of analytical and numerical methods for solving these problems have been developed (the most common of which are the T-matrix method [4] and the discrete source method [5]), the need for modeling diffraction processes is growing quite rapidly and, therefore, the question of developing more universal methods for solving diffraction problems is still relevant. The wide popularity of the T-matrix method is largely due to the fact that it is relatively easy to perform such an important procedure, e.g., in astrophysics, as averaging the characteristics of the scattering of a body by the angles of its orientation relative to the incident plane wave using this method. However, the traditional (classical) version of the T-matrix method [4], as well as some of its recently developed modified versions [5, 6], are applicable to solving diffraction problems only on scatterers with an analytical boundary.

A generalization of the T-matrix method on the basis of the continued boundary conditions method was proposed in [7, 8] for solving the diffraction problem with the Dirichlet condition at the boundary in two- and three-dimensional cases. The two-dimensional case was also considered for the impedance boundary condition [9]. The idea of the continued boundary conditions method is to transfer the boundary condition from surface $S$ of the scatterer to some auxiliary surface ${{S}_{\delta }}$ that is located outside the scatterer at a fairly small distance $\delta$ from its border. The main advantages of the continued boundary conditions method include the absence of restrictions on the geometry of the scatterer (it is also applicable for scatterers that have border breaks and for thin screens). In addition, the continued boundary conditions method offers a unified approach to solving boundary value problems that does not depend on their type or dimension, the surface geometry of the scatterer, or the nature of the scattered field. Note also that the diffraction problem can be reduced to solving a system of integral equations of the first or second kinds within the framework of the method of continued boundary conditions, which is impossible to implement as simply as, e.g., when using the method of surface integral equations.

This article offers a generalization of the method described above for solving the two-dimensional problem of diffraction of electromagnetic waves on a dielectric body. Examples of modeling the characteristics of wave scattering by bodies with a cross section of complex geometry and fractal-like bodies were considered. Formulas and results of calculations of the scattering pattern of bodies of complex geometry located in a homogeneous dielectric half-space are given.

DERIVATION OF THE MAIN RELATIONS

Let primary electromagnetic field ${{{\mathbf{E}}}^{0}}$, ${{{\mathbf{H}}}^{0}}$ be incident on an infinitely long magnetodielectric cylinder with a generator parallel to axis $Oz$ and guide $S$. The geometry of the problem is shown in Fig. 1. Consider the case of E-polarization, when electric field intensity vector ${\mathbf{E}}$ has only one component ${{E}_{z}}$ (below denoted by the letter ${{U}_{ - }}$ or ${{U}_{ + }}$) parallel to the cylindrical body generator. The following coupling conditions will then take place at the boundary of the scatterer:

$${{\left. {{{U}_{ + }}} \right|}_{S}} = {{\left. {{{U}_{ - }}} \right|}_{S}},\quad {{\left. {\frac{{\partial {{U}_{ + }}}}{{\partial n}}} \right|}_{S}} = {{\left. {\boldsymbol{\kappa} \frac{{\partial {{U}_{ - }}}}{{\partial n}}} \right|}_{S}},$$

(1)

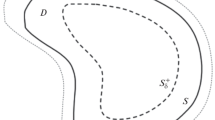
where ${{U}_{ + }}$ is the field inside the cylinder; ${{U}_{ - }} = {{U}^{0}} + {{U}^{1}}$ is the full field outside the body, where ${{U}^{0}}$ is falling and ${{U}^{1}}$ is scattered (secondary) fields; $\frac{\partial }{{\partial n}}$ is differentiation in the direction of the normal internal to $S$; and $\boldsymbol{\kappa} = {{{{\mu }_{i}}} \mathord{\left/ {\vphantom {{{{\mu }_{i}}} {{{\mu }_{e}}}}} \right. \kern-0em} {{{\mu }_{e}}}}$, where ${{\mu }_{i}}$ and ${{\mu }_{e}}$ are the relative magnetic permeabilities of the media inside and outside the body, respectively. The external medium (${{D}_{e}}$ = ${{\mathbb{R}}^{2}}{\backslash }\bar {D}$, $\bar {D}$ = $D \cup S$, where $D$ is the area bounded by curve $S$) and the medium inside the cylinder are assumed to be homogeneous, linear, and isotropic. At infinity, the standard radiation conditions for the scattered field are assumed to be met.

Fig. 1.

The geometry of the diffraction problem on a body located in a homogeneous medium.

We use the following representations to solve the Helmholtz equation in regions $D$ and ${{D}_{e}}$, respectively [5]:

$$\begin{gathered} {{U}_{ - }}({\mathbf{r}}) = {{U}^{0}}({\mathbf{r}}) \\ + \;\int\limits_S {\left\{ {\frac{{\partial {{U}_{ - }}({\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}{{G}_{ - }}({\mathbf{r}},{\mathbf{r}}{\kern 1pt} ') - {{U}_{ - }}({\mathbf{r}}{\kern 1pt} ')\frac{{\partial {{G}_{ - }}({\mathbf{r}},{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right\}ds{\kern 1pt} '} , \\ {{U}_{ + }}({\mathbf{r}}) = - \int\limits_S {\left\{ {\frac{{\partial {{U}_{ + }}({\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}{{G}_{ + }}({\mathbf{r}},{\mathbf{r}}{\kern 1pt} ') - {{U}_{ + }}({\mathbf{r}}{\kern 1pt} ')\frac{{\partial {{G}_{ + }}({\mathbf{r}},{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right\}ds{\kern 1pt} '} , \\ \end{gathered} $$

(2)

in which ${{G}_{ \pm }}({\mathbf{r}};{\mathbf{r}}{\kern 1pt} ') = \frac{1}{{4i}}H_{0}^{{(2)}}({{k}_{ \pm }}\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '} \right|)$ are the fundamental solutions of the scalar Helmholtz equation in ${{\mathcal{R}}^{2}}$ with material parameters of the media ${{D}_{e}}$ and D, respectively, ${{k}_{ + }}$ and ${{k}_{ - }}$ are the wavenumbers of the medium inside and outside the scatterer. By requiring the of conditions Eq. (1) to be met on contour $S_{\delta }^{ - }$ located in $\mathcal{R}{\backslash }\bar {D}$, and on contour $S_{\delta }^{ + }$ located in area $D$ (see Fig. 1) using Eqs. (2), we obtain the following systems of the Fredholm integral equations of the first or second kind, respectively:

$$\int\limits_S {\left\{ {\frac{{\partial U({\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ') + \kappa {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')} \right)} \right.} $$

$$\begin{gathered} \left. { - \;U({\mathbf{r}}{\kern 1pt} ')\left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} + \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)} \right\}ds{\kern 1pt} ' = - {{U}^{0}}({{{\mathbf{r}}}_{ - }}), \\ \int\limits_S {\left\{ {\frac{{\partial U({\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}} + \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}}} \right)} \right.} \\ \end{gathered} $$

(3)

$$\left. { - \;U({\mathbf{r}}{\kern 1pt} ')\left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} + \frac{1}{\kappa }\frac{{{{\partial }^{2}}{{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right)} \right\}ds{\kern 1pt} ' = - \frac{{\partial {{U}^{0}}({{{\mathbf{r}}}_{ - }})}}{{\partial n}},$$

$$U({\mathbf{r}}) = \frac{1}{2}{{U}^{0}}({{{\mathbf{r}}}_{ - }}) + \frac{1}{2}\int\limits_S {\left\{ {\frac{{\partial U({\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ') - \kappa {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')} \right)} \right.} $$

$$\left. { - \;U({\mathbf{r}}{\kern 1pt} ')\left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} - \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)} \right\}ds{\kern 1pt} ',$$

$$\frac{{\partial U({\mathbf{r}})}}{{\partial n}} = \frac{1}{{1 + \kappa }}\frac{{\partial {{U}^{0}}({{{\mathbf{r}}}_{ - }})}}{{\partial n}}$$

(4)

$$ + \;\frac{1}{{1 + \kappa }}\int\limits_S {\left\{ {\frac{{\partial U({\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}} - \kappa \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}}} \right)} \right.} $$

$$\left. { - \;U({\mathbf{r}}{\kern 1pt} ')\left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} - \frac{{{{\partial }^{2}}{{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right)} \right\}ds{\kern 1pt} ',$$

where observation points $M({{{\mathbf{r}}}_{ \pm }})$ belong to contours $S_{\delta }^{ \pm }$ and point $M({\mathbf{r}}) \in S$ and it is denoted that $U = {{U}_{ - }}$. Note that the contours that are separated from S by a fairly small distance $\delta$ are most often chosen as $S_{\delta }^{ \pm }$; i.e., equidistant contours are considered [5, 10]. Let the S boundary equation be given in parametric form:

$$\left\{ \begin{gathered} x = x{\kern 1pt} '(t), \hfill \\ y = y{\kern 1pt} '(t),\quad t \in [0,{{t}_{{\max }}}]. \hfill \\ \end{gathered} \right.$$

(5)

The equations of the displaced contours $S_{\delta }^{ \mp }$ are then written as follows:

$$\left\{ \begin{gathered} x(t) = x{\kern 1pt} '(t) \pm {{n}_{x}}(t)\delta , \hfill \\ y(t) = y{\kern 1pt} '(t) \pm {{n}_{y}}(t)\delta , \hfill \\ \end{gathered} \right.$$

(6)

where ${{n}_{x}}$ and ${{n}_{y}}$ are the coordinates of the normal to the boundary of body S. To solve system of equations (3), (4), we use the Krylov–Bogolyubov method. To do this, we write Eqs. (3) and (4) as

$$\begin{gathered} \int\limits_0^{{{t}_{{\max }}}} {\left( {{{K}_{{11}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{K}_{{12}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} ')} \right)dt{\kern 1pt} ' = {{b}_{1}}(t)} , \\ \int\limits_0^{{{t}_{{\max }}}} {\left( {{{K}_{{21}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{K}_{{22}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} ')} \right)dt{\kern 1pt} ' = {{b}_{2}}(t)} , \\ \end{gathered} $$

(7)

$$\begin{gathered} {{I}_{1}}(t) + \int\limits_0^{{{t}_{{\max }}}} {({{{\tilde {K}}}_{{11}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{{\tilde {K}}}_{{12}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} '))dt{\kern 1pt} ' = {{{\tilde {b}}}_{1}}(t)} , \\ {{I}_{2}}(t) + \int\limits_0^{{{t}_{{\max }}}} {({{{\tilde {K}}}_{{21}}}(t,t{\kern 1pt} '){{I}_{1}}(t{\kern 1pt} ') + {{{\tilde {K}}}_{{22}}}(t,t{\kern 1pt} '){{I}_{2}}(t{\kern 1pt} '))dt{\kern 1pt} ' = {{{\tilde {b}}}_{2}}(t)} , \\ \end{gathered} $$

(8)

in which

$${{I}_{1}}(t{\kern 1pt} ') = U({\mathbf{r}}{\kern 1pt} '(t{\kern 1pt} ')),\quad {{I}_{2}}(t{\kern 1pt} ') = \frac{{\partial U({\mathbf{r}}{\kern 1pt} '(t{\kern 1pt} '))}}{{\partial n{\kern 1pt} '}},$$

$$\xi (t{\kern 1pt} ') = \sqrt {\dot {x}{\kern 1pt} '{{{(t{\kern 1pt} ')}}^{2}} + \dot {y}{\kern 1pt} '{{{(t{\kern 1pt} ')}}^{2}}} ,$$

$${{K}_{{11}}} = - \left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} + \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '),$$

$${{K}_{{12}}} = \left( {{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ') + \kappa {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')} \right)\xi (t{\kern 1pt} '),$$

(9)

$${{K}_{{21}}} = - \left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} + \frac{1}{\kappa }\frac{{{{\partial }^{2}}{{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '),$$

$${{K}_{{22}}} = \left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}} + \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}}} \right)\xi (t{\kern 1pt} '),$$

$${{b}_{1}}(t) = - {{U}^{0}}({{{\mathbf{r}}}_{ - }}(t)),\quad {{b}_{2}}(t) = - \frac{{\partial {{U}^{0}}({{{\mathbf{r}}}_{ - }}(t))}}{{\partial n}},$$

$${{\tilde {K}}_{{11}}} = + \frac{1}{2}\left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}} - \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '),$$

$${{\tilde {K}}_{{12}}} = - \frac{1}{2}\left( {{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ') - \kappa {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')} \right)\xi (t{\kern 1pt} '),$$

$${{\tilde {K}}_{{21}}} = + \frac{1}{{1 + \kappa }}\left( {\frac{{{{\partial }^{2}}{{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}} - \frac{{{{\partial }^{2}}{{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}} \right)\xi (t{\kern 1pt} '),$$

(10)

$${{\tilde {K}}_{{22}}} = - \frac{1}{{1 + \kappa }}\left( {\frac{{\partial {{G}_{ - }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}} - \kappa \frac{{\partial {{G}_{ + }}({{{\mathbf{r}}}_{ + }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}}} \right)\xi (t{\kern 1pt} '),$$

$${{\tilde {b}}_{1}}(t) = + \frac{1}{2}{{U}^{0}}({{{\mathbf{r}}}_{ - }}(t)),\quad {{\tilde {b}}_{2}}(t) = + \frac{1}{{1 + \kappa }}\frac{{\partial {{U}^{0}}({{{\mathbf{r}}}_{ - }}(t))}}{{\partial n}}.$$

The point in Eq. (9) means the $t$-derivative. Let us present unknown functions ${{I}_{{1,2}}}(t{\kern 1pt} ')$ as sums:

$${{I}_{q}}(t{\kern 1pt} ') \cong \sum\limits_{n = 1}^N {c_{n}^{q}{{\Phi }_{n}}(t{\kern 1pt} ')} ,\quad q = 1,2,$$

(11)

where ${{\Phi }_{n}}(t{\kern 1pt} ')$ are pulse functions:

$${{\Phi }_{n}}(t{\kern 1pt} ') = \left\{ \begin{gathered} 1,\quad t \in [{{t}_{n}} - \Delta {\text{/2}},{{t}_{n}} + \Delta {\text{/2}}], \hfill \\ 0,\quad t \notin [{{t}_{n}} - \Delta {\text{/2}},{{t}_{n}} + \Delta {\text{/2}}]. \hfill \\ \end{gathered} \right.$$

(12)

Here, ${{t}_{n}} = \frac{{{{t}_{{\max }}}}}{N}\left( {n - \frac{1}{2}} \right)$, $n = \overline {1,N}$, where $\Delta = \frac{{{{t}_{{\max }}}}}{N}$ is the grid step and $N$ is the number of basic functions. Then, substituting Eq. (11) into system of integral equations (7), (8) and equating the left and right parts at the collocation points with coordinates $(x({{t}_{n}})$, $y({{t}_{n}}))$ selected on curves $S_{\delta }^{ \pm }$, we obtain the following systems of algebraic equations with respect to $c_{n}^{q}$:

$$\begin{gathered} \sum\limits_{n = 1}^N {} (K_{{mn}}^{{11}}c_{n}^{1} + K_{{mn}}^{{12}}c_{n}^{2}) = b_{m}^{1}, \\ \sum\limits_{n = 1}^N {(K_{{mn}}^{{21}}c_{n}^{1} + K_{{mn}}^{{22}}c_{n}^{2})} = b_{m}^{2},\quad m = \overline {1,N} , \\ \end{gathered} $$

(13)

or

$$\begin{gathered} c_{m}^{1} + \sum\limits_{n = 1}^N {(\tilde {K}_{{mn}}^{{11}}c_{n}^{1} + \tilde {K}_{{mn}}^{{12}}c_{n}^{2})} = \tilde {b}_{m}^{1}, \\ c_{m}^{2} + \sum\limits_{n = 1}^N {(\tilde {K}_{{mn}}^{{21}}c_{n}^{1} + \tilde {K}_{{mn}}^{{22}}c_{n}^{2})} = \tilde {b}_{m}^{2},\quad m = \overline {1,N} , \\ \end{gathered} $$

(14)

where the matrix elements and right parts are calculated using the following formulas

$$K_{{mn}}^{{pq}} = \int\limits_{{{t}_{n}} - \Delta /2}^{{{t}_{n}} + \Delta /2} {{{K}_{{pq}}}({{t}_{m}},t)dt} ,\quad b_{m}^{p} = b_{p}^{{}}({{t}_{m}}),$$

(15)

$$\begin{gathered} \tilde {K}_{{mn}}^{{pq}} = \int\limits_{{{t}_{n}} - \Delta /2}^{{{t}_{n}} + \Delta /2} {{{{\tilde {K}}}_{{pq}}}({{t}_{m}},t)dt} , \\ \tilde {b}_{m}^{p} = \tilde {b}_{p}^{{}}({{t}_{m}}),\quad p,q = 1,2. \\ \end{gathered} $$

(16)

Moving on to the asymptotics of the scattered wave field at ${\mathbf{r}} \to \infty$ and taking into account Eqs. (2), (5), (11), and (12), we obtain the following expression for the scattering pattern:

$$\begin{gathered} g(\varphi ) = \frac{{i\Delta }}{4}\sum\limits_{n = 1}^N {(c_{n}^{2} - c_{n}^{1}i{{k}_{ - }}(n_{x}^{'}({{t}_{n}})\cos \varphi } \\ + \;n_{y}^{'}({{t}_{n}})\sin \varphi ))\xi ({{t}_{n}}){{e}^{{i{{k}_{ - }}(x'({{t}_{n}})\cos \varphi + y'({{t}_{n}})\sin \varphi )}}}. \\ \end{gathered} $$

(17)

Equations (13)–(17) yield two numerical algorithms, which are based on the systems of equations of first and second kinds, for solving the formulated diffraction problem.

One criterion for the correctness of the results obtained is the optical theorem, which is written as [11]

$$\sigma = - \operatorname{Re} (g(\varphi = {{\varphi }_{0}})),$$

(18)

where

$$\sigma = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{{\left| {g(\varphi )} \right|}}^{2}}d\varphi } .$$

(19)

As an estimate of the accuracy of the optical theorem, we will calculate a value that represents the relative difference between the left and right parts in Eq. (18):

$${{\Delta }_{{ot}}} \equiv \frac{{\left| {\sigma + \operatorname{Re} (g({{\varphi }_{0}}))} \right|}}{\sigma }.$$

(20)

SCATTERING ON A CYLINDRICAL BODY IMMERSED IN A HOMOGENEOUS DIELECTRIC HALF-SPACE

We generalize the proposed method to the case in which the scattering obstacle is located in a homogeneous magnetodielectric half-space. The geometry of the problem is shown in Fig. 2. Denote the material parameters of the media at $y > d$ and $y < d$ through ${{\varepsilon }_{1}}$, ${{\mu }_{1}}$ and ${{\varepsilon }_{2}}$, ${{\mu }_{2}}$, respectively ($y = d$ is the media interface). The matching condition are assumed to be met at the interface:

$${{\left. U \right|}_{{y = d}}} = {{\left. {{{U}_{ - }}} \right|}_{{y = d}}},\quad \frac{1}{{{{\mu }_{1}}}}{{\left. {\frac{{\partial U}}{{\partial y}}} \right|}_{{y = d}}} = {{\left. {\frac{1}{{{{\mu }_{2}}}}\frac{{\partial {{U}_{ - }}}}{{\partial n}}} \right|}_{{y = d}}},$$

(21)

where $U$ and ${{U}_{ - }}$ are the complete field in the upper and lower half-space, respectively. Let us consider a plane wave incident from the upper half-space $y > d$ as the incident field.

Fig. 2.

The geometry of the problem of diffraction on a body located in a dielectric half-space.

As in the case of diffraction on a body in a homogeneous medium, the complete field in the lower half-space, in which the body is located, and the field inside the scatterer has the form Eq. (2), where Green function ${{G}_{ - }}({\mathbf{r}},{\mathbf{r}}{\kern 1pt} ')$ is replaced by the following one:

$$\begin{gathered} {{G}_{ - }}({\mathbf{r}},{\mathbf{r}}{\kern 1pt} ') = - \frac{i}{4}H_{0}^{{(2)}}({{k}_{ - }}\left| {{\mathbf{r}} - {\mathbf{r}}{\kern 1pt} '} \right|) \\ - \;\frac{i}{{4\pi }}\int\limits_{ - \infty }^\infty {R(w)\exp ( - i{{\gamma }_{ - }}(2d\, - \,y\, - \,y{\kern 1pt} ')\, - \,iw(x\, - \,x{\kern 1pt} '))\frac{{dw}}{{{{\gamma }_{ - }}}}} \\ = G_{ - }^{\operatorname{I} }({\mathbf{r}};{\mathbf{r}}{\kern 1pt} ') + G_{ - }^{{\operatorname{II} }}({\mathbf{r}};{\mathbf{r}}{\kern 1pt} '), \\ \end{gathered} $$

(22)

here, $R(w) = \frac{{{{\gamma }_{ - }} - {{\mu }_{{21}}}\gamma }}{{{{\gamma }_{ - }} + {{\mu }_{{21}}}\gamma }}$, ${{\gamma }_{ - }} = \sqrt {k_{ - }^{2} - {{w}^{2}}}$, $\gamma = \sqrt {k_{{}}^{2} - {{w}^{2}}}$. In this case, the root sign is selected so that its imaginary part is not positive. In these formulas, it is denoted that $k = \omega \sqrt {{{\varepsilon }_{1}}{{\mu }_{1}}}$, ${{k}_{ - }} = \omega \sqrt {{{\varepsilon }_{2}}{{\mu }_{2}}}$, and ${{\mu }_{{12}}} = {{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, ${{\mu }_{{21}}} = {{\mu }_{2}}{\text{/}}{{\mu }_{1}}$.

The further solution of the problem is again reduced to the system of integral equations with respect to the field and its normal derivative at the boundary of the scatterer. We will solve the diffraction problem using, e.g., the system of integral equations of the second kind. As a result, we obtain the system of integral equations in the form of Eq. (8) and the kernels of the integral equations are written as follows:

$${{\tilde {K}}_{{pq}}} = \tilde {K}_{{pq}}^{\operatorname{I} } + \tilde {K}_{{pq}}^{{\operatorname{I} \operatorname{I} }},\quad p,q = 1,2,$$

(23)

where the first terms are the same as for a body in a homogeneous medium with wavenumber ${{k}_{ - }}$ and the additional terms, which are due to the presence of the interface, have the following form:

$$\tilde {K}_{{11}}^{{\operatorname{II} }} = + \frac{1}{2}\frac{{\partial G_{ - }^{{\operatorname{II} }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}\xi (t{\kern 1pt} '),\quad \tilde {K}_{{12}}^{{\operatorname{II} }} = - \frac{1}{2}G_{ - }^{{\operatorname{II} }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')\xi (t{\kern 1pt} '),$$

$$\tilde {K}_{{21}}^{{\operatorname{II} }} = + \frac{1}{{1 + \kappa }}\frac{{{{\partial }^{2}}G_{ - }^{{\operatorname{II} }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n\partial n{\kern 1pt} '}}\xi (t{\kern 1pt} '),$$

(24)

$$\tilde {K}_{{22}}^{{\operatorname{II} }} = - \frac{1}{{1 + \kappa }}\frac{{\partial G_{ - }^{{\operatorname{II} }}({{{\mathbf{r}}}_{ - }};{\mathbf{r}}{\kern 1pt} ')}}{{\partial n}}\xi (t{\kern 1pt} ').$$

In addition, unlike the case of diffraction on a body in a homogeneous medium, under diffraction on a body in a half-space, the primary field is written as follows:

$$\begin{gathered} {{U}^{0}}({\mathbf{r}}) = \frac{{2k\cos {{\theta }_{0}}}}{{k\cos {{\theta }_{0}} + {{\mu }_{{12}}}\sqrt {k_{ - }^{2} - {{k}^{2}}{{{\sin }}^{2}}{{\theta }_{0}}} }} \\ \times \;\exp (ikd\cos {{\theta }_{0}} - id\sqrt {k_{ - }^{2} - {{k}^{2}}{{{\sin }}^{2}}{{\theta }_{0}}} ) \\ \times \;\exp ( - ikx\sin {{\theta }_{0}} + iy\sqrt {k_{ - }^{2} - {{k}^{2}}{{{\sin }}^{2}}{{\theta }_{0}}} ), \\ \end{gathered} $$

(25)

where ${{\theta }_{0}}$ is the angle of incidence of a plane wave. The system of integral equations is again solved by the Krylov–Bogolyubov method, but, because of the fact that the additional kernels of integral equations are slowly changing coordinate functions, the matrix elements of the system of linear equations can be calculated using an approximate formula:

$$\begin{gathered} \tilde {K}_{{mn}}^{{pq}} \approx \int\limits_{{{t}_{n}} - \Delta /2}^{{{t}_{n}} + \Delta /2} {\tilde {K}_{{pq}}^{{\text{I}}}({{t}_{m}},t)dt + \tilde {K}_{{pq}}^{{{\text{II}}}}({{t}_{m}},{{t}_{n}})} \Delta , \\ p,\;q = 1,\;2. \\ \end{gathered} $$

(26)

Here, we have the formulas for calculating the scattering pattern in the upper half-space. The pattern has the form

$$\begin{gathered} g(\varphi ) = \frac{{i\Delta }}{4}\frac{{2k\sin \varphi }}{{{{\mu }_{{21}}}k\sin \varphi + \sqrt {k_{ - }^{2} - {{k}^{2}}{{{\cos }}^{2}}\varphi } }} \\ \times \;\exp (ikd\sin \varphi - id\sqrt {k_{ - }^{2} - {{k}^{2}}{{{\cos }}^{2}}\varphi } ) \\ \times \;\sum\limits_{n = 1}^N {(c_{n}^{2} - c_{n}^{1}(in_{x}^{'}({{t}_{n}})k\cos \varphi + in_{y}^{'}({{t}_{n}})\sqrt {k_{ - }^{2} - {{k}^{2}}{{{\cos }}^{2}}\varphi } ))} \\ \times \;{{e}^{{i(kx'({{t}_{n}})\cos \varphi + y'({{t}_{n}})\sqrt {k_{ - }^{2} - {{k}^{2}}{{{\cos }}^{2}}\varphi } )}}}\xi ({{t}_{n}}). \\ \end{gathered} $$

(27)

NUMERICAL RESULTS

Let us consider the results of numerical modeling. Thereafter, we will assume that the body is irradiated by a plane wave. As an example, let us first consider the diffraction problem on an elliptical cylinder, a cylinder with a quadrifolium cross section, and a cylinder with a rectangular cross-section. The equation of the contour of a body with a section in the form of a quadrifolium has the form (in polar coordinates)

$$r = a(1 + \tau \cos 4\varphi ),\quad 0 < \tau < 1.$$

(28)

Figures 3–5 show the angular dependences of the scattering pattern for the corresponding geometry obtained for the following values of the problem parameters: kδ = 10^–4, φ₀, = 0, μ_i = 1, and ε_i = 4 (the material parameters of the external medium are μ_e = 1 and ε_e = 1 everywhere). The dimensions of the bodies had the following values: the semiaxis or half the side lengths of the rectangle ka = 5 and kb = 1 and the $ka = 5$ and $\tau = 0.5$ parameters for the body with a cross section in the form of a quadrifolium. The results were compared with the patterns constructed using the modified discrete source method [5, 12]. Note that the modified discrete source method cannot be directly applied to the problem of the diffraction on bodies that have boundary breaks, and so the contour of the axial section of the body was approximated by a smooth contour to solve the problem using the modified discrete source method [12]. Note also that the modified discrete source method provides high accuracy of calculation for bodies with a smooth border, such as ellipses, multifoil, etc.

Fig. 3.

The angular dependence of the scattering pattern for an elliptical cylinder. (1) The modified discrete source method and (2) the continued boundary conditions method.

Fig. 4.

The angular dependence of the scattering pattern of a body with a cross section in the form of a quadrifolium. (1) The modified discrete source method and (2) the continued boundary conditions method.

Fig. 5.

The angular dependence of the scattering pattern of a body with a rectangular cross section. (1) The modified discrete source method and (2) the continued boundary conditions method.

Tables 1–3 show the differences in the scattering pattern modules of the specified geometry obtained by two methods: using the modified discrete source method and the continued boundary conditions method. As can be seen from Tables 1–3, the difference in results decreases as the number of basic functions used increases. It also follows from the given data that the use of equations of the first kind for bodies with a smooth boundary is better because of faster convergence. In the case of a body with a rectangular section, using equations of the second kind gives better results.

Table 1. Comparison of the results obtained using the modified discrete source method and the continued boundary conditions method. Diffraction on an elliptical cylinder

Table 2. Comparison of the results obtained using the modified discrete source method and the continued boundary conditions method. Diffraction on the body with a section in the form of a quadrifolium

Table 3. Comparison of the results obtained using the modified discrete source method and the continued boundary conditions method. Diffraction on a body with a rectangular cross section

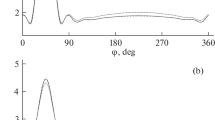
Figure 6 shows the geometry of fractal-like cylinders with a cross section in the form of a Koch snowflake and Sierpinski curve (first iteration) [13]. Figures 7 and 8 illustrate the angular dependences of the scattering pattern for the specified cylinders at the problem parameters of kδ = 10^–4, µ_i = 1, and ε_i = 4. The maximum cross-sectional size of a body with a cross section in the form of the Koch snowflake and a body with a cross section in the form of the Sierpinski curve on the x axis was $kL = 10$. Two different angles of incidence φ₀ = 0° and 45° were considered. As follows from the figures for the geometry under study, the maximum points of the angular dependences of the scattering pattern roughly coincide with the angles of incidence of the plane wave. It can also be seen that the dependences of the pattern for both a body with a section in the form of the Koch snowflake and a body with a section in the form of the Sierpinski curve have quite large side lobes.

Fig. 6.

The geometry of the body with a cross section in the form of (a) a Koch snowflake and (b) Sierpinski curve.

Fig. 7.

Angular dependence of the scattering pattern of a body with a section in the form of a Koch snowflake. The angle of incidence of the wave (1) ${{\varphi }_{0}} = 0$ and (2) ${{\varphi }_{0}}$ = 45°.

Fig. 8.

The angular dependence of the scattering pattern of a body with a cross section in the form of a Sierpinski curve. The angle of incidence of the wave (1) ${{\varphi }_{0}} = 0$ and (2) ${{\varphi }_{0}}$ = 45°.

The accuracy of the optical theorem was verified for the geometry of the scatterers considered above. In all cases, we chose the number of bias functions so that ${{N}_{\lambda }} = 25$, where ${{N}_{\lambda }}$ is the number of collocation points at a single wavelength. In this case, the permittivity of the body medium varied from ${{\varepsilon }_{i}} = 4$ to 10³ and the relative magnetic permeability was chosen equal to 1. As a result of calculations, we found that the relative difference between the right and left parts of Eq. (18), which is the value of ${{\Delta }_{{ot}}}$ (see Eq. (20)), does not exceed 5 × 10^–3; i.e., it is small.

Table 4 shows the results of the calculation of the scattering pattern obtained using the continued boundary conditions method and the modified discrete source method. The diffraction on a body located in a dielectric half-space was considered. The dimensions of the bodies were chosen the same as in the case of diffraction in a homogeneous medium and the material parameters of the media for the upper and lower half-spaces and the cylindrical body had the following values: μ₁ = 1, ε₁ = 1, µ₂ = 1, ε₂ = 2 – i × 10^–3, µ_i = 1, and ε_i = 6. The value of d was chosen so that the shortest distance from the boundary of all bodies to the boundary of the media was 1. Parameter $k\delta = {{10}^{{ - 4}}}$. The table shows that the relative difference between the results obtained using the continued boundary conditions method and the modified discrete source method does not exceed 1.6%. Figure 9 shows the angular dependences of the scattering pattern for cylinders with a cross section in the form of a regular hexagon, Koch snowflake, and Sierpinski curve (first iteration) located in a homogeneous half-space. The pattern dependences are given for the upper half-space. Two different angles of incidence of the plane wave θ₀ = 0° and 45° were considered. It follows from the figure that, in the case of a plane wave normal incidence, the scattering pattern for all bodies has a main lobe (in the direction of backscattering) and two side lobes. In the case of an off-normal incidence, the pattern graph has an oscillating character.

Table 4. Comparison of the results obtained using the modified discrete source method and the continued boundary conditions method. Diffraction on a body located in the dielectric half-space

Fig. 9.

The angular dependence of the scattering pattern of a body located in a dielectric half-space. (1) A cylinder with a section in the form of a Sierpinski curve, (2) a cylinder with a section in the form of a Koch snowflake, and (3) a cylinder with a section in the form of a regular hexagon. The angle of incidence of the wave (1) ${{\theta }_{0}} = 0$ and (2) ${{\theta }_{0}}$ = 45°.

CONCLUSIONS

Two numerical algorithms based on a system of integral equations of the first and second kind have been developed using the continued boundary conditions method, which allow calculating the scattering characteristics of magnetodielectric bodies of arbitrary geometry. The results of calculating the scattering pattern for a large set of bodies with different geometries, including fractal-like scatterers, were obtained. A comparison of the results of the methods based on the continued boundary conditions method with the results obtained using the modified discrete source method was made. The continued boundary conditions method allows getting the results of the calculation of the scattering pattern with high accuracy. In the case of a body with a smooth boundary, the method based on equations of the first kind allows obtaining results with better accuracy. The accuracy of the optical theorem for the geometry under consideration was verified. The accuracy of the optical theorem was 5 × 10^–3. Comparison of the modified discrete source method and the continued boundary conditions method for the case of diffraction on a cylindrical body located in the dielectric half-space showed a good coincidence of the calculation results. Angular dependences of the scattering pattern were constructed for bodies with boundary breaks located in the dielectric half-space.