Acoustic Waves in Multifraction Gas Suspensions in the Presence of Phase Transformations

Abstract

The propagation of acoustic waves in gas mixtures with vapor, monodisperse drops, and solid particles of various materials and sizes has been studied. A mathematical model is presented; the dispersion relation, the equilibrium and frozen speeds of sound, and low- and high-frequency asymptotes for the linear attenuation coefficient are deduced; the dispersion curves are calculated. The influence of particle size and disperse phase parameters on dissipation and dispersion of acoustic waves is analyzed for a mixture of air with vapor, water drops, and aluminum and carbon black particles. Fast Fourier transform is used to calculate the pulse perturbations in the studied media.

INTRODUCTION

The study of the propagation of small perturbations in gas mixtures is a topical problem in the dynamics of multiphase media. The study of the propagation of acoustic waves in gas mixtures is complicated by the fact that gas mixtures are multiphase and polydisperse and that the interphase interaction is nonstationary and nonequilibrial. The main models of the wave dynamics of polydisperse media and several results in this field are presented in a well-known monograph [1]. The authors of [2] studied two-phase flows with solid particles, drops, and bubbles. In [3], problems of the formation of zones with an increased concentration of a disperse phase in multiphase flows were considered. The author of monograph [4] presented a brief review of the results on the study of acoustic perturbations of monodisperse gas mixtures without phase transitions. The authors of [5] studied the influence of a polydisperse composition of a gas mixture on the propagation of monochromatic perturbations in one-component gas mixtures with particles or in vapor mixtures with drops. The authors of [6] studied patterns of the propagation of monochromatic waves in two-component, polydisperse gas mixtures with vapor and liquid drops. The propagation of spherical and cylindrical low-amplitude waves in polydisperse fogs with phase transitions was considered in [7], and a general dispersion dependence of the wavenumber on the oscillation frequency and thermophysical parameters of phases was obtained. The authors of [8] studied an anomalous, nonmonotonic dependence of the dissipation of small harmonic and pulse perturbations on the mass concentration of drops in monodisperse aerosols with heat and mass transfer. A rather full description of the linear propagation theory for plane perturbations in mono- and polydisperse, two-phase gas mixtures with vapor and liquid drops is presented in [9].

The authors of [10, 11] studied propagation of acoustic waves of various shapes in two- and multiphase gas mixtures with particles of various materials and sizes without taking into account phase transitions. The patterns of the propagation of plane, cylindrical, and spherical low-amplitude waves in two-phase, vapor–gas–drop mixtures with solid particles were analyzed in [12, 13].

The present work studies the propagation of low-amplitude waves in mixtures of gas with vapor, monodisperse drops, and solid particles of various materials and sizes.

MAIN EQUATIONS

In describing the motion of a multiphase gas mixture by the methods of continuum mechanics, let us suppose to be valid following assumptions [1]:

• The sizes of inclusions (particles, drops) in the mixture are considerably larger than the molecular-kinetic sizes, i.e., the inclusions contain a large number of molecules.

• The inclusion sizes are considerably lower than distances over which average or macroscopic parameters of the mixture significantly change, i.e., the inclusions are much smaller than typical studied wavelengths.

• We are not taking into account the energy and other effects of the chaotic and internal motion of disperse particles (Brownian and rotational and deformational, respectively).

• There is no coagulation, fragmentation, or formation of new inclusions.

• The viscosity and thermal conductivity are revealed only upon interphase interaction and are not upon macroscopic processes of the energy and impulse transfer.

• The studied acoustic wavelengths considerably exceed the inclusion sizes and distances between them, i.e., the medium is acoustically homogeneous for these waves.

Within the framework of the aforementioned assumptions, let us use the model of multivelocity and a three-temperature continuum [1] to study the propagation of acoustic waves in mixtures of gas with vapor, monodisperse drops, and solid particles of various materials and sizes.

Since the problem is linear, perturbations of the parameters are small. The drop mass is small as well. Thus, evaporation and condensation are weak, and the Stephen flows [14] could be disregarded in the description of the heat transfer.

As in [9], in a coordinate system in which the undisturbed mixture is at rest, the linearized equations of continuity and impulse conservation of phases are as follows:

$$\begin{gathered} \frac{{\partial \rho' _{1}}}{{\partial t}} + {{\rho }_{{10}}}\left( {\frac{{\partial v'_{1}}}{{\partial r}} + \theta \frac{{v'_{1}}}{r}} \right) = - {{n}_{{0l}}}{{j}_{{V\Sigma }}}, \\ \frac{{\partial \rho' _{1}}}{{\partial t}} + {{\rho }_{{V20}}}\left( {\frac{{\partial v'_{1}}}{{\partial r}} + \theta \frac{{v'_{1}}}{r}} \right) = - {{n}_{{0l}}}{{j}_{{V\Sigma }}}, \\ \end{gathered} $$

$$\begin{gathered} \frac{{\partial \rho' _{l}}}{{\partial t}} + {{\rho }_{{l0}}}\left( {\frac{{\partial v'_{l}}}{{\partial r}} + \theta \frac{{v'_{l}}}{r}} \right) = - {{n}_{{0l}}}{{j}_{\Sigma }}, \\ \frac{{\partial \rho' _{j}}}{{\partial t}} + {{\rho }_{{j0}}}\left( {\frac{{\partial v'_{j}}}{{\partial r}} + \theta \frac{{v'_{j}}}{r}} \right) = 0\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \end{gathered} $$

$$\begin{gathered} {{\rho }_{{10}}}\frac{{\partial v'_{1}}}{{\partial t}} + \frac{{\partial p'_{1}}}{{\partial r}} + {{n}_{{0l}}}{{f}_{l}} + \sum\limits_{j = 1}^N {{{n}_{{0sj}}}{{f}_{{sj}}}} = 0, \\ {{\rho }_{{j0}}}\frac{{\partial v'_{j}}}{{\partial t}} = {{n}_{{0j}}}{{f}_{j}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \end{gathered} $$

$$\begin{gathered} {{\rho }_{{j0}}} = {{\alpha }_{{0j}}}\rho _{{j0}}^{^\circ }\,\,\,\,\left( {j = 1,l,\overline {s1,sN} } \right), \hfill \\ {{\rho }_{1}} = {{\rho }_{V}} + {{\rho }_{G}},\,\,\,\,{{p}_{1}} = {{p}_{V}} + {{p}_{G}}, \hfill \\ \end{gathered} $$

$$\begin{gathered} {{k}_{V}} = \frac{{{{\rho }_{V}}}}{{{{\rho }_{1}}}},\,\,\,\,{{k}_{G}} = \frac{{{{\rho }_{G}}}}{{{{\rho }_{1}}}},\,\,\,\,{{k}_{V}} + {{k}_{G}} = 1, \\ {{\alpha }_{{j0}}} = \frac{4}{3}\pi r_{j}^{3}{{n}_{{0j}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ {{\alpha }_{{10}}} + \sum\limits_{j = l,\overline {s1,sN} } {{{\alpha }_{{j0}}}} = 1. \\ \end{gathered} $$

Here and below, index 1 refers to the carrier phase, l refers to drops, sj$\left( {j = \overline {1,N} } \right)$ refers to solid particles, V and G refer to parameters of the vapor and gas components the carrier phase; ${{r}_{j}}$ is the radius of inclusions, ${{n}_{{0j}}}$ is the volume concentration of particles of the jth type, ${{k}_{V}}$ and ${{k}_{G}}$ are the concentrations of vapor and gas in the carrier phase of the mixture, ${{j}_{{V\Sigma }}}$ is the diffusion flow of vapor to the surface of drop “Σ,” and ${{j}_{\Sigma }}$ is the intensity of condensation on the surface of a single drop.

Let us consider the thermophysical parameters of the carrier phase, which are determined by the parameters of vapor and gas:

$$\begin{gathered} {{R}_{1}} = {{k}_{V}}{{R}_{V}} + {{k}_{G}}{{R}_{G}},\,\,\,\,{{c}_{{p1}}} = {{k}_{V}}{{c}_{{pV}}} + {{k}_{G}}{{c}_{{pG}}}, \\ {{\lambda }_{1}} = {{k}_{V}}{{\lambda }_{V}} + {{k}_{G}}{{\lambda }_{G}},\,\,\,\,{{\mu }_{1}} = {{k}_{V}}{{\mu }_{V}} + {{k}_{G}}{{\mu }_{G}}. \\ \end{gathered} $$

Here, R, ${{c}_{p}},$ λ, and μ are the gas constant, heat capacity at constant pressure, and thermal conductivity and dynamic viscosity coefficients, respectively.

At $\sum\nolimits_{j = l,\overline {s1,sN} } {{{\alpha }_{j}} \ll 1}$ and $\rho _{j}^{^\circ } \gg \rho _{1}^{^\circ },$ the Stokes force ${{f}_{\mu }}$ and the Basset force ${{f}_{{\text{B}}}}$ are the main forces acting on a single particle of the disperse phase. Their expressions are as follows:

$${{f}_{j}} = {{f}_{{\mu j}}} + {{f}_{{{\text{B}}j}}},\,\,\,\,{{f}_{{\mu j}}} = 6\pi {{r}_{j}}{{\mu }_{1}}\left( {v'_{1} - v'_{j}} \right),$$

$$\begin{gathered} {{f}_{{{\text{B}}j}}} = {{B}_{j}}\int\limits_{ - \infty }^t {\frac{\partial }{{\partial \tau }}\left( {v'_{1} - v'_{{2j}}} \right)\frac{{d\tau }}{{\sqrt {t - \tau } }}} , \\ {{B}_{j}} = 6r_{j}^{2}\sqrt {\pi {{\mu }_{1}}\rho _{1}^{^\circ }} \,\,\,\,\left( {j = l,\overline {s1,sN} } \right). \\ \end{gathered} $$

Let us present ${{f}_{j}}$ as

$$\begin{gathered} {{f}_{j}} = {{g}_{{0j}}}\frac{1}{{{{\tau }_{{vj}}}}} \\ \times \,\,\left[ {\left( {v'_{1} - v'_{j}} \right) + \sqrt {\frac{{{{\tau }_{{\mu 1j}}}}}{\pi }} \int\limits_{ - \infty }^t {\frac{\partial }{{\partial \tau }}\left( {v'_{1} - v'_{j}} \right)\frac{{d\tau }}{{\sqrt {t - \tau } }}} } \right], \\ \end{gathered} $$

where ${{g}_{{0j}}}$ is the particle mass

$$\begin{gathered} {{g}_{{0j}}} = \frac{4}{3}\pi r_{j}^{3}\rho _{{j0}}^{^\circ },\,\,\,\,{{\tau }_{{\mu 1j}}} = \frac{{\rho _{{10}}^{^\circ }r_{j}^{2}}}{{{{\mu }_{1}}}}, \\ {{\tau }_{{vj}}} = \frac{2}{9}\frac{{\rho _{{j0}}^{^\circ }r_{j}^{2}}}{{{{\mu }_{1}}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right). \\ \end{gathered} $$

The linearized equations for heat influx to the gas phase, drops, solid particles, and the surfaces of a single drop and a single solid particle are as follows:

$$\begin{gathered} {{\rho }_{{V20}}}\frac{{\partial i'_{V}}}{{\partial t}} + {{\rho }_{{G0}}}\frac{{\partial i'_{G}}}{{\partial t}} = {{\alpha }_{{10}}}\frac{{\partial p'_{1}}}{{\partial t}} - \sum\limits_{j = l,\overline {s1,sN} } {{{n}_{{j0}}}{{q}_{{1\Sigma j}}}} , \\ {{\rho }_{{j0}}}\frac{{\partial u'_{j}}}{{\partial t}} = - {{n}_{{0j}}}{{q}_{{2\Sigma j}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ {{q}_{{1\Sigma j}}} + {{q}_{{2\Sigma j}}} = 0\,\,\,\,\left( {j = \overline {s1,sN} } \right),\,\,\,\,{{q}_{{1\Sigma l}}} + {{q}_{{2\Sigma l}}} = - {{j}_{\Sigma }}{{l}_{0}}, \\ \end{gathered} $$

where ${{l}_{0}}$ is the specific heat of evaporation.

The heat fluxes from the outside ${{q}_{{1\Sigma j}}}$ and from within ${{q}_{{2\Sigma j}}}$ of the jth inclusion to its surface and the interphase diffusion flow ${{j}_{{V\Sigma }}}$ are given by the relations [9]

$$\begin{gathered} {{q}_{{1\Sigma j}}} = 2\pi {{r}_{j}}{{\lambda }_{1}}{\text{N}}{{{\text{u}}}_{{1j}}}\left( {T'_{1} - T'_{{\Sigma j}}} \right), \\ {\text{N}}{{{\text{u}}}_{{1j}}} = 2{{r}_{j}}{{\beta _{{1j}}^{T}} \mathord{\left/ {\vphantom {{\beta _{{1j}}^{T}} {{{\lambda }_{1}}}}} \right. \kern-0em} {{{\lambda }_{1}}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \end{gathered} $$

$$\begin{gathered} {{q}_{{2\Sigma j}}} = 2\pi {{r}_{j}}{{\lambda }_{j}}{\text{N}}{{{\text{u}}}_{{2j}}}\left( {T'_{j} - T'_{{\Sigma j}}} \right), \\ {\text{N}}{{{\text{u}}}_{{2j}}} = 2{{r}_{j}}{{\beta _{{2j}}^{T}} \mathord{\left/ {\vphantom {{\beta _{{2j}}^{T}} {{{\lambda }_{j}}}}} \right. \kern-0em} {{{\lambda }_{j}}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \end{gathered} $$

$$\begin{gathered} \left( {1 - {{k}_{V}}} \right){{j}_{{V\Sigma }}} = 2\pi {{r}_{l}}\rho _{1}^{^\circ }{{D}_{1}}{\text{S}}{{{\text{h}}}_{1}}\left( {{{k}_{V}} - {{k}_{{V\Sigma }}}} \right), \\ {\text{S}}{{{\text{h}}}_{1}} = {{2{{r}_{l}}\beta _{1}^{D}} \mathord{\left/ {\vphantom {{2{{r}_{l}}\beta _{1}^{D}} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}. \\ \end{gathered} $$

Here and below, ${{T}_{1}}$ is the career phase temperature, ${{T}_{{\Sigma j}}}$ is the temperature in the surface Σ layer of the $j$th-type particle, ${{T}_{{2j}}}$ is the temperature of the solid jth-type particles, ${\text{N}}{{{\text{u}}}_{{1j}}}$ and $\beta _{{1j}}^{T}$ are the dimensionless (the Nusselt number) and the dimensional coefficients of the career phase heat exchange with the interface of the jth-type inclusion, ${\text{N}}{{{\text{u}}}_{{2j}}}$ and $\beta _{{2j}}^{T}$ are the dimensionless (the Nusselt number) and the dimensional coefficients of the jth-type particle heat exchange with the interface, λ is the thermal conductivity coefficient, ${\text{S}}{{{\text{h}}}_{{\text{1}}}}$ and $\beta _{1}^{D}$ are the dimensionless (the Sherwood number) and dimensional coefficients of the carrier phase mass exchange with the surface Σ layer of the drop, and ${{D}_{1}}$ is the coefficient of the binary diffusion.

The heat fluxes ${{q}_{{1\Sigma j}}}$ and ${{q}_{{2\Sigma j}}}$ are as follows:

$$\begin{gathered} {{q}_{{1\Sigma j}}} = {{g}_{{0j}}}\frac{{{{c}_{{p1}}}}}{{{{m}_{j}}{{\tau }_{{T1j}}}}}{\text{N}}{{{\text{u}}}_{{1j}}}\left( {T'_{1} - T'_{{\Sigma j}}} \right), \\ {{q}_{{2\Sigma j}}} = {{g}_{{0j}}}\frac{{{{c}_{{p1}}}}}{{{{\tau }_{{T2j}}}}}{\text{N}}{{{\text{u}}}_{{2j}}}\left( {T'_{j} - T'_{{\Sigma j}}} \right)\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \end{gathered} $$

where

$$\begin{gathered} {{m}_{j}} = \frac{{{{\rho }_{{j0}}}}}{{{{\rho }_{{10}}}}},\,\,\,\,{{\tau }_{{T1j}}} = \frac{2}{3}\frac{{{{\alpha }_{{10}}}}}{{{{\alpha }_{{j0}}}}}{{\tau }_{{\lambda 1j}}},\,\,\,\,{{\tau }_{{T2j}}} = \frac{2}{3}{{\tau }_{{\lambda 2j}}}, \\ {{\tau }_{{\lambda 1j}}} = \frac{{\rho _{{10}}^{^\circ }r_{j}^{2}{{c}_{{p1}}}}}{{{{\lambda }_{1}}}},\,\,\,\,{{\tau }_{{\lambda 2j}}} = \frac{{\rho _{{j0}}^{^\circ }r_{j}^{2}{{c}_{j}}}}{{{{\lambda }_{j}}}}. \\ \end{gathered} $$

The interphase diffusion flow is [9]

$$\begin{gathered} {{j}_{{V\Sigma }}} = {{g}_{{0l}}}\frac{{m_{l}^{^\circ }}}{{{{p}_{{10}}}}}{\text{S}}{{{\text{h}}}_{1}}\frac{{p'_{V} - p'_{{V\Sigma }}}}{{{{\tau }_{{k1}}}}}, \\ {{\tau }_{{k1}}} = \frac{2}{3}\frac{{{{R}_{V}}}}{{{{R}_{{10}}}}}\left( {1 - {{k}_{V}}} \right){{\tau }_{d}},\,\,\,\,{{\tau }_{d}} = \frac{{r_{l}^{2}}}{{{{D}_{1}}}},m_{l}^{^\circ } = \frac{{\rho _{{10}}^{ \circ }}}{{\rho _{{l0}}^{ \circ }}}. \\ \end{gathered} $$

The intensity of nonequilibrial condensation at the phase interface is given by the Hertz–Knudsen–Langmuir formula [9]:

$${{j}_{\Sigma }} = {{g}_{{0l}}}\frac{{m_{l}^{^\circ }}}{{{{\tau }_{\beta }}}}\frac{{p'_{{V\Sigma }} - p'_{{VS}}}}{{{{p}_{{10}}}}},\,\,\,\,{{\tau }_{\beta }} = \frac{1}{3}\frac{{\sqrt {2\pi } }}{{{{\gamma }_{V}}}}\frac{{{{\gamma }_{{10}}}{{C}_{V}}{{r}_{l}}}}{{\beta C_{{10}}^{2}}}.$$

Here, ${{\tau }_{\beta }}$ is the characteristic time of the equalization of partial vapor pressures on the phase interface with respect to the accommodation coefficient; β and γ are the adiabatic exponents.

Along the phase equilibrium curve, the Clapeyron–Clausius equation [9] is valid:

$$p'_{{VS}} = \frac{{{{l}_{0}}\rho _{{V0}}^{^\circ }}}{{{{T}_{{10}}}}}T'_{{\Sigma l}},$$

where index S relates to parameters on the saturation line.

From the mass balance on the drop surface, we obtain

$${{j}_{{V\Sigma }}} = {{j}_{\Sigma }}.$$

Let us consider the components of the carrier phase to be calorically perfect gases, and we account for the fact that the reduced density perturbations are included into the continuity equations. The equations of state of the career phase are presented in the following linearized form:

$$\begin{gathered} p'_{V} = \frac{{C_{{10}}^{2}}}{{{{\gamma }_{{10}}}{{\alpha }_{{10}}}}}{{{\bar {R}}}_{V}}\rho' _{V} + {{p}_{{V0}}}\frac{{T'_{1}}}{{{{T}_{{10}}}}}, \\ p'_{1} = \frac{{C_{{10}}^{2}}}{{{{\gamma }_{{10}}}{{\alpha }_{{10}}}}}(\rho' _{1} + \Delta \bar {R}(\rho' _{V} - {{k}_{{V0}}}\rho' _{1})) + {{p}_{{10}}}\frac{{T'_{1}}}{{{{T}_{{10}}}}}, \\ \Delta \bar {R} = {{\left( {{{R}_{V}} - {{R}_{G}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{R}_{V}} - {{R}_{G}}} \right)} {{{R}_{{10}}}}}} \right. \kern-0em} {{{R}_{{10}}}}},\,\,\,\,{{{\bar {R}}}_{V}} = \frac{{{{R}_{V}}}}{{{{R}_{{10}}}}}, \\ i'_{V} = {{c}_{{pV}}}T'_{1},\,\,\,\,i'_{G} = {{c}_{{pG}}}T'_{1}\,\,\,\,\left( {{{c}_{{pV}}},{{c}_{{pG}}} = {\text{const}}} \right). \\ \end{gathered} $$

The equations of state of the incompressible disperse phase are

$${\rho _{j}^{\circ}}' = 0,\,\,\,\,u_{j}' = {{c}_{j}}T'_{{2j}}\left( {{{c}_{j}} = {\text{const}},\,\,\,\,j = l,\overline {s1,sN} } \right).$$

Here, ${{c}_{j}}$ is the heat capacity of the disperse phase.

Let us enter the velocity potentials of phases $\left( {v' = \frac{{\partial \varphi '}}{{\partial r}}} \right).$ The linearized system of equations for the perturbed motion of the gas mixture with vapor, identical drops, and solid particles of different types and sizes in the coordinate system in which the unperturbed medium is at rest is then written in the form

$$\begin{gathered} \frac{{\partial \rho' _{1}}}{{\partial t}} + {{\rho }_{{10}}}\left( {\frac{{{{\partial }^{2}}\varphi' _{1}}}{{\partial {{r}^{2}}}} + \frac{\theta }{r}\frac{{\partial \varphi' _{1}}}{{\partial r}}} \right) = - \frac{{{{\rho }_{{l0}}}m_{l}^{^\circ }}}{{{{p}_{{10}}}}}{\text{S}}{{{\text{h}}}_{1}}\frac{{p'_{V} - p'_{{V\Sigma }}}}{{{{\tau }_{{k1}}}}},\,\,\,\, \\ \frac{{\partial \rho' _{V}}}{{\partial t}} + {{\rho }_{{V0}}}\left( {\frac{{{{\partial }^{2}}\varphi' _{1}}}{{\partial {{r}^{2}}}} + \frac{\theta }{r}\frac{{\partial \varphi' _{1}}}{{\partial r}}} \right) = - \frac{{{{\rho }_{{l0}}}m_{l}^{^\circ }}}{{{{p}_{{10}}}}}{\text{S}}{{{\text{h}}}_{1}}\frac{{p'_{V} - p'_{{V\Sigma }}}}{{{{\tau }_{{k1}}}}}, \\ \frac{{\partial \rho' _{l}}}{{\partial t}} + {{\rho }_{{l0}}}\left( {\frac{{{{\partial }^{2}}\varphi' _{l}}}{{\partial {{r}^{2}}}} + \frac{\theta }{r}\frac{{\partial \varphi' _{l}}}{{\partial r}}} \right) = \frac{{{{\rho }_{{l0}}}m_{l}^{^\circ }}}{{{{p}_{{10}}}}}\frac{{p'_{{V\Sigma }} - p'_{{VS}}}}{{{{\tau }_{\beta }}}},\,\,\,\, \\ \frac{{\partial \rho' _{j}}}{{\partial t}} + {{\rho }_{{j0}}}\left( {\frac{{{{\partial }^{2}}\varphi' _{j}}}{{\partial {{r}^{2}}}} + \frac{\theta }{r}\frac{{\partial \varphi' _{j}}}{{\partial r}}} \right) = 0\,\,\,\,\left( {j = \overline {s1,sN} } \right), \\ \frac{{{{\partial }^{2}}\varphi' _{1}}}{{\partial t\partial r}} + \frac{1}{{{{\rho }_{{10}}}}}\frac{{\partial p'_{1}}}{{\partial r}} + \sum\limits_{j \in l,\overline {s1,sN} } {\frac{{{{m}_{j}}}}{{{{\tau }_{{vj}}}}}\left[ {\frac{{\partial \varphi' _{1}}}{{\partial r}} - \frac{{\partial \varphi' _{j}}}{{\partial r}}} \right.} \\ \left. { + \,\,\sqrt {\frac{{{{\tau }_{{\mu 1j}}}}}{\pi }} \int\limits_{ - \infty }^t {\frac{\partial }{{\partial t}}\left( {\frac{{\partial \varphi' _{1}}}{{\partial x}} - \frac{{\partial \varphi' _{j}}}{{\partial x}}} \right)\frac{{d\tau }}{{\sqrt {t - \tau } }}} } \right] = 0, \\ \frac{{{{\partial }^{2}}\varphi' _{j}}}{{\partial t\partial r}} = \frac{1}{{{{\tau }_{{vj}}}}}\left[ {\frac{{\partial \varphi' _{1}}}{{\partial r}} - \frac{{\partial \varphi' _{j}}}{{\partial r}}} \right.\,\,\,\, \\ \left. { + \,\,\sqrt {\frac{{{{\tau }_{{\mu 1j}}}}}{\pi }} \int\limits_{ - \infty }^t {\frac{\partial }{{\partial t}}\left( {\frac{{\partial \varphi' _{1}}}{{\partial x}} - \frac{{\partial \varphi' _{j}}}{{\partial x}}} \right)\frac{{d\tau }}{{\sqrt {t - \tau } }}} } \right]\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \frac{{\partial T'_{1}}}{{\partial t}} = \frac{1}{{\rho _{{10}}^{^\circ }{{c}_{{p1}}}}}\frac{{\partial p'_{1}}}{{\partial t}} - \sum\limits_{j \in l,\overline {s1,sN} } {{\text{N}}{{{\text{u}}}_{{1j}}}\frac{{T'_{1} - T'_{{\Sigma j}}}}{{{{\tau }_{{T1j}}}}}} ,\,\,\,\, \\ \frac{{\partial T'_{j}}}{{\partial t}} = - {\text{N}}{{{\text{u}}}_{{2j}}}\frac{{T'_{j} - T'_{{\Sigma j}}}}{{{{\tau }_{{T2j}}}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \frac{{{{c}_{{p1}}}}}{{{{m}_{l}}}}{\text{N}}{{{\text{u}}}_{{1l}}}\frac{{T'_{1} - T'_{{\Sigma l}}}}{{{{\tau }_{{T1l}}}}} + {{c}_{l}}{\text{N}}{{{\text{u}}}_{{2l}}}\frac{{T'_{l} - T'_{{\Sigma l}}}}{{{{\tau }_{{T2l}}}}} = - \frac{{m_{l}^{^\circ }{{l}_{0}}}}{{{{p}_{{10}}}}}\frac{{p'_{{V\Sigma }} - p'_{{VS}}}}{{{{\tau }_{\beta }}}},\, \\ \frac{{{{c}_{{p1}}}}}{{{{m}_{j}}}}{\text{N}}{{{\text{u}}}_{{1j}}}\frac{{T'_{1} - T'_{{\Sigma j}}}}{{{{\tau }_{{T1j}}}}} + {{c}_{j}}{\text{N}}{{{\text{u}}}_{{2j}}}\frac{{T'_{j} - T'_{{\Sigma j}}}}{{{{\tau }_{{T2j}}}}} = 0\,\,\,\,\left( {j = \overline {s1,sN} } \right), \\ {\text{S}}{{{\text{h}}}_{1}}\frac{{p'_{V} - p'_{{V\Sigma }}}}{{{{\tau }_{{k1}}}}} = \frac{{p'_{{V\Sigma }} - p'_{{VS}}}}{{{{\tau }_{\beta }}}},\,\,\,\,p'_{{VS}} = \frac{{{{l}_{0}}\rho _{{10}}^{^\circ }}}{{{{T}_{{10}}}}}T'_{{\Sigma l}},\, \\ p'_{V} = \frac{{C_{{10}}^{2}}}{{{{\gamma }_{{10}}}{{\alpha }_{{10}}}}}{{{\bar {R}}}_{V}}\rho' _{V} + \frac{{{{p}_{{V0}}}}}{{{{T}_{{10}}}}}T'_{1}, \\ p'_{1} = \frac{{C_{{10}}^{2}}}{{{{\gamma }_{{10}}}{{\alpha }_{{10}}}}}\left( {\rho' _{1} + \Delta \bar {R}\left( {\rho' _{V} - {{k}_{{V0}}}\rho' _{1}} \right)} \right) + \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}T'_{1}. \\ \end{gathered} $$

((1))

The system of equations (1) is closed and might be used to study the propagation of plane, cylindrical, and spherical acoustic perturbations in gas mixtures with vapor, identical drops, and solid particles of different types and sizes.

DISPERSION RELATION

Let us analyze the solutions of the obtained system of equations as the progressive waves for the perturbations

$$\eta = {{A}_{\eta }}\psi .$$

((2))

Here, $\psi = \exp \left[ {i\left( {K_{*}r - \omega t} \right)} \right]$ for plane perturbations, $\psi = H_{0}^{{(1)}}(K_{*}r)\exp \left( { - i\omega t} \right)$ for cylindrical perturbations, $\psi = \frac{1}{r}\exp \left[ {i\left( {K_{*}r - \omega t} \right)} \right]$ for spherical perturbations,

$$K_{*} = K + iK_{**},\,\,\,\,{{C}_{p}} = \frac{\omega }{K},\,\,\,\,\sigma = 2\pi \frac{{K_{**}}}{K},$$

where $H_{0}^{{(1)}}(K_{*}r)$ is the Hankel function, $K_{*}$ is the complex wavenumber, ${{C}_{p}}$ is the phase velocity, and $\sigma$ is the attenuation decrement at the acoustic wavelength.

Substituting solution (2) into system of equations (1) we obtain the following system of linear algebraic equations:

$$\begin{gathered} - i\omega {{A}_{{\rho 1}}} - {{\rho }_{{10}}}K_{ * }^{2}{{A}_{{\varphi 1}}} + {{\eta }_{{k1}}}{{A}_{{pV}}} - {{\eta }_{{k1}}}{{A}_{{pV\Sigma }}} = 0, \\ - i\omega {{A}_{{\rho V}}} - {{\rho }_{{V0}}}iK_{ * }^{2}{{A}_{{\varphi 1}}} + {{\eta }_{{k1}}}{{A}_{{pV}}} - {{\eta }_{{k1}}}{{A}_{{pV\Sigma }}} = 0, \\ - i\omega {{A}_{{\rho l}}} - {{\rho }_{{l0}}}K_{ * }^{2}{{A}_{{\varphi l}}} - {{\eta }_{\beta }}{{A}_{{pV\Sigma }}} + {{\eta }_{\beta }}{{A}_{{pVS}}} = 0, \\ - i\omega {{A}_{{\rho j}}} - {{\rho }_{{j0}}}K_{ * }^{2}{{A}_{{\varphi j}}} = 0\,\,\,\,\left( {j = \overline {s1,sN} } \right), \\ {{\xi }_{{v1}}}{{A}_{{\varphi 1}}} + \frac{1}{{{{\rho }_{{10}}}}}{{A}_{{p1}}} - \sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}}}{{\tau _{{vj}}^{ * }}}{{A}_{{\varphi j}}}} = 0,\, \\ {{\xi }_{{vj}}}{{A}_{{\varphi j}}} - \frac{1}{{\tau _{{vj}}^{ * }}}{{A}_{{\varphi 1}}} = 0\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ {{\xi }_{{T1}}}{{A}_{{T1}}} + \frac{{i\omega }}{{\rho _{{10}}^{^\circ }{{c}_{{p1}}}}}{{A}_{{p1}}} - \sum\limits_{j = l,\overline {s1,sN} } {\frac{1}{{\tau _{{T1j}}^{ * }}}{{A}_{{T\Sigma j}}}} = 0,\, \\ {{\xi }_{{T2j}}}{{A}_{{Tj}}} - \frac{1}{{\tau _{{T2j}}^{ * }}}{{A}_{{T\Sigma j}}} = 0,\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \frac{{{{c}_{{p1}}}}}{{{{m}_{l}}}}\frac{1}{{\tau _{{T1l}}^{ * }}}{{A}_{{T1}}} - {{\xi }_{{T\Sigma l}}}{{A}_{{T\Sigma l}}} + \frac{{{{c}_{l}}}}{{\tau _{{Tl}}^{ * }}}{{A}_{{Tl}}} + {{\eta }_{l}}{{A}_{{pV\Sigma }}} - {{\eta }_{l}}{{A}_{{pVS}}} = 0,\, \\ \frac{{{{c}_{{p1}}}}}{{{{m}_{j}}\tau _{{T1j}}^{ * }}}{{A}_{{T1}}} - {{\xi }_{{T\Sigma j}}}{{A}_{{T\Sigma j}}} + \frac{{{{c}_{j}}}}{{\tau _{{T2j}}^{ * }}}{{A}_{{Tj}}} = 0,\,\,\left( {j = \overline {s1,sN} } \right), \\ \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}{{{\bar {R}}}_{V}}{{A}_{{\rho V}}} + \frac{{{{p}_{{V0}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} - {{A}_{{pV}}} = 0,\,\,\, \\ \,{{\xi }_{{\rho 1}}}{{A}_{{\rho 1}}} + \frac{{C_{1}^{2}}}{{{{\gamma }_{1}}{{\alpha }_{{10}}}}}\Delta \bar {R}{{A}_{{\rho V}}} + \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}{{A}_{{T1}}} - {{A}_{{p1}}} = 0,\, \\ \frac{{{{l}_{0}}\rho _{{V0}}^{^\circ }}}{{{{T}_{{10}}}}}{{A}_{{T\Sigma l}}} - {{A}_{{pVS}}} = 0, \\ \end{gathered} $$

$$\begin{gathered} \left( {\frac{1}{{{{\tau }_{\beta }}}} + \frac{1}{{\tau _{{k1}}^{ * }}}} \right){{A}_{{pV\Sigma }}} - \frac{1}{{{{\tau }_{\beta }}}}{{A}_{{pVS}}} - \frac{1}{{\tau _{{k1}}^{ * }}}{{A}_{{pV}}} = 0, \\ {{\xi }_{{v1}}} = \sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}}}{{\tau _{{vj}}^{ * }}}} - i\omega ,\,\,\,\,{{\xi }_{{T1}}} = \sum\limits_{j = l,\overline {s1,sN} } {\frac{1}{{\tau _{{T1j}}^{ * }}}} - i\omega , \\ {{\xi }_{{\rho 1}}} = \frac{{C_{{10}}^{2}}}{{{{\gamma }_{{10}}}{{\alpha }_{{10}}}}}\left( {1 - \Delta \bar {R}{{k}_{V}}} \right),\,\,\,\,{{\xi }_{{vj}}} = \frac{1}{{\tau _{{vj}}^{ * }}} - i\omega , \\ \,\,\,\,{{\xi }_{{T\Sigma l}}} = \frac{{{{c}_{{p1}}}}}{{{{m}_{l}}\tau _{{T1l}}^{ * }}} + \frac{{{{c}_{l}}}}{{\tau _{{T2l}}^{ * }}},\,\,\,\,{{\xi }_{{T2j}}} = \frac{1}{{\tau _{{Tj}}^{ * }}} - i\omega , \\ \,\,\,\,{{\eta }_{{k1}}} = \frac{{{{\rho }_{{l0}}}m_{l}^{^\circ }}}{{{{p}_{{10}}}\tau _{{k1}}^{ * }}},\,\,\,\,\,{{\eta }_{\beta }} = \frac{{{{\rho }_{{l0}}}m_{l}^{^\circ }}}{{{{p}_{{10}}}{{\tau }_{\beta }}}},\,\,\,\,{{\eta }_{l}} = \frac{{{{l}_{0}}m_{l}^{^\circ }}}{{{{p}_{{10}}}{{\tau }_{\beta }}}},\, \\ {\text{Nu}}_{{1j}}^{ * } = 2\left[ {1 + \frac{{1 - i}}{{\sqrt 2 }}{{{\left( {\omega {{\tau }_{{\lambda 1j}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right], \\ {\text{Nu}}_{{2j}}^{ * } = 2\frac{{{{z}^{2}}\left( {\tanh z - z} \right)}}{{3z - \left( {3 + {{z}^{2}}} \right)\tanh z}}, \\ z = \frac{{1 - i}}{{\sqrt 2 }}{{\left( {\omega {{\tau }_{{\lambda 2j}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\,\,\,\,\left( {j = l,\overline {s1,sN} } \right), \\ \end{gathered} $$

((3))

$$\begin{gathered} \,\,\,{\text{Sh}}_{1}^{ * } = 2\left[ {1 + \frac{{1 - i}}{{\sqrt 2 }}{{{\left( {\omega {{\tau }_{d}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right], \\ \,\,\,\,{{\tau }_{d}} = \frac{{r_{l}^{2}}}{{{{D}_{1}}}},\,\,\,\,\tau _{{T1j}}^{ * } = \frac{{{{\tau }_{{T1j}}}}}{{{\text{Nu}}_{{1j}}^{ * }\left( \omega \right)}}, \\ \tau _{{T2j}}^{ * } = \frac{{{{\tau }_{{T2j}}}}}{{{\text{Nu}}_{{2j}}^{ * }\left( \omega \right)}},\,\,\,\,\tau _{{k1}}^{ * } = \frac{{{{\tau }_{{k1}}}}}{{{\text{Sh}}_{1}^{ * }\left( \omega \right)}}, \\ \,\,\,\,\tau _{{vj}}^{ * } = {{\tau }_{{vj}}}\left[ {1 + \frac{{1 - i}}{{\sqrt 2 }}{{{\left( {\omega {{\tau }_{{\mu 1j}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]. \\ \end{gathered} $$

The system of equations (3) does not depend on parameters $\theta$ and is the same in its description of plane, cylindrical, and spherical waves in the multifraction gas mixture with vapor, identical drops, and solid particles of different types and sizes.

From the condition of the existence of a nontrivial solution for the system of linear algebraic equations (3), we obtain the following dispersion relation:

$${{\left( {\frac{{{{C}_{1}}K_{*}}}{\omega }} \right)}^{2}} = V\left( \omega \right)D\left( \omega \right),$$

((4))

where

$$\begin{gathered} V\left( \omega \right) = 1 + \frac{{{{m}_{l}}}}{{1 - i\omega \tau _{{vl}}^{ * }}} + \sum\limits_{j = 1}^N {\frac{{{{m}_{{sj}}}}}{{1 - i\omega \tau _{{vsj}}^{ * }}}} ,\, \\ D\left( \omega \right) = 1 + \left( {{{\gamma }_{1}} - 1} \right)\,\frac{{{{m}_{{2l}}}\left[ {{{H}_{2}} - {{{\bar {R}}}_{V}}{{k}_{V}}{{\gamma }_{1}}\left( {{{{\bar {c}}}_{1}}{{{\bar {R}}}_{V}}{{H}_{3}} - 2{{{\bar {l}}}_{0}}{{H}_{1}}} \right) - {{M}_{{1l}}}\Lambda } \right] + \left( {1 - {{M}_{{1l}}}{{H}_{3}}} \right)\sum\limits_{i = 1}^N {\frac{{{{m}_{{2si}}}{{e}_{{1si}}}}}{{1 - {{t}_{{esi}}}{{e}_{{1si}}}}}} }}{{\left[ {1 + {{m}_{{2l}}}\left( {{{H}_{2}} - B{{H}_{3}} - {{M}_{{2l}}}\Lambda } \right)} \right] + \left( {1 - {{M}_{{2l}}}{{H}_{3}}} \right)\sum\limits_{i = 1}^N {\frac{{{{m}_{{2si}}}{{e}_{{1si}}}}}{{1 - {{t}_{{esi}}}{{e}_{{1si}}}}}} }}, \\ {{H}_{1}} = eZ,\,\,\,\,{{H}_{2}} = \left( {{{e}_{{1l}}} - Le} \right)Z, \\ \end{gathered} $$

$$\begin{gathered} {{H}_{3}} = e\left( {1 - {{e}_{{1l}}}{{t}_{{el}}}} \right)Z,\,\,\,\,\Lambda = LH_{1}^{2} + {{H}_{2}}{{H}_{3}}, \\ Z = \frac{1}{{1 - {{t}_{{el}}}\left( {{{e}_{{1l}}} - Le} \right)}},\,\,\,\,e = \frac{1}{{i\omega \left( {{{\tau }_{\beta }} + \tau _{{k1}}^{ * }} \right)}}, \\ \,\,\,\,{{{\bar {R}}}_{V}} = \frac{{{{R}_{V}}}}{{{{R}_{{10}}}}},\,\,\,\,{{{\bar {c}}}_{1}} = \frac{{{{c}_{{p1}}}}}{{{{\gamma }_{1}}{{R}_{1}}}} = \frac{1}{{{{\gamma }_{1}} - 1}},\,\,\,\,B = {{{\bar {R}}}_{v}}\left( {1 - {{k}_{V}}{{{\bar {R}}}_{V}}} \right), \\ {{m}_{{2l}}} = {{m}_{l}}m_{l}^{^\circ },\,\,\,\,{{e}_{{1j}}} = \frac{{{{c}_{{2j}}}}}{{m_{j}^{^\circ }{{c}_{{p1}}}\left( {1 - i\omega \tau _{{T2j}}^{ * }} \right)}}, \\ {{t}_{{ej}}} = i\omega \tau _{{\Sigma 1j}}^{ * },\,\,\,\,\tau _{{\Sigma 1j}}^{ * } = \frac{{{{\alpha }_{{20j}}}}}{{{{\alpha }_{{10}}}}} \\ \times \,\,\tau _{{T1j}}^{ * },\,\,\,\,{{m}_{{1j}}} = {{m}_{j}}m_{j}^{^\circ }{{{\bar {R}}}_{V}},\,\,\,\,\left( {j = l,\overline {s1,sN} } \right),\, \\ {{M}_{{2l}}} = {{m}_{{2l}}}{{{\bar {R}}}_{V}}\left( {1 - {{k}_{V}}{{{\bar {R}}}_{V}}} \right), \\ {{M}_{{1l}}} = {{m}_{{1l}}}{{{\bar {c}}}_{1}}\left( {{{\gamma }_{1}} - 1 + {{k}_{V}}{{{\bar {R}}}_{V}}} \right), \\ {{{\bar {l}}}_{0}} = \frac{{{{l}_{0}}}}{{C_{1}^{2}}},\,\,\,\,L = \bar {l}_{0}^{2}{{k}_{V}}{{\gamma }_{1}}\left( {{{\gamma }_{1}} - 1} \right). \\ \end{gathered} $$

EQUILIBRIUM AND FROZEN SPEEDS OF SOUND, LOW- AND HIGH-FREQUENCY ASYMPTOTES OF THE ATTENUATION COEFFCIENT

The expressions for the equilibrium ${{C}_{e}}$ and frozen ${{C}_{f}}$ speeds of sound in a vapor–gas–drop mixture with solid particles can be obtained from dispersion relation (4) at the limiting transitions, ω → 0 and ω → ∞, respectively, and they have the following form:

$${{C}_{f}} = {{C}_{1}},\,\,\,\,{{C}_{e}} = {{C}_{1}}{{\left[ {\frac{{{{\gamma }_{e}}}}{{{{m}_{1}}{{\gamma }_{1}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$$

where

$${{m}_{1}} = 1 + {{m}_{l}} + \sum\limits_{j = 1}^N {{{m}_{{sj}}}} ,$$

$${{\gamma }_{e}} = \frac{{{{{\bar {R}}}_{V}}\left( {1 - {{k}_{V}}{{{\bar {R}}}_{V}}} \right)\left( {\sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{{{c}_{{p1}}}}}} - 1} \right) - L}}{{\left( {2{{{\bar {l}}}_{0}}{{k}_{V}}{{{\bar {R}}}_{V}}\left( {{{\gamma }_{1}} - 1} \right) - L - \frac{{{{{\bar {R}}}_{V}}}}{{{{\gamma }_{1}}}}} \right) + {{{\bar {R}}}_{V}}\sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{{{c}_{{p1}}}}}} }}.$$

The low-frequency asymptotic $K_{**}$ is written as

$$K_{**}^{0}\left( \omega \right) = \frac{1}{{2{{C}_{1}}}}\frac{{\left( {{{m}_{1}}a_{2}^{D} + a_{2}^{V}a_{0}^{D}} \right)}}{{\sqrt {{{m}_{1}}a_{0}^{D}} }}{{\omega }^{2}},$$

where

$$\begin{gathered} {{m}_{1}} = 1 + {{m}_{l}} + \sum\limits_{i = 1}^N {{{m}_{{si}}}} ,\,\,\,\,a_{2}^{V} = {{m}_{l}}{{\tau }_{{vl}}} + \sum\limits_{i = 1}^N {{{m}_{{si}}}{{\tau }_{{vsi}}}} , \\ {{\xi }_{1}} = \sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{{{c}_{{p1}}}}}} ,\,\,\,\,{{\xi }_{2}} = \sum\limits_{j = 1}^N {\frac{{{{m}_{{sj}}}{{c}_{{2sj}}}}}{{{{c}_{{p1}}}}}} , \\ \end{gathered} $$

$$\begin{gathered} a_{0}^{D} = 1 + \left( {{{\gamma }_{1}} - 1} \right)\frac{{2{{{\bar {l}}}_{0}}{{k}_{V}}{{{\bar {R}}}_{V}}{{\gamma }_{1}} - L - B{{{\bar {c}}}_{1}}\left( {{{\xi }_{1}} - {{\gamma }_{1}}} \right)}}{{B\left( {{{\xi }_{1}} - 1} \right) - L}}, \\ a_{2}^{D} = \frac{{\left( {{{\gamma }_{1}} - 1} \right)}}{{{{M}_{{2l}}}\left( {{{\xi }_{1}} - 1} \right) - {{m}_{{2l}}}L}}\left( {{{\zeta }_{1}} - \frac{{\left( {{{m}_{{2l}}}{{\beta }_{1}} + {{M}_{{1l}}}{{\xi }_{2}}} \right){{\eta }_{1}}}}{{{{M}_{{2l}}}\left( {{{\xi }_{1}} - 1} \right) - {{m}_{{2l}}}L}}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{\zeta }_{1}} = {{m}_{{2l}}}{{\beta }_{2}} + {{m}_{{2l}}}\sum\limits_{j = 1}^N {\frac{{{{c}_{{2j}}}{{\tau }_{{\lambda 1j}}}}}{{3m_{j}^{^\circ }{{c}_{{p1}}}}}} {{\beta }_{1}} \\ + \,\,{{M}_{{1l}}}\sum\limits_{j = 1}^N {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{15{{c}_{{p1}}}}}{{\tau }_{{\lambda 2j}}}} - \sum\limits_{j = 1}^N {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{{{c}_{{p1}}}}}} {{\beta }_{3}}, \\ \end{gathered} $$

$$\begin{gathered} {{\eta }_{1}} = {{b}_{2}} + \sum\limits_{j = 1}^N {\frac{{{{c}_{{2j}}}{{\tau }_{{\lambda 1j}}}}}{{3m_{j}^{^\circ }}}} + {{M}_{{2l}}}\sum\limits_{j = 1}^N {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{15{{c}_{{p1}}}}}{{\tau }_{{\lambda 2j}}}} - \sum\limits_{j = 1}^N {\frac{{{{m}_{j}}{{c}_{{2j}}}}}{{{{c}_{{p1}}}}}} {{b}_{3}}, \\ {{\beta }_{1}} = 2{{{\bar {l}}}_{0}}{{k}_{V}}{{{\bar {R}}}_{V}}{{\gamma }_{1}} - L - {{k}_{V}}\bar {R}_{V}^{2}{{\gamma }_{1}}{{{\bar {c}}}_{1}} + {{M}_{{1l}}}\frac{{{{c}_{{2l}}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}}}, \\ \end{gathered} $$

$$\begin{gathered} {{\beta }_{2}} = {{M}_{{1l}}}\frac{{{{c}_{{2l}}}{{\tau }_{{\lambda 2l}}}}}{{15m_{l}^{^\circ }{{c}_{{p1}}}}} - \frac{{{{c}_{{2l}}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}}}\left( {{{\tau }_{\beta }} + \frac{1}{3}{{{\bar {R}}}_{V}}\left( {1 - k{}_{V}} \right){{\tau }_{d}}} \right) \\ - \,\,{{k}_{V}}\bar {R}_{V}^{2}{{\gamma }_{1}}{{{\bar {c}}}_{1}}\frac{{{{c}_{{2l}}}{{\tau }_{{\lambda 1l}}}}}{{3m_{l}^{^\circ }{{c}_{{p1}}}}}, \\ \end{gathered} $$

$${{\beta }_{3}} = {{\tau }_{\beta }} + \frac{1}{3}{{\bar {R}}_{V}}\left( {1 - {{k}_{V}}} \right){{\tau }_{d}} + \frac{1}{3}L{{\tau }_{{\lambda 1l}}} - {{M}_{{1l}}}\frac{{{{c}_{{2l}}}{{\tau }_{{\lambda 1l}}}}}{{3m_{l}^{^\circ }{{c}_{{p1}}}}},$$

$$\begin{gathered} {{b}_{2}} = \left( {{{\tau }_{\beta }} + \frac{1}{3}{{{\bar {R}}}_{V}}\left( {1 - {{k}_{V}}} \right){{\tau }_{d}}} \right)\left( {1 - \frac{{{{m}_{l}}{{c}_{{2l}}}}}{{{{c}_{{p1}}}}}} \right) \\ + \,\,\frac{1}{3}L{{\tau }_{{\lambda 1l}}} - {{M}_{{2l}}}\left( {\frac{{{{c}_{{2l}}}}}{{3m_{l}^{^\circ }{{c}_{{p1}}}}}{{\tau }_{{\lambda 1l}}} + \frac{{{{m}_{l}}{{c}_{{2l}}}}}{{15{{c}_{{p1}}}}}{{\tau }_{{\lambda 2l}}}} \right), \\ \end{gathered} $$

$${{b}_{3}} = {{\tau }_{\beta }} + \frac{1}{3}{{\bar {R}}_{V}}\left( {1 - {{k}_{V}}} \right){{\tau }_{d}} + \frac{1}{3}L{{\tau }_{{\lambda 1l}}} - {{M}_{{2l}}}\frac{{{{c}_{{2l}}}{{\tau }_{{\lambda 1l}}}}}{{3m_{l}^{^\circ }{{c}_{{p1}}}}}.$$

The dissipation of low-frequency perturbations is strongly affected by both the interphase friction and the interphase heat and mass transfer.

The high-frequency asymptotic $K_{**}$ is

$$K_{**}^{\infty } = \frac{{\sqrt {{{a}_{1}}} }}{{\sqrt 2 {{C}_{1}}}}\sqrt \omega + \frac{{{{a}_{2}}}}{{2{{C}_{1}}\sqrt {2{{a}_{1}}} }},$$

where

$$\begin{gathered} {{a}_{1}} = \frac{1}{2}{{\left( {{{\zeta }_{1}} - {{\eta }_{1}}} \right)}^{2}},\,\,\,\,{{a}_{2}} = \left( {{{\zeta }_{1}} - {{\eta }_{1}}} \right) \\ \times \,\,\left[ {{{\eta }_{2}} + {{\zeta }_{2}} - \frac{1}{2}{{{\left( {{{\zeta }_{1}} + {{\eta }_{1}}} \right)}}^{2}}} \right],\,\,\,\,{{\zeta }_{1}} = \sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}}}{{{{\tau }_{{vj}}}}}\sqrt {\frac{{{{\tau }_{{\mu 1j}}}}}{2}} } , \\ \end{gathered} $$

$$\begin{gathered} {{\zeta }_{2}} = \sum\limits_{j = l,\overline {s1,sN} } {\frac{{{{m}_{j}}}}{{{{\tau }_{{vj}}}}}\left( {1 - \frac{{{{\tau }_{{\mu 1j}}}}}{{{{\tau }_{{vj}}}}}} \right)} , \\ {{\eta }_{1}} = \sum\limits_{j = a,l} {\frac{{3{{m}_{j}}{{c}_{{2j}}}\left( {{{\gamma }_{1}} - 1} \right)}}{{{{c}_{{p1}}}\sqrt {2{{\tau }_{{\lambda 2j}}}} }}{{{\left( {1 - \frac{{{{c}_{{2j}}}}}{{m_{j}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1j}}}}}{{{{\tau }_{{\lambda 2j}}}}}} } \right)}}^{{ - 1}}}} , \\ {{\eta }_{2}} = \left( {{{\gamma }_{1}} - 1} \right)\frac{{{{p}_{2}}}}{{{{b}_{0}}}} + 2{{b}_{1}}{{\eta }_{1}}, \\ \end{gathered} $$

$$\begin{gathered} {{p}_{2}} = {{m}_{{2l}}}{{q}_{1}}\left( {1 - \sum\limits_{j = 1}^N {\frac{{{{c}_{{2sj}}}}}{{m_{{sj}}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1sj}}}}}{{{{\tau }_{{\lambda 2sj}}}}}} } } \right) \\ - \,\,\frac{{3{{m}_{l}}{{c}_{{2l}}}}}{{{{c}_{{p1}}}\sqrt {{{\tau }_{{\lambda 2l}}}} }}\sum\limits_{j = 1}^N {\frac{{{{c}_{{2sj}}}\left( {\sqrt {{{\tau }_{{\lambda 1sj}}}} + \sqrt {{{\tau }_{{\lambda 2sj}}}} } \right)}}{{m_{{sj}}^{^\circ }{{c}_{{p1}}}{{\tau }_{{\lambda 2sj}}}}}} \\ + \,\,\left( {1 - \frac{{{{c}_{{2l}}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1l}}}}}{{{{\tau }_{{\lambda 2l}}}}}} } \right)\sum\limits_{j = 1}^N {\frac{{3{{m}_{{sj}}}{{c}_{{2sj}}}}}{{{{c}_{{p1}}}{{\tau }_{{\lambda 2sj}}}}}} \\ - \,\,\left( {\frac{{{{c}_{{2l}}}\left( {\sqrt {{{\tau }_{{\lambda 1l}}}} + \sqrt {{{\tau }_{{\lambda 2l}}}} } \right)}}{{m_{l}^{^\circ }{{c}_{{p1}}}{{\tau }_{{\lambda 2l}}}}} + \frac{{L\sqrt {{{\tau }_{{\lambda 1l}}}} }}{{3{{\tau }_{\beta }}}}} \right)\sum\limits_{j = 1}^N {\frac{{3{{m}_{{sj}}}{{c}_{{2sj}}}}}{{{{c}_{{p1}}}\sqrt {{{\tau }_{{\lambda 2sj}}}} }}} , \\ \end{gathered} $$

$${{b}_{0}} = \left( {1 - \sum\limits_{j = 1}^N {\frac{{{{c}_{{2sj}}}}}{{m_{{sj}}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1sj}}}}}{{{{\tau }_{{\lambda 2sj}}}}}} } } \right)\left( {1 - \frac{{{{c}_{{2l}}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1l}}}}}{{{{\tau }_{{\lambda 2l}}}}}} } \right),$$

$$\begin{gathered} {{b}_{1}} = \sum\limits_{j = 1}^N {\left( {\frac{{{{c}_{{2sj}}}\left( {\sqrt {{{\tau }_{{\lambda 1sj}}}} + \sqrt {{{\tau }_{{\lambda 2sj}}}} } \right)}}{{\sqrt 2 m_{{sj}}^{^\circ }{{c}_{{p1}}}{{\tau }_{{\lambda 2sj}}}}} - \frac{{3{{m}_{{sj}}}{{c}_{{2sj}}}}}{{{{c}_{{p1}}}\sqrt {2{{\tau }_{{\lambda 2sj}}}} }}} \right)} \\ \times \,\,{{\left( {1 - \frac{{{{c}_{{2sj}}}}}{{m_{{sj}}^{ \circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1sj}}}}}{{{{\tau }_{{\lambda 2sj}}}}}} } \right)}^{{ - 1}}} \\ + \,\,\left( {\frac{{{{c}_{{2l}}}\left( {\sqrt {{{\tau }_{{\lambda 1l}}}} + \sqrt {{{\tau }_{{\lambda 2l}}}} } \right)}}{{\sqrt 2 m_{l}^{^\circ }{{c}_{{p1}}}{{\tau }_{{\lambda 2l}}}}} + \frac{L}{{3{{\tau }_{\beta }}}}\sqrt {\frac{{{{\tau }_{{\lambda 1l}}}}}{2}} } \right){{\left( {1 - \frac{{{{c}_{{2l}}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1l}}}}}{{{{\tau }_{{\lambda 2l}}}}}} } \right)}^{{ - 1}}}, \\ \end{gathered} $$

$$\begin{gathered} {{q}_{1}} = \frac{{3{{c}_{{2l}}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}{{\tau }_{{\lambda 2l}}}}} \\ + \,\,\frac{1}{{{{\tau }_{\beta }}}}\left( {L + {{k}_{V}}\bar {R}_{V}^{2}{{\gamma }_{1}}{{{\bar {c}}}_{1}}\left( {1 - \frac{{c{}_{{2l}}}}{{m_{l}^{^\circ }{{c}_{{p1}}}}}\sqrt {\frac{{{{\tau }_{{\lambda 1l}}}}}{{{{\tau }_{{\lambda 2l}}}}}} } \right) - 2{{{\bar {l}}}_{0}}{{k}_{V}}{{{\bar {R}}}_{V}}{{\gamma }_{1}}} \right). \\ \end{gathered} $$

The attenuation of high-frequency perturbations $\omega {{\tau }_{v}} \ll 1$ in the studied gas mixtures is directly proportional to the mass content of the disperse phase. At the propagation of high-frequency perturbations in multifraction gas mixtures, the effects of interphase friction are the governing dissipative effects.

RESULTS

As an example, let us consider the acoustic wave propagation in an air mixture with vapor, water drops, carbon black, and aluminum particles at a temperature of ${{T}_{0}} = 273$ K and a pressure of ${{p}_{{10}}} = 0.1$ MPa and the following thermophysical parameters: for the carrier gas, we have ${{\rho }_{{10}}} = 1.19$ kg/m³, ${{C}_{1}} = 343$ m/s, ${{c}_{{p1}}} = 1007$ m²/(s² K), ${{\lambda }_{1}} = 0.0258$ kg m/(s³ K), ${{\mu }_{1}} = 1.81 \times {{10}^{{ - 5}}}$ kg/(m s), ${{\gamma }_{1}} = 1.4$; for the aluminum particles, we have ${{r}_{a}} = 8 \times {{10}^{{ - 6}}}$ m, ${{\rho }_{{20a}}} = 2700$ kg/m³, ${{c}_{{2a}}} = 896$ m²/(s² K), ${{\lambda }_{{2a}}} = 209$ kg m/(s³ K); for the carbon black particles, we have ${{r}_{s}} = {{10}^{{ - 6}}}$ m, ρ_20s = 1200 kg/m³, ${{c}_{{2s}}} = 0.{\text{8}}$ m²/(s² K), ${{\lambda }_{{2s}}} = 0.{\text{15}}$ kg m/(s³ K); for water drops, we have ${{r}_{l}} = {{10}^{{ - 5}}}$ m, ${{\rho }_{{20l}}} = 1000$ kg/m³, ${{c}_{{2l}}} = 4180$ m²/(s² K), ${{\lambda }_{{2l}}} = 0.602$ kg m/(s³ K).

Figure 1 shows the dependence of the attenuation coefficient on the dimensionless oscillation frequency $\omega {{\tau }_{{va}}}$ for various mass contents of the inclusions. Clearly, an increase in the mass content results in an increase in the value of the attenuation coefficient.

Fig. 1.

Dependences of the attenuation coefficient on the dimensionless oscillation frequency for an air mixture with vapor, water drops, and aluminum and carbon black particles at various mass contents of inclusions: (1) m = 0.15 (m_a = 0.05, m_s = 0.05, m_l = 0.05), (2) m = 0.225 (m_a = 0.075, m_s = 0.075, m_l = 0.075), (3) m = 0.3 (m_a = 0.1, m_s = 0.1, m_l = 0.1); the dashed line is (a) the low-frequency and (b) high-frequency asymptotic.

Figure 2 shows the influence of the inclusion mass content on the dependences of the relative speed of sound and the wavelength attenuation decrement on the dimensionless oscillation frequency $\omega {{\tau }_{{va}}}.$ The calculated dependences are plotted with dispersion relation (4).

Fig. 2.

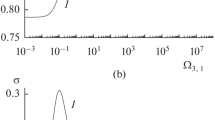
Dependences of (a) the relative speed of sound and (b) the wavelength attenuation decrement on the dimensionless oscillation frequency for an air mixture with vapor, water drops, and aluminum and carbon black particles at various mass contents of the disperse phase (1–3 are the same designations as in Fig. 1).

Note that both the speed of sound dispersion and the wave dissipation increase with an increase in the mass content of the inclusions. Accounting for the three-fraction composition and the difference in the thermophysical properties of the fractions causes characteristic inflections in the dependence of the relative speed of sound within the frequence range that are inversely proportional to the relaxation times for the velocities of phases ${{\tau }_{{va}}},$${{\tau }_{{vl}}},$ and ${{\tau }_{{vs}}}$ (Fig. 2а). Figure 2b shows that the difference in the sizes and the thermophysical parameters of inclusions leads to the occurrence of three maxima in the dependence of the wavelength attenuation decrement at characteristic unity values for each of the three: $\omega {{\tau }_{{va}}},$$\omega {{\tau }_{{vl}}},$ and $\omega {{\tau }_{{vs}}}$ = 1.

Figure 3 shows the dependences of the wavelength attenuation decrement on the dimensionless oscillation frequency $\omega {{\tau }_{{vs}}}.$ Calculations were made for a three-fraction mixture of air with vapor, water drops, and aluminum and carbon black particles with the mass content of drops ${{m}_{l}} = 0.2$, aluminum particles ${{m}_{a}} = 0.2$, carbon black particles ${{m}_{s}} = 0.2$ (curve (1)), and for monodisperse air mixtures with carbon black particles for ${{m}_{s}} = 0.2$ (curve (2)), with aluminum particles for ${{m}_{a}} = 0.2$(curve (3)), and with vapor and water drops for ${{m}_{l}} = 0.2$ (curve (4)). The radius of inclusions was ${{r}_{l}} = {{10}^{{ - 5}}}$m for drops, ${{r}_{a}} = 8 \times {{10}^{{ - 6}}}$ m for aluminum particles, and ${{r}_{s}} = {{10}^{{ - 6}}}$m for carbon black particles.

Fig. 3.

Dependence of the wavelength attenuation decrement on the dimensionless oscillation frequency $\omega {{\tau }_{{va}}}.$

Figure 3 shows that the largest contribution to the dispersion and dissipation of acoustic waves is observed at characteristic unity values for each of the three frequencies $\omega {{\tau }_{{va}}},$$\omega {{\tau }_{{vl}}},$ and $\omega {{\tau }_{{vs}}}$ = 1.

Next, we study the propagation patterns of low-amplitude pulse perturbations in a three-fraction, vapor–gas–drop mixture with solid particles upon phase transitions. The calculations were performed with dispersion relation (4) and the fast Fourier transform software code [15].

Figure 4 shows the influence of the mass content of inclusions on the evolution of a Gaussian pressure pulse in a mixture of air with vapor, water drops, and aluminum and carbon black particles with the mass content of aluminum particles ${{m}_{a}} = 0.2,$ carbon black particles ${{m}_{s}} = 0.2,$ and water drops ${{m}_{l}} = 0.3,$ (curves (1)); ${{m}_{a}} = 0.15,$${{m}_{s}} = 0.15,$ and ${{m}_{l}} = 0.1$ curves (2)); ${{m}_{a}} = 0.25,$${{m}_{s}} = 0.25,$ and ${{m}_{l}} = 0.4$ (curves (3)). The radius of inclusions was ${{r}_{a}} = {{10}^{{ - 6}}}$ m for aluminum particles, ${{r}_{s}} = 8 \times {{10}^{{ - 6}}}$ m for carbon black particles, and ${{r}_{l}} = {{10}^{{ - 5}}}$ m for water drops. The calculated profiles were plotted at distances of 4 and 8 m from the pulse radiating point, respectively.

Fig. 4.

Influence of the mass content on the evolution of the plane Gaussian pulse perturbation.

Clearly, the increase of in the inclusion mass content leads to both increased attenuation and a stronger change in the shape of the pressure pulse due to the larger dispersion of the speed of sound and dissipation of waves.

Figure 5 shows the influence of the three-fraction content of the disperse phase on the evolution of the Gaussian pressure pulse in a mixture of air with vapor, water drops, aluminum and carbon black particles for the mass content ${{m}_{a}},$${{m}_{s}} = 0.2$ and ${{m}_{l}} = 0.3$ (curve (1)); in a two-fraction mixture of air with aluminum and carbon black particles for the entire content of particles $m = 0.7$ (curves (2)); and in a monodisperse mixture of air with vapor and water drops with the mass content of drops $m = 0.7$(curves (3)). The radius of inclusions was ${{r}_{a}} = {{10}^{{ - 6}}}$ m for aluminum particles, ${{r}_{s}} = 8 \times {{10}^{{ - 6}}}$ m for carbon black particles, and ${{r}_{l}} = {{10}^{{ - 5}}}$ m for water drops. The calculated profiles were plotted with dispersion relation (4) and the fast Fourier transform software code [15] at distances of 4 and 8 m from the pulse radiating point, respectively.

Fig. 5.

Influence of the three-fraction content of the disperse phase on the evolution of the plane Gaussian pulse perturbation.

The pulse attenuation in the air mixture with vapor, water drops, and aluminum and carbon black particles with the entire mass content $m = 0.7$ is larger than that in the two-fraction gas mixture with aluminum and carbon black particles and lower than in the air mixture with vapor and water drops. A considerable change in the pulse shape is observed for the air mixture with vapor, water drops, and carbon black and aluminum particles, as well as for the air mixture with vapor and monodisperse drops, due to dispersion of the speed of sound and dissipation of perturbations. Therefore, the presence of contaminations (for instance, aluminum and carbon black particles) significantly influences the dynamics of small waves in air fogs.

CONCLUSIONS

The present work contains a closed system of linear differential equations of motion for a multifraction gas mixture with vapor, liquid drops, and solid particles of different sizes and with different thermophysical properties. We deduced the dispersion relation governing the propagation of plane, spherical, and cylindrical low-amplitude perturbations. The dispersion curves were calculated. We obtained the low- and high-frequency asymptotes for the linear attenuation coefficient, as well as the equilibrium and frozen speeds of sound. We analyzed the influence of the disperse phase parameters for a three-fraction gas mixture with aluminum and carbon black particles, as well as with water drops on dissipation and the dispersion of acoustic waves. We found that the presence of contaminants (solid particles) substantially influences the weak wave dynamics in vapor–gas–drop mixtures, a fact that should be taken into account in the development of methods of acoustic testing of multifraction gas mixtures.