INTRODUCTION

Problems of the wave dynamics of multiphase media are of great interest because of the wide dissemination of such media in nature and their engineering applications. The specifics of the dynamics of multiphase media have been considered in well-known monographs [1–3]. The propagation of acoustic waves in monodisperse gas suspensions was studied [4, 5]. However, real gas suspensions are polydisperse, and the propagation of acoustic waves in polydisperse media was also studied [2, 6]. The characteristics of two-phase media with various inclusions have been described [7–10]. The propagation of acoustic waves in multifraction gas suspensions with polydisperse inclusions differing in size and materials is studied in this work for the first time. The wide application of acoustic methods in engineering emphasizes the relevance of this study.

MAIN EQUATIONS

Let us consider the one-dimensional motion of a multifraction gas suspension, the disperse phase of which includes N fractions. The fractions consist of various materials, have different sizes, and are described by their own size-distribution function of inclusions. The linearized equations for the plane one-dimensional disturbed motion follow from the general equations of the two-phase mixture [1] and have the form [8], but they are written with allowance for N polydisperse fractions as:

$$\begin{gathered} \frac{{\partial \rho _{1}^{'}}}{{\partial t}} + {{\rho }_{{10}}}\frac{{\partial {v}_{1}^{'}}}{{\partial x}} = 0, \\ \frac{{\partial \rho _{{2j}}^{'}}}{{\partial t}} + \int\limits_{\Delta {{r}_{j}}} {\frac{{\partial {v}_{{2j}}^{'}}}{{\partial x}}N_{0}^{j}({{r}_{j}})} g_{0}^{j}({{r}_{j}})d{{r}_{j}} = 0, \\ {{\rho }_{{10}}}\frac{{\partial {v}_{1}^{'}}}{{\partial t}} + \frac{{\partial p_{1}^{'}}}{{\partial x}} + \sum\limits_{j = 1}^N {\int\limits_{\Delta {{r}_{j}}} {{{f}_{j}}N_{0}^{j}({{r}_{j}})} d{{r}_{j}} = 0} , \\ g_{0}^{j}({{r}_{j}})\frac{{\partial {v}_{{2j}}^{'}}}{{\partial t}} = {{f}_{j}},\,\,\,\,j = \overline {1,N} . \\ \end{gathered} $$
((1))

Here and below, strokes designate the parameter perturbations, and subscript 0 corresponds to the initial unperturbed state.

Taking into account N fractions, the equations for the internal energy of the carrier phase, inclusions, and their interface are written as

$${{\rho }_{{10}}}{{c}_{{p1}}}\frac{{\partial T_{1}^{'}}}{{\partial t}} - {{\alpha }_{{10}}}\frac{{\partial p_{1}^{'}}}{{\partial t}} + \sum\limits_{j = 1}^N {\int\limits_{\Delta {{r}_{j}}} {{{q}_{{1j}}}N_{0}^{j}({{r}_{j}})} d{{r}_{j}} = 0} ,$$
$${{\rho }_{{10}}}{{c}_{{p1}}}\frac{{\partial T_{1}^{'}}}{{\partial t}} - {{\alpha }_{{10}}}\frac{{\partial p_{1}^{'}}}{{\partial t}} + \sum\limits_{j = 1}^N {\int\limits_{\Delta {{r}_{j}}} {{{q}_{{1j}}}N_{0}^{j}({{r}_{j}})} d{{r}_{j}} = 0} ,$$
((2))
$$g_{0}^{j}({{r}_{j}}){{c}_{{2j}}}\frac{{\partial T_{{2j}}^{'}}}{{\partial t}} = - {{q}_{{2j}}},\,\,\,\,{{q}_{{1j}}} + {{q}_{{2j}}} = 0,\,\,\,\,j = \overline {1,N} .$$

Let us use expressions for force \(f\) and heat transfer intensity \(q\) similar to [9]. For the carrier phase, the linearized equation of state is written as

$$p_{1}^{'} = \frac{{C_{1}^{2}}}{{{{\gamma }_{{10}}}{{\alpha }_{{10}}}}}\rho ' + \frac{{{{p}_{{10}}}}}{{{{T}_{{10}}}}}T_{1}^{'}.$$
((3))

Here, ρ is the density, \({v}\) is the velocity, \(p\) is the pressure, T is the temperature, γ is the adiabatic exponent, \(\alpha \) is the volume content, \({{c}_{p}}\) is the heat capacity, \({{C}_{1}}\) is the speed of sound in a pure gas, \(N_{0}^{{}}\) is the size-distribution function of inclusions, \(g_{0}^{{}}\) is the mass of a particle, r is the radius of inclusions, and \(\Delta r\) is the variation range of the inclusion radius, Subscript 1 refers to the carrier phase, and subscript 2 refers to the disperse phase.

DISPERSION RELATION

Let us seek the solution of the system of equations (1)–(3) as progressive waves of perturbations

$$\begin{gathered} \phi ' = {{A}_{\phi }}\exp [i(K_{\text{*}}x - \omega t)],\,\,\,\,K_{\text{*}} = K + iK_{\text{**}}, \\ {{C}_{p}} = {\omega \mathord{\left/ {\vphantom {\omega K}} \right. \kern-0em} K},\sigma = {{2\pi K_{\text{**}}} \mathord{\left/ {\vphantom {{2\pi K_{\text{**}}} K}} \right. \kern-0em} K}, \\ \end{gathered} $$
((4))

where \(K_{\text{*}}\) is the complex wavenumber, \(K_{\text{**}}\) is the linear attenuation coefficient, \({{C}_{p}}\) is the phase velocity, \(\sigma \) is the attenuation decrement at a given acoustic wavelength, \(\omega \) is the perturbation frequency, \(i\) is an imaginary unit, and \({{A}_{\phi }}\) is the amplitude.

The dispersion relation determining the dependence of the complex wavenumber on the perturbation frequency is obtained by solving the system of equations (1)–(3) with allowance for (4):

$$\begin{gathered} {{\left( {\frac{{{{C}_{1}}K_{\text{*}}}}{\omega }} \right)}^{2}} = V(\omega )D(\omega ),\,\,\,V(\omega ) = 1 + \sum\limits_{j = 1}^N {{{m}_{j}}} {{\left\langle {\frac{1}{{1 - i\omega \tau _{{{v}j}}^{*}}}} \right\rangle }_{j}}, \\ D(\omega ) = 1 + ({{\gamma }_{1}} - 1)\frac{{{{t}_{d}}}}{{1 + {{t}_{d}}}},\,\,\,{{t}_{d}} = \sum\limits_{j = 1}^N {{{m}_{j}}\frac{{{{c}_{{2j}}}}}{{{{c}_{{p1}}}}}} {{\left\langle {\frac{1}{{1 - i\omega \tau _{{Tj}}^{*}}}} \right\rangle }_{j}}, \\ \tau _{{{v}j}}^{*} = {{\tau }_{{{v}j}}}{{\left[ {1 - \frac{{1 - i}}{{\sqrt 2 }}\sqrt {\omega {{\tau }_{{\mu 1j}}}} } \right]}^{{ - 1}}}, \\ \end{gathered} $$
$${{\tau }_{{{v}j}}} = \frac{2}{9}\frac{{\rho _{{2j}}^{0}r_{j}^{2}}}{{{{\mu }_{1}}}},\,\,\,{{\tau }_{{\mu 1j}}} = \frac{{\rho _{1}^{0}r_{j}^{2}}}{{{{\mu }_{1}}}},\,\,\tau _{{Tj}}^{*} = \tau _{{T2j}}^{*} + {{m}_{j}}\frac{{{{c}_{{p2j}}}}}{{{{c}_{{p1}}}}}\tau _{{T1j}}^{*},$$
((5))
$$\begin{gathered} \tau _{{T1j}}^{*} = \frac{1}{3}\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{{2j}}}}}\frac{{{{\tau }_{{\lambda 1j}}}}}{{1 + {{z}_{{1j}}}}}, \\ \tau _{{T2j}}^{*} = \frac{1}{3}{{\tau }_{{\lambda 2j}}}\frac{{3{{z}_{{2j}}} - \left( {3 + z_{{2j}}^{2}} \right){\text{tanh}}({{z}_{{2j}}})}}{{z_{{2j}}^{2}\left( {{\text{tanh}}({{z}_{{2j}}}) - {{z}_{{2j}}}} \right)}}, \\ {{z}_{k}} = \frac{{1 - i}}{{\sqrt 2 }}\sqrt {\omega {{\tau }_{{\lambda k}}}} ,\,\,\,\,k = 1j,2j, \\ {{\tau }_{{\lambda 1j}}} = \frac{{r_{j}^{2}\rho _{1}^{0}{{c}_{{p1}}}}}{{{{\lambda }_{1}}}},\,\,\,\,{{\tau }_{{\lambda 2j}}} = \frac{{r_{j}^{2}\rho _{{2j}}^{0}{{c}_{{p2j}}}}}{{{{\lambda }_{{2j}}}}}, \\ {{\left\langle h \right\rangle }_{j}} = \frac{1}{{\rho _{{20}}^{j}}}\int\limits_{\Delta {{r}_{j}}} {N_{0}^{j}({{r}_{j}})g_{0}^{j}({{r}_{j}})} {{h}_{j}}d{{r}_{j}},\,\,\,\,j = 1,...,N. \\ \end{gathered} $$

Here, \(m\) is the mass content, \(\tau _{{v}}^{*},\)\(\tau _{T}^{*}\) are the complex relaxation times of the velocity and temperature, respectively [1], \(\lambda \) is the thermal conductivity, \(\left\langle h \right\rangle \) is the linear averaging operator [6], and \(\rho _{{20}}^{{}}\) is the density of the disperse phase. It should be noted that the dispersion relation coincides with that obtained in [8] for a particular case of two fractions.

CALCULATION RESULTS

Let us consider the propagation of acoustic waves in a three-fraction gas mixture with water drops, sand, and aluminum particles. The calculations were made with dispersion relation (5) for the following mixture parameters: \({{p}_{0}} = 0.1\) MPa, and \({{T}_{0}} = 320\) K. The mass contents of inclusions were \({{m}_{a}} = 0.3\) for water drops, \({{m}_{b}} = 0.3\) for sand particles, and \({{m}_{c}} = 0.3\) for aluminum particles. The size distribution function of inclusions were \(N_{0}^{a}({{r}_{a}}) = r_{a}^{{ - 3}}\) for water drops, \(N_{0}^{b}({{r}_{b}}) = r_{b}^{{ - 3}}\) for sand particles, and \(N_{0}^{c}({{r}_{c}}) = r_{c}^{{ - 3}}\) for aluminum particles. The radius of inclusions varied in the range \({{r}_{a}} \in \left[ {5 \times {{{10}}^{{ - 4}}},\;{{{10}}^{{ - 3}}}} \right]\) m for water drops, \({{r}_{b}} \in \left[ {5 \times {{{10}}^{{ - 5}}},\;{{{10}}^{{ - 4}}}} \right]\) m for sand particles, and \({{r}_{c}} \in \left[ {5 \times {{{10}}^{{ - 6}}},\;{{{10}}^{{ - 5}}}} \right]\) m for aluminum particles.

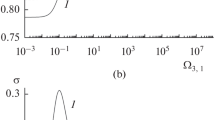
Figure 1 shows the dependence of the relative speed of sound \({{{{C}_{p}}} \mathord{\left/ {\vphantom {{{{C}_{p}}} {{{C}_{1}}}}} \right. \kern-0em} {{{C}_{1}}}}\) on the dimensionless perturbation frequency \({{\Omega }_{{5,3}}} = \omega \tau _{{{v}a}}^{{(5,3)}},\) where \(\tau _{{va}}^{{(5,3)}}\) is the relaxation time of the velocity for the mean radius \(r_{a}^{{(5,3)}} = {{\left( {{{\left\langle {r_{a}^{5}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {r_{a}^{5}} \right\rangle } {\left\langle {r_{a}^{3}} \right\rangle }}} \right. \kern-0em} {\left\langle {r_{a}^{3}} \right\rangle }}} \right)}^{{\frac{1}{2}}}}\) [2]. The presence of three fractions with various inclusion sizes causes three characteristic discontinuities in the dependence of the relative speed of sound on the dimensionless perturbation frequency. At low frequencies (\({{\Omega }_{{5,3}}} < {{10}^{{ - 1}}}\)), the relative speed of sound takes some equilibrium value. At high frequencies (\({{\Omega }_{{5,3}}} > {{10}^{4}}\)), the relative speed of sound tends toward unity, i.e., the phase velocity tends toward the speed of sound in a pure gas.

Fig. 1.
figure 1

Dependence of the relative speed of sound on the dimensionless perturbation frequency.

Full size image

Figure 2 shows the dependences of the attenuation decrement at a given acoustic wavelength, \(\sigma \), on the dimensionless perturbation frequency \({{\Omega }_{{5.3}}};\) curve 1 is obtained with allowance for the heat transfer, and curve 2 is obtained without it. The presence of three fractions with different thermophysical properties causes three local maxima in the dependence of the attenuation decrement on the dimensionless perturbation frequency. When the heat transfer between the fractions and the carrier medium is not taken into account, and the attenuation decrement decreases in the entire range of the perturbation frequencies.

Fig. 2.
figure 2

Dependence of the attenuation decrement on the dimensionless perturbation frequency.

Full size image

CONCLUSIONS

The propagation of sound in multifraction gas suspensions with polydisperse inclusions was considered. We established that the presence of three fractions with inclusions of various sizes causes three typical discontinuities in the dependence of the relative speed of sound on the dimensionless perturbation frequency. Three local maxima in the dependence of the attenuation decrement on given wavelength on the dimensionless perturbation frequency were observed; they were determined by the different radii and thremophysical properties of inclusions of various fractions. When the heat transfer is not taken into account, the attenuation decrement is smaller for the entire range of the studied frequencies.