The investigation of surface oscillations of liquid drops consisting of a liquid kernel and the surrounding layer of another liquid were began significantly later than the investigation of homogeneous drops. One of the pioneer papers is considered to be [1] in which the stability of thin film on the drop surface was investigated. In [2] the oscillations of a density-stratified drop of an ideal liquid were theoretically and experimentally investigated, author’s attention being restricted to analysis of the effect of the wall thickness on the oscillations frequencies. In successive investigations, some additional factors and features of the behavior of compound drops, namely, rotation of fluid [3], damping of oscillations [4], stability of surface [5], and the effect of shape and location of the kernel on the shape of the drop surface [6, 7], were considered. Note that in [2, 4, 7] only the oscillation modes \(n = 2\) were analyzed.

Investigator’s interest in the behavior of a compound drop did not become weaker, oscillations of the compound drop on the horizontal surface were experimentally investigated [8] and the eigenfrequency spectrum of compound drops was analytically studied [9]. The free surface of a compound drop whose equilibrium shape differs from the spherical one was investigated using the numerical simulation methods [10–14].

In the present study, the oscillations of the free surface of a compound drop are considered with the aim to investigate the effect of the main liquid parameters on the oscillations and analyze the effect for typical liquids used in the experiments. The second aim is to obtain simplified expressions for the studied dependences on the parameters. It is also reasonable to consider the oscillations of both basic and higher modes since the modern high-speed cameras and the image processing techniques make it possible to identify and distinguish the third and higher mode characteristics [15].

1. FORMULATION OF THE PROBLEM

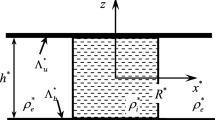
We will consider oscillations of a spherical drop of radius R consisting of two layers of immiscible inviscid incompressible liquids. The upper liquid layer of density \({{\rho }_{1}}\) has the thickness \(h\). The inner liquid which forms the drop “kernel” has the density \({{\rho }_{2}}\). The surface tensions coefficients of the free drop surface and the liquid interface are denoted by \({{\sigma }_{1}}\) and \({{\sigma }_{2}}\), respectively. The oscillations of the disturbed free surface of the drop and the perturbations of the interface between the liquids will be described by the functions \({{\xi }_{1}}(\theta ,t)\) and \({{\xi }_{2}}(\theta ,t)\), respectively. We will restrict our attention to consideration of capillary oscillations of such a drop. The impact of the free-stream air flow is neglected.

The problem is formulated and considered in the spherical coordinate system (\(r\), \(\theta \), \(\varphi \)) with the origin at the center of mass of the drop. We will use the axisymmetric formulation of the problem, i.e., the dependence of the quantities on the azimuthal angle \(\varphi \) is neglected. Such an approach makes it possible to reduce the volume of the algebra without loss of the generality of considerations.

In the mathematical formulation of the problem we will use the following dimensionless variables with three characteristic scales, namely, the radius of the equivalent drop R, the density of the outer liquid layer \({{\rho }_{1}}\), and the surface tension coefficient \({{\sigma }_{1}}\). All remaining quantities in the equations will be expressed in fractions of their characteristic scales:

$${\text{[P] = }}{{\sigma }_{1}}{\text{/}}R;\quad {\text{[}}{\mathbf{V}}{\text{] = }}\sqrt {{{\sigma }_{1}}{\text{/}}{{\rho }_{1}}R} ;\quad {\text{[t] = }}\sqrt {{{\rho }_{1}}{{R}^{3}}{\text{/}}{{\sigma }_{1}}} .$$

The dimensionless quantities conserve the old notation.

We introduce the dimensionless ratios of the layer densities \(\rho \equiv {{\rho }_{2}}{\text{/}}{{\rho }_{1}}\) and the surface tension coefficients \(\sigma \equiv {{\sigma }_{2}}{\text{/}}{{\sigma }_{1}}\).

We will restrict our attention to consideration of irrotational flows \({\text{curl}}{\kern 1pt} {\mathbf{V}} = 0\). Owing to this fact, in the problem considered we can go over from the vector fields of the liquid flow velocities V1, 2 to the corresponding hydrodynamic potentials \({{\psi }_{1}}\) and \({{\psi }_{2}}\): \({{{\mathbf{V}}}_{{1,2}}} = \nabla {{\psi }_{{1,2}}}\).

The system of equations thus scalarized consists of the Euler equations in the Gromeka–Lamb form for irrotational flows:

$${{\partial }_{t}}{{\psi }_{1}} + \frac{{{{{(\nabla {{\psi }_{1}})}}^{2}}}}{2} = - {{P}_{1}} + \operatorname{const} ;\quad {{\partial }_{t}}{{\psi }_{2}} + \frac{{{{{(\nabla {{\psi }_{2}})}}^{2}}}}{2} = - \frac{{{{P}_{2}}}}{\rho } + {\text{const,}}$$

where P1 and P2 are the hydrodynamic pressures in the outer and inner layers of the drop, respectively.

The equations of incompressibility of liquid can be transformed in the Laplace equations for the hydrodynamic potentials

$$\nabla (\nabla {{\psi }_{{1,2}}}) = \Delta {{\psi }_{{1,2}}} = 0.$$

The kinematic and dynamic conditions on the free surface are

$$r = 1 + {{\xi }_{1}}(\theta ,t){\text{:}}\quad \frac{{d{{F}_{1}}(r,\theta ,t)}}{{dt}} = 0;\quad {{P}_{1}} - {{P}_{{\sigma 1}}} = {{P}_{{{\text{ext}}}}},$$

where \({{F}_{1}}(r,\theta ,t) \equiv r - 1 - {{\xi }_{1}}(\theta ,t)\) and \({{P}_{{\sigma 1}}} = \operatorname{div} {{{\mathbf{n}}}_{1}}\) is the pressure of the capillary forces on the free surface and \({{P}_{{{\text{ext}}}}}\) is the hydrodynamic pressure of the surrounding medium. The normal to the free surface of the drop n1 is determined by the formulas

$${{{\mathbf{n}}}_{1}} \equiv \frac{{\nabla {{F}_{1}}(r,\theta ,t)}}{{\left| {\nabla {{F}_{1}}(r,\theta ,t)} \right|}}.$$

The conditions on the interface between the media represent the kinematic and dynamic conditions and the conditions of equality of the normal components of the liquid velocities:

$$r = 1 - h + {{\xi }_{2}}(\theta ,t){\text{:}}\,\,\frac{{d{{F}_{2}}(r,\theta ,t)}}{{dt}} = 0;\quad {{P}_{2}} - {{P}_{{\sigma 2}}} = {{P}_{1}};\quad \nabla {{\psi }_{1}} \times {{{\mathbf{n}}}_{2}} = \nabla {{\psi }_{2}} \times {{{\mathbf{n}}}_{2}},$$

where \({{F}_{2}}(r,\theta ,t) \equiv r - 1 + h - {{\xi }_{2}}(\theta ,t)\) аnd \({{P}_{{\sigma 2}}} = \sigma \operatorname{div} {{{\mathbf{n}}}_{2}}\) is the pressure of the capillary forces on the interface, and n2 is the normal to the interface between the media which can be determined from the expression

$${{{\mathbf{n}}}_{2}} \equiv \frac{{\nabla {{F}_{2}}(r,\theta ,t)}}{{\left| {\nabla {{F}_{2}}(r,\theta ,t)} \right|}}.$$

The integral conditions of conservation of the drop volume are as follows:

$$\mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^\pi \mathop \smallint \limits_0^{1 + {{\xi }_{1}}(\theta ,t)} {{r}^{2}}\sin \theta {\text{d}}r{\text{d}}\theta {\text{d}}\varphi = \frac{4}{3}\pi ;\quad \mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^\pi \mathop \smallint \limits_0^{1 - h + {{\xi }_{2}}(\theta ,t)} {{r}^{2}}\sin \theta {\text{d}}r{\text{d}}\theta {\text{d}}\varphi = \frac{4}{3}\pi \rho {{(1 - h)}^{3}}.$$

The integral condition of immobility of the center of masses of the drop can be written with regard to the expression for \({{{\mathbf{e}}}_{r}} \equiv {\mathbf{r}}{\text{/}}\left| {\mathbf{r}} \right|\) in the Cartesian coordinate system: \({{{\mathbf{e}}}_{r}} = {\mathbf{i}}{\text{sin}}\theta {\text{cos}}\varphi \) + jsinθsinφ + kcosθ. Thereafter, this expression is divided into three integrals {i, j,k} which represent the projections on the Cartesian unit vectors. The integrals representing the projections on the axes determined by the unit vectors \({\mathbf{i}}\) and \({\mathbf{j}}\) vanish after integration with respect to the angle \(\varphi \). After this algebra, the integral condition can be reduced to the form:

$$\mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^\pi \mathop \smallint \limits_0^{1 - h + {{\xi }_{2}}(\theta ,t)} \rho {{r}^{3}}\cos \theta \sin \theta {\text{d}}r{\text{d}}\theta {\text{d}}\varphi + \mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^\pi \mathop \smallint \limits_{1 - h + {{\xi }_{2}}(\theta ,t)}^{1 + {{\xi }_{1}}(\theta ,t)} {{r}^{3}}\cos \theta \sin \theta {\text{d}}r{\text{d}}\theta {\text{d}}\varphi = 0.$$

The problem formulated above can be solved using the asymptotic methods: the wave perturbations of the drop surface and the interface between the media are assumed to be small as compared with the drop dimensions: \(\max \left| {{{\xi }_{{1,2}}}(\theta ,t)} \right|{\text{/}}R \sim \varepsilon \ll 1\). Here, the quantity \(\varepsilon \) which represents the ratio of the surface oscillation amplitude of the drop to its radius is the small parameter of the problem. The liquid velocity fields induced by these perturbations and the hydrodynamic potentials will have the corresponding order of smallness: \({{{\mathbf{V}}}_{{1,2}}}\sim {{\psi }_{{1,2}}}\sim {{\xi }_{{1,2}}}(\theta ,t)\) ~ ε. The hydrodynamic pressures and the pressures of capillary forces can be represented in the form of expansions in the small parameter ε. Here and in what follows, the component of the corresponding order in ε will be denoted by the superscript with an Arabic numeral in parentheses:

$${{P}_{1}} = {{P}_{1}}^{{(0)}} + \varepsilon {{P}_{1}}^{{(1)}} + o({{\varepsilon }^{2}}),\quad {{P}_{2}} = {{P}_{2}}^{{(0)}} + \varepsilon {{P}_{2}}^{{(1)}} + o({{\varepsilon }^{2}}),$$
$${{P}_{{\sigma 1}}} = P_{{\sigma 1}}^{{(0)}} + \varepsilon P_{{\sigma 1}}^{{(1)}} + o({{\varepsilon }^{2}}),\quad {{P}_{{\sigma 2}}} = P_{{\sigma 2}}^{{(0)}} + \varepsilon P_{{\sigma 2}}^{{(1)}} + o({{\varepsilon }^{2}}).$$

We will restrict our attention to the terms of the order of ε1 inclusively. The procedure of linearization is carried out using the standard methods and then the problems of the zeroth and first orders in the perturbations amplitude is formulated.

2. CONSTRUCTION OF THE SOLUTION

The problem of the zeroth order in \(\varepsilon \) consists of Euler’s equations and the dynamic boundary conditions. The additional integral conditions are identically fulfilled. The equilibrium shape of the drop coincides with that specified initially. The solution reduces to finding the hydrodynamic pressures in the undisturbed two-layer spherical drop

$${{P}_{1}}^{{(0)}} = {{P}_{{{\text{ext}}}}} + 2;\quad {{P}_{2}}^{{(0)}} = \frac{2}{{1 - h}}\sigma + {{P}_{{{\text{ext}}}}} + 2.$$

To analyze the oscillations of the disturbed surface of the drop, the problem of the first order in \(\varepsilon \) is investigated:

$$P_{1}^{{(1)}} = - {{\partial }_{t}}{{\psi }_{1}},$$
(2.1)
$$P_{2}^{{(1)}} = - \rho \,{{\partial }_{t}}{{\psi }_{2}},$$
(2.2)
$$\Delta {{\psi }_{1}} = 0,$$
(2.3)
$$\Delta {{\psi }_{2}} = 0,\quad r \to 0{\text{:}}\,\,\left| {\nabla {{\psi }_{2}}} \right| < \infty ,$$
(2.4)
$$r = 1{\text{:}}\quad - \frac{{\partial {{\xi }_{1}}(\theta ,t)}}{{\partial t}} + \frac{{\partial {{\psi }_{1}}}}{{\partial r}} = 0,$$
(2.5)
$$r = 1{\text{:}}\quad {{P}_{1}}^{{(1)}} - {{P}_{{\sigma 1}}}^{{(1)}} = 0,$$
(2.6)
$$r = 1 - h{\text{:}}\quad - \frac{{\partial {{\xi }_{2}}(\theta ,t)}}{{\partial t}} + \frac{{\partial {{\psi }_{2}}}}{{\partial r}} = 0,$$
(2.7)
$$r = 1 - h{\text{:}}\quad {{P}_{2}}^{{(1)}} - {{P}_{{\sigma 2}}}^{{(1)}} = {{P}_{1}}^{{(1)}},$$
(2.8)
$$r = 1 - h{\text{:}}\quad {{\partial }_{r}}{{\psi }_{1}} = {{\partial }_{r}}{{\psi }_{2}},$$
(2.9)
$$P_{{\sigma 1}}^{{(1)}} = - 2{{\xi }_{1}}(\theta ,t) - {{\Delta }_{\theta }}{{\xi }_{1}}(\theta ,t);\quad P_{{\sigma 2}}^{{(1)}} = \frac{{ - 2{{\xi }_{2}}(\theta ,t) - {{\Delta }_{\theta }}{{\xi }_{2}}(\theta ,t)}}{{{{{(1 - h)}}^{2}}}},$$
(2.10)

where \({{\Delta }_{\theta }} \equiv \frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \,\frac{\partial }{{\partial \theta }}} \right)\).

$$\frac{{2\pi }}{3}\mathop \smallint \limits_0^\pi (3{{\xi }_{2}}(\theta ,t)){{(1 - h)}^{2}}\sin \theta {\text{d}}\theta = 0,\quad \frac{{2\pi }}{3}\mathop \smallint \limits_0^\pi 3{{\xi }_{1}}(\theta ,t)\sin \theta \,{\text{d}}\theta = 0,$$
(2.11)
$$\mathop \smallint \limits_0^{2\pi } \mathop \smallint \limits_0^\pi \rho \frac{1}{4}(1 - h + 4{{\xi }_{2}}(\theta ,t))\cos \theta \sin \theta {\text{d}}\theta {\text{d}}\varphi $$
$$ + \;\int\limits_0^{2\pi } {\mathop \smallint \limits_0^\pi \frac{1}{4}(h + 4{{\xi }_{1}}(\theta ,t) - 4{{\xi }_{2}}(\theta ,t))\cos \theta \sin \theta {\text{d}}\theta {\text{d}}\varphi = 0} .$$
(2.12)

The functions describing the perturbations of the free surface \({{\xi }_{1}}(\theta ,t)\) and the interface between the media \({{\xi }_{2}}(\theta ,t)\) can be represented in the form of expansions in the Legendre polynomials:

$${{\xi }_{1}}(\theta ,t) = \mathop \sum \limits_{n = 0}^\infty {{\alpha }_{n}}(t){{P}_{n}}(\theta ),$$
(2.13)
$${{\xi }_{2}}(\theta ,t) = \mathop \sum \limits_{n = 0}^\infty {{\beta }_{n}}(t){{P}_{n}}(\theta ),$$
(2.14)

where the coefficients \({{\alpha }_{n}}(t)\) and \({{\beta }_{n}}(t)\) have the sense of the oscillation amplitudes of the nth mode.

The kinematic problem consists of the Laplace equations for the hydrodynamic potentials with regard to the boundedness conditions of the velocity field (2.3) and (2.4), the kinematic boundary conditions (2.5) and (2.7), and the condition of equality of the normal velocity components (2.9) on the layer interface.

In the spherical coordinate system the solutions of the Laplace equations (2.3) and (2.4) are well known [16] and with regard to the boundedness conditions of the velocity field they take the form:

$${{\psi }_{1}}(r,\theta ,t) = \mathop \sum \limits_{n = 0}^\infty {{A}_{n}}{{r}^{n}}{{P}_{n}}(\theta ) + \mathop \sum \limits_{n = 0}^\infty {{B}_{n}}{{r}^{{ - (n + 1)}}}{{P}_{n}}(\theta );$$
(2.15)
$${{\psi }_{2}}(r,\theta ,t) = \mathop \sum \limits_{n = 0}^\infty {{V}_{n}}{{r}^{n}}{{P}_{n}}(\theta ).$$
(2.16)

The solutions (2.15) and (2.16) and the expressions for the surface perturbation functions (2.13) and (2.14) can be substituted in the kinematic boundary conditions (2.5) and (2.7) and the condition of equality of the normal velocity components (2.9). These conditions must be satisfied for any angle \(\theta \); therefore, we can use the linear independence of the Legendre polynomials by equating the coefficients of the polynomials of the same order, after which the system can be reduced to the form:

$$n{{A}_{n}} + ( - 1 - n){{B}_{n}} - \alpha _{n}^{'}(t) = 0,$$
$${{V}_{n}} = \beta _{n}^{'}(t){\text{/}}n,$$
(2.17)
$${{(1 - h)}^{{ - 1 + n}}}n{{A}_{n}} + {{(1 - h)}^{{ - 2 - n}}}( - 1 - n){{B}_{n}} - {{(1 - h)}^{{ - 1 + n}}}n{{V}_{n}} = 0.$$

Here and in what follows, prime denotes the partial derivative with respect to time.

From the above system (2.17) we can find the following expressions for the coefficients An, Bn, and Vn in terms of the coefficients \({{\alpha }_{n}}(t)\) and \({{\beta }_{n}}(t)\) of the expressions (2.13) and (2.14):

$${{B}_{n}} = \frac{{(1 - h)(\alpha _{n}^{'}(t) - \beta _{n}^{'}(t))}}{{( - {{{(1 - h)}}^{{ - 2n}}} + 1 - h)(1 + n)}},$$
$${{A}_{n}} = \frac{{\alpha _{n}^{'}(t)}}{n} - \frac{{(1 - h)(\alpha _{n}^{'}(t) - \beta _{n}^{'}(t))}}{{ - n + n{{{(1 - h)}}^{{ - 2n}}} + nh}},$$
(2.18)
$${{V}_{n}} = \beta _{n}^{'}(t){\text{/}}n.$$

The additional integral conditions (2.11) and (2.12), written with regard to the expressions (2.13) and (2.14), determine the amplitudes of the zeroth modes α0(t) and \({{\beta }_{0}}(t)\) and give the relation between the amplitudes of the first modes α1(t) and β1(t) of the oscillations of the free surface and the interface

$${{\alpha }_{0}}(t) = 0,\quad {{\beta }_{0}}(t) = 0\quad {{\rho }_{1}}{{\alpha }_{1}}(t) + ({{\rho }_{2}} - {{\rho }_{1}}){{\beta }_{1}}(t) = 0.$$

The absence of oscillations of the zeroth mode of the free surface \({{\alpha }_{0}}(t)\) is determined by the requirement of conservation of the liquid volume. The relation of oscillations of the zeroth mode of the free surface (α1(t)) with oscillations of the zeroth mode of the interface (β1(t)) follows from the introduced reference system located at the center of masses of the drop. Note that the zeroth mode of oscillations of the free surface is related to the displacement of the drop kernel as a whole, while in the experiments [2] it was obtained that the drop kernel is centered during several oscillation periods (i.e., \({{\beta }_{1}}(t)\) and, consequently, also α1(t), become equal to zero). In what follows, we will consider oscillations of the higher modes with \(n \geqslant 2\).

Using expressions (2.15) and (2.16) for the hydrodynamic potentials and the surface perturbation functions (2.13) and (2.14), we can determine the expressions for the components of the pressures entering into the dynamic boundary conditions (2.6) and (2.8).

The component of the hydrodynamic pressure of the outer liquid is determined from expression (2.1) with substitution of the explicit form of the hydrodynamic potential (2.15):

$$P_{1}^{{(1)}} = - \left( {\mathop \sum \limits_{n = 0}^\infty {{r}^{n}}{{P}_{n}}(\theta )A_{n}^{'}(t) + \mathop \sum \limits_{n = 0}^\infty {{r}^{{ - 1 - n}}}{{P}_{n}}(\theta )B_{n}^{'}(t)} \right).$$
(2.19)

The component of the hydrodynamic pressure in the inner liquid can be calculated from formula (2.2) with substitution of expression (2.16):

$$P_{2}^{{(1)}} = - \rho \mathop \sum \limits_{n = 0}^\infty {{r}^{n}}{{P}_{n}}(\theta )V_{n}^{'}(t).$$
(2.20)

The corrections of the order of \(\varepsilon \) to the capillary pressure on the free surface and the interface between the media can be calculated from formulas (2.10) with regard to expressions (2.15) and (2.16):

$${{P}_{{\sigma 1}}} = {{\alpha }_{n}}(t)(n - 1)(n + 2);\quad {{P}_{{\sigma 2}}} = \left( {\frac{\sigma }{{{{{( - 1 + h)}}^{2}}}}} \right)\mathop \sum \limits_{n = 0}^\infty (n - 1)(n + 2){{\beta }_{n}}(t){{P}_{n}}(\theta ).$$
(2.21)

Expressions (2.19)–(2.21) for the pressures are substituted in the boundary conditions (2.6) and (2.8). The pressure balance on the free surface (2.6) with regard to (2.13), (2.18), and the linear independence of the Legendre polynomials

$${{C}_{1}}(n){{\alpha }_{n}}(t) + {{C}_{2}}(n)\alpha _{n}^{{''}}(t) + {{C}_{3}}(n)\beta _{n}^{{''}}(t) = 0,$$
(2.22)
$${{C}_{1}}(n) = (1 - n)(2 + n),$$
(2.23)
$${{C}_{2}}(n) = \left( {\frac{{ - 1}}{{(1 - {{{(1 - h)}}^{{2n}}} + {{{(1 - h)}}^{{2n}}}h)n}} + \frac{{{{{(1 - h)}}^{{ - 1 + n}}}}}{{{{{(1 - h)}}^{{ - 2 - n}}}( - 1 - n) + {{{(1 - h)}}^{{n - 1}}}(1 + n)}}} \right),$$
$${{C}_{3}}(n) = \left( {\frac{{{{{(1 - h)}}^{{2 + n}}}}}{{(1 - {{{(1 - h)}}^{{2n}}} + {{{(1 - h)}}^{{2n}}}h)n}} - \frac{1}{{{{{(1 - h)}}^{{ - 2 - n}}}( - 1 - n) + {{{(1 - h)}}^{{n - 1}}}(1 + n)}}} \right).$$

Using the similar substitution of (2.14) and (2.18) in (2.8), we obtain the evolutionary equation for \({{\alpha }_{n}}(t)\) and \({{\beta }_{n}}(t)\) on the interface between the media:

$${{C}_{4}}(n){{\beta }_{n}}(t) + {{C}_{5}}(n)\alpha _{n}^{{''}}(t) + {{C}_{6}}(n)\beta _{n}^{{''}}(t) = 0,$$
(2.24)
$${{C}_{4}}(n) = - \frac{{( - 1 + n)(2 + n)\sigma }}{{{{{( - 1 + h)}}^{2}}}},$$
(2.25)
$${{C}_{5}}(n) = \left( {\frac{{{{{(1 - h)}}^{n}}}}{{(1 - {{{(1 - h)}}^{{2n}}} + {{{(1 - h)}}^{{2n}}}h)n}}} \right.$$
$$ - \;\left. {\frac{1}{{{{{(1 - h)}}^{2}}({{{(1 - h)}}^{{ - 2 - n}}}( - 1 - n) + {{{(1 - h)}}^{{ - 1 + n}}}(1 + n))}}} \right),$$
$${{C}_{6}}(n) = \left( { - \frac{{{{{(1 - h)}}^{{2 + 2n}}}}}{{(1 - {{{(1 - h)}}^{{2n}}} + {{{(1 - h)}}^{{2n}}}h)n}}} \right.$$
$$ + \;\frac{{{{{(1 - h)}}^{{ - 1 - n}}}}}{{{{{(1 - h)}}^{{ - 2 - n}}}( - 1 - n) + {{{(1 - h)}}^{{ - 1 + n}}}(1 + n)}} + \left. {\frac{{( - 1 + h)\rho }}{n}} \right).$$

The evolutionary equation can be also obtained from the mutual combination of Eqs. (2.22) and (2.24). For this purpose, \(\beta _{n}^{{''}}(t)\) is expressed from (2.22) and the expression obtained is substituted in (2.24). Thereafter, equation (2.24) is solved with respect to \({{\beta }_{n}}(t)\) and the solution obtained is substituted in Eq. (2.22) which takes the form:

$${{D}_{1}}(n){{\alpha }_{n}}(t) + {{D}_{2}}(n)\alpha _{n}^{{''}}(t) + {{D}_{3}}(n)\alpha _{n}^{{(4)}}(t) = 0,$$
(2.26)
$${{D}_{1}}(n) = - {{C}_{1}}(n){\text{/}}{{C}_{3}}(n);$$
$${{D}_{2}}(n) = - \frac{{{{C}_{2}}(n)}}{{{{C}_{3}}(n)}} - \frac{{{{C}_{1}}(n){{C}_{6}}(n)}}{{{{C}_{3}}(n){{C}_{4}}(n)}};$$
(2.27)
$${{D}_{3}}(n) = \frac{{{{C}_{5}}(n)}}{{{{C}_{4}}(n)}} - \frac{{{{C}_{2}}(n){{C}_{6}}(n)}}{{{{C}_{3}}(n){{C}_{4}}(n)}}.$$

The evolutionary equation (2.26) for \({{\alpha }_{n}}(t)\) is the fourth-order homogeneous differential equation and can be reduced to the characteristic equation for the eigenfrequencies \({{\omega }_{n}}\) of individual oscillation modes whose solution can be written in the form of the dispersion relation:

$${{\omega }_{n}} = {{2}^{{ - 1/2}}}{{\left( {\frac{{{{D}_{2}}(n)}}{{{{D}_{3}}(n)}} \pm \frac{{\sqrt {{{D}_{2}}{{{(n)}}^{2}} - 4{{D}_{3}}(n){{D}_{1}}(n)} }}{{{{D}_{3}}(n)}}} \right)}^{{1/2}}},$$
(2.28)

where the coefficients \({{D}_{i}}(n)\) of the evolutionary equation are determined by expressions (2.27) with regard to expressions (2.23) and (2.25) for the coefficients \({{C}_{i}}(n)\). The values of the eigenfrequencies calculated from formulas (2.28) correspond to the results published in [2].

3. ANALYSIS OF THE SOLUTION

We will analyze the case in which the drop is composed from two immiscible liquids taken in approximately equal volumetric proportions. Restricting our attention to consideration of liquids of densities close in the value, we obtain the parameter \(h \approx 0.2\).

As an example, we will consider the water-oil (mineral or vegetable) pair of liquids in which the water forms the inner liquid layer. The surface tension coefficient of water on the interface with air is approximately by 2.5 times greater than the similar coefficient for oils. Taking into account the Antonov rule for the interfacial tension coefficient, we obtain the approximate value of the dimensionless parameter σ = 1.5. We will consider the low modes of oscillations of the free surface of the drop \(2 \leqslant n \leqslant 5\).

As can be seen from Fig. 1, each of the modes of oscillations of the drop surface has two eigenfrequencies, one of which is significantly greater than the other. For the purpose of comparison, curve 3 shows the eigenfrequencies obtained by Lord Rayleigh [17] for the spherical drop of homogeneous liquid.

Fig. 1.
figure 1

Eigenfrequencies of oscillations as functions of the mode number for \(h = 0.2\), \(\sigma = 2\), and \(\rho = 1.2\): curves 1 and 2 correspond to two solutions of the biquadratic evolutionary equation (26); curve 3 corresponds to the eigenfrequencies of surface oscillations of a spherical drop of homogeneous liquid [17].

Full size image

In dimensionless form, for homogeneous liquid (i.e., when the entire drop consists of outer-layer liquid) the eigenfrequencies can be written by the formula \(\omega = \sqrt {n(n - 1)(n + 2)} \). As shown in [2, 5], the high-frequency surface oscillations (curve 1) correspond to the in-phase modes of oscillations of the kernel and the outer layer, while the low-frequency surface oscillations (curve 2) correspond to the out-of-phase modes.

We will now analyze the influence of the problem parameters on oscillations in both regimes. In order to illustrate the difference from the case of homogeneous drop we introduce the parameter \(\delta \) as the ratio of the eigenfrequency (2.28) to the oscillation frequency of homogeneous drop \(\omega = \sqrt {n(n - 1)(n + 2)} \). Such a normalization makes it possible to reproduce the frequencies of several modes at once in the same figure since their absolute values differ strongly from one another. In the further figures the normalized oscillation frequencies of homogeneous drop are equal to unity and the estimates of the oscillation frequencies of compound drop are compared with the frequencies of homogeneous drop.

As can be seen from the dependences reproduced in Fig. 2, as \(h\) increases, in the in-phase regime the normalized oscillation frequencies also increases as compared with homogeneous drop [17]. Variation in the layer thickness affects more significantly the out-of-phase oscillation regime, namely, the frequencies are considerably lower than the Rayleigh frequencies [17] but approach the latter, as the layer thickness increases. Note that for the considered values of the parameters \(\sigma \), \(h\), and \(\rho \) the coefficient \({{D}_{3}}(n)\) is small as compared with \({{D}_{1}}(n)\) and \({{D}_{2}}(n)\) and the normalized frequency of out-of-phase oscillations can be approximately described by the function

$$\delta (n) \approx \frac{{{{D}_{2}}{{{(n)}}^{{1/2}}}{{D}_{3}}{{{(n)}}^{{ - 1/2}}}}}{{\sqrt {\left( { - 1 + n} \right)n\left( {2 + n} \right)} }} - \frac{{{{D}_{1}}(n){{D}_{2}}{{{(n)}}^{{ - 3/2}}}{{D}_{3}}{{{(n)}}^{{1/2}}}}}{{2\sqrt {\left( { - 1 + n} \right)n\left( {2 + n} \right)} }}.$$
(3.1)
Fig. 2.
figure 2

Normalized oscillation frequencies \(\delta \) as functions of the dimensionless layer thickness \(h\) constructed for \(\sigma = 1.5\) and \(\rho = 1.2\): curves 1–4 correspond to \(n = 2,3,\) 4, 5, respectively; I and II correspond to the in-phase and out-of-phase modes, respectively.

Full size image

The rougher approximation which consists of the first term of expression (3.1) leads to junction of the solutions corresponding to different oscillation regimes.

We will estimate the influence of the surface tension coefficients of liquids. In the in-phase regimes the oscillation frequencies become appreciably higher than the Rayleigh frequencies, as the dimensionless ratio of the surface tension coefficients \(\sigma \) increases. The dependences can be described by formulas (2.28); however, correct to 4% they can be also approximated by the linear functions with \(\partial \delta {\text{/}}\partial \sigma = 0.25\) at \(h = 0.2\) and \(1 < \sigma < 2\) for the nth modes at \(2 \leqslant n \leqslant 5\). In the out-of-phase regime, increase in \(\sigma \) affects weakly the oscillation mode amplitudes for the same parameters, increasing them only slightly, while the quantity \(\partial \delta {\text{/}}\partial \sigma \) amounts a few percent. When the liquid densities are close (\(1 < \rho < 1.2\)), for the out-of-phase oscillations when \(1 < \sigma < 2\) the value of \(\partial \delta {\text{/}}\partial \rho \) is lower than \(\delta \) by two orders of magnitude and \(\rho \) has almost no effect on the surface oscillations. For the in-phase oscillations the normalized frequency decreases with increase in \(\rho \) and over the given limitations (\(1 < \rho < 1.2\)) it can be approximated by the linear function with \(\partial \delta {\text{/}}\partial \rho \approx 0.5\) for the low modes (\(n = 2,3,4,5\)).

Note that the presence of the liquid kernel in the drop has the maximum effect on the oscillation frequencies of the basic second mode. This can be seen from Fig. 2, in which the curves corresponding to n = 2 are located farther from those for the eigenfrequences for the homogeneous drop \(\delta = 1\) as compared with the remaining curves. The higher-mode frequencies also differ significantly from the eigenfrequences for the homogeneous drop and this fact must be taken into account in simulating the surface of the oscillating drop which contains a liquid kernel.

SUMMARY

Two values of the eigenfrequencies of oscillations of the free surface of a compound drop are obtained. In the in-phase regime the oscillation frequencies are higher than the oscillation frequencies of homogeneous drop (the case of absent liquid kernel).

In the in-phase oscillation regime, decrease in the dimension of liquid kernel, decrease in the difference between the liquid densities, as well as increase in the ratio of the interfacial tension coefficients \(\sigma \) lead to increase in both the eigenfrequencies and their difference from the eigenfrequencies in the case of homogeneous drop.

In the out-of-phase regime the oscillation frequencies are lower than the frequencies in the case of homogeneous drop and this difference increases as \(\sigma \) and the layer thickness decrease. Variation in the density ratio over the range \(1 < \rho < 1.2\) has an only slight effect on the frequencies in the out-of-phase regime.

Within the framework of the parameter range investigated the dependences of the normalized frequencies on \(\sigma \) can be approximated by the linear functions correct to 4%.

The difference of the oscillation eigenfrequencies from the frequencies of homogeneous drop is essential also for the higher modes. This fact must be taken into account in simulating the surface of a compound drop.