Abstract
This article contributes to research dealing with the optimal dividend policy problem of a firm whose goal is to maximize the expected total discounted dividend payments before bankruptcy. We consider a model of a firm whose cash surplus exhibits regime switching, but unlike the existing literature, we exclude diffusion from our model. We assume that firm’s cash surplus follows the telegraph process, which leads to a problem of singular stochastic control. Surprisingly, this problem turns out to be more complicated than the ones arising in the models involving diffusion. We solve this problem by using the method of variational inequalities and show that the optimal dividend policy can be of three significantly different types depending on the parameters of the model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1. Introduction
The optimal dividend problem was first discussed in [1]. The key idea of [1] was that the goal of a firm is to maximize the expected present value of the flow of dividends before bankruptcy. In the simplest discrete framework, it was shown that the optimal dividend strategy is of a threshold type—the surplus above a certain level should be paid as dividends. If the capital is less than this level, the company should not pay any dividends. Renewed interest in optimal dividend problems was stimulated by the articles [2]–[4], which addressed optimal dividend problems in continuous environment with firm’s cash reserves following the Brownian motion with drift. Numerous works which followed after them considered optimal dividend problems for more complicated dynamics of cash reserves based on the Brownian motion; see, e.g., [5]–[9].
Our point of interest is an optimal dividend problem in the model where the firm’s flow of profits follows the telegraph process. Introduced in [10] and [11], the telegraph process was extensively analyzed, for example, in [12]–[14]. The telegraph process and its generalizations are widely used in finance as alternatives to Brownian motion, since it is free from the limitations of the Brownian motion such as infinite propagation velocities and independence of returns on separated time intervals. For example, in [15], the telegraph process was used in the context of stochastic volatility. In [16], the very basic model of evolution of stock prices based on the telegraph process was presented. In [17], a geometric telegraph process was used to describe the dynamics of the price of risky assets, and an analog of the Black–Scholes equation was derived. In [18]–[20], the jump-telegraph process was used to develop an arbitrage-free model of financial market. In [21], it was used in an option pricing model.
Works devoted to models of optimal dividend policy with regime switching, such as [22]–[26] among others, are closest to ours, but they all consider models involving diffusion, which is absent in our model. For example, our model may be considered as simply a special case of the model of [22] with two states of the world (the first one with positive drift coefficient and the second one with negative drift coefficient) and diffusion coefficients set to zero. But, as we will see, the absence of diffusion significantly changes the mathematical properties of the problem and leads to substantially different results.
The contribution of this paper is twofold. From the point of view of mathematics, we analyze the limiting case of well-known models with diffusion, which cannot be solved directly by standard techniques used in diffusion-based models. Moreover, the solution which we derived has significantly different structure depending on the parameters of the model, which is highly unusual for this class of optimal control problems. From the point of view of economics, we introduce a model with regime switching as the only source of risk, unlike the existing models with diffusion as the only source of risk. Indeed, in all papers cited above, the drift coefficient (or coefficients) is assumed to be positive, and thus, setting diffusion coefficient(s) to zero, we obtain a model of a firm which never goes bankrupt. With two states of the world, the model is obviously highly stylized, but it can be interpreted as a description of a firm working in market conditions switching from favorable to unfavorable ones and vice versa.
2. The Model
2.1. Formulation
We now define our model. Let \((\Omega,\mathcal{F},\mathbb{P})\) be the probability space of trajectories of changes of the state of the world, and let a filtration \(\mathcal{F}(t)\) represent available information up to time \(t\). We assume that cash reserves of a firm \(X(t)\) follow the equation
where \(x\) is the initial level of reserves, \(\pi(u) \in \{0,1\}\) is the state of the world, \(\mu_0<0\) and \(\mu_1>0\) are the drift coefficients, and \(L(t) \in \mathcal{F} (t)\) is the total amount of dividends paid up to the time \(t\), which is nonnegative and nondecreasing and also assumed to be left-continuous with right limits. The switching between the states of the world is defined by frequencies \(\Lambda_0 > 0\) and \(\Lambda_1 > 0\): if the state of the world is 0, then the probability of switching to the state 1 during a short period of time \(\Delta t\) is \(\Lambda_0 \Delta t\), and similarly for the state 1. The goal of a firm is to maximize the expected total amount of dividends paid before a bankruptcy time \(\tau\), which occurs when a firm’s level of reserves becomes negative for the first time:
where \(c>0\). We denote the admissible dividend policy, which maximizes \(J(s,x,L(\,\cdot\,))\), by \(L^*\) and then introduce
2.2. Variational Inequalities
In this subsection, we derive variational inequalities which the solution of the optimal dividend problem must satisfy, following the standard technique described, for example, in [4]. Consider a small interval \([0,\delta]\). Fix some \(\varepsilon>0\) and consider an admissible policy \(L^{s,x} (\,\cdot\,)\) such that, for any \(x>0\) and \(s \in \{0,1\}\),
Let \(W(t)=x+\mu_{\pi(t)}t\). Consider the following policy:
This policy means that we pay no dividends before \(\delta\) and then switch to suboptimal policy. We obtain
By the definition of the telegraph process,
Using this and the arbitrariness of \(\varepsilon\), we can rewrite (2.2) as
Assuming that \(P(s,x)\) is continuously differentiable and using Taylor expansion, we see that
Simplifying this expression and letting \(\delta\) tend to zero, we obtain the first variational inequality:
To obtain another one, we fix \(x, \delta>0\). Consider the policy \(\delta + L^{s,x-\delta} (t)\), which prescribes paying \(\delta\) instantaneously and then switching to suboptimal policy. It yields
Again using Taylor expansion and the fact that \(\varepsilon\) is arbitrary, we obtain the second variational inequality
Now combining (2.3), (2.4), the obvious boundary condition \(P(0,0)=0\), and the fact that at least one inequality should be tight (see [27], [28]), we arrive at the following theorem.
Theorem 1.
Let the function \(P\) be continuously differentiable. Then it satisfies the following Hamilton–Jacobi–Bellman (HJB) equation :
We now solve this equation and show that the dividend strategy associated with the solution is indeed optimal.
2.3. Solution of the Hamilton–Jacobi–Bellman Equation
A standard argument (see, e.g., [22]) proves that \(P(s,\,\cdot\,)\) is concave. This implies that there exists an \(m_s\), \(s \in \{0,1\}\), such that
So the associated dividend policy is of barrier type. We now analyze several cases.
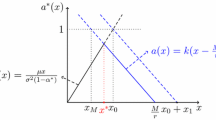
Case 1: \(m_0 \ge m_1 > 0\). We denote \(m=m_1\) and \(M=m_0\). In this case, \(\mathbb{R}_+\) is divided into three domains. In the lower domain \([0,m]\), it follows from (2.3) that the function \(P\) satisfies the equations
with boundary condition \(P(0,0)=0\) for \(s \in \{0,1\}\). This is a linear system of equations, so it can be solved by substitution, but we prefer to use the Laplace transform in order to derive a solution in terms of \(m\). Applying the Laplace transform to (2.6) and inverting it, we obtain
where \(a\) and \(b\) are the negative and the positive root of the quadratic polynomial
We now consider the middle domain \([m,M]\). In this domain, the function \(P(1,\,\cdot\,)\) satisfies the equation \((\partial/\partial x)P(1,x) = 1\). Integrating it and using the obvious boundary condition, we obtain
The function \(P(0,\,\cdot\,)\) satisfies (2.6). Substituting (2.9) into (2.6) and solving the differential equation, we obtain
for \(x \in [m,M]\). Since \(P(0,\,\cdot\,)\) is assumed to be continuously differentiable, we impose two conditions:
but they turn out to be identical:
Substituting (2.11) into (2.10) and also substituting \(P(1,m)\) found from (2.7), we obtain
for \(x \in [m,M]\), where \(B=-b\mu_0+c+\Lambda_0\) and \(A=-a\mu_0+c+\Lambda_0\).
Unlike similar problems involving diffusion, our problem cannot be solved by using only equalities which follow from the Hamilton–Jacobi–Bellmann equation, so we have to impose several conditions which follow from the variational inequalities.
Condition 1.1: \((\partial/\partial x)P(0,x) \ge 1\) for \(x\in [0,m]\). To guarantee the fulfillment of this inequality, we can require that
The first inequality can be rewritten as
The second inequality can be rewritten as
But this condition holds automatically if (2.13) holds. Indeed,
In order to prove the last inequality, note that
Condition 1.2: \((\partial/\partial x)P(1,x) \ge 1\) for \(x \in [0,m]\). This inequality can be rewritten as
which can be guaranteed if the function in the numerator has a negative derivative for any \(x \in [0,m]\). This condition can be rewritten after some simplification as
Condition 1.3. Inequality (2.3) in the middle domain for \(s=1\) has the following form:
It holds as an equality for \(x=m\). To guarantee that it holds for \(x \in [m,m']\) for some \(m'>m\), we impose the following condition:
which is equivalent to
Hence, the only possibility for both (2.14) and (2.15) to be satisfied is
This equation defines the optimal lower threshold level \(m\). In order to prove this, we need, first, to show that it satisfies Condition 1.1. To do so, note that
Hence \(m\) indeed satisfies Condition 1.1. Second, we must check that \(m\) is positive, which is obviously equivalent to the fact that the expression on the right-hand side of (2.16) is greater than 1. After some simplifications, this condition takes the form
where \(\Omega\) is the discriminant of (2.8). Hence we arrive at the following condition for the positivity of \(m\):
And third, we should check that the variational inequalities (2.3) hold for the upper domain \([M,+\infty)\), but this is rather trivial.
In order to find the upper threshold \(M\), we apply the condition
After some rather lengthy computations, we obtain
Note that \(M>m\), and hence (2.17) also guarantees that \(M\) is positive. Hence, if (2.17) holds, then there exists a unique solution for the optimal dividend problem in Case 1, and this solution is defined by the threshold levels (2.16) and (2.19). In the region below \(m\), the firm should not pay any dividends in both states of the world. In the region between \(m\) and \(M\), the firm should immediately pay an excess above \(m\) as dividends if the state of the world is 1 and do not pay anything if the state of world is 0.
This may look a bit counterintuitive—in the state 0, the firm loses money, and when the state of the world switches to 1, it pays the excess above \(m\). Why not pay before switching? The answer is that, in the case of paying dividends before switching, the firm suffers losses after that, because the state of the world is 0, and in the case of paying dividends after switching, the state of the world 1, and the firm makes more money.
Finally, if the firm has more money than \(M\), then, whatever the state of the world, it should immediately pay the excess above \(M\) as dividends (and then also the excess above \(m\) if the state of the world is 1). Also note that if (2.17) does not hold, there are no solutions in this case.
Case 2: \(m_1 > m_0 >0\). We denote \(m=m_0\) and \(M=m_1\). Again, we should consider three domains. In the lower domain \([0,m]\), as in the previous case, the function \(P\) satisfies (2.6), but the boundary condition is now \((\partial/\partial x)P(0,x)=1\). The solution of this system is
For the middle domain, similarly to the Case 1,
The function \(P(1,\,\cdot\,)\) satisfies (2.6). Substituting (2.19) into (2.6) and solving the differential equation, we obtain
Again, we impose the conditions
but they turn out to be identical:
where
Substituting this expression into (2.20), we obtain
Similarly to Case 1, we consider several conditions which follow from the variational inequalities, but in this case, they turn out to be inconsistent.
Condition 2.1: \((\partial/\partial x)P(1,x) \ge 1\) for \(x=m\). After some simplifications, this condition can be rewritten as
Condition 2.2: The concavity of the function \(P(1,x)\) with respect to \(x\) in the middle domain. Taking the second derivative of (2.21) and requiring it to be less than or equal to zero, after some simplifications, we obtain
Now we note that (2.22) and (2.23) cannot hold simultaneously, because
Hence, there are no solutions to the HJB equation in this case.
Case 3: \(m_1=0\) and \(m_0>0\). We set \(m=m_0\) and consider the domain \(x \in [0,m]\). Note that, in this case, we can derive a lower boundary condition for \(P(1,x)\). Indeed,
So, in this domain,
The function \(P(0,x)\) can be found from (2.6), which, together with the boundary condition \(P(0,0)=0\), gives
Equating the derivative of this function to 1, we find the following condition defining the threshold \(m\):
Since the exponent is negative, the expression on the right-hand side must be from 0 to 1. The first condition leads to
and the second one, taken together with (2.25), leads to
but (2.26) obviously implies (2.25).
Condition 3.1: \((\partial/\partial x)P(0,x) \ge 1\) for \(x \in [0,m]\). This condition is equivalent to
If it holds for \(x=0\), it also holds for greater values of \(x\). And for \(x=0\), it can be rewritten as
which is true due to (2.26).
Condition 3.2: inequality (2.3) for the lower domain and for \(s=0\). It has the following form:
Similarly to the previous cases, using the easy-to-verify fact that \(P(0,x)\) is concave, we can guarantee that this inequality holds if the following condition holds:
This condition can be rewritten as
Hence, if the parameters of the model are such that (2.26) and (2.27) hold, then the solution of the HJB equation is determined by the positive threshold \(m\) for the state of the world 0, which is defined by (2.24), and by the zero threshold for the state of the world 1.
Case 4: \(m_1>0\) and \(m_0=0\). We set \(m=m_1\). In this case, \(P(0,x)=x\) and \(P(1,x)\) can be found from Eq. (2.6) for \(s=1\). Solving it, we obtain
Equating the derivative of this function to 1 and finding \(C\), we obtain
But this function is convex, which is impossible for the solution of our HJB equation. So we conclude that there are no solutions in this case.
Case 5: \(m_0=m_1=0\). In this case,
Inequality (2.3) now has the form \(cx \geq 0\) for \(s=1\), which is always true, and
For this inequality to hold for every positive \(x\), we require that
Hence, if (2.28) holds, then the solution of the HJB equation (2.5) is determined by the strategy which prescribes immediately paying all cash reserves as dividends in both states of the world. As we can see, the set of all possible values of the parameters of the model is divided into three subsets with significantly different optimal dividend policies.
Now we unite all the above results in the following theorem.
Theorem 2.
1. Let the parameters of the model be such that (2.17) is satisfied. Then the thresholds \(m\) and \(M\) defined by (2.16) and (2.18), respectively, are positive, and the solution of the HJB equation (2.5) is given by
where \(B=-b\mu_0+c+\Lambda_0\), \(A=-a\mu_0+c+\Lambda_0\), and the associated dividend policy is
2. Let the parameters of the model be such that (2.26) and (2.27) hold. Then the threshold \(m\) defined by (2.24) is positive, and the solution of HJB equation (2.5) is given by
and the associated dividend policy is
3. Let the parameters of the model be such that (2.28) holds. Then the solution of the HJB equation (2.5) is given by
and the associated dividend policy is given by
We now prove that the solution of the HJB equation described in this theorem is a solution of the optimal control problem (2.1).
Theorem 3.
Let \(G\) be a solution of the HJB equation (2.5) presented in Theorem 2. Then \(G\) is the objective function of problem (2.1), and the associated dividend policy is optimal.
Proof.
Let \(L(\,\cdot\,)\) be some admissible control. Denote the set of its points of discontinuity by \(\Phi\) and let
be the discontinuous and continuous parts of \(L\). Also denote \(f(t,s,x)={e}^{-c t}G(s,x)\). Then we have
Integrating this expression, we obtain
where
Taking the conditional expectation, we arrive at
Inequality (2.3) guarantees that the integrand of the first integral is nonpositive, and (2.4) guarantees that, for any \(t \in \Phi\),
It also follows from (2.4) that
Hence
Note that, for the dividend policy \(L^G\), which is associated with the solution of the HJB equation (2.5), this inequality becomes an equality. Indeed, \(R(y)= 0\) a.e. for this strategy, hence the first integral is zero. A continuous flow of dividends corresponds to \(X(t) = m\) and \(s=1\), and we know that
Finally, at the points of discontinuity,
Hence, taking the limit \(t \to +\infty\), we obtain the inequality
for an arbitrary dividend policy, which becomes an equality for the strategy associated with the solution of the HJB equation (2.5).
3. Conclusions
It is shown that the optimal dividend policy in the model of firm’s cash surplus following the telegraph process is of threshold type, which is in line with results for models with diffusion and regime switching. However, we had to perform rather tricky analysis of variational inequalities to find these thresholds. Further research may be related to generalization of our results to an arbitrary number of regimes and an analysis of links between our model and models with diffusion.
References
B. de Finetti, “Su un’lmpostazione alternativa della teoria collettiva del rischio,” in Transactions of the XV International Congress of Actuaries (New York, 1957), pp. 433–443.
R. Radner and L. Shepp, “Risk vs Profit Potential: A Model for Corporate Strategy,” J. Economic Dynamics and Control 20 (8), 1373–1393 (1996).
M. Jeanblanc-Picqué and A. N. Shiryaev, “Optimization of the flow of dividends,” Russian Math. Surveys 50 (2), 257–277 (1995).
S. Asmussen and M. Taksar, “Controlled diffusion models for optimal dividend pay-out,” Insurance Math. Econom. 20 (1), 1–15 (1997).
M. Belhaj, “Optimal dividend payments when cash reserves follow a jump-diffusion process,” Math. Finance 20 (2), 313–325 (2010).
M. I. Taksar, “Dependence of the optimal risk control decisions on the terminal value for a financial corporation,” Ann. Oper. Res. 98 (1), 89–99 (2000).
J.-P. Décamps and S. Villeneuve, “Optimal dividend policy and growth option,” Finance Stoch. 11 (1), 3–27 (2007).
J. Paulsen, “Optimal dividend payments until ruin of diffusion processes when payments are subject to both fixed and proportional costs,” Adv. in Appl. Probab. 39 (3), 669–689 (2007).
S. Sethi and M. Taksar, “Optimal financing of a corporation subject to random returns,” Math. Finance 12 (2), 155–172 (2002).
S. Goldstein, “On diffusion by discontinuous movements, and on the telegraph equation,” Quart. J. Mech. Appl. Math. 4 (2), 129–156 (1951).
M. Kac, “A stochastic model related to the telegrapher’s equation,” Rocky Mountain J. Math. 4 (3), 497–509 (1974).
E. Orsingher, “Probability law, flow function, maximum distribution of wave-governed random motions and their connections with Kirchhoff’s laws,” Stochastic Process. Appl. 34 (1), 49–66 (1990).
S. K. Foong and S. Kanno, “Properties of the telegrapher’s random without a trap,” Stochastic Process. Appl. 53 (1), 147–173 (1994).
L. Beghin, L. Nieddu, and E. Orsingher, “Probabilistic analysis of the telegrapher’s process with drift by means of relativistic transformations,” J. Appl. Math. Stochastic Anal. 14 (1), 11–25 (2001).
G. B. D. Masi, Yu. M. Kabanov, and W. Runggaldier, “Mean-variance hedging of options on stocks with Markov volatilities,” Theory Probab. Appl. 39 (1), 172–182 (1994).
Yu. V. Bondarenko, “A probabilistic model for describing the evolution of financial indices,” Cybernet. Systems Anal. 36 (5), 738–742 (2000).
A. Di Crescenzo and F. Pellerey, “On prices’ evolutions based on geometric telegrapher’s process,” Appl. Stoch. Models Bus. Ind. 18 (2), 171–184 (2002).
N. Ratanov, “A jump telegraph model for option pricing,” Quant. Finance 7 (5), 575–583 (2007).
N. Ratanov and A. Melnikov, “On Financial markets based on telegraph processes,” Stochastics 80 (2-3), 247–268 (2008).
N. Ratanov, “Option pricing model based on a Markov-modulated diffusion with jumps,” Braz. J. Probab. Stat. 24 (2), 413–431 (2010).
O. López and N. Ratanov, “Option pricing driven by a telegraph process with random jumps,” J. Appl. Probab. 49 (3), 838–849 (2012).
L. R. Sotomayor and A. Cadenillas, “Classical and singular stochastic control for the optimal dividend policy when there is regime switching,” Insurance Math. Econom. 48, 344–354 (2011).
J. Zhu and F. Chen, “Dividend optimization for regime-switching general diffusions,” Insurance Math. Econom. 53 (2), 439–456 (2013).
Z. Jiang and M. Pistorius, “Optimal dividend distribution under Markov regime switching,” Finance Stoch. 16 (3), 449–476 (2012).
J. Wei, R. Wang, and H. Yang, “On the optimal dividend strategy in a regime-switching diffusion model,” Adv. in Appl. Probab. 44 (3), 886–906 (2012).
Z. Jiang, “Optimal dividend policy when cash reserves follow a jump-diffusion process under Markov-regime switching,” J. Appl. Probab. 52 (1), 209–223 (2015).
W. H. Fleming and R. W. Rishel, Deterministic and Stochastic Optimal Control (Berlin, 1975).
W. Fleming and H. M. Soner, Stoch. Model. Appl. Probab., Vol. 25: Controlled Markov Processes and Viscosity Solutions (Springer, New York, 2006).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Pospelov, I.G., Radionov, S.A. Optimal Dividend Policy when Cash Surplus Follows the Telegraph Process. Math Notes 109, 125–135 (2021). https://doi.org/10.1134/S0001434621010156
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0001434621010156