Abstract
We develop a stochastic dynamic model of dividend optimization under the conditions of a positive recovery, in which shareholders can recover a portion of their capital, and nonterminal bankruptcy due to private capital infusion or government bailout. In the presence of a recovery, the optimization problem becomes a mixed classical impulse stochastic control problem. We provide a closed-form solution for optimal dividend payout and timing under nonterminal bankruptcy. We take the model to the real data and show that this model explains the dividend puzzle during the financial crisis when the US government bailed out insurance companies and banks.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Corporate dividend policy has long engaged the attention of financial economists. One of the most important decisions for a firm is to set an optimal dividend payout strategy. Miller and Modigliani (1961) provides a valuation model of dividends for an infinite-horizon firm under perfect information. Later studies extend the model to account for information asymmetry, agency cost and other issues (see, for example, Bhattacharya 1979; Miller and Rock 1985; John and Williams 1985; Jensen 1986; Hausch and Seward 1993; Guttman et al. 2010; Baker et al. 2016). Traditional models of optimal dividend decisions for the firm typically build on the non-stochastic framework which is difficult to apply to a more realistic situation of controllable business activities in a stochastic environment. In contrast, stochastic dynamic programming provides a powerful tool for studying intertemporal optimization under uncertainty (see Merton 1990). This approach is ideal for solving the complicated problems of determining the optimal dividend policy in an uncertain world.
The dividend policies of banks and insurance companies during the financial crisis have received considerable attention from academic researchers and practitioners. These companies distributed a large amount of dividends even as losses were mounting. During this period, aggregate dividends paid by banks exceeded aggregate earnings by about 30% (see Floyd et al. 2015). One possible explanation for the dividend policy during the early stages of the financial crisis is that it reflected a form of agency problems. Agency theory suggests that risk shifting, or asset substitution, is a moral hazard problem between shareholders and creditors. After raising debt, shareholders have incentives to transfer wealth away from creditors. The dividend payout policy during the financial crisis may simply reflect that banks engaged in risk shifting by paying dividends to dilute the value of creditors’ claims. An alternative explanation for the large dividend payouts during the financial crisis is these firms were concerned that cutting dividends may induce a run by their short-term creditors and trigger bankruptcy (see Acharya et al. 2012). By maintaining large dividend payouts, banks and insurance companies send out a signal that they have the ability to survive, thereby increasing the confidence of short-term creditors and financial stability.
A number of studies have proposed different models to explain the dividend puzzle during the financial crisis. These studies typically adopt static agency theoretic or signaling models, which is difficult to apply to firms in an uncertain world. In this paper, we develop a stochastic dynamic model of optimal dividend policy to describe the dividend behavior of financial firms facing a bankruptcy risk. This stochastic model is more suitable for studying the intertemporal optimization of dividend payout under uncertainty. Using this approach, we solve the complicated problems of determining the optimal dividend policy in a stochastic environment with bankruptcy risk and recovery, and provide a rational explanation for firms’ dividend behavior during the subprime crisis.
Optimizing dividend payout is a classical problem in actuarial mathematics dated back to de Finetti (1957). In past decades, there has been an increasing interest in diffusion models with controllable risk exposure and optimal dividend distribution (see Cadenillas et al. 2006; Kulenko and Schimidli 2008; Wang and Zhang 2010; Avanzi and Wong 2012; Jin and Yin 2013). While past studies have improved our knowledge of managing risk, the financial system is constantly evolving, and firms have faced new problems never encountered in the traditional dividend optimization models. As an example, a number of large insurance companies were on the verge of collapse and had to be bailed out by the government through capital injections. How to develop a stochastic model of optimal dividend payouts in such an environment is a challenging task. In this paper, we address this issue by constructing a diffusion model with nonterminal bankruptcy to generate an optimal dividend distribution strategy for firms under uncertainty. While our model is very general and applicable to firms of all business types, the framework we propose is particularly suitable for a large insurance company facing obligations of a stream of payouts to policy holders. A key feature in our model is that an adoption of the nonterminal bankruptcy setting in this diffusion framework enables us to capture the unique dividend behavior during the financial crisis when the government injected capitals into financial companies to avert the catastrophe of systemic defaults.
Numerous studies have applied the methods of stochastic control to model the optimal dividend payout problem (see, for example, Sethi et al. 1984; Radner and Shepp 1996; Asmussen and Taksar 1997; Højgaard and Taksar 1998a, b; Cadenillas et al. 2006; Paulsen 2007, 2008; Belhaj 2010; Yao et al. 2011; Avanzi and Wong 2012; Jin and Yin 2013). In most studies, the firm’s liquid asset process is characterized by a Brownian motion in which the drift term corresponds to the expected profit per unit of time, and the diffusion term captures risk exposure. Some studies have allowed firms to replenish their cash reserve through external capital infusion when they are under financial stress (Sethi and Taksar 2002).Footnote 1 In these models, firms go bankrupt when their profits fall short of expenses, and bankruptcy is typically assumed to be terminal with zero recovery value. This assumption is unrealistic because in reality when firms go bankrupt, they may recover some asset value, and can also resurrect from the bankruptcy proceeding (nonterminal bankruptcy) through external capital injection. Even in the models with capital infusion, regardless of whether firms can raise capital by issuing new shares or not, the value functions in traditional models are typically defined on cumulative dividends less predetermined cumulative capital inflows under firms’ control. However, in reality, when firms are in distress, they face tremendous uncertainty and have little control over the amounts of capital they can raise. In this paper, we relax these assumptions to make the diffusion model of dividends more general. With less restrictive assumptions, we develop a stochastic dynamic model of dividends to assess the effects of capital infusion on the firm’s optimization of dividend payout, and use this model to explain the dividend puzzle during the financial crisis that the distressed firms distributed large amounts of dividends shortly after receiving the government bailout money.
However, relaxing these assumptions comes with a price. Specifically, it results in a nonzero boundary condition and a nonlinear value function in the diffusion dividend model and as a consequence, the closed-form solution is difficult to obtain. To overcome this difficulty, we treat the amount of capital inflow at the state of bankruptcy as an external exogenous variable in the value function. Specifically, we permit a capital injection by external funding or bailouts when firms face a possibility of bankruptcy, and the amounts of these aids are beyond their control. This assumption is very realistic because in reality the amounts of government bailout grants are exogenously determined by the political process, which is beyond firms’ control. Bankruptcy is thus not necessarily terminal because the government can step in to bail out ailing big firms as observed during the subprime crisis. Moreover, even if some smaller firms were allowed to bankrupt with no government aids, they typically had positive residual values after they were liquidated, which depend on the circumstance.Footnote 2 Imposing these more realistic assumptions, i.e., nonterminal bankruptcy, politically charged external grants, and positive recovery, will increase the ability of the stochastic dividend model to predict future outcomes. Given this setup, we obtain an analytic solution for the value maximization problem with the aid of an auxiliary problem, in which a terminal model with a residual value at bankruptcy is considered. A candidate solution of the latter problem can be constructed by a series of quasi-variational inequalities with a non-negative boundary condition. Using these procedures, we provide a closed-form solution for the original dividend optimization problem with nonterminal bankruptcy, and determine the optimal dividend strategy and timing of payout in the presence of capital infusion.
Besides the closed-form solution for the diffusion model, we present and verify the concise sufficient and necessary condition for a dividend distribution after the capital infusion. Numerical simulation and empirical tests are provided to verify the model predictions. We employ confidence intervals to determine if a firm’s dividend behavior is rational, instead of taking rationality as given, as in most previous studies. The confidence intervals can reveal the often high sampling error in the statistics, and so are more direct and transparent than standard errors. Another advantage of reporting confidence intervals is that it avoids the tricky problem of deciding on a null hypothesis by simply showing the range of true parameters.
The model generates policy implications for regulators. A concern of the government bailout for troubled firms during the financial crisis is that these firms may use government grants to pay dividends to stockholders or bonuses to management and therefore, induce a risk shifting problem. Our model suggests that to prevent such problem, the capital injection rate should be set at a level lower than the average growth rate of the firm’s future cash flow. Alternatively, the government can impose a penalty on the firm that distributes excessive dividends after receiving financial aids, or put a cap on the dividend payment when the firm is still on the bailout program.
We take the model to the real data to explain the dividend behavior in the subprime crisis. The US government bailed out a number of troubled firms during the crisis to help them continue their operation. However, many of these companies on the government bailout program continued or even increased dividends while they were still on life vest. As an example, AIG incurred heavy losses in providing credit insurance to collateralized debt obligations (CDOs). It took a massive government bailout to help the company remain solvent. However, instead of preserving cash to increase its chance of survival, the company used the government bailout money to actually pay out a total of $218 million dividends and bonuses in March 2009. Many other firms under the government support did the same thing. For example, 19 banks on the Supervisory Capital Assessment Program (SCAP) distributed about 80 billion for dividends and bonuses which represented nearly 50% of the Capital Purchase Program (CPP) funds used to recapitalize banks in the fall of 2008. An important question is whether these firms’ dividend decisions are rational. To answer this question, we test the hypothesis of rationality in firms’ dividend behavior using the confidence interval derived from the dividend optimization model. Interestingly, we find that that firms’ dividend behavior during the crisis period is consistent with rationality and the value-maximization principle. Our study demonstrates that the stochastic dynamic programming model is a valuable tool that can be used to design an optimal payout policy and evaluate firms’ dividend decisions even in a highly uncertain environment as the subprime crisis.
Our paper is related to a growing literature on dividend payouts of financial firms, especially during a financial crisis, and the optimal policy response to external shocks (Hirtle 2014; Floyd et al. 2015; Cziraki et al. 2016; Acharya et al. 2017; Juelsrud and Nenov 2020). Acharya et al. (2017) develop a model of bank dividend payout, whereby the risk shifting incentive of the bank stockholders affects bank dividend payments. They show that when banks are connected through an interbank market, the interaction of risk shifting with a dividend externality may set off a systemic crisis. Juelsrud and Nenov (2020) study the informational role of dividends when banks are exposed to a coordination-based run. They show that banks can use dividends to both risk shift and signal their available liquidity to short-term lenders and influence the lenders’ actions. They suggest that with dividend signaling, there is an additional informational externality that banks fail to internalize in addition to the risk-shifting inefficiencies. Jacob and Michaely (2017) investigate how dividend taxation affects payout. Exploiting an exogenous shock to dividend taxation, they show that absent any frictions, dividend taxation has a large impact on payout. As agency issues and shareholder conflicts increase, the impacts of owners’ tax preferences on dividend payout significantly decrease. Our work complements these studies. Similar to the Jacob and Michaely (2017) study, we consider the effects of taxes on dividend payments. Like the studies of Acharya et al. (2017) and Juelsrud and Nenov (2020), we examine the dividend payout issue during the financial crisis. Our paper differs from these studies in several aspects. First, we employ a stochastic dynamic programming approach to model the dividend behavior under uncertainty. Our modeling considers the effects of bankruptcy risk and differentiates the effects of terminal and nonterminal bankruptcies on firms’ strategic dividend payouts. Second, we construct a model of dividend payout policy that better accommodates the business operation of insurance companies, which were at the center stage of the subprime crisis. Third, we derive the optimal dividend payment strategy with taxation under symmetric information, and show that an optimal payout policy exists without having to deal with the incentive issue related to information signaling.
This paper contributes to the current literature on corporate dividend policy. A number of recent papers have examined various issues of dividend policy related to information, corporate governance, and environmental and social responsibility. Amberger (2023) examines whether the volatility of tax payments is associated with dividend payouts and finds that firms with more volatile tax payments are less likely to pay dividends. An et al. (2022), Chen et al. (2022), and Rubio et al. (2023) investigate the fundamental reasons behind firms’ dividend payments. Corgnet et al. (2023) examine how securities market aggregate the information in dividends and Mazouz et al. (2023) explore the relation between dividend policy, liquidity risk and the cost of equity capital. Aziz et al. (2022) and Wang (2022) examine the effect of ESG concerns on corporate dividend policy. Sikalidis (2022) and Tayachi (2023) investigate the effect of ownership structure on dividend policy. This paper complements these studies by examining how government policy may affect dividend payouts by financial and non-financial firms.
Our work is also related to a recent paper by Lindensjö and Lindskog (2020), which proposes a dividend model that allows for capital injection when insurance companies face the possibility of bankruptcy. Our paper differs from Lindensjö and Lindskog (2020) in several major aspects. First, our paper focuses on the effect of the bailout from the government when the firm faces bankruptcy. Because bailout decisions are largely a political process, we treat the capital injection from the government as an external variable that is beyond the firm’s control. This setup contrasts sharply with Lindensjö and Lindskog (2020) that views the capital injection as an internal control variable, which enters into the objective function of their model. In their model, the firm can control outside funding, e.g., determining how much financing is from issuing new bonds or stocks. In their paper, the capital injection is primarily raising equity capital from the firm’s owners and they do not explicitly consider government bailout. In contrast, we focus on government bailout as the main source of capital injections and aim to explain the dividend puzzle during the period of government intervention. We specifically recognize that when the firm is on the verge of bankruptcy, it is extremely difficult for the company to issue new bonds or new stocks as implied by the Laffer theory. Second, in Lindensjö and Lindskog (2020), the dividend payout barrier is preset, that is, the dividend payment time is not a control variable in their model. In contrast, in our paper, both dividend time and amount are control variables. The optimal dividend payment time and amount are determined by our model through the value optimization, and the dividend payout time is not a preset barrier. This setup is important as we want to investigate whether the dividend payout timing observed during the financial crisis is consistent with rationality. Third, our paper focuses on the effects of capital injections on dividend timing and amount. We construct the model and design empirical tests to investigate whether the dividend decisions are rational during the subprime crisis and government bailout periods, whereas Lindensjö and Lindskog (2020) did not address these issues. Fourth, our paper considers the reinsurance problem, and the proportion of reinsurance is an optimal control variable in our model, whereas Lindensjö and Lindskog (2020) ignore the issue of the proportion of reinsurance. In their model, the proportion of reinsurance is set to zero. Our model is therefore more general and particularly suitable to describe the behavior of insurance companies such as AIG and MBIA, which were at the center of the subprime crisis. Finally, our dividend model can be used to explain the dividend behavior of not only insurance companies but also other financial institutions and firms, while Lindensjö and Lindskog (2020) focus on the problems of insurance companies and their paper does not provide empirical tests.
Our paper makes two major contributions to the dividend literature. First, we develop a rational dividend model based on the stochastic dynamic programming approach. Our generalized optimal stochastic dividend model accounts for the effects of bankruptcy risk and the possibility of capital infusion and recovery from bankruptcy, which have not been considered in traditional financial models. We provide a closed-form solution for this generalized model for the first time. Past studies have not been able to develop a stochastic dividend model so general and yet obtain the closed-form solutions. Second, we provide both numerical simulations and empirical results to support the prediction of the diffusion dividend model. We show that the dividend payout by troubled banks and insurance companies are consistent with the prediction of our dividend model. The empirical evidence uncovered in this paper suggests that the dividend payout policy during the subprime crisis is consistent with rationality and the signaling equilibrium that dividends are used to signal financial firms’ available liquidity and managers’ confidence for resolving their financial problems.
The remainder of this paper is structured as follows. In Sect. 2, we propose a model with bankruptcy for the optimal dividend strategy with capital injections. An auxiliary model is proposed to help solve the complicated optimization problem. In Sect. 3, the relationship between the auxiliary model and the original model is discussed. In Sect. 4, the smooth solution of the original problem is given and in Sect. 5, an explicit form for the optimal dividend policy is listed out along with the closed-form solution for the optimal timing of dividend payments. In Sect. 6, numerical simulations are conducted to provide implications of the theoretical model and in Sect. 7, empirical tests are performed using real data. Finally, Sect. 8 summarizes the main findings and concludes the paper.
2 Dividend optimization models
In this section, we set up the stochastic dividend optimization model and solve for the close-formed solution. In the model, the liquid asset value process of the firm is represented by a Brownian motion with drift and diffusion terms. The drift term corresponds to the expected profit per unit of time generated from firms’ investment and operation, and the diffusion term captures risk exposure. Capital infusion is primarily through government bailout. Firms in our model may retain part of the injected funds and pay out the rest as dividends when there is lack of a profitable investment opportunity. The manager maximizes the expected present value of future dividends from the perspective of shareholder wealth maximization. The value function specified in the model is net of taxes and transaction costs, and capital injection is permissible when a firm faces bankruptcy. This setup paves the way to obtain the solution for the model with nonterminal bankruptcy later.
Let \((\Omega , {\mathcal {F}}, P)\) be a probability space, and a process \(\{W_t \}_{t\ge 0}\) be a standard Brownian motion adapted to a filtration \(\{{\mathcal {F}}_t\}_{t\ge 0}\) defined on this space. The reserve process \(\{X(t)\}_{t\ge 0}\) is a state variable, which denotes the value of a firm’s liquid assets and its changes, \(\Delta X(t)= X(t)-X(t-1)\), follow a normal distribution with mean \(\mu \) and variance \(\sigma ^2\). The firm can invest or reduce risk through risk management using available funds. In such case, we can accommodate simultaneous decreases in the drift and diffusion terms of X(t) by multiplying them by \(u(t)\in [0,1]\), in which profits and risk are reduced concurrently by expending part of reserves (see also Højgaard and Taksar, 1998b). For insurance firms, the term \(1-u(t)\) represents the proportion of re-insurance actions taken to reduce the risk on liquid assets. Let the stream of dividends be described by a series of increasing stopping times \(\tau _i, (i=1,2,...)\) and the amounts of dividends paid to shareholders be denoted by a random variable \(\xi _i, ( i=1,2,...)\). In addition, we define the time of bankruptcy by
Upon bankruptcy, the firm may receive an x amount of external capital. After a capital infusion, the reserve process has a jump, \(\Lambda _b:=X(b_+)-X(b)=x\). Let \(\eta = x/\Delta _t\), where \(\Delta _t\) is the unit time of injection period. In the continuous analogue,
where \(\eta \) is the rate at which the firm receives a capital at the state of bankruptcy.
While we assume the amount of bailout grant is constant, it does not literally mean that capital injection amount is always the same in each bankruptcy case and for each firm. The assumption of a constant x is consistent with the reality that the bailout grant is a lump sum amount determined by the political process. In actuality, the amount of the bailout money in the government capital injection varies by firm and is often positively related to firm size. A bailout is not guaranteed. Whether a firm can receive a bailout grant or not is determined by the political process. Thus, the value of x can be zero. We permit x to vary by firm in our analysis. In empirical investigation, we use the actual amount of bailout grants and frequency, and occurrence for each firm in our tests and these values vary by firm.
To ascertain the relationship between capital injections and its subsequent optimal dividends, we employ a discrete model for dividend events as in Cadenillas et al. (2006). Note that we do not consider the continuous form of dividend events in Asmussen and Taksar (1997) and Sethi and Taksar (2002) here as the optimal dividend time is an important variable to be determined later in this study to explain the timing of dividend payout events during the subprime crisis. The process X(t) after capital injections and before the next bankruptcy can be represented by
where \(dX(t)=\eta dt\) at b, and \(I_{ X(t) = 0}\) is an indicator function at \( X(t) = 0\).
Remark 2.1
To focus on the relationship between capital injection and subsequent dividend events, we posit that the amount of capital injection x is a constant at the time of bankruptcy. The capital injection is a fixed amount determined externally by the political process and the value of x is beyond the firm’s control. Under this condition, it is suitable for us to consider the dividend process as (2), which is the process defined during two bankruptcy states, and so is \(\{\xi _i\}\). The process (2) starts from the time point b, and we set \(b\ge 0\) for generality.
Each dividend event involves transaction cost and taxes. The net amount of money that shareholders receive is denoted by a function \(g:[0,\infty )\rightarrow (-\infty , \infty )\) as
where \(K>0\) is a fixed transaction cost that includes all expenses associated with dividend distribution (except taxes), and \(1-k\in (0,1)\) is the tax rate at which dividends are taxed, and \(\nu \) is a real value variable with respect to the amount of liquid assets withdrawn.
Define a control policy \(\pi \) by
where \(0\le \xi _i\le X(\tau _i-)\). The class of all admissible controls is denoted by \({\mathcal {A}}(x)\). Under each admissible control \(\pi \), we define a performance value functional J for the process (2) by
which represents the total expected discounted value received by shareholders and \(\lambda \) is the discount rate. For capital injection, as it is a debt and the receiver has to pay it back, we deduct the discounted capital injections in the above function. In this paper, we assume that the amount of capital injection is out of the firm’s control at the state of bankruptcy. In the present case, capital injections mainly come from the bailout of government or other investment firms and the amount of injection is determined by these lenders. Therefore, we assume that capital infusion is an external variable, which is a parameter that can be varied to examine the sensitivity of results.
Based on \(J(x,\pi )\), we define a value function V(x) by
We posit that the manger has control over the dividend payments and act for the best interest of shareholders by choosing a policy to maximize the expected value of future dividend payments or equivalently, to maximize the shareholder value. Miller and Modigliani (1961) provide the valuation formula for the firm by discounting dividend payments at an infinite horizon using a similar discount function in a perfect market with certainty and no bankruptcy risk. But in an imperfect market, transaction costs and taxes exist for dividend payments and there is a possibility of bankruptcy. In this paper, we maximize the expected future dividends for shareholders net of transaction costs and taxes in a stochastic environment.
The optimal control \(\pi ^*=(u^*,{\mathcal {T}}^*,\xi ^*)\) is a policy for which the following equality is satisfied:
There is an optimal dividend strategy when the company has excess liquid capitals, which have priority to cover current liabilities. An external capital injection is an installment debt for a firm, and the amount of external capital injection x will affect the optimal dividend payout. Therefore, we cannot just simplify the objective in (3) to solve the problem \(\sup \nolimits _{\pi \in A(x)}{\mathbb {E}}_x \left[ \sum \nolimits _{i=1}^\infty e^{-\lambda \tau _i}g(\xi _i)\cdot I_{(\tau _i>b)}\right] \) by deriving its HJB equation as in classical dividend problems. In addition, an important task is to find out the relationship between the capital injection and the next dividend event. To tackle these issues, we adopt the strategy of constructing an auxiliary problem to approach the original value function in (3).
We first consider the case of terminal bankruptcy, and employ the cash reserve process before bankruptcy as
to define an auxiliary performance function \(J_a\) as
where the definitions of \(\tau _i\), b, \(\lambda \) and \(g(\cdot )\) are the same as in \(J(x,\pi )\), but a is the residual value that has accrued from the sale of non-liquid assets at bankruptcy and the bankruptcy time in this case may be not zero. The control policy \(\pi _a\) is defined by
The class of all admissible controls \(\pi _a\) is denoted by \({\mathcal {A}}_a(x)\).
As mentioned, the assumption of a recovery value upon bankruptcy and the uncontrollable capital infusion amount leads to a nonzero boundary condition and a nonlinear value function in the diffusion dividend model, making it difficult to obtain the closed-form solution of the value function V(x). To facilitate solving the original optimization problem, we define an auxiliary optimal value \(V_a(x)\) as
Note that in past studies, it is usually assumed that \(a=0\), which implies no value left for shareholders at the bankruptcy state. But in reality, firms often have a residual value upon bankruptcy. Thus, we set the condition that \(a\ge 0\).
3 Relationship between V(x) and \(V_a(x)\)
In this section, we demonstrate the relationship between the true value function V(x) and the auxiliary optimal value \(V_a(x)\), which is used to obtain the solution of V(x). We first present the inequalities satisfied by \(V_a(x)\) and then verify that the solution of \(V_a(x)\) can be used to obtain the solution of V(x).
For a function \(\phi : [0,\infty )\rightarrow {\mathbb {R}}\), we define the maximum utility operator M of it by
Then, MV(x) is a local optimal policy, which is equal to or less than the global optimal policy V(x). That is, the following relationship holds,
in which the equality holds when x is a globally dividend intervening point.
Next, we define a differential operator \({\mathcal {L}}^u\) as
By the dynamic programming principle (e.g., Højgaard and Taksar 1998a, b), in the continuation region, which is a region not optimal to intervene, it follows that V(x) satisfies the Hamilton-Jacobi-Bellman (HJB) equation:
By the same argument, \(V_a(x)\) defined in (5) also satisfies (6) and (7). However, the equation in (7) is not sufficient to find the solution of \(V_a(x)\). Besides (7), the boundary condition of \(V_a(x)\) is required. The discussion above and the arguments in (6) and (7) give us an intuition that one analytic form of \(V_a(x)\) satisfies the following statement.
Statement 3.1
Assume that function \(v(x): [0,\infty )\rightarrow [0,\infty )\). For every \(x\in [0,\infty )\) and \(u\in [0,1]\), if we have
we claim that v(x) satisfies the quasi-variational inequalities (QVI) of the control problem.
In the following we provide a clue to obtain the form of V(x) by demonstrating that the solution of V(x) can be expressed by \(V_a(x)\) with the boundary condition \(\eta V'_a(0)-\lambda V_a(0)=0.\)
Lemma 3.1
Let V(x) be a solution of (3) and v(x) be a solution of (QVI). Assume that there exists a positive number P, such that v(x) is a nonnegative \(C^2\)-function on (0, P) with \(v'(x)\) bounded, v(x) is linear on \([P,\infty )\) and v(x) has a mixed boundary condition
Then, it follows
Proof
Denote by \(X(t)=X^{(u,{\mathcal {T}},\xi )}\) the trajectory determined by an admissible control \((u,{\mathcal {T}},\xi )\) and (2). In view of the boundedness of \(v'(x)\) on \([0,\infty )\), then
For dividend events, let n be a positive integer and \(b<\tau _{1}\). Denote \(\tau _0:= b\). In the following, we denote the minimum of any two numbers \(o_1\) and \(o_2\) by \(o_1\wedge o_2 = \min \{o_1, o_2\}\) and the maximum by \(o_1\vee o_2 = \max \{o_1, o_2\}\). After the bankruptcy time b, it follows that
Here and
In addition, for \(i\ge 2\), applying It\(\mathrm {\hat{o}}\)’s formula and combining with \({\mathcal {L}}^{u_s}v(X(s))\le 0\), we have
At the dividend time \(\tau _i\), \(i=1,2,\ldots \), it implies from (8) that
At time b, some capitals can be injected into X(t). Then it follows that
On the other hand,
Combining inequalities and equalities (14)–(18), and taking expectations, we obtain
It can be shown (see also Cadenillas et al. 2006) that \(\tau _n\rightarrow \infty \) a.s. (otherwise, \(v(x,\pi )=-\infty \)). Thus, \(P(\tau _n\rightarrow \infty )=1\), which implies that for \(n\rightarrow \infty \), we have
Then taking supremum over all trajectories with admissible control, \(v(x)\ge V(x)\) is verified as \(t\rightarrow \infty \). \(\square \)
Theorem 3.1
Let V(x) be the solution of (3). Suppose that \(v_{a}(x)\) is the optimal value function for the problem (5) and let \(u(\cdot )\) and \(\{\xi _i\}_{i=1}^\infty \) be corresponding optimal control functions. Let \(\eta \) be provided by
and let \(X^{\pi ^*}_t\) be the solution of (2) with \(\eta \) given by (19), \(u_{\pi ^*}(t)\) given by \(u(X^{\pi ^*}_t)\) and \(\xi _i^{\pi ^*}\) given by \(\xi _i(X^{\pi ^*}_t)\). Then, \(v_a(x)\) presents the optimal value function V(x) with the capital injection rate, \(\eta \).
Proof
As \(v_a(x)\) is the optimal value function (5), the corresponding u(x) forms the argmaxima of Eq. (7). Consequently, it follows that \({\mathcal {L}}^uv_a(x)=0\) and by the definition of (19), we have \(\eta v'_a(0) -\lambda v_a(0)=0\). Repeating the argument used in the proof of Lemma 3.1, we have
As \(t\rightarrow \infty \), by monotone convergence
In the following, we show that \({\mathbb {E}}_x[e^{-\lambda t}v_a(X_t^{\pi ^*})]\rightarrow 0\) for \(t\rightarrow \infty \) and then from (20), the following inequality holds:
From the boundedness of \(v_a'(x)\), it follows that there exists a constant \(\Theta >0\), such that \(v_a(x)\le \Theta (1+x)\). Consequently,
In addition, for the process \(X_t^{\pi ^*}\), we have
Therefore,
As such,
and (21) follows. Additionally, from Lemma 3.1, we have
Thus, \(V_a(x)\) can represent the form of V(x) to obtain the solution for the terminal bankruptcy model. \(\square \)
4 Smooth solutions of (QVI) and V(x)
In this section, we provide a general closed-form solution of (QVI). Then, based on it and Theorem 3.1, we derive a solution of V(x) for the nonterminal bankruptcy model.
4.1 A smooth solution to (QVI) properties
In this subsection, we construct a solution of (QVI) using a method similar to that in Cadenillas et al. (2006), Chen and Li (2017). In Cadenillas et al. (2006), (QVI) has a zero boundary condition, that is, \(v(0)=0\). However, for the nonzero boundary condition as in this paper, (QVI) is a nonlinear problem, and the solution can’t be obtained just by shifting the solution of (QVI) with the zero boundary condition. This is verified in the following, and we show that the case \(v(0)=a>0\) is much more complicated than the case \(a=0\). Nevertheless, the ideas in Cadenillas et al. (2006) are useful and give us a powerful heuristic tool to search for the solution of (QVI) under \(a>0\).
First, we define a dividend intervention point as
Then, at the interval \((0,x_1)\), from (QVI), the following equation is satisfied:
Let \(u(x)\in {\mathbb {R}}\) be the maximizer of \({\mathcal {L}}^uv(x)\). It follows that \({\mathcal {L}}^uv(x)\) reaches its maximum at
Combining (24) with (23), Eq. (23) can be reduced to
A general solution of (25) under the boundary condition \(v(0)=a\) is
where \(\gamma \) is presented by
and C is a free positive constant. \(\gamma \) can be interpreted as a discount factor adjusted for the mean and variance of the cash flow (reserve) process or the squared Sharpe ratio. Substituting (26) into (24), u(x) has the form as
If \(\mu >0\), obviously u(x) in (28) is an increasing linear function; so \(u(x)\le 1\) if and only if \(x\le x_0\), where
and
Thus, if \(x_0>0 \), which implies that for \(x_0<x<x_1\), then \(u(x)\ge 1\). But since the range of u(x) is [0, 1], we must have \(u(x)=1\) for \(x\in (x_0,x_1)\). Consequently, (23) becomes
One general solution to (31) can be written as
where \(C_1\) and \(C_2\) are free constants, and \(\theta _+\) and \(\theta _-\) are given by
Continuity of the function v(x) and its derivative \(v'(x)\) at the point \(x_0\) implies that \(C_1=Ca_1\), \(C_2=Ca_2,\) and \(a_1\) and \(a_2\) are defined by
It can be shown that \(a_1>0\) and \(a_2<0\).
On the other hand, if \(x_0\le 0\), then \(u(x)=1\) for any \(x\in [0,x_1)\), and (23) becomes
with the boundary condition \(v(0)=a\). Solving (35), the general solution can be obtained as follows:
with \(C_1+C_2=a\).
We now summarize the possible structure for the solution of (23) on \([0,x_1)\). If \(x_0>0\), then
where C is a free positive constant. If \(x_0\le 0\), then the structure of v(x) on \([0,x_1)\) is given by (36).
Remark 4.1
The existence of \(x_0\) and \(x_0>0\), is equivalent to that of C, such that
In addition, \(x_0\rightarrow 0_+\) is equivalent to \(C\rightarrow (aX_0^{-\gamma })_+\). For v(x) in (36) and (37), they are consistent at \(x_0=0\). Thus, it follows that \(C_1=Ca_1\). In addition, if the solution (36) exists, it implies \(C\le aX_0^{-\gamma }\). There is no conflict to denote \(C_1\) by \(Ca_1\) when \(C\le aX_0^{-\gamma }\). So, we let \(C_1=Ca_1\) for \(C\le aX_0^{-\gamma }\).
4.2 Smooth solution of (QVI) properties at \(x_1\)
We next discuss the properties of the smooth solution at \(x_1\), which is the critical point for the dividend event. From the definition of \(x_1\), we have that \(v(x_1)=Mv(x_1)\). In addition,
Then at \(x_1\), the supremum on Mv(x) can be taken over \(\eta \in [\epsilon ,x_1]\) for some \(\epsilon >0\). Thus, there exists \(\eta (x_1)\in (\epsilon ,x_1]\), such that
Let \(\widetilde{x}=x_1-\eta (x_1),\) then \(0\le \widetilde{x}< x_1\) and
From (39), it follows that
and
4.3 Uniqueness for the unfixed parameters
In the above discussion, some parameters, such as C, \(C_1\) and \(C_2\), are unfixed numbers. In this section, we discuss the uniqueness of these parameters by two useful integral functions, which can be used to obtain a solution of (QVI).
4.3.1 Two cases of \(x_0\) and two corresponding integral functions
Case I: \(x_0> 0\).
Let \(H^C(x)\) be a function, with constant C, constructed by
where \(x_0\) is also defined in (29) with \(C> aX_0^{-\gamma }\).
Define
where \(x_1^C\) and \(\widetilde{x}^C\) are two nonnegative roots of the equation \(k-CH^C(x)=0\) with \(\widetilde{x}^C<x_1^C\), and \(\widetilde{x}^C\vee 0\) denotes \(\max \{\widetilde{x}^C,0\}\). If \(\widetilde{x}^C\) doesn’t exist on \([0,\infty )\), then set \(\widetilde{x}^C\vee 0=0\).
From the definitions of \(H^C(x)\), it is easy to see that \(CH^{C}(x)\) is a continuous and increasing function of C and \(H^C(x)\) has convexity on \(x\in [0,\infty )\) by \((H^C)''(x)>0\). It follows that \(x_1^C\) is a decreasing function of C and \(\widetilde{x}^C\) is an increasing function of C. Thus, we have the following proposition.
Proposition 4.1
For \(H^C(x)\) defined by (41), we have that \(I_1(C)\) in (42) is a strictly decreasing function with respect to C on \((aX_0^{-\gamma }a_1, +\infty )\). Moreover, there exists \(C^*\in (aX_0^{-\gamma }a_1, +\infty )\), such that \(I_1(C^*) = 0\).
Case II: \(x_0\le 0\).
Let
where \(0<C_1\le aX_0^{-\gamma }a_1\).
Define
where \(x_1^{C_1}\) and \(\widetilde{x}^{C_1}\) are two nonnegative roots of the equation \(k-H^{C_1}(x)=0\) with \(\widetilde{x}^{C_1}<x_1^{C_1}\). If \(\widetilde{x}^{C_1}\) doesn’t exist on \([0,\infty )\), then let \(\widetilde{x}^{C_1}\vee 0=0\).
For (44), taking the derivative of \(I_2(C_1)\) with respect to \(C_1\) gives
For any positive \(C_1\), \(I'_2(C_1)<0\) due to the fact \(\theta _+ >0\) and \(\theta _-<0 \). Thus, we have the following result.
Proposition 4.2
For \(H^{C_1}(x)\) defined by (43), we have that \(I_2(C_1)\) in (44) is strictly decreasing function with respect to \(C_1\) on \((0,aX_0^{-\gamma }a_1]\). Moreover, it follows that \( \lim \nolimits _{C_1\rightarrow 0}x_1^{C_1}=\infty , \) and \( \lim \nolimits _{C_1\rightarrow 0}I_2(C_1)=\infty . \)
4.3.2 Property of two integral functions at \(x_0=0\)
At \(x_0=0\), there are some common properties of \(I_1(C)\) and \(I_2(Ca_1)\). First, \(C_1=Ca_1\) and \(C=aX_0^{-\gamma }\). Then from
we find that at \(x_0=0\), the integrands of \(I_1(C)\) and \(I_2(C_1)\) are the same. Consequently, we can conclude that if \(x_1^{C_1}\) exists at \(C_1=aX_0^{-\gamma }a_1\),
As \(I_1(C)\) is a decreasing function of C, the existence of C, such that \(C>aX_0^{-\gamma }\), is equivalent to that \(I_2(aX_0^{-\gamma }a_1)>0\) is satisfied. To judge whether \(I_2(aX_0^{-\gamma }a_1)>0\), we have the following result.
Proposition 4.3
We have that \(I_2(aX_0^{-\gamma }a_1)>0\) if and only if
where \(M^*\) is given by
Proof
Let \(B(x):=aX_0^{-\gamma }a_1\theta _+e^{\theta _+x}+aX_0^{-\gamma }a_2\theta _-e^{\theta _-x}.\) Notice that \(B''(x)>0\), and so B(x) has convexity. One equivalent condition of \(I_2(aX_0^{-\gamma }a_1)>0\) is that
Solving \(B'(x)=0\), we have
It can be shown that \(\frac{-a_2\theta _-^2}{a_1\theta _+^2}>1\) and \(x>0\) in (50).
Substituting (50) into B(x), we have
By simplification, we can obtain
From (49), (51) and the equality above, it follows that one equivalent condition of \(I_2(aX_0^{-\gamma }a_1)>0\) is \( a<k/M^*.\) \(\square \)
Then, if \(a<k/M^*\), the solution of (QVI) is
On the other hand, if \(a\ge k/M^*\) the solution of (QVI) is given by
where \(C_1\) is a positive parameter.
4.4 Solution of the nonterminal bankruptcy model
We are now in a position to solve the optimization problem for the nonterminal bankruptcy model of dividends. The key is to exploit the relationship between \(V_a(x)\) and V(x) in Sect. 3. Specifically, we employ the solution of the auxiliary value function \(V_a(x)\) to construct the solution of V(x) in the nonterminal bankruptcy model.
From the preceding analysis, we know that \(v_a(x)\) can be given by \(v_1(x)\) in (52) or \(v_2(x)\) in (53). By (52), it is easy to show that
where \(C>aX_0^{-\gamma }\). On the other hand, from (53), we have
where \(C\le aX_0^{-\gamma }\). Let \(\eta =\frac{\lambda v_a(0)}{v'_a(0)}\), then from (54) and (55), we can see that \(\eta \) is an increasing function of the ratio \(\frac{a}{C}\). Consequently, for any \(\eta \in (0,\infty )\), there exists a unique ratio \(\frac{a}{C},\) such that \(\eta =\frac{\lambda v_a(0)}{v'_a(0)}.\) So, for a fixed a, the parameter C is unique, corresponding to the given value of \(\eta \).
From (54), we have \( \eta =\frac{\lambda }{\gamma } (\frac{a}{C})^{\frac{1}{\gamma }}\). It follows that
or \(a=C(\frac{\eta \gamma }{\lambda })^\gamma \). From \(C>aX_0^{-\gamma }\), it implies \(\eta \in (0,\frac{\lambda X_0}{\gamma })\). In reduction, \(\frac{\lambda X_0}{\gamma }=\frac{\mu }{2}\). On the other hand, for \(\eta \in [\frac{\mu }{2},\infty )\) and from (55), \(\eta =\frac{\lambda }{\theta _-+a_1(\theta _+-\theta _-)/(\frac{a}{C})}.\) Consequently,
For simplicity, we denote \(p_\eta =\frac{a_1(\theta _+-\theta _-)}{\frac{\lambda }{\eta }-\theta _-}\). Then, for any given \(\eta >0\), we have the following results.
Proposition 4.4
If \(\eta \in (0,\frac{\mu }{2})\), then the solution v(x) of the nonterminal bankruptcy model with a capital injection \(\eta \) is uniquely given by
where \(x_0=X_0-\frac{\eta \gamma }{\lambda }\). On the other hand, if \(\eta \in [\frac{\mu }{2},\infty )\), the solution v(x) of the nonterminal bankruptcy model with a capital injection \(\eta \) is uniquely given by
4.5 Determination of parameter C
The analysis above shows that the solution of the nonterminal bankruptcy model depends on parameter C. We next discuss how to determine the value of this parameter.
Let \(\widetilde{x}^+\) denote \(\max \{\widetilde{x},0\}\). For the optimal strategy v(x), there exists a point \(\widetilde{x}^+\), such that
It follows that
Define \(I(C)=\int _{\widetilde{x}^+}^{x_1}(k-v'(x))dx,\) then according to the two different cases of v(x) in (56) and (57), we can write I(C) as \(I_1(C)\) and \(I_2(C)\) as follows:
and
where
and \(x_1\) and \(\widetilde{x}\) are two roots of equation \(k-CH_1(x)=0\) or \(k-CH_2(x)=0\) with \(\widetilde{x}<x_1\). If \(\widetilde{x}<0\), we use \(\widetilde{x}^+\) to replace \(\widetilde{x}\). In Appendix A.1, the steps to calculate C are given. The value of \(x_1-\widetilde{x}^+\) represents the amount of dividend payout and I(C) denotes net dividends received by shareholders.
5 Dividend policy and payout timing
Given the results in the preceding sections, we now formally present the optimal dividend policy. in this section, we discuss the time between the bankruptcy state and the subsequent dividend payout predicted by the model and present some useful results.
5.1 Dividend policy
The optimal policy for the nonterminal bankruptcy model is presented below.
Policy 5.1
Suppose that \(\mu \), \(\sigma \), k, K, \(\lambda \) and \(\eta \) are estimated from empirical data. It follows from Proposition 4.4 that parameter values, C, \(x_0\), \(x_1\), and \(\widetilde{x}\) can be calculated. Let \(\tau ^*_0=0\) and \(x_0=X_0-\frac{\eta \gamma }{\lambda }\), then the control \(\pi ^{*}=(u^{*},{\mathcal {T}}^{*},\xi ^{*})\) is defined by
where \(X^*\) is the solution of the stochastic differential equation:
which is the optimal control associated with the function v(x) defined by (56) and (57).
5.2 The expected time between bankruptcy and its subsequent dividend payout
In this part, we firstly provide the expected time between bankruptcy state and its subsequent dividend payout after achieving external capital injections. Then, based on this result we illustrate an interesting application on the explanation of paying dividend immediately. Moreover, we present a sufficient and necessary condition for this event.
5.2.1 Expected time for dividend distribution
If \(\eta \in [0,\frac{\mu }{2})\), from Proposition 4.4, we have \(x_0=X_0-\frac{\eta \gamma }{\lambda }>0\). But for \(\eta \in [\frac{\mu }{2},\infty )\), it implies \(x_0\vee 0=0\). For convenience, we use \(x_0^+\) to denote \(x_0\vee 0\). If \(x_0^+=0\), then all the following functions defined on \([0,x_0^+)\) do not exist. Hence, we just need to consider the case defined on \([x_0^+,\infty )\). We define the stochastic process Y(t) by
where \(u^*:[0,\infty )\rightarrow [0,\infty )\) has the following function:
and \(\mu , \sigma , \gamma \) and \(\lambda \) are as defined before. In \([0,x_0^+)\), the process Y(t) is
whereas in \([x_0^+,\infty )\), the process Y(t) behaves like a Brownian motion
Define a stopping time by
For both processes in (59) and (60), they may first reach the upper boundary \(x_1\) or the lower boundary 0, and we let \(\tau _{x_1} \) and \(\tau _0\) be the corresponding times for these two cases. Let \(x\in (0,x_1]\). We consider auxiliary functions \(\phi _{x_1}(x)\) and \(\psi _{0,x_1}(x)\) defined by
Here, \(\phi _{x_1}(x)\) is the probability that the process Y(t) reaches the boundary \(x_1\) prior to time 0, and \(\psi _{0,x_1}(x)\) is the expected time that the process Y(t) exits from the interval \((0, x_1]\).
Let \(\tau _{x_1}^* = \inf \{t|X(t) = x_1, X(0) = 0\}\). For the dividend policy with capital injections, we denote the expected time duration between bankruptcy state and the next dividend time by \(\psi _0^{x_1}(x)=E_x(\tau _{x_1}^*)\), where x is the position after the capital is injected at the bankruptcy state. In Appendix B.1, for every \(x\in [0,x_1]\), we derive the closed form of \(\psi _0^{x_1}(x)\):
where the closed forms of \(\psi _{0,x_1}(x)\) and \(\phi _{x_1}(x)\) are also obtained.
In addition, in Appendix B.2, the variance of \(\tau _{x_1}^*\) is given and denoted by \(\sigma _{\tau _{x_1}}^2\). This enables us to set the confidence interval for \(\tau _{x_1}^*\) under the assumption of normal distribution for \(\tau _{x_1}^*\) at a given significant level. For instance, under the \(5\%\) significance level (or \(95\%\) confidence level), the confidence interval of \(\tau _{x_1}^*\) is
By It\(\mathrm {\hat{o}}\)’s formula, \(\log (Y^1(t)+\eta \gamma /\lambda )\) is a linear Brownian motion with drift
Thus, if \(1-2\gamma <0\) and \(Y^1(0)\in [0,x_0^+)\), then there is a positive probability that \(Y^1(t)\) never reaches \(x_1\) (see Section 7.5, Karlin and Taylor 1975), which implies \(\psi ^{x_1}_0(x)=\infty \). But if \(x_0^+=0\), the constraint \(1-2\gamma >0\) is not needed. So, in numerical simulations (see below), we only consider the case \(x_0^+=0\) and the case \(x_0^+>0\) with condition \(1-2\gamma >0\). In empirical investigation, we find that all \(\eta \) values are large and satisfy the condition of \(\eta >\frac{\mu }{2}\), which leads to \(x_0^+=\max \{X_0-\frac{\eta \gamma }{\lambda },0\}=0\). Similarly, for the process of \(Y^2(t)\), the feasible condition is \(\mu >0\), which is also satisfied as shown later in our numerical simulations and empirical examples.
5.2.2 The condition of immediate dividend payment after the bailout
When the reserve process X(t) reaches the bankruptcy state, some amounts of capital are expected to be injected in the nonterminal bankruptcy model. A question of interest is how large the injection rate \(\eta \) should be so that a dividend is paid immediately (e.g., as done by banks during the subprime crisis). For clarity, we explain below the statement of dividends being paid immediately.
We set the condition of “immediately” by an arbitrarily small threshold value \(\epsilon _i>0\) for a shareholder i. Specifically, for any shareholder i there exists a \(\epsilon _i\), such that \(\psi _0^{x_1}(x)\le \epsilon _i\), where \(\psi _0^{x_1}(x)\) is the expected dividend payment time after the bailout given by (63). Thus, we can define the event of an immediate dividend payment mathematically as follows.
Statement 5.1
For any shareholder i, there exists an expected value \(\epsilon _i>0\) such that dividends are paid immediately. When the condition \(\psi _0^{x_1}(x)\le \epsilon _i \) holds, we say dividends are paid “immediately”.
From Sect. 5.1, we know that if the process \(X^*(t)\) reaches the point \(x_1\), dividends are distributed. Therefore, the value of \(x_1\) determines dividend payout time. If \(x_1\) is a large number, then there is a high probability that the process \(X^*(t)\) would approach the bankruptcy state many times before reaching \(x_1\); that is, it would take a long time for a dividend event to occur. Thus, for large \(x_1\), the probability for the firm to pay dividends immediately is small. Conversely, if \(x_1\) is small, then it is relatively easy for the process \(X^*(t)\) to reach \(x_1\), or the probability that dividends are paid immediately would be high.
From the analytic solution of \(\psi _0^{x_1}(x)\) given in Appendix B, we notice that \(\psi _0^{x_1}(x)\) is an increasing function with respect to \(x_1\) and \(\psi _0^{x_1}(x) = 0\) at \(x_1 = 0\). Consequently, for any given \(\epsilon _i\), x, \(\mu \), \(\sigma \), k, \(\eta \) and K, there exists a unique solution \(x_1\), such that \(\psi _0^{x_1}(x) = \epsilon _i\). Moreover, from \(I_1(C) = K\) or \(I_2(C) = K\) we can obtain a unique C under given \(\epsilon _i\), x, \(\mu \), \(\sigma \), k, \(\eta \), K and \(x_1\). Therefore, for any immediate dividend time of \(\epsilon _i\), we can obtain a unique solution of the optimal dividend payment.
From the perspective of a rational individual shareholder, an important question is under what parameter condition, especially for the parameter \(\eta \), the optimal immediate dividend payment will occur. In the following, we answer this question.
Theorem 5.1
If the parameters \(\mu \), \(\sigma \) and k are given, then \(x_1\rightarrow 0\) if and only if \(\eta \ge \mu \) and \(K\rightarrow 0\).
Proof
For any given \(\eta \in (0,\frac{\mu }{2})\), \(x_0=X_0-\frac{\eta \gamma }{\lambda }>0\) is a fixed number given parameters \(\mu \), \(\sigma \) and k. As \(x_1\) is the right root of \(H_1'(x) = k\), which makes \(x_1>x_0\). It follows that there is a lower bound \(x_0\) for \(x_1\) such that \(x_1\nrightarrow 0\) for any \(K>0\). So, in the following we only consider the case \(\eta \in [\frac{\mu }{2}, \infty )\), which implies \(x_0^+ = 0\). Then, the optimal dividend strategy can be expressed by \(H_2(x)\).
As \(x_1\) is the right root of \(H_2'(x) = k\) it implies that \(x_1>x_{min}\), where \(x_{min} = \arg \min \limits _{x\ge 0} H_2(x)\). Then from the convexity of \(H_2(x)\) and \(I_2(C)=K\), we have that \(x_1 \rightarrow 0\) if only if \( x_{min}=0 \) and \(K\rightarrow 0\).
We next explore the sufficient and necessary condition of \( x_{min}=0.\) From (43) the derivative of \(H_2(x)\) is
Let \(H'_2(x)=0\), then the criterion for \(x_{min}=\max \left\{ \frac{1}{\theta _+-\theta _-}\ln \left( \frac{(a_1-p_\eta )\theta _-^2}{a_1\theta _+^2}\right) , 0\right\} = 0\) can be shown as
Simplifying the inequality of the right equivalence above, we have
The discussion above suggests that
Thus, the equivalent condition of immediate dividend payment has been proved. \(\square \)
Conversely, if \(0\le \eta <\mu \), then \(x_1\nrightarrow 0^+\), meaning that the event of immediate dividend payment will never occur. This result has a policy implication. It suggests that to prevent the occurence of immediate dividend payment, the government can reduce the capital injection rate \(\eta \) to a low level, or impose a penalty on dividend distribution, which effectively increases the cost of dividend payout K. In the following, we derive a closed-form solution for the expected dividend payout time.
6 Numerical examples
In the preceding section, we derive the theoretical results of dividend payout time \(\psi _0^{x_1}(x)\) and the dividend amount \(\xi _i\) given a bailout rate \(\eta \) at the bankruptcy state. In this section, we provide numerical simulations to assess the effects of model parameters on the optimal time and amount of dividend payout.
We use the following parameter estimates for Fannie Mae in February 2012 as the base values for \(\mu \), \(\sigma \), \(\lambda \), k, \(\eta \) and K in numerical simulations. These base values are \(\mu _0=0.1812\), \(\sigma _0=0.2586\), \(\lambda _0=0.0775\), \(k_0=0.85\), \(\eta _0=2.4431\) and \(K_0 = 0.1\), respectively.Footnote 3
To examine the sensitivity of dividend time and dividend amount to parameter values, we set the ranges of these parameters by the minimum and maximum multipliers in Table 1 times their base values. For the base value \(\eta _0=2.4431\), it is much larger than \(\mu _0=0.1812\). To show the dividend event near the line \(\eta = \mu \), we set the smallest and largest multipliers of \(\eta \) as 0 and 0.2, respectively in Table 1. For the value of k, the proportion of dividends left for shareholders is not small, we set the multipliers as 0.75 and 1.125. This gives a k interval of \([0.75 k_0, 1.125 k_0]\), which is equal to [0.6375, 0.9563]. For the condition \(1-2\gamma > 0\), it is equivalent to \(\mu > \sqrt{2\lambda }\sigma \). As mentioned earlier, if \(x_0^+ = 0\) is satisfied, the condition \(1-2\gamma > 0\) is not needed. We carefully select the multipliers of parameters \(\mu \), \(\sigma \), and \(\lambda \) listed in Table 1 so that at least one of these two conditions is satisfied, which makes the multipliers of \(\mu \) larger than those of the other two parameters. K also has a large impact on the dividend payment time and amount. We choose the smallest multiplier of K as 0.2 so that \(0.2 K_0\) is around zero. To accommodate the effects of K at plausible values, we set the largest multiplier to 5.0.
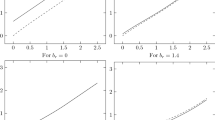
Given different \(\eta \), K and fixed values \(\mu = \mu _0\), \(\sigma = \sigma _0\), \(\lambda = \lambda _0\) and \(k = k_0\), Panels A and B of Fig. 1 plot the expected dividend time \(\psi _0^{x_1}(x)\) and its lower bound of confidence interval at the \(95\%\) level. To save space, the upper bound is omitted. As shown in Panel A, for any \(\eta \) near the transition layer \([\frac{\mu _0}{2}, \mu _0) = [0.0906, 0.1812)\), the value of \(\psi _0^{x_1}(x)\) changes sharply. For instance, at point \((K,\eta ) = (0.4631,0.0752)\), the dividend time is 9.9978,Footnote 4 while at its neighboring point (0.4631, 0.1128), the dividend time changes to 5.3533. For any \(\eta \) in \((0,\frac{\mu _0}{2})\), the dividend time remains high with the minimum value 2.4571 and the maximum value 10.4178, both are far from zero. An interesting result in Panel A is that dividend payout time approaches zero as \(K\rightarrow 0^+\) under the condition \(\eta \ge \mu _0=0.1812\). This finding is consistent with the theoretical result in Theorem 5.1, that is, \(x_1\rightarrow 0^+\) as \(K\rightarrow 0^+\) if \(\eta \ge \mu \). As K gets larger in Panel A, the expected dividend time becomes larger. The result suggests that to generate an immediate dividend payment, K has to be small. Panel B shows that the variance of dividend time becomes larger as K is larger and the value of the lower bound at large K is close to zero. This implies that although the expected dividend time is high at a large K value theoretically, the dividend time may actually approach zero under the condition \(\eta >\mu \).
The base number of \(\mu \), \(\sigma \), \(\lambda \), k, K and \(\eta \) are \(\mu = 0.1812\), \(\sigma = 0.2586\), \(\lambda = 0.0775\), \(k = 0.85\), \(K=0.10\) and \(\eta =2.4431\) respectively. The range of K is formed by the lower and upper bounds which are the base number multiplied by 0.2 and 5
Panels C and D of Fig. 1 present the corresponding dividend amounts and the lower bound of the confidence interval at the \(95\%\) level. At the first glance, the whole surface in Panel C looks much smoother than that in Panel A. Even at the transition layer \(\eta \in [\frac{\mu _0}{2}, \mu _0)\), the change of dividend amount is not large. For instance, corresponding to the points (0.4631, 0.0752) and (0.4631, 0.1128) in Panel A, the dividend amounts are 2.0254 and 1.9499, respectively. The change in the dividends of these two points is only \(3.87\%\), whereas the change in dividend time is \(86.76\%\). Thus, the sensitivity of dividend payment to \(\eta \) is not as high as that of dividend time. The dividend amount increases as K becomes bigger or \(\eta \) becomes smaller in Panel C. As shown in Panels A and C, dividend payment time and amount have the same trend as K and \(\eta \), suggesting that if the dividend is paid less often, the dividend amount will increase to make up the difference. In Panels B and D, there are some values below zero, which is caused by large standard deviation or the significance level. But it also implies that the dividend can be distributed immediately with a very small amount. Panel B shows that the confidence interval of dividend time at large K or small \(\eta \) is wider than that at small K or large \(\eta \). This result shows that the width of the confidence interval depends on K and \(\eta \). For small K and large \(\eta \), the confidence interval of dividend time is quite narrow.
Other parameters of the model also affect the expected dividend payout time and amount. Panels A and D in Fig. 2 show the effects of parameters \(\mu \), \(\sigma \), \(\lambda \) and k on payout time. In Panel A, dividend payout time changes greatly along the line, \(\eta =\mu \). When \(\eta >\mu \), the dividend time is around zero (paid almost instantly) and much smaller than when \(\eta <\mu \). This is consistent with the argument in Theorem 5.1 that if and only if the condition \(\eta > \mu \) is satisfied at small K, then the dividend payment time is close to zero. As revealed in Panel B, volatility \(\sigma \) is another important determinant of payout time. When \(\eta \) and \(\sigma \) are large, dividend payout time is much shorter than when \(\eta \) and \(\sigma \) are small. This finding implies that if volatility is larger, it is sooner to reach the upper bound \(x_1\). This means when it is more uncertain (larger volatility), it is more likely for firms to pay dividend quickly to signal the firm’s probability of survival.Footnote 5 The parameters, \(\lambda \) and k, are another two important factors. In Panel C, when \(\lambda \) approaches zero, it takes longer for firms to pay dividends than when \(\lambda \) is larger. When \(\lambda \) is larger, the discount factor \(e^{-\lambda \tau _i}\) becomes smaller at each \(\tau _i\). To maximize the shareholder value, it is optimal to pay dividends sooner, which is consistent with the case with large \(\lambda \) in Panel C. In Panel D, as k becomes larger or the tax rate is smaller, the dividend payout time is shorter. If the income tax is low, shareholders will prefer to receive dividends earlier.
The base number of \(\mu \), \(\sigma \), \(\lambda \), k, K and \(\eta \) are \(\mu = 0.1812\), \(\sigma = 0.2586\), \(\lambda = 0.0775\), \(k = 0.85\), \(K=0.10\) and \(\eta =2.4431\) respectively. To see the relationship of \(\eta \) and \(\mu \), we shorten the maximal multiple of \(\eta \) to be 0.2 in this figure. From Panel A–D, it shows that along the line \(\eta = \mu \), the dividend times are divided into two parts with obviously different magnitudes
Panels A to D of Fig. 3 plot the expected dividend amounts for different parameters, \(\mu \), \(\sigma \), \(\lambda \) and k. Comparing with Fig. 2, we find that dividend time and amount have the same trend under the same parameters. Moreover, the surface of dividend amounts is much smoother than that of dividend time duration. In addition, from Figs. 1, 2 and 3 we find that \(\eta \) has the largest effects on dividend time and amount. When \(\eta = \eta _0\), sensitivity of dividend time and amount to \(\eta \) is high. Overall, simulation results generate a pattern of dividend timing and payout consistent with the intuition and theoretical predictions.
7 Empirical tests
We next take our model to the real data to investigate why firms in financial distress continue to pay dividends when they are on the bailout program. A number of recent paper has tried to answer this question (see, for example, Acharya et al. 2012, 2016, 2017). To our knowledge, no empirical test based on the real data has been performed on the optimal dividend policy generated from the stochastic dynamic programming models. In this section, we provide empirical tests on the timing \(\psi _0^{x_1}(x)\) of dividends using the data for a sample of firms bailed out by the US government during the sub-prime crisis in 2008–2009.
7.1 Empirical data
The information for bailouts and subsequent events, such as payout of dividends, are provided in a public website.Footnote 6 The bailout events in our empirical test cover the repurchase program and the loan program. We collect the data for the names of companies receiving capital injections, the amount of cash grants, the time and amount of dividend distributions and other related information. We match the bailout data with the firm’s financial statement data in Wharton Research Data Services (WRDS). This matching results in 96 companies with the required data. The sample includes 91 banks, 2 financial service companies, 2 insurance companies and 1 auto company. The sample period runs from January 1980 to February 2012.
While our main purpose is to explain the dividend puzzle during the financial crisis in 2008–2009, our sample period is longer. There are two reasons that our sample period is longer than the subprime crisis period. First, we need to estimate model parameters using historical data. We set the estimation period from 1980 to the onset of the subprime crisis. Setting the sample period for the data to start in January 1980 gives us sufficient observations to obtain reliable parameter estimation. Second, although the severity of the crisis is largely over in the summer of 2009, the government bailout program goes well beyond it. As an example, one of the most important bailout programs, the Troubled Assets Relief Program (TARP) was authorized by the US Congress in October 2008. While the authority to make new financial commitments under TARP ended on October 3, 2010, the government support continued on. For example, the US government continued to hold AIG shares even after 2010, and Fannie Mae received government bailout until February 2012. Therefore, we extend the sample period to February 2012 to capture the full effect of the government bailout program.
Among all firms on the bailout programs, Fannie Mae received the largest number of of government bailout grants, which were multiple times of a typical bank aided. The government injected capitals into Fannie Mae for about three years beginning in March 2009. Panel A of Fig. 4 plots the frequency of capital injections into Fannie Mae from March 2009 to February 2012. In Panel B of Fig. 4, we separately plot the frequency of total capital injections for other firms included in our portfolio each month from October 2008 to July 2009. Panel B shows an interesting contrast in that capital injections for other firms mainly occur from October 2008 to January 2009, which is dramatically different from the case of Fannie Mae. Also, the frequency of capital injections for each of these firms (omitted for brevity) is low, on average only one or two injections for each firm. The low frequency of capital injections makes it difficult to estimate the parameter \(\eta \) (annualized injection rate) precisely for the firm with a smaller number of data points. To overcome the issue of infrequent injections, we form the portfolio on these firms to test the implications of our dividend model. This portfolio approach is quite common in financial research. The results based on the portfolio represent the average of the sample firms selected for our test. Since we are testing the implications of the dividend model for the bailout firms as a whole, this portfolio approach serves well for our purpose. In testing the model implications, we provide the tests using both the portfolio approach and individual firm data, and find that our results are robust.
Panels C–D of Fig. 4 display the total dividend amounts for Fannie Mae and other firms in the portfolio, respectively. In 2009, Federal Reserve Bank conducted the “stress tests” for the 19 largest banks. During this test period, dividends were accumulated and eventually declared on May 31, 2009 for most of these banks. However, dividends were announced regularly over most of our sample period. To measure the dividend time more accurately during this “stress test” period, we collect the regular dividend dates from the website of Yahoo and we divide the total amount of dividends that each firm announced on May 31, 2009 over these dates. Panels C–D of Fig. 4 show that dividend distributions are close to the time that capitals were injected by the government in Panels A–B.
We next use the item of Cash and Short-Term Investments in Compustat as a measure of cash reserve X(t). The discount rate \(\lambda \) can be estimated by the Gordon model: \(\lambda _t = D_t/P_t + g_r\) where \(g_r\) is the growth rate of dividends, and \(D_t\) and \(P_t\) are the dividend and stock price per share at time t, respectively. The growth rate can be estimated from the dividend process \(D_t = D_0 e^{g_rt}\). Taking the log on both sides, we have \(\log D_t = \log D_0 + g_rt \) where t is the time indicator. Running a regression against t, we can get an estimate of the growth rate \(g_r\) for each firm. Then, substituting \(g_r\) in the Gordon model, we can obtain the firm’s discount rate \(\lambda _t\) for each t. Further, we can calculate an average \(\lambda \) over the estimation period for each firm, and average them across firms to represent an average discount rate for the firms in the whole sample.
Dividend tax rates change over time. The Jobs and Growth Tax Relief Reconciliation ActFootnote 7 (JGTRRA) of 2003 allows qualified dividends to be taxed at the same rate as long-term capital gains, which is 15%. We set the tax rate \(1-k\) to \(15\%\) as the tax rate over the bailout period. The \(15\%\) dividend tax rate was introduced by the Bush Administration and carried over to the Obama Administration over the period between 2008 and 2012. Thus, this tax rate is the right rate to test the model implications.
The transaction cost of dividends is the cost related to the distribution of dividends. The cost of dividend distribution is not just the cost of cutting and mailing checks to shareholders. It also includes opportunity cost of paying dividends. The literature has suggested that dividend distribution can incur costs associated with foregone investments and issuing new shares, and increased cost of capital. These costs are hard to measure and can vary substantially across firms. To resolve this difficulty, we assume that the firm’s dividend behavior returns to normal as the economic situation becomes stable toward the end of the sample period. We then back out the transaction cost implied by the optimal condition of the dividend model and use this cost estimate in the empirical test. Finally, we use the item of Capital Surplus in CRSP as a measure of x for individual firms which reflects the amount of capital injection.
7.2 Estimates of \(\mu \), \(\sigma \) and \(\eta \)
The annualized mean and standard deviation of the difference series \(\{X_t-X_{t-1}\}\) are used as measures of \(\mu \) and \(\sigma \). The cash flow (reserve) process of the portfolio is constructed by \(X_p(t)=\frac{1}{n_t}\sum \nolimits _{i=1}^{n_t}X_i(t)\), and the difference series of reserve \(R_p(t)=X_p(t)-X_p(t-1)\) can be written as
where \(n_t\) is the number of firms at time t, \(R_i(t)=X_i(t)-X_i(t-1)\) and \(X_i(t)\) represents the cash reserve process of the survival firm i. The parameters \(\mu _p\) and \(\sigma _p\) of the portfolio are then obtained from the mean and standard deviation of \(\{R_p(t)\}\). For the capital injection rate \(\eta \), we calculate the annualized rate of the portfolio by summarizing over all injections of each firm in their existing time period.Footnote 8
To illustrate, we use Fannie Mae as a special case as the government bailout program separates it from other firms. The sample period of the Fannie Mae data runs from January 1980 to February 2012. We use the rolling-window method to update estimation over time. In this case, the rolling estimation period runs from January 1980 up to each quarter in the test period, which is from August 2009 to February 2012. We start our test period from August 2009 when Lehman Brothers ran into a serious problem and the crisis escalated. We also conduct tests for the constructed portfolio that includes the group of other firms. For the portfolio test, the rolling estimation period is also from January 1980 up to each month in the test period. But we set the test period from January 2009 to July 2009, which is more relevant for the bailout pattern of this group. As shown in Panel B of Fig. 4, government capital injections into this group of firms are more intensive and largely concentrate in the period from October 2008 to January 2009. As such, we start the test period for this group of firms from January 2009 by allowing a two-month lag to capture the full effect of government bailouts.
7.3 Empirical tests
In this section, using the parameters estimated above, we conduct empirical tests first for Fannie Mae and the constructed portfolio and then use AIG as an additional case to ensure robustness of our test results.
7.3.1 Empirical results for Fannie Mae
On September 7, 2008, the government took over Fannie Mae and Freddie Mac and injected billions of dollars to cover their losses. The Fannie and Freddie bailout is separated from the broader $700 billion bailout known as the TARP. Instead, their bailouts are based on the Housing and Economic Recovery Act of 2008 passed in July 2008.Footnote 9 As the frequency of capital injections is much higher for Fannie Mae than for other firms, we can estimate the injection rate for this firm precisely using its data. Thus, we first select Fannie Mae as an example to verify our model predictions.
As mentioned above, transaction cost data are not available. However, as the economic condition stabilized in the first quarter of 2012, we can posit that the dividend distribution by Fannie Mae is back to normal to back out the implied transaction cost for this firm in this quarter and apply this estimate to other quarters in the sample period. We estimate that the implied dividend transaction cost is 16.3 million for Fannie Mae.
We estimate \(\mu \) and \(\sigma \) of the cash reserve process using the data beginning from January 1980, while for \(\eta \), the data of capital injections is available only from March 2009. As mentioned, we choose the period from August 2009 to February 2012 for empirical tests on Fannie Mae. For each quarter in the test period, all available historical data up to that quarter are used to estimate the parameters of \(\mu \), \(\sigma \) and \(\eta \).
Panel A of Fig. 5 plots the estimates of \(\mu \). As shown, \(\mu \) is not constant and tends to decrease over the sample period. By contrast, the estimate of \(\sigma \) (see Panel B of Fig. 5) is relatively stable and almost flat over the period. The estimated \(\sigma \) is somewhat larger than the estimated \(\mu \) which could be due to the small sample size. For the capital injection rate \(\eta \) (see Panel C of Fig. 5), the largest value occurs in August 2009 and the injection rate decreases henceforth as the market condition improves.
In Panel A–C, the parameters \(\mu \), \(\sigma \) and \(\eta \) are estimated respectively for Fannie Mae. In Panel D, the estimated dividend times (grey bars) are calculated using the parameters of Panels A–C and \(\lambda = 7.75\%\), \(k=85\%\), \(K=0.1\). In Panel D, the vertical axis denotes dividend times and the unit is one day. In addition, in Panel D the black bars denote the actual dividend times in each quarter. In these four panels, all notations on the horizontal axis denote the empirical time duration and its unit is one quarter
Given the parameters in Panels A–C of Fig. 5 and the implied transaction cost, Panel D of Fig. 5 plots the estimated (black bars) and actual (grey bars) dividend payout amounts after capital injections where the dividend amount is in billions. It shows that the differences between actual and estimated dividends are quite small and much lower than the volatility, suggesting that the actual dividends are well within the confidence interval of estimated dividends. Thus, the firm’s dividend policy is fully consistent with rationality implied by the model over the sample period. The results suggest that the dividend behavior is rational not only in normal time but also in the crisis period.
Comparing Panel C with Panel A of Fig. 5, we find that the capital injection rate is always greater than the parameter \(\mu \). That is, the condition of \(\eta >\mu \) is well satisfied, which implies the optimal dividend event should take place shortly after the capital injection. The empirical results thus strongly support the prediction of our theoretical dividend model. The estimated time durations increase from the lowest value (about 7.98 days) in the first quarter to the highest value (about 85.92 days) in the last quarter. Although the actual dividend payment time is somewhat flat due to the fact that dividend payments are regular, they are still within the confidence intervals of the estimates. Moreover, as the optimal estimated dividend time duration is longer, the estimated dividend amounts are also larger, which reflects the accumulation of accrued dividends over time.
7.3.2 Empirical results for AIG
After falling into deep trouble in September 2008, AIG received four bailouts from the US government, totaling over $170 billion. Immediately after receiving $30 billion in bailout funds from the US government on March 3, 2009, on the 15th of the same month AIG announced that it would pay a total of $165 million in bonuses to its financial products department executives, which sparked controversy. The issue of distributing bonuses right after receiving government bailouts has been discussed in detail in Thomas (2009). In this paper, we further employ the AIG case to test the implication of our theoretical model. Specifically, we want to test how quickly a company should distribute dividends or bonuses within a rational framework after receiving a large amount of government relief. To do so, we compare the model prediction with the actual bonus payment pattern of AIG.
To estimate \(\mu \) and \(\sigma \) for AIG, we also use the quarterly cash reserve data from January 1980 to March 2009. For parameter \(\eta \), AIG Company received four government bailouts between September 2008 and March 2009. This means we only have four data points of external capital injections. As the sample size is relatively small, we use these four observations as the training sample to estimate parameter \(\eta \). For other parameters, we use the same method to estimate them as in the Fannie Mae case. Considering that the government bailout funds was distributed out within half a year, in order to calculate the capital injection rate within six months, we reduce the scale of original data by multiplying \(2 * 10^{-10} \). We then obtain the estimated parameters \(\mu = 0.0012\) and \(\eta \) = 17.5335. A shown, \(\eta \) is much greater than \(\mu \). The estimated dividend time is: 0.0208 year, which is equivalent to 7.592 days. It is less than the actual observed dividend (bonus) payment time, which is 12 days after receiving the government bailout grant. As shown, AIG quickly distributed cashes after receiving a large amount of funding. This finding is consistent with the prediction of our rational dividend model that when the capital injection rate is greater than the growth rate of the liquid asset, the firm will distribute cash immediately after receiving the bailout grant.
7.3.3 Empirical results for portfolio
As mentioned earlier, most firms receive government grants only a few times and therefore, it is more efficient to form the portfolio in empirical tests for these firms to accommodate the low frequency in grant offers and achieve a dispersion in data points. As revealed in the data of panel B in Fig. 4, most capital injections fall in the period from October 2008 to July 2009. In order to increase the amount of data for the estimated parameter \(\eta \), we start validating our model at monthly points from January 2009 until July 2009.
We similarly posit that the dividend behavior is rational in the last quarter of the sample period to back out the implied cost of dividends K and use it in empirical tests.Footnote 10 Estimates of \(\mu \), \(\sigma \) and \(\eta \) are displayed in Panels A–C of Fig. 6, respectively. Panel A shows that \(\mu \) estimates are stable over time. Panel B of Fig. 6 shows that the estimated \(\sigma \) values are close to a constant. Panel C of Fig. 6 shows that the estimated capital injection decreases as time goes by. In April 2009, there is no capital injection and therefore, we treat the injection rate as a missing data and no dividend amount is estimated at this time point in Panel D. Comparing Panel A with Panel C of Fig. 6, we find that the inequality \(\eta > \mu \) is well satisfied, that is, the capital injection rates are greater than the parameter \(\mu \). Thus, according to Theorem 5.1, the dividends event should occur shortly after the capital injection.
In Panel A–D, the parameters \(\mu \), \(\sigma \) and \(\eta \), and the estimated and actual dividend time for the constructed portfolio are presented. In Panel D, the grey bars denote the estimated dividend days after capital injections and the black bars denote the actual ones. The unit of time duration on horizontal axis in this figure is one month
Panel D of Fig. 6 plots the estimated and actual dividend times represented by grey bars and black bars, respectively. In this panel, the estimated dividend time represents the expected number of days following the capital injection in each month. The actual dividend time is the observed dividend day after the capital injection in each month. The dividend payment day in this panel is mostly no more than 6 days after the capital injection, which is quite short and consistent with the model’s prediction of immediate dividend distribution if the capital injection rate is greater than average growth rate of the firm’s cash reserve. It appears that large capital injections by the US government are the main cause for dividend payments during the crisis period. Importantly, our results show that the estimated dividend time is quite close to the actual dividend payment time with the largest prediction error of only 1.5 days, which is economically insignificant. The results suggest that the dividend behavior of firms on the bailout program is rational and consistent with shareholder value maximization. Thus, the dividend distribution during the subprime crisis period does not appear to be an anomaly. Instead, the dividend payout pattern is consistent with the optimal dividend policy predicted by our dynamic optimization model with nonterminal bankruptcy and capital injections.
8 Conclusion
In this paper, we propose a stochastic dynamic dividend model with nonterminal bankruptcy and a positive residual value when a firm goes bankrupt. The model generates the optimal dividend strategies under capital injections. We derive the sufficient and necessary condition for dividend payout in the case that firms have a positive residual value at the bankruptcy state and can be revived by capital infusion. Numerical simulations and empirical test are used to verify the model prediction.
We use the model to evaluate the dividend behavior of firms receiving the bailout money during the financial crisis. We find that the dividend decisions for firms receiving government bailout money are consistent with the principle of shareholder value maximization. By paying dividends, banks and insurance companies send out a signal that they have the ability to survive, and increase the confidence of short-term creditors to prevent a run. Paying dividends during the crisis period is also consistent with the contention that the firms’ opportunity cost of dividend payout is low at a time when the investment opportunity is meager and the government support is generous. In this circumstance, our model predicts that firms will be prone to pay dividends because the bailout grant results in excess cash flow. This prediction is consistent with the traditional dividend model of free cash flow Jensen 1986. A policy implication generated from the model is that the government can prevent firms from distributing dividends by lowering the amount of capital injection to avoid excess (free) cash inflow to these firms or imposing a sufficient penalty to increase the cost of their dividend payments.
Notes
For example, a diffusion model with random returns has been considered in Sethi and Taksar (2002) for a company that can issue new equity when the surplus becomes negative. Along a similar line, Kulenko and Schimidli (2008), Yao et al. (2011) and Jin and Yin (2013) analyze the optimal dividend problem with capital injections and derive closed-form solutions.
For example, given the too-big-to-fail attitude held by the government, the government did not let big financial companies fail during the financial crisis because it can have huge consequences on the economy. While some monoline insurance companies and regional banks were allowed to bankrupt during the subprime crisis, they were liquidated with residual values distributed to stockholders.
The estimation of these parameters is discussed in Sect. 7. Here, \(1-k_0\) is the tax rate and \(K_0\) is the transaction cost of dividends.
In this and next section, the unit of dividend time we use is a day.
Paying dividends more quickly sends out a signal that firms have the ability to survive, thereby increasing the confidence of short-term creditors.
We normalize the scale of raw data to increase the precision of dividend time and amount estimates in empirical tests.
See bailout for Fannie Mae on website: https://projects.propublica.org.
This is the last quarter in which bailout data are available and represents the best choice for estimating the implied cost of dividends.
References
Acharya VV, Gujral I, Kulkarni N, Shin HS (2012) Dividends and bank capital in the financial crisis of 2007–2009. Working Paper
Acharya VV, Mehran H, Thakor A (2016) Caught between Scylla and Charybdis? Regulating bank leverage when there is rent seeking and risk taking. Rev Corpo Finance Stud 5:36–75
Acharya VV, Le HT, Shin HS (2017) Bank capital and dividend externalities. Rev Financ Stud 30:988–1018
Amberger HJ (2023) Volatility of tax payments and dividend payouts. Contemp Account Rev 40:451–487
An Z, Gao W, Li D, Ye D (2022) Dividend payouts, cash-flow uncertainty and the role of institutions. J Bus Account Finance 49:1356–1390
Asmussen S, Taksar M (1997) Controlled diffusion models for optimal dividend payout. Insurance Math Econ 20:1–15
Avanzi B, Wong B (2012) On a mean reverting dividend strategy with Brownian motion. Insurance Math Econ 51:229–238
Aziz N, Hossain B, Lamb L (2022) Does green policy pay dividends? Environ Econ Policy Stud 24:147–172
Baker M, Mendel B, Wurgler J (2016) Dividends as reference points: a behavioral signaling approach. Rev Financ Stud 29:697–738
Belhaj M (2010) Optimal dividend payments when cash reserves follow a jump-diffusion process. Math Finance 20:313–325
Bhattacharya S (1979) Imperfect information, dividend policy, and “the bird in the hand’’ fallacy. Bell J Econ 10:259–270
Cadenillas A, Choulli T, Taksar M, Zhang L (2006) Classical and impulse stochastic control for the optimization of the dividend and risk policies of an insurance firm. Math Finance 16:181–202
Chen B, Chen H, Chen H, Lin F (2022) Corporate growth and strategic payout policy. Rev Quant Finance Account 59:641–669
Chen P, Li B (2017) Classical and impulse stochastic control on the optimization of dividends with residual capital at bankruptcy. Discrete Dyn Nat Soc 2017, Article ID 2693568
Corgnet B, Deck C, DeSantis M, Hampton K, Kimbroughe EO (2023) When do security markets aggregate dispersed information. Manag Sci 69:3697–3729
Cziraki P, Laux C, Loranth G (2016) Bank payout policy, performance, and insider trading in the financial crisis of 2007–2009. Mimeo, New York
de Finetti B (1957) Su un’impostazione alternativa dell teoria collectiva del rischio. In: Transactions of the 15th International Congress of Actuaries. New York vol 2, pp 433–443
Floyd E, Li E, Skinner DJ (2015) Payout policy through the financial crisis: the growth of repurchases and the resilience of dividends. J Financ Econ 118:299–316
Guttman I, Kadan O, Kandel E (2010) Dividend stickiness and strategic pooling. Rev Financ Stud 23:4455–4495
Hausch DB, Seward JK (1993) Signaling with dividends and share repurchases: a choice between deterministic and stochastic cash disbursements. Rev Financ Stud 6:121–154
Hirtle B (2014) Bank holding company dividends and repurchases during the financial crisis. FRB of New York Staff Report
Højgaard B, Taksar M (1998) Optimal proportional reinsurance policies for diffusion models with transaction costs. Insurance Math Econ 22:41–51
Højgaard B, Taksar M (1998) Optimal proportional reinsurance policies for diffusion models. Scand Actuar J 2:166–168
Jacob M, Michaely R (2017) Taxation and dividend policy: the muting effect of agency issues and shareholder conflicts. Rev Financ Stud 30:3176–3222
Jensen MC (1986) Agency costs of free cash flow, corporate finance, and takeovers. Am Econ Rev 76:323–329
Jin Z, Yin G (2013) An optimal dividend policy with delayed capital injections. Aust N Z Ind Appl Math J 55:129–150
John K, Williams J (1985) Dividends, dilution, and taxes: a signalling equilibrium. J Finance 40:1053–1070
Juelsrud RE, Nenov PT (2020) Dividend payouts and rollover crises. Rev Financ Stud 33:4139–4185
Karlin S, Taylor HM (1975) A first course in stochastic processes. Academic Press, New York
Karlin S, Taylor HM (1981) A second course in stochastic processes. Academic Press, New York
Kulenko N, Schimidli H (2008) Optimal dividend strategies in a Cramer–Lundberg model with capital injections. Insurance Math Econ 43:270–278
Lindensjö K, Lindskog F (2020) Optimal dividends and capital injection under dividend restrictions. Math Methods Oper Res 92(3):461–487
Mazouz K, Mazouz K, Wu Y, Rabab E, Sharma A (2023) Dividend policy, systematic liquidity risk, and the cost of equity capital. Rev Quant Finance Account 60:839–876
Merton R (1990) Continuous-time finance. Blackwell Publishers, Oxford
Miller MH, Modigliani F (1961) Dividend policy, growth, and the valuation of shares. J Bus 34:411–433
Miller MH, Rock K (1985) Dividend policy under asymmetric information. J Finance 40:1031–1051
Paulsen J (2007) Optimal dividend payments until ruin of diffusion processes when payments are subject to both fixed and proportional costs. Adv Appl Probab 39:669–689
Paulsen J (2008) Optimal dividend payments and reinvestments of diffusion process with both fixed and proportional costs. SIAM J Control Optim 47:2201–2226
Radner R, Shepp L (1996) Risk versus profit potential: a model for corporate strategy. J Econ Dyn Control 20:1373–1393
Rubio G, Jakob K, Castillo A, Niño J (2023) Why do firms heap dividends? New evidence on the key role of firm characteristics. J Corp Account Finance 34:80–95
Sethi SP, Taksar M (2002) Optimal financing of a corporation subject to random returns. Math Finance 12:155–172
Sethi SP, Derzko NA, Lehoczky J (1984) General solution of the stochastic price-dividend integral equation: a theory of financial valuation. SIAM J Math Anal 15:1100–1113
Sikalidis A, Bozos K, Chantziaras A, Grose C (2022) Influences of family ownership on dividend policy under mandatory dividend rules. Rev Quant Finance Account 59:939–967
Tayachi T (2023) How does ownership structure affect the financing and dividend decisions of firm? J Financ Report Account 21:729–746
Thomas TA (2009) Bailouts, Bonuses, and the Return of Unjust Gains. Comments, Washington University-St. Louis, 2009, U of Akron Legal Studies Research Paper No. 09-14. (Available at SSRN: https://ssrn.com/abstract=1549913)
Wang W, Zhang C (2010) Optimal dividend strategies in the diffusion model with stochastic return on investments. J Syst Sci Complex 23:1071–1085
Wang Y, Li M, Kamar A (2022) Environmental concerns and impression offsetting: new evidence on dividend payout. Financ Mark Inst Instrum 31:87–118
Yao D, Yang H, Wang R (2011) Optimal dividend and capital injection problem in the dual model with proportional and fixed transaction costs. Eur J Oper Res 211:568–576
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Some properties of the optimal control function
1.1 A.1. Estimate parameter C
In the optimal policies of (56) and (57), the parameter C is an unknown parameter. In the real practical problems, we need to determine it.
1.1.1 A.1.1. Steps for computing parameter C
For the nonterminal model, we assume that the parameters \(\mu \), \(\sigma \), k, K and \(\eta \) are known already. Then, the steps to compute C are given as follows.
-
Step 1.
Compare \(\eta \) with \(\frac{\mu }{2} \).
-
Step 2.
If \(0\le \eta <\frac{\mu }{2}\), using the bisection method or Newton method to calculate C such that \(I_1(C)=K\).
-
Step 3.
If \(\eta \ge \frac{\mu }{2}\), using the bisection method or Newton method to calculate C such that \(I_2(C)=K\).
By these steps, the uncertain parameter C can be obtained. Meanwhile, we can get other parameters, such as \(x_1^C\) and \(\widetilde{x}^{C}\), which are the left and right roots of equation \(CH_1(x)=k\) or \(CH_2(x)=k\), respectively.
Appendix B: Property of dividend events
1.1 B.1. Expected first dividend times after capital injections
Let \(\phi _{x_1}(x)\) and \(\psi _{0,x_1}(x)\) be defined as in (61) and (62) respectively, then the expected time \(\psi _0^{x_1}(x)\) first reaches \(x_1\) can be given by
Proof
As in Chapter 15 of Karlin and Taylor (1981), the equations satisfied by \(\phi _{x_1}(x)\) and \(\psi _{0,x_1}(x)\) for \(x\in (0, x_1)\) can be presented as,
and
respectively.
To solve these two equations above, we define the function \(s:(0,\infty )\rightarrow [0,\infty )\) by
the function \(S:(0,\infty )\rightarrow [0,\infty )\) by
and the function \(m:(0,\infty )\rightarrow [0,\infty )\) by
Then, by the similar method of Karlin and Taylor (1981), it follows that
For \(x\in (0, x_0^+]\), let
for \(x\in [x_0^+,x_1]\), let
for \(x\in (0,x_0^+]\), let
for \(x\in [x_0^+,x_1]\), let
Then, by the formula as in Chapter 15 of Karlin and Taylor (1981), \(\psi _{0,x_1}(x)\) can be obtained as
Let \(\psi _{x_1}(x)\) be the expected time for both processes, which reach the boundary \(x_1\) prior to 0. Meanwhile, for \(\psi _0(x)\), it denotes the expected time the processes reach 0 prior to \(x_1\). Then we have
For the processes defined in (59) and (60), both of them have positive probability to reach zero points. But if the zero points are touched, then some capitals from outside will be injected to save the company. So, the expected time \(\psi _0^{x_1}(x)\) for both processes, which finally reach the bound \(x_1\), even they reach the lower bound 0 first, is complicated to calculate. If the process starting from bankruptcy state, then after a huge capital injection it would recover to the position x in a stochastic time period \(\tau _s\), which is assumed to be a random variable with small mean and in simplification be neglected in our simulation examples. So, it follows that
From (64) and (65), we have that
So, the closed form of \(\psi _0^{x_1}(x)\) is obtained. \(\square \)
1.2 B.2. Variance of \(\tau _{x_1}^*\)
Before X(t) reaches the upper boundary \(x_1\), it may arrive at the lower boundary 0 first, and in this case we assume that the process X(t) would rebound to the original position x in a negligible time after bailouts. Similar to (64), it follows that
Then, we have that
Consequently,
To derive \(E_x(\tau _{0, x_1}^2)\), let \(U(x) = E_x(\tau _{0, x_1}^2)\), then as in Chapter 15 of Karlin and Taylor (1981), the function U(x) satisfies
As in Appendix B.1, the solution of the equation above can be derived and given as follows
where \(\phi _{x_1}(x)\), S(t), m(t) and \(\psi _{0, x_1}(t)\) are presented in Appendix B.1 and we don’t list them out again. Then the variance of \(\tau _{x_1}^*\) can be obtained from (66) and
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhang, S., Chen, P. & Wu, C. Optimal dividend decisions with capital infusion in a dynamic nonterminal bankruptcy model. Rev Quant Finan Acc 62, 911–951 (2024). https://doi.org/10.1007/s11156-023-01229-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11156-023-01229-1