1 Introduction

Vector control based on a PI controller is widely used in wind power generation systems to realize maximum power point tracking (MPPT) [1,2,3]. It is a passive way to eliminate errors based on error feedback, which lags behind the influence of a disturbance [4]. It may cause serious overshoot of the system due to an excessive initial control force, and fall into a contradiction between 'rapidity' and 'overshoot' [5, 6]. In wind power generation, it is necessary for the speed to track a given value quickly to ensure that the unit runs at the maximum power point. The speed tracking dynamic process of PI controllers is slow, which reduces the power generation efficiency [7,8,9]. In addition, PI controllers rely on an accurate mathematical model of a system, which it is often difficult. Therefore, its robustness is poor and it is prone to saturation. These factors make it difficult for PI controllers to achieve the desired effect [10,11,12]. Therefore, a number of scholars have introduced many nonlinear control algorithms in systems, among which the active disturbance rejection control (ADRC) algorithm has outstanding effects [13,14,15,16].

In recent years, the ADRC algorithm has had some good research results in the control systems of permanent magnet synchronous motors (PMSMs) [17,18,19]. In [20], LADRC was designed for the speed loop control of a PMSM. The results show that when compared with a PI controller, this method has better control performance, can achieve zero overshoot startup, and has strong anti-load disturbance capability. In [21], ADRC and passive control were used to form a double closed loop system that controls the speed and current loop, respectively. Thus, the control system has good dynamic performance and robustness. In [22], based on the traditional speed loop ADRC, a model-assisted ADRC controller was designed to improve the response speed of a system. Based on this model, a speed observer was designed. This composite control scheme significantly improved the control performance and anti-interference capability. In addition, the difficulty in terms of the parameter tuning of ADRC has always been an important reason that hinders its development. Most of literature on the subject has not specifically analyzed its tuning method. The second-order nonlinear active disturbance rejection control (NLADRC) mathematical model of a PMSM speed control system was established in [23]. With the help of the frequency domain method and a large quantity of system simulation data, by comparing and analyzing the influence of parameter changes on system performance, the physical meaning and tuning direction for each of the parameters are summarized. To sum up, although there have been many ADRC studies on PMSM control systems, there are few ADRC studies for permanent magnet synchronous wind power generation systems. In particular, reports on current loop ADRC are relatively rare [24].

In this paper, a speed loop FLADRC controller is established to speed up the dynamic process of speed tracking and to improve the generating efficiency of the unit. Then on the basis of the traditional FLADRC, after considering the influence of the inverter, the control object is re-modeled, and the second-order current state equation is obtained to build a new SLADRC, which effectively improves the anti-disturbance capability of the system. In addition, a convergence analysis of the newly designed controller and the control parameter configuration method are given. The proposed method can operate stably under all of the working conditions of a PMSG. In addition, it has a better performance improvement when compared with PI controllers, which makes it significant for engineering applications.

2 PMSG mathematical model

A PMSG is a high-order coupling and nonlinear system. To simplify the modeling process, the following assumptions are made [17].

  1. 1.

    The magnetic circuit saturation, core loss, hysteresis loss, and eddy current loss are ignored.

  2. 2.

    The three-phase stator windings are symmetrical, and the magnetic field is sinusoidal in space, when ignoring the space high-order harmonics.

  3. 3.

    The influences of frequency, temperature, and other changes on the motor parameters are not considered.

Under the synchronous rotation \(dq\) coordinate system, the voltage equation is:

$$\left[ {\begin{array}{*{20}c} {u_{d} } \\ {u_{q} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} R & 0 \\ 0 & R \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d} } \\ {i_{q} } \\ \end{array} } \right] + \frac{{\text{d}}}{{{\text{d}}t}}\left[ {\begin{array}{*{20}c} {\psi_{d} } \\ {\psi_{q} } \\ \end{array} } \right] + \omega_{{\text{e}}} \left[ {\begin{array}{*{20}c} { - \psi_{q} } \\ {\psi_{d} } \\ \end{array} } \right]$$
(1)

The flux linkage equation is:

$$\left[ {\begin{array}{*{20}c} {\psi_{d} } \\ {\psi_{q} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {L_{d} } & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & {L_{q} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{d} } \\ {i_{q} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\psi_{{\text{f}}} } \\ 0 \\ \end{array} } \right]$$
(2)

The electromagnetic torque equation is:

$$T_{{\text{e}}} = 1.5n_{{\text{p}}} \left( {\psi_{d} i_{q} - \psi_{q} i_{d} } \right),$$
(3)

where \(u_{d}\) and \(u_{q}\) are the components of the stator voltage vector in the \(d\)-axis and \(q\)-axis (V); \(i_{d}\) and \(i_{q}\) are the components of the stator current vector in the \(d\)-axis and \(q\)-axis (A); \(\psi_{d}\) and \(\psi_{q}\) are the components of the stator flux vector in the \(d\)-axis and \(q\)-axis (Wb); \(R\) is the stator winding resistance (Ω); and \(\omega_{{\text{e}}}\) is the electrical angular velocity of the generator (rad/s). \(L_{d}\) and \(L_{q}\) are the inductance components of the \(d\)-axis and \(q\)-axis (H), and they are both equal; \(\psi_{{\text{f}}}\) is the flux linkage of the permanent magnet (Wb); \(n_{{\text{p}}}\) is the polar logarithm; and \(T_{{\text{e}}}\) is the electromagnetic torque (N m).

In the synchronous rotating coordinate system, the equation coefficients are constant, and the physical quantities are also direct flow, which is convenient for the design of the control scheme.

3 LADRC design

3.1 FLADRC speed loop design

The motion equation of PMSG is:

$$Jp\omega_{m} = T_{{\text{e}}} - T_{{\text{L}}} - B\omega_{m} ,$$
(4)

where \(J\) is the moment of inertia (kg m2); \(p\) is the differential factor; \(T_{L}\) is the load torque of the motor (N m); and \(B\) is the damping coefficient.

According to Eq. (4), the FLADRC design process is as follows [25]:

① Linear tracking differentiator (LTD): To solve the contradiction between the speed and overshoot in a PI regulator, the following transition process is arranged for the reference signal using a tracking differentiator:

$$\left\{ \begin{gathered} e_{1} = v_{1} - \omega_{m}^{*} \hfill \\ \dot{v}_{1} = - re_{1} \hfill \\ \end{gathered} \right.,$$
(5)

where \(\omega_{m}^{*}\) is the speed reference value; and \(v_{1}\) is the speed value of the LTD output. In this paper, \(\dot{x}\) represents the derivative of \(x\), where \(x\) represents any variable. In addition, \(e_{1}\) is the error between \(\omega_{m}^{*}\) and \(v_{1}\); \(r\) is the speed factor, and its size affects the speed of tracking a given value. The larger the value, the faster the tracking speed. However, it should also be noted that if the value is too large, the transition effect is lost.

② Linear extended state observer (LESO): A PMSG generally uses \(i_{d}^{*} = 0\), which is substituted into Eqs. (2) and (3) to obtain:

$$T_{{\text{e}}} = 1.5n_{{\text{p}}} \psi_{{\text{f}}} i_{q}$$
(6)

Combining Eqs. (6) and (4), the motion equation is rewritten as follows:

$$\dot{\omega }_{m} = f_{\omega } + b_{\omega } i_{q} ,$$
(7)

where \(\omega_{m}\) and \(i_{q}\) are the input and output of the LESO respectively. In addition, \(b_{\omega }\) is the current proportional coefficient, which is partially known; \(f_{\omega }\) is the total disturbance of the speed loop, and \(f_{\omega } = \frac{1}{J}\left( {1.5n_{p} i_{q} \psi_{{\text{f}}} - T_{{\text{L}}} - B\omega_{m} } \right) - b_{\omega } i_{q}\).

From Eq. (7), it can be seen that the speed loop is a first-order system. Thus, it is necessary to design a second-order LESO to observe the state variables and disturbance variables. The following state variables are selected \(x_{1} = \omega_{m}\), \(x_{2} = f_{\omega }\), \(y_{1}\) as output variables. Then the extended state equation expression is:

$$\left\{ \begin{gathered} \dot{x}_{1} = x_{2} + b_{\omega } i_{q} \hfill \\ \dot{x}_{2} = \dot{f}_{\omega } \hfill \\ y_{1} = x_{1} \hfill \\ \end{gathered} \right.$$
(8)

According to this new expansion system, the following LESO can be designed:

$$\left\{ \begin{gathered} e_{2} = z_{1} - \omega_{m} \hfill \\ \dot{z}_{1} = z_{2} - \beta_{\omega 1} e + b_{\omega } i_{q} \hfill \\ \dot{z}_{2} = - \beta_{\omega 2} e \hfill \\ \end{gathered} \right.,$$
(9)

where \(e_{2}\) is the error between the real speed and the estimated speed; \(z_{1}\) is used to estimate the value of \(\omega_{m}\), which performs certain denoising processing and tracking; \(z_{2}\) is used to estimate the value of the total disturbance; and \(\beta_{\omega 1} ,\;\beta_{\omega 2}\) is the output error correction gain.

③ Linear state error feedback (LSEF): This primarily controls the reference input and error feedback, and counteracts disturbances.

Proportional control can be used in a simple first-order LADRC. Thus:

$$u_{01} = k_{p\omega } \left( {v_{1} - z_{1} } \right),$$
(10)

where \(k_{p\omega }\) is the control parameter, and \(u_{01}\) is the equivalent control quantity.

Then the estimated disturbance is compensated to obtain the output \(u_{1}\) of the speed LADRC. That is:

$$u_{1} = \frac{1}{{b_{\omega } }}\left( {u_{01} - z_{2} } \right)$$
(11)

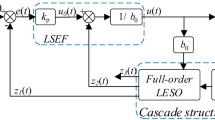
A speed loop LADRC structure diagram is shown in Fig. 1.

Fig. 1
figure 1

FLADRC control block diagram of the PMSG speed loop

Full size image

3.2 FLADRC current loop design

Taking the \(q\)-axis current loop as an example, the current loop LADRC is designed. The current state equation obtained from Eqs. (1) and (2) is:

$$\dot{i}_{q} = \frac{1}{{L_{q} }}\left[ {u_{q} - Ri_{q} - \omega_{r} \left( {L_{d} i_{d} + \psi_{{\text{f}}} } \right)} \right],$$
(12)

where \(i_{q}\) and \(u_{q}\) are the input and output of LADRC respectively. \(b_{q}\) is the q-axis voltage proportional coefficient, \(f_{q}\) is the total disturbance quantity, and \(f_{q} = \frac{1}{{L_{q} }}\left[ {u_{q} - Ri_{q} - \omega_{r} \left( {L_{d} i_{d} + \psi_{f} } \right)} \right] - b_{q} u_{q}\). Then the \(q\)-axis current state equation is rewritten as:

$$\dot{i}_{q} = f_{q} + b_{q} u_{q}$$
(13)

Since the current loop requires a fast response, a transition process is not set here for the current reference. The \(d\)-axis reference current is 0, and the q-axis reference current is generated by the speed loop controller.

The following state variables are selected \(x_{3} = i_{q}\) and \(x_{4} = f_{q}\). The current loop expansion state equation is:

$$\left\{ \begin{gathered} \dot{x}_{3} = x_{4} { + }b_{q} u_{q} \hfill \\ \dot{x}_{4} = \dot{f}_{q} \hfill \\ y_{2} = x_{3} \hfill \\ \end{gathered} \right.$$
(14)

In terms of the LADRC design scheme of the speed ring, the specific design process is not described here. The \(q\)-axis LADRC discrete equation of the current loop can be summarized as follows:

$$\left\{ \begin{gathered} e_{3} = z_{3} - i_{q} \hfill \\ \dot{z}_{3} = z_{4} - \beta_{q1} e_{3} + b_{q} u_{q} \hfill \\ \dot{z}_{4} = - \beta_{q2} e_{3} \hfill \\ u_{02} = k_{pq} \left( {i_{q}^{*} - z_{3} } \right) \hfill \\ u_{2} = \frac{1}{{b_{q} }}\left( {u_{02} - z_{4} } \right) \hfill \\ \end{gathered} \right.,$$
(15)

where \(e_{3}\) is the error between the \(q\)-axis real current and the estimated current; \(z_{3}\) is used to estimate the value of \(i_{q}\), which performs certain denoising processing and tracking; \(z_{4}\) is used to estimate the value of the total disturbance; and \(\beta_{q1} ,\beta_{q2}\) is the output error correction gain. In addition, \(k_{pq}\) is the control parameter; \(u_{02}\) is the equivalent control quantity; \(u_{2}\) is the output of the current LADRC.

Similarly, the current loop LADRC discrete equation of the \(d\)-axis can be obtained, which is given as follows:

$$\left\{ \begin{gathered} e_{4} = z_{5} - i_{d} \hfill \\ \dot{z}_{5} = z_{6} - \beta_{d1} e_{4} + b_{d} u_{d} \hfill \\ \dot{z}_{6} = - \beta_{d2} e_{4} \hfill \\ u_{03} = k_{pd} \left( {i_{d}^{*} - z_{5} } \right) \hfill \\ u_{3} = \frac{1}{{b_{d} }}\left( {u_{03} - z_{6} } \right) \hfill \\ \end{gathered} \right.,$$
(16)

where \(e_{4}\) is the error between the d-axis real current and the estimated current; \(z_{5}\) is used to estimate the value of \(i_{d}\), which performs certain denoising processing and tracking; \(z_{6}\) is used to estimate the value of the total disturbance; and \(\beta_{d1} ,\beta_{d2}\) is the output error correction gain. In addition, \(k_{pd}\) is the control parameter; \(u_{03}\) is the equivalent control quantity; and \(u_{3}\) is the output of the current LADRC.

3.3 SLADRC design considering the influence of the converter

Equation (1) is rewritten into vector matrix form:

$${\mathbf{u}} = R{\mathbf{i}} + L{\dot{\mathbf{i}}} + \Delta {\mathbf{u}},$$
(17)

where \({\mathbf{i}} = \left[ {i_{d} ,i_{q} } \right]^{{\text{T}}}\) and \({\mathbf{u}} = \left[ {u_{d} ,u_{q} } \right]^{{\text{T}}}\) are the stator current and voltage vector matrices of the PMSG; \({\dot{\mathbf{x}}}\) denotes the first derivative of any vector matrix \({\mathbf{x}}\); \({\mathbf{\ddot{x}}}\) represents the second derivative of the corresponding vector matrix \({\mathbf{x}}\); and \(\Delta {\mathbf{u}} = \left[ {\Delta u_{d} ,\Delta u_{q} } \right]\) is the cross-coupling term of the PMSG, where \(\Delta u_{d} { = } - \omega_{r} L_{q} i_{q}\) and \(\Delta u_{q} = \omega_{r} \left( {L_{d} i_{d} + \psi_{f} } \right)\).

Equation (17) only reflects the characteristics of the motor itself. It also considers that the output voltage of the current loop is the stator voltage of the PMSG, without considering the influence of the nonlinearity of the converter on the control system. In this paper, the motor and converter are the object of mathematical modeling. In the new control system, the current loop outputs the voltage value through the converter to the motor stator. The transfer function of the converter is generally considered to be [26]:

$$\frac{{{\mathbf{u}}\left( s \right)}}{{{\mathbf{u}}_{{{\text{inv}}}} \left( s \right)}} = G_{{{\text{inv}}}} \left( s \right) = \frac{1}{{T_{{{\text{inv}}}} s + 1}},$$
(18)

where \(T_{inv}\) is the control cycle of the converter, and \({\mathbf{u}}_{{{\text{inv}}}} = \left[ {u_{{d{\text{inv}}}} ,u_{{q{\text{inv}}}} } \right]^{{\text{T}}}\) is the value of the output from the current loop to the converter.

Equation (18) is rewritten into differential equation form as follows:

$${\mathbf{u}}_{{{\text{inv}}}} = T_{{{\text{inv}}}} {\dot{\mathbf{u}}} + {\mathbf{u}}$$
(19)

Combining Eqs. (17) and (19), a new voltage equation is obtained:

$${\mathbf{u}}_{{{\text{inv}}}} = R{\mathbf{i}} + \left( {T_{{{\text{inv}}}} R + L} \right){\dot{\mathbf{i}}} + T_{{{\text{inv}}}} L{\mathbf{\ddot{i}}} + \left( {T_{{{\text{inv}}}} \Delta {\dot{\mathbf{u}}} + \Delta {\mathbf{u}}} \right)$$
(20)

It can be seen from Eq. (20) that the current state equation becomes a second-order system. Thus, a SLADRC control system needs to be constructed to meet the control requirements.

The specific design process of the SLADRC is divided into three main parts, as described below.

① Design a third-order linear extended state observer (TLESO): Taking the \(q\)-axis current loop as an example, it is necessary to rewrite Eq. (20) into a current state equation. Selecting \(x_{5} = i_{q}\), \(x_{6} = \dot{i}_{q}\) and \(x_{7} = f_{qs}\) as state variables, the expansion current state equation can be expressed as:

$$\left\{ \begin{gathered} \dot{x}_{5} = x_{6} \hfill \\ \dot{x}_{6} = x_{7} + b_{qs} u_{q} \hfill \\ \dot{x}_{7} = \dot{f}_{qs} \hfill \\ y_{3} = x_{5} \hfill \\ \end{gathered} \right.,$$
(21)

where \(b_{qs} \approx {1 \mathord{\left/ {\vphantom {1 {T_{{{\text{inv}}}} L_{q} }}} \right. \kern-0pt} {T_{{{\text{inv}}}} L_{q} }}\) is the voltage proportional coefficient, \(u_{q}\) is the output of SLADRC, and the total disturbance \(f_{qs}\) includes the external disturbance, the internal uncertainty disturbance, and \(- \frac{1}{{T_{{{\text{inv}}}} L_{q} }}\left[ {Ri_{q} + \left( {T_{{{\text{inv}}}} R + L_{q} } \right)\dot{i} + \left( {T_{{{\text{inv}}}} \Delta \dot{u}_{q} + \Delta u_{q} } \right)} \right]\).

From the above expansion of the current state equation, the discrete TLESO can be designed by the forward Euler discretization method:

$$\left\{ \begin{gathered} e_{5} \left( k \right) = z_{7} \left( k \right) - y_{3} \left( k \right) \hfill \\ z_{7} \left( {k + 1} \right) = z_{7} \left( k \right) + h\left[ {z_{8} \left( k \right) - \beta_{qs1} e_{5} \left( k \right)} \right] \hfill \\ z_{8} \left( {k + 1} \right) = z_{8} \left( k \right) + h\left[ {z_{9} \left( k \right) - \beta_{qs2} e_{5} \left( k \right) + bu_{q} \left( k \right)} \right] \hfill \\ z_{9} \left( {k + 1} \right) = z_{9} \left( k \right) - h\beta_{qs3} e_{5} \left( k \right) \hfill \\ \end{gathered} \right.,$$
(22)

where \(z_{7} \left( k \right)\), \(z_{8} \left( k \right)\),\(z_{9} \left( k \right)\), and \(y_{3} \left( k \right)\) are the observed variables of TLESO, which corresponding to the discretization of \(x_{5}\),\(x_{6}\),\(x_{7}\), and \(y_{3}\), respectively. In addition, \(h\) is the integral step length; \(\beta_{qs1} ,\beta_{qs2} ,\beta_{qs3}\) is the output error correction gain. With the proper selection of the correction gain, TLESO can better estimate the state variables of the system.

The extended state variable \(z_{9}\) contains the internal uncertainties and external disturbances of the system. If \(z_{9}\) is compensated to the control system, the nonlinear and uncertain original system can be simplified to an integral series structure, which realizes the linearization and determinacy of the system.

② Convergence analysis of TLESO [27, 28]

Rewrite the continuous equation matrix of TLESO:

$$\left\{ \begin{gathered} e_{5} = \hat{y}_{3} - y_{3} \hfill \\ \dot{\user2{z}} = {\varvec{Az}} + {\varvec{B}}u + {\varvec{E}}\dot{f}_{qs} + {\varvec{L}}e_{5} \hfill \\ \hat{y}_{3} = {\varvec{Cz}} \hfill \\ \end{gathered} \right.,$$
(23)

where \({\varvec{z}} = \left[ {z_{7} ,z_{8} ,z_{9} } \right]^{{\text{T}}}\), \({\varvec{A}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array} } \right]\), \({\varvec{B}} = \left[ {0,b,0} \right]^{{\text{T}}}\),\({\varvec{E}} = \left[ {0,0,1} \right]^{{\text{T}}}\), \({\varvec{C}} = \left[ {1,0,0} \right]\), and \({\varvec{L}} = \left[ {\beta_{qs1} ,\beta_{qs2} ,\beta_{qs3} } \right]^{{\text{T}}}\).

In Eq. (23), the total disturbance term \(f_{qs}\) is unknown, and is estimated by the expansion state variable and compensated in the control system. Therefore, it can be omitted when calculating the transfer function. The three equations in Eq. (23) are rewritten as:

$$\left\{ \begin{gathered} \dot{\user2{z}} = \left[ {{\varvec{A}} - {\varvec{LC}}} \right]{\varvec{z}} + \left[ {{\varvec{B}},{\varvec{L}}} \right]{\varvec{u}}_{{\text{c}}} \hfill \\ {\varvec{y}}_{{\text{c}}} = {\varvec{z}} \hfill \\ \end{gathered} \right.,$$
(24)

where \({\varvec{u}}_{{\text{c}}} = \left[ {u,y} \right]^{{\text{T}}}\) is the combined input, and \({\varvec{y}}_{{\text{c}}}\) is the output.

According to Eq. (24), the TLESO transfer function can be obtained:

$$G\left( s \right) = \frac{{\left[ {{\varvec{B}},{\varvec{L}}} \right]}}{{s{\varvec{I}} - \left( {\user2{\rm A} - {\varvec{LC}}} \right)}}$$
(25)

The characteristic equation of the observer is obtained as:

$$\lambda_{1} \left( s \right) = \left| {s{\varvec{I}} - \left( {{\varvec{A}} - {\varvec{LC}}} \right)} \right|{ = }s^{3} + \beta_{qs1} s^{2} + \beta_{qs2} s + \beta_{qs3}$$
(26)

The necessary condition for the stability of the observer is that the eigenvalues of Eq. (26) are in the left half plane of the \(s\) domain. In addition, the above conditions can be satisfied by selecting an appropriate observer gain. To facilitate the design of the controller parameters, the eigenvalues of the characteristic equation are placed in the same position \(s = - \omega_{o}\), where \(\omega_{o}\) is the observer bandwidth, and the correction gain is \(\left[ {\beta_{qs1} ,\beta_{qs2} ,\beta_{qs3} } \right] = \left[ {3\omega_{o} ,3\omega_{o}^{2} ,\omega_{o}^{3} } \right]\). At this time, the output error correction gain is only related to the observer bandwidth, which makes the TLESO design simpler.

③ Design the second-order linear state error feedback (SLSEF): The SLSEF is designed by a classical PID combination. The TLESO can estimate the total disturbance to make up for the system error. Therefore, the integral link used to eliminate the static error in the PID combination can be omitted, and the SLSEF can be further simplified into the PD combination control as follows:

$$u_{04} = k_{pqs} \left( {i_{q}^{*} - z_{7} } \right) - k_{dqs} z_{8}$$
(27)

In this equation, \(k_{pqs}\) and \(k_{dqs}\) are the amplification coefficients of the proportional and differential links, respectively.

Finally, the estimated value of the disturbance is compensated at the control input:

$$u_{4} = \frac{1}{{b_{qs} }}\left( {u_{04} - z_{9} } \right)$$
(28)

The parameter design process in Eq. (27) is as follows.

From the above SLADRC design process, the second-order state equation of the control system can be expressed as:

$$\ddot{y}_{3} = f_{qs} + b_{qs} u_{4}$$
(29)

If the TLESO can track the state variables accurately, Eq. (28) is substituted into Eq. (29) and the estimation error of the disturbance is ignored. Then:

$$\ddot{y}_{3} = f - z_{9} + u_{04} \approx u_{04}$$
(30)

At this time, the control system is simplified to a double integral series structure. Substituting Eq. (27) into Eq. (30) yields:

$$\ddot{y}_{3} + k_{dqs} \dot{y}_{3} + k_{pqs} y_{3} = k_{pqs} i_{q}^{*}$$
(31)

By an analogy with the above SLESO parameter configuration method, the characteristic equation can be obtained from Eq. (31):

$$\lambda_{2} \left( s \right) = \left| {s^{2} + k_{dqs} s + k_{pqs} } \right|$$
(32)

Rational allocation of the amplification factor \(k_{pqs} ,k_{dqs}\) can ensure the stability of the system. To simplify the parameter design process, the poles are configured on \(s = - \omega_{{\text{c}}}\), where \(\omega_{{\text{c}}}\) is the system bandwidth. At this point it can be found that \(k_{pqs} = \omega_{{\text{c}}}^{2}\) and \(k_{dqs} = 2\omega_{{\text{c}}}\).

It can be seen from the above that the configuration problem of the SLADRC control parameters has been simplified to the selection of \(\omega_{{\text{o}}}\) and \(\omega_{{\text{c}}}\).

The above is the design process of the SLADRC. When combined with the vector control strategy of the PMSG, a control system block diagram can be obtained as shown in Fig. 2.

Fig. 2
figure 2

SLADRC control block diagram of the PMSG current loop

Full size image

4 Simulation and experimental results

4.1 FLADRC simulation verification

To verify the superiority of the FLADRC algorithm proposed in this paper, a PMSG simulation model is built in MATLAB/Simulink. The specific parameters of the unit are shown in Table 1.

Table 1 PMSG parameters
Full size table

The simulation conditions are set as follows. The wind speed is 7 m/s when the wind turbine starts. It increases to 10 m/s at 0.5 s, increases to 12 m/s at 1 s, decreases to 9 m/s at 1.5 s, and the simulation ends at 2 s. The PI speed regulation curve and the FLADRC speed regulation curve are shown in Fig. 3. From this figure, it can be seen that in the steady-state process, both the PI controller and the LADRC controller can make the rotor speed accurately track the given speed value without errors. However, the dynamic process is obviously different. This is mainly reflected in the fact that the speed of the PI control dynamic process has obvious overshoot. Meanwhile, in the speed loop FLADRC due to the LTD transition process, the speed is smooth, no overshoot reaches the reference value, and the FLADRC reaches steady state faster. For example, when the speed changes at 0.5 s, the overshoot of the PI control is 11.79%, and the PI and LADRC controls reach the steady state in 0.18 s and 0.1 s, respectively.

Fig. 3
figure 3

Comparison diagrams of the speed response between PI and FLADRC controllers: a overall speed waveforms; b amplified waveforms of a speed change at 0.5 s

Full size image

4.2 SLADRC simulation verification

To verify the superiority of the proposed SLADRC algorithm, a PMSG simulation model is built in the MATLAB/Simulink environment, and the proposed current loop SLADRC, the FLADRC, and the PI control strategies are compared. The control bandwidths of the three controllers are consistent. In the three groups of simulations, except for the current loop controller, the conditions are the same. The simulation results are as follows. The legends REAL-PI, REAL-1st, and REAL-2nd represent the response curves of the PI, the FLADRC, and the SLADRC, respectively.

In this section, the anti-interference performance of the proposed SLADRC controller is verified by an external additional disturbance signal. At the output end of the controller, a sinusoidal signal with an amplitude of 100 V and a frequency of 200 Hz is superimposed. The frequency of the signal is lower than the bandwidth frequency of the current controller, hereafter referred to as low-frequency disturbance. Taking the \(q\)-axis current response as an example, the resulting waveforms are shown in Fig. 4.

Fig. 4
figure 4

Current control performance of three controllers under low-frequency disturbances: a speed response waveforms; b amplified waveforms of the dynamic response; c amplified waveform of the static response

Full size image

From the steady-state response waveforms of the current in Fig. 4b, it can be seen that due to the influence of an external low-frequency disturbance, there are 200 Hz sinusoidal pulsations in the three current curves, and the current pulsation amplitude of the PI is about 25 A. The FLADRC and the SLADRC have similar pulsation suppression effects, and their current pulsation amplitudes are both about 10A. It can be seen from the current dynamic response of Fig. 4c that the response speeds of the three controllers are almost the same.

The above simulation results show that when compared with the PI controller, the two LADRCs have an inhibitory effect on low-frequency disturbances. The main principle is that the extended state observer in the LADRC strategy can observe the input disturbance, and compensate for it in the feedback control link. Figure 5 compares output voltage waveforms under the actions of the three controllers. The lower images are part of the enlarged upper images, where the blue curve is the added disturbance signal \(u_{h} \cos \left( {\omega_{h} t} \right)\), the red curve is the voltage signal \(u_{q}\) output by the controller, and the black curve is the voltage signal \(u_{q}^{^{\prime}}\) superimposed by the disturbance signal and the output voltage signal. In addition, the specific positions of the three signals are shown in Fig. 2. Figure 5a shows that the \(u_{q}\) and \(u_{h} \cos \left( {\omega_{h} t} \right)\) of the PI controller are anti-phase, and that the superpositions have the effect of canceling each other out. However, the fluctuation amplitude of \(u_{q}\) is small, which fails to completely cancel the low-frequency disturbance, and \(u_{q}^{^{\prime}}\) still presents a large sinusoidal pulsation form. Thus, the sinusoidal pulsation characteristics in the current response are obvious. The interference signal estimations in Fig. 5b and Fig. 5c are more accurate. After compensation, the voltage \(u_{q}^{^{\prime}}\) of the input converter is basically a constant value. Thus, the pulsation suppression effect is relatively strong.

Fig. 5
figure 5

Output voltage response and amplified waveforms of three controllers under low-frequency disturbances: a PI; b FLADRC; c SLADRC

Full size image

The disturbance signal is changed to a sinusoidal signal with an amplitude of 100 V and a frequency of 700 Hz, which is higher than the bandwidth frequency of the current controller, here after referred to as high-frequency disturbance. Similar to the low-frequency disturbance analysis, the \(q\)-axis current response is taken as an example, and its waveform is shown in Fig. 6.

Fig. 6
figure 6

Current control performance of three controllers under high-frequency disturbances: a speed response waveforms; b amplified waveforms of the dynamic response; c amplified waveforms of the static response

Full size image

From the current steady-state response waveforms in Fig. 6b, it can be seen that due to the influence of external high-frequency disturbances, the three current curves all have a sinusoidal pulsation of 700 Hz. The current pulsation amplitude of the PI is about 16A, and the FLADRC current pulsation amplitude is about 20A. The SLADRC has the most obvious pulsation suppression, and the current pulsation amplitude is about 2 A. It can be seen from the current dynamic response in Fig. 6c that the response speeds of the three controllers are almost the same.

The above simulation results show that the PI and the FLADRC have poor suppression effects on high-frequency disturbances, and that the SLADRC has the strongest suppression effect on high-frequency disturbances. Figure 7 shows a comparison of output voltage waveforms under the action of the three controllers. Figure 7a and b shows that the phases of \(u_{q}\) and \(u_{h} \cos \left( {\omega_{h} t} \right)\) of the PI and the FLADRC controllers are not anti-phase, and that there is a phase deviation. After superposition, they cannot cancel each other out, and \(u_{q}^{^{\prime}}\) still shows a large sinusoidal pulsation form. Thus, the sinusoidal pulsation characteristics in the current response are obvious. The interference signal estimation in Fig. 7c is more accurate. After compensation, \(u_{q}^{^{\prime}}\) is basically a constant value. Thus, the pulsation suppression effect is relatively strong.

Fig. 7
figure 7

Output voltage response and amplified waveforms of three controllers under high-frequency disturbances: a PI; b FLADRC; c SLADRC

Full size image

To show the anti-disturbance performance of the three controllers with respect to the current response more intuitively, the A-phase stator current of the PMSG is analyzed by a FFT, and total harmonic distortion (THD) data are obtained as shown in Table 2. The THD of the current is calculated by Eq. (33):

$$I_{{{\text{THD}}}} = I_{{\text{H}}} /I_{{\text{F}}} ,$$
(33)

where \(I_{{\text{H}}} = \sqrt {I_{2}^{2} + I_{3}^{2} + \cdots + I_{n}^{2} }\) is the RMS value of the harmonic n, and \(I_{{\text{F}}}\) is the RMS value of the fundamental current.

Table 2 FFT analysis of the PMSG stator A-phase current
Full size table

In the above Table 2, THD1 is the THD of the A-phase stator current without disturbance, THD2 is the THD of the A-phase stator current with a low-frequency disturbance, and THD3 is the THD of the A-phase stator current with a high-frequency disturbance. It can be seen from the table that the current THDs of the two LADRCs are smaller than that of the PI under the same control bandwidth before perturbation. After adding a low-frequency disturbance, the current THD of the PI increased significantly, and the current THD of the two LADRCs increased slightly, In addition, the two were close. After adding a high-frequency disturbance, the current THD of the SLADRC is smaller than that of the low-frequency disturbance, while the current THD of the PI and the FLADRC increases greatly. In addtion, the current THD of the FLADRC is higher than that of the PI controller.

4.3 Experimental verification

In this paper, a low-power PMSG towing platform was built to verify the effectiveness of the proposed algorithm. Figure 8 is a schematic diagram of the experimental platform.

Fig. 8
figure 8

Experiment platform of a PMSG

Full size image

The generator is a 3 kW surface mounted PMSG. A 3.8 kW asynchronous motor (AM) is used to simulate a wind turbine, and a SCIYON-KD200 frequency converter is used to control the AM, which can operate in both torque and speed modes. The AM drives the PMSG to rotate and generate electricity. The back-to-back converter uses two RTI-INV6030IRs, and the DC terminals of the two RTIs are connected. The control algorithm of the two converters is processed in a RTUBOX-204, and it sends pulse signals to control the IGBT switch. The main processor of the RTUBOX-204 is a 32-bit floating point TMS320C28346 of TI Inc., with a main frequency of 300 MHz. The variable frequency AC generated by the PMSG is rectified and controlled by one RTI, and the inverter is controlled by the other RTI to generate AC to meet grid connection standards. The inverter output terminal is connected to the grid after filtering by a three-phase reactor.

During the experiment, the speed reference value \(N_{{{\text{ref}}}}\) was reduced from 250 to 150 r/min, and then increased to 250 r/min. The dynamic and steady-state performances of the speed were analyzed. The relevant experimental waveforms are shown in Fig. 9.

Fig. 9
figure 9

Experimental waveforms of the control performance of two controllers in a speed loop: a PI; b LADRC

Full size image

Figure 9a and b shows speed waveforms when the PI and the LADRC controllers are used in the outer loop of the speed loop, respectively. Both of the controllers can realize tracking control of the speed, but the dynamic performance of the PI controller is poor. When the reference value of the speed changes, the PI takes 1.5 s to reenter the stable state, and the speed has a large overshoot in the dynamic process. By changing the PI parameters, the overshoot and the stabilization time can be adjusted in the dynamic process. However, the two control objectives of reducing both the overshoot and the stabilization time are contradictory, and the parameter setting is complex. The LADRC controller can completely eliminate the overshoot phenomenon in the dynamic process of the speed, and reduce the time for the speed to reach a stable state. The speed can be stabilized again in about 0.9 s. It is worth noting that an increase of the LADRC bandwidth leads to an amplification of observation noise. Thus, its bandwidth needs to be properly selected.

The speed loop controller bandwidth is kept consistent. In addition, the current loop PI, FLADRC, and SLADRC current control performances are verified. A sinusoidal interference signal with an amplitude of 5 V, and frequencies of 200 Hz and 700 Hz is added to the output link of the \(q\)-axis current controller. This verifies the anti-disturbance capability of the three controllers when the system input has an interference signal. Figure 10a–c shows current waveforms of the PI controller, the FLADRC, and the SLADRC before and after adding a 200 Hz interference, respectively. Figure 10d–f is corresponding waveforms after adding a 700 Hz interference.

Fig. 10
figure 10

Experimental waveforms of the control performance of three controllers in a current loop: a PI-200 Hz; b FLADRC-200 Hz; c SLADRC-200 Hz; d PI-700 Hz; e FLADRC-700 Hz; f SLADRC-700 Hz

Full size image

From Fig. 10, it can be seen that before the disturbance was added, under the same controller bandwidth, the current harmonic of the PI controller is larger. The THD is about 4.4%, and the current harmonics of the FLADRC and the SLADRC controllers are smaller than that of the PI controller at about 3.0% and 4.0%. respectively. After adding a 200 Hz disturbance, the THD of the current harmonics of the three controllers are 20.1%, 11.6%, and 9.2%, respectively. After adding a 700 Hz disturbance, the THD of the current harmonics of the three are 5.9%, 5.3%, and 4.9%, respectively. It can be seen that the PI controller has the worst anti-interference performance. The two kinds of ADRCs have obvious suppression effects on external disturbances. However, the SLADRC has better anti-interference performance than the FLADRC.

5 Conclusion

To improve the dynamic performance and anti-disturbance performance of the speed loop and current loop of a permanent magnet synchronous wind turbine, a dual active disturbance rejection control system was designed. First, the FLADRC of the speed loop and the current loop were designed to control the speed and current tracking processes, respectively. The LTD link in the speed loop performs transition processing on the speed reference value, and the current loop needs the fast response of the current value. Thus, the transition process is not set. The LESO estimates the total disturbance of the system and compensates it through the LSEF. Then considering the nonlinear influence of the converter, a new second-order current state equation was established, and a new current loop SLADRC was designed. The new controller includes TLSESO to estimate the disturbance, and SLSEF to compensate the disturbance. In addition, the convergence performance and parameter configuration method of the SLADRC were analyzed. The proposed control strategy was comprehensively compared with the traditional PI control strategy on a 3 kW experimental platform and 2 MW simulation system. The results show that there is no overshoot in the speed tracking process of the proposed control system, and that the time to reach the steady state is short. The anti-interference performance of the current loop based on FLADRC is stronger than that of the traditional PI controller. In addition, the SLADRC further enhances the high-frequency and low-frequency interference suppression capabilities of the current loop.