1 Introduction

Permanent-magnet synchronous motor (PMSM) has the advantages of simple structure, high efficiency, and high torque-to-inertia ratio, so it has superiority in low-speed tracking and high-speed flux-weakening performance [1]. In recent years, PMSM has been widely used in high-precision servo control. The high-precision and stable drive system put forward higher requirements for the smooth operation of the motor. However, the non-ideal factors of the motor and its drive system will cause torque ripple, which affects the application of permanent magnet synchronous motors in high-precision servo control systems [2,3,4].

At present, torque ripple suppression is mainly achieved through the optimization and design of the motor structure and the improvement of the control method. From the point of view of motor design, it is practical to analyze the magnetization method of permanent magnets to optimize the pole-arc coefficient and the pole-slot coordination. In terms of optimal control methods, it is mainly divided into two ways: relying on the strong robustness of the controller andfeed-forward compensation [5].

In recent years, many researchers have conducted research on optimizing the robustness of controllers and suppressing disturbances. A hybrid robust resonance control strategy is studied in [6]. It improves the vector resonance controller with the fractional order method, making the controller have good robustness and harmonic suppression performance. However, predictive control and sliding mode control also have strong robustness. A harmonic suppression method combining dead-band control and sliding mode control is proposed in [7], which exhibits good torque ripple suppression capability. In [8], the researchers analyzed the dead-band as a cause of torque ripple. Therefore, the motor drive system adopted the dead-band effect compensation algorithm based on a Proportional Resonance (PR) controller. Designing a feed-forward compensation link is also an effective way to suppress torque ripple. A method of extracting nonlinear disturbances is analyzed in [9], and a proportional-integral (PI) controller is used to feed-forward the disturbances. After compensation, the sixth harmonic component is suppressed, and torque ripple is reduced. In [10], an improved Non-homogeneous Disturbance Observer (NHDO) is proposed to converge the d-q axis current error to zero. This compensation method has a faster compensation speed and can maintain an excellent current tracking performance when the main motor parameters do not match. The fifth and seventh harmonics in the three-phase static coordinate system are caused by the dead-band and lead to the torque ripple. Therefore, a filtering method was studied in [11] to weaken the dead-band effect, thereby reducing the torque ripple. Also, a torque ripple suppression method based on harmonic current control is proposed in [12]. It analyzes the optimal harmonic current solution, and the method also utilizes a least mean square (LMS) based adaptive filter (AF), which effectively suppresses torque ripple. In particular, the harmonic voltage injection method is a typical feed-forward suppression scheme. The harmonic voltage model is established under the multi-synchronous coordinate system [13]. Then the feed-forward harmonic voltage and feedback harmonic current control phase combined, torque ripple is effectively suppressed.

In [14], an extended state observer (ESO) based current harmonic suppression strategy is proposed. It is demonstrated in detail that ESO is superior to traditional proportional-integral controllers and advanced proportional resonance (PR) controllers in harmonic suppression. Professor Gao Zhiqiang proposed LADRC after linearizing ADRC [15]. With LESO as the core, LADRC estimates and compensates for the total disturbance of the system, which has reasonable rapidity and anti-disturbance performance. The ability of LADRC to observe disturbances determines its anti-disturbance performance. Therefore, a correction link for total disturbances is added in [16] to improve the anti-disturbance performance of LADRC. However, improving the observation ability of the controller is often accompanied by an increase in the sensitivity of noise. Therefore, the observation pressure of the observer is reduced in [17] by connecting two LESOs in parallel to prevent the amplification of noise.

In this paper, an Enhanced LADRC is proposed, which improves the anti-disturbance ability of the controller and has strong anti-noise performance. The structure of this paper is as follows, the second chapter describes the conventional LADRC and its limitations, the third chapter designs and analyzes the Enhanced LADRC, and strengthens the anti-disturbance performance and noise suppression performance in two parts. In addition, the parameter setting method or selection range after increasing order are also given. Finally, its effectiveness is verified by simulation and experiment.

2 PMSM Mathematical Model and LADRC

Under the ideal work conditions, the mathematical model of PMSM in the synchronously rotating reference frame [18] can be described as:

$$\left\{ {\begin{array}{*{20}{l}} {{u_{\text{d}}}={L_{\text{d}}}\frac{{{\text{d}}{i_{\text{d}}}}}{{{\text{d}}t}} - {\omega _{\text{e}}}{L_{\text{q}}}{i_{\text{q}}}+{R_{\text{s}}}{i_{\text{d}}}} \\ {{u_{\text{q}}}={L_{\text{q}}}\frac{{{\text{d}}{i_{\text{q}}}}}{{{\text{d}}t}}+{\omega _{\text{e}}}\left( {{L_{\text{d}}}{i_{\text{d}}}+{\varphi _{\text{f}}}} \right)+{R_{\text{s}}}{i_{\text{q}}}} \end{array}} \right.$$
(1)
$${T_{\text{e}}}=\frac{{3p}}{2}\left[ {{\varphi _{\text{f}}}+\left( {{L_{\text{d}}} - {L_{\text{q}}}} \right){i_{\text{d}}}} \right]{i_{\text{q}}}$$
(2)

where \({i}_{d}\), \({i}_{q}\) represent the dq-axis currents; \({u}_{d}\), \({u}_{q}\) represent the dq-axis voltages; \({L}_{d}\), \({L}_{q}\) represent the dq-axis inductances; \({R}_{s}\), \({\omega }_{e}\), and \({\phi }_{f}\) represent the stator resistance, the rotor angular speed, and permanent magnet flux linkage. \(p\) represent the number of pole pairs.

In (2), the interference of the dq-axis current will increase the difficulty of electromagnetic torque control and easily cause torque ripple [19]. Input disturbance and measurement noise are included in the current loop. According to (1), the current loop of the PMSM drive system is a first-order system [20]. The current loop is rewritten into a first-order controlled system, and the q-axis current can be expressed as:

$$\frac{{d{i_q}}}{{dt}}=\frac{1}{{{L_q}}}[{u_q} - {R_s}{i_q} - {\omega _e}({L_d}{i_d}+{\varphi _{\text{f}}})]$$
(3)

The form of (3) written as an equation of state can be expressed as:

$$\left\{ {\begin{array}{*{20}{l}} {\dot {x}(t)=Ax(t)+Bu(t)+Ch} \\ {y=Ex(t)} \end{array}} \right.$$
(4)

where \(x\left(t\right)={\left[\begin{array}{cc}{x}_{1}\left(t\right)& {x}_{2}\left(t\right)\end{array}\right]}^{T}\). \(A=\left[ {\begin{array}{*{20}{c}} 1&0 \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} 0&1 \end{array}} \right]^T}\). \(B={\left[\begin{array}{cc}{b}_{0}& 0\end{array}\right]}^{T}\). \(C={\left[\begin{array}{cc}0& 1\end{array}\right]}^{T}\). \(E=\left[ {\begin{array}{*{20}{l}} 1&0 \end{array}} \right]\). \({x}_{1}={\omega }_{\text{e}}\). \(f=-{R}_{s}{i}_{q}-{\omega }_{e}\left({L}_{d}{i}_{d}+{\phi }_{\text{f}}\right)\). \({x}_{2}=f\). \(f\) contains load torque disturbance and viscous friction coefficient disturbance. \(u={i}_{\text{q}}\). \(h=\dot{f}\). \({b}_{0}=1/{L}_{q}\) can be expressed as controller gain.

$$\left\{ {\begin{array}{*{20}l} {z_{1} (k + 1) = z_{1} (k) + h\left( {z_{2} (k) - \beta _{1} e(k) + b_{0} u(t)} \right)} \hfill \\ {z_{2} (k + 1) = z_{2} (k) - h\beta _{2} e(k)} \hfill \\ {e(k) = z_{1} (k) - y(k)} \hfill \\ \end{array} } \right.$$
(5)

where \({z}_{1}\left(k\right)\) and \({z}_{2}\left(k\right)\) are expressed as estimates of \({x}_{1}\) and \({x}_{2}\), respectively. \(y\left(k\right)\) is represented as the output of the control object. \({\beta }_{1}\) and \({\beta }_{2}\) are observer parameters.

According to the above formula, the transfer function of.

Fig. 1
figure 1

Block diagram of the enhanced LADRC

Full size image

the estimated value z with respect to the system output y and the control value u can be obtained. Then, the system’s ability to suppress current loop disturbance and measurement noise disturbance can be obtained. According to [18], LADRC can suppress disturbances in the whole frequency domain, especially in low and high-frequency bands. However, improving the interference immunity in the mid-band requires increasing the observer bandwidth, which leads to the noise sensitivity of LADRC.

Therefore, it is necessary to find an improvement measure to the conventional LADRC, which can strengthen the ability to suppress disturbance and effectively suppress the measurement noise.

3 Design and Analysis of Enhanced LADRC

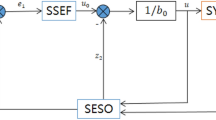
An Enhanced LADRC is designed in this section, including Linear Tracking Differentiator (LTD), Linear State Error Feedback (LSEF), Full-order LESO, and Fal-Filter. The block diagram of the ELADRC is shown in Fig. 1.

3.1 Design of Linear Tracking Differentiator

In the vector control system of PMSM, there will be some high-frequency noise signals in the input signal, and LTD can extract continuous signals from the superimposed signals of various signals. However, inappropriate LTD parameters can lead to high-frequency chattering, which in severe cases can reduce the controllability of the system. Therefore, this paper uses the first-order inertial link to replace the LTD, and its digital form can be expressed as:

$$c(k)=c(k - 1)+h\left[ {2\pi {f_c}(r(k) - c(k - 1))} \right]$$
(6)

where \(T=1/\left(2\pi {f}_{\text{c}}\right)\) is expressed as the inertia time constant. \({f}_{\text{c}}\) is defined as the cutoff frequency. \(r\left(k\right)\) is defined as the speed given value. \(c\left(k\right)\) is defined as the output of the inertial component. \(h\) is expressed as the sampling step. \(k\) is defined as the kth sampling moment.

Fig. 2
figure 2

The structure of Full-order LESO

Full size image

3.2 Design of Full-Order Observer

The differential of the disturbance reflects the changing trend of the error and can determine the output value at the next moment. To enhance the observation performance of the LESO, so the differential equation of the total disturbance is added in (5). The structure of the full-order observer is shown in Fig. 1. The observer can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {z_{1} (k + 1) = z_{1} (k) + h\left( {z_{2} (k) - \beta _{1} e(k) + b_{0} u(t)} \right)} \hfill \\ {z_{2} (k + 1) = z_{2} (k) + h(z_{3} (k) - \beta _{2} e(k))} \hfill \\ {z_{3} (k + 1) = z_{3} (k) - h\beta _{3} e(k)} \hfill \\ {e(k) = z_{1} (k) - y(k)} \hfill \\ \end{array} } \right.$$
(7)

The transfer function of the system can be expressed as:

$${z_1}=\frac{{({\beta _1}{s^2}+{\beta _2}s+{\beta _3})y+{b_0}{s^2}u}}{{{s^3}+{\beta _1}{s^2}+{\beta _2}s+{\beta _3}}}$$
(8)

The poles of (8) are configured according to the bandwidth method in [15]. Its characteristic equation and expected form can be written as:

$$\left\{ {\begin{array}{*{20}l} {\Delta (s) = s^{3} + \beta _{1} s^{2} + \beta _{2} s + \beta _{3} = 0} \hfill \\ {\Delta (s) = (s + \omega _{0} )^{3} } \hfill \\ \end{array} } \right.$$
(9)

By configuring the parameters, \({\beta }_{1}\), \({\beta }_{2}\) and \({\beta }_{3}\) can be determined as:

$${\beta _1}=3{\omega _0},{\text{ }}{\beta _2}=3{\omega _0}^{2},{\text{ }}{\beta _3}={\omega _0}^{3}$$
(10)

The LESO can track the system state variables accurately by selecting the observer bandwidth [21, 22]. The system control rate is expressed as:

Fig. 3
figure 3

Total disturbance observation capability

Full size image
$$\left\{ {\begin{array}{*{20}{l}} {{u_0}(k)={K_p}\left( {r(k) - {z_1}(k)} \right)} \\ {u(k)=\frac{{{u_0}(k) - {z_2}(k)}}{{{b_0}}}} \end{array}} \right.$$
(11)

where \({k}_{p}\) is represented as the controller proportional coefficient, and \(r\left(k\right)\) is defined as the given reference variable of the system. The structure of the Full-order LESO is shown in Fig. 2.

3.3 Disturbance estimation and suppression

The observation ability of the total disturbance can determine the compensation effect of the observer, and the timely output of the observation value can improve the anti-interference ability. According to (1) and (2), the relationship between the total disturbance’s estimated value and its actual value can be expressed as:

$$\frac{{{{\text{z}}_2}}}{{{x_2}}}=\frac{{3{\omega _0}^{2}s+\omega _{0}^{3}}}{{{{(s+{\omega _0})}^3}}}$$
(12)

In Fig. 3, the observation speed of the total disturbance of the full-order observer is faster, and the observation results of the conventional observer are included. To simplify the following analysis, let the system disturbance is \({\delta }_{c}\), and the measurement noise disturbance is denoted by \({\delta }_{0}\). According to (7), the transfer function of the observer to the system disturbance and measurement noise can be represented as:

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{z}}_{1} }}{{\delta _{c} }} = \frac{{b_{0} s^{2} }}{{(s + \omega _{0} )^{3} }}} \hfill \\ {\frac{{{\text{z}}_{1} }}{{\delta _{0} }} = \frac{{3\omega _{0} s^{2} + 3\omega _{0} ^{2} s + \omega _{0}^{3} }}{{(s + \omega _{0} )^{3} }}} \hfill \\ \end{array} } \right.$$
(13)
Fig. 4
figure 4

System disturbance rejection performance

Full size image
Fig. 5
figure 5

Measuring noise suppression performance

Full size image

According to the above formula, make its amplitude-frequency characteristic curve. The disturbance rejection performance of the full-order observer is reflected in Fig. 4, and its noise rejection performance is shown in Fig. 5. Under the same bandwidth parameters, the anti-disturbance capability of Full-order LESO in the middle and low-frequency bands is significantly higher than that of conventional LESO. Also, the dynamic characteristics of full-order observers can maintain good performance. However, the analysis of Fig. 5 shows that the full-order LESO does not have a good improvement in noise suppression performance. Therefore, this paper is further improved by cascading Full-order LESO and Fal-Filter.

3.4 Design of the Fal-Filter

The Fal-Filter can be formed by the Fal function and the integral link. By constructing the feedback structure, the measurement noise at the observer’s input can be reduced. The structure of the Fal-Filter as shown in Fig. 6. It can be represented as:

Fig. 6
figure 6

Block diagram of the Fal-Filter

Full size image
Fig. 7
figure 7

Block diagram of the control system

Full size image
Fig. 8
figure 8

Photos of the experimental platform

Full size image
$$\left\{ {\begin{array}{*{20}l} {\dot{x} = g\text{fal} \left( {(y_{0} - x),m,n} \right)} \hfill \\ {y = x,{\text{ }}E{\text{ = }}y_{0} - x} \hfill \\ \end{array} } \right.$$
(14)

where the Fal function is given by:

$$fal(E,m,n) = \left\{ {\begin{array}{*{20}l} {\left| E \right|^{m} sign(E),\left| E \right| > n} \hfill \\ {\frac{E}{{n^{{1 - m}} }},\left| E \right| \le {\text{ }}n} \hfill \\ \end{array} } \right.$$
(15)

where \(g\) is the proportional coefficient, \(m\) is the constant between 0 and 1, \(n\) is designed as the filtering factor, y is the input signal of the Fal function, and \({y}_{0}\) is expressed as the output signal of the Fal-Filter. y denoted as \({y}_{0}=Fal\_Filter(y,g,m,n)\).

According to the characteristics of the Fal function, there are two different processing methods for errors of different sizes. The error is more evident at a certain moment (\(\left|E\right|>n\)), and the signal can be quickly converged to the input signal through the sign function and small gain, until the error value is reduced to \(n\).

After the error converges to a smaller range (\(\left|E\right|<n\)), the role of the Fal function changes from fast convergence to a low-pass filter. At this time,\(\dot{x}=gE/{n}^{1-m}\).T, e value of \(\dot{x}\) is represented by k, according to (15), it can be described as:

$$\frac{{{y_0}}}{y}=\frac{{k/{\text{s}}}}{{1+k/s}}=\frac{k}{{s+k}}=\frac{1}{{s/k+1}}$$
(16)

The cutoff frequency of this filter decreases as the error decreases, which is suitable when AC disturbances accompany the DC input signal.

In addition, the conventional low-pass filter has a significant phase delay [23], and the Fal-Filter takes advantage of its nonlinear filtering. It can switch between fast approaching the input signal and filtering, so the Fal-Filter has both fastness and filtering performance.

4 Simulation and Experiment

The simulations and experiments are carried out in the vector control system to verify the effectiveness of the Enhanced LADRC. The system control block diagram is shown in Fig. 7. A simulation model was built in MATLAB/Simulink, and the experimental platform was the dSPACE platform. The photo of the experimental platform is shown in Fig. 8. The experimental platform mainly consists of PMSM, control cabinet, and induction motor as load. The control cabinet includes the dSPACE-DS1202 control board, signal converter, and drive circuit. In addition, the motor control platform can be connected with PC, real-time display current, torque, and other information. A PI controller controls the speed loop in simulation and experiment. The PI controller, conventional LADRC, and Enhanced LADRC are used in the current loop controller, and the three algorithms are compared. The parameters of the PMSM are listed as follows Rated power = 5.5 kW, Rated speed = 1500 rpm, \({L}_{d}=7.45 mH\), \({L}_{q}=1.78 mH\), \({R}_{s}=0.26\)Ω, φf = 0.201 Wb, Bus voltage = 546 V, \(p\)= 4.

4.1 Simulation Results

The PMSM works under the condition of rated speed, the initial torque is 5 N·m, and then the given step torque is 15 N·m. A random measurement noise signal is applied on the feedback path of the motor output current to verify the noise suppression performance.

In Fig. 9, the control performances under the three control methods are shown. By comparing the phase currents of the three methods, it can be found that the current distortion under the conventional PI algorithm is significant.

Fig. 9
figure 9

Phase current, FFT analysis and torque under three control methods a PI controller b conventional LADRC c Enhanced LADRC

Full size image
Fig. 10
figure 10

Control performances under three control methods a PI controller b conventional LADRC c Enhanced LADRC

Full size image

and contains high-frequency components. This phenomenon is caused by the inverter’s high-frequency noise and nonlinear factors [20]. Similarly, although the current is stable under the traditional LADRC control method, it still contains some disturbance components. However, the Enhanced LADRC enables smoother phase currents, better sinusoids, and significantly fewer high-frequency components. Then, the phase currents under the three control methods are analyzed by FFT, and it can also be found that the disturbances under the Enhanced LADRC are reduced.

By comparing the torque performance under the three control methods, it can be seen that the stability of the PI controller is insufficient, and the torque ripple is noticeable. Compared with the PI controller, the torque ripple under the LADRC method is suppressed, but there are still high-frequency components. However, Enhanced LADRC not only suppresses torque ripple, but also reduces high-frequency disturbances.

4.2 Experimental Results

The Enhanced LADRC algorithm is built in the PMSM vector control system to verify the control method. The speed and torque set in the experiment are the same as in the simulation.

In Fig. 10, the disturbance immunity of the three control methods is demonstrated. The PI controller contradicts rapidity and overshoot, so the torque has a significant overshoot. In terms of anti-disturbance, the PI controller cannot effectively suppress current distortion and noise, resulting in more considerable torque disturbance. Compared with the PI controller, the dynamic performance of the conventional LADRC is better, but it cannot suppress the noise and the internal disturbance of the system at the same time. However, the Enhanced LADRC strengthens noise suppression and better suppresses the system disturbance so that the torque ripple will be more minor. In addition, it also inherits the dynamic performance of the conventional LADRC.

5 Conclusions

The Enhanced LADRC control method was proposed in this paper to improve the measurement noise and disturbance rejection performance of PMSMs. It was verified on the MATLAB/Simulink and dSPACE motor control platforms, and the following conclusions were obtained.

  1. 1)

    The Full-order LESO and Fal-Filter deal with mid-and low-frequency disturbances and high-frequency noise. Therefore, the Enhanced LADRC can solve the problem that conventional LADRC is difficult to balance measurement noise and system disturbance.

  2. 2)

    Through the Enhanced LADRC method, the motor’s torque is smoother, and the sine of the phase currents is strengthened. According to the experimental results, compared with the traditional PI controller, the total current harmonic distortion rate is reduced by about 5.24%. When compared with LADRC, the distortion rate dropped by about 1.72%. In addition, the smoothness of phase current and torque is significantly enhanced by the method in this paper.