Keywords

1 Introduction

In recent years, there has been an evolution of the electricity production based on wind energy. As a result, the wind energy is the subject of several researches. Although this energy source is inexhaustible and environmental friendly, its relatively cost stay interesting and its efficiency is still low compared to conventional sources [1,2,3,4].

The DFIG is broadly used for variable speed wind power generation system thanks to its several advantages over other generators. These advantages are easiness of speed control, operation at over a large range of wind speeds of 30% around the synchronous speed and an inverter rated at 20–30% of the total system power [2,3,4, 6, 8]. Contrary, the DFIG is subject to many constraints, such as the effects of parametric uncertainties (due to overheating, saturation …) and the disturbance of the speed variation, which could divert the system from its optimal functioning. Therefore, the control of DFIG has become a very important research subject [4, 11].

In this paper we start with the description and modeling the components of the Wind Energy Conversion System based on the DFIG. Then, a special linear control system called ADRC is applied to the control of the rotor side converter and tested at a variable wind speed. Finally, we conclude our work by interpretations of the simulation results.

2 Modeling of the Wind Energy Conversion System

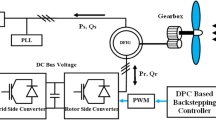
Our wind energy conversion system is shown in Fig. 1 [1,2,3,4].

Fig. 1.
figure 1

Model of the variable speed wind turbine conversion chain.

Full size image

2.1 Wind Turbine

The turbine transforms the wind energy into a mechanical energy. The aerodynamic power available on a wind turbine rotor is given by the following equation [1,2,3,4,5,6]:

$$ P_{aer} = \frac{1}{2}C_{p} \left( {\lambda ,\beta } \right)\rho \pi R^{2} V^{3} $$
(1)

Where ρ is the air density, R is the turbine radios and V is the wind velocity.

According to [8], the power coefficient Cp is given by:

$$ C_{p} \left( {\lambda ,\beta } \right) = C_{1} (\frac{{C_{2} }}{{\lambda_{i} }} - C_{3} \beta - C_{4} )e^{{\left( { - \frac{{C_{5} }}{{\lambda_{i} }}} \right)}} + C_{6} \lambda $$
(2)

Where

$$ \lambda = \frac{{ \varOmega_{t} R}}{ V}\frac{1}{{\lambda_{i} }} = \frac{1}{\lambda + 0.08\beta } - \frac{0.035}{{1 + \beta^{3} }} $$
(3)
$$ C_{1} = 0.5176, \, C_{2} = 116, \, C_{3} = 0.4, \, C_{4} = 5, \, C_{5} = 21, \, C_{6} = 0.0068 $$

The mechanical model between the turbine and shaft generator is defined by [1,2,3,4,5,6,7,8]:

$$ T_{mec} = J\frac{{d\varOmega_{g} }}{dt} = T_{g} - T_{em} - f_{v} \varOmega_{g} \,{\text{With}}\,J = \frac{{J_{t} }}{{G^{2} }} + J_{g} $$
(4)

Where Tg, Tem and Tmec are respectively the torque of the fast shaft, the electromagnetic torque and the mechanical torque of generator, J is total moment of inertia and fv is the viscous friction coefficient.

To extract the maximum power generated, we must fix the speed ratio to its optimal value λopt and the power coefficient to its maximum value Cpmax [14]. The wind speed and the electromagnetic torque reference are determined by the following equations [1, 3, 7].

$$ T_{em - ref} = \frac{1}{{2G\Omega _{t} }}C_{pmax} \,\rho \pi R^{2} \widehat{V}^{3} \,{\text{With}}\,\widehat{V} = \frac{{R\widehat{\varOmega }_{t} }}{{\lambda_{opt} }} $$
(5)

The next figure represents the block diagram model of the turbine with MPPT (Fig. 2):

Fig. 2.
figure 2

Block diagram model of the turbine without wind velocity measurement

Full size image

2.2 Modeling of the DFIG

In this paper, we use a vector control of DFIG based on the stator field oriented control (SFOC). We have adopted a stator flux aligned on the d-axis [1,2,3,4,5,6,7,8, 13]. Therefore:

$$ \left\{ {\begin{array}{*{20}l} {\phi_{ds} = \phi_{s} = L_{s} I_{ds} + MI_{dr} } \hfill \\ {\phi_{qs} = 0 = L_{s} I_{qs} + MI_{qr} } \hfill \\ \end{array} } \right. $$
(6)

The d-axis is aligned with the supply voltage Vs, thus \( V_{sd } = V_{s } = \omega_{s} \phi_{sd} \) and Vsq = 0. In addition, the stator resistance Rs can be neglected since this is a realistic assumption for the high power generators [1,2,3,4,5].

The expressions of the active and reactive power are given by:

$$ \begin{array}{*{20}c} {P_{s} = - V_{s} \frac{M}{{L_{s} }}I_{qr} } \\ {} \\ \end{array} Q_{s} = - V_{s} \frac{M}{{L_{s} }}I_{dr} + \frac{{V_{s}^{2} }}{{L_{s} \omega_{s} }} $$
(7)

For power control of DFIG, the expressions of the rotor voltages are established according to the rotor currents (Eq. 8).

$$ \left\{ {\begin{array}{*{20}c} {V_{dr} = R_{r} I_{dr} + L_{r} \sigma \frac{{dI_{rd} }}{dt} - g\omega_{s} L_{r} \sigma I_{qr} } \\ {V_{qr} = R_{r} I_{qr} + L_{r} \sigma \frac{{dI_{rq} }}{dt} - g\omega_{s} L_{r} \sigma I_{rd} + g\omega_{s} \frac{{V_{s} M}}{{L_{s} \omega_{s} }}} \\ \end{array} } \right. $$
(8)

Where: \( \upsigma = 1 - \frac{{{\text{M}}^{2} }}{{{\rm{L}}_{\rm{s}} {\text{L}}_{\rm{r}} }} \)

Therefore, the simplified model of DFIG is given in Fig. 3.

Fig. 3.
figure 3

Simplified theoretical model of DFIG

Full size image

3 Synthesis of the ADRC Control and Its Application to DFIG

3.1 Synthesis of ADRC Controller

The Extended State Observer (ESO) is the key of the ADRC, which allows to estimate all real disturbances and modeling uncertainties, this estimate is used in the generation of the control signal in order to decouple the system of the disturbance acting on the actual process [2, 9, 10].

Consider a first order system time-varying dynamic system with single input denoted u, and single-output denoted y (Eq. 9).

$$ \frac{dy}{dt} = f\left( {y,d,t} \right) + b_{0} u $$
(9)

Where f(y, d, t) represents the combined effect of internal and external disturbance, b0 is a parameter gain and d represents the external disturbance.

The following mathematical system (Eq. 10) describes the state space of the process as [2, 9, 12]:

$$ \left\{ {\begin{array}{*{20}c} {\dot{x}_{1} = x_{2} + b_{0} u } \\ {x_{2} = f ; y = x_{1} } \\ \end{array} } \right. $$
(10)

The system of equations (Eq. 11) presents the state-space representation of the ESO [2, 9, 10].

$$ \left\{ {\begin{array}{*{20}c} {\mathop {\widehat{x}}\limits^{ \cdot } {}_{1} = \widehat{x}_{2} + \beta_{1} \left( {y - \widehat{x}_{1} } \right) + b_{0} u} \\ {\mathop {\widehat{x}}\limits^{ \cdot } {}_{2} = \beta_{2} \left( {y - \widehat{x}_{1} } \right)} \\ \end{array} } \right. $$
(11)

Where [β1, β2] is the vector of the observer gain values are given as [12]:

$$ \left[ {\begin{array}{*{20}c} {\beta_{1} } \\ {\beta_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 2S_{ESO} } \\ {S_{ESO}^{2} } \\ \end{array} } \right] $$
(12)

SESO is the pole of the observer is defined by the technique of placement of the poles.

The control input is given by (Eq. 13) [12]:

$$ u = \frac{{u_{0} - \widehat{f}}}{{b_{0} }} = \frac{{u_{0} - \widehat{x}_{2} }}{{b_{0} }} $$
(13)

According to [12], the plant has approximately integrating behavior, which can easily be controlled, by a simple proportional controller (Eq. 14) with gain values Kp [2, 12]. The input signal reference denoted r.

$$ u_{0} = K_{p} \left( {r - \widehat{y}} \right) = K_{p} \left( {r - \widehat{x}_{1} } \right) $$
(14)

Where, Kp = SCL. Where, SCL denotes the desired closed loop pole. Usually the controller regulation is done by observing the desired closed loop pole. Generally, SESO = 3~10 SCL and consequently, SCL is the only setting parameter [12].

The Fig. 4 shows the structure of the linear ADRC controller for a first order system [2, 9, 12].

Fig. 4.
figure 4

Control structure of ADRC

Full size image

3.2 Applying the ADRC for Control of the Active and Reactive Power of the DFIG

The direct and quadratic rotor current is controlled by the ADRCcontroller, by imposing reference voltages direct and quadratic of the rotor to the rotor side converter (RSC) which generates the control signals using the Pulse Width Modulation (PWM) (Fig. 5) [2].

Fig. 5.
figure 5

Scheme of power control of DFIG using ADRC controller

Full size image

The rotor currents are rearranged to be in the following form:

$$ \left\{ {\begin{array}{*{20}c} {\frac{{dI_{rd} }}{dt} = - \frac{{R_{r} }}{{\sigma L_{r} }}I_{rd} + \omega_{r} I_{rq} + \frac{1}{{\sigma L_{r} }}V_{rd} } \\ {\frac{{dI_{rq} }}{dt} = - \frac{{R_{r} }}{{\sigma L_{r} }}I_{rq} - \omega_{r} I_{rd} - \omega_{r} \frac{M}{{\sigma L_{r} L_{s} }}\phi_{sq} + \frac{1}{{\sigma L_{r} }}V_{rd} } \\ \end{array} } \right. $$
(15)

We can write these expressions in the following form:

$$ \frac{{dI_{rdq} }}{dt} = f\left( {I_{rdq} ,d,t} \right) + b_{0} u(t) $$
(16)

Where:

$$ \left\{ {\begin{array}{*{20}l} {f(I_{rd} ,d,t) = - \frac{{R_{r} }}{{\sigma L_{r} }}I_{rd} + \omega_{r} I_{rq} + (\frac{1}{{\sigma L_{r} }} - b_{0} )V_{rd} } \hfill \\ {\quad \quad \,\,\,u\left( t \right) = V_{rd} \quad \quad \quad and\,\,\,\,b_{0} = \frac{1}{{\sigma L_{r} }}} \hfill \\ \end{array} } \right. $$
(17)
$$ \left\{ {\begin{array}{*{20}l} {f(I_{rq} ,d,t) = - \frac{{R_{r} }}{{\sigma L_{r} }}I_{rq} - \omega_{r} I_{rd} - \omega_{r} \frac{M}{{\sigma L_{r} L_{s} }}\phi_{sq} + (\frac{1}{{\sigma L_{r} }} - b_{0} )V_{rd} } \hfill \\ {\quad \quad \quad \quad \quad u\left( t \right) = V_{rq} \quad \quad \quad \,\,\,and\,\,\,\,b_{0} = \frac{1}{{\sigma L_{r} }}} \hfill \\ \end{array} } \right. $$
(18)

4 Simulation with MATLAB/Simulink and Results

In [2] the performance test of the ADRC was realized at fixed speed, although our work comprised of the wind turbine dynamic modeling and power extraction technique (MPPT).

The wind speed is modeled in the determinist form by a sum of several harmonics, according to [4], its expression is given by the following equation:

$$ \begin{aligned} V\left( { t } \right) & = V_{0} + 2\sin \left( {\omega t} \right) - 1.75\sin \left( {3\omega t} \right) + 1.5\sin \left( {5\omega t} \right) - 1.25\sin \left( {10\omega t} \right) \\ & + \sin \left( {30\omega t} \right) + 0.5\sin \left( {50\omega t} \right) + 0.25\sin \left( {100\omega t} \right) \\ \end{aligned} $$
(19)

Where V0 is the average wind speed and ω = 2π/10

Figure 6 shows the simulated wind profile with an average speed of 4.5 m/s, this figure shows that the turbine has a good adaptation to the variation of the wind thanks to the MPPT control.

Fig. 6.
figure 6

Wind Speed and Mechanical Rotor Speed

Full size image

The reference reactive power is chosen as follow (Fig. 7):

Fig. 7.
figure 7

Active and reactive powers of stator and their references.

Full size image

  • From t = 0 to t = 1 s and from t = 1.5 to t = 2 s: Qs-ref = 0 VAR

  • From t = 1 to t = 1.5 s: Qs-ref = -5e5VAR

4.1 Test of Reference Tracking

Figure 7 shows that the active and reactive powers track with high and very good performances as their references.

4.2 Test of Robustness

This test is to show the robustness of the ADRC controller by varying the internal DFIG parameters by increasing the resistance Rr by 100% and the inductance Lr and Ls by 20% and decreasing M by 10%.

The Fig. 8 shows that the increases in the resistance and inductance of rotor of DFIG have not almost any influence on the operation of the generator because the ADRC controller allows automatically compensate for the disturbance due to these variations and the stability has not affected. Moreover, the outputs of our system track their reference with high performances.

Fig. 8.
figure 8

Active and reactive power of stator with varying the internal DFIG parameters

Full size image

5 Conclusion

In this work, we presented the modeling of the wind turbine based on the DFIG, developing ADRC controller and using the MPPT technic to extract the maximum power generated in order to optimize the capture wind energy by tracking the optimal speed. In addition, we have carried out a simulation in MATLAB/Simulink.

Finally, we can conclude through the results of simulation that the ADRC controller is very efficient in terms of tracking performances and more robust to internal parameters changes because this control strategy deletes in real time the effect of all disturbances which can affect our system.