$C^1$-Conforming Quadrilateral Spectral Element Method for Fourth-Order Equations

Abstract

This paper is devoted to Professor Benyu Guo’s open question on the $C^1$-conforming quadrilateral spectral element method for fourth-order equations which has been endeavored for years. Starting with generalized Jacobi polynomials on the reference square, we construct the $C^1$-conforming basis functions using the bilinear mapping from the reference square onto each quadrilateral element which fall into three categories—interior modes, edge modes, and vertex modes. In contrast to the triangular element, compulsively compensatory requirements on the global $C^1$-continuity should be imposed for edge and vertex mode basis functions such that their normal derivatives on each common edge are reduced from rational functions to polynomials, which depend on only parameters of the common edge. It is amazing that the $C^1$-conforming basis functions on each quadrilateral element contain polynomials in primitive variables, the completeness is then guaranteed and further confirmed by the numerical results on the Petrov–Galerkin spectral method for the non-homogeneous boundary value problem of fourth-order equations on an arbitrary quadrilateral. Finally, a $C^1$-conforming quadrilateral spectral element method is proposed for the biharmonic eigenvalue problem, and numerical experiments demonstrate the effectiveness and efficiency of our spectral element method.

1 Introduction

Fourth-order partial differential equations are widely used mathematical models in physics, engineering, and geological science such as physical flows, fluids in lungs, the elastic vibration and the plate deviation theory. There is an abundant literature on various numerical methods to solve fourth-order equations because of their great importance to scientists and engineers. These numerical methods mainly fall into several categories. The first type uses classical nonconforming elements such as the Adini element [1] and the Morley element [31, 33, 37]. A disadvantage of this method is that such elements do not come in a natural hierarchy and existing nonconforming elements only involve low-order polynomials which are not efficient for capturing smooth solutions. The second type is the mixed finite-element method [14, 30] which only requires $C^0$-conforming elements to approximate the solution. However, for the simply supported boundary condition, some mixed finite-element methods may result in spurious solutions on non-convex domains [15, 18, 43]. Besides, the solution of the saddle point problems resulting from the use of mixed finite-element method is also more involved than that for a direct discretization of the fourth-order operator. The third type is the interior penalty Galerkin method [11, 17] which is a discontinuous Galerkin method based on standard $C^0$-conforming approximation spaces usually used for second-order elliptic problems. Alternatively, researchers also expect $C^1$-conforming elements such as the Argyris/Bell triangular elements [2, 4] and the Bogner–Fox–Schmit [10] or Melkes/Watkins [29, 39] rectangular elements for a direct approximation to fourth equations. The advantage of the direct approximation is obvious, however, it requires $C^1$-conforming basis functions which are more difficult to construct and implement than $C^0$-conforming finite elements.

There is a growing trend toward the use of high-order methods to directly solve fourth-order equations owing to their high accuracy; see [5, 6, 12, 16, 21, 24, 25, 34,35,36, 40, 41] and the references therein. In [34, 35], Shen proposed some efficient spectral methods using basis functions in compact combinations of Legendre/Chebyshev polynomials for fourth-order equations, the algorithm of which was subsequently studied in [7, 8]. Aimed at the numerical solutions of high-order equations in a one-dimensional interval together with high-dimensional tensorial domains, Guo et al. developed generalized Jacobi polynomials [22, 23]. Spectral methods using generalized Jacobi polynomials lead to straightforward and well-conditioned implementations, and can be analyzed with a unified approach leading to more precise error estimates. Recently, Yu and Guo [41] proposed a spectral method for fourth-order problems on an arbitrary convex quadrilateral based on a bilinear mapping from the reference square to the computational domain. Inspired by the success of these direct and efficient spectral methods, some tentative progress has also been made in extending spectral methods to $C^1$-conforming spectral elements for more flexibility.

Indeed, spectral element methods were first introduced by Patera [32]. Analogue to p- and hp-finite-element methods, spectral element methods inherit the high order of convergence of the traditional spectral methods, while preserving the flexibility of the low-order finite-element methods. Theoretical and numerical evidences on second-order equations [13, 27, 28, 32] approve that spectral element methods can enjoy some essential priorities over the traditional spectral method and most of low-order methods. Although great efforts have been made on the $C^1$- and $H^k$-conforming finite elements on rectangles and cuboids (see [26, 42] and the references therein), few achievements have been reported on $C^1$-conforming spectral element methods [3, 40, 44], especially on the $C^1$-conforming spectral element method on the commonly used quadrangulated meshes, for solving fourth-order problems. After all, the construction of basis functions of the $C^1$-conforming approximation space is usually difficult. In particular, it has remained for years a question on how to construct the $C^1$-conforming spectral elements on an arbitrarily quadrangulated mesh.

The purpose of the current paper is to make efforts to construct the $C^1$-conforming quadrilateral basis and then to propose a $C^1$-conforming quadrilateral spectral element method for solving fourth-order partial differential equations. Similar to $C^0$-conforming basis, $C^1$-conforming basis functions can be divided into vertex modes, edge modes, and interior modes. The interior modes themselves together with their normal derivatives are identically zero on all edges. The edge modes involve eight one-dimensional trace functions constituted of function values and normal derivatives on four edges. For each edge basis function, all trace functions but one vanish identically. In analogy to Argyris [2] or Bell [4] triangles, the vertex modes on a given quadrilateral adopt 24 degrees of freedom constituted of all partial derivatives up to second order in primitive variables at four vertices. For each vertex basis function, all the 24 quantities but one are enforced zero.

With the help of the bilinear mapping from the reference square to the physical element, it is always easy to construct the interior mode basis. Starting with the corresponding basis functions on the reference square, it is also not difficult to derive such a type of mapped polynomial that all but one of their traces up to first-order on four edges vanish identically. Moreover, by searching in the space of all mapped polynomials of separate degree equal or less than 5, one can also obtain such functions that all but one of 24 partial derivatives at four vertices are zero.

Nevertheless, apart from the tedious procedure above, one of the main challenges of the construction of $C^1$-continuous basis on an unstructured quadrilateral mesh lies in that any first-order partial derivative of a piecewise mapped polynomial with respect to primitive variables is generally piecewise rational functions in the reference coordinates, whose denominator is exactly the Jacobi of the bilinear transformation on each quadrilateral. Hence, to guarantee the $C^1$-continuity of a piecewise mapped polynomial across the common edge of two adjacent quadrilaterals, the normal derivatives along the common edge from both sides should be reduced to the same polynomial. This compulsive requirement is fulfilled on each element by sacrificing one degree of freedom per common edge. However, this would cast some doubts upon the completeness of our $C^1$-conforming basis. Fortunately, owing to the polynomial inclusion of our basis functions, the completeness can be easily proved, and then confirmed by numerical experiments on the spectral method on a single quadrilateral for non-homogeneous boundary value problems and the $C^1$-conforming quadrilateral spectral element method on a multi-domain for biharmonic eigenvalue problems.

The next section is for preliminaries on the bilinear mapping and the generalized Jacobi polynomials. In Sect. 3, we construct the $C^1$-conforming quadrilateral basis functions for interior modes, edge modes, and vertex modes. The completeness of the $C^1$-conforming quadrilateral basis is first proved in Sect. 4, then a quadrilateral spectral method is proposed for the non-homogeneous boundary value problem of fourth-order equations to confirm the completeness theory. Finally, a $C^1$-conforming quadrilateral spectral element method is proposed for biharmonic eigenvalue problems. Numerical experiments are also presented to demonstrate the effectiveness and efficiency of our spectral element method.

2 Preliminaries

2.1 Mapping from the Reference Square onto Quadrilateral

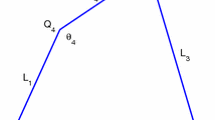
Let Q be an arbitrary convex quadrilateral with the vertices $P_i (x_i,y_i)$, the edges $\Gamma _i$ and the inner angles $\theta _i$, $i\le i\le 4$; see Fig. 1. The side length of $\Gamma _i$ is denoted by $l_i$. Further let ${\hat{Q}}=[-1,1]^2$ be the reference square with the vertices ${\hat{P}}_i$ and the edges ${\hat{\Gamma }}_i$, $1\le i\le 4$. We now make the variable transformation $F_{Q}: {\hat{Q}} \mapsto Q$,

$$\begin{aligned} \begin{pmatrix} x \\ y \end{pmatrix} = F_{Q} \begin{pmatrix} \xi \\ \eta \end{pmatrix} := \begin{pmatrix} x_1 \sigma _{1}(\xi ,\eta ) + x_2 \sigma _{2}(\xi ,\eta ) + x_3 \sigma _{3}(\xi ,\eta ) + x_4 \sigma _{4}(\xi ,\eta )\\ y_1 \sigma _{1}(\xi ,\eta ) + y_2 \sigma _{2}(\xi ,\eta ) + y_3 \sigma _{3}(\xi ,\eta ) + y_4 \sigma _{4}(\xi ,\eta ) \end{pmatrix}, \end{aligned}$$

(2.1)

where

$$\begin{aligned}&\sigma _{1}(\xi ,\eta ) = \frac{(1-\xi )(1-\eta )}{4} , \quad \sigma _{2}(\xi ,\eta ) = \frac{(1+\xi )(1-\eta )}{4} ,\\&\sigma _{3}(\xi ,\eta ) = \frac{(1+\xi )(1+\eta )}{4}, \quad \sigma _{4}(\xi ,\eta ) =\frac{(1-\xi )(1+\eta )}{4}. \end{aligned}$$

Fig. 1

Arbitrary convex quadrilateral (left) and the reference square $[-1,1]^2$ (right)

Throughout this paper, we always associate a function $\phi$ defined on Q with its partner

$$\begin{aligned} {\hat{\phi }} :=\phi \circ F_{Q} \end{aligned}$$

(2.2)

defined on ${\hat{Q}}$. For simplicity, we hereafter write

$$\begin{aligned}&x_{ji} = x_j - x_i,&y_{ji} = y_j - y_i. \end{aligned}$$

It is easy to see from the chain rule that

$$\begin{aligned} \partial _{\xi } {\hat{\phi }} =&A_{11}(\eta )\partial _{x}\phi +A_{12}(\eta )\partial _{y}\phi , \qquad \partial _{\eta } {\hat{\phi }} =A_{21}(\xi )\partial _{x}\phi +A_{22} (\xi )\partial _{y}\phi \end{aligned}$$

(2.3)

under (2.1), (2.2), where

$$\begin{aligned} A_{11}=A_{11}(\eta ) :=&\frac{x_{21}}{2} \frac{1-\eta }{2}+\frac{x_{34}}{2} \frac{1+\eta }{2} ,\quad A_{12}=A_{12}(\eta ) :=\frac{y_{21}}{2} \frac{1-\eta }{2}+\frac{y_{34}}{2} \frac{1+\eta }{2} ,\\ A_{21}=A_{21}(\xi ) :=&\frac{x_{41}}{2} \frac{1-\xi }{2}+\frac{x_{32}}{2} \frac{1+\xi }{2} ,\quad A_{22}=A_{22}(\xi ) :=\frac{y_{41}}{2} \frac{1-\xi }{2}+\frac{y_{32}}{2} \frac{1+\xi }{2} . \end{aligned}$$

We denote by $\nabla$, $\partial _{n}$ and $\partial _{\tau }$ the gradient operator, the outward normal derivative operator, and the anti-clockwise tangent derivative operator, respectively; while we adopt the symbols ${\hat{\nabla }}$, $\partial _{{\hat{n}}}$ and $\partial _{{\hat{\tau }}}$ for differentiation operators in the reference coordinates throughout the current paper for clarity. Then, one can simply write (2.3) as

$$\begin{aligned} {\hat{\nabla }} {\hat{\phi }} = \begin{pmatrix} A_{11} &{} A_{12} \\ A_{21} &{} A_{22} \end{pmatrix} \nabla \phi . \end{aligned}$$

The Jacobian of the variable transformation reads

$$\begin{aligned} J =J(\xi ,\eta ):=&\frac{x_{21} y_{41} - y_{21}x_{41}}{4} \frac{(1-\xi )(1-\eta )}{4} +\frac{x_{32}y_{12} -y_{32}x_{12}}{4} \frac{(1+\xi )(1-\eta )}{4}\\&+\frac{ x_{43}y_{23}- y_{43}x_{23}}{4} \frac{(1+\xi )(1+\eta )}{4} +\frac{x_{14}y_{34}-y_{14}x_{34}}{4} \frac{(1-\xi )(1+\eta )}{4} \\ =&\frac{l_{2}l_{1}\sin \theta _{1}}{4} \sigma _{1}(\xi ,\eta ) +\frac{l_{3}l_{2}\sin \theta _{2}}{4} \sigma _{2}(\xi ,\eta ) +\frac{l_{4}l_{3}\sin \theta _{3}}{4} \sigma _{3}(\xi ,\eta )\\&+\frac{l_{1}l_{4}\sin \theta _{4}}{4} \sigma _{4}(\xi ,\eta ). \end{aligned}$$

Although we write J as a combination of bilinear polynomials in $\xi$ and $\eta$, J is indeed linear since its leading term is exactly zero. For Q being convex, the bilinear mapping $F_{Q}$ is a bijection and thus admits an inverse mapping since $J>0$ on Q.

Conversely, we also have

$$\begin{aligned} \partial _{x} {\phi } = \frac{A_{22}(\xi )}{J(\xi ,\eta )} \partial _{\xi } {{\hat{\phi }}} - \frac{A_{12}(\eta )}{J(\xi ,\eta )}\partial _{\eta } {{\hat{\phi }}}, \qquad \partial _{y} {\phi } = -\frac{A_{21}(\xi )}{J(\xi ,\eta )}\partial _{\xi } {{\hat{\phi }}} + \frac{A_{11}(\eta )}{J(\xi ,\eta )}\partial _{\eta } {{\hat{\phi }}}. \end{aligned}$$

Specifically, at the vertex $P_1$, i.e., $(\xi ,\eta )=(-1,-1)$, one has

$$\begin{aligned} \partial _x {\phi } = \frac{2y_{41}}{l_1l_2\sin \theta _1}\partial _{\xi }{\hat{\phi }} - \frac{2y_{21}}{l_1l_2\sin \theta _1}\partial _{\eta } {\hat{\phi }} ,\qquad \partial _y {\phi } = -\frac{2x_{41}}{l_1l_2\sin \theta _1}\partial _{\xi }{\hat{\phi }} +\frac{2x_{21}}{l_1l_2\sin \theta _1}\partial _{\eta } {\hat{\phi }}. \end{aligned}$$

(2.4)

We are interested in the normal derivatives along the four edges of Q. To this end, we introduce the following bilinear function:

$$\begin{aligned} K=K(\xi ,\eta ) :=& -\frac{l_{2}l_{1}\cos \theta _{1}}{4} \sigma _{1}(\xi ,\eta ) +\frac{l_{3}l_{2}\cos \theta _{2}}{4} \sigma _{2}(\xi ,\eta ) \\&-\frac{l_{4}l_{3}\cos \theta _{3}}{4} \sigma _{3}(\xi ,\eta ) +\frac{l_{1}l_{4}\cos \theta _{4}}{4} \sigma _{4}(\xi ,\eta ) , \end{aligned}$$

and then arrive at the following lemma.

Lemma 2.1

It holds that

$$\begin{aligned} \partial _{\mathrm {n}}{\phi }\big |_{\Gamma }&= \left[ -\dfrac{l_{1} \partial _{\xi } {{\hat{\phi }}} }{2J} - \dfrac{2 K \partial _{\eta }{{\hat{\phi }}} }{l_1J} \Bigg|_{{\hat{\Gamma }}_1}, \ -\dfrac{l_{2} \partial _{\eta }{{\hat{\phi }}} }{2J} - \dfrac{2 K \partial _{\xi }{{\hat{\phi }}}}{l_2J} \Bigg |_{{\hat{\Gamma }}_2},\ \dfrac{l_{3} \partial _{\xi }{{\hat{\phi }}} }{2J} \nonumber \right. \\&\left. \quad + \dfrac{2 K \partial _{\eta }{{\hat{\phi }}} }{l_3J} \Bigg |_{{\hat{\Gamma }}_3}, \ \dfrac{l_{4} \partial _{\eta }{{\hat{\phi }}} }{2J} + \dfrac{2 K \partial _{\xi }{{\hat{\phi }}}}{l_4J} \Bigg |_{{\hat{\Gamma }}_4}\right] , \end{aligned}$$

(2.5)

hereafter, we use the tetrads for the trace on four edges, i.e., ${\phi } \big |_{\Gamma }=\left[ {{\hat{\phi }}} |_{\hat{\Gamma }_1},{\hat{\phi }} |_{{\hat{\Gamma }}_2},{\hat{\phi }} |_{{\hat{\Gamma }}_3},{\hat{\phi }} |_{{\hat{\Gamma }}_4}\right]$.

Proof

We start with the directional derivative ${ \begin{pmatrix} y_{14} \\ x_{41} \end{pmatrix} \cdot \nabla }$,

$$\begin{aligned} l_{1}\partial _{\mathrm {n}} {\phi }=&\, { \begin{pmatrix} y_{14} \\ x_{41} \end{pmatrix} \cdot \nabla \phi = \begin{pmatrix} y_{14} \\ x_{41} \end{pmatrix} \cdot \begin{pmatrix} A_{11} &{} A_{12} \\ A_{21} &{} A2_{22} \end{pmatrix} ^{-1} {\hat{\nabla }} {\hat{\phi }} } \\ =&\left( -\frac{y_{41}^2 + x_{41}^2 }{2} \frac{1-\xi }{2J} - \frac{y_{41}y_{32} + x_{41}x_{32} }{2} \frac{1+\xi }{2J} \right) {\partial _{\xi }} {{\hat{\phi }}} \\&+\left( \frac{y_{41}y_{21} +x_{41} x_{21} }{2} \frac{1-\eta }{2J} + \frac{y_{41}y_{34} + x_{41}x_{34} }{2} \frac{1+\eta }{2J} \right) {\partial _{\eta }} {{\hat{\phi }}} \\ =&\left[ -l_1^2 \frac{1-\xi }{4J} + l_{1}l_{3}\cos (\theta _{3}+\theta _{4}) \frac{1+\xi }{4J}\right] \partial _{\xi } {{\hat{\phi }}} \\&+ \left( l_1l_2\cos \theta _1 \frac{1-\eta }{4J} - l_{1} l_{4} \cos \theta _{4} \frac{1+\eta }{4J}\right) \partial _{\eta } {{\hat{\phi }}}. \end{aligned}$$

Hence on $\Gamma _1$,

$$\begin{aligned} \partial _{\mathrm {n}} {\phi } \big |_{\Gamma _1} =\,&-\frac{l_{1}}{2J} \partial _{\xi }{{\hat{\phi }}} +\left( l_2\cos \theta _1 \frac{1-\eta }{4J} - l_{4} \cos \theta _{4} \frac{1+\eta }{4J}\right) \partial _{\eta }{{\hat{\phi }}},\\ J\big |_{{\hat{\Gamma }}_1}=\,&\frac{1}{8} \left[ l_{2}l_{1}\sin \theta _{1} (1-\eta ) + l_{1}l_{4}\sin \theta _{4} (1+\eta ) \right] . \end{aligned}$$

Similar reductions give $\partial _{\mathrm {n}}{\phi }\big |_{\Gamma _2}$, $\partial _{\mathrm {n}}{\phi }\big |_{\Gamma _3}$ and $\partial _{\mathrm {n}}{\phi }\big |_{\Gamma _4}$ in Lemma 2.1, and thus completes the proof.

Let us now turn to the second-order derivatives. One gets from (2.1)–(2.3) that

$$\begin{aligned} \partial _{\xi }^2 {{\hat{\phi }}} =&A_{11}^2(\eta ) \partial _x^2{\phi } +2 A_{11}(\eta )A_{12}(\eta ) \partial _x\partial _y{\phi } +A_{12}^2(\eta ) \partial _y^2{\phi }, \\ \partial _{\eta }^2{{\hat{\phi }}} =&A_{21}^2(\xi ) \partial _x^2{\phi } +2 A_{21}(\xi )A_{22}(\xi ) \partial _x\partial _y{\phi } +A_{22}^2(\xi ) \partial _y^2{\phi }, \\ \partial _{\xi }\partial _{\eta } {{\hat{\phi }}}= &A_{11}(\eta )A_{21}(\xi ) \partial _x^2{\phi } +\left[ A_{12}(\eta )A_{21}(\xi )\right. \\&\left. +\, A_{11}(\eta )A_{22}(\xi ) \right] \partial _x\partial _y{\phi } +A_{12}(\eta )A_{22}(\xi ) \partial _y^2{\phi } \\&+\,A_{11}'(\eta )\partial _x{\phi } + A_{22}'(\xi )\partial _y{\phi }. \end{aligned}$$

Conversely,

$$\begin{aligned} \partial _{x}^2{\phi } =&\frac{2A_{12} A_{22} (-A_{22}' A_{21} + A_{22} A_{11}' )}{J^3} \partial _{\xi }{{\hat{\phi }}} + \frac{2A_{12} A_{22} (-A_{12} A_{11}' + A_{11} A_{22}' )}{J^3} \partial _{\eta } {{\hat{\phi }}} \\&+ \frac{A_{22}^2}{J^2} \partial _{\xi }^2{{\hat{\phi }}} - \frac{2A_{12}A_{22}}{J^2} \partial _{\xi }\partial _{\eta } {\hat{\phi }} +\frac{A_{12}^2}{J^2} \partial _{\eta }^2 {{\hat{\phi }}}, \\ \partial _{x}\partial _{y} {\phi }=&-\frac{(-A_{22}'A_{21}+A_{22}A_{11}')(A_{12}A_{21} + A_{11} A_{22} )}{J^3} \partial _{\xi }{{\hat{\phi }}} \\&- \frac{(-A_{11}'A_{12}+A_{11}A_{22}') (A_{12} A_{21} + A_{11} A_{22} )}{J^3} \partial _{\eta }{{\hat{\phi }}} \\&- \frac{A_{21}A_{22}}{J^2} \partial _{\xi }^2 {{\hat{\phi }}} + \frac{ A_{12} A_{21} + A_{11} A_{22} }{J^2} \partial _{\xi }\partial _{\eta }{{\hat{\phi }}} -\frac{A_{11}A_{12}}{J^2} \partial _{\eta }^2{{\hat{\phi }}}, \\ \partial _{y}^2{\phi } =&\frac{2A_{11} A_{21} (-A_{22}' A_{21} + A_{22} A_{11}' )}{J^3} \partial _{\xi }{{\hat{\phi }}} + \frac{2A_{11} A_{21} (-A_{12} A_{11}' + A_{11} A_{22}' )}{J^3} \partial _{\eta }{{\hat{\phi }}} \\&+ \frac{A_{21}^2}{J^2} \partial _{\xi }^2 {{\hat{\phi }}} - \frac{2A_{11}A_{21}}{J^2} \partial _{\xi }\partial _{\eta }{\hat{\phi }} +\frac{A_{11}^2}{J^2} \partial _{\eta }^2{{\hat{\phi }}}. \end{aligned}$$

In particular, at the corner $(\xi ,\eta )=(-1,-1)$,

$$\left\{\begin{aligned} &{\begin{aligned} \partial _x^2 {\phi }&= -\frac{4y_{41}y_{21} l_1l_3\sin \theta _5 }{(l_1l_2\sin \theta _1)^3} \partial _{\xi }{{\hat{\phi }}} + \frac{4y_{41}y_{21}l_2l_4\sin \theta _6}{(l_1l_2\sin \theta _1)^3}\partial _{\eta }{{\hat{\phi }}} \\&\quad + \frac{4y_{41}^2}{(l_1l_2\sin \theta _1)^2}\partial _{\xi }^2{{\hat{\phi }}} - \frac{8y_{41}y_{21}}{(l_1l_2\sin \theta _1)^2}\partial _{\xi }\partial _{\eta } {{\hat{\phi }}} + \frac{4y_{21}^2}{(l_1l_2\sin \theta _1)^2}\partial _{\eta }^2{\hat{\phi }}, \end{aligned}}\\& {\begin{aligned}\partial _x\partial _y {\phi }&= \frac{2 l_1l_3\sin \theta _5 (x_{21}y_{41}+y_{21}x_{41}) }{(l_1l_2\sin \theta _1)^3} \partial _{\xi }{{\hat{\phi }}} - \frac{ 2l_2l_4\sin \theta _6 (x_{21}y_{41}+y_{21}x_{41}) }{(l_1l_2\sin \theta _1)^3}\partial _{\eta }{{\hat{\phi }}} \\&\quad - \frac{4x_{41} y_{41}}{(l_1l_2\sin \theta _1)^2}\partial _{\xi }^2{{\hat{\phi }}} + \frac{4 (x_{21}y_{41}+y_{21}x_{41}) }{(l_1l_2\sin \theta _1)^2}\partial _{\xi }\partial _{\eta } {{\hat{\phi }}} - \frac{4x_{21}y_{21}}{(l_1l_2\sin \theta _1)^2}\partial _{\eta }^2{{\hat{\phi }}}, \end{aligned}}\\& {\begin{aligned}\partial _y^2 {\phi }&= -\frac{4x_{41}x_{21} l_1l_3\sin \theta _5 }{(l_1l_2\sin \theta _1)^3} \partial _{\xi }{{\hat{\phi }}} + \frac{4x_{41}x_{21}l_2l_4\sin \theta _6}{(l_1l_2\sin \theta _1)^3}\partial _{\eta }{{\hat{\phi }}} \\&\quad + \frac{4x_{41}^2}{(l_1l_2\sin \theta _1)^2}\partial _{\xi }^2{{\hat{\phi }}} - \frac{8x_{41}x_{21}}{(l_1l_2\sin \theta _1)^2}\partial _{\xi }\partial _{\eta } {{\hat{\phi }}} + \frac{4x_{21}^2}{(l_1l_2\sin \theta _1)^2}\partial _{\eta }^2{\hat{\phi }}, \end{aligned}} \end{aligned}\right.$$

(2.6)

where $\theta _5$ (resp. $\theta _6$) is defined as the angles between the edges $\Gamma _1$ and $\Gamma _3$ (respectively, $\Gamma _2$ and $\Gamma _4$),

$$\begin{aligned}&\sin \theta _{5} =\frac{y_{23}x_{14}-x_{23}y_{14} }{l_1l_3},&\cos \theta _{5} = \frac{y_{23}y_{14}+x_{23}x_{14} }{l_1l_3},\\&\sin \theta _{6} = \frac{y_{34}x_{21}-x_{34}y_{21} }{l_2l_4},&\cos \theta _{6} = \frac{y_{34}y_{21}+x_{34}x_{21} }{l_2l_4}. \end{aligned}$$

First and second-order partial derivatives at other vertices can be readily derived by parity.

2.2 Generalized Jacobi Polynomials

For any $\alpha ,\beta >-1$, denote by $J^{\alpha ,\beta }_n(\zeta )$ the n-th classic Jacobi polynomial with respect to the weight function $(1-\zeta )^{\alpha }(1+\zeta )^{\beta }$ on $[-1,1]$. Various generalizations have been introduced to allow $\alpha$ and/or $\beta$ being negative integers [23, 24, 38]. In the current paper, we define the following generalized Jacobi polynomials:

$$\begin{aligned} J^{-2,-2}_n(\zeta ) ={\left\{ \begin{array}{ll} \frac{(1-\zeta )^2(2+\zeta )}{4}, &{} n=0,\\ \frac{(1-\zeta )^2(1+\zeta )}{4}, &{} n =1,\\ \frac{(1+\zeta )^2(2-\zeta )}{4} , &{} n=2,\\ \frac{(1+\zeta )^2(\zeta -1)}{4}, &{}n=3,\\ \left( \frac{\zeta ^2-1}{4}\right) ^{2}J^{2,2}_{n-4}(\zeta ), &{} n \ge 4; \end{array}\right. } \qquad J^{-3,-3}_n(\zeta ) = {\left\{ \begin{array}{ll} \frac{(1-\zeta )^3(3\zeta ^2+9\zeta +8)}{16}, &{} n=0,\\ \frac{(1-\zeta )^3(3\zeta +5)(\zeta +1)}{16}, &{} n =1,\\ \frac{(1-\zeta )^3(\zeta +1)^2}{16} , &{} n=2,\\ \frac{(1+\zeta )^3(3\zeta ^2-9\zeta +8)}{16}, &{}n=3,\\ -\frac{(1+\zeta )^3(3\zeta -5)(\zeta -1)}{16}, &{}n=4,\\ \frac{(1+\zeta )^3(\zeta -1)^2}{16}, &{}n=5,\\ \left( \frac{\zeta ^2-1}{4}\right) ^{3}J^{3,3}_{n-6}(\zeta ), &{} n \ge 6. \end{array}\right. } \end{aligned}$$

It is readily checked that $\{ J^{-2,-2}_n: n\ge 4\}$ and $\{ J^{-3,-3}_n: n\ge 6\}$ coincide, up to a constant, with the generalized Jacobi polynomials in [23], while $\{ J^{-2,-2}_n: 0\le n\le 3\}$ and $\{ J^{-3,-3}_n: 0\le n\le 5\}$ are exactly the Hermite or Birkhoff interpolating basis functions on $[-1,1]$ up to the first and second derivatives, respectively. More precisely,

$$\begin{aligned}&\partial _{\zeta }^l J^{-2,-2}_n(-1) = \delta _{l, n} , \qquad \partial _{\zeta }^l J^{-2,-2}_n(1) = \delta _{l+2, n} , \qquad 0\le l\le 1, \ 0\le n\le 3, \end{aligned}$$

(2.7)

$$\begin{aligned}&\partial _{\zeta }^l J^{-3,-3}_n(-1) = \delta _{l, n} , \qquad \partial _{\zeta }^l J^{-3,-3}_n(1) = \delta _{l+3, n} , \qquad 0\le l\le 2, \ 0\le n\le 5. \end{aligned}$$

(2.8)

Besides, it holds that

$$\begin{aligned}&J^{-2,-2}_0(\zeta ) + J^{-2,-2}_2(\zeta ) = 1, \end{aligned}$$

(2.9)

$$\begin{aligned}&J^{-3,-3}_0(\zeta ) + J^{-3,-3}_3(\zeta ) = 1, \end{aligned}$$

(2.10)

$$\begin{aligned}&4J^{-2,-2}_4(\zeta ) + J^{-2,-2}_1(\zeta ) = {(1+\zeta )} J^{-2,-2}_0(\zeta ) , \end{aligned}$$

(2.11)

$$\begin{aligned}&\partial _{\zeta } J^{-3,-3}_1(\zeta ) =-15 J^{-2,-2}_4(\zeta ) + J^{-2,-2}_0(\zeta ), \end{aligned}$$

(2.12)

$$\begin{aligned}&\partial _{\zeta } J^{-3,-3}_0(\zeta ) = -15 J^{-2,-2}_4(\zeta ) . \end{aligned}$$

(2.13)

3 $C^1$-Conforming Quadrilateral Elements

In this section, we present our main theory on the construction of $C^1$-conforming basis functions on an arbitrary convex quadrilateral element Q. All basis functions are derived from polynomials on the reference square ${\hat{Q}}$, and thus are referred to as mapped polynomials. The $C^1$-conforming basis functions are divided into vertex modes, edge modes and interior modes. The interior modes themselves together with their normal derivatives are identically zero on all edges. The edge modes are further divided into two groups, the first group has magnitudes on one and only one edge while their normal derivatives are enforced zero on all edges; the second group vanishes identically on all edges while their normal derivatives have magnitudes on one and only one edge. The vanishment up to order two at four vertices is then characteristic of our $C^1$-conforming interior and edge basis functions.

In analogy to the Argyris/Bell triangle [2, 4] and the Melkes/Watkins rectangle [29, 39], the vertex modes are defined such that all the function values, first-order derivatives and second derivatives are enforced as zero at four vertices except one quantity at one vertex.

3.1 Interior Modes

It is easy to find the interior modes on an arbitrary quadrilateral Q.

Theorem 3.1

Define the interior mode basis $\phi _{m,n}, m,n\ge 4$ such that

$$\begin{aligned}&{{\hat{\phi }}_{m,n}}= J^{-2,-2}_m(\xi ) J^{-2,-2}_n(\eta ), \quad m,n\ge 4. \end{aligned}$$

Then,

$$\begin{aligned}&\phi _{m,n} \big |_{\Gamma }= \left[ 0,0,0,0\right] , \qquad \partial _{\mathrm {n}}\phi _{m,n} \big |_{\Gamma }= \left[ 0, 0, 0,0\right] , \qquad \qquad m,n\ge 4. \end{aligned}$$

3.2 Edge Modes

3.2.1 Derivative Edge Modes

To construct normal derivative edge modes on $\Gamma _1$, we also start with the basis functions on a rectangular element. By Lemma 2.1 and (2.7),

$$\left\{\begin{aligned}&\left[ J^{-2,-2}_{m}(\eta ) J^{-2,-2}_1(\xi ) \right] \big |_{\Gamma } = [0,0,0,0], \qquad m\ge 4, \\&\partial _{\mathrm {n}} \left[ J^{-2,-2}_{m}(\eta ) J^{-2,-2}_1(\xi ) \right] \big |_{\Gamma } = \left[ -\frac{l_1}{2J(-1,\eta )} J^{-2,-2}_{m}(\eta ),0,0,0 \right] ,\qquad m\ge 4. \end{aligned}\right. $$

(3.1)

Owing to the fact that

$$\begin{aligned} J\big |_{\hat \Gamma _1}=\frac{1}{8} \left[ l_{2}l_{1}\sin \theta _{1} (1-\eta ) + l_{1}l_{4}\sin \theta _{4} (1+\eta ) \right] , \end{aligned}$$

we find that the normal derivative on $\Gamma _1$ relies on the geometric quantities $l_2,\,{l_4},\, \theta _1$ and $\theta _4$. While the normal derivative of a typical $C^1$-conforming basis function on $\Gamma _i$ only relies on geometric quantities of the edge $\Gamma _i$. This observation motivates us to add a multiplier $J(-1,\eta )$ to basis function above,

$$\begin{aligned} \begin{aligned}&\partial _{\mathrm {n}}\left[ \frac{2}{l_1}J(-1,\eta ) J^{-2,-2}_{m}(\eta ) J^{-2,-2}_1(\xi ) \right] \Bigg |_{\Gamma _1} = -\frac{1}{J(-1,\eta )} J(-1,\eta ) J^{-2,-2}_{m}(\eta ) \partial _{\xi } J^{-2,-2}_{1}(-1)\\&\quad - \frac{4 K(-1,\eta ) }{l_1^2J(-1,\eta )} J^{-2,-2}_{1}(-1) \partial _{\eta } \left[ J(-1,\eta ) J^{-2,-2}_{m}(\eta )\right] = - J^{-2,-2}_{m}(\eta ). \end{aligned} \end{aligned}$$

(3.2)

We now end up with the desired basis functions and summarize our main theory on the normal derivative edge modes.

Theorem 3.2

Define the derivative edge mode basisby their partners

$$\begin{aligned}&{{\hat{\phi }}_{m,0}} =\frac{2}{l_1} J(-1,\eta ) J^{-2,-2}_{m}(\eta ) J^{-2,-2}_1(\xi ) ,\qquad m\ge 4 , \\&{{\hat{\phi }}_{m,1}} =\frac{2}{l_2} J(\xi ,-1) J^{-2,-2}_{m}(\xi ) J^{-2,-2}_1(\eta ) ,\qquad m\ge 4 , \\&{{\hat{\phi }}_{m,2}} =\frac{2}{l_3} J(1,\eta ) J^{-2,-2}_{m}(\eta ) J^{-2,-2}_3(\xi ) ,\qquad m\ge 4 , \\&{{\hat{\phi }}_{m,3}} =\frac{2}{l_4} J(\xi ,1) J^{-2,-2}_{m}(\xi ) J^{-2,-2}_3(\eta ) ,\qquad m\ge 4 . \end{aligned}$$

Then, for$m\ge 4$,

$$\begin{aligned}&\phi _{m,0} \big |_{\Gamma }= [0,0,0,0], \qquad \partial _{\mathrm {n}}\phi _{m,0} \big |_{\Gamma }= \left[ -J^{-2,-2}_{m}(\eta ), 0,0,0\right] , \\&\phi _{m,1} \big |_{\Gamma }= [0,0,0,0], \qquad \partial _{\mathrm {n}}\phi _{m,1} \big |_{\Gamma }= \left[ 0, -J^{-2,-2}_{m}(\xi ), 0,0\right] , \\&\phi _{m,2} \big |_{\Gamma }= [0,0,0,0], \qquad \partial _{\mathrm {n}}\phi _{m,2} \big |_{\Gamma }= \left[ 0, 0,J^{-2,-2}_{m}(\eta ),0\right] , \\&\phi _{m,3} \big |_{\Gamma }= [0,0,0,0], \qquad \partial _{\mathrm {n}}\phi _{m,3} \big |_{\Gamma }= \left[ 0, 0,0,J^{-2,-2}_{m}(\xi )\right] . \end{aligned}$$

3.2.2 Function Edge Modes

Let us concentrate on the construction of function edge modes. Once again, we start with a combination of edge modes on a rectangle: ${\hat{\phi }} =\frac{(n-5)(n-4)}{(2n-5)(2n-4)}J^{-2,-2}_{n}(\eta ) J^{-2,-2}_0(\xi ) -\frac{(n-3)(n-2)}{(2n-5)(2n-4)} \cdot J^{-2,-2}_{n-2}(\eta ) J^{-2,-2}_0(\xi ) =J^{-3,-3}_{n}(\eta ) J^{-2,-2}_0(\xi )$. By (2.7) and (2.5), it is readily checked that

$$\begin{aligned}&\phi \big |_{\Gamma } = [J^{-3,-3}_{n}(\eta ) , 0,0,0],\\&\partial _{\mathrm {n}} \phi \big |_{\Gamma } =\left[ - \frac{ (n-5)K(-1,\eta ) }{l_1J(-1,\eta )} J^{-2,-2}_{n-1}(\eta ) ,0,0,0\right] . \end{aligned}$$

Inspired by (3.2), we find that

$$\begin{aligned}&\left[ K(-1,\eta ) J^{-2,-2}_{m-1}(\eta ) J^{-2,-2}_1(\xi )\right] \big |_{\Gamma } = [0,0,0,0],\\&\partial _{\mathrm {n}} \left[ K(-1,\eta ) J^{-2,-2}_{m-1}(\eta ) J^{-2,-2}_1(\xi )\right] \big |_{\Gamma } = \left[ -\frac{l_1\, K(-1,\eta )}{2J(-1,\eta )} J^{-2,-2}_{m-1}(\eta ), 0,0,0\right] . \end{aligned}$$

This allows us to modify ${\hat{\phi }}$ as

$$\begin{aligned} {\hat{\phi }}=J^{-3,-3}_{n}(\eta ) J^{-2,-2}_0(\xi ) - 2(n-5) l_1^{-2}\, K(-1,\eta ) J^{-2,-2}_{n-1}(\eta ) J^{-2,-2}_1(\xi ), \end{aligned}$$

and finally get that

$$\begin{aligned}&\phi \big |_{\Gamma } = \left[ J^{-3,-3}_{n}(\eta ) , 0,0,0\right] ,\qquad \partial _{\mathrm {n}} \phi \big |_{\Gamma } =\left[ 0,0,0,0\right] . \end{aligned}$$

Theorem 3.3

Define the function edge mode basisby their partners

$$\begin{aligned} {{\hat{\phi }}_{0,n}}&= J^{-3,-3}_n(\eta )J^{-2,-2}_{0}(\xi ) - \frac{2(n-5)}{l_1^2} K(-1,\eta ) J^{-2,-2}_{n-1}(\eta ) J^{-2,-2}_1(\xi ) , \quad n\ge 6, \\ {{\hat{\phi }}_{1,n}}&= J^{-3,-3}_n(\xi )J^{-2,-2}_{0}(\eta ) - \frac{2(n-5)}{l_2^2} K(\xi ,-1) J^{-2,-2}_{n-1}(\xi ) J^{-2,-2}_1(\eta ) , \quad n\ge 6, \\ {{\hat{\phi }}_{2,n}}&= J^{-3,-3}_n(\eta )J^{-2,-2}_{2}(\xi ) - \frac{2(n-5)}{l_3^2} K(1,\eta ) J^{-2,-2}_{n-1}(\eta ) J^{-2,-2}_3(\xi ) , \quad n\ge 6, \\ {{\hat{\phi }}_{3,n}}&= J^{-3,-3}_n(\xi )J^{-2,-2}_{2}(\eta ) - \frac{2(n-5)}{l_4^2} K(\xi ,1) J^{-2,-2}_{n-1}(\xi ) J^{-2,-2}_3(\eta ) , \quad n\ge 6. \end{aligned}$$

Then, for$n\ge 6$,

$$\begin{aligned} \phi _{0,n}&\big |_{\Gamma } =\left[ J^{-3,-3}_n(\eta ), 0, 0 ,0\right] , \qquad \partial _{\mathrm {n}} \phi _{0,n}\big |_{\Gamma } =[0,0,0,0], \\ \phi _{1,n}&\big |_{\Gamma } =\left[ 0, J^{-3,-3}_n(\xi ), 0 ,0\right] , \qquad \partial _{\mathrm {n}} \phi _{1,n} \big |_{\Gamma } =[0,0,0,0], \\ \phi _{2,n}&\big |_{\Gamma } =\left[ 0, 0,J^{-3,-3}_n(\eta ), 0 \right] , \qquad \partial _{\mathrm {n}} \phi _{2,n} \big |_{\Gamma } =[0,0,0,0], \\ \phi _{3,n}&\big |_{\Gamma } =\left[ 0, 0, 0, J^{-3,-3}_n(\xi )\right] , \qquad \partial _{\mathrm {n}} \phi _{3,n} \big |_{\Gamma } =[0,0,0,0]. \end{aligned}$$

It is worthy to note that all interior modes and edge modes are charactered by the homogeneity of their function values together with the first and the second derivatives at the four vertices.

3.3 Vertex Modes

We now concentrate on the vertex modes, which actually are the Hermite or Birkhoff interpolation basis on the arbitrary quadrilateral Q. For simplicity, we use the sextuplet $\varvec {\phi }= [\phi , \partial _x \phi , \partial _y \phi , \partial _x^2 \phi , \partial _x\partial _y \phi , \partial _y^2 \phi ]$ for the derivatives up to second order of a given function $\phi$ defined on Q, and further use the tetrad $\varvec {\phi }\big |_{V}= [ \varvec {\phi }(P_1),\varvec {\phi }(P_2), \varvec {\phi }(P_3), \varvec {\phi }(P_4)]$ to denote all the derivatives up to second order at the four vertices. For simplicity, we abbreviate $\cos \theta _i$ as $c_i$ and $\sin \theta _i$ as $s_i$, and write

$$\begin{aligned} \begin{array}{lll} &{}x_{ji} = x_j - x_i, &{} y_{ji} = y_j - y_i,\\ &{}x_{*i} = (-1)^i (x_{1} +x_{3} -x_2 - x_4), &{}y_{*i} = (-1)^i (y_{1} +y_{3} -y_2 - y_4). \end{array} \end{aligned}$$

Each vertex mode basis function $\phi$ associated with a given vertex $P_i$ has one and only one unit entry in $\varvec {\phi }$ at $P_i$ and has a zero sextuplet $\varvec {\phi }$ at any other vertices. Thus, there are a total of 24 vertex mode basis functions just as the second type of Melkes rectangle [29]. We shall search all the vertex mode basis functions in the space $\mathrm {span}\{\xi ^m\eta ^n: 0\le m,n\le 5, \min (m,n)\le 3 \}$ and write them as symmetrically as possible in a combination of

$$\begin{aligned}&J^{-2,-2}_m(\xi ) J^{-3,-3}_n(\eta ),\quad J^{-2,-2}_m(\eta ) J^{-3,-3}_n(\xi ),\quad J^{-2,-2}_m(\xi ) J^{-2,-2}_n(\eta ). \end{aligned}$$

The 24 vertex modes can be divided into six groups, according to the non-vanishing entry (i.e., the non-vanishing partial derivative) of $\varvec {\phi }$ at four vertices.

3.3.1 Function Vertex Modes

We only need to explicitly construct the function vertex mode $\phi$ associate with $P_1$ such that

$$\begin{aligned}&\varvec {\phi }\big |_{V}=[[1,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0]],\\&\phi \big |_{\Gamma _3\cup \Gamma _4} = \partial _{\mathrm {n}}\phi \big |_{\Gamma _3\cup \Gamma _4} =0. \end{aligned}$$

The last equation above states that the partner ${{\hat{\phi }}}$ of $\phi$ has a polynomial factor $(1-\xi )^2 (1-\eta )^2$ and thus is a combination of the following generalized Jacobi polynomials:

$$\left\{\begin{aligned} \begin{aligned}&J^{-2,-2}_m(\xi ) J^{-3,-3}_n(\eta ),\ J^{-2,-2}_m(\eta ) J^{-3,-3}_n(\xi ), \quad m\in \{ 0,1\},\, n\in \{ 0,1,2,5\},\\&J^{-2,-2}_m(\xi ) J^{-2,-2}_n(\eta ), \quad \quad m,n\in \{ 0,1\}. \end{aligned} \end{aligned}\right.$$

(3.3)

To proceed, we calculate the partial derivatives with respect to $\xi$ and $\eta$ of order up to two of the above low-order Jacobi polynomials at four vertices, and list them in Tables 1, 2 and 3.

Table 1 Partial derivatives $(\mathrm {I},\partial _{\xi },\partial _{\eta },\partial _{\xi }^2,\partial _{\xi }\partial _{\eta },\partial _{\eta }^2)$ of $J^{-2,-2}_m(\xi ) J^{-3,-3}_n(\eta )$ for $m\in \{0,1\}$ and $n\in \{0,1,2,5\}$ at four vertices

Table 2 Partial derivatives $(\mathrm {I},\partial _{\xi },\partial _{\eta },\partial _{\xi }^2,\partial _{\xi }\partial _{\eta },\partial _{\eta }^2)$ of $J^{-2,-2}_m(\eta ) J^{-3,-3}_n(\xi )$ for $m\in \{0,1\}$ and $n\in \{0,1,2,5\}$ at four vertices

Table 3 Partial derivatives $(\mathrm {I},\partial _{\xi },\partial _{\eta },\partial _{\xi }^2,\partial _{\xi }\partial _{\eta },\partial _{\eta }^2)$ of $J^{-2,-2}_m(\xi ) J^{-2,-2}_n(\eta )$ for $m,n\in \{0,1\}$ at four vertices

In the sequel, we start the construction with the following polynomial:

$$\begin{aligned} {{\hat{\phi }}}=&J^{-2,-2}_0(\xi ) J^{-3,-3}_0(\eta ) +J^{-2,-2}_0(\eta ) J^{-3,-3}_0(\xi ) - J^{-2,-2}_0(\xi )J^{-2,-2}_0(\eta ). \end{aligned}$$

It is readily checked from Tables 1, 2 and 3 that

$$\begin{aligned} \begin{aligned}&{\hat{\phi }}(-1,-1)=1, \qquad {\hat{\phi }}(1,-1)={\hat{\phi }}(1,1)={\hat{\phi }}(-1,1)=0, \\&\partial _{\eta }{\hat{\phi }}(\pm 1, \pm 1)=\partial _{\xi }{\hat{\phi }}(\pm 1, \pm 1)=0, \\&\partial _{\eta }^2{\hat{\phi }}(\pm 1, \pm 1)=\partial _{\xi }^2{\hat{\phi }}(\pm 1, \pm 1)=\partial _{\xi }\partial _{\eta }{\hat{\phi }}(\pm 1, \pm 1)=0. \end{aligned} \end{aligned}$$

Further by (2.4) and (2.6), one has

$$\begin{aligned} \varvec {\phi }\big |_{V}=[[1,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0]]. \end{aligned}$$

However, by (2.7), (2.8) and (2.5),

$$\begin{aligned}&\phi \big |_{\Gamma }=[J^{-3,-3}_0(\eta ) , J^{-3,-3}_0(\xi ), 0,0],\\&\partial _{\mathrm {n}} \phi \big |_{\Gamma }=\left[ \frac{30 K}{l_1 J} J^{-2,-2}_4(\eta ), \frac{30 K}{l_2 J} J^{-2,-2}_4(\xi ), 0,0\right] . \end{aligned}$$

The awkward dependence of $\partial _{\mathrm {n}} \phi \big |_{\Gamma _1}$ and $\partial _{\mathrm {n}} \phi \big |_{\Gamma _2}$ on $\frac K{J}$ make $\phi$ hard to be a globally $C^1$-continuous basis function across the edges $\Gamma _1$ and $\Gamma _2$. To conquer this difficulty, we resort to the “kernerl” functions defined in (3.1). Indeed, in view of (3.1), we simply change ${{\hat{\phi }}}$ to

$$\begin{aligned} \begin{aligned} {{\hat{\phi }}} =&J^{-2,-2}_0(\xi ) J^{-3,-3}_0(\eta ) +J^{-2,-2}_0(\eta ) J^{-3,-3}_0(\xi ) - J^{-2,-2}_0(\xi )J^{-2,-2}_0(\eta ) \\&+\frac{60}{l_1^2} K(-1,\eta )J^{-2,-2}_4(\eta ) J^{-2,-2}_1(\xi ) + \frac{60}{l_2^2} K(\xi ,-1)J^{-2,-2}_4(\xi ) J^{-2,-2}_1(\eta ), \end{aligned} \end{aligned}$$

(3.4)

and find that

$$\begin{aligned}&\partial _{\mathrm {n}} \phi \big |_{\Gamma }=[0,0, 0,0]. \end{aligned}$$

This finally completes the construction of the vertex mode of order zero at $P_1$.

By a parity analysis, we obtain the vertex mode of order zero at $P_2$ (respectively, $P_3$ and $P_4$) by replacing $(\xi ,\eta )$ by $(\eta ,-\xi )$ (respectively, $(-\xi ,-\eta )$ and $(-\eta ,\xi )$), and the subscripts (1, 2, 3, 4) of c, s and l by (2, 3, 4, 1) (respectively, (3, 4, 1, 2) and (4, 1, 2, 3)).

Theorem 3.4

Define the basis of the function vertex modeby their partners

$$\begin{aligned} {{\hat{\phi }}_{0,0}} =&J^{-2,-2}_0(\xi ) J^{-3,-3}_0(\eta ) +J^{-2,-2}_0(\eta ) J^{-3,-3}_0(\xi ) - J^{-2,-2}_0(\xi )J^{-2,-2}_0(\eta ) \\&+ \frac{60 }{l_1^2} K(-1,\eta )J^{-2,-2}_4 (\eta ) J^{-2,-2}_1(\xi ) + \frac{60 }{l_2^2} K(\xi ,-1)J^{-2,-2}_4 (\xi ) J^{-2,-2}_1(\eta ), \\ {\hat{\phi }_{1,0}}=&J_{0}^{-2,-2}(\eta )J_{3}^{-3,-3}(\xi )+J_{2}^{-2,-2}(\xi )J_{0}^{-3,-3}(\eta )-J_{0}^{-2,-2}(\eta )J_{2}^{-2,-2}(\xi ) \\&- \frac{60 }{l_2^2} K(\xi ,-1)J^{-2,-2}_4 (\xi ) J_{1}^{-2,-2}(\eta ) +\frac{60 }{l_3^2} K(1,\eta )J^{-2,-2}_4 (\eta ) J_{3}^{-2,-2}(\xi ), \\ {\hat{\phi }_{2,0}}=&J_{2}^{-2,-2}(\xi )J_{3}^{-3,-3}(\eta )+J_{2}^{-2,-2}(\eta )J_{3}^{-3,-3}(\xi )-J_{2}^{-2,-2}(\xi )J_{2}^{-2,-2}(\eta ) \\&-\frac{60 }{l_3^2} K(1,\eta )J^{-2,-2}_4 (\eta ) J_{3}^{-2,-2}(\xi ) -\frac{60 }{l_4^2} K(\xi ,1)J^{-2,-2}_4 (\xi ) J_{3}^{-2,-2}(\eta ) , \\ {\hat{\phi }_{3,0}}=&J_{2}^{-2,-2}(\eta )J_{0}^{-3,-3}(\xi )+J_{0}^{-2,-2}(\xi )J_{3}^{-3,-3}(\eta )-J_{2}^{-2,-2}(\eta )J_{0}^{-2,-2}(\xi ) \\&+\frac{60 }{l_4^2} K(\xi ,1)J^{-2,-2}_4 (\xi ) J_{3}^{-2,-2}(\eta ) -\frac{60 }{l_1^2} K(-1,\eta )J^{-2,-2}_4 (\eta ) J_{1}^{-2,-2}(\xi ) . \end{aligned}$$

Then, it holds that

$$\begin{aligned} \phi _{0,0} \big |_{\Gamma }&= [J^{-3,-3}_0(\eta ), J^{-3,-3}_0(\xi ),0,0], \qquad \partial _{\mathrm {n}} \phi _{0,0} \big |_{\Gamma } =[0,0,0,0], \\ \phi _{1,0} \big |_{\Gamma }&= [0, J^{-3,-3}_3(\xi ),J^{-3,-3}_0(\eta ),0], \qquad \partial _{\mathrm {n}} \phi _{1,0} \big |_{\Gamma } =[0,0,0,0], \\ \phi _{2,0} \big |_{\Gamma }&= [0,0,J^{-3,-3}_3(\eta ), J^{-3,-3}_3(\xi )], \qquad \partial _{\mathrm {n}} \phi _{2,0} \big |_{\Gamma } =[0,0,0,0],\\ \phi _{3,0} \big |_{\Gamma }&= [J^{-3,-3}_3(\eta ), 0,0,J^{-3,-3}_0(\xi )], \qquad \partial _{\mathrm {n}} \phi _{3,0} \big |_{\Gamma } =[0,0,0,0]; \end{aligned}$$

and

$$\begin{aligned} \varvec {\phi }_{0,0}\big | _{V}&=[ [1,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{1,0}\big | _{V}&=[ [0,0,0,0,0,0],[1,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{2,0}\big | _{V}&=[ [0,0,0,0,0,0],[0,0,0,0,0,0],[1,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{3,0}\big | _{V}&=[ [0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[1,0,0,0,0,0]]. \end{aligned}$$

3.3.2 Gradient Vertex Modes

Among the generalized Jacobi polynomials listed in (3.3), we are interested in $J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi )$ and $J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta )$, which vanish up to order 2 at $P_2$, $P_3$ and $P_4$. By (2.4) and (2.6), the partial derivatives $[\mathrm {I}, \partial _x, \partial _y, \partial _{x}^2, \partial _{x}\partial _{y}, \partial _y^2]$ of $J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta )$ and $J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi )$ at $P_1$ are

$$\begin{aligned}&\left[ 0, \frac{2y_{41}}{l_1l_2\sin \theta _1}, -\frac{2x_{41}}{l_1l_2\sin \theta _1}, -\frac{4y_{41}y_{21} l_1l_3\sin \theta _5 }{(l_1l_2\sin \theta _1)^3}, \right. \\&\quad \left. \frac{2 l_1l_3\sin \theta _5 (x_{21}y_{41} \quad +y_{21}x_{41}) }{(l_1l_2\sin \theta _1)^3} , -\frac{4x_{41}x_{21} l_1l_3\sin \theta _5 }{(l_1l_2\sin \theta _1)^3}\right] \end{aligned}$$

and

$$\begin{aligned}&\left[ 0, - \frac{2y_{21}}{l_1l_2\sin \theta _1}, \frac{2x_{21}}{l_1l_2\sin \theta _1}, \frac{4y_{41}y_{21}l_2l_4\sin \theta _6}{(l_1l_2\sin \theta _1)^3}, \right. \\&\left. \quad - \frac{ 2l_2l_4\sin \theta _6 (x_{21}y_{41}+y_{21}x_{41}) }{(l_1l_2\sin \theta _1)^3} , \frac{4x_{41}x_{21}l_2l_4\sin \theta _6}{(l_1l_2\sin \theta _1)^3}\right] , \end{aligned}$$

respectively. Thus, taking

$$\begin{aligned} {{\hat{\phi }}}=\frac{x_{21}}{2} J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) +\frac{x_{41}}{2} J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ), \end{aligned}$$

we have

$$\begin{aligned} \varvec {\phi } \big |_{P_1} = \left[ 0,1,0, -\frac{ 2y_{41}y_{21} x_{*,1} }{(l_1l_2\sin \theta _1)^2} , \frac{ (x_{21}y_{41}+y_{21}x_{41}) x_{*,1} }{(l_1l_2\sin \theta _1)^2}, -\frac{2x_{41}x_{21} x_{*,1} }{(l_1l_2\sin \theta _1)^2} \right] , \end{aligned}$$

(3.5)

where the following identity has been used for deriving the equality sign:

$$\begin{aligned} x_{21} l_1 l_3 \sin \theta _5 -x_{41}l_2l_4\sin \theta _6 =x_{*,1} l_1l_2\sin \theta _1 . \end{aligned}$$

Fortunately, one finds that the last three entries in (3.5) are respective multiples of three coefficients of $\partial _{\xi }\partial _{\eta }$ in (2.6). Looking up Tables 1, 2 and 3, one also finds that $J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )$ vanishes up to order 2 at four vertices except for its unit mixed derivative with respect to $\xi$ and $\eta$ at $P_1$ such that the derivative tetrad reads

$$\begin{aligned}&\left[ \left[ 0,0,0, -\frac{ 8y_{41}y_{21} }{(l_1l_2\sin \theta _1)^2} , \frac{ 4(x_{21}y_{41}+y_{21}x_{41}) }{(l_1l_2\sin \theta _1)^2}, -\frac{8x_{41}x_{21} x_{*,1} }{(l_1l_2\sin \theta _1)^2} \right] ,\right. \\&\quad \left. [0,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0] \vphantom{-\frac{ 8y_{41}y_{21} }{(l_1l_2\sin \theta _1)^2} }\right] . \end{aligned}$$

Thus, we modify ${{\hat{\phi }}}$ as

$$\begin{aligned} {{\hat{\phi }}} = -\frac{x_{*1}}{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) +\frac{x_{21}}{2} J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) +\frac{x_{41}}{2} J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ), \end{aligned}$$

and then get

$$\begin{aligned} \varvec {\phi }\big |_{V} =[ [0,1,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0]]. \end{aligned}$$

Next, we evaluate $\phi$ and its normal derivative on $\Gamma _1\cup \Gamma _2$. By (2.7) and (2.8),

$$\begin{aligned}&\phi \big |_{\Gamma _1} = \frac{x_{41}}{2} J_{1}^{-3,-3}(\eta ) , \qquad \qquad \phi \big |_{\Gamma _2} =\frac{x_{21}}{2} J_{1}^{-3,-3}(\xi ). \end{aligned}$$

Meanwhile, by (2.5), (2.7), (2.8), (2.11) and (2.12),

$$\begin{aligned} \partial _{\mathrm {n}}\phi \big |_{\Gamma _1} =&-\frac{l_{1}}{2J(-1,\eta )} \left[ -\frac{x_{*1}}{4} J^{-2,-2}_1(\eta ) +\frac{x_{21}}{2} J^{-2,-2}_0(\eta )\right] \\&- \frac{2 K(-1,\eta ) }{l_1J(-1,\eta )} \frac{x_{41}}{2} \partial _{\eta } J^{-3,-3}_1(\eta ) \\ =&\left[ \frac{ l_{1}^2 x_{*1} }{8l_1J(-1,\eta )} (1+\eta ) J^{-2,-2}_0(\eta ) - \frac{ l_{1}^2 x_{*1} }{2l_1J(-1,\eta )} J^{-2,-2}_4(\eta )\right] \\&+\frac{l_1^2 x_{21}}{4l_1J(-1,\eta )} J^{-2,-2}_0(\eta ) \\&+\left[ \frac{15 x_{41} K(-1,\eta ) }{l_1J(-1,\eta )} J^{-2,-2}_4(\eta ) - \frac{x_{41} K(-1,\eta ) }{l_1J(-1,\eta )} J^{-2,-2}_0(\eta )\right] \\ =&-\frac{l_1 J^{-2,-2}_4(\eta )}{2J(-1,\eta )} \left[ -\frac{30 x_{41} }{l_1^2}K(-1,\eta ) +x_{*1} \right] \\&+ \frac{ l_{1}^2 x_{*1} (1+\eta ) -2 l_1^2 x_{21} -8x_{41} K(-1,\eta ) }{8l_1J(-1,\eta )} J^{-2,-2}_0(\eta ). \end{aligned}$$

Further using (3.1) together with the following identity:

$$\begin{aligned} 8y_{41} J(-1,\eta ) - 8x_{41} K(-1,\eta ) = l_{1}^2 x_{21} (1-\eta ) + l_{1}^2 x_{34} (1+\eta ), \end{aligned}$$

one derives that

$$\begin{aligned} \partial _{\mathrm {n}}\phi \big |_{\Gamma _1} =&\partial _{\mathrm {n}} \left[ \left( -\frac{30 x_{41} }{l_1^2}K(-1,\eta ) +x_{*1} \right) J^{-2,-2}_4(\eta ) J^{-2,-2}_1(\xi ) \right] \bigg |_{\Gamma _1} + \frac{ y_{14} }{l_1} J^{-2,-2}_0(\eta ). \end{aligned}$$

A parity argument also yields

$$\begin{aligned} \partial _{\mathrm {n}}\phi \big |_{\Gamma _2} =&\partial _{\mathrm {n}} \left[ -\left( \frac{30x_{21}}{l_2^2} K(\xi ,-1) -x_{*1} \right) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) \right] \bigg |_{\Gamma _2} + \frac{ y_{21} }{l_2} J^{-2,-2}_0(\eta ). \end{aligned}$$

Hence, we modify ${{\hat{\phi }}}$ once again as

$$\begin{aligned} {{\hat{\phi }}} =&-\frac{x_{*1}}{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) +\frac{x_{21}}{2} J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) +\frac{x_{41}}{2} J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ) \\&+\frac{30x_{41}}{l_1^2} K(-1,\eta ) J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) -x_{*1} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) \\&+\frac{30x_{21}}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) -x_{*1} J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) , \end{aligned}$$

and then find that

$$\begin{aligned}&\varvec {\phi } \big |_{\Gamma } = [[0,1,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\&\phi \big |_{\Gamma } =\left[ \frac{x_4-x_1}{2} J^{-3,-3}_1(\eta ), \frac{x_2-x_1}{2} J^{-3,-3}_1(\xi ), 0,0\right] ,\\&\partial _{\mathrm {n}}\phi \big |_{\Gamma } = \left[ \frac{y_1-y_4}{l_1} J^{-2,-2}_0(\eta ), \frac{y_2-y_1}{l_2} J^{-2,-2}_0(\xi ) ,0,0 \right] . \end{aligned}$$

We now draw our conclusion on the gradient modes with the following two theorems.

Theorem 3.5

Define the following gradient vertex mode basisby their partners:

$$\begin{aligned} {{\hat{\phi }}_{0,1}}=&\frac{x_{41}}{2} J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ) +\frac{x_{21}}{2} J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) -\frac{x_{*1}}{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) \\&+\frac{30x_{41}}{l_1^2} K(-1,\eta ) J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) -x_{*1} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) \\&+\frac{30x_{21}}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) -x_{*1} J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) , \\ {{\hat{\phi }}_{1,1}}=&-\frac{x_{12}}{2} J_{4}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) +\frac{x_{32}}{2} J_{1}^{-3,-3}(\eta ) J_{2}^{-2,-2}(\xi ) +\frac{x_{*2}}{4} J_{1}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) \\&-\frac{30x_{12}}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) -x_{*2} J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) \\&+\frac{30x_{32}}{l_3^2} K(1,\eta ) J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) +x_{*2} J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) , \\ {{\hat{\phi }}_{2,1}}=&-\frac{x_{23}}{2} J_{4}^{-3,-3}(\eta ) J_{2}^{-2,-2}(\xi ) -\frac{x_{43}}{2} J_{4}^{-3,-3}(\xi ) J_{2}^{-2,-2}(\eta ) -\frac{x_{*3}}{4} J_{3}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) \\&-\frac{30x_{23}}{l_3^2} K(1,\eta ) J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) +x_{*3} J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) \\&-\frac{30x_{43}}{l_4^2} K(\xi ,1) J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) +x_{*3} J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) , \\ {{\hat{\phi }}_{3,1}}=&\frac{x_{34}}{2} J_{1}^{-3,-3}(\xi ) J_{2}^{-2,-2}(\eta ) -\frac{x_{14}}{2} J_{4}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ) +\frac{x_{*4}}{4} J_{3}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) \\&+\frac{30x_{34}}{l_4^2} K(\xi ,1) J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) +x_{*4} J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) \\&-\frac{30x_{14}}{l_1^2} {K(-1,\eta )} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) -x_{*4} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ). \end{aligned}$$

Then,

$$\begin{aligned} \phi _{0,1} \big |_{\Gamma }&=\left[ \frac{x_{41}}{2} J^{-3,-3}_1(\eta ), \frac{x_{21}}{2} J^{-3,-3}_1(\xi ) ,0,0 \right] , \\ \phi _{1,1} \big |_{\Gamma }&=\left[ 0,\frac{x_{21}}{2} J^{-3,-3}_4(\xi ), \frac{x_{32}}{2} J^{-3,-3}_1(\eta ) ,0 \right] , \\ \phi _{2,1} \big |_{\Gamma }&=\left[ 0,0,\frac{x_{32}}{2} J^{-3,-3}_4(\eta ) ,\frac{x_{34}}{2} J^{-3,-3}_4(\xi )\right] , \\ \phi _{3,1} \big |_{\Gamma }&=\left[ \frac{x_{41}}{2} J^{-3,-3}_4(\eta ) ,0,0,\frac{x_{34}}{2} J^{-3,-3}_1(\xi )\right] ,\\ \partial _{\mathrm {n}}\phi _{0,1} \big |_{\Gamma }&= \left[ \frac{y_{14}}{l_1} J^{-2,-2}_0(\eta ), \frac{y_{21}}{l_2} J^{-2,-2}_0(\xi ) ,0,0 \right] , \\ \partial _{\mathrm {n}}\phi _{1,1} \big |_{\Gamma }&= \left[ 0, \frac{y_{21}}{l_2} J^{-2,-2}_2(\xi ) , \frac{y_{32}}{l_3} J^{-2,-2}_0(\eta ),0 \right] , \\ \partial _{\mathrm {n}}\phi _{2,1} \big |_{\Gamma }&= \left[ 0, 0, \frac{y_{32}}{l_3} J^{-2,-2}_2(\eta ), \frac{y_{43}}{l_4} J^{-2,-2}_2(\xi )\right] , \\ \partial _{\mathrm {n}}\phi _{3,1} \big |_{\Gamma }&= \left[ \frac{y_{14}}{l_1} J^{-2,-2}_2(\eta ), 0, 0, \frac{y_{43}}{l_4} J^{-2,-2}_0(\xi )\right] , \end{aligned}$$

and

$$\begin{aligned} \varvec {\phi }_{0,1}\big |_{V}&= [ [0,1,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{1,1}\big |_{V}&= [ [0,0,0,0,0,0],[0,1,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{2,1}\big |_{V}&= [ [0,0,0,0,0,0],[0,0,0,0,0,0],[0,1,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{3,1}\big |_{V}&= [ [0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,1,0,0,0,0]]. \end{aligned}$$

Theorem 3.6

Define the following gradient vertex mode basisby their partners:

$$\begin{aligned} {{\hat{\phi }}_{0,2}}=&\frac{y_{41}}{2} J_{1}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ) +\frac{y_{21}}{2} J_{1}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) -\frac{y_{*1}}{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{30y_{41}}{l_1^2} K(-1,\eta ) J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) -y_{*1} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi )\\&+\frac{30y_{21}}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) -y_{*1} J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) ,\\ {{\hat{\phi }}_{1,2}}=&-\frac{y_{12}}{2} J_{4}^{-3,-3}(\xi ) J_{0}^{-2,-2}(\eta ) +\frac{y_{32}}{2} J_{1}^{-3,-3}(\eta ) J_{2}^{-2,-2}(\xi ) +\frac{y_{*2}}{4} J_{1}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{30y_{12}}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta ) -y_{*2} J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta )\\&+\frac{30y_{32}}{l_3^2} K(1,\eta ) J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) +y_{*2} J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) ,\\ {{\hat{\phi }}_{2,2}}=&-\frac{y_{23}}{2} J_{4}^{-3,-3}(\eta ) J_{2}^{-2,-2}(\xi ) -\frac{y_{43}}{2} J_{4}^{-3,-3}(\xi ) J_{2}^{-2,-2}(\eta ) -\frac{y_{*3}}{4} J_{3}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&-\frac{30y_{23}}{l_3^2} K(1,\eta ) J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) +y_{*3} J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi )\\&-\frac{30y_{43}}{l_4^2} K(\xi ,1) J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) +y_{*3} J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) ,\\ {{\hat{\phi }}_{3,2}}=&\frac{y_{34}}{2} J_{1}^{-3,-3}(\xi ) J_{2}^{-2,-2}(\eta ) -\frac{y_{14}}{2} J_{4}^{-3,-3}(\eta ) J_{0}^{-2,-2}(\xi ) +\frac{y_{*4}}{4} J_{3}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi )\\&+\frac{30y_{34}}{l_4^2} K(\xi ,1) J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) +y_{*4} J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta )\\&-\frac{30y_{14}}{l_1^2} {K(-1,\eta )} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) -y_{*4} J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ). \end{aligned}$$

Then, there hold that

$$\begin{aligned} \phi _{0,2} \big |_{\Gamma }&=\left[ \frac{y_{41}}{2} J^{-3,-3}_1(\eta ), \frac{y_{21}}{2} J^{-3,-3}_1(\xi ) ,0,0 \right] ,\\ \phi _{1,2} \big |_{\Gamma }&=\left[ 0,\frac{y_{21}}{2} J^{-3,-3}_4(\xi ), \frac{y_{32}}{2} J^{-3,-3}_1(\eta ) ,0 \right] ,\\ \phi _{2,2} \big |_{\Gamma }&=\left[ 0,0,\frac{y_{32}}{2} J^{-3,-3}_4(\eta ) ,\frac{y_{34}}{2} J^{-3,-3}_4(\xi )\right] ,\\ \phi _{3,2} \big |_{\Gamma }&=\left[ \frac{y_{41}}{2} J^{-3,-3}_4(\eta ) ,0,0,\frac{y_{34}}{2} J^{-3,-3}_1(\xi )\right] ,\\ \partial _{\mathrm {n}}\phi _{0,2} \big |_{\Gamma }&= \left[ \frac{x_{41}}{l_1} J^{-2,-2}_0(\eta ), \frac{x_{12}}{l_2} J^{-2,-2}_0(\xi ) ,0,0 \right] ,\\ \partial _{\mathrm {n}}\phi _{1,2} \big |_{\Gamma }&= \left[ 0, \frac{x_{12}}{l_2} J^{-2,-2}_2(\xi ) , \frac{x_{23}}{l_3} J^{-2,-2}_0(\eta ),0 \right] ,\\ \partial _{\mathrm {n}}\phi _{2,2} \big |_{\Gamma }&= \left[ 0, 0, \frac{x_{23}}{l_3} J^{-2,-2}_2(\eta ), \frac{x_{34}}{l_4} J^{-2,-2}_2(\xi )\right] ,\\ \partial _{\mathrm {n}}\phi _{3,2} \big |_{\Gamma }&= \left[ \frac{x_{41}}{l_1} J^{-2,-2}_2(\eta ), 0, 0, \frac{x_{34}}{l_4} J^{-2,-2}_0(\xi )\right] , \end{aligned}$$

and

$$\begin{aligned} \varvec {\phi }_{0,2}\big |_{V}&= [ [0,0,1,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{1,2}\big |_{V}&= [ [0,0,0,0,0,0],[0,0,1,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{2,2}\big |_{V}&= [ [0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,1,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{3,2}\big |_{V}&= [ [0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,1,0,0,0]]. \end{aligned}$$

3.3.3 Hessian Vertex Modes

We start our construction of the xx-Hessian vertex mode basis functions at $P_1$ with

$$\begin{aligned} {\hat{\phi }}= \alpha _{11}J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )+ \alpha _{20} J_{2}^{-3,-3}(\xi )J_0^{-2,-2}(\eta )+ \alpha _{02} J_{2}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) \end{aligned}$$

for certain coefficients to be determined such that

$$\begin{aligned} \varvec {\phi } \big |_{V}=[[0,0,0,1,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0]]. \end{aligned}$$

Then, we mend ${\hat{\phi }}$ by adding the “kernel” terms with the unknown coefficients $\alpha _{41}$ and $\alpha _{14}$,

$$\begin{aligned} \alpha _{41}(\xi )J_{4}^{-2,-2}(\xi ) J_{1}^{-2,-2}(\eta ) +\alpha _{14}(\eta ) J_{4}^{-2,-2}(\eta ) J_{1}^{-2,-2}(\xi ) \end{aligned}$$

such that the function value and the normal derivative of $\phi$ on $\Gamma _i$ are dependent on the geometric parameters of $\Gamma _i$ ($i=1,2$). We shall omit the details, and simply draw the conclusion with the following three theorems.

Theorem 3.7

Define the followingxx-Hessian vertex mode basisby their partners:

$$\begin{aligned} {{\hat{\phi }}_{0,3}} =&\frac{x_{41}^2}{4} J_{2}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) +\frac{x_{21}^2}{4} J_{2}^{-3,-3}(\xi )J_0^{-2,-2}(\eta ) +\frac{x_{21} x_{41} }{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{5 x_{41}^2K(-1,\eta )}{l_1^2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) -\frac{x_{41}x_{*1} }{2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi )\\&+\frac{5x_{21}^2 K(\xi ,-1)}{l_2^2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) -\frac{ x_{21} x_{*1} }{2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ),\\ {{\hat{\phi }}_{1,3}} =&\frac{x_{12}^2}{4} J_{5}^{-3,-3}(\xi )J_0^{-2,-2}(\eta ) +\frac{x_{32}^2}{4} J_{2}^{-3,-3}(\eta )J_2^{-2,-2}(\xi ) -\frac{x_{32} x_{12} }{4} J_{3}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&-\frac{5x_{12}^2 K(\xi ,-1)}{l_2^2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) -\frac{ x_{12} x_{*2} }{2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{5x_{32}^2K(1,\eta ) }{l_3^2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) +\frac{x_{32} x_{*2} }{2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ),\\ {{\hat{\phi }}_{2,3}} =&\frac{x_{23}^2}{4} J_{5}^{-3,-3}(\eta )J_2^{-2,-2}(\xi ) +\frac{x_{43}^2}{4} J_{5}^{-3,-3}(\xi )J_2^{-2,-2}(\eta ) +\frac{x_{43} x_{23} }{4} J_{3}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{5x_{32}^2K(1,\eta ) }{l_3^2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) +\frac{x_{23} x_{*3} }{2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{5x_{43}^2K(\xi ,1) }{l_4^2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) +\frac{x_{43} x_{*3} }{2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ),\\ {{\hat{\phi }}_{3,3}} =&\frac{x_{34}^2}{4} J_{2}^{-3,-3}(\xi )J_2^{-2,-2}(\eta ) +\frac{x_{14}^2}{4} J_{5}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) -\frac{x_{14} x_{34} }{4} J_{1}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&+\frac{5x_{34}^2K(\xi ,1) }{l_4^2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) +\frac{x_{34} x_{*4} }{2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&-\frac{5 x_{14}^2K(-1,\eta ) }{l_1^2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) -\frac{x_{14} x_{*4} }{2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ). \end{aligned}$$

Then, we have

$$\begin{aligned}&\phi _{0,3} \big |_{\Gamma } = \left[ \frac{x_{41}^2}{4} J_2^{-3,-3}(\eta ), \frac{x_{21}^2}{4} J_2^{-3,-3}(\xi ), 0,0\right] ,\\&\phi _{1,3} \big |_{\Gamma } = \left[ 0, \frac{x_{12}^2}{4} J_5^{-3,-3}(\xi ), \frac{x_{32}^2}{4} J_2^{-3,-3}(\eta ),0\right] ,\\&\phi _{2,3} \big |_{\Gamma } = \left[ 0, 0,\frac{x_{23}^2}{4} J_5^{-3,-3}(\eta ), \frac{x_{43}^2}{4} J_5^{-3,-3}(\xi )\right] ,\\&\phi _{3,3} \big |_{\Gamma } = \left[ \frac{x_{14}^2}{4} J_5^{-3,-3}(\eta ),0, 0, \frac{x_{34}^2}{4} J_2^{-3,-3}(\xi )\right] , \\&\partial _{\mathrm {n}}\phi _{0,3} \big |_{\Gamma } =\left[ - \frac{ x_{41} y_{41}}{2l_1} J_1^{-2,-2}(\eta ), \frac{ x_{21} y_{21}}{2l_2} J_1^{-2,-2}(\xi ), 0, 0\right] ,\\&\partial _{\mathrm {n}}\phi _{1,3} \big |_{\Gamma } =\left[ 0, \frac{ x_{12} y_{12}}{2l_2} J_3^{-2,-2}(\xi ), \frac{ x_{32} y_{32}}{2l_3} J_1^{-2,-2}(\eta ), 0\right] ,\\&\partial _{\mathrm {n}}\phi _{2,3} \big |_{\Gamma } =\left[ 0, 0, \frac{ x_{23} y_{23}}{2l_3} J_3^{-2,-2}(\eta ), - \frac{ x_{43} y_{43}}{2l_4} J_3^{-2,-2}(\xi )\right] ,\\&\partial _{\mathrm {n}}\phi _{3,3} \big |_{\Gamma } =\left[ - \frac{ x_{14} y_{14}}{2l_1} J_3^{-2,-2}(\eta ), 0, 0, - \frac{ x_{34} y_{34}}{2l_4} J_1^{-2,-2}(\xi )\right] , \end{aligned}$$

and

$$\begin{aligned} \varvec {\phi }_{0,3}\big |_V&=[[0,0,0,1,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{1,3}\big |_V&=[[0,0,0,0,0,0],[0,0,0,1,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{2,3}\big |_V&=[[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,1,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{3,3}\big |_V&=[[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,1,0,0]]. \end{aligned}$$

Theorem 3.8

Define the followingxy-Hessian vertex mode basisby their partners:

$$\begin{aligned} {{\hat{\phi }}_{0,4}} =&\frac{x_{41} y_{41}}{2} J_{2}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) +\frac{x_{21}y_{21}}{2} J_{2}^{-3,-3}(\xi )J_0^{-2,-2}(\eta ) \\&+\frac{x_{21} y_{41} + y_{21} x_{41}}{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{10 x_{41} y_{41} K(-1,\eta )}{l_1^2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) -\frac{x_{41}y_{*1} +y_{41}x_{*1} }{2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi )\\&+\frac{10x_{21} y_{21} K(\xi ,-1)}{l_2^2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) -\frac{ x_{21} y_{*1} + y_{21} x_{*1} }{2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ),\\ {{\hat{\phi }}_{1,4}} =&\frac{x_{12} y_{12}}{2} J_{5}^{-3,-3}(\xi )J_0^{-2,-2}(\eta ) +\frac{x_{32} y_{32}}{2} J_{2}^{-3,-3}(\eta )J_2^{-2,-2}(\xi ) \\&-\frac{x_{32} y_{12} +y_{32} x_{12}}{4} J_{3}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&-\frac{10x_{12}y_{12} K(\xi ,-1)}{l_2^2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) -\frac{ x_{12} y_{*2}+y_{12} x_{*2} }{2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{10x_{32}y_{32}K(1,\eta ) }{l_3^2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) +\frac{x_{32} y_{*2} +y_{32} x_{*2} }{2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ),\\ {{\hat{\phi }}_{2,4}} =&\frac{x_{23}y_{23}}{2} J_{5}^{-3,-3}(\eta )J_2^{-2,-2}(\xi ) +\frac{x_{43}y_{43}}{2} J_{5}^{-3,-3}(\xi )J_2^{-2,-2}(\eta ) \\&+\frac{x_{43} y_{23}+y_{43} x_{23} }{4} J_{3}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{10x_{32}y_{32} K(1,\eta ) }{l_3^2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) +\frac{x_{23} y_{*3}+y_{23} x_{*3} }{2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{10x_{43}y_{43} K(\xi ,1) }{l_4^2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) +\frac{x_{43} y_{*3} +y_{43} x_{*3} }{2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ),\\ {{\hat{\phi }}_{3,4}}=&\frac{x_{34}y_{34}}{2} J_{2}^{-3,-3}(\xi )J_2^{-2,-2}(\eta ) +\frac{x_{14}y_{14}}{2} J_{5}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) \\&-\frac{x_{14} y_{34} +y_{14} x_{34} }{4} J_{1}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&+\frac{10x_{34} y_{34} K(\xi ,1) }{l_4^2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) +\frac{x_{34} y_{*4}+y_{34} x_{*4} }{2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&-\frac{10 x_{14} y_{14} K(-1,\eta ) }{l_1^2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) -\frac{x_{14} y_{*4} +y_{14} x_{*4} }{2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ). \end{aligned}$$

Then, we have

$$\begin{aligned}&\phi _{0,4} \big |_{\Gamma } = \left[ \frac{x_{41}y_{41}}{2} J_2^{-3,-3}(\eta ), \frac{x_{21}y_{21}}{2} J_2^{-3,-3}(\xi ), 0,0\right] ,\\&\phi _{1,4} \big |_{\Gamma } = \left[ 0, \frac{x_{12}y_{12}}{2} J_5^{-3,-3}(\xi ), \frac{x_{32}y_{32}}{2} J_2^{-3,-3}(\eta ),0\right] ,\\&\phi _{2,4} \big |_{\Gamma } = \left[ 0, 0,\frac{x_{23}y_{23}}{2} J_5^{-3,-3}(\eta ), \frac{x_{43}y_{43}}{2} {J_5^{-3,-3}(\xi )}\right] ,\\&\phi _{3,4} \big |_{\Gamma } = \left[ \frac{x_{14}y_{14}}{2} J_5^{-3,-3}(\eta ),0, 0, \frac{x_{34}y_{34}}{2} J_2^{-3,-3}(\xi )\right] ,\\&\partial _{\mathrm {n}}\phi _{0,4} \big |_{\Gamma } =\left[ \frac{ x_{41}^2- y_{41}^2}{2l_1} J_1^{-2,-2}(\eta ), \frac{ y_{21}^2-x_{21}^2 }{2l_2} J_1^{-2,-2}(\xi ), 0, 0\right] ,\\&\partial _{\mathrm {n}}\phi _{1,4} \big |_{\Gamma } =\left[ 0, \frac{y_{12}^2- x_{12}^2 }{2l_2} J_3^{-2,-2}(\xi ), \frac{ y_{32}^2- x_{32}^2 }{2l_3} J_1^{-2,-2}(\eta ), 0\right] ,\\&\partial _{\mathrm {n}}\phi _{2,4} \big |_{\Gamma } =\left[ 0, 0, \frac{y_{23}^2- x_{23}^2 }{2l_3} J_3^{-2,-2}(\eta ), \frac{ x_{43}^2-y_{43}^2 }{2l_4} J_3^{-2,-2}(\xi )\right] ,\\&\partial _{\mathrm {n}}\phi _{3,4} \big |_{\Gamma } =\left[ \frac{ x_{14}^2-y_{14}^2 }{2l_1} J_3^{-2,-2}(\eta ), 0, 0, \frac{x_{34}^2- y_{34}^2 }{2{l_4}} J_1^{-2,-2}(\xi )\right] , \end{aligned}$$

and

$$\begin{aligned} \varvec {\phi }_{0,4}\big |_V&=[[0,0,0,0,1,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{1,4}\big |_V&=[[0,0,0,0,0,0],[0,0,0,0,1,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{2,4}\big |_V&=[[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,1,0],[0,0,0,0,0,0]],\\ \varvec {\phi }_{3,4}\big |_V&=[[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,1,0]]. \end{aligned}$$

Theorem 3.9

Define theyy-Hessian mode basisby their partners

$$\begin{aligned} {{\hat{\phi }}_{0,5}} =&\frac{y_{41}^2}{4} J_{2}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) +\frac{y_{21}^2}{4} J_{2}^{-3,-3}(\xi )J_0^{-2,-2}(\eta ) +\frac{y_{21} y_{41} }{4} J_{1}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{5 y_{41}^2K(-1,\eta )}{l_1^2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) -\frac{y_{41}y_{*1} }{2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi )\\&+\frac{5y_{21}^2 K(\xi ,-1)}{l_2^2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) -\frac{ y_{21} y_{*1} }{2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ),\\ {{\hat{\phi }}_{1,5}} =&\frac{y_{12}^2}{4} J_{5}^{-3,-3}(\xi )J_0^{-2,-2}(\eta ) +\frac{y_{32}^2}{4} J_{2}^{-3,-3}(\eta )J_2^{-2,-2}(\xi ) -\frac{y_{32} y_{12} }{4} J_{3}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&-\frac{5y_{12}^2 K(\xi ,-1)}{l_2^2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta ) -\frac{ y_{12} y_{*2} }{2} J_{4}^{-2,-2}(\xi )J_{1}^{-2,-2}(\eta )\\&+\frac{5y_{32}^2K(1,\eta ) }{l_3^2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) +\frac{y_{32} y_{*2} }{2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ),\\ {{\hat{\phi }}_{2,5}} =&\frac{y_{23}^2}{4} J_{5}^{-3,-3}(\eta )J_2^{-2,-2}(\xi ) +\frac{y_{43}^2}{4} J_{5}^{-3,-3}(\xi )J_2^{-2,-2}(\eta ) +\frac{y_{43} y_{23} }{4} J_{3}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{5y_{32}^2K(1,\eta ) }{l_3^2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi ) +\frac{y_{23} y_{*3} }{2} J_{4}^{-2,-2}(\eta )J_{3}^{-2,-2}(\xi )\\&-\frac{5y_{43}^2K(\xi ,1) }{l_4^2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) +\frac{y_{43} y_{*3} }{2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ),\\ {{\hat{\phi }}_{3,5}} =&\frac{y_{34}^2}{4} J_{2}^{-3,-3}(\xi )J_2^{-2,-2}(\eta ) +\frac{y_{14}^2}{4} J_{5}^{-3,-3}(\eta )J_0^{-2,-2}(\xi ) -\frac{y_{14} y_{34} }{4} J_{1}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&+\frac{5y_{34}^2K(\xi ,1) }{l_4^2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta ) +\frac{y_{34} y_{*4} }{2} J_{4}^{-2,-2}(\xi )J_{3}^{-2,-2}(\eta )\\&-\frac{5 y_{14}^2K(-1,\eta ) }{l_1^2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ) -\frac{y_{14} y_{*4} }{2} J_{4}^{-2,-2}(\eta )J_{1}^{-2,-2}(\xi ). \end{aligned}$$

Then, we have

$$\begin{aligned}&\phi _{0,5} \big |_{\Gamma } = \left[ \frac{y_{41}^2}{4} J_2^{-3,-3}(\eta ), \frac{y_{21}^2}{4} J_2^{-3,-3}(\xi ), 0,0\right] ,\\&\phi _{1,5} \big |_{\Gamma } = \left[ 0, \frac{y_{12}^2}{4} J_5^{-3,-3}(\xi ), \frac{y_{32}^2}{4} J_2^{-3,-3}(\eta ),0\right] ,\\&\phi _{2,5} \big |_{\Gamma } = \left[ 0, 0,\frac{y_{23}^2}{4} J_5^{-3,-3}(\eta ), \frac{y_{43}^2}{4} J_5^{-3,-3}(\xi )\right] ,\\&\phi _{3,5} \big |_{\Gamma } = \left[ \frac{y_{14}^2}{4} J_5^{-3,-3}(\eta ),0, 0, \frac{y_{34}^2}{4} J_2^{-3,-3}(\xi )\right] ,\\&\partial _{\mathrm {n}}\phi _{0,5} \big |_{\Gamma } =\left[ \frac{ x_{41} y_{41}}{2l_1} J_1^{-2,-2}(\eta ), -\frac{ x_{21} y_{21}}{2l_2} J_1^{-2,-2}(\xi ), 0, 0\right] ,\\&\partial _{\mathrm {n}}\phi _{1,5} \big |_{\Gamma } =\left[ 0, - \frac{ x_{12} y_{12}}{2l_2} J_3^{-2,-2}(\xi ), -\frac{ x_{32} y_{32}}{2l_3} J_1^{-2,-2}(\eta ), 0\right] ,\\&\partial _{\mathrm {n}}\phi _{2,5} \big |_{\Gamma } =\left[ 0, 0, -\frac{ x_{23} y_{23}}{2l_3} J_3^{-2,-2}(\eta ), \frac{ x_{43} y_{43}}{2l_4} J_3^{-2,-2}(\xi )\right] ,\\&\partial _{\mathrm {n}}\phi _{3,5} \big |_{\Gamma } =\left[ \frac{ x_{14} y_{14}}{2l_1} J_3^{-2,-2}(\eta ), 0, 0, \frac{ x_{34} y_{34}}{2l_4} J_1^{-2,-2}(\xi )\right] , \end{aligned}$$

and

$$\begin{aligned}&\varvec {\phi }_{0,5}\big |_V=[[0,0,0,0,0,1],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\&\varvec {\phi }_{1,5}\big |_V=[[0,0,0,0,0,0],[0,0,0,0,0,1],[0,0,0,0,0,0],[0,0,0,0,0,0]],\\&\varvec {\phi }_{2,5}\big |_V=[[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,1],[0,0,0,0,0,0]],\\&\varvec {\phi }_{3,5}\big |_V=[[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,0],[0,0,0,0,0,1]]. \end{aligned}$$

4 Applications to Fourth-Order Equations

In the section, we shall propose the $C^1$-conforming quadrilateral spectral element methods for fourth-order equations. To this end, we start with the discussion of the completeness and the $C^1$-global continuity of the quadrilateral basis functions together with the spectral method using our $C^1$-conforming basis for solving non-homogeneous boundary value problems of fourth-order equations on an arbitrary quadrilateral.

4.1 Completeness and Global $C^1$-Continuity of the Quadrilateral Basis

We first explore the completeness of our quadrilateral basis. It is easy to see that all the basis functions constructed in the former section are linearly independent. Let N be an integer $\ge 5$. Denote by $\mathbb {P}_N(\Omega )$ be the mapped polynomial space of separate degree $\le N$ on $\Omega$. We list in Table 4 all the $C^1$-conforming basis functions which have a separate degree of $\le N$.

Table 4 The statistics on the basis of degree $\le N$ on an arbitrary quadrilateral Q

Let us introduce the corresponding mapped polynomial space

$$\begin{aligned}&V_N(Q) = \mathrm {span} \left\{ \phi _{m,n}: 0\le m\le M_n ,\ 0\le n \le N \right\} , \end{aligned}$$

where $M_n=N-1$ if $0\le n\le 3$ and $M_n=N$ if $4\le n\le N$. It is obvious that

$$\begin{aligned} \dim V_N(Q) = (N+1)^2-4 < (N+1)^2=\dim \mathbb {P}_N(Q). \end{aligned}$$

It then seems that $\{\phi _{m,n}: m,n\ge 0\}$ is not necessarily complete in $C^1(Q)$ or $H^2(Q)$. Nevertheless, the following lemma states that $V_N(Q), \, N\ge 5$ contains lower-order polynomials on Q.

Lemma 4.1

It holds that

$$\begin{aligned}&1=\phi _{0,0}+\phi _{1,0}+\phi _{2,0}+\phi _{3,0}, \end{aligned}$$

(4.1)

$$\begin{aligned}&x=x_1 \phi _{0,0}+x_2\phi _{1,0}+x_3\phi _{2,0}+x_4\phi _{3,0} + \phi _{0,1}+\phi _{1,1}+\phi _{2,1}+\phi _{3,1}, \end{aligned}$$

(4.2)

$$\begin{aligned}&y=y_1 \phi _{0,0}+y_2\phi _{1,0}+y_3\phi _{2,0}+y_4\phi _{3,0} + \phi _{0,2}+\phi _{1,2}+\phi _{2,2}+\phi _{3,2}. \end{aligned}$$

(4.3)

Proof

One readily obtains from Theorem 3.4, (2.9) and (2.10) that

$$ \begin{aligned} { \phi _{0,0}}+{{\hat{\phi }}_{1,0}}+{{\hat{\phi }}_{2,0}}+{\hat{\phi }_{3,0}}=&\, J^{-2,-2}_0(\xi ) J^{-3,-3}_0(\eta ) +J^{-2,-2}_0(\eta ) J^{-3,-3}_0(\xi ) - J^{-2,-2}_0(\xi )J^{-2,-2}_0(\eta )\\&+J_{0}^{-2,-2}(\eta )J_{3}^{-3,-3}(\xi )+J_{2}^{-2,-2}(\xi )J_{0}^{-3,-3}(\eta )-J_{0}^{-2,-2}(\eta )J_{2}^{-2,-2}(\xi )\\&+J_{2}^{-2,-2}(\xi )J_{3}^{-3,-3}(\eta )+J_{2}^{-2,-2}(\eta )J_{3}^{-3,-3}(\xi )-J_{2}^{-2,-2}(\xi )J_{2}^{-2,-2}(\eta )\\&+J_{2}^{-2,-2}(\eta )J_{0}^{-3,-3}(\xi )+J_{0}^{-2,-2}(\xi )J_{3}^{-3,-3}(\eta )-J_{2}^{-2,-2}(\eta )J_{0}^{-2,-2}(\xi )\\ =&\,\left[ J^{-2,-2}_0(\xi )+J^{-2,-2}_2(\xi )\right] \left[ J^{-3,-3}_0(\eta )+ J^{-3,-3}_3(\eta )\right] \\&+\left[ J^{-2,-2}_0(\eta )+J^{-2,-2}_2(\eta )\right] \left[ J^{-3,-3}_0(\xi )+ J^{-3,-3}_3(\xi )\right] \\&-\left[ J^{-2,-2}_0(\eta )+J^{-2,-2}_2(\eta )\right] \left[ J^{-2,-2}_0(\xi )+ J^{-2,-2}_2(\xi )\right] \\ =&\, 1+1-1=1, \end{aligned}$$

which exactly gives (4.1).

Further by Theorems 3.4 and 3.5, one finds

$$\begin{aligned}&x_1{{\hat{\phi }}_{0,0}}+x_2{{\hat{\phi }}_{1,0}}+x_3{\hat{\phi }_{2,0}}+x_4{{\hat{\phi }}_{3,0}}\\&=\, x_1\left[ J^{-2,-2}_0(\xi ) J^{-3,-3}_0(\eta ) +J^{-2,-2}_0(\eta ) J^{-3,-3}_0(\xi ) - J^{-2,-2}_0(\xi )J^{-2,-2}_0(\eta ) \right] \\&\qquad +x_2\left[ J_{0}^{-2,-2}(\eta )J_{3}^{-3,-3}(\xi )+J_{2}^{-2,-2}(\xi )J_{0}^{-3,-3}(\eta )-J_{0}^{-2,-2}(\eta )J_{2}^{-2,-2}(\xi )\right] \\&\qquad +x_3\left[ J_{2}^{-2,-2}(\xi )J_{3}^{-3,-3}(\eta )+J_{2}^{-2,-2}(\eta )J_{3}^{-3,-3}(\xi )-J_{2}^{-2,-2}(\xi )J_{2}^{-2,-2}(\eta )\right] \\&\qquad +x_4\left[ J_{2}^{-2,-2}(\eta )J_{0}^{-3,-3}(\xi )+J_{0}^{-2,-2}(\xi )J_{3}^{-3,-3}(\eta )-J_{2}^{-2,-2}(\eta )J_{0}^{-2,-2}(\xi )\right] \\&\qquad -\frac{60(x_{4}-x_{1})}{l_1^2} K(-1,\eta ) J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi )\\&\qquad -\frac{60(x_{2} -x_{1})}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta )\\&\qquad -\frac{60(x_{3}-x_{2})}{l_3^2} K(1,\eta ) J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) \\&\qquad -\frac{60(x_{3}-x_{4})}{l_4^2} K(\xi ,1) J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) , \end{aligned}$$

and

$$\begin{aligned}&{ {\hat\phi} _{0,1}}+{ {\hat\phi} _{1,1}}+{ {\hat \phi} _{2,1}}+{ {\hat \phi} _{3,1}}\\& = \, \frac{x_1-x_2+x_3-x_4}{4} [ J_1^{ -2,-2}(\xi )+J_3^{-2,-2}(\xi )] {[} J_1^{ -2,-2}(\eta )+J_3^{-2,-2}(\eta )]\\&\qquad +\frac{x_{4}-x_{1}}{2} [J_{1}^{-3,-3}(\eta ) + J_{4}^{-3,-3}(\eta )] J_{0}^{-2,-2}(\xi ) \\&\qquad +\frac{x_{2} -x_{1}}{2} [J_{1}^{-3,-3}(\xi )+J_{4}^{-3,-3}(\xi ) ] J_{0}^{-2,-2}(\eta )\\&\qquad +\frac{x_{3}-x_{2}}{2} \left[ J_{1}^{-3,-3}(\eta )+J_{4}^{-3,-3}(\eta ) \right] J_{2}^{-2,-2}(\xi ) \\&\qquad +\frac{x_{3}-x_{4}}{2} \left[ J_{1}^{-3,-3}(\xi )+J_{4}^{-3,-3}(\xi )\right] J_{2}^{-2,-2}(\eta )\\&\qquad +\frac{60(x_{4}-x_{1})}{l_1^2} K(-1,\eta ) J^{-2,-2}_4(\eta ) J_{1}^{-2,-2}(\xi ) \\&\qquad +\frac{60(x_{2} -x_{1})}{l_2^2} K(\xi ,-1) J^{-2,-2}_4(\xi ) J_{1}^{-2,-2}(\eta )\\&\qquad +\frac{60(x_{3}-x_{2})}{l_3^2} K(1,\eta ) J^{-2,-2}_4(\eta ) J_{3}^{-2,-2}(\xi ) \\&\qquad +\frac{60(x_{3}-x_{4})}{l_4^2} K(\xi ,1) J^{-2,-2}_4(\xi ) J_{3}^{-2,-2}(\eta ) , \end{aligned}$$

respectively. On the other hand, it is readily checked that

$$\begin{aligned}&\frac{1}{4} \left[ J_1^{ -2,-2}(\xi )+J_3^{-2,-2}(\xi )\right] [ J_1^{ -2,-2}(\eta )+J_3^{-2,-2}(\eta )] - J_0^{ -2,-2}(\xi ) J_0^{ -2,-2}(\eta )\\& \,+\frac{1}{2} J_0^{ -2,-2}(\eta ) [ 2J_0^{ -3,-3}(\xi ) -J_1^{ -3,-3}(\xi )-J_4^{-3,-3}(\xi ) ] \\ &\,+\frac{1}{2} J_0^{ -2,-2}(\xi ) [2J_0^{ -3,-3}(\eta )- J_1^{ -3,-3}(\eta )-J_4^{-3,-3}(\eta ) ]\\&\quad =\, \frac{ ( \xi +1) \xi ( \xi -1 ) ( \eta +1) \eta ( \eta -1 ) }{16} -\frac{( \xi -1 ) ^{2} ( \xi +2 ) ( \eta -1 ) ^{2} ( \eta +2 ) }{16}\\&\qquad \, - \frac{ ( \eta -1 ) ^{2} ( \eta +2 ) ( \xi -1 ) }{8} -\frac{ ( \xi -1 ) ^{2} ( \xi +2 ) ( \eta -1 ) }{8}\\&\quad =\,\frac{(1-\xi )(1-\eta )}{4} = \sigma _1(\xi ,\eta ),\\&\qquad -\frac{1}{4} [ J_1^{ -2,-2}(\xi )+J_3^{-2,-2}(\xi )] [ J_1^{ -2,-2}(\eta )+J_3^{-2,-2}(\eta )] - J_2^{ -2,-2}(\xi ) J_0^{ -2,-2}(\eta )\\&\qquad \,+\frac{1}{2} J_0^{ -2,-2}(\eta ) [ 2J_3^{ -3,-3}(\xi ) +J_1^{ -3,-3}(\xi )+J_4^{-3,-3}(\xi ) ]\\&\qquad \,+\frac{1}{2} J_2^{ -2,-2}(\xi ) [2J_0^{ -3,-3}(\eta )- J_1^{ -3,-3}(\eta )-J_4^{-3,-3}(\eta ) ]\\&\quad =\,\frac{(1-\xi )(1-\eta )}{4} = \sigma _2(\xi ,\eta ),\\&\frac{1}{4} [ J_1^{ -2,-2}(\xi )+J_3^{-2,-2}(\xi )] [ J_1^{ -2,-2}(\eta )+J_3^{-2,-2}(\eta )] - J_2^{ -2,-2}(\xi ) J_2^{ -2,-2}(\eta )\\&\qquad \,+\frac{1}{2} J_2^{ -2,-2}(\eta ) [ 2J_3^{ -3,-3}(\xi ) +J_1^{ -3,-3}(\xi )+J_4^{-3,-3}(\xi ) ]\\&\qquad \,+\frac{1}{2} J_2^{ -2,-2}(\xi ) [2J_3^{ -3,-3}(\eta )+ J_1^{ -3,-3}(\eta )+J_4^{-3,-3}(\eta ) ]\\&\quad =\,\frac{(1+\xi )(1+\eta )}{4} = \sigma _3(\xi ,\eta ),\\&\qquad -\frac{1}{4} [ J_1^{ -2,-2}(\xi )+J_3^{-2,-2}(\xi )] [ J_1^{ -2,-2}(\eta )+J_3^{-2,-2}(\eta )] - J_0^{ -2,-2}(\xi ) J_2^{ -2,-2}(\eta )\\&\qquad \,+\frac{1}{2} J_2^{ -2,-2}(\eta ) [ 2J_0^{ -3,-3}(\xi ) -J_1^{ -3,-3}(\xi )-J_4^{-3,-3}(\xi ) ]\\&\qquad \,+\frac{1}{2} J_0^{ -2,-2}(\xi ) [2J_3^{ -3,-3}(\eta )+ J_1^{ -3,-3}(\eta )+J_4^{-3,-3}(\eta ) ]\\&\quad =\,\frac{(1-\xi )(1+\eta )}{4} = \sigma _4(\xi ,\eta ). \end{aligned}$$

In the sequel, one derives

$$\begin{aligned} &x_1{{\hat{\phi }}_{0,0}}+x_2{{\hat{\phi }}_{1,0}}+x_3{\hat{\phi }_{2,0}}+x_4{{\hat{\phi }}_{3,0}} +{{\hat{\phi }}_{0,1}}+{\hat{\phi }_{1,1}}+{{\hat{\phi }}_{2,1}}+{{\hat{\phi }}_{3,1}}\\&\,= x_1\sigma _1(\xi ,\eta )+x_2\sigma _2(\xi ,\eta )+x_3\sigma _3(\xi ,\eta )+x_4\sigma _4(\xi ,\eta )=x, \end{aligned}$$

which states (4.2).

A parity analysis also yields (4.3). The proof is now complete.

Remark 4.1

Define the Hermite interpolation operator $I_5: C^2(Q)\mapsto V_5(Q)$ such that

$$\begin{aligned} {[}I_5 u](x,y) =&u(x_1,y_1)\phi _{0,0}+ u(x_2,y_2)\phi _{1,0}+ u(x_3,y_3) \phi _{2,0}+ u(x_4,y_4)\phi _{3,0}\\&+\partial _x u(x_1,y_1) \phi _{0,1}+ \partial _x u(x_2,y_2) \phi _{1,1}+\partial _x u(x_3,y_3) \phi _{2,1}+\partial _x u(x_4,y_4) \phi _{3,1}\\&+\partial _y u(x_1,y_1) \phi _{0,2}+ \partial _y u(x_2,y_2) \phi _{1,2}+\partial _y u(x_3,y_3) \phi _{2,2}+\partial _y u(x_4,y_4) \phi _{3,2}\\&+\partial _x^2 u(x_1,y_1) \phi _{0,3}+ \partial _x^2 u(x_2,y_2) \phi _{1,3}+\partial _x^2 u(x_3,y_3) \phi _{2,3}+\partial _x^2 u(x_4,y_4) \phi _{3,3}\\&+\partial _x\partial _y u(x_1,y_1) \phi _{0,4}+ \partial _x\partial _y u(x_2,y_2) \phi _{1,4}\\&+\partial _x\partial _y u(x_3,y_3) \phi _{2,4}+\partial _x\partial _y u(x_4,y_4) \phi _{3,4}\\&+\partial _y^2 u(x_1,y_1) \phi _{0,5}+ \partial _y^2 u(x_2,y_2) \phi _{1,5}+\partial _y^2 u(x_3,y_3) \phi _{2,5}+\partial _y^2 u(x_4,y_4) \phi _{3,5}. \end{aligned}$$

Then, $I_5$ recovers polynomials of total degree no greater than 3 on Q,

$$\begin{aligned} {[}I_5 u](x,y) = u(x,y), \qquad u \in \Pi _3(Q), \end{aligned}$$

(4.4)

where $\Pi _N(Q)=\{ x^iy^j: 0\le i,j, i+j\le N \}$. We do not intend to give a tedious proof for (4.4) in this paper, however, it can be verified using a symbolic computational software such as MAPLE.

Generally, for $u\in {\Pi _N}(Q)$, we have the following hypothesis:

$$\begin{aligned} u(x,y)-[I_5u](x,y) = \sum _{m=4}^N \sum _{n=4}^N c_{m,n} \phi _{m,n} + \sum _{m=4}^{N-1}\sum _{i=0}^3 c_{m,i} \phi _{m,i} + \sum _{n=6}^{N}\sum _{i=0}^3 c_{i,n} \phi _{i,n}, \end{aligned}$$

(4.5)

where the coefficients $c_{m,n}=c_{m,n}(u)$ are defined by

$$\begin{aligned} c_{m,n}(u) =&\, \frac{\int _{-1}^{1} \int _{-1}^{1} \partial _{\xi }^2 \partial _{\eta }^2 {{\hat{u}}(\xi ,\eta )} \cdot \partial _{\xi }^2 \partial _{\eta }^2 {{\hat{\phi }}_{m,n}(\xi ,\eta )} \,\mathrm {d}\xi \,\mathrm {d}\eta }{\int _{-1}^{1} \int _{-1}^{1} \left[ \partial _{\xi }^2 \partial _{\eta }^2{{\hat{\phi }}_{m,n}(\xi ,\eta )} \right] ^2 \,\mathrm {d}\xi \,\mathrm {d}\eta } \end{aligned}$$

for $m,n \ge 4$, and

$$\begin{aligned}&c_{m,0}(u)=\frac{\int _{-1}^1 ( \partial _{\eta }^2 \partial _{\mathrm {n}} {{\hat{u}}} \cdot \partial _{\eta }^2 \partial _{\mathrm {n}}{{\hat{\phi }}_{m,0}} )(-1,\eta ) \,\mathrm {d}\eta }{ \int _{-1}^1 ( \partial _{\eta }^2 \partial _{\mathrm {n}}{\hat{\phi }_{m,0} } )^2(-1,\eta ) \,\mathrm {d}\eta },&c_{0,n}(u)=\frac{\int _{-1}^1 ( \partial _{\eta }^3 { {\hat{u}}} \cdot \partial _{\eta }^3 {{\hat{\phi }}_{0,n} })(-1,\eta ) \,\mathrm {d}\eta }{ \int _{-1}^1 ( \partial _{\eta }^3 {{\hat{\phi }}_{0,n} } )^2(-1,\eta ) \,\mathrm {d}\eta },\\&c_{m,1}(u)=\frac{\int _{-1}^1 ( \partial _{\xi }^2 \partial _{\mathrm {n}}{{\hat{u}}} \cdot \partial _{\xi }^2 \partial _{\mathrm {n}}{{\hat{\phi }}_{m,1} })(\xi ,-1) \,\mathrm {d}\xi }{ \int _{-1}^1 ( \partial _{\xi }^2 \partial _{\mathrm {n}}{\hat{\phi }_{m,1}} )^2(\xi ,-1) \,\mathrm {d}\xi },&c_{1,n}(u)=\frac{\int _{-1}^1 ( \partial _{\xi }^3 {{\hat{u}}} \cdot \partial _{\xi }^3 {{\hat{\phi }}_{1,n} })(\xi ,-1) \,\mathrm {d}\xi }{ \int _{-1}^1 ( \partial _{\xi }^3{ {\hat{\phi }}_{1,n}} )^2(\xi ,-1) \,\mathrm {d}\xi },\\&c_{m,2}(u)=\frac{\int _{-1}^1 ( \partial _{\eta }^2 \partial _{\mathrm {n}} {{\hat{u}}} \cdot \partial _{\eta }^2 \partial _{\mathrm {n}} {{\hat{\phi }}_{m,2}} )(1,\eta ) \,\mathrm {d}\eta }{ \int _{-1}^1 ( \partial _{\eta }^2 \partial _{\mathrm {n}}\hat{\phi }_{m,2} )^2(1,\eta ) \,\mathrm {d}\eta },&c_{2,n}(u)=\frac{\int _{-1}^1 ( \partial _{\eta }^3 u \cdot \partial _{\eta }^3{\hat{\phi }}_{2,n} )(1,\eta ) \,\mathrm {d}\eta }{ \int _{-1}^1 ( \partial _{\eta }^3{ {\hat{\phi }}_{2,n}} )^2(1,\eta ) \,\mathrm {d}\eta },\\&c_{m,3}(u)=\frac{\int _{-1}^1 ( \partial _{\xi }^2 \partial _{\mathrm {n}}{{\hat{u}}} \cdot \partial _{\xi }^2 \partial _{\mathrm {n}}{{\hat{\phi }}_{m,3} })(\xi ,1) \,\mathrm {d}\xi }{ \int _{-1}^1 ( \partial _{\xi }^2 \partial _{\mathrm {n}}{\hat{\phi }_{m,3}} )^2(\xi ,1) \,\mathrm {d}\xi },&c_{3,n}(u)=\frac{\int _{-1}^1 ( \partial _{\xi }^3{{\hat{u}}} \cdot \partial _{\xi }^3{\hat{\phi }_{3,n}} )(\xi ,1) \,\mathrm {d}\xi }{ \int _{-1}^1 ( \partial _{\xi }^3 {{\hat{\phi }}_{3,n}} )^2(\xi ,1) \,\mathrm {d}\xi } \end{aligned}$$

for $m\ge 4$ and $n\ge 6$. The hypothesis (4.5) can be partially (up to $N=5$, for instance) verified using the MAPLE software. In particular, for $0\le i,j; i+j\le 4$,

$$\begin{aligned} x^i y^{{j}} = I_5(x^i y^{{j}}) + \frac{(i+j-3)_4}{4!} (x_1-x_2+x_3-x_4)^i (y_1-y_2+y_3-y_4)^j \phi _{4,4}, \end{aligned}$$

(4.6)

where we have used the Pochhammer symbol $(a)_k= a(a+1)\cdots (a+k-1)$. It then indicates all polynomials of total degree no greater than 4 on Q are in $V_5(Q)$.

Now let us turn to the completeness of our basis functions. To this end, we define

$$\begin{aligned} V(Q) = \bigcup \limits _{N=5}^{\infty } V_N(Q), \end{aligned}$$

which is exactly the set of all functions with a finite expansion in $\phi _{m,n}, m,n \ge 0$. Then, V(Q) is characterized by those mapped polynomials whose trace functions up to first order on each edge are polynomials depending on only the geometric parameters of the edge. As a result, we claim that V(Q) is an algebra of functions on Q. Indeed, for any $f,g\in V(Q)$ and $c\in \mathbb {R}$, it is obvious that $cf, cg, f+g\in V(Q)$. Moreover, fg is also a mapped polynomial on Q, and $(fg)\big |_{\Gamma _i}= f\big |_{\Gamma _i} \cdot g\big |_{\Gamma _i}$ and $\partial _{\mathrm {n}}(fg)\big |_{\Gamma _i} =(g\partial _{\mathrm {n}}f)\big |_{\Gamma _i} +(f\partial _{\mathrm {n}}g)\big |_{\Gamma _i}$ are certainly polynomials depending on only the geometric quantities of $\Gamma _i$, $i=1,2,3,4$. This clearly states that $fg\in V(Q)$. Hence, by Lemma 4.1, any monomial $x^iy^j$, $i,j\ge 0$, is a function in V(Q).

In return, we claim our main theory on the completeness of our basis functions.

Theorem 4.1

V(Q) includes all polynomials onQ, and thus is complete onQ.

Let us concentrate on the global $C^1$-continuity of the quadrilateral basis before concluding this subsection. It suffices to explore the trace of $I_5u$ and show its global $C^1$-continuity. Indeed, one readily finds that

$$\begin{aligned} (I_5u) \big |_{\Gamma _1}&= u(x_1,y_1) J^{-3,-3}_0(\eta ) + u(x_4,y_4) J^{-3,-3}_3(\eta )\\&\quad -\frac{l_1}{2} \partial _{\tau _1}u(x_1,y_1) J^{-3,-3}_1(\eta ) -\frac{l_1}{2} \partial _{\tau _1}u(x_4,y_4) J^{-3,-3}_4(\eta )\\&\quad +\frac{l_1^2}{4} \partial _{\tau _1}^2 u(x_1,y_1) J^{-3,-3}_2(\eta ) + \frac{l_1^2}{4} \partial _{\tau _1}^2 u(x_4,y_4) J^{-3,-3}_5(\eta ); \end{aligned}$$

$$\begin{aligned}\partial _{\rm {n}} (I_5u) \big |_{\Gamma _1} = &\partial _{n_1}u(x_1,y_1) J^{-2,-2}_0(\eta ) + \partial _{n_1}u(x_4,y_4) J^{-2,-2}_2(\eta )\\ &-\frac{l_1}{2} \partial _{\tau _1}\partial _{n_1} u(x_1,y_1) J^{-2,-2}_1(\eta ) -\frac{l_1}{2} \partial _{\tau _1}\partial _{n_1} u(x_4,y_4) J^{-2,-2}_3(\eta ), \end{aligned}$$

where $n_i$ is the unit outward normal vector of $\Gamma _i$, $\tau _i$ is the unit tangent vector to $\Gamma _i$ following the positive orientation with respect to Q. It turns out that $(I_5u) |_{\Gamma _1}$ is the second-order Hermite interpolation of u on $\Gamma _1$, and $\partial _{\text{n}}(I_5u) |_{\Gamma _1}$ is the standard first-order Hermite interpolation of $\partial _{\text{n}} u$ on $\Gamma _1$. And this states that $I_5u$ is globally continuous on $\Gamma _1$.

Similar arguments lead to the global continuity of $I_5u$ on $\Gamma _2$, $\Gamma _3$ and $\Gamma _4$. In return, one derives the global continuity of all the quadrilateral basis functions.

4.2 Quadrilateral Spectral Method for Non-homogeneous Boundary Value Problems

To testify our completeness theory, we consider the following non-homogeneous boundary value problem of the biharmonic equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta ^2 u = f &{}\text { in } Q, \\ u = g_i &{} \text { on } \Gamma _i, \ i=1,2,3,4,\\ \partial _{\mathrm {n}}u = h_i &{} \text { on } \Gamma _i, \ i=1,2,3,4, \end{array}\right. } \end{aligned}$$

(4.7)

where Q is a given convex quadrilateral; while f is supposed to be in $H^{-2}(Q)$, and $(g_i, h_i) \in H^{\frac{3}{2}}(\Gamma _i)\times H^{\frac{1}{2}}(\Gamma _i)$, $i=1,2,3,4$, are compatible boundary data. The equivalent variational form reads: to find $u\in H^2(\Omega )$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} ( \Delta u, \Delta v) = (f,v) , &{} v\in H^2_0(Q), \\ u = g_i &{} \text { on } \Gamma _i, \ 1\le i\le 4,\\ \partial _{\mathrm {n}}u = h_i &{} \text { on } \Gamma _i, \ 1\le i\le 4. \end{array}\right. } \end{aligned}$$

By the extension theorem and the Lax–Milgram lemma, it admits a unique solution $u\in H^2(Q)$.

4.2.1 Approximation Scheme and Implementation

Assume that $f\in H^k(Q)$ and $(g_i,h_i) \in H^{k+\frac{7}{2}}(\Gamma _i)\times H^{k+\frac{5}{2}}(\Gamma _i), \, 1\le i\le 4, \ k \ge -1$ with the following compatibility conditions:

$$\left\{\begin{aligned} \begin{aligned}&g_i(P_i) = g_{\bar{i}}(P_{i}), \\&\partial _{\tau _i} g_i (P_i) = -\cos \theta _i \partial _{\tau _{\bar{i}}} g_{\bar{i}} + \sin \theta _i h_{\bar{i}} (P_i), \\&h_i (P_i) = -\sin \theta _i \partial _{\tau _{\bar{i}}} g_{\bar{i}} - \cos \theta _i h_{\bar{i}} (P_i), \end{aligned}&1\le i\le 4, \end{aligned}\right.$$

(4.8)

where $\bar{i}=i+1$ if $1\le i\le 3$ and $\bar{i}=1$ if $i=4$. In addition, assume that

$$\begin{aligned}&-\cos \theta _i \,\partial _{\tau _i}^2 g_i (P_i) - \sin \theta _i \, \partial _{\tau _i} h_i (P_i) = -\cos \theta _i \,\partial _{\tau _{\bar{i}}}^2 g_{\bar{i}} (P_i) + \sin \theta _i \, \partial _{\tau _{\bar{i}}} h_{\bar{i}} (P_i),\quad 1\le i\le 4, \end{aligned}$$

(4.9)

when $k\ge 0$ and

$$\begin{aligned} \begin{aligned}&\int _{0}^{1} \Big | \cos \theta _i \left[ -\partial _{\tau _i}^2 g_i (P_i-s l_i\tau _i) + \partial _{\tau _{\bar{i}}}^2 g_{\bar{i}} (P_i+s l_{\bar{i}} \tau _{\bar{i}})\right] \\&\qquad + \sin \theta _i \left[ -\partial _{\tau _i} h_i (P_i-s l_{i}\tau _i) - \partial _{\tau _{\bar{i}}} g_{\bar{i}} (P_i+s _{\bar{i}} \tau _{\bar{i}}) \right] \Big |^2 \frac{\text{d} s}{s} <\infty , \end{aligned} \end{aligned}$$

(4.10)

when $k=-1$. Further assume that the equations

$$\begin{aligned} \sinh (\lambda \theta _i) = \lambda ^2 \sin ^2 \theta _i, \qquad 1\le i\le 4 \end{aligned}$$

have no root (other than $-\mathrm {i}$) on the line $\mathrm {Im}\, \lambda = -k-2$ excluding the case $k=-1$ whenever $\tan \theta _i=\theta _i$ for some i. Then, the solution $u\in H^{k+4}(Q)$ owing to the lifting theory [6, 9, 19].

For $N\ge 5$, define the approximation space

$$\begin{aligned}&V_N^{2,0}(Q) = V_N(Q)\cap H_0^2(Q)= \left\{ \phi _{m,n}: 4\le m,n \le N \right\} . \end{aligned}$$

Then, the (Petrov–Galerkin) spectral approximation scheme is, to find $u_N\in V_N(Q)$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} (\Delta u_N, \Delta v) = (f,v) , &{} v\in V_N^{2,0}(Q), \\ u_N = \pi ^{-3,-3}_N g_i &{} \text { on }\Gamma _i, \ 1\le i\le 4, \\ \partial _{\mathrm {n}}u = \pi ^{-2,-2}_N h_i &{} \text { on } \Gamma _i, \ 1\le i\le 4, \end{array}\right. } \end{aligned}$$

(4.11)

where $[\pi _N^{-\sigma ,-\sigma } g_i ](P_i- \frac{ l_i}{2} (1-\zeta )\tau _i) = \pi _{N,\zeta }^{-\sigma ,-\sigma } g_i(P_i- \frac{ l_i}{2} (1-\zeta )\tau _i)$ with $\pi _{N,\zeta }^{-\sigma ,-\sigma }: H^{\sigma }(-1,1)\mapsto \mathbb {P}_{N}(-1,1)$ being defined such that

$$\begin{aligned}&\partial _{\zeta }^j [\pi _{N,\zeta }^{-\sigma ,-\sigma } g-g] (\pm 1) = 0 , \qquad 0\le j\le \sigma -1,\\&\left( \partial _{\zeta }^{\sigma } [\pi _{N,\zeta }^{-\sigma ,-\sigma } g-g], \partial _{\zeta }^{\sigma } h\right) = 0, \quad h\in \mathbb {P}_{N}(I)\cap H^{\sigma }_0(I). \end{aligned}$$

Assume that

$$\begin{aligned}&u_N(x,y) = \sum _{n=0}^N\sum _{m=0}^{M_n}{\hat{u}}_{m,n} \phi _{m,n}(x,y),\\&g\left( P_i-l_i\frac{1-\zeta }{2}\tau _i\right) = \sum _{n=0}^{\infty } {\hat{g}}_{i-1,n}J^{-3,-3}_n(\zeta ), \\&h\left( P_i-l_i\frac{1-\zeta }{2}\tau _i\right) = \sum _{n=0}^{\infty } {\hat{h}}_{i-1,n}J^{-2,-2}_n(\zeta ). \end{aligned}$$

Then, the coefficients $\{{\hat{u}}_{m,n}\}$ of the vertex and the edge modes are given by

$$\begin{aligned}&{\hat{u}}_{i-1,0} = {\hat{g}}_{i,3} = {\hat{g}}_{\bar{i},0} , \qquad 1\le i\le 4,\\&{\hat{u}}_{i-1,1} = \frac{2x_{i\underline{i}}}{l_i^2} {\hat{h}}_{i,2} + \frac{y_{i\underline{i}}}{l_i} {\hat{g}}_{i,4} = \frac{2x_{\bar{i}i}}{l_{\bar{i}}^2} {\hat{h}}_{i,2} + \frac{y_{\bar{i}i}}{l_{\bar{i}}} {\hat{g}}_{\bar{i},1}, \qquad 1\le i\le 4,\\&{\hat{u}}_{i-1,2} = \frac{2 y_{\bar{i}i}}{l_{\bar{i}}^2} {\hat{h}}_{i,2} - \frac{x_{\bar{i}i}}{l_{i}} {\hat{g}}_{\bar{i},1}= \frac{2y_{\bar{i}i}}{l_{\bar{i}}^2} {\hat{h}}_{i,2} - \frac{y_{\bar{i}i}}{l_{\bar{i}}} {\hat{g}}_{\bar{i},1}, \qquad 1\le i\le 4,\\&{\hat{u}}_{i-1,3} = -\frac{4 y_{i\bar{i}} (x_{i\underline{i}} s_i +y_{i\underline{i}} c_i )}{ l_i^3 l_{\bar{i}} s_i^2} {\hat{g}}_{i,5} - \frac{4 y_{i\bar{i}} y_{i\underline{i}} }{ l_{i}^2 l_{\bar{i}} s_i } {\hat{h}}_{i,3} + \frac{4 y_{i\underline{i}}^2 }{ l_i^2 l_{\bar{i}}^2 s_i^2} {\hat{g}}_{\bar{i},2}, \qquad 1\le i\le 4,\\&{\hat{u}}_{i-1,4} = -\frac{4 y_{i\underline{i}} x_{i\underline{i}} }{ l_i^4 s_i^2} {\hat{g}}_{i,5} +\frac{2 y_{i,\underline{i}} x_{i\bar{i}} + 2x_{i\underline{i}} y_{i\bar{i}} }{ l_{i}^2 l_{\bar{i}} s_i } {\hat{h}}_{i,3} - \frac{4 y_{i\underline{i}}x_{i\underline{i}} }{l_i^2 l_{\bar{i}}^2 s_i^2} {\hat{g}}_{\bar{i},2}, \quad 1\le i\le 4,\\&{\hat{u}}_{i-1,5} = \frac{4 x_{i\bar{i}} (y_{i\underline{i}} s_i -x_{i\underline{i}} c_i )}{ l_i^3 l_{\bar{i}} s_i^2} {\hat{g}}_{i,5} - \frac{4 x_{i\bar{i}} x_{i\underline{i}} }{ l_{i}^2 l_{\bar{i}} s_i } {\hat{h}}_{i,3} + \frac{4 x_{i\underline{i}}^2 }{ l_i^2 l_{\bar{i}}^2 s_i^2} {\hat{g}}_{\bar{i},2}, \qquad 1\le i\le 4,\\&{\hat{u}}_{m,i-1} = {\hat{h}}_{i,m},\qquad \qquad {\hat{u}}_{i-1,n} = {\hat{g}}_{i,n}, \qquad \qquad \ \ m\ge 4, n\ge 6,\ i=2,3,\\&{\hat{u}}_{m,i-1} = (-1)^m {\hat{h}}_{i,m},\quad {\hat{u}}_{i-1,n} = (-1)^n {\hat{g}}_{i,n}, \qquad m\ge 4, n\ge 6,\ i=1,4, \end{aligned}$$

where $\underline{i}=i-1$ if $2\le i\le 4$ and $\underline{i}=4$ if $i=1$; while solving the first equation in (4.11) yields the coefficients $\{{\hat{u}}_{m,n}\}$ of the interior modes.

4.2.2 Numerical Experiment

Now we take the computational domain Q as the quadrilateral with four vertices $(1, -1), (1,-\frac{3}{2}),$$(2,0), (-2,2)$ in our numerical experiment (see the left side of Fig. 2). The source term f and the boundary data $(g_i,h_i)$, $1\le i\le 4$, are determined by the exact solution

$$\begin{aligned} u(x,y) = \sin (k_1x) \sin (k_2y). \end{aligned}$$

The surface plots of the exact solution with $k_1=k_2=\pi$ and the numerical solution with $N=32$ are demonstrated in the center and the right side of Fig. 2. Maximum errors are reported in Table 5 with various N, where an exponential order of convergence is clearly observed. This partially validates the completeness of our basis functions.

Fig. 2

The computational domain Q (left), the surface plots of the exact solution (center) and the numerical solution (right)

Table 5 Maximum errors of the $C^1$-conforming spectral element method vs. N

4.3 $C^1$-Conforming Quadrilateral Spectral Elements for Biharmonic Eigenvalue Problems

We shall propose the quadrilateral spectral element method and show its effectiveness for fourth-order equations. It is better for us to consider the following biharmonic eigenvalue problem on a polygon $\Omega$:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta ^2 u = \lambda u &{} \text { in } \Omega ,\\ u = \partial _{\mathrm {n}}u = 0 &{} \text { on } \partial \Omega . \end{array}\right. } \end{aligned}$$

(4.12)

The weak form for (4.12) is to find $u\in H_0^2(\Omega ),$ such that

$$\begin{aligned} (\Delta u,\Delta v)=\lambda (u,v), \quad \forall v\in H_0^2(\Omega ). \end{aligned}$$

(4.13)

4.3.1 Approximation Scheme and Implementation

Let $\Sigma =\{Q_i\}$ be a quadrilateral partition of $\Omega$, where each element $Q_i$ is a convex quadrilateral. $\Sigma$ is regular in the sense that the intersection $\overline{Q}_i\cap \overline{Q}_j,\ i\ne j$ is either empty or a node or an entire edge of both $Q_i$ and $Q_j$.

We now define the approximation spaces $W_{N}(\Sigma )$ as follows:

$$\begin{aligned} W_N(\Sigma ) = \mathrm {span} \{ u\in H_0^2(\Omega ): u|_{Q} \in V_N(Q), Q\in \Sigma \}. \end{aligned}$$

Then, the $C^1$-conforming quadrilateral spectral element approximation scheme for the biharmonic eigenvalue problem of (4.13) reads: to find $\lambda _N\in \mathbb {R}$ and $u_N\in W_N(\Sigma )$, such that

$$\begin{aligned} (\Delta u_{N},\Delta \psi ) =\lambda _N(u_{N},\psi ), \quad \psi \in W_N(\Sigma ). \end{aligned}$$

(4.14)

Assembling the global “stiffness” and mass matrices A, B, we arrive at the following equivalent algebraic eigenvalue system:

$$\begin{aligned} A{\hat{u}}=\lambda _N B {\hat{u}}, \end{aligned}$$

(4.15)

where ${\hat{u}}$ is a column vector of expansion coefficients of the unknown eigenfunction in global basis. Note that the matrices on both sides of the algebraic eigen-equation (4.15) are nonsingular, thus can be efficiently solved by algebraic eigenvalue packages such as ARPACK or FEAST.

4.3.2 Numerical Experiment

We simply carry out our numerical experiment of the $C^1$-conforming quadrilateral spectral element method for the biharmonic eigenvalue problem (4.12) on $\Omega =[-1,1]^2$. The computational domain is partitioned with four convex quadrilaterals with five random grid points, see Fig. 3a.

We take $\lambda _1=80.933\,373\,724\,482\,024,\ \lambda _2=\lambda _3=336.666\,035\,048\,621\,5,\ \lambda _4=731.925\,702\,387\,858,$$\lambda _5=1082.093\,732\,611\,044$ as the reference values of the 5 smallest eigenvalues of (4.12) on $\Omega =[-1,1]^2$ which are obtained by the classic rectangular spectral method with a polynomial degree of 200. The errors $|\lambda _i-\lambda _{i,\delta }|,i=1,\cdots ,5$ versus the polynomial degree N are then plotted in Fig. 3c in semi-log scale. It can be observed from Fig. 3c, our conforming quadrilateral spectral element method possesses a high order of convergence. As a comparison, we also plot in Fig. 3b the errors of the classic spectral method for the first five biharmonic eigenvalues. Roughly speaking, our $C^1$-conforming spectral element method exhibits the same order of convergence as the classic spectral method, although it has a relatively lower accuracy with the same degrees of freedom. This reflects the effectiveness and efficiency of the our $C^1$-conforming quadrilateral spectral element method.

Fig. 3

a Partition of $\Omega =[-1,1]^2$ with four quadrilaterals; b eigenvalue errors of the spectral method; c eigenvalue errors of the quadrilateral spectral element method