Spectral Method for Fourth-Order Problems on Quadrilaterals

Abstract

In this paper, we investigate the spectral method for fourth-order problems defined on quadrilaterals. Some results on the Legendre irrational orthogonal approximations are established, which play important roles in the related spectral method on quadrilaterals. As examples of applications, we provide spectral schemes for a model problem with various boundary conditions. The spectral accuracy of suggested algorithms are proved. Numerical results demonstrate the effectiveness of suggested algorithms, and confirm the analysis well. The approximation results and techniques developed in this paper are also applicable to other fourth-order problems defined on quadrilaterals.

1 Introduction

The spectral method has gained increasing popularity in scientific computations, see [2, 8, 12–15, 17–19, 28] and the references therein. The standard spectral method is traditionally confined to periodic problems and problems defined on rectangular domains. However, many practical problems are set on complex domains. We usually use finite element methods for such problems. For obtaining accurate numerical results, we may adopt spectral method and other high order methods, see, e.g., [3, 9, 16, 20, 24, 25]. We consider second-order problems mostly. But, it is also interesting and important to study fourth-order problems, see [4, 10, 23, 26, 27]. Some authors proposed the spectral method for fourth-order problems defined on rectangular domains, see [5, 6, 11]. We also refer to the work of [1]. Whereas, there has been few work in the spectral method for fourth-order problems defined on non-rectangular domains.

In this paper, we investigate the spectral method for fourth-order problems defined on quadrilaterals. We introduce the orthogonal approximation defined on quadrilaterals, by using an orthogonal system of irrational functions. Then, we establish the basic results on such approximation, which play important roles in the related spectral method. As example of applications, we provide the spectral schemes for a model problem with Dirichlet boundary condition and mixed boundary condition respectively, and prove their spectral accuracy. Numerical results demonstrate the high effectiveness of proposed algorithms, and confirm the analysis well. The approximation results and the techniques developed in this paper are also applicable to other fourth-order problems defined on quadrilaterals.

The paper is organized as follows. The next section is for preliminaries. In Sect. 3, we study the irrational orthogonal approximation on quadrilaterals. In Sect. 4, we provide the spectral schemes for a model problems with the convergence analysis, and present some numerical results. The last section is for concluding remarks. The appendix is devoted to the lifting technique.

2 Preliminaries

We first recall some results on the one-dimensional Legendre orthogonal approximation. Let $I_\xi =\{~\xi ~|-1<\xi <1\}$ and $\chi (\xi )$ be a certain weight function. For integer $r\ge 0$, we define the weighted Sobolev spaces $H^r_\chi (I_\xi )$ as usual, with the semi-norm $|v|_{r,\chi ,I_\xi }$ and the norm $\Vert v\Vert _{r,\chi ,I_\xi }$. In particular, $H^0_\chi (I_\xi )=L^2_\chi (I_\xi )$ with the inner product $(u,v)_{\chi ,I_\xi }$ and the norm $\Vert v\Vert _{\chi ,I_\xi }$. We omit the subscript $\chi$ whenever $\chi (\xi )\equiv 1$. We denote by $L_l(\xi )$ the Legendre polynomial of degree $l$. The set of all Legendre polynomials is a complete $L^2(I_\xi )-$orthogonal system.

Let $N$ be any positive integer. $\mathcal {P}_N(I_\xi )$ stands for the set of all algebraic polynomials of degree at most $N$, and $\mathcal {P}^0_N(I_\xi )=\mathcal {P}_N(I_\xi )\cap H^2_0(I_\xi )$. Throughout this paper, we denote by $c$ a generic positive constant independent of any function and the mode $N$.

The orthogonal projection $P^{2,0}_{N,I_\xi }:H^2_0(I_\xi )\rightarrow \mathcal {P}^0_N(I_\xi )$, is defined by

$$\begin{aligned} (\partial ^2_\xi (P^{2,0}_{N,I_\xi }v-v),\partial ^2_\xi \phi )_{I_\xi }=0,\qquad \forall \phi \in \mathcal {P}^0_N(I_\xi ). \end{aligned}$$

Let $\alpha ,\beta >-1$. The Jacobi weight function $\chi ^{(\alpha ,\beta )}(\xi )=(1-\xi )^\alpha (1+\xi )^\beta$. According to Theorem 2.5 of [22], we know that if $v\in H^2_0(I_\xi ),\,\partial ^m_\xi v\in L^2_{\chi ^{(m-2,m-2)}}(I_\xi )$, integers $2\le m\le N+1$ and $N\ge 2$, then

$$\begin{aligned} \Vert \partial ^k_\xi (P^{2,0}_{N,I_\xi }v-v)\Vert _{I_\xi }\le cN^{k-m}\Vert \partial ^m_\xi v\Vert _{\chi ^{(m-2,m-2)},I_\xi },\qquad k=0,1,2. \end{aligned}$$

(2.1)

In the numerical analysis of spectral method for mixed boundary value problems, we need other orthogonal approximations. Let

$$\begin{aligned} {}_0H^2(I_\xi )=\{v\in H^2(I_\xi )~|~v(\pm 1)=\partial _\xi v(-1)=0\}, \qquad {}_0\mathcal {P}_N(I_\xi )=\mathcal {P}_N(I_\xi )\cap {}_0H^2(I_\xi ). \end{aligned}$$

The orthogonal projection ${}_0P^{2}_{N,I_\xi }:{}_0H^2(I_\xi )\rightarrow {}_0\mathcal {P}_N(I_\xi )$, is defined by

$$\begin{aligned} (\partial ^2_\xi ({}_0P^{2}_{N,I_\xi }v-v),\partial ^2_\xi \phi )_{I_\xi }=0,\qquad \forall \phi \in {}_0\mathcal {P}_N(I_\xi ). \end{aligned}$$

By a slight modification of proof of Theorem 2.5 of [22], we have that if $v\in {}_0H^2(I_\xi ),~\partial ^m_\xi v\in L^2_{\chi ^{(m-2,m-2)}}(I_\xi )$, integers $2\le m\le N+1$ and $N\ge 2$, then

$$\begin{aligned} \Vert \partial ^k_\xi (_0P^{2}_{N,I_\xi }v-v)\Vert _{I_\xi }\le cN^{k-m}\Vert \partial ^m_\xi v\Vert _{\chi ^{(m-2,m-2)},I_\xi },\qquad k=0,1,2. \end{aligned}$$

(2.2)

We may also let

$$\begin{aligned} {}^0H^2(I_\xi )=\{v\in H^2(I_\xi )~|~v(\pm 1)=\partial _\xi v(1)=0\}, \qquad {}^0\mathcal {P}_N(I_\xi )=\mathcal {P}_N(I_\xi )\cap {}^0H^2(I_\xi ). \end{aligned}$$

The orthogonal projection ${}^0P^{2}_{N,I_\xi }:{}^0H^2(I_\xi )\rightarrow {}^0\mathcal {P}_N(I_\xi )$, is defined by

$$\begin{aligned} (\partial ^2_\xi ({}^0P^{2}_{N,I_\xi }v-v),\partial ^2_\xi \phi )_{I_\xi }=0,\qquad \forall \phi \in {}^0\mathcal {P}_N(I_\xi ). \end{aligned}$$

If $v\in {}^0H^2(I_\xi ),~\partial ^m_\xi v\in L^2_{\chi ^{(m-2,m-2)}}(I_\xi )$, integers $2\le m\le N+1$ and $N\ge 2$, then

$$\begin{aligned} \Vert \partial ^k_\xi ({}^0P^{2}_{N,I_\xi }v-v)\Vert _{I_\xi }\le cN^{k-m}\Vert \partial ^m_\xi v\Vert _{\chi ^{(m-2,m-2)},I_\xi },\qquad k=0,1,2. \end{aligned}$$

(2.3)

We now turn to the Legendre approximation on the square. Let $I_\eta =\{\eta ~|~-1<\eta <1\}$ and $S=I_\xi \otimes I_\eta$. For integer $r\ge 0$, we define the weighted Sobolev spaces $H^r_\chi (S)$ in the usual way, with the semi-norm $|v|_{r,\chi ,S}$ and the norm $\Vert v\Vert _{r,\chi ,S}$. The inner product and the norm of $L^2_\chi (S)$ are denoted by $(u,v)_{\chi ,S}$ and $||v||_{\chi ,S}$, respectively. We also omit the subscript $\chi$ whenever $\chi (\xi )\equiv 1$. Moreover, $\mathcal {P}_N(S)=\mathcal {P}_N(I_\xi )\otimes \mathcal {P}_N(I_\eta )$ and $\mathcal {P}^0_N(S)=\mathcal {P}_N(S)\cap H^2_0(S)$.

Let $d$ be a non-negative constant. We introduce the bilinear form

$$\begin{aligned} a_d(u,v)=(\Delta u,\Delta v)_S+d(u,v)_S,\qquad \forall u,v\in H^2(S). \end{aligned}$$

Indeed, $||\Delta v||_S=|v|_{2,S}$ for any $v\in H^2_0(S)$. Moreover,

$$\begin{aligned} a_d(u,v)=(\partial ^2_{\xi } u,\partial ^2_{\xi } v)_S +2(\partial _{\xi }\partial _{\eta }u,\partial _{\xi }\partial _{\eta }v)_S+(\partial ^2_{\eta } u,\partial ^2_{\eta } v)_S+d( u, v)_S,\qquad \forall u,v\in H_0^2(S). \end{aligned}$$

The orthogonal projection $P^{2,0}_{N,S}:H^2_0(S)\rightarrow \mathcal {P}^0_N(S)$, is defined by

$$\begin{aligned} a_d(P^{2,0}_{N,S}v-v,\phi )=0,\qquad \forall \phi \in \mathcal {P}^0_N(S), \end{aligned}$$

(2.4)

Let $\chi ^{(\alpha ,\beta )}_1(\xi )=(1-\xi )^\alpha (1+\xi )^\beta$ and $\chi ^{(\alpha ,\beta )}_2(\eta )=(1-\eta )^\alpha (1+\eta )^\beta$. For description of approximation errors, we introduce the quantity $D_{r,S}(v)$. $D_{r,S}(v)=\Vert v\Vert _{r,S}$ for $r=2,3$. For $r\ge 4$,

$$\begin{aligned} D_{r,S}(v)= & {} \Vert \partial ^r_\xi v\Vert _{\chi ^{(r-2,r-2)}_1,S}+\Vert \partial ^{r-1}_\xi \partial _\eta v\Vert _{\chi ^{(r-3,r-3)}_1,S} +\Vert \partial ^{r-2}_\xi \partial ^2_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S} \\&+\,\Vert \partial ^r_\eta v\Vert _{\chi ^{(r-2,r-2)}_2,S} +\Vert \partial _\xi \partial ^{r-1}_\eta v\Vert _{\chi ^{(r-3,r-3)}_2,S} +\Vert \partial ^2_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}. \end{aligned}$$

Theorem 2.1

If $v\in H^2_0(S)$ and $D_{r,S}(v)$ is finite for integers $2\le r\le N+1$ and $N\ge 2$, then

$$\begin{aligned} \Vert P^{2,0}_{N,S}v-v\Vert _{\mu ,S}\le cN^{\mu -r}D_{r,S}(v),\qquad \mu =0,1,2. \end{aligned}$$

(2.5)

Proof

Let $\phi =P^{2,0}_{N,I_\xi }(P^{2,0}_{N,I_\eta }v)=P^{2,0}_{N,I_\eta }(P^{2,0}_{N,I_\xi }v)\in \mathcal {P}^0_N(S)$. We use projection theorem to obtain

$$\begin{aligned} |P^{2,0}_{N,S}v-v|_{2,S}+d||P^{2,0}_{N,S}v-v||_S\le |\phi -v|_{2,S}+d||\phi -v||_{S}. \end{aligned}$$

(2.6)

Clearly,

$$\begin{aligned} \Vert \partial ^{k_1}_\xi \partial ^{k_2}_\eta (\phi -v)\Vert _S\le F_1(v)+F_2(v)+F_3(v), \end{aligned}$$

(2.7)

with

$$\begin{aligned} F_1(v)= & {} \Vert \partial ^{k_1}_\xi (P^{2,0}_{N,I_\xi }\partial ^{k_2}_\eta (P^{2,0}_{N,I_\eta }v-v) -\partial ^{k_2}_\eta (P^{2,0}_{N,I_\eta }v-v))\Vert _S,\\ F_2(v)= & {} \Vert \partial ^{k_1}_\xi \partial ^{k_2}_\eta (P^{2,0}_{N,I_\xi }v-v)\Vert _S, \qquad F_3(v)=\Vert \partial ^{k_1}_\xi \partial ^{k_2}_\eta (P^{2,0}_{N,I_\eta }v-v)\Vert _S. \end{aligned}$$

Also, we have

$$\begin{aligned} \Vert \partial ^{k_1}_\xi \partial ^{k_2}_\eta (\phi -v)\Vert _S\le \widetilde{F}_1(v)+F_2(v)+F_3(v), \end{aligned}$$

with

$$\begin{aligned} \widetilde{F}_1(v)=\Vert \partial ^{k_2}_\eta (P^{2,0}_{N,I_\eta }\partial ^{k_1}_\xi (P^{2,0}_{N,I_\xi }v-v) -\partial ^{k_1}_\xi (P^{2,0}_{N,I_\xi }v-v))\Vert _S. \end{aligned}$$

We use (2.1) with $k=k_1$ and $m=2$, and (2.1) with $k=k_2$ and $m=r-2$ successively, to derive that for $r\ge 4$,

$$\begin{aligned} F_1(v)\le cN^{k_1-2}\Vert \partial ^2_\xi \partial ^{k_2}_\eta (P^{2,0}_{N,I_\eta }v-v)\Vert _S \le cN^{k_1+k_2-r}\Vert \partial ^2_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}. \end{aligned}$$

Similarly,

$$\begin{aligned} \widetilde{F}_1(v)\le cN^{k_1+k_2-r}\Vert \partial ^{r-2}_\xi \partial ^2_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S}. \end{aligned}$$

Next, we use (2.1) with $k=k_1$ and $m=r-k_2$ to obtain

$$\begin{aligned} F_2(v)\le cN^{k_1+k_2-r}\Vert \partial ^{r-k_2}_\xi \partial ^{k_2}_\eta v\Vert _{\chi ^{(r-k_2-2,r-k_2-2)}_1,S}. \end{aligned}$$

Also, thanks to (2.1) with $k=k_2$ and $m=r-k_1$, we have

$$\begin{aligned} F_3(v)\le cN^{k_1+k_2-r}\Vert \partial ^{k_1}_\xi \partial ^{r-k_1}_\eta v\Vert _{\chi ^{(r-k_1-2,r-k_1-2)}_2,S}. \end{aligned}$$

The previous statements, together with (2.7), lead to that

$$\begin{aligned} \Vert \partial ^{2}_\xi (P^{2,0}_{N,I_\xi }(P^{2,0}_{N,I_\eta }v)-v)\Vert _S\le & {} cN^{2-r}\left( \Vert \partial ^2_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}+\Vert \partial ^{r-2}_\xi \partial ^2_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S} \right. \\&\left. +\,\Vert \partial ^{r}_\xi v\Vert _{\chi ^{(r-2,r-2)}_1,S}+\Vert \partial ^{2}_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}\right) , \\ \Vert \partial ^{2}_\eta (P^{2,0}_{N,I_\xi }(P^{2,0}_{N,I_\eta }v)-v)\Vert _S\le & {} cN^{2-r}\left( \Vert \partial ^2_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}+\Vert \partial ^{r-2}_\xi \partial ^2_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S} \right. \\&\left. +\,\Vert \partial ^{r-2}_\xi \partial ^{2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S}+\Vert \partial ^{r}_\eta v\Vert _{\chi ^{(r-2,r-2)}_2,S}\right) , \\ \Vert \partial _\xi \partial _\eta (P^{2,0}_{N,I_\xi }(P^{2,0}_{N,I_\eta }v)-v)\Vert _S\le & {} cN^{2-r}\left( \Vert \partial ^2_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}+\Vert \partial ^{r-2}_\xi \partial ^2_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S} \right. \\&\left. +\,\Vert \partial ^{r-1}_\xi \partial _\eta v\Vert _{\chi ^{(r-3,r-3)}_1,S}+\Vert \partial _\xi \partial ^{r-1}_\eta v\Vert _{\chi ^{(r-3,r-3)}_2,S}\right) ,\\ \Vert P^{2,0}_{N,I_\xi }(P^{2,0}_{N,I_\eta }v)-v\Vert _S\le & {} cN^{-r}\left( \Vert \partial ^2_\xi \partial ^{r-2}_\eta v\Vert _{\chi ^{(r-4,r-4)}_2,S}+\Vert \partial ^{r-2}_\xi \partial ^2_\eta v\Vert _{\chi ^{(r-4,r-4)}_1,S} \right. \\&\left. +\,\Vert \partial ^{r}_\xi v\Vert _{\chi ^{(r-2,r-2)}_1,S}+\Vert \partial ^{r}_\eta v\Vert _{\chi ^{(r-2,r-2)}_2,S}\right) . \end{aligned}$$

Then the result (2.5) with $\mu =2$ and $r\ge 4$ comes from (2.6) and the Poincaré inequality.

In order to derive the result (2.5) with $\mu =2$ and $r=2,3$, we should use the interpolation of operators, as described in Brenner and Scott [7]. To do this, we define the linear operator ${\mathcal {L}}$, which maps $v$ to the error $P^{2,0}_{N,S}v-v$. In other words, ${\mathcal {L}}v=P^{2,0}_{N,S}v-v$. Clearly, $\mathcal {L}$ maps $H^2_0(S)$ to $H^2_0(S)$, with the norm

$$\begin{aligned} \Vert \mathcal {L}\Vert _{H_0^2(S)\rightarrow H^2_0(S)}\le c. \end{aligned}$$

(2.8)

On the other hand, by virtue of (2.5) with $\mu =2$ and $r=4$, we obtain

$$\begin{aligned} \Vert P^{2,0}_{N,S}v-v\Vert _{ H^2_0(S)}\le cN^{-2}D_{4,S}(v)\le cN^{-2}||v||_{H^4(S)\cap H^2_0(S)}. \end{aligned}$$

It means that ${\mathcal {L}}$ maps $H^4(S)\cap H^2_0(S)$ to $H^2_0(S)$, with the norm

$$\begin{aligned} ||{\mathcal {L}}||_{H^4(S)\cap H^2_0(S)\rightarrow H^2_0(S)}\le cN^{-2}. \end{aligned}$$

(2.9)

As is well known, the space $H^3(S)\cap H^2_0(S)$ is the interpolation between the spaces $H^2_0(S)$ and $H^4(S)\cap H^2_0(S)$, see page 14 of [13]. Thus, the operator ${\mathcal {L}}$ mapping $H^3(S)\cap H^2_0(S)$ to $H^2_0(S)$ could be regarded as an interpolation between the operator mapping $H^2_0(S)$ to $H^2_0(S)$ and the operator mapping $H^4(S)\cap H^2_0(S)$ to $H^2_0(S)$. Accordingly, by virtue of Proposition 14.1.5 with $\theta =\frac{1}{2}$ and $p=2$ of [7], we have

$$\begin{aligned} \Vert {\mathcal {L}}\Vert _{H^3(S)\cap H^2_0(S) \rightarrow H^2_0(S)}\le \Vert {\mathcal {L}}\Vert _{H^2_0(S)\rightarrow H^2_0(S)}^{\frac{1}{2}} \Vert {\mathcal {L}}||_{H^4(S)\cap H^2_0(S)\rightarrow H^2_0(S)}^{\frac{1}{2}}. \end{aligned}$$

This, along with (2.8) and (2.9), leads to $\Vert {\mathcal {L}}\Vert _{H^3(S)\cap H^2_0(S)\rightarrow H^2_0(S)}\le cN^{-1}$. A combination of the previous statements implies the validity of the desired result (2.5) with $\mu =2$ and $r\ge 2$.

We now derive the result (2.5) with $\mu =0$. Let $g\in L^2(S)$ and consider an auxiliary problem. It is to find $w\in H^2_0(S)$ such that

$$\begin{aligned} a_d( w, z)=(g,z)_{S},\qquad \forall z\in H^2_0(S). \end{aligned}$$

(2.10)

Taking $z=w$ in (2.10) and using the Poincaré inequality, we obtain $\Vert w\Vert _{2,S}\le c\Vert g\Vert _S$. Due to the property of elliptic equation, we have $\Vert w\Vert _{4,S}\le c\Vert g\Vert _{S}$. Thereby, using (2.5) with $\mu =2$ yields that

$$\begin{aligned} \Vert P^{2,0}_{N,S}w-w\Vert _{2,S}\le cN^{-2}D_{4,S}(w)\le cN^{-2}\Vert w\Vert _{4,S}\le cN^{-2}\Vert g\Vert _S. \end{aligned}$$

(2.11)

Now, by taking $z=P^{2,0}_{N,S}v-v$ in (2.10), we use (2.5) with $\mu =2$, (2.11) and the Poincaré inequality to verify that

$$\begin{aligned} |(P^{2,0}_{N,S}v-v,g)_{S}|= & {} |a_d(P^{2,0}_{N,S}v-v,P^{2,0}_{N,S}w-w)| \\\le & {} c|P^{2,0}_{N,S}v-v|_{2,S}|P^{2,0}_{N,S}w-w|_{2,S}\le cN^{-r}D_{r,S}(v)||g||_{S}. \end{aligned}$$

Consequently,

$$\begin{aligned} \Vert P^{2,0}_{N,S}v-v\Vert _{S}=\sup _{g\in L^2(S), g\ne 0} \displaystyle \frac{|(P^{2,0}_{N,S}v-v,g)_S|}{||g||_S}\le cN^{-r}D_{r,S}(v). \end{aligned}$$

Finally, we use the interpolation of spaces, together with the results (2.5) with $\mu =0,2$, to deduce that $\Vert P^{2,0}_{N,S}v-v\Vert _{1,S}\le cN^{1-r}D_{r,S}(v)$. The proof is completed. $\square$

In the numerical analysis of spectral method for mixed boundary value problems of fourth-order, we need other orthogonal approximations. For instance, let $\partial ^{**}S=\{ (\xi ,\eta )~|~\xi =1 \mathrm{~or~} \eta =-1\}$, and $\partial _nv(\xi ,\eta )$ be the normal derivative of $v(\xi ,\eta )$ on the boundary of $S$. We set

$$\begin{aligned} {}^0H^2(S)=H^2(S)\cap \{v~|~v(-1, \eta )=v(\xi ,1)=0\},\qquad {}^0\mathcal {P}_N(S)={}^0H^2(S)\cap \mathcal {P}_N(S). \end{aligned}$$

Let $d,\beta \ge 0$, and

$$\begin{aligned} a_{d,\beta }(u,v)=(\Delta u,\Delta v)_S +d( u, v)_S+\beta \int _{\partial ^{**}S}\partial _nu\partial _nvds,\qquad \forall u,v\in H^2(S). \end{aligned}$$

(2.12)

It can be shown that $||\Delta v||_S=|v|_{2,S}$ for any $v\in {}^0H^2(S)$. Moreover,

$$\begin{aligned} a_{d,\beta }(u,v)= & {} (\partial ^2_{\xi } u,\partial ^2_{\xi } v)_S +2(\partial _{\xi }\partial _{\eta }u,\partial _{\xi }\partial _{\eta }v)_S+(\partial ^2_{\eta } u,\partial ^2_{\eta } v)_S \\&+\,d( u, v)_S+\beta \displaystyle \int _{\partial ^{**}S}\partial _nu\partial _nvds,\qquad \forall u,v\in {}^0H^2(S). \end{aligned}$$

The orthogonal projection ${}^0P^{2}_{N,S}:{}^0H^2(S)\rightarrow {}^0\mathcal {P}_N(S)$, is defined by

$$\begin{aligned} a_{d,\beta }({}^0P^{2}_{N,S}v-v, \phi )=0,\qquad \forall \phi \in {}^0\mathcal {P}_N(S). \end{aligned}$$

(2.13)

With the aid of (2.2) and (2.3), we could follow the same line as in the proof of Theorem 2.1 to reach the following result.

Theorem 2.2

If $v\in {}^0H^2(S)$ and $D_{r,S}(v)$ is finite for integers $2\le r\le N+1$ and $N\ge 2$, then

$$\begin{aligned} \Vert {}^0P^{2}_{N,S}v-v\Vert _{\mu ,S}\le cN^{\mu -r}D_{r,S}(v),\qquad \mu =0,1,2. \end{aligned}$$

(2.14)

3 Legendre Orthogonal Approximation on Quadrilaterals

In this section, we consider the Legendre irrational quasi-orthogonal approximations on quadrilaterals.

3.1 Some Praperations

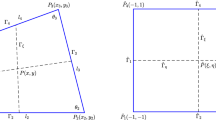
Let $\Omega$ be a convex quadrilateral with the edges $L_i$, the vertices $Q_i=(x_i,y_i)$, and the angles $\theta _i,~1\le i\le 4$, see Fig. 1. We make the following variable transformation

$$\begin{aligned} x=a_0+a_1\xi +a_2\eta +a_3\xi \eta ,\qquad y=b_0+b_1\xi +b_2\eta +b_3\xi \eta \end{aligned}$$

(3.1)

where

$$\begin{aligned} a_0= & {} \frac{1}{4}(x_1+x_2+x_3+x_4),\qquad b_0=\frac{1}{4}(y_1+y_2+y_3+y_4), \nonumber \\ a_1= & {} \frac{1}{4}(-x_1+x_2+x_3-x_4),\quad b_1=\frac{1}{4}(-y_1+y_2+y_3-y_4), \nonumber \\ a_2= & {} \frac{1}{4}(-x_1-x_2+x_3+x_4),\quad b_2=\frac{1}{4}(-y_1-y_2+y_3+y_4), \nonumber \\ a_3= & {} \frac{1}{4}(x_1-x_2+x_3-x_4),\qquad b_3=\frac{1}{4}(y_1-y_2+y_3-y_4). \end{aligned}$$

(3.2)

Fig. 1

Quadrilateral $\Omega$

Then, the quadrilateral $\Omega$ is changed to the reference square $S$ as in the last section. The Jacobi matrix of transformation (3.1) is as follows,

$$\begin{aligned} M_\Omega =\left( \begin{array}{cc} \partial _\xi x &{}\quad \partial _\xi y \\ \partial _\eta x &{}\quad \partial _\eta y\\ \end{array}\right) =\left( \begin{array}{cc} a_1+a_3\eta &{}\quad b_1+b_3\eta \\ a_2+a_3\xi &{}\quad b_2+b_3\xi \\ \end{array}\right) . \end{aligned}$$

(3.3)

Its Jacobian determinant is

$$\begin{aligned} J_\Omega (\xi ,\eta )= & {} \left| \begin{array}{cc} a_1+a_3\eta &{}\quad b_1+b_3\eta \\ a_2+a_3\xi &{}\quad b_2+b_3\xi \end{array}\right| \nonumber \\= & {} (a_1+a_3\eta )(b_2+b_3\xi )-(b_1+b_3\eta )(a_2+a_3\xi ). \end{aligned}$$

(3.4)

Due to the convexity of $\Omega$, there exist positive constants $\delta _{\Omega }$ and $\delta _{\Omega }^*$, such that

$$\begin{aligned} 0 <\delta _{\Omega }\le J_\Omega (\xi ,\eta )\le \delta _{\Omega }^*. \end{aligned}$$

(3.5)

The inverse of transformation (3.1) is given by $\xi =\xi (x,y)$ and $\eta =\eta (x,y)$. Their explicit expressions were given in Appendix of [16], which are irrational functions generally. The Jacobi matrix of the above inverse transformation is

$$\begin{aligned} M_S=M^{-1}_{{\Omega }}=\left( \begin{array}{cc} \partial _x \xi &{}\quad \partial _x\eta \\ \partial _y\xi &{}\quad \partial _y\eta \\ \end{array}\right) =\frac{1}{J_{{\Omega }}(\xi ,\eta )}\left( \begin{array}{cc} b_2+b_3\xi &{}\quad -b_1-b_3\eta \\ -a_2-a_3\xi &{}\quad a_1+a_3\eta \\ \end{array}\right) . \end{aligned}$$

(3.6)

Thanks to (3.5), we have

$$\begin{aligned} 0<\frac{1}{\delta _\Omega ^*}\le J_S(x,y)=J_{{\Omega }}^{-1}(\xi ,\eta )\le \frac{1}{\delta _\Omega }. \end{aligned}$$

(3.7)

Let $x_5=x_1$ and $y_5=y_1$. We set

$$\begin{aligned} \sigma _\Omega= & {} \displaystyle \max _{(\xi ,\eta )\in S}(|b_2+b_3\xi |,|b_1+b_3\eta |,|a_2+a_3\xi |,|a_1+a_3\eta |) \nonumber \\= & {} \displaystyle \frac{1}{2}\max _{1\le j\le 4}(|x_j-x_{j+1}|,|y_j-y_{j+1}|). \end{aligned}$$

(3.8)

Due to (3.2), we have (see [16])

$$\begin{aligned} \gamma _\Omega =\max _{1\le i\le 3}(|a_i|,|b_i|)\le \sigma _\Omega . \end{aligned}$$

(3.9)

On the other hand, thanks to the Poincaré inequality, there exists a positive constant $c_\Omega$ such that

$$\begin{aligned} ||v||_\Omega \le c_\Omega ||v||_{1,\Omega },\qquad \forall v\in H^1_0(\Omega ). \end{aligned}$$

(3.10)

Let $d$ be a non-negative constant as before. By virtue of the property of elliptic equation, there exists a positive constant $\eta _{\Omega }$ such that

$$\begin{aligned} \Vert v\Vert _{4,\Omega }\le \eta _{\Omega }\Vert \Delta ^2v+dv\Vert _{\Omega }.\qquad \forall v\in H^2_0(\Omega ). \end{aligned}$$

(3.11)

3.2 Legendre Irrational Orthogonal Approximation in $H^2_0(\Omega )$

For any integer $r\ge 0$, we define the weighted Sobolev spaces $H^r_\chi (\Omega )$ as usual, with the semi-norm $|v|_{r,\chi ,\Omega }$ and the norm $\Vert v\Vert _{r,\chi ,\Omega }$. The inner product and the norm of $L^2_\chi (\Omega )$ are denoted by $(u,v)_{\chi ,\Omega }$ and $||v||_{\chi ,\Omega }$, respectively. We omit the subscript $\chi$ whenever $\chi (\xi )\equiv 1$.

We shall use the following family of irrational functions given in [16],

$$\begin{aligned} \psi _{l,m}(x,y)=L_l\big (\xi (x,y)\big )L_m\big (\eta (x,y)\big ), \qquad l,m\ge 0, \end{aligned}$$

which are mutually orthogonal with the weight function $J^{-1}_{\Omega }(\xi (x,y),\eta (x,y))$. Moreover,

$$\begin{aligned} V_N(\Omega )=\mathrm{Span}\{\psi _{l,m}(x,y)~|~ 0\le l,m\le N\},\qquad V_N^0(\Omega )=H^2_0(\Omega )\cap V_N(\Omega ). \end{aligned}$$

We introduce the bilinear form with $d\ge 0$,

$$\begin{aligned} a_d(u,v)=(\Delta u,\Delta v)_\Omega +d(u,v)_\Omega ,\qquad \forall u,v\in H^2(\Omega ). \end{aligned}$$

(3.12)

The orthogonal projection $P^{2,0}_{N,\Omega }:H^2_0(\Omega )\rightarrow V^0_N(\Omega )$, is defined by

$$\begin{aligned} a_d(P^{2,0}_{N,\Omega }v-v, \phi )=0,\qquad \forall \phi \in V^0_N(\Omega ). \end{aligned}$$

(3.13)

For description of approximation error, we shall use the quantity $B_{r,\Omega }(v)$. $B_{r,\Omega }(v)=\delta _\Omega ^{-\frac{1}{2}}\sum _{j=1}^r\sigma _\Omega ^{j}|v|_{j,\Omega }$ for $r=2,3$. Meanwhile $B_{r,\Omega }(v)=\sum _{j=1}^5B_{r,\Omega }^{(j)}(v)$ for $r\ge 4$, with

$$\begin{aligned} B_{r,\Omega }^{(1)}(v)= & {} \delta _\Omega ^{-\frac{1}{2}}\sigma ^r_\Omega \displaystyle \sum ^r_{j=0}(||(1-\xi ^2)^{\frac{r-2}{2}}\partial ^j_x\partial ^{r-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-2}{2}}\partial ^j_x\partial ^{r-j}_yv||_\Omega ), \\ B_{r,\Omega }^{(2)}(v)= & {} \delta _\Omega ^{-\frac{1}{2}}\sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-1}(||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega )\\&+\,\delta _\Omega ^{-\frac{1}{2}}\sigma _\Omega ^{r-1}\displaystyle \sum _{j=0}^{r-2}(||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega ),\\ B_{r,\Omega }^{(3)}(v)= & {} \delta _\Omega ^{-\frac{1}{2}}\sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-1}(||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-j}_yu||_\Omega ) \\&+\,\delta _\Omega ^{-\frac{1}{2}}\sigma _\Omega ^{r-1}\displaystyle \sum _{j=0}^{r-2}(||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega ),\\ B_{r,\Omega }^{(4)}(v)= & {} \delta _\Omega ^{-\frac{1}{2}}\sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-2}(||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega \\&+\,||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega )\\&+\,\delta _\Omega ^{-\frac{1}{2}}\sigma _\Omega ^{r-1}\displaystyle \sum _{j=0}^{r-3}(||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-3-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega \\&+\,||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega )\\&+\,\delta _\Omega ^{-\frac{1}{2}}\sigma _\Omega ^{r-2}\displaystyle \sum _{j=0}^{r-4}(||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-4-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-3-j}_yv||_\Omega \\&+\,||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-2-j}_yv||_\Omega ),\\ \end{aligned}$$

$$\begin{aligned} B_{r,\Omega }^{(5)}(v)= & {} \delta _\Omega ^{-\frac{1}{2}}\sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-2}(||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega \\&+\,||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega )\\&+\,\delta _\Omega ^{-\frac{1}{2}}\sigma _\Omega ^{r-1}\displaystyle \sum _{j=0}^{r-3}(||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-3-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega \\&+\,||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega )\\&+\,\delta _\Omega ^{-\frac{1}{2}}\sigma _\Omega ^{r-2}\displaystyle \sum _{j=0}^{r-4}(||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-4-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-3-j}_yv||_\Omega \\&+\,||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-2-j}_yv||_\Omega ). \end{aligned}$$

For notational convenience, we also set

$$\begin{aligned} C_{0, \Omega }= & {} \eta _{\Omega }\sigma ^{4}_\Omega \delta ^{-\frac{7}{2}}_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})^2(1+dc_\Omega ^2)^3(\sigma _\Omega +1)^4, \\ C_{1, \Omega }= & {} \eta _{\Omega }^{\frac{1}{2}}\sigma ^3_\Omega \delta ^{-\frac{5}{2} }_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})^{\frac{3}{2}} (1+dc_\Omega ^2)^2(\sigma _\Omega +1)^2(1+c_\Omega ), \\ C_{2, \Omega }= & {} \sigma ^2_\Omega \delta ^{-\frac{3}{2}}_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})(1+dc_\Omega ^2)(1+c_\Omega )^2. \end{aligned}$$

Theorem 3.1

If $v\in H^2_0(\Omega )$ and $B_{r,\Omega }(v)$ is finite for integer $2\le r\le N+1$ and $N\ge 2$, then

$$\begin{aligned} ||P_{N,\Omega }^{2,0}v-v||_{\mu ,\Omega }\le cC_{\mu ,\Omega }N^{\mu -r}B_{r,\Omega }(v),\qquad \mu =0,1,2. \end{aligned}$$

(3.14)

Proof

For any $v\in H^2_0(\Omega )$, we set $u(\xi ,\eta )=v(x(\xi ,\eta ),y(\xi ,\eta ))\in H^2_0(S)$. Let

$$\begin{aligned} \psi (\xi ,\eta )=P^{2,0}_{N,S}u(\xi ,\eta ),\qquad \phi (x,y)=\psi (\xi (x,y),\eta (x,y)). \end{aligned}$$

(3.15)

Since $\phi \in V^0_N(\Omega )$, we use projection theorem and (3.10) to obtain that

$$\begin{aligned} |P^{2,0}_{N,S}v-v|_{2,\Omega }+d||P^{2,0}_{N,S}v-v||_\Omega\le & {} |\phi -v|_{2,\Omega }+d||\phi -v||_{\Omega } \nonumber \\\le & {} (1+dc_\Omega ^2)|\phi -v|_{2,\Omega }. \end{aligned}$$

(3.16)

For estimating the right side of (3.16), we need some preparations. Firstly, a direct calculation shows that

$$\begin{aligned} \partial _x v= & {} \partial _\xi u\partial _x\xi +\partial _\eta u\partial _x\eta ,\qquad \partial _y v=\partial _\xi u\partial _y\xi +\partial _\eta u\partial _y\eta , \nonumber \\ \partial ^2_x v= & {} \partial ^2_\xi u(\partial _x\xi )^2 +2\partial _\xi \partial _\eta u \partial _x\xi \partial _x\eta +\partial ^2_\eta u(\partial _x\eta )^2+\partial _\xi u\partial ^2_x\xi +\partial _\eta u\partial ^2_x\eta , \nonumber \\ \partial ^2_y v= & {} \partial ^2_\xi u(\partial _y\xi )^2 +2\partial _\xi \partial _\eta u \partial _y\xi \partial _y\eta +\partial ^2_\eta u(\partial _y\eta )^2 +\partial _\xi u\partial ^2_y\xi +\partial _\eta u\partial ^2_y\eta , \\ \partial _x\partial _y v= & {} \partial ^2_\xi u\partial _x\xi \partial _y\xi +\partial _\xi \partial _\eta u \partial _x\xi \partial _y\eta +\partial _\xi \partial _\eta u \partial _y\xi \partial _x\eta +\partial ^2_\eta u\partial _x\eta \partial _y\eta +\partial _\xi u\partial _x\partial _y\xi \nonumber \\&+\,\partial _\eta u\partial _x\partial _y\eta .\nonumber \end{aligned}$$

(3.17)

Next, by virtue of (3.6), we have that

$$\begin{aligned} \begin{aligned} \partial _x\xi&= J^{-1}_\Omega (\xi ,\eta )(b_2+b_3\xi ),\qquad \partial _y\xi =-J^{-1}_\Omega (\xi ,\eta )(a_2+a_3\xi ), \\ \partial _x\eta&= -J^{-1}_\Omega (\xi ,\eta )(b_1+b_3\eta ),\qquad \partial _y\eta =J^{-1}_\Omega (\xi ,\eta )(a_1+a_3\eta ). \end{aligned} \end{aligned}$$

(3.18)

Thanks to (3.4), we have $\partial _\xi J_\Omega (\xi ,\eta )=a_1b_3-a_3b_1$ and $\partial _\eta J_\Omega (\xi ,\eta )=a_3b_2-a_2b_3$. Thus,

$$\begin{aligned} \partial _x J_\Omega (\xi ,\eta )= & {} J^{-1}_\Omega (\xi ,\eta )((a_1b_3-a_3b_1)(b_2+b_3\xi )-(a_3b_2-a_2b_3)(b_1+b_3\eta )),\nonumber \\ \partial _y J_\Omega (\xi ,\eta )= & {} -J^{-1}_\Omega (\xi ,\eta )((a_1b_3-a_3b_1)(a_2+a_3\xi )-(a_3b_2-a_2b_3)(a_1+a_3\eta )). \end{aligned}$$

The above facts lead to that

$$\begin{aligned} \begin{aligned} \partial ^2_x\xi&= 2J^{-3}_\Omega (\xi ,\eta )(b_1+b_3\eta )(b_2+b_3\xi )(a_3b_2-a_2b_3), \\ \partial ^2_x\eta&= 2J^{-3}_\Omega (\xi ,\eta )(b_1+b_3\eta )(b_2+b_3\xi )(a_1b_3-a_3b_1), \\ \partial ^2_y\xi&= 2J^{-3}_\Omega (\xi ,\eta )(a_1+a_3\eta )(a_2+a_3\xi )(a_3b_2-a_2b_3), \\ \partial ^2_y\eta&= 2J^{-3}_\Omega (\xi ,\eta )(a_1+a_3\eta )(a_2+a_3\xi )(a_1b_3-a_3b_1), \\ \partial _x\partial _y\xi&= J^{-3}_\Omega (\xi ,\eta )((a_1+a_3\eta )(b_2+b_3\xi )+(b_1+b_3\eta )(a_2+a_3\xi ))(a_2b_3-a_3b_2), \\ \partial _x\partial _y\eta&= J^{-3}_\Omega (\xi ,\eta )((a_1+a_3\eta )(b_2+b_3\xi )+(b_1+b_3\eta )(a_2+a_3\xi ))(a_3b_1-a_1b_3). \end{aligned} \end{aligned}$$

(3.19)

Accordingly, we use (3.15) and (3.17)–(3.19) to deduce that

$$\begin{aligned} \partial ^2_x(\phi -v)= & {} \partial ^2_\xi (\psi -u)(\partial _x\xi )^2+\partial ^2_\eta (\psi -u)(\partial _x\eta )^2 +2\partial _\xi \partial _\eta (\psi -u)\partial _x\xi \partial _x\eta \nonumber \\&+\,\partial _\xi (\psi -u)\partial ^2_x\xi +\partial _\eta (\psi -u)\partial ^2_x\eta \nonumber \\= & {} J^{-2}_\Omega (\xi ,\eta )(b_2+b_3\xi )^2\partial ^2_\xi (\psi -u) +J^{-2}_\Omega (\xi ,\eta )(b_1+b_3\eta )^2\partial ^2_\eta (\psi -u) \nonumber \\&-\,2J^{-2}_\Omega (\xi ,\eta )(b_2+b_3\xi )(b_1+b_3\eta )\partial _\xi \partial _\eta (\psi -u) \nonumber \\&+\,2J^{-3}_\Omega (\xi ,\eta )(b_1+b_3\eta )(b_2+b_3\xi )(a_3b_2-a_2b_3)\partial _\xi (\psi -u) \nonumber \\&+\,2J^{-3}_\Omega (\xi ,\eta )(b_1+b_3\eta )(b_2+b_3\xi )(a_1b_3-a_3b_1)\partial _\eta (\psi -u). \end{aligned}$$

The above equality, together with (3.7)- (3.9), leads to

$$\begin{aligned} \Vert \partial ^2_x(\phi -v)\Vert ^2_\Omega\le & {} c\sigma ^4_\Omega \delta ^{-3}_\Omega (\Vert \partial ^2_\xi (\psi -u)\Vert ^2_S+\Vert \partial ^2_\eta (\psi -u)\Vert ^2_S+\Vert \partial _\xi \partial _\eta (\psi -u)\Vert ^2_S) \\&+\,c\sigma ^8_\Omega \delta ^{-5}_\Omega (\Vert \partial _\xi (\psi -u)\Vert ^2_S+\Vert \partial _\eta (\psi -u)\Vert ^2_S). \end{aligned}$$

We can estimate $\Vert \partial ^2_x(\phi -v)\Vert ^2$ and $\Vert \partial _x\partial _y(\phi -v)\Vert ^2$ in the same manner. Consequently, we use (3.16) and Theorem 2.1 to reach that

$$\begin{aligned} |P_{N,\Omega }^{2,0}v-v|_{2,\Omega }\le & {} c\sigma ^2_\Omega \delta ^{-\frac{3}{2}}_\Omega (1+dc_\Omega ^2) (|P^{2,0}_{N,S}u-u|_{2,S}+\sigma _\Omega ^2\delta ^{-1}_\Omega |P^{2,0}_{N,S}u-u|_{1,S}) \nonumber \\\le & {} c\sigma ^2_\Omega \delta ^{-\frac{3}{2}}_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})(1+dc_\Omega ^2)N^{2-r}D_{r,S}(u). \end{aligned}$$

(3.20)

We next estimate the up-bound of $D_{r,S}(v)$. By (3.13) and (3.14) of [24], we know that

$$\begin{aligned} \begin{aligned} \partial ^r_\xi u&= \displaystyle \sum _{j=0}^rC_r^j(a_1+a_3\eta )^j(b_1+b_3\eta )^{r-j}\partial ^j_x\partial ^{r-j}_y v, \\ \partial ^r_\eta u&= \displaystyle \sum _{j=0}^rC_r^j(a_2+a_3\xi )^j(b_2+b_3\xi )^{r-j}\partial ^j_x\partial ^{r-j}_y v. \end{aligned} \end{aligned}$$

(3.21)

Furthermore, we have from (3.3) that

$$\begin{aligned} \partial _\xi x=a_1+a_3\eta ,\qquad \partial _\eta x=a_2+a_3\xi ,\qquad \partial _\xi y=b_1+b_3\eta ,\qquad \partial _\eta y=b_2+b_3\xi . \end{aligned}$$

Thereby, we differentiate the two equalities of (3.21) to obtain that

$$\begin{aligned} \partial ^{r-1}_\xi \partial _\eta u= & {} \displaystyle \sum _{j=0}^{r-1}C_{r-1}^j(a_1+a_3\eta )^j(b_1+b_3\eta )^{r-1-j} ((a_2+a_3\xi )\partial ^{j+1}_x\partial ^{r-1-j}_yv \nonumber \\&+\,(b_2+b_3\xi )\partial ^{j}_x\partial ^{r-j}_yv) \nonumber \\&+\,(r-1)\displaystyle \sum _{j=0}^{r-2}C_{r-2}^j(a_1+a_3\eta )^j(b_1+b_3\eta )^{r-2-j} (a_3\partial ^{j+1}_x\partial ^{r-2-j}_yv \nonumber \\&+\,b_3\partial ^{j}_x\partial ^{r-1-j}_yv), \nonumber \\ \partial _\xi \partial ^{r-1}_\eta u= & {} \displaystyle \sum _{j=0}^{r-1}C_{r-1}^j(a_2+a_3\xi )^j(b_2+b_3\xi )^{r-1-j} ((a_1+a_3\eta )\partial ^{j+1}_x\partial ^{r-1-j}_yv \nonumber \\&+\,(b_1+b_3\eta )\partial ^{j}_x\partial ^{r-j}_yv) \nonumber \\&+\,(r-1)\displaystyle \sum _{j=0}^{r-2}C_{r-2}^j(a_2+a_3\xi )^j(b_2+b_3\xi )^{r-2-j} (a_3\partial ^{j+1}_x\partial ^{r-2-j}_yv +b_3\partial ^{j}_x\partial ^{r-1-j}_yv). \end{aligned}$$

(3.22)

Similarly, we derive that

$$\begin{aligned} \partial ^{r-2}_\xi \partial ^2_\eta u= & {} \displaystyle \sum _{j=0}^{r-2}C_{r-2}^j(a_1+a_3\eta )^j(b_1+b_3\eta )^{r-2-j}((a_2+a_3\xi )^2\partial ^{j+2}_x\partial ^{r-2-j}_y v \nonumber \\&+\,2(a_2+a_3\xi )(b_2+b_3\xi )\partial ^{j+1}_x\partial ^{r-1-j}_y v+(b_2+b_3\xi )^2\partial ^{j}_x\partial ^{r-j}_y v) \nonumber \\&+\,2(r-2)\displaystyle \sum _{j=0}^{r-3}C_{r-3}^j(a_1+a_3\eta )^j(b_1+b_3\eta )^{r-3-j}(a_3(a_2+a_3\xi )\partial ^{j+2}_x\partial ^{r-3-j}_y v \nonumber \\&+\,(a_3b_2+a_2b_3+2a_3b_3\xi )\partial ^{j+1}_x\partial ^{r-2-j}_y v+b_3(b_2+b_3\xi )\partial ^j_x\partial ^{r-1-j}_y v) \nonumber \\&+\,(r-2)(r-3)\displaystyle \sum _{j=0}^{r-4}C_{r-4}^j(a_1+a_3\eta )^j(b_1+b_3\eta )^{r-4-j} \nonumber \\&\cdot \,(a^2_3\partial ^{j+2}_x\partial ^{r-4-j}_y v +2a_3b_3\partial ^{j+1}_x\partial ^{r-3-j}_y v+b^2_3\partial ^{j}_x\partial ^{r-2-j}_y v), \nonumber \\ \partial ^2_\xi \partial ^{r-2}_\eta u= & {} \displaystyle \sum _{j=0}^{r-2}C_{r-2}^j(a_2+a_3\xi )^j(b_2+b_3\xi )^{r-2-j}((a_1+a_3\eta )^2\partial ^{j+2}_x\partial ^{r-2-j}_y v \nonumber \\&+\,2(a_1+a_3\eta )(b_1+b_3\eta )\partial ^{j+1}_x\partial ^{r-1-j}_y v+(b_1+b_3\eta )^2\partial ^{j}_x\partial ^{r-j}_y v) \nonumber \\&+\,2(r-2)\displaystyle \sum _{j=0}^{r-3}C_{r-3}^j(a_2+a_3\xi )^j(b_2+b_3\xi )^{r-3-j}(a_3(a_1+a_3\eta )\partial ^{j+2}_x\partial ^{r-3-j}_yv \nonumber \\&+\,(a_3b_1+a_1b_3+2a_3b_3\eta )\partial ^{j+1}_x\partial ^{r-2-j}_y v+b_3(b_1+b_3\eta )\partial ^j_x\partial ^{r-1-j}_y v) \nonumber \\&+\,(r-2)(r-3)\displaystyle \sum _{j=0}^{r-4}C_{r-4}^j(a_2+a_3\xi )^j(b_2+b_3\xi )^{r-4-j} \nonumber \\&\cdot \,(a^2_3\partial ^{j+2}_x\partial ^{r-4-j}_y v +a_3b_3\partial ^{j+1}_x\partial ^{r-3-j}_y v+b^2_3\partial ^{j}_x\partial ^{r-2-j}_y v). \end{aligned}$$

(3.23)

Now, we use (3.21) and (3.7)–(3.9) to verify that

$$\begin{aligned} \begin{aligned} \Vert \partial ^r_\xi u\Vert _{\chi ^{(r-2,r-2)}_1,S}&\le c\delta ^{-\frac{1}{2}}_\Omega \sigma ^r_\Omega \displaystyle \sum ^r_{j=0}||(1-\xi ^2)^{\frac{r-2}{2}}\partial ^j_x\partial ^{r-j}_yv||_\Omega , \\ \Vert \partial ^r_\eta u\Vert _{\chi ^{(r-2,r-2)}_2,S}&\le c\delta ^{-\frac{1}{2}}_\Omega \sigma ^r_\Omega \displaystyle \sum ^r_{j=0}||(1-\eta ^2)^{\frac{r-2}{2}}\partial ^j_x\partial ^{r-j}_yv||_\Omega . \end{aligned} \end{aligned}$$

(3.24)

Next, we use (3.22) and (3.7)–(3.9) to derive that

$$\begin{aligned}&\Vert \partial ^{r-1}_\xi \partial _\eta u\Vert _{\chi ^{(r-3,r-3)}_1,S}\nonumber \\&\quad \le c\delta ^{-\frac{1}{2}}_\Omega \sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-1} (||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega ) \nonumber \\&\qquad +\,c\delta ^{-\frac{1}{2}}_\Omega \sigma ^{r-1}_\Omega \displaystyle \sum _{j=0}^{r-2} (||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega ), \nonumber \\&\Vert \partial _\xi \partial ^{r-1}_\eta u\Vert _{\chi ^{(r-3,r-3)}_2,S}\nonumber \\&\quad \le c\delta ^{-\frac{1}{2}}_\Omega \sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-1} (||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega ) \nonumber \\&\qquad +\,c\delta ^{-\frac{1}{2}}_\Omega \sigma ^{r-1}_\Omega \displaystyle \sum _{j=0}^{r-2} (||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-3}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega ), \end{aligned}$$

(3.25)

Similarly, we use (3.23) and (3.7)–(3.9) to obtain that

$$\begin{aligned} \Vert \partial ^{r-2}_\xi \partial ^2_\eta u\Vert _{\chi ^{(r-4,r-4)}_1,S}\le & {} c\delta ^{-\frac{1}{2}}_\Omega \sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-2} (||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-2-j}_yv||_\Omega \nonumber \\&+\,||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega ) \nonumber \\&+\,c\delta ^{-\frac{1}{2}}_\Omega \sigma ^{r-1}_\Omega \displaystyle \sum _{j=0}^{r-3} (||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-3-j}_yv||_\Omega \nonumber \\&+\,||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega ) \nonumber \\&+\,c\delta ^{-\frac{1}{2}}_\Omega \sigma ^{r-2}_\Omega \displaystyle \sum _{j=0}^{r-4} (||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-4-j}_yv||_\Omega \nonumber \\&+\,||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-3-j}_yv||_\Omega +||(1-\xi ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-2-j}_yv||_\Omega ), \nonumber \\ \Vert \partial ^2_\xi \partial ^{r-2}_\eta u\Vert _{\chi ^{(r-4,r-4)}_2,S}\le & {} c\delta ^{-\frac{1}{2}}_\Omega \sigma ^r_\Omega \displaystyle \sum _{j=0}^{r-2} (||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-2-j}_yv||_\Omega \nonumber \\&+\,||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-1-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-j}_yv||_\Omega ) \nonumber \\&+\,c\delta ^{-\frac{1}{2}}_\Omega \sigma ^{r-1}_\Omega \displaystyle \sum _{j=0}^{r-3} (||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-3-j}_yv||_\Omega \nonumber \\&+\,||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-2-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-1-j}_yv||_\Omega ) \nonumber \\&+\,c\delta ^{-\frac{1}{2}}_\Omega \sigma ^{r-2}_\Omega \displaystyle \sum _{j=0}^{r-4} (||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+2}_x\partial ^{r-4-j}_yv||_\Omega \nonumber \\&+\,||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j+1}_x\partial ^{r-3-j}_yv||_\Omega +||(1-\eta ^2)^{\frac{r-4}{2}}\partial ^{j}_x\partial ^{r-2-j}_yv||_\Omega ). \end{aligned}$$

(3.26)

A combination of (3.24)–(3.26) implies

$$\begin{aligned} D_{r,S}(u)\le cB_{r,\Omega }(v),\qquad r\ge 4. \end{aligned}$$

(3.27)

Moreover, according to the definitions of $D_{r,S}(u)$ and $B_{r,\Omega }(v)$, we use (3.21)–(3.23) to find that the inequality (3.27) is also valid for $r=2,3$. Consequently, we use (3.20) and (3.10) to reach that for $r\ge 2$,

$$\begin{aligned} ||P_{N,\Omega }^{2,0}v-v||_{2,\Omega }\le & {} (1+c_\Omega )^2|P_{N,\Omega }^{2,0}v-v|_{2,\Omega } \nonumber \\\le & {} c\sigma ^2_\Omega \delta ^{-\frac{3}{2}}_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})(1+dc_\Omega ^2)(1+c_\Omega )^2 N^{2-r} B_{r,\Omega }(v). \end{aligned}$$

(3.28)

This is the desired result (3.14) with $\mu =2$.

We are now in position of deriving the optimal estimate for $||P_{N,\Omega }^{2,0}v-v||_{\Omega }$. Let $g\in L^2(\Omega )$ and consider an auxiliary problem. It is to find $w\in H^2_0(\Omega )$ such that

$$\begin{aligned} a_d( w, z)=(g,z)_{\Omega },\qquad \forall z\in H^2_0(\Omega ). \end{aligned}$$

(3.29)

By taking $z=P^{2,0}_{N,\Omega } v-v$ in (3.29), we use (3.13), (3.10) and the second equality of (3.28) successively to verify that

$$\begin{aligned} |(P^{2,0}_{N,\Omega } v-v,g)|= & {} |a_d(w,P^{2,0}_{N,\Omega } v-v)|=|a_d(P^{2,0}_{N,\Omega } w-w,P^{2,0}_{N,\Omega } v-v)| \nonumber \\\le & {} |P^{2,0}_{N,\Omega } v-v|_{2,\Omega }|P^{2,0}_{N,\Omega }w-w|_{2,\Omega } +d||P^{2,0}_{N,\Omega } v-v||_{\Omega }||P^{2,0}_{N,\Omega }w-w||_{\Omega } \nonumber \\\le & {} c(1+dc_\Omega ^2)|P^{2,0}_{N,\Omega } v-v|_{2,\Omega }|P^{2,0}_{N,\Omega } w-w|_{2,\Omega } \nonumber \\\le & {} c\sigma ^{4}_\Omega \delta ^{-3}_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})^2(1+dc_\Omega ^2)^3 N^{-r}B_{r,\Omega }(v)B_{4,\Omega }(w). \end{aligned}$$

(3.30)

Furthermore, the Eq. (3.29) implies $\Delta ^2 w+dw=g$ in sense of distribution. Thus, due to (3.11), we assert that

$$\begin{aligned} B_{4,\Omega }(w)\le c\delta _\Omega ^{-\frac{1}{2} }(\sigma _\Omega +1)^4\Vert w\Vert _{4,\Omega } \le c \eta _{\Omega }\delta _\Omega ^{-\frac{1}{2} }(\sigma _\Omega +1)^4\Vert g\Vert _{\Omega }. \end{aligned}$$

(3.31)

Consequently, we use (3.30) and (3.31) to deduce that for $r\ge 2$,

$$\begin{aligned} \Vert P^{2,0}_{N,\Omega }v-v\Vert _{\Omega }= & {} \displaystyle \sup _{g\in L^2(\Omega ), g\ne 0}\frac{|(P^{2,0}_{N,\Omega }v-v,g)_\Omega |}{\Vert g\Vert _\Omega } \nonumber \\\le & {} c\sigma ^{4}_\Omega \delta ^{-3}_\Omega (1+\sigma _\Omega \delta ^{-1}_\Omega N^{-1})^2(1+dc_\Omega ^2)^3 N^{-r}\frac{B_{r,\Omega }(v)B_{4,\Omega }(w)}{\Vert g\Vert _{\Omega }} \nonumber \\\le & {} c\eta _{\Omega }\sigma ^{4}_\Omega \delta ^{-\frac{7}{2}}_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})^2(1+dc_\Omega ^2)^3(\sigma _\Omega +1)^4 N^{-r}B_{r,\Omega }(v). \end{aligned}$$

Finally, we use the interpolation of spaces to derive that

$$\begin{aligned}&\Vert P^{2,0}_{N,\Omega }v-v\Vert _{1,\Omega }\\&\quad \le \Vert P^{2,0}_{N,\Omega }v-v\Vert ^{\frac{1}{2}}_\Omega \Vert P^{2,0}_{N,\Omega }v-v\Vert ^{\frac{1}{2}}_{2,\Omega } \nonumber \\&\quad \le c\eta _{\Omega }^{\frac{1}{2}}\sigma ^3_\Omega \delta ^{-\frac{5}{2} }_\Omega (1+\sigma _\Omega ^2\delta ^{-1}_\Omega N^{-1})^{\frac{3}{2}} (1+dc_\Omega ^2)^2(\sigma _\Omega +1)^2(1+c_\Omega ) N^{1-r}B_{r,\Omega }(v). \end{aligned}$$

The proof is completed. $\square$

Remark 3.1

In the norms involved in the error estimations (3.14), there are some weight functions which tend to zero as the points go to the corners of domain. It is useful for covering certain singularities of the approximated functions and their derivatives at the corners.

3.3 Other Legendre Irrational Orthogonal Approximations

We consider other Legendre irrational orthogonal approximations. For example, we set

$$\begin{aligned} {}^0H^2(\Omega )=H^2(\Omega )\cap \{v~|~v=0 \mathrm{~on~} \partial \Omega , \partial _n v=0 \mathrm{~on~}L_1\cup L_4 \},\quad {}^0V_N(\Omega )={}^0H^2(\Omega )\cap V_N(\Omega ). \end{aligned}$$

According to the Poincaré inequality, there exists a positive constant, which is denoted by $c_\Omega$ also, such that

$$\begin{aligned} \Vert v\Vert _\Omega \le c_\Omega | v|_{1,\Omega }, \qquad \forall v\in H^1(\Omega )\cap \{v\,|\,v=0\,\mathrm{on}\,L_1\cup L_4 \}. \end{aligned}$$

(3.32)

Let $d,\beta \ge 0$, and

$$\begin{aligned} a_{d,\beta }(u,v)=(\Delta u,\Delta v)_\Omega +d( u, v)_\Omega +\beta \int _{L_2\cup L_3}\partial _nu\partial _nvds,\qquad \forall u,v\in H^2(\Omega ). \end{aligned}$$

(3.33)

We define the operator ${}^0P^{2}_{N,\Omega }:{}^0H^2(\Omega )\rightarrow {}^0V_N(\Omega )$, by

$$\begin{aligned} a_{d,\beta }({}^0P^{2}_{N,\Omega }v-v, \phi )=0,\qquad \forall \phi \in {}^0V_N(\Omega ). \end{aligned}$$

(3.34)

It can be shown that

$$\begin{aligned} a_{d,\beta }({}^0P^{2}_{N,\Omega }v-v,{}^0P^{2}_{N,\Omega }v-v)\le a_{d,\beta }(\phi -v,\phi -v ),\qquad \forall \phi \in {}^0V_N(\Omega ). \end{aligned}$$

Let $u(\xi ,\eta )=v(x(\xi ,\eta ),y(\xi ,\eta )),\,\psi (\xi ,\eta )=P^{2,0}_{N,S}u(\xi ,\eta )$ and $\phi (x,y)=\psi (\xi (x,y),\eta (x,y))$ in the above inequality. Then, with the aid of (3.32), the trace theorem and Theorem 2.2, we could follow the same line as in the proof of Theorem 3.1 to reach the following result.

Theorem 3.2

If $v\in {}^0H^2(\Omega )$ and $B_{r,\Omega }(v)$ is finite for integer $2\le r\le N+1$ and $N\ge 2$, then

$$\begin{aligned}&||\Delta ({}^0P^{2}_{N,\Omega }v-v)||_{\Omega }+\beta ^{\frac{1}{2}}\left( \int _{L_2\cup L_3}(\partial _n({}^0P^{2}_{N,\Omega }v-v))^2ds \right) ^{\frac{1}{2}} \nonumber \\&\quad \le c(1+\beta )C_{2, \Omega }N^{2-r} B_{r,\Omega }(v). \end{aligned}$$

(3.35)

4 Spectral Method for Fourth-Order Problems

In this section, we propose the spectral method for fourth-order problems defined on quadrilaterals.

Let $\partial \Omega =\overline{\partial ^*\Omega \cup \partial ^{**}\Omega },\partial ^*\Omega \cap \partial ^{**}\Omega =\emptyset$ and $d, \beta$ be non-negative constants. We consider the following model problem,

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta ^2 U(x,y)+dU(x,y)=F(x,y), &{}\quad \,\mathrm{in}\,\Omega ,\\ \Delta U(x,y)+\beta \partial _nU(x,y)=G_2(x,y), &{}\quad \,\mathrm{on}\,\partial ^{**}\Omega ,\\ \partial _n U(x,y)=G_1(x,y),&{}\quad \,\mathrm{on}\,\partial ^*\Omega ,\\ U(x,y)=G_0(x,y), &{}\quad \,\mathrm{on}\,\partial \Omega . \end{array}\right. \end{aligned}$$

(4.1)

If $\partial ^*\Omega =\partial \Omega$, then the above problem is a Dirichlet boundary value problem. Otherwise, it is a mixed inhomogeneous boundary value problem. In this case, if $\partial ^{**}\Omega =\partial \Omega$ and $d=\beta =0$, then we require the following additional condition for ensuring the existence of solution,

$$\begin{aligned} \int \int _\Omega F(x,y)dx_1dx_2=\int _{\partial \Omega }\partial _n G_2(x,y)ds. \end{aligned}$$

4.1 Dirichlet Boundary Value Problems

We first consider the homogeneous Dirichlet boundary value problems, namely, $\partial ^*\Omega =\partial \Omega$ and $G_0(x,y)=G_1(x,y)\equiv 0$. Let $a_d(u,v)$ be the same as in (3.12). The weak form of problem (4.1) is to seek the solution $U\in H^2_0(\Omega )$ such that

$$\begin{aligned} a_d(U,v)=(f,v)_\Omega ,\qquad \forall v\in H^2_0(\Omega ). \end{aligned}$$

(4.2)

The Legendre irrational spectral scheme for solving (4.2) is to find $u_N\in V^0_N(\Omega )$ such that

$$\begin{aligned} a_d(u_N,\phi )=(f,\phi )_\Omega ,\qquad \forall \phi \in V_N^0(\Omega ). \end{aligned}$$

(4.3)

We now estimate the error of numerical solution. Let $P^{2,0}_{N,\Omega }U$ be the same as in (3.13). Then

$$\begin{aligned} a_d(P^{2,0}_{N,\Omega }U,\phi )=(f,\phi )_\Omega ,\qquad \forall \phi \in V_N^0(\Omega ). \end{aligned}$$

Subtracting the above equality from (4.3), we obtain

$$\begin{aligned} a_d(u_N-P^{2,0}_{N,\Omega }U,\phi )=0,\qquad \forall \phi \in V_N^0(\Omega ). \end{aligned}$$

(4.4)

Taking $\phi =u_N-P^{2,0}_{N,\Omega }U$ in (4.4), we find that $\Delta (u_N-P^{2,0}_{N,\Omega }U)\equiv 0$ in $\Omega$. Since $u_N-P^{2,0}_{N,\Omega }U= 0$ on $\partial \Omega$, we assert that $u_N-P^{2,0}_{N,\Omega }U\equiv 0$ on $\bar{\Omega }$, i.e., $u_N=P^{2,0}_{N,\Omega }U$. Finally, we use Theorem 3.1 to conclude that

$$\begin{aligned} ||U-u_N||_{\mu ,\Omega }\le cC_{\mu , \Omega }N^{\mu -r} B_{r,\Omega }(U),\qquad \mu =0,1,2. \end{aligned}$$

(4.5)

Remark 4.1

In the norms involved in the above estimations, there are some weight functions which tend to zero as the points go to the corners of domain. It is useful for covering certain singularities of the exact solutions and their derivatives at the corners.

We next describe the numerical implementations and present some numerical results confirming the analysis in the last section. To do this, let $L_l(\xi )(-1\le l\le 1)$ be the standard Legendre polynomials as before, and

$$\begin{aligned} \phi _l(\xi )=\displaystyle \frac{1}{\sqrt{2(2l+3)^2(2l+5)}}\left( L_l(\xi ) -\frac{2(2l+5)}{2l+7}L_{l+2}(\xi )+\frac{2l+3}{2l+7}L_{l+4}(\xi )\right) . \end{aligned}$$

Obviously $\phi _l(\pm 1)=\partial _\xi \phi _l(\pm 1)=0$. Therefore, all of the functions $\phi _l(\xi (x,y))\phi _m(\eta (x,y)) (0\le l,m \le N-4)$ conform the basis of $V^0_N(\Omega )$. In actual computations, we expand the numerical solution of (4.3) as

$$\begin{aligned} u_N(x,y)=\displaystyle \sum ^{N-4}_{l=0}\displaystyle \sum ^{N-4}_{m=0}a_{l,m}\phi _l(\xi (x,y))\phi _m(\eta (x,y)). \end{aligned}$$

By inserting the above expression into (4.3), we obtain a linear system of algebraic equations with the unknown coefficients $a_{l,m}$.

Let $\xi _{N,l}~(0\le l\le N)$ be the zeros of the Legendre polynomial $L_{N+1}(\xi )$. Meanwhile, $\omega _{N,l}\,(0\le l\le N)$ stand for the Christoffel numbers of the Legendre–Gauss interpolation. Moreover, $x_{N,l,m}=x(\xi _{N,l},\eta _{N,m})$ and $y_{N,l,m}=y(\xi _{N,l},\eta _{N,m})$. We measure the errors of numerical solutions by the discrete average norm

$$\begin{aligned} E_{ave,N}=\left( \displaystyle \sum ^{N-4}_{l=0}\displaystyle \sum ^{N-4}_{m=0}(U(x_{N,l,m},y_{N,l,m})-u_N(x_{N,l,m},y_{N,l,m}))^2\omega _{N,l}\omega _{N,m}\right) ^{\frac{1}{2}}, \end{aligned}$$

and the discrete maximum norm

$$\begin{aligned} E_{max,N}=\displaystyle \max _{0\le l \le N-4}\max _{0\le m \le N-4}|U(x_{N,l,m},y_{N,l,m})-u_N(x_{N,l,m},y_{N,l,m})|. \end{aligned}$$

We first use (4.3) to solve (4.2) with $d=1$ and $\beta =0$. We take the domain $\Omega =\Omega ^{(1)}$ with the vertices $Q_1=(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$, $Q_2=(\frac{\sqrt{6}}{2},-\frac{\sqrt{6}}{2})$, $Q_3=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ and $Q_4=(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$. The smallest angle $\theta _2=\frac{\pi }{3}$, and the two largest angles $\theta _1=\theta _3=\frac{7}{12}\pi$. The equations of the four edges of $\Omega ^{(1)}$ are as follows,

• $L_1: l_1(x,y)=x+\frac{\sqrt{2}}{2}=0$,

• $L_2: l_2(x,y)=(\sqrt{3}-2)x-y-\frac{3\sqrt{2}}{2}+\frac{\sqrt{6}}{2}=0$,

• $L_3: l_3(x,y)=(\sqrt{3}+2)x+y-\frac{3\sqrt{2}}{2}-\frac{\sqrt{6}}{2}=0$,

• $L_4: l_4(x,y)=y-\frac{\sqrt{2}}{2}=0$.

We take the following test function,

$$\begin{aligned} U(x,y)=l^2_1(x,y)l^2_2(x,y)l^2_3(x,y)l^2_4(x,y)\cos (x+y). \end{aligned}$$

(4.6)

Clearly, $U(x,y)\in H^2_0(\Omega )$. In Table 1, we list the discrete errors $E_{ave,N}$ and $E_{max,N}$ versus the mode $N$. They demonstrate that the numerical errors decay rapidly as $N$ increases. This confirms the analysis.

Table 1 The numerical errors of scheme (4.3) with domain $\Omega ^{(1)}$

Table 2 The numerical errors of scheme (4.3) with domain $\Omega ^{(2)}$

We next use (4.3) to solve (4.2) with $d=1$ and $\beta =0$, defined on the domain $\Omega =\Omega ^{(2)}$ with the vertices $Q_1=(-\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2})$, $Q_2=(\sqrt{2}+\frac{\sqrt{6}}{2},-\sqrt{2}-\frac{\sqrt{6}}{2})$, $Q_3=(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$ and $Q_4=(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$. The smallest angle $\theta _2=\frac{\pi }{6}$, and the largest angles $\theta _1=\theta _3=\frac{2\pi }{3}$. The equations of the four edges of $\Omega ^{(2)}$ are as follows,

• $L_1: l_1(x,y)=x+\frac{\sqrt{2}}{2}=0$,

• $L_2: l_2(x,y)=-\frac{\sqrt{3}}{3}x-y-\frac{\sqrt{6}}{6}-\frac{\sqrt{2}}{2}=0$,

• $L_3: l_3(x,y)=-\sqrt{3}x-y+\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2}=0$,

• $L_4: l_4(x,y)=y-\frac{\sqrt{2}}{2}=0$.

The test function is given by (4.6) with the above new functions $l_i(x,y), 1\le i\le 4$. In Table 2, we list the discrete errors $E_{ave,N}$ and $E_{max,N}$ versus the mode $N$. They also demonstrate that the numerical errors decay rapidly as $N$ increases. By comparing Table 1 with Table 2, we find that the numerical errors depend on the quantity $\min _{1\le i\le 4}( \theta _i, \pi -\theta _i)$. Indeed, the bigger this quantity, the smaller the numerical errors.

4.2 Mixed Boundary Value Problems

In this subsection, we consider mixed boundary value problems. For fixedness, let $\partial ^{*}\Omega =L_1\cup L_4,$ and $\partial ^{**}\Omega =L_2\cup L_3$. Moreover, $G_0(x,y)\equiv 0$ on $\Omega$, and $G_1(x,y)\equiv 0$ on $\partial ^{*}\Omega$. The space ${}^0H^2(\Omega )$ and the set ${}^0V_N(\Omega )$ are the same as in Sect. 3.3. Let $a_{d,\beta }(u,v)$ be the same as in (3.33). The weak formulation of (4.1) is to seek solution $U\in {}^0H^2(\Omega )$ such that

$$\begin{aligned} a_{d,\beta }(U,v)=(f,v)_\Omega +\int _{\partial ^{**}\Omega }G_2\partial _nvds,\qquad \forall v\in {}^0H^2(\Omega ). \end{aligned}$$

(4.7)

The Legendre irrational spectral scheme for solving (4.7) is to find $u_N\in {}^0V_N(\Omega )$ such that

$$\begin{aligned} a_{d,\beta }(u_N,\phi )=(f,\phi )_\Omega +\int _{\partial ^{**}\Omega }G_2\partial _n\phi ds,\qquad \forall \phi \in {}^0V_N(\Omega ). \end{aligned}$$

(4.8)

Let ${}^0P^2_{N,\Omega }U$ be the same as in (3.34). Then

$$\begin{aligned} a_{d,\beta }({}^0P^2_{N,\Omega }U,\phi )=(f,\phi )_\Omega +\int _{\partial ^{**}\Omega }G_2\partial _n\phi ds,\qquad \forall \phi \in {}^0V_N(\Omega ). \end{aligned}$$

By subtracting the above equality from (4.8), we obtain

$$\begin{aligned} a_d(u_N-{}^0P^2_{N,\Omega }U,\phi )=0,\qquad \forall \phi \in {}^0V_N(\Omega ). \end{aligned}$$

(4.9)

Taking $\phi =u_N-{}^0P^2_{N,\Omega }U$ in (4.9), we find that $\Delta (u_N-{}^0P^2_{N,\Omega }U)\equiv 0$ in $\Omega$. Since $u_N-{}^0P^2_{N,\Omega }U= 0$ on $\partial \Omega$, we derive that $u_N={}^0P^2_{N,\Omega }U$. Finally, we use Theorem 3.2 to obtain

$$\begin{aligned} ||\Delta (U-u_N)||_{\Omega }+\beta ^{\frac{1}{2}}\left( \int _{\partial ^{**}\Omega }(\partial _n(U-u_N))^2ds \right) ^{\frac{1}{2}}\le c(1+\beta )C_{2, \Omega }N^{2-r} B_{r,\Omega }(v). \end{aligned}$$

(4.10)

We now present some numerical results. Let $\phi _l(\xi )$ be the same as in the last subsection, and

$$\begin{aligned} h_-(x)=\displaystyle \frac{1}{4}(\xi ^3-\xi ^2-\xi +1),\qquad h_+(\xi )=\frac{1}{4}(\xi ^3+\xi ^2-\xi -1). \end{aligned}$$

It was shown in [21] that $h_-(\pm 1)=h_+(\pm 1)=\partial _\xi h_-(1)=\partial _\xi h_+(-1)=0$. Thus, all $\phi _l(\xi (x,y))\phi _m(\eta (x,y))$, $\phi _l(\xi (x,y))h_-(\eta (x,y)),h_+(\xi (x,y))\phi _l(\eta (x,y))~(0\le l,m \le N-4)$ and $h_+(\xi (x,y))h_-(\eta (x,y))$ conform the basis of ${}^0V_N(\Omega )$. In actual computations, we expand the numerical solution of (4.8) as

$$\begin{aligned} u_N(x,y)= & {} \displaystyle \sum ^{N-4}_{l=0}\displaystyle \sum ^{N-4}_{m=0}a_{l,m}\phi _l(\xi (x,y))\phi _m(\eta (x,y))+\displaystyle \sum ^{N-4}_{l=0}b_l\phi _l(\xi (x,y))h_-(\eta (x,y)) \\&+\,\displaystyle \sum ^{N-4}_{l=0}c_lh_+(\xi (x,y))\phi _l(\eta (x,y)) +qh_+(\xi (x,y))h_-(\eta (x,y)). \end{aligned}$$

By inserting the above expression into (4.8), we obtain a linear system of algebraic equations with the unknown coefficients $a_{l,m},b_l,c_l$ and $q$.

We now use (4.8) to solve (4.7) with $d=1$ and $\beta =0$, defined on the domain $\Omega =\Omega ^{(1)}$. The test function is

$$\begin{aligned} U(x,y)=l^2_1(x,y)l_2(x,y)l_3(x,y)l^2_4(x,y)\cos (x+y). \end{aligned}$$

(4.11)

Clearly, $U\in {}^0H^2(\Omega )$. In Table 3, we list the discrete errors $E_{ave,N}$ and $E_{max,N}$ versus the mode $N$. They show the rapid convergence of scheme (4.8).

Table 3 The numerical errors of scheme (4.8) with domain $\Omega ^{(1)}$

Table 4 The numerical errors of scheme (4.8) with domain $\Omega ^{(2)}$

We next use (4.8) to solve (4.7) with $d=1$ and $\beta =0$, defined on the domain $\Omega =\Omega ^{(2)}$. The test function is given by (4.11), with the functions $l_i(x,y), 1\le i\le 4$, which correspond to the domain $\Omega ^{(2)}$ as before. In Table 4, we list the discrete errors $E_{ave,N}$ and $E_{max,N}$ versus the mode $N$. They also show the rapid convergence of scheme (4.8). By comparing Table 3 with Table 4, we observe again that the numerical errors depend on the quantity $\min _{1\le i\le 4}( \theta _i, \pi -\theta _i)$.

In the error estimates (4.5) and (4.10), there exist the weights vanishing on some parts of the edges. It would be useful to cover certain weak singular behaviors at the edges or vertices. To show this, we use (4.8) to solve (4.7) with $d=1$ and $\beta =0$, defined on the domain $\Omega =\Omega ^{(1)}$ as before. We take the test function as

$$\begin{aligned} U(x,y)=\rho ^\gamma (x,y)l^2_1(x,y)l_2(x,y)l_3(x,y)l^2_4(x,y)\cos (x+y), \end{aligned}$$

(4.12)

where $\rho (x,y)=\sqrt{\left( x-\frac{\sqrt{6}}{2}\right) ^2+\left( y+\frac{\sqrt{6}}{2}\right) ^2}$ and $\gamma >0$. Clearly, the singularities of $U(x,y)$ occur at the vertices $Q_2\left( \frac{\sqrt{6}}{2},-\frac{\sqrt{6}}{2}\right)$, except that $\gamma$ is an even number. Also, $U\in {}^0H^2(\Omega )\cap H^{3+\gamma -\omega }(\Omega )$ with arbitrary $\omega >0$.

Table 5 The numerical errors of scheme (4.8) with domain $\Omega ^{(1)}$ and $\gamma =1$

In Tables 5, 6 and 7, we list the discrete errors $E_{ave,N}$ and $E_{max,N}$ versus the mode $N$ with $\gamma =1,~3,~5$, respectively. We see that for the same modes $N$, the numerical results with bigger $\gamma$ are more accurate than those with smaller $\gamma$. More precisely, since $U\in H^{2+\gamma }(\Omega )$, we obtain from (4.10) that the numerical errors are of the order $N^{-\gamma }$. Therefore, as indicated by Tables 5, 6 and 7, the numerical errors with bigger $\gamma$ decrease faster than those with small $\gamma$.

4.3 Inhomogeneous Boundary Value Problems

We now turn to problem (4.1) with $G_0(x,y)\not \equiv 0$ and $G_1(x,y)\not \equiv 0$. According to the lifting, there exists the function ${\widetilde{U}}(x,y)$ such that ${\widetilde{U}}(x,y)=G_0(x,y)$ on $\partial \Omega$, and $\partial _n {\widetilde{U}}(x,y)=G_1(x,y)$ on $\partial ^{*}\Omega$. We make the following variable transformation,

$$\begin{aligned} U(x,y)= & {} W(x,y)+{\widetilde{U}}(x,y),\qquad f(x,y)=F(x,y)-\Delta ^2 {\widetilde{U}}(x,y)-d {\widetilde{U}}(x,y), \nonumber \\ g_2(x,y)= & {} G_2(x,y)-\Delta {\widetilde{U}}(x,y)-\beta \partial _n{\widetilde{U}}(x,y). \end{aligned}$$

(4.13)

Then, the problem (4.1) is reformulated to

$$\begin{aligned} \left\{ \begin{array}{ll} \Delta ^2 W(x,y)+d W(x,y)=f(x,y), &{}\quad \,\mathrm{in}\,\Omega ,\\ \Delta W(x,y)+\beta \partial _nW(x,y)=g_2(x,y), &{}\quad \,\mathrm{on}\,\partial ^{**}\Omega ,\\ \partial _n W(x,y)=0,&{}\quad \,\mathrm{on}\,\partial ^{*}\Omega ,\\ W(x,y)=0, &{}\quad \,\mathrm{on}\,\partial \Omega . \end{array}\right. \end{aligned}$$

(4.14)

We can solve this alternative problem numerically by the methods proposed in Sects. 4.1 or 4.2. Its numerical solution is denoted by $w_N(x,y)$. The numerical solution of the original problem is given by $u_N(x,y)=W_N(x,y)+{\widetilde{U}}(x,y)$.

Table 6 The numerical errors of scheme (4.8) with domain $\Omega ^{(1)}$ and $\gamma =3$

Table 7 The numerical errors of scheme (4.8) with domain $\Omega ^{(1)}$ and $\gamma =5$

The key point is how to construct the lifting function ${\widetilde{U}}(x,y)$. This is a difficult and open problem for fourth-order problem. Fortunately, we solve this problem, see “Appendix” of this paper.

We now present some numerical results. We consider the inhomogeneous Dirichlet boundary value problem (4.1) with $d=1$ and $\beta =0$, define on the quadrilaterals $\Omega =\Omega ^{(3)}$ with the vertices $Q_1=(0,0),\, Q_2=(2,0),\, Q_3=(1,1)$ and $Q_4=(0,1)$. We take the following test function,

$$\begin{aligned} U(x,y)=(x-1)^3(x-2)^3(y-2)^3sin(x-y). \end{aligned}$$

(4.15)

Clearly, $U\in H^2(\Omega )$, and $U$ possesses inhomogeneous boundary condition on $\partial \Omega$. We list the discrete errors $E_{ave,N}$ and $E_{max,N}$ versus the mode $N$ in Table 8. They show the rapid convergence of spectral scheme.

Table 8 The numerical errors of inhomogeneous problem with domain $\Omega ^{(3)}$

5 Concluding Remarks

In this paper, we proposed the spectral method for fourth-order problems defined on quadrilaterals. We provided the spectral schemes for a model problem with Dirichlet boundary condition and mixed boundary condition, and proved their spectral accuracy. We also developed the lifting technique, by which we could deal with inhomogeneous boundary value problems reasonably. Numerical results demonstrated the high effectiveness of the suggested algorithms. As the mathematical foundation of our new spectral method, we introduced the orthogonal irrational approximation defined on quadrilaterals, and established the basic approximation results, which plays an essential role in designing and analyzing the related spectral method. The approximation results and techniques developed in this paper are also applicable to other fourth-order problems defined on quadrilaterals.

As we know, Guo and Jia [16] first proposed the spectral element method for second-order problems defined on quadrilateral arbitrary polygons with quadrilateral partition, while Yu and Guo [29] investigated the spectral element method for fourth-order problems with rectangle partition of domains. An important problem is how to generalize the approach of this work to fourth-order problems with quadrilateral partition of domains. Like conforming finite element method, the main difficulty of designing such method is how to ensure the continuity of the derivatives of numerical solutions at all common edges of adjacent elements. It seems hopeful to solve this problem by using the quasi orthogonal approximation similar to the work of [16], coupled with the lifting technique presented in “Appendix” of this paper. We shall report the related results in the future.

Appendix

This appendix is devoted to the lifting technique. The edges $L_i$ of domain $\Omega$ are as follows (see Fig. 1),

$$\begin{aligned} L_i:\,l_i(x,y)=a_i x+b_i y+c_i=0,\qquad 1\le i\le 4. \end{aligned}$$

(A.1)

Let $l_{i+4}(x,y)=l_i(x,y),~i=1,2,3,4$. We could rewrite the equations corresponding to the edges as $x=x_i(y)$ for $L_i,i=1,3$, and $y=y_i(x)$ for $L_i,i=2,4$. Clearly,

$$\begin{aligned} \frac{dx_i}{dy}=-\frac{b_i}{a_i}\,\mathrm{for }\,i=1,3,\qquad \frac{dy_i}{dx}=-\frac{a_i}{b_i} \,\mathrm{for}\,i=2,4. \end{aligned}$$

(A.2)

We denote the normal vector of edges $L_i$ by $n_i=(\cos \alpha _i,\cos \beta _i)^T,~1\le i\le 4$. Besides, $Q_i$ stand for the four corners of domain $\Omega$ as in Fig. 1.

Our aim is to design the lifting function $v_b(x,y)$ such that

$$\begin{aligned} v_b(x,y)|_{L_i}= & {} v_b(x_i(y),y) = g_i(y),\qquad \partial _{n_i} v_b(x,y)|_{L_i}=h_i(y),\qquad i=1,3, \nonumber \\ v_b(x,y)|_{L_i}= & {} v_b(x,y_i(x))=g_i(x),\qquad \partial _{n_i} v_b(x,y)|_{L_i}=h_i(x),\qquad i=2,4, \end{aligned}$$

(A.3)

where $g_i(y),h_i(y) (i=1,3)$ and $g_i(x),h_i(x)(i=2,4)$ are given functions. In addition, the functions $g_i(y)$ and $g_i(x)$ fulfill certain consistent conditions ensuring the continuity of $v_b(x,y)$ at the corners of domain.

In the forthcoming discussions, we introduce the following polynomials,

$$\begin{aligned} s_i(x,y)= & {} \displaystyle \prod _{1\le j\le 4,j\ne i}(a_j x+b_j y+c_j)^2=\displaystyle \frac{l_1^2(x,y)l_2^2(x,y)l_3^2(x,y)l_4^2(x,y)}{l_i^2(x,y)}, \nonumber \\ t_i(x,y)= & {} (a_i x+b_i y+c_i)s_i(x,y)=l_i(x,y)s_i(x,y),\qquad i=1,2,3,4. \end{aligned}$$

(A.4)

It can be checked that

$$\begin{aligned} \partial _n s_i(x,y)\ne & {} 0,\quad s_i(x,y)\ne 0,\quad \partial _n t_i(x,y)\ne 0,\quad t_i(x,y)=0,\quad \,\mathrm{on}\,L_i,\,i=1,2,3,4, \nonumber \\ \partial _n s_i(x,y)= & {} s_i(x,y)=\partial _n t_i(x,y)=t_i(x,y)=0,\quad \mathrm{~on~}\cup ^{4}_{j=1,j\ne i}L_j, \end{aligned}$$

(A.5)

We also introduce the following polynomials,

$$\begin{aligned} \sigma _{i1}(x,y)= & {} l^2_{i+2}(x,y)l^2_{i+3}(x,y),\qquad \sigma _{i2}(x,y)=l_{i+1}(x,y)\sigma _{i1}(x,y), \nonumber \\ \sigma _{i3}(x,y)= & {} l_{i}(x,y)\sigma _{i1}(x,y),\,\,\,\quad \qquad \sigma _{i4}(x,y)=l_{i}(x,y)l_{i+1}(x,y)\sigma _{i1}(x,y), \nonumber \\ i= & {} 1,2,3,4. \end{aligned}$$

(A.6)

It can be verified that

$$\begin{aligned} \sigma _{12}(x,y)|_{L_2}= & {} \sigma _{13}(x,y)|_{L_1}=\sigma _{14}(x,y)|_{L_1\cup L_2}=0, \nonumber \\ \partial _n \sigma _{1j}(x,y)|_{L_3\cup L_4}= & {} \sigma _{1j}(x,y)|_{L_3\cup L_4}=0,\quad 1\le j\le 4. \end{aligned}$$

(A.7)

We can also verify that $\sigma _{ij}(x,y),2\le i,j\le 4$ have the same properties. Accordingly, we design the desired lifting function $v_b(x,y)$ satisfying (A.3) as follows,

$$\begin{aligned} v_b(x,y)= & {} \widetilde{g}_1(y)s_1(x,y)+\widetilde{h}_1(y)t_1(x,y) +\widetilde{g}_2(x)s_2(x,y)+\widetilde{h}_2(x)t_2(x,y) \nonumber \\&+\,\widetilde{g}_3(y)s_3(x,y)+\widetilde{h}_3(y)t_3(x,y) \nonumber \\&+\,\widetilde{g}_4(x)s_4(x,y)+\widetilde{h}_4(x)t_4(x,y)+\displaystyle \sum ^4_{i,j=1}p_{ij}\sigma _{ij}(x,y), \end{aligned}$$

(A.8)

where $\widetilde{g}_i,\widetilde{h}_i$ and $p_{ij}, 1\le i,j\le 4$ are undetermined functions and constants. We shall construct those undetermined quantities properly in the following four steps.

Step 1 According to (A.3), we use (A.5) and (A.7) to derive that

$$\begin{aligned} v_b(x,y)|_{L_1}= & {} \widetilde{g}_1(y)s_1(x_1(y),y)+p_{11}\sigma _{11}(x_1(y),y)+p_{12}\sigma _{12}(x_1(y),y) \nonumber \\&+\,p_{41}\sigma _{41}(x_1(y),y)+p_{43}\sigma _{43}(x_1(y),y)=g_1(y), \nonumber \\ v_b(x,y)|_{L_2}= & {} \widetilde{g}_2(x)s_2(x,y_2(x))+p_{21}\sigma _{21}(x,y_2(x))+p_{22}\sigma _{22}(x,y_2(x)) \nonumber \\&+\,p_{11}\sigma _{11}(x,y_2(x))+p_{13}\sigma _{13}(x,y_2(x))=g_2(x),\qquad \mathrm {etc.} \end{aligned}$$

(A.9)

Furthermore, the corner $Q_1=L_1\cap L_2$. Thus we know from (A.5) and (A.7) that

$$\begin{aligned} s_1(x_1(y),y)= & {} s_2(x,y_2(x))=\sigma _{12}(x_1(y),y)=\sigma _{13}(x,y_2(x)) \\= & {} \sigma _{21}(x,y_2(x))=\sigma _{22}(x,y_2(x))=\sigma _{41}(x_1(y),y)\\= & {} \sigma _{43}(x_1(y),y)=0, \qquad \,\mathrm{at} \,Q_1. \end{aligned}$$

Therefore

$$\begin{aligned} v_b(x,y)|_{Q_1}=p_{11}\sigma _{11}(x,y)|_{Q_1}=g_1(y)|_{Q_1}=g_2(x)|_{Q_1}. \end{aligned}$$

In other words,

$$\begin{aligned} p_{11}=\frac{g_1(y)|_{Q_1}}{\sigma _{11}(x,y)|_{Q_1}}=\frac{g_2(x)|_{Q_1}}{\sigma _{11}(x,y)|_{Q_1}}. \end{aligned}$$

(A.10)

Due to the continuity of $v_b(x,y)$, we have $g_1(y)|_{Q_1}=g_2(x)|_{Q_1}$. Thereby, the above expression is meaningful and so determines the constant $p_{11}$. In the same manner, we can calculate the constants $p_{i1},\,i=2,3,4$.

Step 2 For simplicity, let $\partial _x s_1(x_1(y),y)=\partial _x s_1(x,y)|_{x=x_1(y)}$, etc. By differentiating the two equations of (A.9), we derive that

$$\begin{aligned} \partial _y(v_b(x_1(y),y))= & {} \partial _y\widetilde{g}_1(y)s_1(x_1(y),y) +\widetilde{g}_1(y)(\partial _xs_1(x_1(y),y)\frac{dx_1}{dy}+\partial _y s_1(x_1(y),y)) \nonumber \\&+\,p_{11}(\partial _x\sigma _{11}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{11}(x_1(y),y)) \nonumber \\&+\,p_{12}(\partial _x\sigma _{12}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{12}(x_1(y),y)) \nonumber \\&+\,p_{41}(\partial _x\sigma _{41}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{41}(x_1(y),y)) \nonumber \\&+\,p_{43}(\partial _x\sigma _{43}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{43}(x_1(y),y))=\partial _yg_1(y), \nonumber \\ \partial _x(v_b(x,y_2(x)))= & {} \partial _x\widetilde{g}_2(x)s_2(x,y_2(x)) +\widetilde{g}_2(x) \left( \partial _xs_2(x,y_2(x))+\partial _ys_2(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{21} \left( \partial _x\sigma _{21}(x,y_2(x))+\partial _y\sigma _{21}(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{22}\left( \partial _x\sigma _{22}(x,y_2(x))+\partial _y\sigma _{22}(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{11}\left( \partial _x\sigma _{11}(x,y_2(x))+\partial _y\sigma _{11}(x,y_2(x))\frac{dy_2}{dx}\right) \nonumber \\&+\,p_{13}\left( \partial _x\sigma _{13}(x,y_2(x))+\partial _y\sigma _{13}(x,y_2(x))\frac{dy_2}{dx}\right) =\partial _xg_2(x). \end{aligned}$$

(A.11)

Moreover, we know from (A.5) and (A.7) that at the corner $Q_1$,

$$\begin{aligned} s_1(x_1(y),y)= & {} \partial _x s_1(x_1(y),y)=\partial _y s_1(x_1(y),y)=0 \\ s_2(x,y_2(x))= & {} \partial _x s_2(x,y_2(x))=\partial _y s_2(x,y_2(x))=0, \\ \partial _x\sigma _{41}(x_1(y),y)= & {} \partial _y\sigma _{41}(x_1(y),y)=\partial _x\sigma _{43}(x_1(y),y)=\partial _y\sigma _{43}(x_1(y),y)=0, \\ \partial _x\sigma _{21}(x,y_2(x))= & {} \partial _y\sigma _{21}(x,y_2(x))=\partial _x\sigma _{22}(x,y_2(x))=\partial _y\sigma _{22}(x,y_2(x))=0. \end{aligned}$$

Therefore

$$\begin{aligned} \partial _yv_b(x_1(y),y)|_{Q_1}= & {} p_{11}(\partial _x\sigma _{11}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{11}(x_1(y),y))|_{Q_1} \nonumber \\&+\,p_{12}(\partial _x\sigma _{12}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{12}(x_1(y),y))|_{Q_1}=\partial _yg_1(y)|_{Q_1}, \nonumber \\ \partial _xv_b(x,y_2(x))|_{Q_1}= & {} p_{11}(\partial _x\sigma _{11}(x,y_2(x))+\partial _y\sigma _{11}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1} \nonumber \\&+\,p_{13}(\partial _x\sigma _{13}(x,y_2(x))+\partial _y\sigma _{13}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1} \nonumber \\= & {} \partial _xg_2(x)|_{Q_1}. \end{aligned}$$

(A.12)

Consequently,

$$\begin{aligned} p_{12}= & {} \displaystyle \frac{\partial _yg_1(y)|_{Q_1}-p_{11}(\partial _x\sigma _{11}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{11}(x_1(y),y))|_{Q_1}}{(\partial _x\sigma _{12}(x_1(y),y)\frac{dx_1}{dy}+\partial _y\sigma _{12}(x_1(y),y))|_{Q_1}}, \nonumber \\ p_{13}= & {} \displaystyle \frac{\partial _xg_2(x)|_{Q_1}-p_{11}(\partial _x\sigma _{11}(x,y_2(x))+\partial _y\sigma _{11}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1}}{(\partial _x\sigma _{13}(x,y_2(x))+\partial _y\sigma _{13}(x,y_2(x))\frac{dy_2}{dx})|_{Q_1}}. \end{aligned}$$

(A.13)

These expressions with (A.10) determine the constants $p_{12}$ and $p_{13}$. We can calculate the $p_{i2}$ and $p_{i3},~i=2,3,4$ in the same way.

Furthermore, we obtain from the first equation of (A.9) that

$$\begin{aligned}&\widetilde{g}_1(y)\nonumber \\&\quad =\displaystyle \frac{g_1(y)-p_{11}\sigma _{11}(x_1(y),y)-p_{12}\sigma _{12}(x_1(y),y) -p_{41}\sigma _{41}(x_1(y),y)-p_{43}\sigma _{43}(x_1(y),y)}{s_1(x_1(y),y)}. \end{aligned}$$

(A.14)

Since $p_{ij},\,1\le i\le 4,1\le j\le 3$ are given already by (A.10) and (A.13), the above expressions determine the functions $\widetilde{g}_1(y)$. We also can determine the functions $\widetilde{g}_2(x),\widetilde{g}_3(y)$ and $\widetilde{g}_4(x)$.

Step 3 According to (A.3), we use (A.5) and (A.7) to derive that

$$\begin{aligned} h_1(y)= & {} \partial _{n_1}u(x,y)|_{L_1}=\partial _xu(x_1(y),y)\cos \alpha _1+\partial _yu(x_1(y),y)\cos \beta _1,\\ h_2(x)= & {} \partial _{n_2}u(x,y)|_{L_2}=\partial _xu(x,y_2(x))\cos \alpha _2+\partial _yu(x,y_2(x))\cos \beta _2. \end{aligned}$$

Then, we have

$$\begin{aligned} \partial _yh_1(y)|_{Q_1}= & {} (\partial ^2_xu(x,y)\frac{d x_1}{d y}+\partial _{xy}u(x,y))|_{Q_1}\cos \alpha _1 +(\partial _{xy}u(x,y)\frac{d x_1}{d y} \nonumber \\&+\,\partial ^2_yu(x,y))|_{Q_1}\cos \beta _1, \nonumber \\ \partial _xh_2(x)|_{Q_1}= & {} \left( \partial ^2_xu(x,y)+\partial _{xy}u(x,y)\frac{dy_2}{dx}\right) |_{Q_1}\cos \alpha _2 \nonumber \\&+\,\left( \partial _{xy}u(x,y)+\partial ^2_yu(x,y)\frac{dy_2}{dx}\right) |_{Q_1}\cos \beta _2. \end{aligned}$$

(A.15)

Moreover, due to $g_1(y)=u(x_1(y),y),~g_4=u(x,y_4(x))$ and (A.4), we find that

$$\begin{aligned} \partial ^2_yg_1(y)|_{Q_1}= & {} \partial ^2_xu(x,y)|_{Q_1}\left( \frac{dx_1}{dy}\right) ^2 +2\partial _{xy}u(x,y)|_{Q_1}\frac{d x_1}{d y}+\partial ^2_yu(x,y)|_{Q_1}, \nonumber \\ \partial ^2_xg_2(x)|_{Q_1}= & {} \partial ^2_xu(x,y)|_{Q_1}+2\partial _{xy}u(x,y)|_{Q_1}\frac{dy_2}{dx} +\partial ^2_yu(x,y)|_{Q_1}\left( \frac{dy_2}{dx}\right) ^2. \end{aligned}$$

(A.16)

From the first equation of (A.15) and (A.16), we have

$$\begin{aligned} A_{Q_1}= & {} \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \partial _yh_1(y)|_{Q_1} \nonumber \\&+\,\left( \cos \beta _1-\frac{dx_1}{dy}\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _1\right) \partial ^2_yg_1(y)|_{Q_1} \nonumber \\&+\,\left( \frac{dx_1}{dy}\cos \alpha _1-\left( \frac{dx_1}{dy}\right) ^2\cos \beta _1\right) \partial ^2_xg_4(x)|_{Q_1}, \nonumber \\ B_{Q_1}= & {} \left( \cos \alpha _1+\frac{dx_1}{dy}\cos \beta _1\right) \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \nonumber \\&+\,2\frac{dx_1}{dy}\frac{dy_4}{dx}\cos \alpha _1+2\frac{dx_1}{dy}\cos \beta _1 \nonumber \\&-\,2\left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _1 -2\left( \frac{dx_1}{dy}\right) ^2\frac{dy_4}{dx}\cos \beta _1. \nonumber \\ \partial _{xy}u(x,y)|_{Q_1}= & {} \frac{A_{Q_1}}{B_{Q_1}}. \end{aligned}$$

(A.17)

From the second equation of (A.15) and (A.16), we have

$$\begin{aligned} C_{Q_1}= & {} \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \partial _yh_4(y)|_{Q_1} \nonumber \\&+\,\left( \frac{dy_4}{dx}\cos \beta _4-\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _4\right) \partial ^2_yg_1(y)|_{Q_1} \nonumber \\&+\,\left( \cos \alpha _4-\left( \frac{dx_1}{dy}\right) ^2\frac{dy_4}{dx}\cos \beta _4\right) \partial ^2_xg_4(x)|_{Q_1}, \nonumber \\ D_{Q_1}= & {} \left( \frac{dy_4}{dx}\cos \alpha _4+\cos \beta _4\right) \left( \left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2-1\right) \nonumber \\&+\,2\frac{dy_4}{dx}\cos \alpha _4+2\frac{dx_1}{dy}\frac{dy_4}{dx}\cos \beta _4 \nonumber \\&-\,2\frac{dx_1}{dy}\left( \frac{dy_4}{dx}\right) ^2\cos \alpha _4 -2\left( \frac{dx_1}{dy}\right) ^2\left( \frac{dy_4}{dx}\right) ^2\cos \beta _4. \nonumber \\ \partial _{xy}u(x,y)|_{Q_1}= & {} \frac{C_{Q_1}}{D_{Q_1}}. \end{aligned}$$

(A.18)

Then, we obtain the compatibility conditions as $\partial _{xy}u(x,y)|_{Q_1}=\frac{A_{Q_1}}{B_{Q_1}}=\frac{C_{Q_1}}{D_{Q_1}}$.

Next, by differentiating the (A.8) twice, we derive that

$$\begin{aligned} \partial _{xy}v(x,y)= & {} \partial _y\widetilde{g}_1(y)\partial _xs_1(x,y)+\widetilde{g}_1(y)\partial _{xy}s_1(x,y) +\partial _y\widetilde{h}_1(y)\partial _xt_1(x,y) \\&+\,\widetilde{h}_1(y)\partial _{xy}t_1(x,y) +\partial _x\widetilde{g}_2(x)\partial _ys_2(x,y)+\widetilde{g}_2(x)\partial _{xy}s_2(x,y)\\&+\,\partial _x\widetilde{h}_2(x)\partial _yt_2(x,y)+\widetilde{h}_2(x)\partial _{xy}t_2(x,y)+\partial _y\widetilde{g}_3(y)\partial _xs_3(x,y)\\&+\,\widetilde{g}_3(y)\partial _{xy}s_3(x,y) +\partial _y\widetilde{h}_3(y)\partial _xt_3(x,y)+\widetilde{h}_3(y)\partial _{xy}t_3(x,y)\\&+\,\partial _x\widetilde{g}_4(x)\partial _ys_4(x,y)+\widetilde{g}_4(x)\partial _{xy}s_4(x,y) +\partial _x\widetilde{h}_4(x)\partial _yt_4(x,y)\\&+\,\widetilde{h}_4(x)\partial _{xy}t_4(x,y) +\sum ^4_{i,j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y). \end{aligned}$$

Moreover, we know form (A.5) and (A.7) that

$$\begin{aligned} \partial _xs_i(x,y)|_{Q_1}= & {} \partial _xt_i(x,y)|_{Q_1} = \partial _{xy}t_i(x,y)|_{Q_1}=\partial _{xy}\sigma _{i4}(x,y)|_{Q_1}=0,\qquad 1\le i\le 4, \\ \partial _{xy}s_3(x,y)|_{Q_1}= & {} \partial _{xy}s_4(x,y)|_{Q_1}=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \partial _{xy}u(x,y)|_{Q_1}= & {} \partial _{xy}v(x,y)|_{Q_1} \\= & {} \widetilde{g}_1(y)\partial _{xy}s_1(x,y)|_{Q_1}+\widetilde{g}_2(x)\partial _{xy}s_2(x,y)|_{Q_1} +\displaystyle \sum ^4_{i=1}\displaystyle \sum ^3_{j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y)|_{Q_1}. \end{aligned}$$

Consequently,

$$\begin{aligned} p_{14} = \frac{\partial _{xy}u(x,y)|_{Q_1} -(\widetilde{g}_1(y)\partial _{xy}s_1(x,y) +\widetilde{g}_2(x)\partial _{xy}s_2(x,y) +\sum \nolimits ^4_{i=1}\sum \nolimits ^3_{j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y))|_{Q_1}}{\partial _{xy}\sigma _4(x,y)|_{Q_1}}. \end{aligned}$$

(A.19)

In the same manner, we can determine the constants $p_{i4},~1\le i\le 4$.

Step 4 According to (A.3), we use (A.5) and (A.7) to derive that

$$\begin{aligned} \partial _nv_b(x,y)|_{L_1}= & {} \partial _n(\widetilde{g}_1(y)s_1(x,y) +\widetilde{h}_1(y)t_1(x,y)+\displaystyle \sum ^4_{i,j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y))|_{L_1} \nonumber \\= & {} h_1(y). \end{aligned}$$

(A.20)

Moreover, with the aid of (A.5), we deduce that

$$\begin{aligned} \partial _n(\widetilde{h}_1(y)t_1(x,y))|_{L_1}= & {} (\widetilde{h}_1(y)\partial _xt_1(x,y)\cos \alpha _1+\partial _y\widetilde{h}_1(y)t_1(x,y)\cos \beta _1\\&+\,\widetilde{h}_1(y)\partial _yt_1(x,y)\cos \beta _1)|_{L_1} \\= & {} \widetilde{h}_1(y)(\partial _xt_1(x,y)\cos \alpha _1+\partial _yt_1(x,y)\cos \beta _1)|_{L_1}\\= & {} \widetilde{h}_1(y)\partial _nt_1(x,y)|_{L_1}. \end{aligned}$$

By substituting the above equality into (A.20), we obtain

$$\begin{aligned} \widetilde{h}_1(y)=\frac{h_1(y)-\partial _n(\widetilde{g}_1(y)s_1(x,y))|_{L_1} -\left( \displaystyle \sum \nolimits ^4_{i,j=1}p_{ij}\partial _{xy}\sigma _{ij}(x,y)\right) |_{L_1}}{\partial _nt_1(x,y)|_{L_1}}, \end{aligned}$$

(A.21)

which determines the function $\widetilde{h}_1(y)$.

In the same way, we can determine the functions $\widetilde{h}_2(x),\,\widetilde{h}_3(y)$ and $\widetilde{h}_4(x)$.

Finally, a combination of (A.10), (A.13), (A.14), (A.19) and (A.21) leads to the desired lifting function (A.8).

Remark 5.1

We can construct the lifting function for the boundary condition corresponding to the mixed inhomogeneous boundary value problems of fourth order.