On relaxing the distributional assumption of stochastic frontier models

Abstract

Stochastic frontier models have been considered as an alternative to deterministic frontier models in that they attribute the deviation of the output from the production frontier to both measurement error and inefficiency. However, such merit is often dimmed by strong assumptions on the distribution of the measurement error and the inefficiency such as the normal-half normal pair or the normal-exponential pair. Since the distribution of the measurement error is often accepted as being approximately normal, here we show how to estimate various stochastic frontier models with a relaxed assumption on the inefficiency distribution, building on the recent work of Kneip and his coworkers. We illustrate the usefulness of our method with data on Japanese local public hospitals.

1 Introduction

Productivity analysis consists in a series of analytical methods that allow to measure the performance of production units in terms of output versus input. Efficiency in productivity analysis is often defined as the ratio of the actual achieved output to the maximum possible output from the input, assuming that the inefficiency of the unit is the cause of its production not reaching its maximum output. However, from the recognition that many uncontrolled factors need to be considered in efficiency analysis, Aigner and Chu (1968) and Meeusen and van den Broeck (1977) first proposed the stochastic frontier analysis, which allows for both unobserved variation in output, the technical inefficiency (u) of the production unit and the noise (v) which represents the effect of innumerable uncontrollable factors.

Although the initial stochastic frontier analysis has the advantage of considering the role of unforeseen/uncontrollable factors, it was assumed that the frontier function had a specific parametric form such as the Cobb–Douglas and translog function. In addition, often specific parametric distributions for the inefficiency and the error were assumed. Over the last 20 years, studies have been conducted to relax the assumption of a parametric form of the frontier function in stochastic frontier analysis and there have been some remarkable achievements such as Fan et al. (1996), Kumbhakar et al. (2007) and Martins-Filho and Yao (2015). However, much less research has been done on relaxing the parametric assumption on the inefficiency and the noise. This is the starting point of our work. Since the distribution of the noise is often accepted as being approximately normal, here we focus on developing a method for estimating various stochastic frontier models with a relaxed assumption on the inefficiency distribution.

In general, it is known that the estimate of firm level efficiency proposed in Jondrow et al. (1982) is given by a monotonic function of the overall error ($\epsilon =v-u$) estimate when the noise (v) follows a normal distribution (see Ondrich and Ruggiero 2001). Since the ranking of the estimates of the overall error ($\epsilon$) can be obtained through ordinary least squares residuals as mentioned in Bera and Sharma (1999) and Parmeter and Kumbhakar (2014), if the rank of the individual inefficiency is the main concern, we do not have to pay much attention to the assumption on the inefficiency distribution. However, if our main interest lies in the value itself of the production function or the inefficiency function when the inefficiency is affected by other variables, then the appropriate modeling of the inefficiency distribution becomes important. Motivated by this observation we will discuss how to estimate the frontier function under relaxed assumptions on the inefficiency distribution so that the estimation results become less sensitive to the specification of the inefficiency distribution. The key idea of this paper is to extend the work in Kneip et al. (2015), who studied the estimation of the constant frontier under the setting of our interest. Actually, Hall and Simar (2002) considered a similar problem with a different method but their method has the uncorrected bias depending on the magnitude of the noise variance in the estimation of the frontier function, even in large samples. In contrast, the method in Kneip et al. (2015) does not have such problem provided that the noise follows a normal distribution.

The rest of the paper is structured as follows. Section 2 briefly explains the method of Kneip et al. (2015), which is important for understanding our proposals. Section 3 introduces our methods as an extension of Kneip et al. (2015)’s work and provides some heuristics for the theoretical understanding of the proposed methods. We present the small sample performance of the proposed methods in Sect. 4 and illustrate how the proposed methods can be used for efficiency and productivity analysis in Sect. 5. Some conclusions are given in Sect. 6.

2 Background

In this section, following Kneip et al. (2015) we briefly review how the constant frontier can be reconstructed with a relaxed assumption on the inefficiency when the noise follows a normal distribution. Suppose that we have i.i.d. observations $Y_1,Y_2,\ldots ,Y_n$ from the model

$$\begin{aligned} Y_i = \tau \exp (-U_i) \cdot \exp (V_i), \quad i=1,\ldots ,n, \end{aligned}$$

(1)

where $\tau >0$, $U_i$ is a positive random variable that represents the inefficiency and whose density makes a jump at the origin, and where $V_i$ follows a normal distribution with mean zero and unknown variance $\sigma ^2$. Note that Model (1) can be rewritten as

$$\begin{aligned} \log Y_i = \log \tau + V_i - U_i, \quad i=1,\ldots ,n. \end{aligned}$$

(2)

Kneip et al. (2015) proposed a method to estimate $\tau$ and $\sigma ^2$ based on a penalized profile likelihood. The estimation procedure can be summarized as follows.

Let $g(\cdot )$ and $f(\cdot )$ be the densities of the observed variable $Y_i$ and the latent variable $X_i=\tau \exp (-U_i)$, respectively. Note that the density $f(\cdot )$ is defined on $[0,\tau ]$ with $f(\tau )>0$. As in Kneip et al. (2015), we use a sub-index 0 to indicate the true quantities. For all $y>0$, we can write the true density of Y,

$$\begin{aligned} g_0(y) = \frac{1}{\sigma _0 y} \int _0^1 h_0(t) \phi \left( \frac{1}{\sigma _0} \log \frac{y}{t \tau _0} \right) dt, \end{aligned}$$

(3)

where $h_0(t) = \tau _0 f_0(t \tau _0)$ for $0 \le t \le 1$ and $\phi (\cdot )$ is the standard normal density. From expression (3), we consider the following probability density model to estimate $\tau _0$ and $\sigma _0^2$ based on $Y_1,Y_2,\ldots ,Y_n$:

$$\begin{aligned} \left\{ g_{h,\tau ,\sigma }(\cdot )~:~h~\hbox {is a probability density on}~[0,1],~\tau>0,~\sigma >0 \right\} , \end{aligned}$$

(4)

where

$$\begin{aligned} g_{h,\tau ,\sigma }(y) = \frac{1}{\sigma y} \int _0^1 h(t) \phi \left( \frac{1}{\sigma } \log \frac{y}{t \tau } \right) dt. \end{aligned}$$

(5)

Since $g_{h,\tau ,\sigma }(y)$ depends on the underlying density $h(\cdot )$, Kneip et al. (2015) considered the approximation of h by

$$\begin{aligned} \left\{ h_{\varvec{\gamma }}(t) = \gamma _1 I(t=0) + \sum _{k=1}^M \gamma _k I(q_{k-1} < t\le q_k): \gamma _k > 0~\hbox {for all }k~\hbox {and} \sum _{k=1}^M \gamma _k = M \right\} ,\nonumber \\ \end{aligned}$$

(6)

where $q_k = k/M~(k=0,1,\ldots ,M)$ and M is a pre-specified natural number. The final density model is

$$\begin{aligned} g_{h_{\varvec{\gamma }},\tau ,\sigma }(y) = \frac{1}{\sigma y} \sum _{k=1}^M \gamma _k \int _{q_{k-1}}^{q_k} \phi \left( \frac{1}{\sigma } \log \frac{y}{t \tau } \right) dt. \end{aligned}$$

(7)

Estimators ${\hat{\tau }}$ and ${\hat{\sigma }}$ of $\tau _0$ and $\sigma _0$ are obtained by maximizing the following penalized likelihood:

(8)

where $\lambda \ge 0$ is a fixed value independent of n, $\text{ pen }(g_{h_{\varvec{\gamma }},\tau ,\sigma })=\max _{3 \le j \le M} |\gamma _j - 2 \gamma _{j-1}+\gamma _{j-2}|$ and $\Gamma = \left\{ \varvec{\gamma }= (\gamma _1,\ldots ,\gamma _M)^\top :\gamma _k >0~\hbox {for all }k~\hbox {and} \sum _{k=1}^M \gamma _k = M\right\}$. Note that the penalty is introduced to account for the smoothness of the function $h_0$. Also note that $\lambda$ can be taken equal to zero, which means that we consider both penalized and non-penalized estimators. However, it can be seen that the penalized estimator attains a better rate of convergence.

3 Our proposals

In this section, building upon the work of Kneip et al. (2015), we propose how to estimate the frontier function with a relaxed assumption on the inefficiency for three stochastic frontier models. Additionally, we provide some heuristics for the theoretical understanding of the proposed methods.

3.1 Linear model

Assume the stochastic frontier model with a linear frontier function

$$\begin{aligned} Y_i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }+ \epsilon _i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }+ V_i - U_i, \quad i=1,\ldots ,n, \end{aligned}$$

(9)

where $\varvec{\beta }= (\beta _1,\ldots ,\beta _p)^\top$ and $\mathbf{X}_i = (X_{1,i},\ldots ,X_{p,i})^\top$. Concerning $U_i$ and $V_i$, we make the same assumption as in Kneip et al. (2015). Our interest lies in estimating both $\beta _0$ and $\varvec{\beta }$. Horrace and Parmeter (2011) considered the same model with the same assumption on $V_i$ but they tried to estimate the density of $U_i$ with a relaxed assumption on $U_i$, which is that the distribution of $U_i$ is a member of the family of ordinary smooth densities (see Fan 1991).

Since $Y_i = (\beta _0 - E(U_i))+\mathbf{X}_i^\top \varvec{\beta }+ (V_i -(U_i - E(U_i))$ with $\epsilon _i^* = V_i -(U_i - E(U_i))$ having zero mean, we can estimate $\varvec{\beta }$ and $\beta _0-E(U_i)$ via least squares using the fact that $E(\epsilon _i^*|X_i)=0$, provided that $V_i$ and $U_i$ are independent of $X_i$. Once we have obtained $\hat{\varvec{\beta }}$, we calculate $Y_i - \mathbf{X}_i^\top \hat{\varvec{\beta }}$, which is expected to be similar to $\beta _0 + V_i - U_i$. From the observation

$$\begin{aligned} \exp (Y_i - \mathbf{X}_i^\top \hat{\varvec{\beta }}) \approx \exp (\beta _0) \exp (-U_i) \exp (V_i), \end{aligned}$$

(10)

we apply the estimation method of Kneip et al. (2015) with $\exp (Y_i - \mathbf{X}_i^\top \hat{\varvec{\beta }})$ to obtain the estimate of $\exp (\beta _0)$ and $\sigma _V = \sqrt{Var(V_i)}$. After obtaining , we can obtain , , . If we are only interested in ranking production units or in ranking firm-specific inefficiency estimates, the estimate $\hat{\varvec{\beta }}$ is enough and we don’t need to go further with the method of Kneip et al. (2015). However, if we have specific interest in firm level inefficiency, then it is necessary to have the estimate $\hat{\epsilon }_i$ for which the distributional assumption about the inefficiency is usually utilized. We propose here how to obtain $\hat{\epsilon }_i$ with the relaxed assumption on the inefficiency. Traditionally, one estimates the firm-specific inefficiency using the formula of $E(U_i|\epsilon _i)$ derived from the distributional assumption on $U_i$ and $V_i$. In our case, instead of using the formula of $E(U_i|\epsilon _i)$ we use the best linear predictor of $U_i$ given $\epsilon _i$, $a + b\, \epsilon _i$, which was analyzed in detail in Waldman (1984). A simple calculation leads to $b = -Var(U_i)/(Var(U_i)+Var(V_i))$ and $a=E(U_i)(1+b)$.

3.2 Partially linear model

Another stochastic frontier model that we would like to consider is the model that Parmeter et al. (2017) studied. They considered the same model as in Sect. 3.1 but assume that the inefficiency is directly influenced by observable exogenous determinants, $Z_i$:

$$\begin{aligned} Y_i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }+ \epsilon _i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }+ V_i - U_i, \quad i=1,\ldots ,n, \end{aligned}$$

(11)

where $V_i \sim N(0,\sigma _V^2)$, $U_i \ge 0$, $E(U_i | \mathbf{X}_i,Z_i) = E(U_i|Z_i) = g(Z_i)$. For simplicity, we assume that $Z_i$ is a scalar. We will deal with the case where $Z_i$ is a vector of dimension q in Sect. 3.3. Model (11) can be rewritten as

$$\begin{aligned} Y_i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }-g(Z_i) +\epsilon _i^* = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }-g(Z_i) + (V_i - (U_i-g(Z_i))).\qquad \end{aligned}$$

(12)

Since $E(\epsilon _i^* | \mathbf{X}_i,Z_i)=0$ provided $V_i$ is independent of $(X_i,Z_i)$, we can estimate $\varvec{\beta }$ and $g(\cdot )$ using estimation techniques for partially linear models. More precisely, the conditional mean function $g(\cdot )$ representing the inefficiency can be estimated up to a constant because it is mixed up with the intercept $\beta _0$. Parmeter et al. (2017) discussed that the intercept $\beta _0$ cannot be separately identified from $g(Z_i)$ but this is not a concern as differences between $g(Z_i)$ across firms can be used as measures of relative inefficiency. However, if we would like to evaluate the exact impact of the exogenous determinants on the inefficiency, we have to know the value of $\beta _0$ so that we can estimate the function $g(\cdot )$ consistently. Here we try to estimate the exact level of $\beta _0$ and $g(\cdot )$ applying the method in Kneip et al. (2015). The idea is to calculate $Y_i - \mathbf{X}_i^\top {\varvec{\beta }} = \beta _0 + V_i -U_i$. Let ${\hat{\varvec{\beta }}}$ be the estimator of $\varvec{\beta }$ obtained from the partial linear model fitting of Model (11). Then, since $\hat{\varvec{\beta }}$ is $\sqrt{n}$-consistent under appropriate regularity conditions, $Y_i - \mathbf{X}_i^\top \hat{\varvec{\beta }}$ is expected to be similar to $\beta _0 + V_i -U_i$. So we apply the method of Kneip et al. (2015) to estimate $\beta _0$ and $\sigma _V = \sqrt{Var(V_i)}$ with $\exp (Y_i - \mathbf{X}_i^\top \hat{\varvec{\beta }})$ as in Sect. 3.1. In our simulation, we implemented the method in Speckman (1988) to estimate the partially linear model but used two smoothing parameters as proposed in Aneiros-Pérez et al. (2004). We chose the two smoothing parameters based on generalized cross-validation.

3.3 Partially linear single-index model

In this section, we consider a similar stochastic frontier model to the one in Sect. 3.2 but we assume that there is more than one observable determinant which affects the inefficiency, i.e.$\mathbf{Z}_i = (Z_{1,i},\ldots ,Z_{q,i}) \in {\mathbb {R}}^q$. In this case, we could consider various models for $g(\mathbf{Z}_i)$ such as additive models, single-index models and so on. Here we consider the single-index model where $g(\mathbf{Z}_i)$ can be expressed as $g_1(\mathbf{Z}_i^\top \varvec{\alpha })$ for a certain univariate function $g_1(\cdot )$ and a q-dimensional vector $\varvec{\alpha }$. Specifically, our stochastic frontier model can be written as

$$\begin{aligned} Y_i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }+ \epsilon _i = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }+ V_i - U_i, \quad i=1,\ldots ,n, \end{aligned}$$

(13)

where $E(U_i | \mathbf{X}_i,\mathbf{Z}_i) = E(U_i|\mathbf{Z}_i) = g_1(\mathbf{Z}_i^\top \varvec{\alpha })$. A more convenient form for estimation is

$$\begin{aligned} Y_i= & {} \beta _0 + \mathbf{X}_i^\top \varvec{\beta }-g_1(\mathbf{Z}_i^\top \varvec{\alpha }) +\epsilon _i^* = \beta _0 + \mathbf{X}_i^\top \varvec{\beta }-g_1(\mathbf{Z}_i^\top \varvec{\alpha })\nonumber \\&+ (V_i - (U_i-g_1(\mathbf{Z}_i^\top \varvec{\alpha }))). \end{aligned}$$

(14)

Since $E(\epsilon _i^* | \mathbf{X}_i,\mathbf{Z}_i)=0$ provided $V_i$ is independent of $(X_i,Z_i)$, we can estimate $\varvec{\beta }$, $g_1(\cdot )$ (up to a constant) and $\varvec{\alpha }$ using estimation techniques for partially linear single-index models. Following the same idea as in Sects. 3.1 and 3.2, we can estimate $\beta _0$ and $\sigma _V = \sqrt{Var(V_i)}$ from application of the method of Kneip et al. (2015) to $\exp (Y_i - \mathbf{X}_i^\top \hat{\varvec{\beta }})$. In our simulation, we implemented the method in Liang et al. (2010) to estimate the partially linear single-index model. We used 5-fold cross-validation to choose the bandwidth for the single-index estimation.

3.4 Theoretical understanding of the proposed methods

Let us now look at some asymptotic properties of the proposed estimators. Following the results in Kneip et al. (2015) we first need to show that $H^2({\hat{g}},g_0) = O_P(M_n^{-2})$ (see their Theorem 3.1), where for any densities $g_1$ and $g_2$ the Hellinger distance $H^2(g_1,g_2)$ is defined by

$$\begin{aligned} H^2(g_1,g_2) = \frac{1}{2} \int \big (\sqrt{g_1(y)} - \sqrt{g_2(y)}\big )^2 \, dy, \end{aligned}$$

and where ${\hat{g}} = g_{h_{{\hat{\gamma }}},{\hat{\tau }},{\hat{\sigma }}}$ and $M=M_n$ is the number of grid points used to estimate the function h. To prove that Theorem 3.1 in Kneip et al. (2015) remains valid in our context, we need to check what changes in the proof of this theorem when $Y_i$ is replaced by $Y_i - \mathbf{X}_i^\top {\hat{\varvec{\beta }}}$. Since ${\hat{\varvec{\beta }}}$ converges to $\varvec{\beta }$ with parametric rate, it can be seen that ${\hat{\varvec{\beta }}}$ does not disturb the rate of $H^2({\hat{g}},g_0)$, and so the result of Theorem 3.1 in Kneip et al. (2015) remains valid provided the regularity conditions (A1)-(A4) hold true. Next, Theorem 3.2 in Kneip et al. (2015), which states the main result of the paper, namely that

$$\begin{aligned} {\hat{\sigma }}_V - \sigma _V = O_P((\log n)^{-2}) \quad \text{ and } \quad {\hat{\beta }}_0-\beta _0 = O_P((\log n)^{-3/2}) \end{aligned}$$

remains valid in our context since it only requires that the result of Theorem 3.1 is valid. In particular, our estimator ${\hat{\beta }}_0$ has a logarithmic rate of convergence, as in the case where the variance $\sigma _V^2$ would be known.

4 Simulation evidence

In this section, we present the small sample performance of the proposed methods.

4.1 Simulation setup

Our data generating process follows the simple stochastic frontier model:

$$\begin{aligned} Y_i = \beta _0 + \beta _1 \log I_{1,i} + \beta _2 \log I_{2,i} + V_i - U_i, \quad i=1,\ldots ,n, \end{aligned}$$

where $X_{1,i} = \log I_{1,i},~X_{2,i} = \log I_{2,i}$. For all the settings below, $V_i$ is distributed i.i.d. $N(0,\sigma _V^2)$. The vector $(I_{1,i},I_{2,i},W_{1,i},W_{2,i})$ is i.i.d. multivariate normal with all the correlations being $\rho =0.5$. The mean vector for the covariates is (4, 8, 0, 0) and all four random variables have unit variance. We define observable determinants as $Z_{1,i}=\Phi (W_{1,i})$ and $Z_{2,i}=\Phi (W_{2,i})$, where $\Phi (\cdot )$ is the distribution function of a standard normal variable. To generate the inefficiency $U_i$, we consider a positive random variable $U_i^*$, which follows an exponential distribution $\text{ Exp }(a)$ or a half-normal distribution $N^+(\mu ,\sigma ^2)$. Here, $U_i^* \sim \text{ Exp }(a)$ means that the density of $U_i^*$ is

$$\begin{aligned} f_{U^*}(u) = a^{-1} \exp (-a^{-1} u) I(u>0), \end{aligned}$$

and $U_i^* \sim N^+(\mu ,\sigma ^2)$ means that the density of $U_i^*$ is given as

$$\begin{aligned} f_{U^*}(u) = \frac{\Phi ^{-1}(\mu /\sigma )}{\sqrt{2 \pi } \sigma } \exp \left\{ - \frac{1}{2} \left( \frac{u-\mu }{\sigma }\right) ^2\right\} I(u>0). \end{aligned}$$

We consider three scenarios for $U_i^*$: (1) $N^+(0,0.5^2)$ (2) $N^+(0.25,0.4^2)$ (3) $\text{ Exp }(0.3014)$. Depending on the type of model of interest, we define $U_i$ as a function of $U_i^*$, $Z_{1,i}$ and $Z_{2,i}$. Finally, we set the vector of $\beta$’s as $\beta _0 = 5,~\beta _1=1.5$ and $\beta _2=2$ and choose $\sigma _V = \rho _{nts} \sigma _U$ with $\rho _{nts}=0.05,0.25,0.5$ and $\sigma _U = \sqrt{Var(U_i)}$.

4.1.1 Linear model

For this model, we simply let $U_i = U_i^*$.

4.1.2 Partially linear model

In this model, we define the inefficiency $U_i$ as $U_i = 0.2\exp (Z_{1,i})U^*_i$. Hence, $g(Z_{1,i})=E(U_i|\mathbf{X}_i,Z_{1,i})=0.2E(U_i^*)\exp (Z_{1,i})$ provided $U_i^*$ is independent of $(\mathbf{X}_i,Z_{1,i})$.

4.1.3 Partially linear single-index model

In this model, we define the inefficiency $U_i$ as $U_i = \sin (\sqrt{2} Z_{1,i}+\sqrt{2} Z_{2,i})U^*_i$. Hence, $g(Z_{1,i},Z_{2,i}) = E(U_i|\mathbf{X}_i,Z_{1,i},Z_{2,i}) =E(U_i^*)\sin (\sqrt{2} Z_{1,i}+\sqrt{2} Z_{2,i})$ provided $U_i^*$ is independent of $(\mathbf{X}_i,Z_{1,i},Z_{2,i})$.

4.2 Evaluation of the performance of ${\hat{\beta }}_0$ and ${\hat{\sigma }}_V$

For the three simulation models, we perform 500 Monte Carlo experiments with n equal to 100, 200 or 400, and $\rho _{nts}$ equal to 0.05, 0.25 or 0.5. We calculate the Root Mean Squared Error (RMSE) of ${\hat{\beta }}_0$ and ${\hat{\sigma }}_V$ over the grid $\log _{10}\lambda = -4,-3,-2,-1,0,1,2,3,4$. For the sake of space, we only display the smallest RMSEs of ${\hat{\beta }}_0$ and ${\hat{\sigma }}_V$ in each model (Tables 1, 2, 3) but the whole results can be found in the supplementary material. For the number of bins, we used the rule $M = \max (3,2\times {\text{ round }}(n^{1/5}))$ as in Kneip et al. (2015). Here, $\text{ round }(a)$ means the nearest integer to a. The tables show that the performance is as expected: when the sample size increases the performance of the estimators improves for both $\beta _0$ and $\sigma _V$. When increasing the noise from $\rho _{nts}=0.05$ to 0.50, the performance deteriorates. This effect is stronger for estimating $\beta _0$ than for estimating $\sigma _V$ as observed in Kneip et al. (2015). Finally, the selection of the penalty parameter $\lambda$ seems not to be crucial for the performance (see the supplementary material). This phenomenon will also be observed in our data analysis in Sect. 5.

Table 1 RMSEs of ${\hat{\beta }}_0$ and ${\hat{\sigma }}_V$ in the linear model

Table 2 RMSEs of ${\hat{\beta }}_0$ and ${\hat{\sigma }}_V$ in the partially linear model

Table 3 RMSEs of ${\hat{\beta }}_0$ and ${\hat{\sigma }}_V$ in the partially linear single-index model

4.3 Estimation of the firm level inefficiency

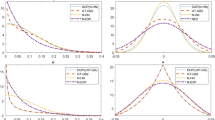
One of the merits of the proposed method is that one can calculate the firm level inefficiency in the relaxed models. To illustrate this aspect, we did a small simulation study to estimate the firm level efficiency $U_i$ of the linear model in Sect. 4.1.1 with $U_i \sim N^+(0,0.5^2)$ and $U_i \sim \text{ Exp }(0.3014)$. We present the result only when $\rho _{nts}=0.25$ but the results with other $\rho _{nts}$ values were more or less similar in trend. We estimate $U_i$ by using the best linear predictor $U_i$ given $\epsilon _i$ as described in Sect. 3.1. For estimation of $\beta _0$, we use the average value of all ${\hat{\beta }}_0(\lambda )$ over the grid $\log _{10}\lambda = -4,-3,-2,-1,0,1,2,3,4$. Table 4 shows the average of the RMSEs between ${\hat{U}}_i$ and $U_i$ over 500 repetitions for $n=100,200$ and 400 when $\rho _{nts}=0.25$. Our method seems to be able to estimate the firm level efficiency under the relaxed assumption about the inefficiency. Our finding is also supported by the scatter plots between ${\hat{U}}_i$ and $U_i$ in Fig. 1.

Table 4 Average of the RMSEs for the linear model when $\rho _{nts}=0.25$

Fig. 1

One instance of the scatter plots between ${\hat{U}}_i$ and $U_i$ with $U_i^* \sim N^+(0,0.5^2)$ and $U_i^* \sim \text{ Exp }(0.3014)$. The solid line is $y=x$

4.4 Comparison with the fully nonparametric method

For estimation of the frontier function in the linear model of Sect. 4.1.1, we can consider the fully-nonparametric estimation method proposed by Kneip et al. (2015), which relies on some “local linear” approximation of the frontier function. Hence, we would like to compare our proposal with their method. For comparison, we consider the same model as in Sect. 4.1.1. In our method, we first obtain the estimates ${\hat{\beta }}_0$ and ${\hat{\varvec{\beta }}}$ and construct the estimate of the frontier function as ${\hat{\tau }}(\mathbf{X}_i) = {\hat{\beta }}_0 + \mathbf{X}_i^\top {\hat{\varvec{\beta }}}$. In contrast, Kneip et al. (2015) estimate nonparametrically the frontier function at a given point $\mathbf{X}_i$ combining the idea of local linear approximation and the recovery of a constant frontier function in the presence of measurement error. Since both function estimators are presumably expected to have the same logarithmic rates of convergence, one may think that our method and the method of Kneip et al. (2015) will not show a significant difference in estimation performance. To check this, we estimate the frontier function at every data point $\mathbf{X}_i$ and calculate $n^{-1}\sum _{i=1}^n ({\hat{\tau }}(\mathbf{X}_i) - \tau (\mathbf{X}_i))^2$ as a measure of performance. The sample size n equals 100, 200 or 400 and $\rho _{nts}$ is fixed to 0.5. For the inefficiency we use $U_i \sim N^+(0,0.5^2)$. The other components of the model are the same as in the model of Sect. 4.1.1. Finally, we display the performance measure for the two estimation methods over the grid $\log _{10}\lambda = -4,-3,-2,-1,0,1,2,3,4$ in Table 5 (the quantity $\log _{10}\lambda ^*$ is the value of $\log _{10}\lambda$ that gives the best performance). The results suggest that our method has better performance than Kneip’s method when the frontier function is linear. However, the difference in performance gets smaller as the sample size increases.

Table 5 Comparison between the performance of our method and that of Kneip’s method when the frontier function is linear

5 Data analysis

In this section, we illustrate how the proposed methods can be used for efficiency and productivity analysis. We will analyze an administrative dataset for financial variables and selected characteristics of Japanese local public hospitals, which is available in the R package rDEA, and we will estimate the inefficiency function of the observable environmental variable using the method described in Sect. 3.2.

Table 6 The estimates of $\beta _0$ depending on the tuning parameter $\lambda$

The dataset contains anonymous observations for 958 local public hospitals, identified by a researcher-generated variable “firm-id”. The output variable ($Y_i$) is the logarithm of the sum of the annual number of inpatients and outpatients, where an inpatient is a hospital patient who occupies a bed for at least one night and an outpatient is a patient who receives treatment at a hospital but does not spend the night there. The two input variables ($X_{1,i}$ and $X_{2,i}$) are the logarithm of the total labor cost per year (total number of employees times per capita annual salary) and the logarithm of the total capital cost (total number of beds times the sum of depreciation and interest per bed). The environmental variable ($Z_i$) is the number of examinations per patient, which represents the severity of the illness in which each hospital is primarily responsible for treatment. We assume the following partially linear model in Sect. 3.2 for this dataset:

$$\begin{aligned} Y_i= & {} \beta _0 + \beta _1 X_{1,i} + \beta _2 X_{2,i} +V_i - U_i \nonumber \\= & {} \beta _0 + \beta _1 X_{1,i} + \beta _2 X_{2,i} -g(Z_i) + (V_i - (U_i-g(Z_i))) \nonumber \\\equiv & {} \beta _0 + \beta _1 X_{1,i} + \beta _2 X_{2,i} -g(Z_i) +\epsilon _i^*, \end{aligned}$$

(15)

where $U_i$ is the inefficiency, $V_i \sim N(0,\sigma _V^2)$ is the noise that is supposed to be independent of $(X_{1,i},X_{2,i},Z_i)$ and $E(U_i | \mathbf{X}_i,Z_i) = E(U_i|Z_i) = g(Z_i)$ is the inefficiency function. Since some hospitals are known to have characteristics that are different from those of other hospitals in this dataset, we conduct outlier detection and remove 26 observations before fitting Model (15). The method used for outlier detection consists in first obtaining the residuals by fitting the partially linear median regression model to the data $(Y_i,X_{1,i},X_{2,i},Z_i)$, and then doing univariate outlier detection based on the residuals applying the methods available in the R package extremevalues.

First, we estimate $\beta _1$ and $\beta _2$ using the method in Speckman (1988), which yields ${\hat{\beta }}_1= 0.240$ and ${\hat{\beta }}_2=0.500$. Then, we estimate $\beta _0$ using the method outlined in Sect. 3.2 and obtain the estimates of $\beta _0$ given in Table 6, depending on the tuning parameter $\lambda$. After estimating $\beta _0$ by the average value of all ${\hat{\beta }}_0(\lambda )$, which is $-$ 3.106, we estimate the inefficiency function $g(\cdot )$ using local linear regression. In Fig. 2, we plot the estimate of the inefficiency function $g(Z_i)$ using our method (solid curve) and the method of Parmeter et al. (2017) assuming $\beta _0=0$ (dotted curve). As expected, in both cases the inefficiency function increases as the severity of illness increases (actually, the two estimated curves have only a constant difference). The result suggests that if we ignore $\beta _0$ by assuming that $\beta _0=0$, then we overestimate the level of the inefficiency function. Hence, if one is interested in the exact level of the inefficiency function and is not sure that $\beta _0$ is zero, we recommend to use our method as a safer option.

Fig. 2

The estimates of the inefficiency function $g(\cdot )$. The solid curve is obtained using our method and the dotted one is from Parmeter et al. (2017) assuming $\beta _0=0$

6 Conclusion

This paper proposes a new method to estimate various stochastic frontier models with a relaxed assumption on the inefficiency distribution. Previous research relied on the work of Hall and Simar (2002), which is known to work well in low noise settings only. Instead, we proposed estimators building on the recent work of Kneip and his coworkers and showed in the numerical study that the proposed methods work well for various levels of the noise.