Stochastic frontier models using the Generalized Exponential distribution

Abstract

We present a new, single-parameter distributional specification for the one-sided error components in single-tier and two-tier stochastic frontier models. The distribution has its mode away from zero, and can represent cases where the most likely outcome is non-zero inefficiency. We present the necessary formulas for estimating production, cost and two-tier stochastic frontier models in logarithmic form. We pay particular attention to the use of the conditional mode as a predictor of individual inefficiency. We use simulations to assess the performance of existing models when the data include an inefficiency term with non-zero mode, and we also contrast the conditional mode to the conditional expectation as measures of individual (in)efficiency.

1 Introduction and motivation

In the founding papers of stochastic frontier analysis (SFA), Aigner et al. (1977) and Meeusen and van den Broeck (1977), the authors considered two distributions for the inefficiency term, the Half Normal and the Exponential, creating organically the Normal-Half Normal (NHN) and the Normal-Exponential (NE) specifications for the composite error term. The first would go on and have a spectacular future outside SFA also, after Azzalini (1985) baptized it as the Skew Normal distribution and presented it to the statistical community. The second had already a well established past, since a variant of it under the name “Exponentially modified Gaussian” was being used already from the ’60s in chromatography (for a review see Grushka, 1972).

But no one is a prophet in their own land: Stevenson (1980) noted that in both specifications the inefficiency distribution had its mode at zero, imposing a specific economic/structural assumption: that the most likely occurrence was near-zero inefficiency. While such an assumption could be justified to a degree by invoking purposeful optimizing behavior as well as the forces of competition, Stevenson linked inefficiency to managerial competence and argued that the latter is not distributed monotonically in the population (of managers at least). Based on this argument, the author proposed the use of the Truncated Normal distribution for the inefficiency term as an alternative, as well as the Gamma distribution, restricting the values of its shape parameter so as to obtain a closed-form density for the composite error term.¹ To this day, these are the main specifications that allow for a non-zero mode of the inefficiency component.² But both these distributions have issues: the maximum likelihood estimator (MLE) has often difficulties converging under a Truncated Normal specification, while the Gamma specification in its general formulation has a non closed-form density that makes it less appealing for empirical implementations. Moreover, Ritter and Simar (1997) found that the shape parameter of the Gamma distribution is weakly identified and imprecisely estimated when the sample size is not really large. But this is the very parameter that allows us to have a non-zero mode.

In this paper we present production and cost stochastic frontier models as well as the two-tier extension (2TSF), where we specify the one sided component(s) to follow the Generalized Exponential distribution, which is a single-parameter distribution that has always a non-zero mode. Assuming in addition that the noise term follows a zero-mean Normal distribution, we obtain the Normal-Generalized Exponential specification (NGE).

Since concerns related to the mode of the inefficiency distribution is what generated this research, it is fitting that we will also pay particular attention to the conditional mode as a measure of individual inefficiency. These measures are sometimes called “JLMS” measures from the paper of Jondrow et al. (1982) where both the conditional expected value and the conditional mode were considered as predictors of individual inefficiency.³ In fact this paper dealt with predicting the error component of the logarithmic specification. It was Battese and Coelli (1988) that presented the conditional expectation expressions for the exponentiated error, i.e. for a prediction at the original measurement scale. We extend the approach by examining the conditional modes for the exponentiated case. In practice, the conditional expectation, being an optimal predictor under the Mean-Squared Error criterion, appears to have prevailed as the inefficiency measure of choice. But by considering the mode of the inefficiency distribution we essentially propose a more elaborate investigation of the inefficiency terms, since by having available their (marginal and conditional) distributions, we can go beyond obtaining some predictor of their value and instead form a more complete picture of their stochastic behavior. In addition, the mode always exists and it may also be easier to derive.

In most cases the regression specification used in empirical SFA papers has the dependent variable in logarithmic form, and it is for this equation that distributional assumptions are made. This implies that inefficiency measures ultimately relate to the exponentiated variables. We will focus on this model and present JLMS measures only for the exponentiated inefficiency terms. This is also a way to contain to some degree the sprawling mass of mathematical expressions, since we will develop in detail three different models.

In Section 2 we present the distribution for the one-sided error components that we will use, and provide its main properties. In Section 3, we address certain concerns that are often raised when new specifications for SF models are proposed. In Sections 4 and 5 we present the production and cost SF models respectively, and in Section 6 the two-tier stochastic frontier model. Section 7 concludes with simulations that explore how the familiar NHN and NE specifications perform when the data come from an NGE process and vice-versa, but also, how the conditional expectation and the conditional mode fare as measures of individual inefficiency.

2 The Generalized Exponential distribution

We consider the distribution that has the following density:

$$\begin{array}{l}{f}_{u}\left(u\right)\,=\,\frac{2}{{\theta }_{u}}\exp \left\{-u/{\theta }_{u}\ \right\}\left(1-\exp \left\{-u/{\theta }_{u}\ \right\}\right),\\ \qquad\qquad\;{\theta }_{u}\,>\,{0},\ {u}\,\ge\, {0}\ \ .\end{array}$$

(1)

Note that the density is two times an Exponential density times the Exponential distribution function with the same scale parameter. Let h_E(u; θ_u) denote the Exponential density with scale parameter θ_u. Then we can write equivalently,

$${f}_{u}\left(u\right)=2{h}_{E}(u;{\theta }_{u})-{h}_{E}(u;{\theta }_{u}/2).$$

(2)

This additive form will prove convenient in calculating expressions that involve integration, exploiting the linearity of integrals and the already known results from the NE specification. The distribution function is

$${F}_{u}(u)={\left(1-\exp \left\{-u/{\theta }_{u}\right\}\right)}^{2}.$$

(3)

There are at least three ways to obtain the above distribution. First, as a general consequence of the Probability Integral Transform that states that for every continuous random variable X with support S_X, distribution function F_X(x) and density f_X(x), we have that ${F}_{X}(X) \sim U\left(0,1\right)$. This then implies that

$$\begin{array}{l}E\left[{F}_{X}\left(X\right)\right]={\int}_{{S}_{X}}{f}_{X}\left(x\right){F}_{X}\left(x\right)dx=\frac{1}{2}\\ \qquad\qquad\quad\Rightarrow {\int}_{{S}_{X}}2{f}_{X}\left(x\right){F}_{X}\left(x\right)dx=1\ .\end{array}$$

So the function $2{f}_{X}\left(x\right){F}_{X}\left(x\right)$ is non-negative in the support of X and integrates to unity over it, therefore it is a density. We take this general result and apply it to the Exponential distribution.

Second, $2{f}_{X}\left(x\right){F}_{X}\left(x\right)$ is the density of the maximum of two i.i.d. random variables—indeed, since its distribution function is ${\left[{F}_{X}\left(x\right)\right]}^{2}$. This representation provides a straightforward way of generating draws from the distribution for simulation purposes.

Third, it can be seen as a special case of the “Generalized Exponential” distribution introduced by Gupta and Kundu (1999), with shape parameter equal to 2 (their α), scale parameter equal to θ_u (their λ) and location parameter equal to zero (their μ). We will write $u \sim GE\left(2,{\theta }_{u},0\right)$, and use this name to identify our distribution.

2.1 Moments and other properties

Yet another representation of this distribution, based on results from Gupta and Kundu (1999) and for the specific values of the parameters, is the following: let e_i, i = 1, 2 be two i.i.d. Exponentials with scale parameter equal to 1. Then

$$u \sim {\theta }_{u}{e}_{1}+{\theta }_{u}{e}_{2}/2.$$

This makes the derivation of the basic moments of u very simple by using cumulants κ, for which we have κ_r(cz) = c^rκ(z), and under independence, κ_r(e₁ + e₂) = κ_r(e₁) + κ_r(e₂). It follows that

$${\kappa }_{r}(u)=(1+{2}^{-r}){\kappa }_{r}(e){\theta }_{u}^{r},$$

$${\kappa }_{1}(e)={\kappa }_{2}(e)=1,\ {\kappa }_{3}(e)=2,\ {\kappa }_{4}(e)=6.$$

Then

$$E(u)={\kappa }_{1}(u)=\frac{3}{2}{\theta }_{u},\ {\rm{Var}}(u)={\kappa }_{2}(u)=\frac{5}{4}{\theta }_{u}^{2},$$

$${\rm{Skewness}}(u)={\gamma }_{1}(u)=\frac{{\kappa }_{3}(u)}{{\kappa }_{2}^{3/2}(u)}=\frac{18}{\sqrt{125}}\approx 1.61,$$

$${\rm{Ex.}}\;{\rm{Kurtosis}}(u)={\gamma }_{2}(u)=\frac{{\kappa }_{4}(u)}{{\kappa }_{2}^{2}(u)}=\frac{102}{25}=4.08.$$

We see that the distribution has lower skewness and excess kurtosis compared to the Exponential distribution (for which they are 2 and 6 respectively), but exceeds in both the Half-Normal (0.995 and 0.869 respectively). Paired with a Normal error component, these values represent the maximum skewness and kurtosis the composed SF error can accommodate under an NGE specification. Papadopoulos and Parmeter (2021) presented the empirical skewness and kurtosis of the OLS residuals for eight representative SF empirical studies, and in none of them did they exceeded the values of the GE distribution. This is an indication that although lower than the corresponding values for the Exponential distribution, they do not restrict in practice the applicability of the GE distribution.

Further, it is a simple exercise to find the argmax of the density,

$${\rm{mode}}(u)={\theta }_{u}\mathrm{ln}\,2.$$

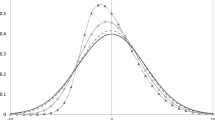
The mode of this distribution is equal to the median of an Exponential distribution with the same scale parameter, and it locates the point where 0.25 of probability mass lies to the left of it. In other words, it is equal to the 1st quartile. We also see that the mode cannot be zero, and in that sense the labeling of the distribution as “Generalized Exponential” could be considered as a misnomer, since it does not nest the Exponential.

The quantile function is

$${Q}_{u}(p)=-{\theta }_{u}\mathrm{ln}\,\left(1-\sqrt{p}\right),\ \ \ p\in [0,1),$$

from which we can obtain the median and other quantiles.

Finally, by using the additive expression eq. (2) for the density, it is easy to determine that it is log-concave (and therefore so is its distribution function). Since we will combine this distribution with a Normal random-noise component, the resulting composite error density will also be log-concave, since the Normal density is log-concave, and convolutions of log-concave functions retain the property.

3 Why use yet another distributional specification?

Now that we have familiarized ourselves with the aspiring newcomer, it is time to confront certain issues that are routinely raised in relation to distributional specifications like the one we propose here: a fully parametric specification with a log-concave density.

The first issue is the risk that, in case of distributional mis-specification, inference would be unreliable. But this is an argument in favor of abandoning parametric inference altogether. For those scholars that find a net benefit in using it though, increasing the number of available specifications mitigates this problem since it increases the diversity of available models and so our ability to get within tolerable distance from the true data generating process (DGP).

Still under the spectre of distributional misspecification, we can avoid this particular risk when “determinants of inefficiency” are available. Then we can model the distribution parameters of the inefficiency components as functions of observed data (as long as a valid economic argument supports it). Moreover, one can exploit the “scaling property” (see Wang and Schmidt, 2002, for the single-tier and Parmeter, 2018, for the two-tier SF model respectively), that always holds for single-parameter distributions, and, instead of using maximum likelihood estimation, implement non-linear least squares (NLLS) that does not require distributional assumptions. An issue in this approach is the finite-sample reliability of the NLLS estimates: in his simulations, Parmeter (2018) has found a persistent upward bias in the estimates of the coefficients for the determinants of inefficiency for small and medium samples, which would lead to an under-estimation of technical efficiency, if we were to calculate the corresponding exponentiated measure: firms appear less efficient than they actually are.⁴

A third issue relates to all SF models that assume a log-concave density for the random noise component: in standard notation, in an SF production model we would have a composite error term ε = v − u, E(v) = 0, u ≥ 0. Ondrich and Ruggiero (2001) have proven that, if the random noise component has a log-concave density, then the expected value of the inefficiency term conditional on the composite error, E(u∣ε), is a monotonic function of the conditioning variable.⁵ This has the implication that as regards ranking of the observations in the sample with respect to inefficiency, we might as well use the estimation residuals instead of E(u∣ε), and anticipate negligible differences (under correct specification). Moreover, the OLS residuals are more robust in ranking observations according to inefficiency, since they are free of possible misspecification from distributional assumptions.

We respond here by noting that ranking may be important and more safe as an inferential result, but there is more to efficiency analysis than a beauty contest to congratulate the more efficient firms and frown at the less efficient ones. The actual quantitative measurement of inefficiency is what matters as regards the efficient use of scarce resources, and for this we need to go beyond the estimation residuals.

In any case, the result of Ondrich and Ruggiero (2001) relates to the conditional expectation. We will provide proof that it holds also for the conditional mode of the production NGE frontier, and we will obtain simulation evidence as regards differences in ranking.

From a technical point of view, the NGE specification responds to the Stevenson (1980) critique of the NHN and NE specifications by offering a more convenient and, let’s say a more “user-friendly” solution to the non-zero mode desideratum, compared to the specifications involving the Truncated Normal or the Gamma distributions: in single-tier SF models the unknown parameters of the NGE specification are only two and not three, while in the 2TSF NGE model they are only three and not five. Moreover, the fixed investment cost in time and intellectual energy that the NGE specification requires (as any new tool does) is modest.

A weakness of the GE distribution is that it does not nest the zero-mode case. This in theory is an undesirable inflexibility, but the existence of a non-zero mode for the one-sided component is mostly an issue for economic debate rather than a statistical matter. We may not “let the data decide”, but knowledge of the particular industry/market under study in each case should allow for a convincing argument and a safe choice on this matter.

From a statistical point of view, the NGE specification, in addition of having a non-zero mode, is characterized by higher values of skewness and excess kurtosis in the composed error term compared to the NHN specification, and so it can accommodate a larger set of real-world data samples.

Finally, from an economics point of view, by representing the maximum of two i.i.d. underlying random variables it allows us to picture the economic mechanism as operating at high intensity: if notionally there are two possible inefficiency values, the GE specification “selects” the strongest one to affect the outcome. To some, this may appear as unjustified negative bias; to others it would be classified as prudential, connected informally with the concept of entropy and the tendency of things to get to a lower state of energy, which in business terms translates into disorganization and loss of efficiency.

4 The production frontier

In a production frontier setting, the original model is

$${y}_{i}=f({{\bf{x}}}_{i})\exp \{{v}_{i}-{u}_{i}\},\ i=1,...,n.$$

Typically, y is some measure of output and the regressors are production inputs. We focus on its estimation in logarithms, so the composite error term is ε = v − u and we assume v ~ N(0, σ_v), u ~ GE(2, θ_u, 0).

The additive representation of the density of u, eq. (2), means that the density of ε can be obtained as the difference of two convolutions of the Normal density with the Exponential, each being nothing else than the familiar Normal-Exponential SF specification, (see e.g. Kumbhakar and Lovell 2000, for the density formula). So we can easily obtain

$$\begin{array}{l}{f}_{\varepsilon }\left(\varepsilon \right)=\frac{2}{{\theta }_{u}}\left[\exp \left\{{a}_{u}\right\}\Phi \left({b}_{u}\right)\right.\\\qquad\qquad\! -\left.\;\exp \left\{2{a}_{u}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\right\}\Phi \left({b}_{u}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right)\right],\end{array}$$

(4)

where Φ is the standard Normal distribution function, and

$${a}_{u}=\frac{\varepsilon }{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{2{\theta }_{u}^{2}}\ ,\ \ \ \ \ \ {b}_{u}=-\left(\frac{\varepsilon }{{\sigma }_{v}}+\frac{{\sigma }_{v}}{{\theta }_{u}}\right).$$

This formula is nested in the formulas for the 2TSF model presented in Section 6, by setting there θ_w = 0. The same holds for the distribution function, which in the production frontier case is

$$\begin{array}{l}{F}_{\varepsilon }\left(\varepsilon \right)=\Phi \left(\frac{\varepsilon }{{\sigma }_{v}}\right)+2\exp \left\{{a}_{u}\right\}\Phi \left({b}_{u}\right)\ \ \ \\ \qquad\qquad\!-\exp \left\{2{a}_{u}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\right\}\Phi \left({b}_{u}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right).\end{array}$$

(5)

The distribution function will be needed in modeling sample selection bias, and also in models where regressor endogeneity is handled using Copulas rather than instrumental variables (see Tran and Tsionas 2015; Papadopoulos 2020a).

Due to the independence of the error components, the mean and variance of the composed error term are immediately obtained. Regarding skewness and excess kurtosis, Papadopoulos and Parmeter (2021) have shown that they can be expressed as follows:

$${\gamma }_{1}(\varepsilon )=-{\gamma }_{1}(u){\left(\frac{{s}_{u}}{{s}_{\varepsilon }}\right)}^{3},\ {\gamma }_{2}(\varepsilon )={\gamma }_{2}(u){\left(\frac{{s}_{u}}{{s}_{\varepsilon }}\right)}^{4},$$

where the symbol s represents the standard deviation. The skewness expression depends on the assumption that the distribution of v is symmetric, while the excess kurtosis expression on the assumption that it is Normal. Their maximum values (in absolute terms) are the skewness and excess kurtosis of the one-sided component. The authors present a powerful specification test using only sample moments of OLS residuals that is suitable for distributions with constant skewness and excess kurtosis.

Past this stage, the density can be used to implement maximum likelihood estimation. Alternatively, one can apply the Corrected Least Squares estimator (COLS), equating in the first stage the sample means of the 2nd and 3rd power of the OLS residuals with the 2nd and 3rd cumulant of the composite error term respectively, which are,

$${\kappa }_{2}(\varepsilon )\,=\,{\sigma }_{v}^{2}\,+\,\frac{5}{4}{\theta }_{u}^{2},\ \ \ {\kappa }_{3}(\varepsilon )\,=\,-\frac{9}{4}{\theta }_{u}^{3}.$$

We note that the COLS estimator is vulnerable to the “wrong skew” issue: the case where the OLS residuals exhibit skew with the opposite sign than the one assumed. Here if ${\widehat{\kappa }}_{3}(\varepsilon )\,>\,{0}$, we cannot compute θ_u which is constrained to be strictly positive. On the other hand, the simulations presented later showed that the MLE under the NGE specification does not break down when the skew is wrong: in such cases, the value of θ_u is estimated by MLE as really small but away from zero, around the values 0.03–0.04. But these are not reliable estimates, and so if the sample skew is wrong and the researcher decides to treat is as a sample problem, special treatment is required (for different such methods see Cai et al. 2020; Hafner et al. 2018; Simar and Wilson 2009).

4.1 Assessing and measuring technical (in)efficiency

For the single-output production frontier model estimated in logarithms, the standard measure of technical efficiency is Shephard’s output distance function that here equals $\exp \{-u\}\equiv {q}_{u}$, q_u ∈ (0, 1] (see Sickles and Zelenyuk 2019, pp. 20–24), which is the ratio of actual to maximum output. This is a random variable on its own. To obtain its marginal distribution, we apply the distribution method and we have

$${F}_{{q}_{u}}({q}_{u})=\Pr \left(\exp \{-u\}\le {q}_{u}\right)=\Pr (u\ge -\mathrm{ln}\,{q}_{u})$$

$$=1-{F}_{u}(-{\mathrm{ln}}\,{q}_{u})\ \Rightarrow \ {F}_{{q}_{u}}({q}_{u})=1-{\left(1-{q}_{u}^{1/{\theta }_{u}}\right)}^{2},$$

(6)

while the density is

$${f}_{{q}_{u}}({q}_{u})=\frac{2}{{\theta }_{u}}\left({q}_{u}^{-1+1/{\theta }_{u}}-{q}_{u}^{-1+2/{\theta }_{u}}\right).$$

(7)

This is the distribution of the minimum of two i.i.d. Beta random variables, with parameters α = 1/θ_u, β = 1. Unlike what happens to the Beta distribution when the parameter β is equal to unity, here, the distribution does not have always a monotonic density. This will depend on the actual value of θ_u. Specifically we have

$$\,\text{mode}\,[\exp \{-u\}]=\left\{\begin{array}{ll}{\left[(1-{\theta }_{u})/(2-{\theta }_{u})\right]}^{{\theta }_{u}}&{\theta }_{u}\,<\,{1}\\ \sim 0&{\theta }_{u}\,\ge\, 1.\end{array}\right.$$

We note that except when θ_u = 1 where the distribution becomes the minimum of two i.i.d U(0, 1) random variables, for θ_u > 1 the density has an asymptote at zero. Also, note that the zero-mode result for θ_u ≥ 1 is for the variable $\exp \{-u\}$, so with stronger inefficiency parameter (higher θ_u) comes lower technical efficiency.

Having the distribution function available allows us also to compute a full representative spectrum of quantiles (not just the median), through the quantile function

$${Q}_{q}(p)={\left(1-\sqrt{1-p}\right)}^{{\theta }_{u}},\ \ p\in [0,1].$$

Turning to moments, by using the additive expression for the f_u(u) density, the unconditional expected value can be calculated through the moment generating function of the Exponential distribution and it is

$$E(\exp \{-u\})={\frac{2}{(1+{\theta }_{u})(2+{\theta }_{u})}}_{.}$$

We can obtain its variance from

$$\,{\text{Var}}\,(\exp \{-u\})=E[\exp \{-2u\}]-{\left[E(\exp \{-u\})\right]}^{2}.$$

The mirror property of the Beta distribution is inherited here, so if one wants to study the relative technical inefficiency $1-\exp \{-u\}$, the distribution will be that of the minimum of two i.i.d. Betas with parameters α = 1, β = 1/θ_u.

Closing this section, we mention that the ratio of maximum output over actual, $\exp \{u\}$, is the “output-oriented Farrell measure of technical efficiency”, and for businesses it is a meaningful measure and perhaps more meaningful to their management, although not as a measure of efficiency but as a guidance for efficiency improvement: a value, say, of $E(\exp \{u\})=1.15$ would tell us that on average, firms in the sample need to increase their output by 15%, in order to be fully efficient, holding inputs constant. At the level of an individual firm, such a measure would be more relatable to the business mindset, and more directly translatable to specific actions in the pursuit of efficiency (“with given inputs, find new ways to combine and coordinate them better so a to increase output—and you have a 15% increase to chase”). To our knowledge it has not been explored in the efficiency literature and we will not examine it further here. We just note that the results on the marginal distribution of the variable “k” in Section 5.1 apply also for the $\exp \{u\}$ variable (but not the individual measures of Section 5.2).

4.2 Individual measures

We can obtain information on ${q}_{u,i}=\exp \{-{u}_{i}\},\ i=1,...,n$ through ε_i. By standard techniques, the conditional density f_u,ε(u_i∣ε_i) is

$${f}_{u| \varepsilon }({u}_{i}| {\varepsilon }_{i})=\frac{{f}_{v,u}({\varepsilon }_{i}+{u}_{i},{u}_{i})}{{f}_{\varepsilon }({\varepsilon }_{i})}=\frac{\phi (({\varepsilon }_{i}+{u}_{i})/{\sigma }_{v}){f}_{u}({u}_{i})}{{\sigma }_{v}{f}_{\varepsilon }({\varepsilon }_{i})},$$

where ϕ is the standard Normal density. We show in the Appendix that

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right) =\frac{2}{{\theta }_{u}{f}_{\varepsilon }(\varepsilon )}\exp \left\{\frac{1+{\theta }_{u}}{{\theta }_{u}}\varepsilon +\frac{{\sigma }_{v}^{2}}{2}{\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right)}^{2}\right\} \\ \qquad\qquad\qquad\quad\!\!\times \left[\Phi \left(-\frac{\varepsilon }{{\sigma }_{v}}-{\sigma }_{v}\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right)\right)\right.\\ \qquad\qquad\qquad\quad\!\!\left.-\exp \left\{\frac{\varepsilon }{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\left({\theta }_{u}+\frac{3}{2}\right)\right\}\Phi \left(-\frac{\varepsilon }{{\sigma }_{v}}-{\sigma }_{v}\left(\frac{2+{\theta }_{u}}{{\theta }_{u}}\right)\right)\right].\end{array}$$

(8)

We will use this expected value in our simulations alongside the conditional mode as predictors of inefficiency (we won’t present formulas for conditional expectations for the other models that we deal with here).

Turning to the conditional mode, in order to compute it we need the conditional density of ${f}_{{q}_{u}| \varepsilon }(q_u| {\varepsilon }_{i})$ which we can readily obtain by applying a change-of-variables in f_u∣ε(u_i∣ε_i) to arrive at

$${f}_{{q}_{u}| \varepsilon }({q}_{u}| {\varepsilon }_{i})=\frac{\phi \left(({\varepsilon }_{i}-{\mathrm{ln}}\,{q}_{u})/{\sigma }_{v}\right){f}_{{q}_{u}}({q}_{u})}{{\sigma }_{v}{f}_{\varepsilon }({\varepsilon }_{i})}.$$

(9)

This can be maximized numerically with respect to q_u (for each estimated value ${\hat{\varepsilon }}_{i}$), to get the conditional mode as an alternative predictor of individual efficiency. Note that this requires maximizing only the numerator in eq. (9), since the denominator does not include the q_u variable.

4.2.1 Monotonicity of the conditional mode in the conditioning variable

We show in the Appendix that the conditional mode q_u,* in the NGE production frontier satisfies the following implicit equation:

$${q}_{u,* }:\left({q}_{u,* }^{-1/{\theta }_{u}}-1\right)\cdot \left[\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,{q}_{u,* }}{{\sigma }_{v}^{2}}-1+1/{\theta }_{u}\right]-1/{\theta }_{u}=0\ .$$

The variable q_u ranges in (0, 1]. This implies that the term in parenthesis is always positive, meaning that the LHS expression is increasing in ε_i. Also, it is evident that both the term in parenthesis and the term in brackets is decreasing in q_u,*. So if we increase the value of ε_i the LHS will tend to increase, and in order to restore equality with zero we must decrease the LHS and so increase q_u,*. But this proves that the conditional mode is monotonically increasing in the conditioning variable. This shows that the result of Ondrich and Ruggiero (2001) mentioned earlier related to conditional expectations extends to the conditional mode of the NGE production specification.

5 The cost frontier

In a cost frontier setting, the original equation is of the form

$${y}_{i}=f({{\bf{x}}}_{i})\exp \{{v}_{i}+{w}_{i}\},\ i=1,...,n\ .$$

Here the dependent variable represents production costs, and the regressors are typically input prices and output, and again we focus on its estimation in logarithms. So the composite error term is ε = v + w and we assume v ~ N(0, σ_v), w ~ GE(2, θ_u, 0).

The density and distribution function of the composite error term are respectively

$$\begin{array}{l}{f}_{\varepsilon }\left(\varepsilon \right)=\frac{2}{{\theta }_{w}}\left[\exp \left\{{a}_{w}\right\}\Phi \left({b}_{w}\right)\right.\\ \qquad\,\,\,\left.-\exp \left\{2{a}_{w}+{\left({\sigma }_{v}/{\theta }_{w}\right)}^{2}\right\}\Phi \left({b}_{w}-{\sigma }_{v}/{\theta }_{w}\ \right)\right],\end{array}$$

(10)

and

$$\begin{array}{l}{F}_{\varepsilon }\left(\varepsilon \right)=\Phi \left(\frac{\varepsilon }{{\sigma }_{v}}\right)-2\exp \left\{{a}_{w}\right\}\Phi \left({b}_{w}\right)\ \\ \qquad\qquad\!+\exp \left\{2{a}_{w}+\frac{{\sigma }_{v}^{2}}{{\theta }_{w}^{2}}\right\}\Phi \left({b}_{w}-\frac{{\sigma }_{v}}{{\theta }_{w}}\right),\end{array}$$

(11)

with

$${a}_{w}=\frac{{\sigma }_{v}^{2}}{2{\theta }_{w}^{2}}-\frac{\varepsilon }{{\theta }_{w}}, \qquad {b}_{w}=\frac{\varepsilon }{{\sigma }_{v}}-\frac{{\sigma }_{v}}{{\theta }_{w}}.$$

As before these can be used in maximum likelihood estimation, while we can also implement the COLS estimator (only, κ₃(ε) would be positive here).

5.1 Assessing and measuring cost (in)efficiency

The standard measure of cost efficiency, is the ratio of minimum cost to actual, in our setting $CE\equiv {q}_{w}=\exp \{-w\}\in (0,1]$ (see Sickles and Zelenyuk 2019 pp. 80–81). The measure enjoys certain theoretical desirable properties, not least being confined in the (0, 1] interval.⁶ For CE all the formulas from the marginal analysis of the section on the production frontier applies as is (Section 4.1), inserting everywhere w in place of u.

Somewhat more intuitive but less well-behaved would be the ratio of actual cost to minimum, which we could think of as a measure of cost inefficiency. This would give us a “gross inefficiency mark up”: a value, say, 1.25 of this ratio would tell us that actual costs are 25% higher than minimum. In our setting this measure is represented by $k=\exp \{w\},\ k\in [1,\infty )$. Here we have

$${F}_{k}(k)=\Pr \left(\exp \{w\}\le k\right)=\Pr (w\le {\mathrm{ln}}\,k)={F}_{w}({\mathrm{ln}}\,k)$$

$$\ \Rightarrow \ {F}_{k}(k)={\left(1-{k}^{-1/{\theta }_{w}}\right)}^{2}.$$

This is the distribution of the maximum of two i.i.d Pareto random variables (of “Type I”), with minimum value/scale parameter equal to 1, and shape parameter 1/θ_w. Its density is

$${f}_{k}(k)=\frac{2}{{\theta }_{w}}\left({k}^{-1-1/{\theta }_{w}}-{k}^{-1-2/{\theta }_{w}}\right).$$

The mode of this distribution is

$${\rm{mode}}\left(\exp \{w\}\right)={\left(\frac{2+{\theta }_{w}}{1+{\theta }_{w}}\right)}^{{\theta }_{w}},$$

while its quantile function is

$${Q}_{k}(p)={\left(1-\sqrt{p}\right)}^{-{\theta }_{w}},\ \ p\in [0,1].$$

Here, the existence of moments depends on the value of θ_w: as it is the case for the Pareto distribution itself, for the r-th moment of k to exist and be finite, we must have θ_w < 1/r. So if θ_w ≥ 1 not even the mean will exist, while to have a variance we would need θ_w < 1/2.

In cases where θ_w < 1, the mean of this distribution is given by

$$E(\exp \{w\})=\frac{2}{(1-{\theta }_{w})(2-{\theta }_{w})}\ ,$$

and if moreover θ_w < 1/2, the variance can be obtained from

$$\,{\text{Var}}\,(\exp \{w\})=E[\exp \{2w\}]-{\left[E(\exp \{w\})\right]}^{2}.$$

The net mark-up on costs due to inefficiency is $\exp \{w\}$−1, and this is the maximum of two i.i.d random variables following the Lomax distribution with scale parameter equal to unity (the Lomax distribution is essentially a Pareto law shifted so as its support starts at zero).

5.2 Individual measures

For the cost efficiency measure $CE=\exp \{-w\}$ the conditional density is

$${f}_{{q}_{w}| \varepsilon }({q}_{w}| {\varepsilon }_{i})=\frac{\phi \left(({\varepsilon }_{i}+{\mathrm{ln}}\,{q}_{w})/{\sigma }_{v}\right){f}_{{q}_{w}}({q}_{w})}{{\sigma }_{v}{f}_{\varepsilon }({\varepsilon }_{i})}.$$

(12)

Turning to the cost inefficiency measure $k=\exp \{w\}$, we note that if θ_w > 1 and the marginal distribution does not possess moments, we are left only with the conditional mode as an individual measure. This is because the conditional expectation is fundamentally defined only for variables that are absolutely integrable and have finite expected value (see e.g. Williams 1991, Theorem 9.2, p. 84). The conditional density here is

$${f}_{k| \varepsilon }(k| {\varepsilon }_{i})=\frac{\phi \left(({\varepsilon }_{i}-\mathrm{ln}\,k)/{\sigma }_{v}\right){f}_{k}(k)}{{\sigma }_{v}{f}_{\varepsilon }({\varepsilon }_{i})}.$$

(13)

Numerical maximization of the numerator in both expressions with respect to k gives the conditional mode, for given ε_i.

6 The two-tier frontier

The mathematical derivations of this section can be found in the Technical Appendix of Papadopoulos (2018, pp. 409–444).

The two-tier stochastic frontier (2TSF) model was introduced by Polachek and Yoon (1987) in order to measure informational inefficiency of both employers and employees related to the determination of the wage. Since then it has been applied to many other markets apart from the labor market, notably the housing market and the health services market, but also as a method to measure bargaining power in a bilateral bargaining setting (see Papadopoulos 2020c, for a comprehensive survey).

The model is represented by the equation

$${y}_{i}=f({{\bf{x}}}_{i})\exp \{{\varepsilon }_{i}\},\ {\varepsilon }_{i}={v}_{i}+{w}_{i}-{u}_{i},\ i=1,...,n\ ,$$

and as before we assume that it will be estimated in logarithmic form. The error components follow v ~ N(0, σ_v), w ~ GE(2, θ_w, 0), u ~ GE(2, θ_u, 0), and are jointly independent. Then we have,

$$\begin{array}{l}{f}_{\varepsilon }\left(\varepsilon \right)=\frac{2}{{\theta }_{w}+{\theta }_{u}}\left[\frac{2{\theta }_{u}\exp \left\{{a}_{u}\right\}\Phi \left({b}_{u}\right)}{{\theta }_{w}+2{\theta }_{u}}\right.\\\qquad\,\,\, -\frac{{\theta }_{u}\exp \left\{2{a}_{u}+{\left({\sigma }_{v}/{\theta }_{u}\right)}^{2}\right\}\Phi \left({b}_{u}-{\sigma }_{v}/{\theta }_{u}\right)}{2{\theta }_{w}+{\theta }_{u}}\\ \qquad\,\,\,+\frac{2{\theta }_{w}\exp \left\{{a}_{w}\right\}\Phi \left({b}_{w}\right)}{2{\theta }_{w}+{\theta }_{u}}\\ \qquad\,\,\,\left.-\frac{{\theta }_{w}\exp \left\{2{a}_{w}+{\left({\sigma }_{v}/{\theta }_{w}\right)}^{2}\right\}\Phi \left({b}_{w}-{\sigma }_{v}/{\theta }_{w}\ \right)}{{\theta }_{w}+2{\theta }_{u}}\right]\ .\end{array}$$

(14)

The distribution function is

$$\begin{array}{l}{F}_{\varepsilon }\left(\varepsilon \right)=\frac{2}{{\theta }_{w}\;+\;{\theta }_{u}}\left[\frac{2{\left({\theta }_{w}\;+\;{\theta }_{u}\right)}^{3}\;+\;{\theta }_{w}{\theta }_{u}^{\,}\left({\theta }_{w}\;+\;{\theta }_{u}\right)}{2\left({\theta }_{w}\;+\;2{\theta }_{u}\right)\left(2{\theta }_{w}\;+\;{\theta }_{u}\right)}\Phi \left(\frac{\varepsilon }{{\sigma }_{v}}\right)\ \right.\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\frac{2{\theta }_{u}^{2}}{{\theta }_{w}\;+\;2{\theta }_{u}}\exp \left\{{a}_{u}\right\}\Phi \left({b}_{u}\right)\ \ \ \\ \qquad\,\,\,\,\,\,\,\,\,\,-\frac{{\theta }_{u}^{2}}{2\left(2{\theta }_{w}\;+\;{\theta }_{u}\right)}\exp \left\{2{a}_{u}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\right\}\Phi \left({b}_{u}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right)\\ \ \ \ \ \ \ \ \ \,\,\,\,\,\,\,\,\,-\frac{2{\theta }_{w}^{2}}{2{\theta }_{w}\;+\;{\theta }_{u}}\exp \left\{{a}_{w}\right\}\Phi \left({b}_{w}\right)\end{array}$$

$$\left.+\ \ \frac{{\theta }_{w}^{2}\exp \left\{2{a}_{w}+{\sigma }_{v}^{2}/{\theta }_{w}^{2}\right\}}{2\left({\theta }_{w}+2{\theta }_{u}\right)}\Phi \left({b}_{w}-\frac{{\sigma }_{v}}{{\theta }_{w}}\right)\ \right]\ .$$

(15)

It is straightforward to obtain the moments of ε using the cumulant expressions, since the three components are independent. We have

$$\begin{array}{l}{\kappa }_{2}(\varepsilon )={\sigma }_{v}^{2}+\frac{5}{4}({\theta }_{w}^{2}+{\theta }_{u}^{2}),\ \ \ {\kappa }_{3}(\varepsilon )=\frac{9}{4}({\theta }_{w}^{3}-{\theta }_{u}^{3}),\\ {\kappa }_{4}(\varepsilon )=\frac{51}{8}({\theta }_{w}^{4}+{\theta }_{u}^{4}).\end{array}$$

Implementing the COLS estimator here requires also the use of the sample mean of the 4th power of the OLS residuals that estimates consistently the 4th central moment of the composed error term, and it must be set equal to ${\kappa }_{4}(\varepsilon )+3{\kappa }_{2}^{2}(\varepsilon )$.

The two-tier frontier specification faces no problems with “wrong skew” samples, because its theoretical skewness can be positive or negative. Papadopoulos (2020b) develops a 2TSF model for production in order to measure the effects that unobservable management has on output (management being represented by the error component w).

6.1 Assessing and measuring the net effect

To analyze each one-sided component individually, we can use the results from the single-tier frontiers as regards the marginal distributions, but not the results on individual measures, since these depend on the composite error term which here is different.

But specific to the 2TSF model is the joint presence of opposing forces w and u on the outcome, and so of special interest is their net effect z = w − u, and, for the logarithmic model we are considering, the exponentiated one, $\xi =\exp \{w-u\}$. After deriving the density and distribution function of z, which we do not present here, we can obtain the density and distribution function of ξ with the same techniques as before,

$$\begin{array}{l}{F}_{\xi }\left(\xi \right)=\left\{\begin{array}{ll}\frac{{\theta }_{u}^{2}}{{\theta }_{w}\;+\;{\theta }_{u}}\left[\frac{4{\xi }^{1/{\theta }_{u}}}{{\theta }_{w}\;+\;2{\theta }_{u}}-\frac{{\xi }^{2/{\theta }_{u}}}{2{\theta }_{w}\;+\;{\theta }_{u}}\right]&\xi\, \le \,1\\ 1\ -\ \frac{{\theta }_{w}^{2}}{{\theta }_{w}\;+\;{\theta }_{u}}\left[\frac{4{\xi }^{-1/{\theta }_{w}}}{2{\theta }_{w}\;+\;{\theta }_{u}}-\frac{{\xi }^{-2/{\theta }_{w}}}{{\theta }_{w}\;+\;2{\theta }_{u}}\right]&\xi\,>\,1\ .\end{array}\right.\end{array}$$

(16)

From this, one can obtain probabilistic events of interest like for example,

$$\begin{array}{l}\Pr \left(\exp \{w-u\}\le 1\right) =\frac{{\theta }_{u}^{2}}{{\theta }_{w}\;+\;{\theta }_{u}}\left(\frac{4}{{\theta }_{w}\;+\;2{\theta }_{u}}-\frac{1}{2{\theta }_{w}\;+\;{\theta }_{u}}\right).\end{array}$$

The marginal density of ξ is

$$\begin{array}{l}{f}_{\xi }\left(\xi \right)=\frac{2}{{\theta }_{w}\;+\;{\theta }_{u}} \\ \qquad\qquad\times \left\{\begin{array}{ll}{\theta }_{u}\cdot \left[\frac{2{\xi }^{-1+1/{\theta }_{u}}}{{\theta }_{w}\;+\;2{\theta }_{u}}\ -\ \frac{{\xi }^{-1+2/{\theta }_{u}}}{2{\theta }_{w}\;+\;{\theta }_{u}}\ \right]&{0}\,<\,\xi \le 1\\ {\theta }_{w}\cdot \left[\frac{2{\xi }^{-1-1/{\theta }_{w}}}{2{\theta }_{w}\;+\;{\theta }_{u}}\ -\ \frac{{\xi }^{-1-2/{\theta }_{w}}}{{\theta }_{w}\;+\;2{\theta }_{u}}\right]&\xi\,>\,{1}\ .\end{array}\right.\end{array}$$

(17)

The mode of this density is

$$\begin{array}{l}{\rm{mode}}\left(\exp \left\{w-u\right\}\right)=\left\{\begin{array}{ll}0&{\theta }_{u}\,\ge\,{1}\\ \max \left\{{q}_{0}I\left\{{q}_{0}\,\le \,{1}\right\},\ {q}_{1}I\left\{{q}_{1}\,>\,{1}\right\}\right\}&{\theta }_{u}\,<\,{1},\end{array}\right.\end{array}$$

(18)

with

$${q}_{0}={\left(\frac{1-{\theta }_{u}}{2-{\theta }_{u}}\cdot\frac{4{\theta }_{w}+2{\theta }_{u}}{{\theta }_{w}+2{\theta }_{u}}\right)}^{{\theta }_{u}},\ {q}_{1}={\left(\frac{2+{\theta }_{w}}{1+{\theta }_{w}}\cdot \frac{2{\theta }_{w}+{\theta }_{u}}{2{\theta }_{w}+4{\theta }_{u}}\right)}^{{\theta }_{w}},$$

and where $I\left\{\cdot \right\}$ is the indicator function. One can determine that

$$\,{\text{mode}}\,\left(\exp \{w-u\}\right)\,\ne\,\,{\text{mode}}\,\left(\exp \{w\}\right)\,{\text{mode}}\,\left(\exp \{-u\}\right).$$

The proper predictor of the net effect of the two opposing one-sided components is the mode of the difference, not the difference of the marginal modes, since, even if they are independent, the two error components happen concurrently and so we must consider their variation jointly. But the marginal modes are also useful since they predict the value of each component, if it operated without the presence of the other.

As regards expected values, due to independence we have,

$$E[\exp \{w-u\}]=E(\exp \{w\})E(\exp \{-u\}),$$

and it will exist if θ_w < 1.

6.2 Individual measures

In the 2TSF setting, of main interest are the variables

$$k=\exp \{w\},\ {q}_{w}=\exp \{-w\},$$

$${q}_{u}=\exp \{-u\},\ \xi =\exp \{w-u\}.$$

Closed-form expressions for the one-sided conditional expectations for the 2TSF NE and NHN specifications have been collected in Papadopoulos (2018, ch.3). Up to now no attention has been given to the conditional mode as a predictor at the individual level. For the NGE specification, closed-formed expressions for conditional expectations can be derived, but they are much more involved and lengthy than for the single-tier models. We also note that even though w and u are assumed independent, they stop being so conditional on ε, so

$$E\left[\exp \{w-u\}| \varepsilon \right]\,\ne \,{E}\left[\exp \{w\}| \varepsilon \right]E\left[\exp \{-u\}| \varepsilon \right].$$

To obtain predictors based on the mode we need four conditional densities. These are

$$\begin{array}{l}{f}_{k\left|\varepsilon \right.}\left(k\left|\varepsilon \right.\right)=\frac{2{f}_{k}(k)}{{\theta }_{u}{f}_{\varepsilon }\left(\varepsilon \right)}\times \left[{k}^{-1/{\theta }_{u}}\exp \left\{{a}_{u}\right\}\Phi \left(\frac{{\mathrm{ln}}\,k}{{\sigma }_{v}}+{b}_{u}\right)\right.\\ \left.\ \ \ \ \ \ \ \ \qquad\quad-{k}^{-2/{\theta }_{u}}\exp \left\{2{a}_{u}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\ \right\}\Phi \left(\frac{{\mathrm{ln}}\,k}{{\sigma }_{v}}+{b}_{u}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right)\right]\ .\end{array}$$

(19)

$$\begin{array}{l}{f}_{{q}_{w}\left|\varepsilon \right.}\left({q}_{w}\left|\varepsilon \right.\right)=\frac{2{f}_{{q}_{w}}({q}_{w})}{{\theta }_{u}{f}_{\varepsilon }\left(\varepsilon \right)} \\ \qquad\qquad\qquad\times \left[{{q}_{w}}^{1/{\theta }_{u}}\exp \left\{{a}_{u}\right\}\Phi \left(\frac{-\mathrm{ln}\,{q}_{w}}{{\sigma }_{v}}+{b}_{u}\right)\right.\\ \qquad\qquad\qquad\left.-{{q}_{w}}^{2/{\theta }_{u}}\exp \left\{2{a}_{u}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\ \right\}\Phi \left(\frac{-\mathrm{ln}\,{q}_{w}}{{\sigma }_{v}}+{b}_{u}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right)\right]\ ,\end{array}$$

(20)

where ${f}_{{q}_{w}}({q}_{w})$ is ${f}_{{q}_{u}}({q}_{u})$ (eq. (7)) with the symbol w in place of the symbol u. Also,

$$\begin{array}{l}{f}_{{q}_{u}| \varepsilon }\left({q}_{u}| \varepsilon \right)=\frac{2{f}_{{q}_{u}}({q}_{u})}{{\theta }_{w}{f}_{\varepsilon }\left(\varepsilon \right)} \\ \qquad\qquad\quad\times\left[{{q}_{u}}^{1/{\theta }_{w}}\exp \left\{{a}_{w}\right\}\Phi \left(\frac{-{\mathrm{ln}}\,{q}_{u}}{{\sigma }_{v}}+{b}_{w}\right)\right.\\ \qquad\qquad\quad-\left.{{q}_{u}}^{2/{\theta }_{w}}\exp \left\{2{a}_{w}+\frac{{\sigma }_{v}^{2}}{{\theta }_{w}^{2}}\right\}\Phi \left(\frac{-{\mathrm{ln}}\,{q}_{u}}{{\sigma }_{v}}+{b}_{w}-\frac{{\sigma }_{v}}{{\theta }_{w}}\right)\right]\ ,\end{array}$$

(21)

and finally,

$${f}_{\xi \left|\varepsilon \right.}\left(\xi \left|\varepsilon \right.\right)=\frac{\phi \left(\left(\varepsilon -\mathrm{ln}\,\xi \right)/{\sigma }_{v}\right)}{{\sigma }_{v}{f}_{\varepsilon }\left(\varepsilon \right)}\ \times {f}_{\xi }(\xi ).$$

(22)

As before, obtaining the conditional mode series requires numerical maximization of these expressions with respect to their variable, for each estimated value of ε_i.

7 Simulation studies

In this section we provide simulation results related to the NGE production frontier model, using maximum likelihood estimation.

In all simulations the regression equation is

$$y=1+{x}_{1}+{x}_{2}+\varepsilon ,\quad \varepsilon =v-u,$$

with ${x}_{1} \sim {\chi }_{1}^{2},\ {x}_{2} \sim \,\text{Bern}\,(0.65),v \sim N(0,1).$

In each simulation we run 1000 replications and we report sample averages over them. We consider two sample sizes n = 200, 1000 and two different values of θ_u = 0.5, 1.5. For each value we report also the “signal-to-noise” ratio (SNR), the ratio of the standard deviation of the inefficiency error component over that of the random component. This is a model-free measure that summarizes well how strong is the signal that interests us (the inefficiency), relative to noise. Note that it equals the familiar λ = σ_u/σ_v only for the NE specification.

We observed that when the data generating process was NGE, the correctly specified MLE failed to converge 2–5% of the times, while when the sample size was small and the SNR large, this percentage rose to ≈15%. We noted earlier that this is not related to the “wrong skew” issue. Rather, it indicates a sensitivity of the NGE likelihood to starting values, and in empirical studies many different sets of initial values for the parameters should be tried.

7.1 Performance when the DGP is NGE

In the first part of our simulation study, the DGP has an NGE composite error term. We report OLS, NHN, and NE estimates also, to see how these fare when the true specification is NGE. Essentially we attempt to answer the question “suppose that the DGP is indeed NGE. Does it matter for inference?” We certainly expect that the correctly specified MLE will fare better compared to a misspecified likelihood, but how much better?

In order to have comparable results between specifications, we present not estimates of the scale parameters of the inefficiency component, but calculated moments based on these estimates and on the assumed specification in each case.

The results are presented in Table 1. They validate the robustness/consistency property for the Skew Normal quasi-MLE (the NHN specification) as regards the regression slope coefficients, proven in Papadopoulos and Parmeter (2020). The same robustness property appears to characterize the NE specification. Regarding the performance of the misspecified likelihoods, we see that the MLE under the NHN specification does remarkably well, perhaps against expectations, with rather small bias in the estimation of average Technical Efficiency. On the other hand, the NE specification leads to high overestimation of TE.

Table 1 Production frontier—Data generating process is NGE

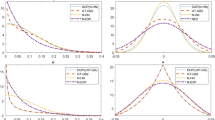
Probing deeper we computed also JLMS conditional expectations for the NHN and NGE models. In each replication we obtained the conditional expectation series, and computed the 0.2, 0.4, 0.6, 0.8 quintiles.

Table 2 presents the median estimate of each quintile over all replications. We observe that sample size does not appear to affect behavior. When the SNR is low, the predictor coming from the NHN misspecified model tends to underestimate Technical Efficiency: for example, it places 40% of firms at a Technical Efficiency level below 0.48–0.49 (1st column 2nd row), while the correctly specified NGE predictor does that for only 20% of firms (2nd column 1st row). When the SNR is large, the two predictors allocate probability mass essentially in the same way up to cumulative probability 0.6, but then the NHN tends to overestimate Technical Efficiency since its 0.8-quantile value is 0.46 while the corresponding quantile value of the NGE predictor is only 0.38.

Table 2 Production frontier—Data generating process is NGE. Empirical medians of Quintiles of JLMS measures E[exp{−u}]

7.2 Performance when the DGP is NHN

Here the DGP includes a NHN composite error term, and we are interested to see how misleading could estimation be if it is carried based on a misspecified NGE likelihood.

The results from the NHN DGP are in Table 3. When the SNR is low, the now misspecified NGE model leads to an overestimation of Technical Efficiency, but not as much as the misspecified NE model. With high SNR, the NGE model performs comparably with the NHN model in the previous simulation, while the NE model continues to be highly biased.

Table 3 Production frontier—Data generating process is NHN

7.3 Performance when the DGP is NE

Here the DGP includes a NE error term, and the goal is the same as in the previous subsection.

From Table 4 we see that the now misspecified NHN and NGE models perform comparably, and both underestimate the average Technical Efficiency measure.

Table 4 Production frontier—Data generating process is NE

Overall, there appears to be a certain degree of congruence and “mutual robustness” between the NGE and the NHN specifications, and exploring whether this has some deeper theoretical justification could be an interesting topic of study. When we misspecify the one against the other, results are not that different, although of course it is always preferable to use the correct specification, especially when one is interested not just in sample averages but individual estimates of inefficiency. On the other hand the misspecified NE likelihood visibly overestimates Technical Efficiency against both an NGE and a NHN data generating process, and these two return the favor by underestimating TE when the true model is NE.

7.4 Rankings and correlation

In this subsection we examine how close are the firm rankings obtained by the NGE predictor compared to the rankings based on OLS residuals. We included an additional sample size, n = 5000, and two additional values for θ_u = 1.0, 2.0. We computed individual efficiency measures for the NGE specification, both conditional expectations and conditional modes (for the exponentiated variable). In Table 5, we compare the observation rankings obtained using them, to those based on OLS residuals. We report the proportion of observations that changed rank, but also the proportion of observations that moved by a ventile, namely those that moved at least five percentiles in the ranking distribution.⁸ We consider this a realistic criterion in order to conclude that the rankings differ in a substantial manner from an economic point of view, since, moving a few positions among hundreds of observations does not signal that the two measures rank really differently an observation.

Table 5 Production frontier—NGE ranking changes compared to OLS ranking

What we observe in Table 5 is that while the large majority, and even almost all of observations change rank under the JLMS measures from the NGE specification compared to the OLS ranking, very few or even none move by a ventile. This does not invalidate the Ondrich and Ruggiero (2001) result, it just clarifies it appropriately: rankings coming from log-concave densities in SF models don’t differ from OLS rankings in an economically important way. We also see that the conditional mode behaves much like the conditional expectation in that respect, as anticipated from the related theoretical result obtained earlier.

Finally, we examined how close are the two JLMS measures of inefficiency, but also how they correlate with the true value $\exp \{-{u}_{i}\}$. The results are presented in Table 6.

Table 6 Production frontier—NGE specification. Individual efficiency measures

The first two rows of Table 6 in each block are analogous to the first two rows of Table 5: they tell us how many observations in percentage terms changed rank and how many moved at least by a ventile, when ranked by the conditional expectation and when ranked by the conditional mode. Except when the sample size is small and the inefficiency parameter is the lowest simulated, in all other cases these proportions are both negligible or even zero, indicating that the two JLMS measures result in almost identical rankings, both from a statistical but also from an economic point of view.

The 3rd row gives the average absolute difference in efficiency percentage points, as measured by the two measures. This difference is not negligible: it tells us that on average, the two measures differ in the assessment of individual efficiency by 5 to 10 points (in the 1–100 scale that $100\times \exp \{-u\}$ lives), which in relative terms may translate to an efficiency score that differs by more than 10–15%, depending on which measure is used.

The 4th and 5th row provide association measures of the JLMS scores with the true variable they predict. The differences are minor to none, with the Conditional Expectation showing a slightly higher linear correlation with $\exp \{-u\}$. We also note that the sample size appears not to matter for how well these measures correlate with the true variable, but the strength of inefficiency (the values of θ_u) does. Overall, the behavior of the two measures is very close, which does not help us to choose among them, in light of their previous difference as regards the actual quantitative estimation of the efficiency score.

But perhaps this is as it should be, since each measure may be appropriate for different situations: mid- and long-term analysis of repeated actions may be more secure using the conditional expectation and the approach of “averaging” that it represents, while short-term one-off decisions may be served better by the “most likely” prediction, and hence by the conditional mode.

Appendix

1.1 The conditional expectation in the NGE production frontier

In the production SF model we want to compute

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right)=\displaystyle{\int\nolimits_{0}^{\infty }}{e}^{-u}{f}_{u| \varepsilon }(u| \varepsilon )du\\ \qquad\qquad\qquad\,\,\,=\frac{2}{{\sigma }_{v}{f}_{\varepsilon }(\varepsilon )}\displaystyle{\int\nolimits_{0}^{\infty }}{e}^{-u}\phi ((\varepsilon +u)/{\sigma }_{v}){h}_{E}(u;{\theta }_{u})du\\ \qquad\qquad\qquad\quad\,\,\,-\frac{1}{{\sigma }_{v}{f}_{\varepsilon }(\varepsilon )}\displaystyle{\int\nolimits_{0}^{\infty }}{e}^{-u}\phi ((\varepsilon +u)/{\sigma }_{v}){h}_{E}(u;{\theta }_{u}/2)du,\end{array}$$

where we have used the additive form of the GE density, eq. (2). Decomposing the integrands,

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right)=\frac{2\exp \{-{\varepsilon }^{2}/2{\sigma }_{v}^{2}\}}{{\theta }_{u}{\sigma }_{v}{f}_{\varepsilon }(\varepsilon )\sqrt{2\pi }}\times ({I}_{1}-{I}_{2}),\\ {I}_{1}=\displaystyle{\int\nolimits_{0}^{\infty }}\exp \left\{-{u}^{2}/2{\sigma }_{v}^{2}-\left(\varepsilon /{\sigma }_{v}^{2}+1+1/{\theta }_{u}\right)u\right\}du\\ {I}_{2}=\displaystyle{\int\nolimits_{0}^{\infty }}\exp \left\{-{u}^{2}/2{\sigma }_{v}^{2}-\left(\varepsilon /{\sigma }_{v}^{2}+1+2/{\theta }_{u}\right)u\right\}du.\end{array}$$

Combining formulas from Gradshteyn and Ryzhik (2007) and Erdelyi et al. (1954), we have (for a > 0),

$${\int\nolimits_{0}^{\infty }}\exp \{-a{z}^{2}-bz\}dz=\frac{\sqrt{\pi }}{\sqrt{a}}\exp \left\{\frac{{b}^{2}}{4a}\right\}\Phi \left(-\frac{b}{\sqrt{2a}}\right).$$

For both integrals, we have the common mapping

$$a=1/2{\sigma }_{v}^{2}\ \Rightarrow \ \frac{1}{\sqrt{a}}={\sigma }_{v}\sqrt{2},\ \frac{1}{\sqrt{2a}}={\sigma }_{v},\ \frac{1}{4a}={\sigma }_{v}^{2}/2.$$

Moreover we have, using indices 1 and 2 for the two integrands,

$${b}_{1}=\varepsilon /{\sigma }_{v}^{2}+1+1/{\theta }_{u},\ {b}_{2}={b}_{1}+1/{\theta }_{u}$$

$$\ \Rightarrow \ {b}_{2}^{2}={b}_{1}^{2}+2{b}_{1}/{\theta }_{u}+1/{\theta }_{u}^{2}.$$

Exploiting these results to make some initial simplifications we can write

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right) =\frac{2\exp \{-{\varepsilon }^{2}/2{\sigma }_{v}^{2}\}}{{\theta }_{u}{f}_{\varepsilon }(\varepsilon )}\exp \left\{\frac{{\sigma }_{v}^{2}{b}_{1}^{2}}{2}\right\}\times ({A}_{1}-{A}_{2}),\\ {A}_{1}=\Phi \left(-{\sigma }_{v}{b}_{1}\right),\\ {A}_{2}=\exp \left\{\frac{{\sigma }_{v}^{2}{b}_{1}}{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{2{\theta }_{u}^{2}}\right\}\Phi \left(-{\sigma }_{v}{b}_{1}-\frac{{\sigma }_{v}}{{\theta }_{u}}\right).\end{array}$$

Now,

$${b}_{1}^{2}=\frac{{\varepsilon }^{2}}{{\sigma }_{v}^{4}}+2\frac{1+{\theta }_{u}}{{\theta }_{u}}\frac{\varepsilon }{{\sigma }_{v}^{2}}+{\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right)}^{2}$$

$$\ \Rightarrow \ \frac{{\sigma }_{v}^{2}{b}_{1}^{2}}{2}=\frac{{\varepsilon }^{2}}{2{\sigma }_{v}^{2}}+\frac{1+{\theta }_{u}}{{\theta }_{u}}\varepsilon +\frac{{\sigma }_{v}^{2}}{2}{\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right)}^{2}.$$

Also,

$${\sigma }_{v}{b}_{1}=\frac{\varepsilon }{{\sigma }_{v}}+{\sigma }_{v}\left(\frac{1+{\theta }_{u}}{{\theta }_{u}}\right),\ \frac{{\sigma }_{v}^{2}}{{\theta }_{u}}{b}_{1}=\frac{\varepsilon }{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}.$$

Combining all, we arrive at

$$\begin{array}{l}E\left(\exp \{-u\}| \varepsilon \right) =\frac{2}{{\theta }_{u}{f}_{\varepsilon }(\varepsilon )}\exp \left\{\frac{1\;+\;{\theta }_{u}}{{\theta }_{u}}\varepsilon +\frac{{\sigma }_{v}^{2}}{2}{\left(\frac{1\;+\;{\theta }_{u}}{{\theta }_{u}}\right)}^{2}\right\} \\ \qquad\qquad\qquad\qquad\!\times\left[\Phi \left(-\frac{\varepsilon }{{\sigma }_{v}}-{\sigma }_{v}\left(\frac{1\;+\;{\theta }_{u}}{{\theta }_{u}}\right)\right)\right.\\ \qquad\qquad\qquad\qquad\left.-\exp \left\{\frac{\varepsilon }{{\theta }_{u}}+\frac{{\sigma }_{v}^{2}}{{\theta }_{u}^{2}}\left({\theta }_{u}+\frac{3}{2}\right)\right\}\Phi \left(-\frac{\varepsilon }{{\sigma }_{v}}-{\sigma }_{v}\left(\frac{2\;+\;{\theta }_{u}}{{\theta }_{u}}\right)\right)\right].\end{array}$$

1.2 The conditional mode in the NGE production frontier

We want to maximize the conditional density in eq. (9) with respect to q. Ignoring the terms that do not include q, the derivative we want to set equal to zero is

$$\frac{\partial }{\partial q}\left[\phi \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right)\cdot \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\right]$$

$$\begin{array}{l}=\phi ^{\prime} \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right)\left(-1/q{\sigma }_{v}\right)\cdot \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\\ \quad+\,\frac{1}{q}\phi \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right) \times \left[\left(-1+\frac{1}{{\theta }_{u}}\right){q}^{-1+1/{\theta }_{u}}-\left(-1+\frac{2}{{\theta }_{u}}\right){q}^{-1+2/{\theta }_{u}}\right]\end{array}$$

Using the property of the standard Normal density $\phi ^{\prime} (z)=-z\phi (z)$ we obtain

$$\begin{array}{l}...=\frac{1}{q}\phi \left(\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}}\right) \times \left\{\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}^{2}}\cdot \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\right.\\ \qquad\,\,\left.+\,\left(-1+\frac{1}{{\theta }_{u}}\right){q}^{-1+1/{\theta }_{u}}-\left(-1+\frac{2}{{\theta }_{u}}\right){q}^{-1+2/{\theta }_{u}}\right\}.\end{array}$$

Setting this expression equal to zero is equivalent to setting the expression in curly brackets equal to zero since the term outside is always positive. Manipulating further,

$$\begin{array}{l}...\ \Rightarrow \ \left({q}^{-1+1/{\theta }_{u}}-{q}^{-1+2/{\theta }_{u}}\right)\cdot \left[\frac{{\varepsilon }_{i}-{\mathrm{ln}}\,q}{{\sigma }_{v}^{2}}-1+\frac{1}{{\theta }_{u}}\right]\\ \qquad\quad\,\,\,\,-\frac{1}{{\theta }_{u}}{q}^{-1+2/{\theta }_{u}}=0.\end{array}$$

Taking ${q}^{-1+2/{\theta }_{u}}$ out as common factor we arrive at the expression used in the main text.