Introduction The aging of the agroforestry workforce, combined with the ongoing trend of urbanization, prompts significant concerns about a food shortfall soon. Mitigating the resultant workforce imbalance requires the implementation of mechanization in agroforestry processes, with autonomous wheeled mobile robots (WMR) emerging as a promising solution [21]. For example, WMRs can implement changeable transport paths, overcoming the limitations associated with fixed conveyor belts [16]. In this scenario, the primary objective of a WMR, viewed through the lens of control engineering, is cast as a nonlinear tracking control problem.

The authors of [13] developed an adaptive sliding mode control approach for a WMF with uncertainties. In [14], they further deliberated the (electric) actuator dynamics in adaptive controller design for WMRs. In [10], the authors addressed the trajectory tracking problem for a WMR, using the extended Kalman filter to observe disturbances along nonlinear dynamics. A sliding mode control for path-tracking unmanned agricultural vehicles with adaption laws was presented in [2]. These endeavors underscore that most control techniques for WMRs rely on variable structures or adaptive mechanisms.

Takagi–Sugeno (T–S) fuzzy model-based strategy is well recognized as an efficient solution for nonlinear control systems [6, 7, 9], including WMRs. Sun et al. [15] proposed a continuous-time T–S fuzzy control design for WMR with visual odometry. This paper continues these efforts to develop a sampled-data approach for WMRs with disturbances and uncertainties using the T–S framework. The focal points of consideration are twofold: (i) disturbance attenuation and (ii) sampled-data burden.

(i) While WMRs conventionally assume pure rolling of wheels, local floor irregularities may cause a slip, which can be identified by \(\mathcal {L}_{2}\) disturbances. The driving task of a WMR is, therefore, defined as the energy-to-peak disturbance attenuation problem in trajectory tracking. In [1], the robust energy-to-peak filtering problem for uncertain continuous-time T–S fuzzy models was studied. In [18], a continuous-time energy-to-peak output-tracking controller was developed for nonlinearly perturbed systems. However, few research efforts are found devoted to the \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) disturbance attenuation problem for WMRs.

(ii) Given the prevalence of low-cost digital microprocessors for driving electric actuators, discrete-time model-based sampled-data control methodologies have become imperative. However, deriving an exact discrete-time model for a WMR proves often unattainable due to the nonlinear nature of the initial value problem [8]. In [4], a predictive control technique was examined, where an approximate discrete-time error posture model of a WMR was used; thereby, actual performance may be degraded. Fast sampling is essential for preventing the performance degradation of sampled-data control. However, it significantly strains the network bandwidth and computing capability of the microprocessor. The event-triggered—rather than the ordinary fixed time-triggering—control (ETC), which changes the control input only when a specific event occurs, can be a resolution [3]. Previous work [11] polished an ETC scheme with a nonlinear sliding mode control technique for WMRs, validating the theoretical development through experimentation.

This paper offers a robust fuzzy sampled-data ETC approach for path tracking of uncertain nonholonomic WMRs that achieves energy-to-peak disturbance attenuation. The kinematic model of a nonlinear WMR is represented in the T–S fuzzy form with no modeling errors. The suggested scheme analyzes closed-loop stability in the continuous-time domain, hence removing the need for a discrete-time model of a WMR. The design condition is stated in terms of linear matrix inequalities and ensures the Zeno-free behavior of the event triggering. A numerical example of a WMR demonstrates the efficacy of the proposed method.

Notation: The index set is defined as \(\mathcal {I}_{R}:=\{1,\dots ,r\}\subset \mathbb {N}\). \(\mathcal {I}_{J}\times \mathcal {I}_{R}\) denotes all pairs \((i,j)\in \mathcal {I}_{R}\times \mathcal {I}_{R}\) such that \(1\leqslant i<j\leqslant r\). The shorthand \(\textrm{He}\left\{ X\right\} :=X+X^{\textrm{T}}\) is adopted, and the transposed element in symmetric positions is denoted by \(*\).

1 Kinematics of a WMF and its T–S Fuzzy Modeling

For a mechanical kinematics with the n-dimensional generalized coordinates q, the m nonholonomic independent constraints can be expressed as:

$$\begin{aligned} A(q)\dot{q} = 0 \end{aligned}$$

where \(A(q):\mathbb {R}^{n}\rightarrow \mathbb {R}^{m\times n}\) is a function matrix with full row rank. For \(n-m\) linear independent vector fields \(s_{i}(q)\) that comprise the basis for the nullspace of A(q), we obtain

$$\begin{aligned}&A(q) \underbrace{ \begin{bmatrix} s_{1}(q)&\cdots&s_{n-m}(q) \end{bmatrix}}_{=:J(q)} = 0 \\&\implies \dot{q} \in \textrm{span}\{s_{1}(q),\dots ,s_{n-m}(q)\}. \end{aligned}$$

Then, there exists a velocity vector \(p\in \mathbb {R}^{n-m}\) [13, 19] such that

$$\begin{aligned} \dot{q}=J(q)p. \end{aligned}$$

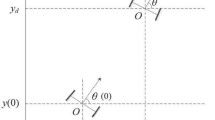
In this study, as shown in Fig. 1, we consider a two-wheeled mobile robot whose posture is represented by the generalized coordinate \(q:=(x,y,\phi )\in \mathbb {R}^{3}\) in the world X–Y frame. In this case, (x, y) is the Cartesian coordinates of the center of mass of the vehicle, and \(\phi \) is the counterclockwise angle between the heading direction and the X-axis.

Fig. 1
figure 1

The posture of WMR

Full size image

Assumption 1

([19]) The WMR purely rolls and does not slip in a lateral direction.

Assumption 1 poses a nonholonomic restriction in which the velocity in the lateral direction of a WMR is null, which is represented by

$$\begin{aligned}&-\dot{x}\sin (\phi )+\dot{y}\cos (\phi )=0 \\&\iff \underbrace{\begin{bmatrix}-\sin (\phi )&\cos (\phi )&0 \end{bmatrix}}_{{A(q)}}\dot{q}=0. \end{aligned}$$

Two vector fields, \(s_{1}=(\cos (\phi ), \sin (\phi ), 0)\) and \(s_{2}=(0, 0, 1)\) are linearly independent and lie in the nullspace of A(q). We define \(p:=(v, \omega )\), where v represents the linear velocity in the heading direction and \(\omega \) denotes the angular velocity. The kinematics model is constructed as

$$\begin{aligned} \underbrace{ \begin{bmatrix} \dot{x} \\ \dot{y} \\ \dot{\phi } \end{bmatrix}}_{\dot{q}} = \underbrace{ \begin{bmatrix} \cos (\phi ) &{} 0 \\ \sin (\phi ) &{} 0 \\ 0 &{} 1 \end{bmatrix}}_{J(q)} \underbrace{ \begin{bmatrix} v \\ \omega \end{bmatrix}} _{p} \end{aligned}$$
(1)

The reference posture \(q_ {\textrm{r}}:=(x_{\textrm{r}},y_{\textrm{r}},\phi _{\textrm{r}})\) that the WMR is to follow is subject to

$$\begin{aligned} \begin{bmatrix} \dot{x}_{\textrm{r}} \\ \dot{y}_{\textrm{r}} \\ \dot{\phi }_{\textrm{r}} \end{bmatrix} = \begin{bmatrix} \cos (\phi _{\textrm{r}}) &{} 0 \\ \sin (\phi _{\textrm{r}}) &{} 0 \\ 0 &{} 1 \end{bmatrix} \begin{bmatrix} v_{\textrm{r}} \\ \omega _{\textrm{r}} \end{bmatrix} \end{aligned}$$
(2)

where \((v_{\textrm{r}},\omega _{\textrm{r}})=:p_{\textrm{r}}\) is a reference velocity vector.

The error posture (i.e. the tracking error with respect to the frame of the WMR defined as the Cartesian coordinate system with an origin of (x, y) and X-axis in the direction of \(\phi \)) is calculated by

$$\begin{aligned} e=\begin{bmatrix} e_{x} \\ e_{y} \\ e_{\phi } \end{bmatrix} := \begin{bmatrix} \cos (\phi ) &{} \sin (\phi ) &{} 0 \\ -\sin (\phi ) &{} \cos (\phi ) &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} (q_{\textrm{r}}-q). \end{aligned}$$
(3)

Considering Eq. 1, the dynamic behavior of Eq. 3 is represented as follows:

$$\begin{aligned} \begin{bmatrix} \dot{e}_{x} \\ \dot{e}_{y} \\ \dot{e}_{\phi } \end{bmatrix} = \begin{bmatrix} \cos (e_{\phi }) &{} 0 \\ \sin (e_{\phi }) &{} 0 \\ 0 &{} 1 \end{bmatrix} \begin{bmatrix} v_{\textrm{r}} \\ \omega _{\textrm{r}} \end{bmatrix} + \begin{bmatrix} -1 &{} e_{y} \\ 0 &{} -e_{x} \\ 0 &{} -1 \end{bmatrix} \begin{bmatrix} v \\ \omega \end{bmatrix}. \end{aligned}$$

We take p in the form of

$$\begin{aligned} p := \begin{bmatrix} v_{\textrm{r}}\cos (e_{\phi }) \\ \omega _{\textrm{r}} \end{bmatrix} +u. \end{aligned}$$
(4)

Overall, the nonlinear error-posture model of a WMR is constructed as follows:

$$\begin{aligned} \dot{e} = \begin{bmatrix} 0 &{} \omega _{\textrm{r}} &{} 0 \\ -\omega _{\textrm{r}} &{} 0 &{} \frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }} \\ 0 &{} 0 &{} 0 \end{bmatrix}e + \begin{bmatrix} -1 &{} e_{y} \\ 0 &{} -e_{x} \\ 0 &{} -1 \end{bmatrix}u. \end{aligned}$$
(5)

The four nonlinear parameters that appeared in Eq. 5 can be expressed by the following convex combinations:

$$\begin{aligned} \omega _{\textrm{r}}&= \sum _{j=1}^{2}\mu _{1}^{j}a_{1}^{j}, \quad \frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }} = \sum _{j=1}^{2}\mu _{2}^{j}a_{2}^{j} \\ e_{y}&= \sum _{j=1}^{2}\mu _{3}^{j}a_{3}^{j}, \quad e_{x} = \sum _{j=1}^{2}\mu _{4}^{j}a_{4}^{j}. \end{aligned}$$

Using the sector nonlinearity technique [5], we solve these equations to obtain:

$$\begin{aligned}&\mu _{1}^{i} = \left\{ \begin{aligned}&\frac{\omega _{\textrm{r}}-a_{1}^{2}}{a_{1}^{1}-a_{1}^{2}}, \quad \text {for}~i=1, \\&1-\mu _{1}^{1}, \quad \text {otherwise} \end{aligned} \right. \\&\mu _{2}^{i} = \left\{ \begin{aligned}&\frac{\frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }}-a_{2}^{2}}{a_{2}^{1}-a_{2}^{2}}, \quad \text {for}~i=1, \\&1-\mu _{2}^{1}, \quad \text {otherwise} \end{aligned} \right. \\&\mu _{3}^{i} = \left\{ \begin{aligned}&\frac{e_{y}-a_{3}^{2}}{a_{3}^{1}-a_{3}^{2}}, \quad \text {for}~i=1, \\&1-\mu _{3}^{1}, \quad \text {otherwise} \end{aligned} \right. \\&\mu _{4}^{i} = \left\{ \begin{aligned}&\frac{e_{x}-a_{4}^{2}}{a_{4}^{1}-a_{4}^{2}}, \quad \text {for}~i=1, \\&1-\mu _{4}^{1}, \quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

where \(a_{j}^{i}\), \((i,j)\in \mathcal {I}_{2}\times \mathcal {I}_{4}\) are determined as follows:

$$\begin{aligned}&\left. \begin{aligned}&a_{1}^{1} \geqslant \sup _{\omega _{\textrm{r}}\in [a_{1}^{1},a_{1}^{2}]}\omega _{\textrm{r}} \\&a_{1}^{2} \leqslant \inf _{\omega _{\textrm{r}}\in [a_{1}^{1},a_{1}^{2}]}\omega _{\textrm{r}} \end{aligned} \right\} \implies \mu _{1}^{i}\in \mathbb {R}_{[0,1]} \\&\left. \begin{aligned}&a_{2}^{1} \geqslant \sup _{\frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }}\in [a_{2}^{1},a_{2}^{2}]}\frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }} \\&a_{2}^{2} \leqslant \inf _{\frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }}\in [a_{2}^{1},a_{2}^{2}]}\frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }} \end{aligned} \right\} \implies \mu _{2}^{i}\in \mathbb {R}_{[0,1]} \\&\left. \begin{aligned}&a_{3}^{1} \geqslant \sup _{e_{y}\in [a_{3}^{1},a_{3}^{2}]}e_{y} \\&a_{3}^{2} \leqslant \inf _{e_{y}\in [a_{3}^{1},a_{3}^{2}]}e_{y} \end{aligned} \right\} \implies \mu _{3}^{i}\in \mathbb {R}_{[0,1]} \\&\left. \begin{aligned}&a_{4}^{1} \geqslant \sup _{e_{x}\in [a_{4}^{1},a_{4}^{2}]}e_{x} \\&a_{4}^{2} \leqslant \inf _{e_{x}\in [a_{4}^{1},a_{4}^{2}]}e_{x} \end{aligned} \right\} \implies \mu _{4}^{i}\in \mathbb {R}_{[0,1]}. \end{aligned}$$

We set \(z:=\left( \omega _{\textrm{r}},\frac{v_{\textrm{r}}\sin (e_{\phi })}{e_{\phi }},e_{y},e_{x}\right) \in \mathbb {R}^{4}\) as the premise variables for the T–S fuzzy model of Eq. 5. If the membership function \(\varGamma _{j}^{i}\) of \(z_{j}\) in the ith fuzzy inference rule is set as follows:

$$\begin{aligned}&\varGamma _{1}^{i} = \left\{ \begin{aligned}&\mu _{1}^{1}, \quad \text {for}~i=\{1,\dots ,8\} \\&\mu _{1}^{2}, \quad \text {otherwise} \end{aligned} \right. \\&\varGamma _{2}^{i} = \left\{ \begin{aligned}&\mu _{2}^{1}, \quad \text {for}~i=\{1,\dots ,4, 9,\dots ,12\} \\&\mu _{2}^{2}, \quad \text {otherwise} \end{aligned} \right. \\&\varGamma _{3}^{i} = \left\{ \begin{aligned}&\mu _{3}^{1}, \quad \text {for}~i=\{1,2,5,6,9,10,13,14\} \\&\mu _{3}^{2}, \quad \text {otherwise} \end{aligned} \right. \\&\varGamma _{4}^{i} = \left\{ \begin{aligned}&\mu _{4}^{1}, \quad \text {for}~i=\{1,3,5,7,9,11,13,15\} \\&\mu _{4}^{2}, \quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

the following state equation

$$\begin{aligned} \dot{e} = \sum _{i=1}^{16}\theta _{i}(A_{i}e+B_{i}u) \end{aligned}$$
(6)

is the modeling error-free T–S fuzzy model for Eq. 5 on the domain \([a_{1}^{1},a_{1}^{2}]\times [a_{2}^{1},a_{2}^{2}]\times [a_{3}^{1},a_{3}^{2}]\times [a_{4}^{1},a_{4}^{2}]\subset \mathbb {R}^{4}\), where

$$\begin{aligned} \theta _{i}(z) := \frac{\prod \limits _{j=1}^{4}\varGamma _{j}^{i}(z_{j})}{\sum \limits _{i=1}^{16}\Bigg (\prod \limits _{j=1}^{4}\varGamma _{j}^{i}(z_{j})\Bigg )} \end{aligned}$$

and

$$\begin{aligned} A_{i} = \begin{bmatrix} 0 &{} (2,1) &{} 0 \\ -(2,1) &{} 0 &{} (2,3) \\ 0 &{} 0 &{} 0 \end{bmatrix}, \quad B_{i} = \begin{bmatrix} -1 &{} (1,2) \\ 0 &{} (2,2) \\ 0 &{} -1 \end{bmatrix} \end{aligned}$$

where

$$\begin{aligned}&(2,1) = \left\{ \begin{aligned}&a_{1}^{1}, \quad \text {for}~i=\{1,\dots ,8\} \\&a_{1}^{2}, \quad \text {otherwise} \end{aligned} \right. \\&(2,3) = \left\{ \begin{aligned}&a_{2}^{1}, \quad \text {for}~i=\{1,\dots ,4, 9,\dots ,12\} \\&a_{2}^{2}, \quad \text {otherwise} \end{aligned} \right. \\&(1,2) = \left\{ \begin{aligned}&a_{3}^{1}, \quad \text {for}~i=\{1,2,5,6,9,10,13,14\} \\&a_{3}^{2}, \quad \text {otherwise} \end{aligned} \right. \\&(2,2) = \left\{ \begin{aligned}&a_{4}^{1}, \quad \text {for}~i=\{1,3,5,7,9,11,13,15\} \\&a_{4}^{2}, \quad \text {otherwise}. \end{aligned} \right. \end{aligned}$$

2 Robust \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) ETC Design

To strengthen the robustness to uncertainties and disturbances attenuation performance in design, we modify (6) as follows:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{e}=\sum _{i=1}^{r}\theta _{i}((A_{i}+\varDelta A_{i})e+B_{i}u+B_{w_{i}}w) \\&z=\sum _{i=1}^{r}\theta _{i}C_{z_{i}}e \end{aligned} \right. \end{aligned}$$
(7)

where \(\varDelta A_{i}\) denotes the system uncertainty and \(z\in \mathbb {R}\) is the performance output.

With a slight abuse of notation, the Lebesgue space \(\mathcal {L}_{p}^{n}[0,\infty )\) of measurable functions \(f:[0,\infty )\rightarrow \mathbb {R}^{n}\) satisfies

$$\begin{aligned} \left\| f\right\| _{\mathcal {L}_{p,r}^{n}}:=\!\left\{ \begin{aligned}&\left( \int _{0}^{\infty }\left\| f(t)\right\| _{r}^{p}\,\textrm{d}t\right) ^{1/p}<\infty \!\quad \text {for} 1\!\leqslant \! p<\infty \\&\sup _{t\in \mathbb {R}_{\geqslant 0}}\left\| f(t)\right\| _{r}<\infty \quad \text {for} p=\infty \end{aligned} \right. \end{aligned}$$

where the following conventional vector r-norm is adopted [12]:

$$\begin{aligned} \left\| f\right\| _{r}:=\left\{ \begin{aligned}&\left( \sum _{i=1}^{n}\left| f_{i}(t)\right| ^{r}\right) ^{1/r}<\infty \quad \text {for} 1\leqslant r<\infty \\&\max _{i\in \mathcal {I}_{R}}\left| f_{i}(t)\right| <\infty \quad \text {for} r=\infty . \end{aligned} \right. \end{aligned}$$

In this study, we consider a continuous-time disturbance \(w\in \mathcal {L}_{2,2}^{p}\) and a continuous-time performance output \(z\in \mathcal {L}_{\infty ,2}^{q}\) (simply denoted as \(\mathcal {L}_{2}\) and \(\mathcal {L}_{\infty }\), respectively). In addition, their norms \(\left\| w\right\| _{\mathcal {L}_{2,2}^{p}}\) and \(\left\| z\right\| _{\mathcal {L}_{\infty ,2}^{q}}\) are denoted by \(\left\| w\right\| _{2}\) and \(\left\| z\right\| _{\infty }\), respectively.

Assumption 2

There exist known compatible constant matrices D and E and an unknown time-varying diagonal matrix \(\varDelta \) satisfying \(\varDelta ^{\textrm{T}}\varDelta \preccurlyeq I, \forall t\in \mathbb {R}_{\geqslant 0}\) such that

$$\begin{aligned} \varDelta A=D\varDelta E. \end{aligned}$$

Lemma 1

([17]) Given compatible matrices D, E, \(S=S^{\textrm{T}}\), with \(\varDelta \ni \varDelta ^{\textrm{T}}\varDelta \preccurlyeq I\), there exists \(\epsilon \in \mathbb {R}_{>0}\) such that

$$\begin{aligned}&S+\textrm{He}\left\{ D\varDelta E\right\} \prec 0 \\&\iff S+ \begin{bmatrix} D&E^{\textrm{T}} \end{bmatrix} \begin{bmatrix} \epsilon ^{-1}I &{} * \\ 0 &{} \epsilon I \end{bmatrix} \begin{bmatrix} D^{\textrm{T}} \\ E \end{bmatrix} \prec 0. \end{aligned}$$

Lemma 2

([9]) Given compatible matrices D, \(Q=Q^{\textrm{T}}\succ 0\), \(S=S^{\textrm{T}}\), the following equivalence is true:

$$\begin{aligned} S+D^{\textrm{T}}QD \prec 0 \iff \begin{bmatrix} S &{} * \\ D &{} -Q^{-1} \end{bmatrix} \prec 0. \end{aligned}$$

We employ the following event-triggered aperiodic sam-pled-data controller:

$$\begin{aligned} u=u_{k}:=\sum _{i=1}^{r}\theta _{i_{k}}K_{i}e(t_{k}), \quad t\in [t_{k},t_{k+1}) \end{aligned}$$
(8)

where \(t_{k}\), \(k\in \mathbb {Z}_{\geqslant 0}\) represents the time at which the control input is updated and \(\theta _{i_{k}}:=\theta _{i}(z(t_{k}))\). The subsequent execution time \(t_{k+1}\) is determined by the following event-triggering mechanism:

$$\begin{aligned} t_{k+1}&:= \inf \Bigg \{ t\in \mathbb {R}_{\geqslant 0}:t >t_{k} \wedge \nonumber \\&\quad \sigma e^{\text {T}}Pe \leqslant 2e^{\text {T}} \Bigg ( \sum _{i,j=1}^{r}\theta _{i}\theta _{j_{k}}PB_{i}K_{j} \Bigg )\epsilon _{e} \Bigg \} \end{aligned}$$
(9)

where \(\epsilon _{e}:=e(t_{k})-e\), \(\sigma \in \mathbb {R}_{>0}\) is a given threshold, and P is a positive definite matrix.

The problem of interest is expressed as follows:

Problem 1

Find \(K_{i}\) such that the uncertain fuzzy model (7) closed by the aperiodic sampled-data controller (8) updated by the event-triggering mechanism (9) exhibits the following \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) disturbance attenuation performance

$$\begin{aligned} \left\| z\right\| _{\infty }\leqslant e^{\textrm{T}}(0)Pe(0)+\gamma \left\| w\right\| _{2} \end{aligned}$$
(10)

and is robustly asymptotically stable against the norm-bounded parametric uncertainties when \(w=0\).

The close-loop system of Eqs. 7, 8, and 9 is constructed as

$$\begin{aligned} \dot{e}= \sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}((A_{i}+\varDelta A_{i}+B_{i}K_{j})e+B_{i}K_{j}\epsilon _{e}+B_{w_{i}}w) \end{aligned}$$
(11)

for \(t\in [t_{k},t_{k+1})\). Similar to [20], we introduce the following relation about the asynchronous firing strengths

$$\begin{aligned} \theta _{i_{k}} = \rho _{i}^{k}\theta _{i}, \quad t\in [t_{k},t_{k+1}) \end{aligned}$$

and suppose the existence of \(\underline{\rho },\overline{\rho }\in \mathbb {R}_{>0}\) such that

$$\begin{aligned} \underline{\rho }:= \min \limits _{(i,k)\in \mathcal {I}_{R}\times \mathbb {Z}_{\geqslant 0}}\rho _{i}^{k}, \quad \overline{\rho }:= \max \limits _{(i,k)\in \mathcal {I}_{R}\times \mathbb {Z}_{\geqslant 0}}\rho _{i}^{k}. \end{aligned}$$
(12)

Then, it straightforwardly follows that

$$\begin{aligned} \frac{\underline{\rho }}{\overline{\rho }} \leqslant \frac{\rho _{i}^{k}}{\rho _{j}^{k}} \leqslant \frac{\overline{\rho }}{\underline{\rho }}. \end{aligned}$$

The following theorem proposes a design condition for Problem 1.

Theorem 1

Given \(\gamma \), \(\kappa _{i}\), \(\lambda \), \(\sigma \), \(\underline{\rho }\), and \(\overline{\rho }\), the uncertain fuzzy model (7) closed by the aperiodic sampled-data controller (8) updated by the event-triggering mechanism (9) (i) exhibits the \(\gamma \)-\(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) disturbance attenuation performance (10) and (ii) is implementable if there exist \(M_{i}\), \(Q=Q^{\textrm{T}}\succ 0\) such that

$$\begin{aligned}&\varXi _{ii} \prec 0, \quad i\in \mathcal {I}_{R} \end{aligned}$$
(13)
$$\begin{aligned}&\varXi _{ij}+\frac{\underline{\rho }}{\overline{\rho }}\varXi _{ji} \prec 0 \end{aligned}$$
(14)
$$\begin{aligned}&\varXi _{ij}+\frac{\overline{\rho }}{\underline{\rho }}\varXi _{ji} \prec 0, \quad (i,j)\in \mathcal {I}_{J}\times \mathcal {I}_{R} \end{aligned}$$
(15)
$$\begin{aligned}&\begin{bmatrix} Q &{} * \\ C_{z_{i}}Q &{} I \end{bmatrix} \succ 0, \quad i\in \mathcal {I}_{R} \end{aligned}$$
(16)

where

$$\begin{aligned} \varXi _{ij}:= \begin{bmatrix} \begin{pmatrix} \textrm{He}\left\{ A_{i}Q+B_{i}M_{j}\right\} \\ +(\lambda +\sigma )Q \end{pmatrix} &{} * &{} * &{} * \\ B_{w_{i}}^{\textrm{T}} &{} -\gamma ^{2}I &{} * &{} * \\ D_{i}^{\textrm{T}} &{} 0 &{} -\kappa _{i}I &{} * \\ E_{i}Q &{} 0 &{} 0 &{} -\kappa _{i}^{-1}I \end{bmatrix}. \end{aligned}$$

In this case, the gain is given by \(K_{i}=M_{i}Q^{-1}\).

Proof

(i) To prove stability, we define \(V:=e^{\textrm{T}}Pe\) with \(P=P^{\textrm{T}}\succ 0\). The time derivative of V is computed as

$$\begin{aligned} \dot{V}&= e^{\textrm{T}} \left( \textrm{He}\left\{ \sum _{i,j=1}^{r}\theta _{i}\theta _{j_{k}}P(A_{i}+\varDelta A_{i}+B_{i}K_{j})\right\} \right) e \\&\quad + 2e^{\textrm{T}} \left( \sum _{i,j=1}^{r}\theta _{i}\theta _{j_{k}}PB_{i}K_{j}\! \right) \epsilon _{e}\!+\! 2e^{\textrm{T}} \left( \sum _{i=1}^{r}\theta _{i}PB_{w_{i}}\! \right) w \end{aligned}$$

for \(t\in [t_{k},t_{k+1})\). Using Eq. 9, we can majorize

$$\begin{aligned} \dot{V}&\leqslant e^{\textrm{T}} \left( \textrm{He}\left\{ \sum _{i,j=1}^{r}\theta _{i}\theta _{j_{k}}P(A_{i}+\varDelta A_{i}+B_{i}K_{j})\right\} \right) e \\&\quad + \sigma e^{\textrm{T}}P\epsilon _{\textrm{e}} + 2e^{\textrm{T}} \left( \sum _{i=1}^{r}\theta _{i}PB_{w_{i}} \right) w \\&= \begin{bmatrix} e \\ w \end{bmatrix}^{\textrm{T}} \left( \sum _{i,j=1}^{r}\theta _{i}\theta _{j_{k}}\bar{\varXi }_{ij} \right) \begin{bmatrix} e \\ w \end{bmatrix} -\lambda V+\gamma ^{2}w^{\textrm{T}}w \\&= \begin{bmatrix} e \\ w \end{bmatrix}^{\textrm{T}} \left( \sum _{i=1}^{r}\theta _{i}\theta _{i}\rho _{i}^{k}\bar{\varXi }_{ii} +\sum _{i<j}^{r}\theta _{i}\theta _{j} \left( \rho _{j}^{k}\bar{\varXi }_{ij}+\rho _{i}^{k}\bar{\varXi }_{ji} \right) \right) \\&\quad \times \begin{bmatrix} e \\ w \end{bmatrix}-\lambda V+\gamma ^{2}w^{\textrm{T}}w \\&= \begin{bmatrix} e \\ w \end{bmatrix}^{\textrm{T}} \!\left( \sum _{i=1}^{r}\theta _{i}\theta _{i}\rho _{i}^{k}\bar{\varXi }_{ii} +\!\sum _{i<j}^{r}\theta _{i}\theta _{j}\rho _{j}^{k} \left( \bar{\varXi }_{ij}+\frac{\rho _{i}^{k}}{\rho _{j}^{k}}\bar{\varXi }_{ji} \right) \!\right) \\&\quad \times \begin{bmatrix} e \\ w \end{bmatrix} -\lambda V+\gamma ^{2}w^{\textrm{T}}w \end{aligned}$$

where

$$\begin{aligned} \bar{\varXi }_{ij} := \begin{bmatrix} \textrm{He}\left\{ P(A_{i}+\varDelta A_{i}+B_{i}K_{j})\right\} +(\sigma +\lambda )P &{} * \\ B_{w_{i}}^{\textrm{T}}P &{} -\gamma ^{2}I \end{bmatrix}. \end{aligned}$$

Define

$$\begin{aligned} \eta _{1}:= \frac{\frac{\overline{\rho }}{\underline{\rho }}-\frac{\rho _{i}^{k}}{\rho _{j}^{k}}}{\frac{\overline{\rho }}{\underline{\rho }}-\frac{\underline{\rho }}{\overline{\rho }}},\quad \eta _{2} := \frac{\frac{\rho _{i}^{k}}{\rho _{j}^{k}}-\frac{\underline{\rho }}{\overline{\rho }}}{\frac{\overline{\rho }}{\underline{\rho }}-\frac{\underline{\rho }}{\overline{\rho }}} \end{aligned}$$

where one knows that \(\eta _{1},\eta _{2}\in \mathbb {R}_{[0,1]}\) and \(\eta _{1}+\eta _{2}=1\). Applying a similarity transformation with \(\textrm{diag}(Q^{-1},I,I,I)\), Lemmas 1 and 2, and Assumption 2 to Eqs. 14 and 15 and denoting \(Q^{-1}=P\) and \(M_{i}=K_{i}Q\) results in

$$\begin{aligned}&\eta _{1}\left( \bar{\varXi }_{ij}+\frac{\underline{\rho }}{\overline{\rho }}\bar{\varXi }_{ji} \right) +\eta _{2}\left( \bar{\varXi }_{ij}+\frac{\overline{\rho }}{\underline{\rho }}\bar{\varXi }_{ji} \right) \prec 0 \\&\implies \bar{\varXi }_{ij}+\frac{\rho _{i}^{k}}{\rho _{j}^{k}}\bar{\varXi }_{ji} \prec 0. \end{aligned}$$

Similarly, it holds that Eq. 13\(\implies \bar{\varXi }_{ii}\prec 0\). As a result

$$\begin{aligned} \dot{V}< -\lambda V+\gamma ^{2}w^{\textrm{T}}w. \end{aligned}$$
(17)

By the comparison lemma, we know that

$$\begin{aligned} V < V(0)+\gamma ^{2}\int _{0}^{\infty }w^{\textrm{T}}w\,\textrm{d}\tau . \end{aligned}$$

Next, performing a similarity transformation with \(\textrm{diag}(P^{-1},\) \(I)\) and applying Lemma 2 to Eq. 16, we derive

$$\begin{aligned} \text {(16)}&\iff P -\left( \sum _{i}^{r}\theta _{i}C_{z_{i}} \right) ^{\textrm{T}} \left( \sum _{i}^{r}\theta _{i}C_{z_{i}} \right) \succ 0 \\&\iff V-z^{\textrm{T}}z > 0, \quad \forall t\in \mathbb {R}_{\geqslant 0}. \end{aligned}$$

Then, we arrive at

$$\begin{aligned} \left\| z\right\| _{\infty } = \sup _{t\in \mathbb {R}_{\geqslant 0}}\left\| z\right\|&< \sqrt{V(0)+\gamma ^{2}\int _{0}^{\infty }w^{\textrm{T}}w\,\textrm{d}\tau } \\&\leqslant \sqrt{e^{\textrm{T}}(0)Pe(0)}+\gamma \left\| w\right\| _{2}. \end{aligned}$$

When \(w=0, \forall t\in \mathbb {R}_{>0}\), Eq. 17 can be expressed as \(\dot{V}+\lambda V<0 \Longrightarrow \dot{V}<0\). Therefore, Eq. 11 is robustly asymptotically stable.

(ii) To demonstrate the implementability of Eq. 8, we investigate the existence of a nonzero lower bound of the minimum event-triggering interval in Eq. 9. Because \(e(t_{k})\) is a constant for any interval \([t_{k},t_{k+1})\), we construct

$$\begin{aligned} \dot{\epsilon }_{e}&= \dot{e}(t_{k})-\dot{e} \\&= 0-\left( \sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}((A_{i}+\varDelta A_{i})e+B_{i}K_{j}e(t_{k})+B_{w_{i}}w) \right) \\&= \sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}((A_{i}+\varDelta A_{i})\epsilon _{e}-(A_{i}+\varDelta A_{i}+B_{i}K_{j})e(t_{k}) \\&\quad -B_{w_{i}}w) \end{aligned}$$

and we derive the following differential inequality:

$$\begin{aligned} \frac{\textrm{d}\left\| \epsilon _{e}\right\| }{\textrm{d}t}&= \frac{\textrm{d} \left( \sqrt{\epsilon _{e}^{\textrm{T}}\epsilon _{e}} \right) }{\textrm{d}t} = \frac{\epsilon _{e}^{\textrm{T}}\dot{\epsilon }_{e}}{\left\| \epsilon _{e}\right\| } \\&\leqslant \left\| \frac{\textrm{d}\epsilon _{e}}{\textrm{d}t}\right\| \\&= \Bigg \Vert \sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}((A_{i}+\varDelta A_{i})\epsilon _{e} \\&\quad -(A_{i}+\varDelta A_{i}+B_{i}K_{j})e(t_{k})-B_{w_{i}}w) \Bigg \Vert \\&\leqslant \sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}\left\| A_{i}+\varDelta A_{i}\right\| \left\| \epsilon _{e}\right\| \\&\quad +\sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}\left\| (A_{i}+\varDelta A_{i}+B_{i}K_{j})\right\| \left\| e(t_{k})\right\| \\&\quad +\sum _{i=1}^{r}\theta _{i}\theta _{j_{k}}\left\| B_{w_{i}}\right\| \left\| w\right\| \\&\leqslant c_{1}\left\| \epsilon _{e}\right\| +c_{2}\left\| e\right\| +c_{3}\left\| w\right\| \end{aligned}$$

where

$$\begin{aligned} c_{1}&:= \max _{i\in \mathcal {I}_{R}} \left( \left\| A_{i}\right\| +\left\| D_{i}\right\| \left\| E_{i}\right\| \right) \\ c_{2}&:= \max _{(i,j)\in \mathcal {I}_{R}\times \mathcal {I}_{R}} \left( \left\| A_{i}\right\| +\left\| D_{i}\right\| \left\| E_{i}\right\| +\left\| B_{i}K_{j}\right\| \right) \\ c_{3}&:= \max _{i\in \mathcal {I}_{R}}\left\| B_{w_{i}}\right\| . \end{aligned}$$

Because of \(\epsilon _{e}(t_{k})=0\), the comparison lemma yields

$$\begin{aligned} \left\| \epsilon _{e}\right\| \leqslant \frac{1}{c_{1}} \left( c_{2}\left\| e\right\| +c_{3}\left\| w\right\| \right) \left( \textrm{e}^{c_{1}(t-t_{k})}-1 \right) . \end{aligned}$$

Solving the inequality, we obtain

$$\begin{aligned} t_{k+1}&> t_{k}+\frac{1}{c_{1}}\ln \left( 1+\frac{c_{1}\left\| \epsilon _{e}\right\| }{c_{2}\left\| e\right\| +c_{3}\left\| w\right\| } \right) \\&> t_{k}+\frac{1}{c_{1}}\ln \left( 1+\frac{c_{1}\left\| P\right\| \left\| e\right\| }{c_{2}\left\| e\right\| +c_{3}\left\| w\right\| } \right) \end{aligned}$$

where \(c_{1},c_{2},c_{3}\) are positively finite. Therefore, for any \(k\in \mathbb {Z}_{\geqslant 0}\), \(t_{k+1}-t_{k}>0\). This completes the proof. \(\square \)

3 A Numerical Example

The parameters for Eq. 6 are set as follows:

$$\begin{aligned} a_{1}^{1}&= 0.7, \quad a_{1}^{2} = 2.1, \quad a_{2}^{1} = 1.7, \quad a_{2}^{2} = 5.1 \\ a_{3}^{1}&= -0.2, \quad a_{3}^{2} = 0.2, \quad a_{4}^{1} = -0.2, \quad a_{4}^{2} = 0.2. \end{aligned}$$

In addition, we introduce the following uncertainty, the disturbance, and the controlled output for Eq. 7, parameterized as

$$\begin{aligned}&\varDelta A_{i} = \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0.09\delta &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix}, \quad B_{w_{i}} = \begin{bmatrix} 0.1 \\ 0.1 \\ 0.1 \end{bmatrix} \\&C_{z_{i}} = \begin{bmatrix} 0.1&0.1&0.1 \end{bmatrix} \end{aligned}$$

where \(\delta \ni \left| \delta \right| \leqslant 1\) randomly varies over time. According to Assumption 2, \(\varDelta A_{i}\) is decomposed as

$$\begin{aligned} D_{i} = \begin{bmatrix} 0 \\ 0.3 \\ 0 \end{bmatrix}, \quad \varDelta _{i} = \delta , \quad E_{i} = \begin{bmatrix} 0.03&0&0 \end{bmatrix}. \end{aligned}$$
Fig. 2
figure 2

Time responses of the closed-loop error posture of the WMR

Full size image
Fig. 3
figure 3

Energy-to-peak disturbance attenuation performance: \(\sqrt{e^{\textrm{T}}(0)Pe(0)}+\gamma \left\| w\right\| _{2}\) (dashed (red)) and \(\left\| z\right\| _{\infty }\) (solid (blue))

Full size image
Fig. 4
figure 4

Time responses of firing strengths: \(\theta _{i}\) (dashed-red), \([\underline{\rho }\theta _{i},\overline{\rho }\theta _{i}]\) (filled-light red), \(\theta _{k_{i}}\) (solid-blue)

Full size image

For Problem 1, the following \(\mathcal {L}_{2}\) disturbance

$$\begin{aligned} w = \left\{ \begin{aligned}&0.2\sin (5t), \quad \text {for}~0.5 \leqslant t \leqslant 2.5 \\ {}&0, \quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

is considered.

Let \(\gamma = 0.5\), \(\kappa _{i}=0.1\), \(\lambda = 0.05\), \(\sigma = 0.05\), \(\underline{\rho }=0.4\), and \(\overline{\rho }=2\). The following controller gains are obtained through Theorem 1

$$\begin{aligned} K_{1}&= \begin{bmatrix} 0.3504 &{} -0.3492 &{} -8.3397 \\ 0.0213 &{} 0.3603 &{} 9.0552 \end{bmatrix} \\ K_{2}&= \begin{bmatrix} 0.3667 &{} -0.4126 &{} -10.3738 \\ 0.0491 &{} 0.4022 &{} 9.5734 \end{bmatrix} \\ K_{3}&= \begin{bmatrix} 0.3741 &{} -0.3005 &{} -7.0670 \\ 0.0248 &{} 0.3988 &{} 10.1102 \end{bmatrix} \\ K_{4}&= \begin{bmatrix} 0.3729 &{} -0.2095 &{} -5.1207 \\ -0.0117 &{} 0.4600 &{} 10.7983 \end{bmatrix} \\ K_{5}&= \begin{bmatrix} 0.3929 &{} -0.4072 &{} -9.7786 \\ 0.0286 &{} 0.4743 &{} 11.4819 \end{bmatrix} \\ K_{6}&= \begin{bmatrix} 0.4193 &{} -0.5125 &{} -12.9243 \\ 0.0735 &{} 0.5254 &{} 12.4182 \end{bmatrix} \\ K_{7}&= \begin{bmatrix} 0.4241 &{} -0.3340 &{} -7.8688 \\ 0.0239 &{} 0.5425 &{} 13.3227 \end{bmatrix} \\ K_{8}&= \begin{bmatrix}0.4232 &{} -0.1951 &{} -4.6053 \\ -0.0333 &{} 0.6183 &{} 14.5886 \end{bmatrix} \\ K_{9}&= \begin{bmatrix}0.5294 &{} -0.5946 &{} -14.2628 \\ 0.0564 &{} 0.6087 &{} 15.7089 \end{bmatrix} \\ K_{10}&= \begin{bmatrix} 0.5808 &{} -0.7989 &{} -20.0466 \\ 0.1388 &{} 0.6732 &{} 17.1337 \end{bmatrix} \\ K_{11}&= \begin{bmatrix} 0.5989 &{} -0.5320 &{} -12.5214 \\ 0.0629 &{} 0.7208 &{} 18.7482 \end{bmatrix} \\ K_{12}&= \begin{bmatrix} 0.6021 &{} -0.2888 &{} -6.6145 \\ -0.0411 &{} 0.8237 &{} 20.6653 \end{bmatrix} \\ K_{13}&= \begin{bmatrix} 0.6701 &{} -0.7829 &{} -18.9559 \\ 0.0874 &{} 0.9009 &{} 22.9529 \end{bmatrix} \\ K_{14}&= \begin{bmatrix} 0.7650 &{} -1.1476 &{} -28.9424 \\ 0.2326 &{} 1.0011 &{} 25.6495 \end{bmatrix} \\ K_{15}&= \begin{bmatrix} 0.7873 &{} -0.6738 &{} -15.9035 \\ 0.0731 &{} 1.1158 &{} 28.6405 \end{bmatrix} \\ K_{16}&= \begin{bmatrix} 0.8039 &{} -0.2641 &{} -5.4255 \\ -0.1122 &{} 1.3003 &{} 32.7024 \end{bmatrix}. \end{aligned}$$
Fig. 5
figure 5

Event-triggered aperiodic sampled-data control inputs

Full size image

(i) Reference velocities are set as

$$\begin{aligned} \begin{bmatrix} v_{\textrm{r}} \\ \omega _{\textrm{r}} \end{bmatrix} = \begin{bmatrix} 5(1-0.5\textrm{e}^{-0.1t}) \\ 2(1-0.5\textrm{e}^{-0.1t}) \end{bmatrix} \end{aligned}$$

to generate the reference trajectory (dash-red) for Eq. 2 with \(q_{\textrm{r}}(0)=(5,0,0)\) shown in the lower-right subfigure of Fig. 2. It is also shown that the controlled trajectory (solid-blue) with \(q(0)=(5.1.0.1,0)\) is accurately directed to the reference trajectory. The other subfigures in Fig. 2 depict the closed-loop time responses of Eqs. 5, 8, 9, where all the error posture variables are well bounded in the presence of the \(\mathcal {L}_{2}\) disturbance and parametric uncertainties. As shown in Fig. 3, \(\left\| z\right\| _{\infty }\) is smaller than \(\sqrt{e^{\textrm{T}}(0)Pe(0)}+\gamma \left\| w\right\| _{2}\) for all \(t_{f}\in \mathbb {R}_{\geqslant 0}\), implying the proposed controller satisfies the \(\mathcal {L}_{2}\)–\(\mathcal {L}_{\infty }\) disturbance attenuation performance in Eq. 10 over the entire simulation time horizon. It is visible from Fig. 4 that every \(\theta _{i_{k}}\) (solid-blue) is present between the interval \([\underline{\rho }\theta _{i},\overline{\rho }\theta _{i}]\) (filled-light red). Hence, Eq. 12 holds.

Fig. 6
figure 6

Event-triggering instants and intervals

Full size image

(ii) Figure 5 illustrates the ETC inputs for Eq. 8, where the control inputs are piecewise-constant but their time intervals are uneven. Figure 6 depicts the event-triggering interval versus the event-triggering instant. The discrete-time signal does not converge to zero, indicating that the proposed controller operates well in a sampled-data manner without the Zeno behavior affecting the sampling process. Thus, the proposed controller is implementable. In summary, Problem 1 is solved.

4 Conclusions

Leveraging the T–S fuzzy technique, this paper tackled the sampled-data nonlinear tracking control problem in WMRs. It is stressed that (i) the energy-to-peak disturbance attenuation was taken into consideration; and (ii) the ETC technique was adopted to overcome the unavailability of the exact discrete-time model of a WMR dynamics. The numerical example demonstrated the efficacy of the proposed method, highlighting its potential to enhance the performance of autonomous agricultural vehicles and contributing valuable insights to the field of agroforestry automation.