Introduction

The elastic constants of unidirectional composites are essential material properties in composite laminate analysis. These properties can be determined either experimentally or numerically. With regard to experimental approaches, many experimental standards have been developed to apply loads and to properly measure the elastic constants of fiber composites [1]. Furthermore, with regard to numerical approaches, micromechanical models have been developed to describe the mechanical properties of fiber composites in terms of the ingredient properties and fiber volume fractions [2, 3]. The simplified micromechanical model is the rule of mixture [4], according to which the properties of composites are expressed in a simple formula. Subsequently, more generalized micromechanical models that account for the dimensions and shapes of fibers have been proposed [5, 6]. Notably, in the aforementioned models, the effects of the fiber arrays were not taken into account. The high-fidelity generalized method of cells (HFGMC) model [7, 8], which can calculate the effective constants of the repeating unit cell (RUC) modestly based on the fiber deployment, was adopted in this study. In the HFGMC analysis, the RUC of unidirectional composites was selected and divided into many subcells, each of which represents either the fiber phase or the matrix phase. The complex microstructures of fiber composites can be characterized by the subcells. From the HFGMC analysis, data sets relating the microstructure images to the effective constants of the fiber composites can be easily generated. In addition to the micromechanical analysis, with developments in artificial intelligence, the mechanical properties of composites can be predicted using machine learning [9, 10]. Rao and Liu [11] used a three-dimensional (3D) convolutional neural network (CNN) model (3D-CNN) to predict the elastic constants of particulate composites with random inclusions. The results indicated that a CNN model trained using a data set of 2000 entries generated from finite element analysis reproduced the effective properties of composites with high accuracy. Yang et al. [12] used a 3D-CNN to characterize the elastic constant of composites with high-contrast ingredient properties. The results showed that the effective stiffness of the composites as predicted using the trained CNN is highly accurate. Chen et al. [13] used finite-volume direct averaging micromechanics [14, 15] to generate the input data sets used for training the CNN model. The thermal expansion coefficients and elastic moduli of graphite/epoxy and glass/epoxy composites predicted using the trained CNN model coincided with the theoretical values obtained from finite-volume micromechanics. Ye et al. [16] used a deep neutral network to predict the mechanical properties of composites with complex microstructures. The CNN model trained using the data sets generated by the finite element method can accurately predict the properties of composites with complex inclusions. Nevertheless, the data set generated by the finite element method is a time consuming task. In light of the above-described investigations, the training data sets used for machine learning have been typically obtained using finite element analysis but rarely obtained using the semi-analytical micromechanical model. In our study, the relationship between the microstructure images of fiber arrays and the mechanical properties of fiber composites were generated using the HFGMC model. The data sets were then used to train the CNN model. The mechanical properties predicted using the trained CNN model were compared with those obtained directly from HFGMC analysis.

Methodology

HFGMC Micromechanical Model

Unidirectional composites are heterogeneous materials consisting of a fiber and a matrix, the morphology and properties of which are distinct. Through the micromechanical analysis, the effective material properties of the unidirectional composites can be evaluated in consideration of the ingredient properties, fiber volume fractions, and microstructural pattern. The microstructural image of the fiber composites was characterized using the RUC with a periodic boundary condition. In this study, the HFGMC micromechanical model proposed by Paley and Aboudi [8] was used to model the behaviors of unidirectional composites. In the HFGMC analysis, the RUC of fiber composites was divided into \(N_{\alpha } \times N_{\beta } \times N_{\gamma }\) subcells, as shown in Fig. 1(a). The dimension of each subcell denoted by (\(\alpha ,\beta ,\gamma\)) was defined as \(d_{\alpha } \times h_{\beta } \times l_{\gamma }\), and the local coordinate (\(\overline{y}_{1}^{(\alpha )} ,\overline{y}_{2}^{(\beta )} ,\overline{y}_{3}^{(\gamma )}\)) was set at the center of the subcell, as shown in Fig. 1(b). Based on the displacement continuity and averaged stress continuity at the interface of adjacent subcells in conjunction with the periodicity condition of the RUC, the relation between the overall strain of the RUC and the subcell strain is expressed as [17]

$$\left\{ \varepsilon \right\}^{(\alpha \beta \gamma )} = \left[ {A^{*} } \right]^{(\alpha \beta \gamma )} \left\{ {\overline{\varepsilon }} \right\}$$
(1)

where \(\left\{ \varepsilon \right\}_{{}}^{{\left( {\alpha \beta \gamma } \right)}} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{11}^{{\left( {\alpha \beta \gamma } \right)}} } \\ {\varepsilon_{22}^{{\left( {\alpha \beta \gamma } \right)}} } \\ {\varepsilon_{33}^{{\left( {\alpha \beta \gamma } \right)}} } \\ {2\varepsilon_{23}^{{\left( {\alpha \beta \gamma } \right)}} } \\ {2\varepsilon_{31}^{{\left( {\alpha \beta \gamma } \right)}} } \\ {2\varepsilon_{12}^{{\left( {\alpha \beta \gamma } \right)}} } \\ \end{array} } \right\}\) indicates the strain components of the subcell \({(}\alpha ,\beta {,}\gamma {)}\),

Fig. 1
figure 1

a Repeating unit cell (RUC) divided into \(N_{\alpha } \times N_{\beta } \times N_{\gamma }\) subcells. b Dimensions and local coordinates of the subcell

Full size image

\(\left\{ {\overline{\varepsilon }} \right\} = \left\{ {\begin{array}{*{20}c} {\overline{\varepsilon }_{11} } \\ {\overline{\varepsilon }_{22} } \\ {\overline{\varepsilon }_{33} } \\ {2\overline{\varepsilon }_{23} } \\ {2\overline{\varepsilon }_{13} } \\ {2\overline{\varepsilon }_{12} } \\ \end{array} } \right\}\) indicates the effective strain components of RUC, and \(\left[ {A^{*} } \right]^{(\alpha \beta \gamma )}\) is the strain concentration tensor [18]. In addition, the effective stress of the RUC was derived by averaging the stress components within the RUC as

$$\left\{ {\overline{\sigma }} \right\} = \frac{1}{dhl}\sum\limits_{\alpha = 1}^{{N_{\alpha } }} {\sum\limits_{\beta = 1}^{{N_{\beta } }} {\sum\limits_{\gamma = 1}^{{N_{\gamma } }} {d_{\alpha } h_{\beta } l_{\gamma } \left\{ \sigma \right\}_{{}}^{{\left( {\alpha \beta \gamma } \right)}} } } }$$
(2)

where \(\left\{ {\overline{\sigma }} \right\}\) is the effective stress of the RUC and \(\left\{ \sigma \right\}^{(\alpha \beta \gamma )}\), the stress state in subcell \({(}\alpha ,\beta {,}\gamma {)}\). Furthermore, d, h, and l are the dimensions of the RUC. For each subcell, the constitutive relation is expressed as

$$\left\{ \sigma \right\}^{(\alpha \beta \gamma )} = \left[ C \right]^{(\alpha \beta \gamma )} \left\{ \varepsilon \right\}^{(\alpha \beta \gamma )}$$
(3)

where \(\left[ C \right]^{(\alpha \beta \gamma )}\) is the stiffness matrix for the subcell (\(\alpha ,\beta ,\gamma\)). Substituting Eqs. (1) and (2) into Eq. (3) gives the effective stress and effective strain relation of the RUC as

$$\left\{ {\overline{\sigma }} \right\} = \frac{1}{dhl}\sum\limits_{\alpha = 1}^{{N_{\alpha } }} {\sum\limits_{\beta = 1}^{{N_{\beta } }} {\sum\limits_{\gamma = 1}^{{N_{\gamma } }} {d_{\alpha } h_{\beta } l_{\gamma } \left[ C \right]_{{}}^{{\left( {\alpha \beta \gamma } \right)}} } } } \left[ {A^{*} } \right]_{{}}^{{\left( {\alpha \beta \gamma } \right)}} \left\{ {\overline{\varepsilon }} \right\}$$
(4)

and the stiffness of matrix \(\left[ {\overline{C}} \right]\) of the RUC as

$$\left[ {\overline{C}} \right] = \frac{1}{dhl}\sum\limits_{\alpha = 1}^{{N_{\alpha } }} {\sum\limits_{\beta = 1}^{{N_{\beta } }} {\sum\limits_{\gamma = 1}^{{N_{\gamma } }} {d_{\alpha } h_{\beta } l_{\gamma } \left[ C \right]_{{}}^{{\left( {\alpha \beta \gamma } \right)}} } } } \left[ {A^{*} } \right]_{{}}^{{\left( {\alpha \beta \gamma } \right)}}$$
(5)

As a result, with Eq. (5), the effective constants of the RUC can be evaluated from the ingredient properties \(\left[ C \right]^{(\alpha \beta \gamma )}\) and microstructural configurations \(d_{\alpha } ,h_{\beta } ,l_{\gamma }\).

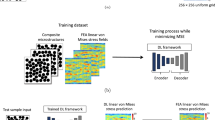
In the HFGMC micromechanical analysis, Young’s modulus and Poisson’s ratio of the fiber were assumed to be 240 GPa and 0.3, respectively. By contrast, for the matrix material, Young’s modulus and Poisson’s ratio were 4 GPa and 0.3, respectively. To generate a data set that is sufficiently large for training and validation, we performed 1000 micromechanical analyses of the fiber composites with fiber volume fractions of 10%–75%. In this analysis, the fibers were assumed to deploy randomly within the matrix, and the morphology of the microstructures for the fiber composites was generated using MATLAB commercial code with a random number. In the HFGMC method, the displacement field in each subcell was expressed by Legendre polynomial. The displacement in each subcell must satisfy displacement continuity and averaged stress continuity at the interface of adjacent subcells as well as periodic boundary condition. The properties of the ingredients, the array of the fiber and microstructural configurations were the input in the analysis. We developed our MATLAB code to solve the groups of systems of equations to obtain the displacement field in each subcell and calculated the relation between the overall strain of the RUC and the subcell strain. The effective properties of the composites were then evaluated from Eq. (5). Figure 2(a) shows the cross section of the fiber composites created with a fiber volume of 10%, where black and white regions respectively indicate the fiber and the matrix. The fiber is aligned in the x3 direction, and x1 and x2 denote the lateral directions of the fiber composite. For each microstructural image of the cross section, the effective material constants of the fiber composites were calculated using HFGMC. In other words, 1000 micromechanical images were generated, and each one correlated to a set of effective material constants. Notably, in the machine learning process, 90% of the data set was used for model training and the remaining 10% was used for model validation.

Fig. 2
figure 2

a Illustration of a microstructural image of fiber composites. b CNN process

Full size image

Machine Learning Approach

Based on the data sets generated from the HFGMC, the CNN model was trained [19, 20]. The distributions of the fibers and the matrix was represented by a 65 × 65 matrix in which the special positions of the fibers and matrix were marked specifically, as shown in Fig. 2a. It is noted that the microstructural images of the fiber were assumed to be invariant along the fiber direction, and thus, the 2D image was employed to represent the microstructures of the long fiber composites. The 65 × 65 matrix served as an input for the convolutional layer and was then convolved by 64 filters. The size of the filter is 3 × 3, and the stride is equal to 1. Subsequently, the output feature map resulting from the convolutional layer was passed through a 2 × 2 MaxPooling filter with a stride of 2 to reduce the size of the feature map. The same process was repeated two times, after which one convolutional layer with 64 filters was applied. The feature map output from the third convolutional layer became a one-dimensional feature vector. This feature vector was then input to the fully connected layer. The fully connected layer contained two layers, one with 50 neurons and the other with 6 neurons. The dropout rate was set to 0% in both layers. The six neurons in the second fully connected layer correspond to the six mechanical properties of the unidirectional composites. In addition, a ReLU function was used as the activation function in both the convolutional layer and the fully connected layer [21]. The CNN model was trained with 60 repeated epochs first, and the predictions based on the trained CNN model were then validated. The prediction error E between the predicted values from the trained CNN and the values directly calculated from HFGMC (10% data) was calculated as [22]

$$E = \frac{100\% }{n}\sum\limits_{i = 1}^{n} {\frac{{\left| {y_{i} - \hat{y}_{i} } \right|}}{{y_{i} }}}$$
(6)

where n is the total number of samples; yi, the value of the ith sample obtained using HFGMC; and \(\hat{y}_{i}\), the corresponding ith value predicted using the CNN. Figure 2b shows the complete CNN process.

Results and Discussion

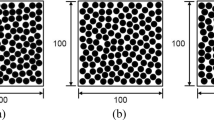
Figure 3 shows the validation of the trained CNN model. The orthotropic material constants for the unidirectional composites—E11, E22, E33, G13, G23, and G12—were considered in the analysis. The frequency distribution associated with the prediction error shown in Fig. 3 indicates the percentage of occurrence of that error in our analysis. The results indicate that the material constants obtained using the trained CNN model are quite close to those calculated directly using HFGMC. In addition, although the maximum prediction error was 6%, most CNN model predictions were within 2%. Subsequently, we predicted the elastic constants of the fiber composites with the randomly generated microstructure. The fiber volume fractions are 15%, 30%, 55%, 65% and 70%, respectively, and the corresponding microstructural images are shown in Fig. 4. The material constants of the unidirectional composites derived using the trained CNN model and the HFGMC model are listed respectively from Tables 1, 2, 3, 4, and 5. Young’s moduli and shear moduli obtained from the two models were very similar, with a maximum error of 3%. Thus, the trained CNN model could be used to predict the elastic constants of the fiber composites with different volume fractions. In addition, three microstructural images with different fiber distributions as shown in Fig. 5 were taken into account. The fiber volume fractions for the microstructure are all 15%. It is noted that the fiber distributions were generated randomly in corresponding to the engineering implication of the fiber composites. The model predictions as listed in Tables 6, 7, and 8 are also close to the results obtained from HFGMC micromechanical analysis. It can be seen that when the fibers are distributed randomly, the elastic constants of the fiber composites are not dramatically affected by the fiber distribution. Furthermore, the computing time to solve each microstructural image using HFGMC model is 30 min with Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz. With the same hardware resources, it takes 3 s to solve the same problem using CNN model. If many microstructural images need to be solved, CNN model would be more efficient than the HFGMC model.

Fig. 3
figure 3figure 3

Validation and prediction error of the CNN model: a E11, b E22, c E33, d G13, e G23, and f G12

Full size image
Fig. 4
figure 4

Microstructural image of fiber composites with different fiber volume fractions a 15% b 30% c 55% d 65% e 70%

Full size image
Table 1 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 15%
Full size table
Table 2 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 30%
Full size table
Table 3 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 55%
Full size table
Table 4 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 65%
Full size table
Table 5 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 70%
Full size table
Fig. 5
figure 5

Microstructural image of fiber composites with three different fiber distributions a Model 1 b Model 2 c Model 3

Full size image
Table 6 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 15% (Model 1)
Full size table
Table 7 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 15% (Model 2)
Full size table
Table 8 Comparison of CNN model and HFGMC for composites with a fiber volume fraction of 15% (Model 3)
Full size table

Conclusion

The elastic constants of unidirectional composites with different fiber volume fractions were predicted using the trained CNN model. For model training and validation, 1000 data sets generated using HFGMC micromechanical analysis were used. The validation revealed that most differences between the CNN prediction and the HFGMC results were less than 2%. Furthermore, we randomly generated the microstructures of unidirectional composites with fiber volume fractions from 15 to 70%, and compared the results predicted using the trained CNN model and the HFGMC micromechanical analysis. The maximum errors were within 3%, indicating that the machine learning approach could accurately characterize the elastic properties of the unidirectional composites with both accuracy and efficiency.