Introduction

Long fiber composites are widely used in industry, but it takes a lot of time and cost to obtain the mechanical properties through experiments and simulation. Therefore, building a neural network model has become a new trend to predict the mechanical properties of fiber composites using artificial intelligence. For example, the artificial neural network (ANN) [1] is a computing model that mimics the neurons of the human brain. It can fit the neural network model parameters through input numerical information to establish nonlinear function approximation of input and output and achieve optimal estimation. Kim et al. [2] generated long fiber models with fixed fiber quantities using the random sequential expansion (RSE) method [3], and produced the models with different fiber volume fraction by changing the fiber radius. They solved the equivalent modulus of the composites through ABAQUS commercial software with periodic boundary conditions [4, 5]. Subsequently, they used the fiber centroid co-ordinates and volume percentage as input and the equivalent modulus as output to establish the ANN neural network. They also compared the effect of database size on prediction accuracy. Results showed that the prediction error was mostly less than 1%, and the correlation coefficient was above 0.96 [6]. Moreover, the accuracy of the model increased with larger database training. Although the ANN neural network model can accurately predict the equivalent modulus of composite materials, when the fiber quantity in the fiber model changes, the input values and neuron quantities may not match, leading to model failure. The convolutional neural network (CNN) [7, 8] can analyze input images without this limitation. Therefore, Chen et al. [9] used glass and graphite fibers as reinforcing materials in composite materials, and used a two-dimensional convolutional neural network to analyze the equivalent modulus of randomly distributed long fiber composite materials. They predicted the Young's modulus, shear modulus, Poisson's ratio, and thermal expansion coefficient in three directions by analyzing the fiber distribution position in the cross-sectional shape. The results showed that regardless of the fiber type, the median absolute prediction error was about 2%. In addition to predicting the equivalent modulus of composite materials, convolutional neural networks are also suitable for other engineering applications. Kim et al. [10] generated unidirectional fiber models with the consideration of fiber matrix interfacial debonding and simulated the stress–strain curve of transverse tensile test using finite element method. They divided the stress–strain curve equally into 40 parts based on strain values and used corresponding stress values as target values. They input the fiber cross-sectional shape into the convolutional neural network (CNN) to predict the stress at each strain. Sorini et al. [11] developed a long fiber model with variable fiber and matrix material properties. They used the high-fidelity generalized method of cells (HFGMC) [12] micromechanical analysis of the composite material's equivalent stiffness matrix as the target value, while with fiber cross-sectional images as input and the convolutional neural network was used to predict the equivalent stiffness matrix values. The results showed that most predicted values were close to the label values, but the analysis time was 25,000 times faster, indicating that neural networks can significantly reduce the time cost of numerical analysis.

Although neural network models can quickly and accurately obtain the mechanical properties of materials, generating sufficient training data often requires a significant time cost. Therefore, transfer learning methods, which involve training a pre-trained neural network model with additional databases, were developed to improve the accuracy of neural networks. Shin et al. [13] used image recognition convolutional neural networks as an example to explore how to enhance the accuracy of neural networks through different methods, including transfer learning. By fine-tuning the parameters in the neural network through transfer learning, and comparing the prediction errors of different neural network models, it was found that the transfer learning neural network model had better prediction performance than the original model, demonstrating that transfer learning can enhance the prediction ability of neural network models. Jung et al. [14] calculated the stress–strain curves of particle and short fiber composite materials under axial tension and cyclic loading, and used material properties and stress–strain curves as inputs and outputs for training deep neural network models. They also built a transfer learning database through the finite element method, and fine-tuned the parameters of the pre-trained neural network model with a small amount of data. The results showed that the deep neural network model fine-tuned through the transfer learning database had a coefficient of determination [15] increased from 0.9744 to 0.9966, indicating that the transfer learning model had better prediction ability.

In this study, the CNN model was trained by the dataset generated from the finite element method and then modified by the transfer learning dataset. The microstructural images directly obtained from experiment and literatures were used to validate the trained CNN model. The accuracy of the CNN model after the transfer learning process was discussed.

CNN Model

Generate Dataset for CNN Model

In order to generate a database for the CNN model, we created the fiber composites master models at first. The master models were generated by setting a 100-unit square model and randomly filling it with fibers with a diameter of 7.5 units until no new fibers could be placed within the model range. In addition, contact between fibers or with the frame was avoided in the master model. Three sets of main models are shown in Fig. 1, each with a side length of 100 units and containing 137, 133, and 127 fibers with different distributions, with volume percentages of 60.5%, 58.7%, and 56.5%, respectively. To increase model diversity, each set of main models was mirrored and flipped in three directions, as shown in Fig. 2. Taking the 90° mirror image as an example, the x-co-ordinate of the fiber center is obtained through a formula to obtain the new fiber center x-co-ordinate, while the y-co-ordinate remains unchanged, forming the new center co-ordinates, which is the 90° mirror image fiber model. The 0° and 45° mirror images are obtained in the same way to allow fibers to appear at different positions within the model range and to avoid the time and cost required to re-design the main models. Random fiber removal was then performed using 10 different random seeds, by assigning numbers to the fibers in the model and removing them in different order. The matrix was utilized to fill the gaps created by the removed fibers. A total of 35 fibers were removed, resulting in 36 different models with different fiber volume fractions and distributions, as shown in Fig. 3. Through this method, a total of 4320 microstructural models of fiber composites was generated for the database, with fiber volume percentages ranging from 41 to 60.5%.

Fig. 1
figure 1

Three master microstructures a Vf = 60.5%, b Vf = 58.7%, c Vf = 56.5

Full size image
Fig. 2
figure 2

Four sub-microstructures were generated from the master microstructure through mirror image process

Full size image
Fig. 3
figure 3

The fibers were removed from the sub-microstructure gradually based on random seed process

Full size image

Subsequently, a fiber structure matrix was generated through image pre-processing to present the cross-sectional structure of the fiber model and serve as input for the neural network model. The fiber cross-section image with extension of image JPG was imported into Python 3.8.8. At this time, the image is a three-color image (RGB figure) with a size of 560 × 560 pixels, as shown in Fig. 4a. The color of each pixel cell in the image was represented by three colors: red, green, and blue, and the color intensity is represented by values ranging from 0 to 255. Afterwards, the image was converted to a grayscale image using grayscale conversion [16], as shown in Eq. (1):

$${\text{I}}_{{\text{y}}} = 0.333{\text{F}}_{{\text{r}}} + 0.5{\text{F}}_{{\text{g}}} + 0.1666{\text{F}}_{{\text{b}}}$$
(1)

where, Iy represents the grayscale value, Fr, Fg, and Fb represent the intensity of red, green, and blue, respectively. At this time, the pixel cells in the image were presented by grayscale values ranging from 0 to 255. The matrix material is white with a grayscale value of 255, while the fiber is black with a grayscale value of 0. The pixel cells at the interface between the fiber and matrix will appear as gray with varying depths depending on the ratio of the fiber and matrix. The grayscale values range from 1 to 254 to define the boundary position of the fiber. The binary images of the microstructures were created through the binarization thresholding process [17] with the proper threshold value. By changing the proper threshold value, the proportion of fiber in the binary image output can be made to approach the volume percentage of the fiber composite model. The threshold value was set to 200 as the boundary standard and the result is shown in Fig. 4b. Then, the image size was unified to a matrix of 200 × 200 through the nearest interpolation [18] to fit the neural network input size. Subsequently, the Min–max normalization [19] was used to normalize the fiber pixel cells to 0 and the matrix pixel cells to 1 to avoid a large difference between the matrix values and the equivalent modulus values, which can make it difficult for the neural network to converge, while reducing the required resources and training time. Finally, the fiber structure was stored as a matrix form for the database.

Fig. 4
figure 4

The image of the microstructure a before binarization, b after binarization

Full size image

Finite Element Analysis

The equivalent properties for the aforementioned microstructures were calculated through finite element analysis. The fiber centroid co-ordinates were entered into the ANSYS (2016 version) numerical software to construct a finite element RUC model. By utilizing periodic boundary conditions, the three corresponding periodic surfaces of the model exhibited the same local strain field. Assuming that the RUC model has n nodes on the periodic surface with the normal vector x1, the relative displacement of all nodes on surfaces + 1 and − 1 can be expressed as [4, 5]

$${}^{{\left( { + 1} \right)}}{\text{u}}_{{\text{i}}}^{{\left( {\text{n}} \right)}} - {}^{{\left( { + 1} \right)}}{\text{u}}_{{\text{i}}}^{{\left( {1} \right)}} = {}^{{\left( { - 1} \right)}}{\text{u}}_{{\text{i}}}^{{\left( {\text{n}} \right)}} - {}^{{\left( { - 1} \right)}}{\text{u}}_{{\text{i}}}^{{\left( {1} \right)}}$$
(2)

where \({}^{{\left( { + {1}} \right)}}\text{u}_{i}^{\left( \text{n} \right)}\) represents the global displacement vector of node n on the periodic surface + 1, while \({}^{{\left( { - 1} \right)}}\text{u}_{i}^{\left( \text{n} \right)}\) represents the global displacement vector of node n on the periodic surface − 1. Similarly, the same formula can be derived for the other two sets of periodic surfaces. The FEM model assumes isotropic materials with a fiber Young's modulus of 240 GPa and a Poisson's ratio of 0.3, and a matrix Young's modulus of 4 GPa and a Poisson's ratio of 0.3. The model uses SOLID187 elements, which are 10-node tetrahedral elements with degrees of freedom in the x, y, and z directions. A finite element model with dimensions of 2 × 100 × 100 is constructed, and a cylinder with a diameter of 7.5 units and a length of 2 units is generated at the fiber centroid co-ordinates to represent the fiber within the composites model.

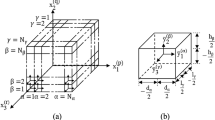
To calculate the equivalent Young's modulus E1, we considered a cube model with edge length a, where the displacement is applied in the x1 direction. The loading is applied as shown in Fig. 5 where the line segment that intersects the x1 = 0 plane and the x2 = a plane was constrained in the x1 direction. The line segment that intersects the x1 = 0 plane and the x2 = 0 plane was constrained in both the x1 and x2 directions, and the origin was constrained in the x1, x2, and x3 directions. Two line segments intersecting the x1 = a plane and the x2 = 0 plane, as well as the x1 = a plane and the x2 = a plane, were given displacement in the x1 direction. The formula for the equivalent Young's modulus is evaluated as follows:

$${\text{E}} = \frac{{\sum {{\text{V}}_{{{\text{element}}}} \times \upsigma_{{{\text{element}}}} } }}{{\sum {{\text{V}}_{{{\text{element}}}} \times \varepsilon_{{{\text{element}}}} } }} = \frac{{\upsigma_{{{\text{model}}}} }}{{\varepsilon_{{{\text{model}}}} }}$$
(3)

where \(\text{V}_\text{element}\) represents the element volume, \(\upsigma_\text{element}\) represents the normal stress on the element, \(\varepsilon_\text{element}\) represents the normal strain on the element, \(\upsigma_{\text{model}}\) represents the normal stress on the model, and \(\varepsilon_{\text{model}}\) represents the normal strain on the model. The similar procedure was employed for the equivalent moduli E2 and E3. For the equivalent shear modulus G12, we take the x2 = a as the shear plane. The loading is set up as shown in Fig. 6, where the x1 direction on the intersection line of x1 = 0 and x2 = a is constrained, while both x1 and x2 directions are constrained on the intersection line of x1 = 0 and x2 = 0. The origin (x1 = x2 = x3 = 0) is constrained in all three directions. Two lines on the intersection of x1 = a and x2 = 0 and x1 = a and x2 = a are given displacement in the x2 direction. The equation for the equivalent shear modulus G is shown below:

$${\text{G}} = \frac{{\sum {{\text{V}}_{{{\text{element}}}} \times \tau_{{{\text{element}}}} } }}{{\sum {{\text{V}}_{{{\text{element}}}} \times \gamma_{{{\text{element}}}} } }} = \frac{{\tau_{{{\text{model}}}} }}{{\gamma_{{{\text{model}}}} }}$$
(4)

where \(\uptau_\text{element}\) is the shear stress of the element, \(\gamma_\text{element}\) is the shear strain of the element, \(\uptau_\text{model}\) is the shear stress of the model, and \(\upgamma_\text{model}\) is the shear strain of the model. We applied the similar procedure to calculate the equivalent shear moduli G13 and G23. The obtained values of the equivalent modulus were employed as the output dataset for training the neural network.

Fig. 5
figure 5

Boundary condition for the calculation of Young’s moduli in FEM analysis

Full size image
Fig. 6
figure 6

Boundary condition for the calculation of shear moduli in FEM analysis

Full size image

Training and Validation of CNN model

When the database design was completed, we began to construct the neural network model. During the training phase, 90% of the database, a total of 3888 sets, were used as training data. The neural network model CNN has a structure as shown in Fig. 7, consisting of three convolutional layers, each with 32 3 × 3 filters with a stride of 1. Padding was set to maintain the same size of input images and output feature maps, and rectified linear units (ReLU) [20, 21] were used as activation functions for the model. A pooling layer (MaxPooling) [22] was added after the first and second convolutional layers to reduce the dimensionality of the output feature maps. A filter size of 2 × 2 was used, and the stride was set to 2. The output data from the third convolutional layer was flattened to form a one-dimensional feature map, which was then inputted into the fully connected layer. The first fully connected layer had 50 neurons to receive the feature vector outputted from the front end, and the second layer had 6 neurons corresponding to the 6 equivalent modulus values. The dropout rate [23] was set to 0. The mean absolute error (MAE) [24] was used as the loss function, and the optimizer used was the Adam gradient descent method [25] with a learning rate decay [26]. The initial learning rate was set to 0.001, and if the training error did not decrease after three epochs, the learning rate was reduced by half. The minimum learning rate was set to 10–5. Finally, hyper-parameters for the neural network were optimized, with a batch size of 30. The data was shuffled and regrouped when entering the next epoch, and a total of 80 training epochs were used. The training was conducted on a computer with an Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz, and the training time was 93 min.

Fig. 7
figure 7

The structure of CNN model

Full size image

During the validation phase, 10% of the validation data is fed into the trained neural network model, and the difference between the label values and predicted values were calculated using the mean absolute percentage error (MAPE) [27]. The comparison of label and predicted values and the error frequency are shown in Fig. 8a–c. It can be seen that the average error is within 0.4%. For shear moduli, the label and predicted values are shown in Fig. 8d–f and the average error is around 0.42%. Thus, the results validate the applicability of the trained CNN model for the predictions of the fiber composites.

Fig. 8
figure 8

Validation of CNN model and prediction error frequency for a E11, b E22, c E33, d G12, e G13, f G23

Full size image

Testing the Microstructures from Experiments

Subsequently, two sets of cross-sectional images of long-fiber composite materials were obtained through journals and optical microscopy (OM) as test data. The two sets are Microstructure-1 [28] and Microstructure-2, as shown in Fig. 9 respectively. The label values of these images were calculated through finite element method. In addition, the fiber structure matrices were generated through image preprocessing and were then used as input to the convolutional neural network for prediction. The accuracy of the neural network predictions was then compared with the label values to explore its predictive ability. Table 1 shows the MAPE error between the label values and predicted values for the selected microstructures. The average prediction error for Microstructure-1 was 3.53%, while that for Microstructure-2 was 3.32%. The results indicate that the convolutional neural network model can still maintain a certain degree of predictive ability.

Fig. 9
figure 9

Microstructural images obtained from a literature [25] (microstructure-1), b experiment (microstructure-2)

Full size image
Table 1 Comparison of CNN model to the label values for unidirectional composites with two different microstructures
Full size table

In order to enhance the accuracy of the model prediction, we adopted the transfer learning technique in the CNN model. Transfer learning is a method of retraining a pre-trained neural network model using a small dataset. This approach involves fine-tuning the parameters within the pre-trained neural network to increase its generalizability, reduce prediction errors, address difficulties in collecting large datasets, and shorten the overall training time required for the network.

In this study, a transfer learning database was created by generating random distribution long fiber RUC models using Material Designer. Material parameters were set to be the same as before, and a single-direction long fiber model was used as the reference, with a fiber diameter of 7.5 units, an inclination angle of 0°, a model cross-section of 100 × 100 units, and a default thickness value. When the volume percentage exceeded 40%, the model was prone to meshing failures due to fiber proximity, so models with 64 and 81 fibers were designed, with volume percentages of 28.24% and 35.74%, respectively. fifty different models were generated for each. Tetrahedral 10-node elements with x, y, and z degrees of freedom were used, and periodic boundary conditions were applied to obtain label numerical values. The fiber structure matrix was then generated using image preprocessing. The Material Designer output model image was first cropped using Python to produce a 412 × 412 pixel RGB image. It was then converted to a gray level image with values ranging from 0 to 255. The gray value of the base material in the image was 213. All pixel values with a gray value of 213 were set to 0, while the remaining pixel values were set to 1, marking the positions of the base material and fibers in the model to form a fiber structure matrix. A transfer learning database consisting of 100 sets of data was then created.

The hyper-parameters and parameters in the trained binary neural network model were loaded into Python as the source model. The training hyper-parameter settings were kept the same as the original model, except for batch size and epoch. The transfer learning database was then inputted into the source model for transfer training, with a batch size of 25 and 150 epochs. Fine-tuning was performed on the weights and biases of the neural network model's fully connected layer using the transfer learning database, allowing the transfer learning model to learn the structural characteristics of the fiber models in the transfer learning database. The training time using a computer with the same configuration was approximately 8 min.

Results and Discussion

By using the two microstructure models mentioned above, a transfer learning model (CNN-T) was tested to explore its predictive accuracy. Table 2 shows the MAPE error between the label values and predicted values for both models. The average test error for microstructure-1 was 3.25%, while the average prediction error for microstructure-2 was 2.44%. These results indicate that the transfer learning model has lower prediction errors than the original model for both microstructure models, demonstrating that transfer learning can effectively enhance the predictive accuracy of neural network models for microstructure models and can be applied in practical engineering applications. It is noted that the equivalent moduli of fiber composites could be estimated by simple area proportion method, so called rule of mixture. The method only considers the volume fraction of the fibers instead of the distribution of the fibers. We calculated E11, E22 and G12 for the microstructures 1 and 2, respectively. For the microstructure 1, the calculated values are E11 = 114.81 GPa, E22 = 8.16 GPa and G12 = 2.86 GPa; for the microstructure 2, the corresponding values are E11 = 112.18 GPa, E22 = 7.97 GPa and G12 = 2.5 GPa. As compared to the data shown in Table 2, it can be seen that the results obtained from the rule of mixture, except the value of E11, deviate from FEM (label) solutions and the CNN predictions. Thus, the neural network model illustrates the advantage for characterizing the mechanical properties of the fiber composites with accuracy, especially in the transverse and shearing directions.

Table 2 Comparison of transfer learning CNN model (CNN-T) to the label values for unidirectional composites with two different microstructures
Full size table

Conclusion

The average prediction errors of the convolutional neural network (CNN) for the two microstructure models were 3.53% and 3.32%, respectively, while those of the transfer learning model (CNN-T) were 3.25% and 2.44%. It can be observed that the transfer learning model had lower prediction errors than the CNN, indicating that it can effectively learn the relationship between the fiber model features and the equivalent modulus in the new database. This enables the transfer learning model to make more accurate predictions for the microstructure models, making it suitable for engineering applications.