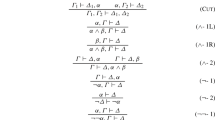On quantum implication

Abstract

Logic is an algebraic structure that defines a set of abstract rules which govern an area of interest. The abstraction property of the rules makes them reusable tools to model different problems and to reason with them. The proliferation of quantum theory brought attention to quantum logic which is a lattice of projectors and it is of importance to quantum computing. Unfortunately, basic tools like implication are not sufficiently studied in that logic, which prevents us from exploiting the power of quantum mechanics in reasoning. This note investigates the implication issue in quantum logic and defines a quantum implication operator for compatible events as well as for incompatible events. The suggested operator depends both on the angle between the vector sub-spaces of the involved events and the angles between the system state and the vector sub-spaces. It differentiates between three cases depending on the angle between the events’ sub-spaces. The article further shows through an example that some classical reasoning rules such as Modus Ponens and Modus Tollens hold given the suggested implication.

1 Introduction

The emergence of Quantum Theory (QM) is promising a new era of computing. So researchers in computer science in general and in database and information retrieval, in particular, are seeking to use quantum formalism to build new and more effective information processing systems (Schmitt 2008).

Relational database systems are the most common database systems. Their query language which is known as SQL (Structured Query Language) is founded on relational algebra and first order (predicate) logic. Predicate logic builds on classical logic which is linked to classical mechanics (Heelan 1970). Now, one open question in information technology is how to use Quantum Logic (QL), the logic that is based on quantum theory, to build information processing systems that enable us to represent data and reason new facts out of them.

In their seminal paper, Birkoff and Von Neumann have introduced quantum logic as a lattice of projectors (Birkhoff and Neumann 1936). Later many algebraic structures were considered as quantum logic but none of them provides a solid basis for a logical system that can be used for reasoning; because those logics still have problems with the basic reasoning tools like implication. Although there are five QL implication operators in the literature, none of them addressed the difference between compatible and incompatible events (Dalla Chiara et al. 2013) (Megill and Pavičić 2003).

The contributions of this article are threefold. First, it shows the limitations of available implication operators that prevent us from using them as QL implication operators due to the special properties of QL. Second, It defines a quantum implication that can be used for compatible as well as for incompatible events. Third, it shows, by an example, how the new operator preserves some of the classical reasoning rules for the compatible case.

The roadmap of this paper is as follows. Section 2 presents an overview of the probability theory and QM. Next, Section 3 introduces quantum logic. After that, the different types of implications are listed along with some criticism in Section 4. Then, a quantum implication operator is introduced in Section 5. Finally, we conclude in Section 6 by indicating directions for future research.

2 Background

In order to make the paper self-contained and reachable to a wide audience, this section provides a quick reminder of probability theory and quantum mechanics. If you are familiar with these concepts, feel free to skip or skim through this section.

2.1 Probability theory

This subsection provides a quick and detailed overview of the probability theory showing its relation to the measure theory (the theory which studies measures). After that, it recalls the different types of events, probability distributions and finishes by introducing the copula concept.

Probability theory is the science behind randomness. The sample space Ω is the set of all possible outcomes of a random experiment. An event A is a subset of the sample space i.e. A ⊆Ω and it occurs when the outcome ω of the experiment belongs to it ω ∈ A. An algebra F is a collection of subsets of Ω that includes the empty set ϕ and is closed under complement (if A ∈ F, then ∼A ∈ F) and finite unions (if A₁,A₂,...A_n ∈ F then $\cup _{i=1}^{n} A_{i} \in F$). If F is also closed under countable unions (if A₁,A₂.... ∈ F then $\cup _{i=1}^{\infty } A_{i}{\in }F$) then we call it σ-Algebra, the subsets of F are called F-measurable sets and (Ω,F) is a measurable-space. A measure is a function μ that maps F-measurable sets to the interval [0,∞[ and satisfies the countable additive axiom ($P({\cup _{i}^{n}} E_{i})={\sum }_{i=1}^{n} P(E_{i})$ where E_i are n disjoint events) and μ(ϕ) = 0. If the measure μ satisfies μ(Ω) = 1 then it is called a probability measure and denoted by P, the space (Ω,F,P) is a probability space and the F-measurable sets are events. Depending on that probability theory is a special case of measure theory that works on a σ-Algebra defined over Ω (Ross 2006).

Since events are subsets of Ω, we can distinguish between different types of them based on the relation between their corresponding subsets as depicted in Fig. 1. Mutual exclusive events do not occur simultaneously and are represented by disjoint subsets like A and B whose intersection is Φ so P(A ∩ B) = 0. In contrast, non-mutual exclusive events are represented by overlapping sets like C and D. The union’s probability of two independent events is defined as:

$$ P(X\cup Y) = P(X) + P(Y) - P(X\cap Y) $$

(1)

Independent events have no effect on each other’s probability of occurrence like tossing a coin and rolling a dice. The joint probability of such events is defined as

$$ P(X\cap Y)=P(X)*P(Y) $$

(2)

Dependent events affect the probabilities of each other like in the experiment of drawing two cards from a deck. The first card will affect the probability of the second. The last type of events is the subsumed events, like E and F, is the essence of material implication (E→ F) in classical logic.

Fig. 1

Relation types of two events

In classical probability, there are three different types of multivariate probability distributions. First, the marginal probability of an event Q is the probability that Q occurs regardless of the results of other experiments. Second, the joint probability of two events Q and R is the probability of their intersection. Third, the conditional probability is the measure of the probability that an event Q will occur given that another event R occurred. It is defined when (P(R)≠ 0) as

$$ P(Q|R) = \frac{P(Q\cap R)}{P(R)} $$

(3)

Copula is the last concept that we want to mention here. It is a function C from I² to I (I = [0,1]) that couples multivariate distribution functions to their one-dimensional marginal distribution functions (Nelsen 2007). It has the following properties:

• 1. For every u,v in I, C(u,0) = 0 = C(0,v) , C(u,1) = u and C(1,v) = v

• 2. For every u₁,u₂,v₁,v₂ in I such that u₁ ≤ u₂ and v₁ ≤ v₂,

  $$ C(u_{2},v_{2})-C(u_{2},v_{1})-C(u_{1},v_{2})+C(u_{1},v_{1})\geq 0 $$

Copula provides a way to study scale-free measures of independence and allow the construction of bivariate distributions (Nelsen 2007). It was proven by Sklar’s theory that a copula could be found to map any two marginal probabilities to their joint probabilities (Grzegorzewski 2013). There are many families of copulas such as Gaussian’s family and Archimedean’s family.

2.2 Quantum mechanics

This subsection introduces the basic ingredients of quantum mechanics. We start by defining QM. Then, we present Dirac’s notation before we list the quantum postulates. Finally, we show how probabilities are used in QM.

Quantum Mechanic is an inherently probabilistic and contextual theory that works at the microscopic level (Bub 2016). Its mathematical framework is a complex separable vector space equipped with inner product called Hilbert space. In Hilbert space, vectors and vector sub-spaces are the basic tools to deal with; that is why a neat way was needed to express such notions. Dirac or Bra(c)ket notation came as a solution to this issue (Ross 2006) which is as follows:

• A column vector $\left (\begin {array}{l}1\\0 \end {array}\right )$ is represented by the ket |0〉, while its complex transpose (10) is expressed by the bra 〈0|.

• The inner product between two vectors x and y is a scalar and is denoted by 〈x|y〉 whereas the result of their outer product is a matrix and delineated as |x〉〈y|.

• The tensor product is a method to form large matrices out of smaller ones. For more information on this topic readers can refer to Nielsen and Chuang (2002) and Svozil (1998).

The connection between the quantum mathematical formalism and the physical world is the following four postulates:

• 1. State space: An isolated physical system is represented by a separable Hilbert space called the state space. The state vector is just a unit vector in the state space that provides a full description of the system.

• 2. Evolution: An isolated quantum system evolves according to a unitary transformation U which preserves the norm of the state vector ∥U|ψ〉∥ = ∥|ψ^′〉∥ where |ψ〉 and |ψ^′〉 are the state vector before and after evolution respectively.

• 3. Measurement: Let Q be a closed quantum system in state ψ. there is a Hermitian operator O_i, here we use projectors, for each possible outcome i of measuring the system. These operators work on the state space of Q to calculate the probability of an outcome i as follows

  $$ p(i) = \langle{\psi}|O_{i}^{\dagger} O_{i}|{\psi}\rangle $$

  (4)

  where $O_{i}^{\dag }$ is the complex transpose of O_i. This measurement results also in changing the state of the system and the post-measurement state as

  $$ \frac{O_{i} |{\psi}\rangle}{\sqrt{|{\psi}\langle O_{i}^{\dagger} O_{i}|{\psi}\rangle}} $$

  (5)

  Since measurement results are probabilities and due to the completeness relation of the Hermitian operators (${\sum }_{i} O_{i}^{\dagger } O_{i} = I$), we get

  $$\sum\limits_{i}p(i)=\sum\limits_{i}{\langle{\psi}| O_{i}^{\dagger} O_{i}|{\psi}\rangle} = 1$$

• 4. Composite Systems: The tensor product is used to assemble different quantum systems into a larger one. The state of the generated system is the tensor product of its generating systems.

Quantum theory brought with it some new terms and phenomena that were not known before like Entanglement, Incompatibility, Entwinement and Contextuality. Next, we clarify those concepts.

Entanglement is a non-classical correlation between two particles (Bub 2016). An entangled state is the result from composing two systems using the tensor product and then applying some rotation. The resulting composite state can not be expressed as a product of two states of the involved systems. For example, let us have the entangled state $|{\psi }\rangle = \frac {1}{\sqrt {2}}|{00}\rangle + \frac {1}{\sqrt {2}}|{11}\rangle$. When we try to decompose it to a product of two states, we will get something like (α₀|0〉 + α₁|1〉)(β₀|0〉 + β₁|1〉)) after multiplication we get (α₀β₀|00〉 + α₀β₁|01〉 + α₁β₀|10〉 + α₁β₁|11〉 to get the entangled state we have to solve the following equations:

$$ \begin{array}{@{}rcl@{}} \alpha_{0}\beta_{0}&=&\frac{1}{\sqrt{2}}\\ \alpha_{0}\beta_{1}&=&0\\ \alpha_{1}\beta_{0}&=&0\\ \alpha_{1}\beta_{1}&=&\frac{1}{\sqrt{2}} \end{array} $$

which is impossible.

In quantum, we can distinguish between two types of observables (physical quantities). Those are compatible and incompatible observables which are represented by Hermitian operators (projectors) (Nielsen and Chuang 2002). Compatible observables can be measured simultaneously while incompatible ones cannot because they are represented using different bases of the vector space. That is why sometimes they are being referred to as simultaneously and non-simultaneously decidable observables respectively (Bub 2016). Two observables A and B are incompatible when their corresponding projectors do not commute, i.e. (P_AP_B≠P_BP_A). That occurs when the enclosed angle between their corresponding vector sub-spaces is acute. The speed and momentum of a particle is a famous example of incompatible observables.

Entwinement refers to the meshing of compatible and incompatible observables. Two observables are said to be entwined if they have a basis vector in common as depicted in the Fig. 2. A direct result of entwinement is contextuality. Contextuality means that observables do not have definite values before they are measured and their assigned values vary according to the context. The Kochen-Specker theorem states that observables of a qutrit system or higher are contextual due to Entwinement (Bub 2016; Peres 1991).

Fig. 2

Entwinement

Now we state how probabilities are used within the quantum formalism. Figure 3 displays a qubit system in state |ψ〉. The probability of getting |0〉 is b² which is the square length of the projection of the state vector |ψ〉 on |0〉. Since a and b are the two right sides of a right triangle, then Pythagoras’ theory comes into play (i.e. a² + b² = 1). Before we close, we should mention that the same probability values can be obtained by taking squared cosine of the minimum angle between the state vector and the measured subspace in this case cos2(σ) = b².

Fig. 3

Quantum probabilities

3 Quantum logic

This section presents the algebraic foundations of quantum logic along with its connection to some other logics. Then, it discusses quantum logic as it was introduced by its founders.

Let us have a set of elements B and a binary ordering relation ≤ between its elements. The structure (B,≤) is called a poset (partially ordered set) when the ordering relation satisfies the reflexive, transitive and anti-symmetry properties (Dalla Chiara et al. 2013). A lattice (B,≤,∧,∨) is a poset supplied with a meet ∧ and join ∨ operations. A lattice forms the mathematical foundation for any bivalent logic. A lattice with fuzzy negation forms a fuzzy logic that in turn forms a logic when it satisfies the law of non-contradiction (a ∧∼a = 0) (de Vries 2007). Boolean logic is a logic in which the distributive law a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) and the double negation law a = ∼∼a hold. Quantum logic is a logic that satisfies the orthomodularity (ifa ≤ c, then a ∨ (∼ a ∧ c) = c (Birkhoff and Neumann 1936).

Birkhoff and Von Neuman introduced quantum logic based on the lattice (P,⊆,∧,∨) of all closed sub-spaces P (projectors) of a Hilbert space greater than two dimensions (Birkhoff and Neumann 1936). The negation operator is defined as ∼p = I − p. The meet of two sub-spaces, as in the boolean logic, is their intersection; while the join of two sub-spaces is the closure of their union. In other words, the join contains the two involved sub-spaces along with any linear combination of them.

Boolean logic is a special case of quantum logic because orthomodularity is a weak form of distributivity (Dalla Chiara et al. 2013). The reason behind the failure of distributive law in quantum logic is the way in which the join operation was defined. In quantum join operation, it is possible for a vector neither to belong to a subspace P nor to a subspace Q but it could belong to their union (P ∨ Q).

4 Literature review and criticism

This section starts by showing the difference between absolute and approximate reasoning. Then, it presents the different types of implications that are available in the literature along with their limitations from the viewpoint of QL.

Absolute reasoning derives absolute conclusions out of absolute premises, whereas approximate reasoning works on uncertain premises to find uncertain conclusions. The word absolute refers to boolean values, while the word approximate refers to uncertain values where the uncertainty could be modelled by fuzzy (membership) values or probability values (Grzegorzewski 2013). In approximate reasoning, neither completeness nor soundness, in their classical sense, are guaranteed due to uncertainty (Garson 2013). The goal of approximate reasoning is to make the benefits overcome the losses incurred by the process. For example in web search, there is a trade-off between quick and accurate responses (Rudolph et al. 2008).

The implication operator I(A,B), in general, is a logical relation between two propositions A and B where the second is considered as a conclusion of the first. In the literature, we can find many implication operators and the following paragraphs outline them and discuss their feasibility to be used as quantum implications.

In classical logic, we can distinguish between two absolute implication operators those are material implication and strict implication. Material implication is constructed based on subsumed events. It is defined as (A → B ≡∼A ∨ B) and is pronounced (IF A then B). The truth values of this implication is shown in Table 1. As we can see from the table, it is evaluated based on the boolean truth values of the involved propositions but not on their meanings. For example the implication “snow is green → fishes can fly” is evaluated as true even though there is no relationship between the premise and conclusion. C.I. Lewis realized this problem and introduced the strict implication which takes the semantics of the propositions into account (Garson 2013). The strict implication uses the necessity modal operator and possible worlds to avoid the material implication problem. It is denoted by (A ≺ B ≡∼ ♢(A∧∼ B)) and interpreted as (it is not possible that A is true and B is false). The main difference between those two implications is that material implication works at the object level because it considers the truth values of two sentences in one fixed model, while the strict implication works at the meta level since it considers the truth values in all possible models.

Table 1 Material implication

The importance of implication stems from the fact that it can be used to define reasoning rules. For example, the classical reasoning rules Modus Ponens (MP) and Modus Tollens (MT) are defined based on material implication as shown in Table 2. The problem with absolute operators, like material and strict implications, is that they work only with two truth values (T and F), so they fail to address the superposition principle which is one of the corner stones of QM. In addition to that, strict implication uses the necessity operator which is not available in QL.

Table 2 Classical inference rules

A second type of implication operators is the fuzzy implication. It is an approximate implication and is used in fuzzy logic. It is defined in Baczyński and Jayaram (2008) as follows:

A function I : [0,1]² → [0,1] is a fuzzy implication if it satisfies the following conditions:

(I1):

If x₁ ≤ x₂ then I(x₁,y) ≥ I(x₂,y)

(I2):

If y₁ ≤ y₂ then I(x,y₁) ≤ I(x,y₂)

(I3):

I(0,0) = 1

(I4):

I(1,1) = 1

(I5):

I(1,0) = 0

for all x,x₁,x₂,y,y₁,y₂ ∈ [0,1].

From the definition, we can see that a fuzzy implication is a generalization of material implication that works on the interval [0,1]. It also satisfies the properties of left antitonicity (I1) and right isotonicity (I2). In the literature (Mas et al. 2007; Oh and Bandler 1987), there are many fuzzy operators like Standard sharp, Lukasiewicz, Gaines 43, and Willmott. The limitation of this type of operators is that fuzzy logic works on fuzzy sets and membership values and obeys neither the law of contradiction nor orthomodularity (de Vries 2007). As a result, the fuzzy implications cannot be used in the quantum logic which obeys these rules.

A third type of implication operators, known as Probabilistic Implications (PI), is a binary function I_C : [0,1]² → [0,1] defined as

$$ I_{C}(u,v) = \left\{\begin{array}{lr} 1 & \text{if } u=0\\ \frac{C(u,v)}{u} & \text{if } u>0, \end{array}\right. $$

(6)

where C is a copula, u,v are probabilities of two events Y and X respectively, and I_C is a probabilistic implication based on copula C.

It was shown in Grzegorzewski (2013) that the probabilistic implication is the natural counter part of the conditional probability. There are many probabilistic implications due to the abundance of copula functions. The problem with these operators is that they do not take into consideration the peculiarities of QL. For example, let I_C be an PI operator based on the product copula, then the truth value of the implication (A → B) will be calculated by multiplying the probabilities of both A and B whether the involved events are compatible or incompatible.

Finally, The founders of quantum logic have already used the concept of subsumed events to define quantum implication using the containment between vector sub-spaces (Birkhoff and Neumann 1936). But since their operator is an absolute one, it fails to address the superposition principle and it is not suitable for incompatible events.

H. Reichenbach managed to account for the superposition principle by using three-valued logic; he suggested three quantum implication operators those are standard implication, alternative implication and quasi implication (Reichenbach 1998). But he did not integrate them into the quantum formalism which leaves them as a mere philosophical view. In addition, the existence of three operators leaves us with the question “Which one should we use?”.

Later Jauch defined implication as the partial ordering relation in the lattice (Jauch 1968). But Zeman objected on this definition because it results in violation of the metalanguage/object language distinction (Zeman et al. 1979). Before we close, we should mention that there are five implications in an orthomodular lattice (quantum lattice) (Megill and Pavičić 2003). Here there are:

• 1. $a\rightarrow _{1} b^{\underset {=}{\text {def}}}\sim a \cup (a\cap b)$ (Sasaki)

• 2. $a\rightarrow _{2} b^{\underset {=}{\text {def}}} b \cup (\sim a \cap \sim b)$ (Dischkant)

• 3. $a\rightarrow _{3} b^{\underset {=}{\text {def}}} ((\sim a \cap b) \cup (\sim a \cap \sim b)) \cup (a \cap (\sim a \cup b))$ (Kalmbach)

• 4. $a\rightarrow _{4} b^{\underset {=}{\text {def}}} ((a\cap b) \cup (\sim a \cap b)) \cup ((\sim a \cup b)\cap \sim b)$ (non-tollens)

• 5. $a\rightarrow _{5} b^{\underset {=}{\text {def}}} ((a\cap b)\cup (\sim a \cap b))\cup (\sim a \cap \sim b)$ (relevance)

As we can see from the definitions, they do not take into consideration the difference between compatible and incompatible events. The above discussion leads us to the conclusion that we need to define new implication operator that accounts for the various properties of quantum logic which is the topic of the next section.

5 Quantum implication and inference

This section is the key section whose goal is to define a quantum implication operator. It starts by clarifying the special properties of quantum logic, then it suggests a quantum implication operator and put it into action by an example.

As in the case of classical reasoning, quantum reasoning needs an implication operator to be used as the basis for its deduction rules. To define such operator, we need to understand the peculiarities of quantum logic. These peculiarities come from its underlying quantum theory. The following list contains the main concepts that distinguish quantum logic from others.

• 1. Quantum theory is probabilistic because the outcome of a quantum measurement is a probability.

• 2. QM is contextual meaning that observables take different values depending on the context. The context is the set of commuting observables one is trying to measure.

• 3. Incompatible observables, which are incomeasurable, raises a real challenge in quantum logic. If observables cannot be measured simultaneously, then some of the classical rules of logic, like distributivity, and probability rules like, total probability, do not apply to them. That is because incompatible observables are represented by different bases of the vector space.

• 4. There is a dependence relation between all quantum events. This is a direct result of the measurement postulate which states that measurements change the state of the system; so the occurrence of one event has an effect on the probability of subsequent events.

• 5. Entwinement is a special relationship between compatible and incompatible events and should be considered by the implication.

It should be mentioned that compatible events form a boolean logic. For this reason, quantum logic is considered as a collection of boolean logics each of which is defined by a set of compatible events (Bub 2016).

Based on the above discussion, we define quantum reasoning as follows:

Definition 1

Quantum reasoning is a kind of approximate reasoning that builds on quantum logic where the imprecision is modeled by quantum probabilities.

In the following, P_A is a projector that defines the vector subspace corresponding to event A. Since there is a one-to-one correspondence between projectors and closed sub-spaces (Dalla Chiara et al. 2013), we will use P_A to represent both of them, for simplicity, and the meaning will be clear from the context.

In addition, the truth value of a quantum event A will be denoted by QLV(A) which stands for Quantum Logical Valuation. QLV(A) is the squared length of the projection of a unit state vector |ψ〉 onto its subspace P_A. This squared length varies between zero and one, depending on the smallest angle between |ψ〉 and P_A. To facilitate things, we will discriminate between three truth values. Two certain truth values T:= 1 and F:= 0 where T means |ψ〉∈ P_A and F means |ψ〉∈ P_∼A. This is equivalent to what we have in the boolean logic. The third truth value is the uncertain value U which means the system state vector is in a superposition with P_A. In other words, the minimum angle θ between |ψ〉 and P_A is in the range ]0,90[. As a result, the QLV(A) is a probabilistic value in the interval ]0,1[ which is symbolized by U. The following definition summaries these states:

$$ QLV(A) = \left\{\begin{array}{lr} T & \text{if } \theta = 0\\ F & \text{if } \theta =90\\ U & \text{if } 0<\theta<90 \end{array}\right. $$

(7)

where θ is the angle between the system state and P_A.

In the previous section, we have shown that the containment relation between vector sub-spaces is used to define quantum implication for compatible events since they constitute a boolean algebra (Schmitt 2008). That is an event A implies B if their corresponding vector sub-spaces satisfy the condition (P_A ⊆ P_B). This requires that the dimension of the vector subspace corresponding to A is less than or equal to that of B i.e.; dim(P_A) ≤ dim(P_B). Since the containment between two vector sub-spaces is equivalent to saying that the confined angle between them is zero; And to make the implication operator usable for incompatible events, we are going to define the implication between two events A and B based on two factors. The first of which is the confined angle between their corresponding sub-spaces which we will denote by ϕ. Because when the event A occurs the system state will change to be in P_A according to the measurement postulate. For a discussion on how to calculate this angle, the reader can refer to Gunawan et al. (2005). The second factor is the minimum angle between the system state |ψ〉 and the sub-spaces P_A and P_B which we will denote by θ₁ and θ₂ respectively. These two angles determine the probabilistic truth values of the events A and B. But some truth combination of A and B are not possible for a certain angle ϕ. Based on that, the Quantum Logical Valuation (QLV) of the implication between A and B is defined as QLV (A → B) = y ∗ x where y = cos2ϕ; and x is the answer to the question “Is the truth combination of A and B possible?” It takes a binary value as follows:

$$ x = \left\{\begin{array}{lr} 1 & \text{if } QLV(A) \text{ and } QLV(B) \text{ are possible together}\\ 0 & \text{otherwise } \end{array}\right. $$

(8)

With this being said, we can differentiate between three cases depending on the angle ϕ:

• 1. ϕ = 0

  This means that the vector subspace P_A is contained in P_B, since dim(P_A) ≤ dim(P_B) and the events A and B are subsumed and compatible events. This is how the material implication was defined between classical events and it was also adopted by the founders of quantum logic. Here the angle ϕ plays no role because y = cos2ϕ = 1. The implication evaluation becomes QLV (A → B) = x which depends only on the angles θ₁ and θ₂ as will be shown shortly.

  Given the three truth values (T, F, and U), we have nine possibilities. To discuss them, let us have the system in Fig. 4 where event A is represented by the subspace defined by projector P_A = |A〉〈A| and event B by subspace defined by projector P_B = P_A ∨ P_C. The angles θ₁,θ₂ are the angles between the system state |ψ〉 and the sub-spaces P_A,P_B respectively. Events A and B are subsumed events and the angle ϕ between their sub-spaces is zero so the implication A → B is interpreted like “Is the truth combination of A and B possible?” The answer to this question is either yes (T) or no (F) and we will get this answer using the truth values of A and B. The following list discusses all possible cases:

  • (a) θ₁ = 90 and θ₂ = 90

    |ψ〉 is orthogonal to both P_A and P_B and the length of projecting |ψ〉 on both of them is zero. That corresponds to having QLV(A) = F and QLV(B) = F. This case occur when |ψ〉 = |D〉 and the implication is true i.e. QLV(A → B) = T.

  • (b) θ₁ = 90 and θ₂ = 0

    This means that |ψ〉⊥ P_A and |ψ〉∈ P_B. Expressed in QLV terms, QLV(A)= F and QLV(B)= T. This occur when |ψ〉 = |C〉 and QLV(A → B) = T.

  • (c) θ₁ = 90 and θ₂ ∈]0,90[

    Here we have QLV(A) = F and QLV(B) ∈ U. This is possible when ∃Events X,Y ;P_X ⊥ P_A,P_X ∧ P_B = P_Y and the angle between |ψ〉 and P_Y is a non-zero acute angle (i.e. 0 < θ < 90). For example, this occurs when |ψ〉 = |s〉 and QLV(A → B) = T.

  • (d) θ₁ = 0 and θ₂ = 90

    The angles indicate that |ψ〉∈ P_A and |ψ〉⊥ P_B. In QLV terms, we write QLV(A) = T and QLV(B) = F. This is impossible when A and B are subsumed so QLV(A → B) = F.

  • (e) θ₁ = 0 and θ₂ = 0

    According to the angles, |ψ〉 belongs to both sub-spaces so QLV(A)= T and QLV(B)= T. This is possible when |ψ〉 = |A〉 and the QLV(A → B) = T.

  • (f) θ₁ = 0 and θ₂ ∈]0,90[

    From the angles, we get QLV(A)= T and QLV(B) ∈ U. This case happens when there is a non-zero acute angle between P_A and P_B which is impossible when A and B are subsumed as a result QLV(A → B) = F.

  • (g) θ₁ ∈]0,90[ and θ₂ = 90

    Again from the angles, QLV(A) ∈ U and QLV(B) = F. This occurs when |ψ〉⊥ P_B and at the same time holds an acute angle with P_A. This case is also impossible when P_A ⊆ P_B and QLV(A → B) = F.

  • (h) θ₁ ∈]0,90[ and θ₂ = 0

    In QLV terms, we get QLV(A) ∈ U and QLV(B) = T. This occurs when |ψ〉∈ P_B but not in P_A. The implication is true and QLV(A → B) = T.

  • (i) θ₁ ∈]0,90[ and θ₂ ∈]0,90[

    QLV(A) ∈ U and QLV(B) ∈ U. This is possible, for example, when |ψ〉 = |f〉 So QLV(A → B) = T.

  These cases are summarized in Table 3. As we can see, Table 1 is included in Table 3. We also notice that the truth value of the implication between two A and B can be decided based on the truth values of the involved events as follows:

  $$ \begin{array}{@{}rcl@{}} &&QLV(A\rightarrow B) \\ &=& \left\{\begin{array}{lr} T & \text{if } QLV(A)\leq QLV(B)\\ F & \text{if } QLV(A) > QLV(B) \end{array}\right. \text{where } F<U<T\\ \end{array} $$

  (9)

• 2. ϕ = 90

  This means that A and B are compatible but mutually exclusive events. In other words, when A is true, B is false and vice verse. So it is impossible to have the case F → F as true which can be seen as a solution to the material implication problem that annoyed C.I. Lewis and was mentioned in Section 4. Since y = cos2ϕ = 0, the implication as we have defined it is always false and we do not need to discuss the possible cases.

• 3. ϕ ∈]0,90[

  This means that events A and B are incompatible. As a result, the implication between them is always not certain. Putting it another way, the truth value of the implication cannot be T or F instead it is always U. So we will express the logical values using the squared cosine of the angles. Figure 5 will be used to discuss the possible cases as follows:

  • (a) θ₁ = 90 and θ₂ = 90

    This case is possible when the system state is in the subspace P_C and the evaluation of the events is QLV(A) = QLV(B) = cos290 = 0. Since the case is possible then x = 1 and QLV (A → B) = cos²ϕ

  • (b) θ₁ = 90 and θ₂ = 0

    Depending on the angles, QLV(A) = 0 and QLV(B) = 1. Such a case is only possible between compatible events which means x = 0 and QLV (A → B) = 0

  • (c) θ₁ = 90 and θ₂ ∈]0,90[

    Here we have QLV(A) = cos290 = 0 and QLV(B)= cos2θ₂. This is possible when the system state is in the subspace corresponding to the projector P_D so x = 1 and QLV (A → B) = cos2ϕ = cos2(90 − θ₂).

  • (d) θ₁ = 0 and θ₂ = 90

    It is impossible to have such case between incompatible events so x = 0 and QLV (A → B) = 0.

  • (e) θ₁ = 0 and θ₂ = 0

    This is the containment case which is also not possible between incompatible events and QLV (A → B) = 0.

  • (f) θ₁ = 0 and θ₂ ∈]0,90[

    It occurs when |ψ〉 is in the subspace corresponding to the event A. That makes x = 1 and θ₂ = ϕ. As a result, QLV (A → B) = cos²θ₂.

  • (g) θ₁ ∈]0,90[ and θ₂ = 90

    This case is possible so x = 1 and QLV (A → B) = cos²(ϕ) = cos2(90 − θ₁).

  • (h) θ₁ ∈]0,90[ and θ₂ = 0

    In QLV terms, we get QLV(A)= cos2(θ₁) ∈ U and QLV(B) = cos20 = 1. It occurs when |ψ〉 is in the subspace corresponding to the event B. That makes x = 1 and θ₁ = ϕ. As a result, QLV (A → B) = cos²θ₁.

  • (i) θ₁ ∈]0,90[ and θ₂ ∈]0,90[

    QLV(A)=cos2θ₁ and QLV(B)= cos2θ₂. This is possible, for example, ϕ > θ₁ and So x = 1 and QLV(A → B) = cos2ϕ.

The implication can always be evaluated using the cos2ϕ but depending on the case, we can express the angle ϕ using θ₁ and θ₂ as shown in Table 4.

Fig. 4

Compatible events

Table 3 Implication for compatible events

Fig. 5

Incompatible events

Table 4 Implication for incompatible events with numbers

Table 5 presents the implication operator for incompatible events but using the terms of three-valued logic. As we can see, the logical evaluation of the operator is either false or uncertain which confirms the uncertainty principle.

Table 5 Three-valued logic implication for incompatible events

To make things more concrete, the following hypothetical experiment, which tests if a man is lucky or not, will be used to illustrate some of the possibilities of Table 3.

Let us have an urn that contains three unbiased balls whose colors are red, green, and blue respectively. A man say, John, chooses a ball from the urn randomly. John will be considered lucky, if he chooses the red or the green ball; otherwise, he is considered unlucky.

There are two main events in this experiment. The first event is “John chooses a colored ball” which we will denote by C; while the second event is “John is lucky” which we will denote by L. There are three disjoint possibilities for the event C; those are CR, CG, or CB for choosing red, green, or blue balls respectively. Since CR, CG, and CB are mutually exclusive, they represent an orthogonal basis for the three-dimensional system as shown in Fig. 6. The event L is defined based on the balls’ colors as P_L = P_CR ∨ P_CG = P_CR∪CG. The balls are unbiased so they have equal probabilities of being selected and that is depicted by the system state $|{\psi }\rangle = \left (1/\sqrt {3},1/\sqrt {3},1/\sqrt {3}\right )^{t}$. This three-dimensional system represent the simplest quantum logic. Now, let us see how the Table 3 holds.

• 1. The balls are unbiased which means QLV(CR) = QLV(CB) = QLV(CG) = (0.5773)² = 0.333. If John chooses the red ball then he is lucky. This can be expressed logically by (CR → L) because P_CR ⊆ P_L. The events CR and L are an example of quantum subsumed events. The same thing applies to the green ball i.e., (CG → L). Du to the definition of L, we can write (CR or CG → L) because P_CR∪CG ⊆ P_L. According to Schmitt (2008), P_L = |CR〉〈CR| + |CG〉〈CG| so we calculate the logical truth value or the probability of John being lucky using Eq. 4 as $QLV(L) = p(L) = \langle {\psi }|P_{L}^{\dagger } P_{L}|{\psi }\rangle$ after substitution we get

  $$QLV(L)= \left( \begin{array}{lll} 1/\sqrt{3}&1/\sqrt{3}&1/\sqrt{3} \end{array}\right) \left( \begin{array}{lll} 1&0&0\\0&1&0\\0&0&0 \end{array}\right) \left( \begin{array}{l}1/\sqrt{3}\\1/\sqrt{3}\\1/\sqrt{3}\\ \end{array}\right) $$

  The result QLV(L) = 0.667 ∈ U and we have QLV(CR) = 0.333 ∈ U. Since P_CR ⊆ P_L then QLV(CR → L) = T. This case is an implementation of the last possibility of Table 3.

• 2. Suppose John is lucky, that means the event L has occurred and the new system state |ψ^′〉 resides in P_L. This new state is calculated, using Eq. 5, as follows

  $$|{\psi^{\prime}\rangle}= \frac{1}{\sqrt{0.667}} \times \left( \begin{array}{lll} 1&0&0\\0&1&0\\0&0&0 \end{array} \right) \times \left( \begin{array}{l} \frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{3}} \end{array}\right) = \left( \begin{array}{l}0.7071\\0.7071\\0 \end{array}\right)$$

  Being in P_L, the new state |ψ^′〉 guaranties that the blue ball was not chosen by giving the zero weight to the subspace P_CB. At the same time it gives an equal weight of 0.7071 for both P_CR and P_CG. The truth value of an event is obtained by squaring the weights of their corresponding sub-spaces. We know that QLV(L) = T and we also know that QLV(CR → L) = T. But QLV(CR)=T when the red ball is chosen, or QLV(CR)=F when the green ball is chosen or uncertain (0.7071 ∈ U) when we do not know whether the red or green ball was chosen.

• 3. If John chooses the red ball, then the system state becomes |CR〉 and the truth value of John being lucky calculated using Eq. 4 is one. We have (CR → L) and CR occurs then L also occurs. In other words, the classical MP rule holds (see Section 5).

• 4. John is unlucky is the event ∼L which occurs when the color of the chosen ball is blue. Its corresponding subspace is ∼ L = I − P_L means that the system state could belong to any subspace except P_L. If John is unlucky, the the system state |ψ^′〉 will be |CB〉 as computed below. Since P_CB ⊥ P_CR the truth value of the event CR is F.

  $$|{\psi^{\prime}\rangle}= \frac{1}{\sqrt{0.333}} \times \left( \begin{array}{lll} 0&0&0\\0&0&0\\0&0&1\\ \end{array} \right) \times \left( \begin{array}{l} \frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{3}} \end{array}\right) = \left( \begin{array}{l} 0\\0\\1 \end{array}\right)$$

  In logical expression, we had CR → L and ∼L then we get ∼CR. This means the classical MT rule also holds.

Fig. 6

The experiment

6 Conclusion and future work

In this paper, we reviewed the existing implication operators and discussed their usability in the quantum case. We also defined a quantum implication operator that works for compatible and incompatible events. It turned out that the suggested operator satisfies some of the classical reasoning rules like Modus Ponens and Modus Tollens when it is used with compatible events.

In future research, we intend to discuss the special case when the events are entwined. We also want to define quantum specific reasoning rules based on the suggested operator and use them for reasoning on real data.