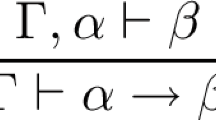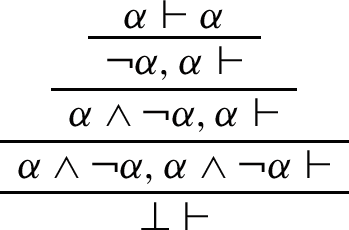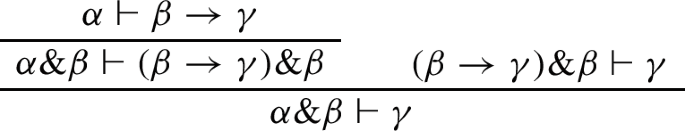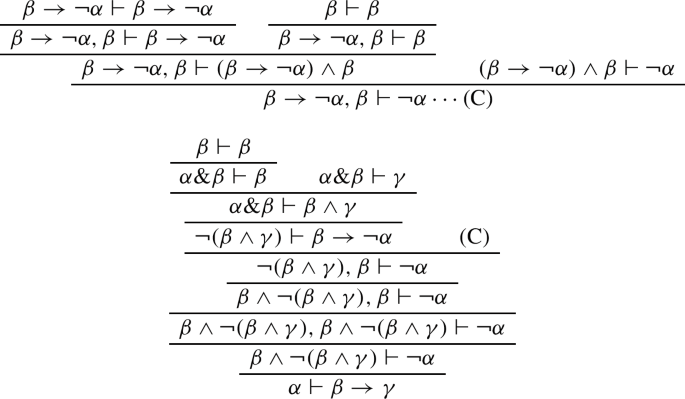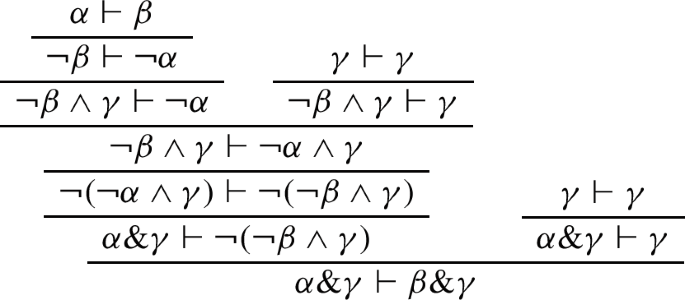Implicational quantum logic

Abstract

A non-classical subsystem of orthomodular quantum logic is proposed. This system employs two basic operations: the Sasaki hook as implication and the and-then operation as conjunction. These operations successfully satisfy modus ponens and the deduction theorem. In other words, they form an adjunction in terms of category theory. Two types of semantics are presented for this logic: one algebraic and one physical. The algebraic semantics deals with orthomodular lattices, as in traditional quantum logic. The physical semantics is given as a procedure for deriving a final segment of a series of yes-no experiments.

1 Introduction

Traditional quantum logic has been studied as a logical system with an algebraic structure of modular lattice, ortholattice, or orthomodular lattice (Birkhoff and von Neumann 1936; Dalla Chiara and Giuntini 2002).

An important property that characterizes quantum logic is that the distributive law of conjunction over disjunction does not always hold, which makes it impossible to have any satisfactory implication operator (Hardegree 1974). Since implication is one of the most fundamental operations for performing inference and computation, this defect has been a major obstacle to the application of quantum logic from a practical point of view.

Another problem with quantum logic is that the operation of conjunction may not have the proper meaning in the conventional interpretation. A proposition in quantum logic corresponds to an observable operator and, essentially the same thing, to a closed subspace that is the range of that operator. Conjunction corresponds to the set-theoretical intersection of the closed subspaces, but it becomes a proposition only when the operators corresponding to those closed subspaces are simultaneously observable, i.e. commutative. Thus, it has long been argued that if the corresponding operators are not commutative, it may not make sense to construct conjunction formally (Jauch 1968; Jammer 1974).

The following operation, called the Sasaki hook, is well known as an implication operation in quantum logic: $\alpha \rightarrow \beta := \lnot \alpha \vee (\alpha \wedge \beta )$. The Sasaki hook is a prime candidate for the next best implication operation, since it has a proper meaning in quantum theory, and it makes modus ponens hold with the help of orthomodularity. However, this operation is still not completely satisfactory for use in inference and computation because it lacks desirable properties such as transitivity and the deduction theorem (Hardegree 1974; Herman and Piziak 1975).

To solve this problem, several methods have been proposed to make an implication behave like in classical logic. However, in most cases, such methods work well only in classical subsystems that consist of mutually commutative propositions (Ying 2015; Tokuo 2019). The other option is to change the conjunction side so that the Sasaki hook satisfies the deduction theorem even in quantum logic. Then the modified conjunction operation, called the and-then operation, has a natural empirical interpretation in quantum logic, at the expense of commutativity and associativity (Finch 1969, 1970; Román and Rumbos 1991; Lehmann et al. 2006; Lehmann 2008).

Following this second approach, we formalize a system of quantum logic whose basic operations are the Sasaki hook and the and-then operation. These operations successfully satisfy modus ponens and the deduction theorem. In other words, they form an adjunction in terms of category theory (Heunen and Jacobs 2011). The proposed system, with an ideal implication at its core, is expected to contribute to viable theories of inference and computation. In the following sections of this paper, this system will be introduced in the style of sequent calculus, and two types of semantics will be given: one algebraic and one physical.

2 Nishimura’s Sequent Calculus

Nishimura’s GOM is known as a system of sequent calculus for orthomodular quantum logic (Nishimura 1980). For reference, the axioms and the inference rules of GOM are listed below.¹ Here, lower-case Greek letters such as $\alpha$ and $\beta$ are logical formulas, and upper-case Greek letters such as $\varGamma$ and $\varDelta$ are (possibly empty) sets of formulas. $\lnot \varDelta$ shall be $\{ \lnot \alpha \mid \alpha \in \varDelta \}$.

This system has been shown to be sound and complete with respect to the semantics of orthomodular quantum logic.

GOM employs conjunction and negation as basic operations. If the Sasaki hook is defined as $\alpha \rightarrow \beta := \lnot \alpha \vee (\alpha \wedge \beta ) = \lnot (\alpha \wedge \lnot (\alpha \wedge \beta ))$, the following are derived rules of GOM.

These correspond to modus ponens and the deduction theorem, respectively. Note that this deduction theorem is of a restricted form. In fact, in ordinary logic such as classical logic, a more general rule of the following form holds.

Now, restricting $\varGamma$ to the empty set leads to the deduction theorem of quantum logic. This restriction may seem like a minor difference, but it is a major obstacle to performing inference and computation in quantum logic. For example, even the transitive law of implication, i.e. $\alpha \rightarrow \beta , \beta \rightarrow \gamma \vdash \alpha \rightarrow \gamma$, cannot be proved in GOM .

3 Syntax of Implicational Quantum Logic

In this paper, we propose a non-classical subsystem of orthomodular quantum logic in which implication and conjunction are the basic operations and modus ponens and the deduction theorem hold for these operations. To keep the system from collapsing into classical logic, this alternative conjunction, i.e. the and-then operation, must be non-commutative and non-associative (Lehmann 2008).

A language of the proposed system consists of the following:

• A denumerable set of propositional variables.

• A propositional constant: $\bot$ (falsity).

• Logical connectives: $\rightarrow$ (implication), & (conjunction).

Formulas are inductively defined as follows:

• A propositional variable is a formula.

• A propositional constant is a formula.

• If $\alpha$ and $\beta$ are formulas, then $(\alpha \rightarrow \beta )$ and $(\alpha \& \beta )$ are formulas.

Parentheses are omitted unless ambiguity arises, but note that&, unlike $\wedge$, is non-associative. The set of all formulas is denoted by ${\mathcal {F}}$.

A sequent of the proposed system is a sequence of symbols with at most one formula on each side of $\vdash$. That is, a sequent is one of the following forms:

• $\alpha \vdash \beta$

• $\alpha \vdash$

• $\vdash \beta$

• $\vdash$

The axioms and the inference rules of our system are as follows:

Identities We could introduce corresponding rules of inference for the idempotency of conjunction and the elimination of double negation (note: $\alpha \rightarrow \bot$ corresponds to $\lnot \alpha$), but to avoid complications, we will consider the equivalence classes of formulas with respect to the following identities:

In other words, the above formulas connected by $\equiv$ are considered identical.

Theorem 1

The axioms and the inference rules of the proposed system can be derived in GOM.

Proof

The proof is deferred to the appendix. $\square$

This implies that any theorem of the proposed system is also a theorem in traditional quantum logic. By contraposition, any proposition which is not a theorem in traditional quantum logic (e.g. the distributive law) is not a theorem in the proposed system.

Corollary 1

The proposed system is a non-classical subsystem of orthomodular quantum logic.

4 Semantics of Implicational Quantum Logic

In this section, we present two types of semantics for the proposed system: one algebraic and one physical.

4.1 Algebraic semantics

We start by giving an algebraic semantics in terms of lattice theory. An orthocomplemented poset is a 4-tuple $\varPi = \langle P, \le , \bot , *\rangle$ which satisfies the following:

• P: a set.

• $\le$: a partial order on P.

• $\bot$: the minimum element of P.

• $*$: a unary operator on P satisfying:

  • $X^{**} = X$.

  • $X\le Y \Leftrightarrow Y^*\le X^*$.

  • if $Y \le X$ and $Y \le X^*$ then $Y=\bot$.

Next, we define the binary operation $\wedge$ on P as $X \wedge Y := \inf \{X,Y\}$. Although infima do not always exist, we will assume below that any finite subset of P has an infimum i.e. $\varPi$ is a meet-semilattice. Then, in fact, given the existence of $*$, we see that $\varPi$ is not just a semilattice, but necessarily a lattice. An orthocomplemented lattice $\varPi$ is called an orthomodular lattice if it satisfies the following orthomodular law: if $X \le Y$, then $Y=(X^*\wedge (X^*\wedge Y)^*)^*$. In what follows, we will assume that $\varPi$ is an orthomodular lattice.

An interpretation $\iota$ in $\varPi$ is a map from ${\mathcal {F}}$ to P which satisfies the following:

• $\iota (\alpha )\in P$    for any propositional variable $\alpha$.

• $\iota (\bot ) = \bot$.

• $\iota (\alpha \rightarrow \beta ) =(\iota (\alpha )\wedge (\iota (\alpha )\wedge \iota (\beta ))^*)^*$.

• $\iota (\alpha \& \beta ) =(\iota (\alpha )^*\wedge \iota (\beta ))^*\wedge \iota (\beta )$.

We say that a sequent $\alpha \vdash \beta$ is valid in $\varPi$ if $\iota (\alpha )\le \iota (\beta )$ for any interpretation $\iota$ in $\varPi$.² We say that a sequent is universally valid if it is valid in $\varPi$ for any orthomodular lattice $\varPi$.

Theorem 2

Every provable sequent is universally valid.

Proof

Assuming that a sequent is provable in the proposed system, we have, by Theorem 1, that it is also provable in GOM. Then the soundness of GOM (Nishimura 1980) immediately implies that the sequent is universally valid. $\square$

4.2 Physical semantics

An experiment with only a binary output of yes or no is called a yes-no experiment. An ordinary experiment performed by a physicist can be reduced, at least in principle, to multiple yes-no experiments. In a typical example, a single yes-no experiment determines whether a measurement of a physical quantity takes a value within a certain range of real numbers or not. By dividing this range into smaller parts and performing multiple yes-no experiments, we can obtain a measurement value with arbitrary accuracy. A yes-no experiment that determines the measurement value of a physical quantity is called a filter for that physical quantity.

A filter corresponds to a logical proposition. For example, let X be the proposition that a particle is located in region A, and let Y be the proposition that a particle is located in region B. If $A \subseteq B$, then whenever X outputs yes, Y will also output yes. In other words, if X is true, then Y is also true. Let us denote this relation by $X \le Y$. If $X \le Y$ and $Y \le X$, we define the two filters X and Y to be equal ($X=Y$). With this order, the set of all filters becomes a poset.

The filter that uses the same measurement device as X, but just inverts the output, is denoted by $X^*$. Then the following properties hold:

• $X^{**} = X$.

• $X\le Y \Leftrightarrow Y^*\le X^*$.

• if $Y \le X$ and $Y \le X^*$ then $Y=\bot$.

Here, $\bot$ is a filter that always outputs no. Thus, the set of all filters acquires the structure of an orthocomplemented poset.

The infimum of filters X and Y with regard to $\le$ is written as $X\wedge Y$ (if it exists). In classical physical systems, it is not difficult to obtain a concept of the filter corresponding to $X\wedge Y$ by measuring X and Y independently and combining the results. That is, we can specify that $X\wedge Y$ outputs yes if and only if both X and Y output yes. However, in a quantum physical system, a measurement may change the state of the system and affect subsequent measurements. For example, if the output of X is yes and the output of Y is yes, and then the measurement of X is performed again, the output may be no this time. Therefore, $X\wedge Y$ cannot be consistently defined by simply combining X and Y, except when X and Y are simultaneously measurable, i.e. commutative. Jauch (1968) suggested that the infinite sequence of alternating filters $XYXYX\dots$ is the infimum of X and Y, and this idea was mathematically justified by Shimony (1971). He proved that the infinite sequence is indeed the infimum of X and Y if we impose the condition that the set of all filters is isomorphic to the set of all projection operators in a Hilbert space. In what follows, we will assume Shimony’s condition. Then, $X^*$ corresponds to the projection of X onto its orthogonal complement, and the set of all filters forms an orthomodular lattice. Interpretation and validity can be defined as in the previous section.

The interpretation of the implication operation ($\rightarrow$) is defined as $\iota (\alpha \rightarrow \beta )=(\iota (\alpha )\wedge (\iota (\alpha )\wedge \iota (\beta ))^*)^*$. The right-hand side is known to have the meaning of counterfactual conditional (the Stalnaker conditional). More details can be found in Hardegree (1974), but we will put it in our context here. Let X and Y be filters. By Y/X, we denote the counterfactual proposition “If X were the case, then Y would be the case.”³ Note that a projection operator X in a Hilbert space ${\mathcal {H}}$ can be identified with the closed subspace of ${\mathcal {H}}$, which is the range of X. A state i in ${\mathcal {H}}$ (or a world, the terminology of possible world semantics) in which X is true is called an X-world, and let $S_X (i)$ denote the X-world closest to i.⁴ Now we define Y/X to be true at i if any X-world closest to i is also a Y-world. That is, $i \in Y/X \, \Leftrightarrow \, S_X (i) \in Y$. Then, we can show that $Y/X = (X\wedge (X\wedge Y)^*)^*$.⁵

The interpretation of the conjunction operation $( \& )$ is defined as $\iota (\alpha \& \beta )=(\iota (\alpha )^*\wedge \iota (\beta ))^{*}\wedge \iota (\beta )$. This is called the and-then operation, which physically means to perform one measurement X, followed by the next measurement Y(Finch 1969, 1970; Lehmann 2008). Abbreviated as $X\circ Y = (X^*\wedge Y)^{*}\wedge Y$, we have:

• $X\circ X = X$.

• $X\circ Y \le Y$.

• $X\circ Y \le Z \,\Leftrightarrow \, X \le Z/Y$.

Now let us define a final segment of a filter recursively as follows:

• X is a final segment of X.

• A final segment of Z is a final segment of $Y \circ Z$.

For example, the final segments of $U\circ (V\circ W)$ are $U\circ (V\circ W)$, $V\circ W$ and W. Then, from the relation $X\circ Y \le Y$ above and the transitivity of $\le$, it follows that $X \le Y$ if Y is a final segment of X. This means that from an assumption X, we can conclude a final segment of X. Furthermore, from the relation $X\circ Y \le Z \,\Leftrightarrow \, X \le Z/Y$ above, it follows that Z is a final segment of $X \circ Y$ if and only if the counterfactual conditional “If Y were the case, then Z would be the case.” is a final segment of X. Thus, the physical meaning of the proposed system can be simply viewed as a procedure for deducing a final segment of a sequence of filters.

5 Conclusion

In this paper, we have proposed a non-classical subsystem of orthomodular quantum logic that focuses on an implication operation, and have presented two types of semantics. The proposed system employs Sasaki hook as an implication operation and the and-then operation as a conjunction operation. This combination has desirable properties: modus ponens and the deduction theorem. Algebraically, the proposed system can be interpreted in terms of orthomodular lattice, as in the case of traditional quantum logic, while physically it can be interpreted as a procedure of deriving a final segment from a series of yes-no experiments.

The future plans of this study include the development of inference and computational theories that exploit the positive properties of this implication. Specifically, we are looking at the possibility of constructing theories in which implication plays an important role, such as natural deduction and $\lambda$-calculus.

Appendix

We provide a proof of Theorem 1.

Proof

Formulas of the proposed system which contain $\bot$, $\rightarrow$, or & will be identified with the formulas of GOM as follows:

• $\bot \equiv \lnot \alpha \wedge \alpha$.

• $\alpha \rightarrow \beta \equiv \lnot (\alpha \wedge \lnot (\alpha \wedge \beta ))$.

• $\alpha \& \beta \equiv \lnot (\lnot \alpha \wedge \beta )\wedge \beta$.

It should be pointed out in advance that modus ponens in a single sequent form, i.e. $(\alpha \rightarrow \beta )\wedge \alpha \vdash \beta$, holds in GOM, as shown in the following diagram:⁶

From this and the following identities, we can immediately see that modus ponens also holds for the combination of $\rightarrow$ and & in GOM: $(\alpha \rightarrow \beta ) \& \alpha = \lnot (\alpha \wedge \lnot (\alpha \wedge \beta )) \& \alpha =\lnot ((\alpha \wedge \lnot (\alpha \wedge \beta ))\wedge \alpha )\wedge \alpha =\lnot (\alpha \wedge \lnot (\alpha \wedge \beta ))\wedge \alpha =(\alpha \rightarrow \beta )\wedge \alpha$.

Axioms

•  Axiom-1. For each formula $\alpha$, $\alpha \vdash \alpha$ is an axiom of GOM.

•  Axiom-2.

  

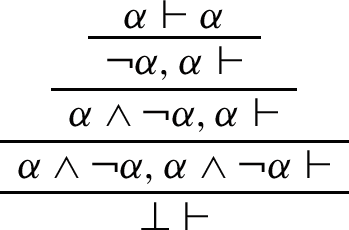
Rules

•  Weakening-1, Weakening-2 and Cut . We can simply apply Weakening and Cut rules of GOM.

•  $\rightarrow$ -1. Using modus ponens and&-2 rule, we have:

  

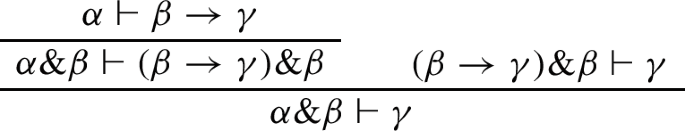
•  $\rightarrow$ -2. Using modus ponens and&-1 rule , we have:

  

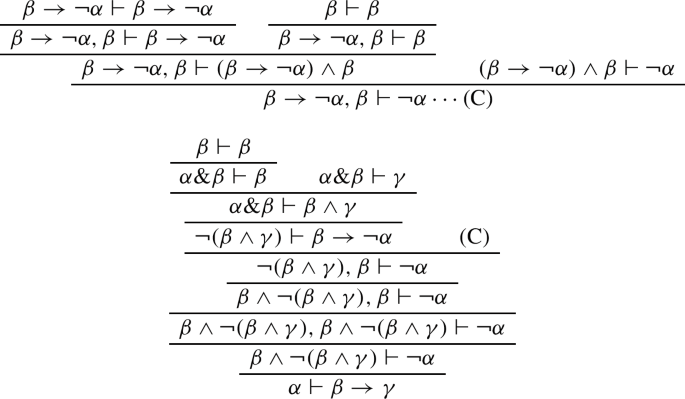
•  &-1. We can simply apply $\wedge$ -1R rule of GOM.

•  &-2. Using &-1 rule, we have:

  

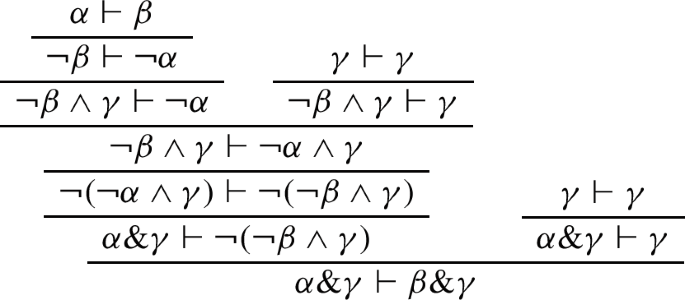
Identities

•  &-idempotency. Since we can prove $\alpha \& \alpha \vdash \alpha$ and $\alpha \vdash \alpha \& \alpha$ in GOM, we are justified in regarding $\alpha \& \alpha$ and $\alpha$ as identical.

•  Double Negation. Since we can prove $\alpha \rightarrow \bot \vdash \lnot \alpha$ and $\lnot \alpha \vdash \alpha \rightarrow \bot$ in GOM, we are justified in regarding $\alpha \rightarrow \bot$ and $\lnot \alpha$ as identical. Then, by using $\lnot \lnot$-1 and $\lnot \lnot$ -2 rules of GOM, we are justified in regarding $(\alpha \rightarrow \bot )\rightarrow \bot$ and $\alpha$ as identical. $\square$