Introduction

The development of advanced technology has necessitated the use of high-quality materials for cutting-edge applications. These requirements have led to the emergence of advanced composite materials, such as functionally graded materials (FGMs). FGMs differ from conventional fiber-reinforced composites, because they do not have fibers and a matrix. Instead, FGMs are made by mixing two different materials, and their composition smoothly and continuously varies from one side to the other. This seamless transition results in a material without any discontinuity and eliminates inter-laminar stresses. Typically, FGMs are composed of ceramics and metals. The ceramic side can withstand high-temperature or chemically aggressive environments, making FGMs ideal for heat shielding applications. In the 1980s, Japanese researchers pioneered the development of FGM materials for thermal insulation purposes. Initially, functionally graded materials found use in the nuclear and aerospace industries for heat shielding. Over time, their applications expanded to various other sectors, including electronic sensors, wear-resistant coatings, biomedical implants, and chemical plants. [1]

Fabricating functionally graded plates (FG plates) presents significant challenges and introduces uncertainty in material properties. This uncertainty stems from many involved parameters, ultimately leading to variations in material parameters, geometry, and boundary conditions. The inherent variability in material properties gives rise to randomness in the structural response [2]. Consequently, it becomes imperative to account for this material property variability in the analysis to ensure safe design and structural integrity. The variability in Young’s modulus and Poisson’s ratio is recognized as uncertain material parameters in stochastic analysis. Over the last few decades, researchers have addressed the stochastic analysis of FGM plates by considering material randomness. For example, Rahman et al. [3] developed a probabilistic model for nonlinear fracture mechanics problems within a finite element framework. Tomar and Zhou et al. [4] explored perturbation fracture analysis to understand the variations in constituent properties at the microscopic level. Nouy et al. [5] introduced an extended stochastic FEM (XFEM) for stochastic analysis. Chakraborty and Rahman et al. [6] conducted reliability analysis using stochastic multiscale models. Lal and Palekar et al. [7] performed stochastic simulations of cracked plates by employing the second-order perturbation technique with XFEM. Khatri and Lal et al. [8] implemented a second-order perturbation technique for analyzing stochastic crack growth.

Over the past decade, researchers have dedicated significant efforts to analyzing the stochastic vibration responses of plates while considering randomness in material parameters. Among the probabilistic techniques employed, the First-Order Perturbation Technique (FOPT) has garnered attention for its computational efficiency in stochastic simulations. For instance, Cha and Gu et al. [9] utilized FOPT to compute perturbed natural frequencies and compared the results with a deterministic approach. Shaker et al. [10] implemented a second-order perturbation technique into a finite element framework to investigate stochastic free vibrations. Yang et al. [11] applied FOPT to analyze the behavior of Functionally Graded (FG) plates under bending. Bhardwaj et al. [12] introduced a stochastic XIGA method for simulating crack growth in the FGM domain. Pathak et al. [13] employed a coupled FE-EFG method in a stochastic medium to simulate crack growth. Singh et al. [14] conducted stochastic simulations to analyze the post-buckling behavior of plates. Lal et al. [15] utilized stochastic simulations to investigate fracture and crack growth by employing FOPT. Talha and Singh [16] performed stochastic simulations to explore the buckling behavior of FG plates in the presence of material randomness. Jagtap et al. [17] performed stochastic simulations to investigate the nonlinear free vibrations of FG plates. Lal et al. [18, 19] employed a second-order perturbation technique (SOPT) to simulate cracked composite plates and determine the stochastic stress intensity factor. Talha and Singh [20] used FOPT to study the free vibrations of higher-order FG plates. Lal and Palekar [21] conducted stochastic simulations to analyze the stress intensity factor, employing a first-order perturbation technique while considering uncertainty in system properties. Lal et al. [22] utilized FOPT for stochastic simulations of non-linear bending, considering uncertainties in material properties and thermal coefficients. Pandit et al. [23] implemented FOPT for stochastic analysis of free vibration. Shakir and Talha [24] employed FOPT for stochastic simulations of free vibrations in panels reinforced with graphene, considering uncertainty in material properties. Lal et al. [25] utilized FOPT for stochastic simulations of stress intensity factors, accounting for uncertainty in material properties. Amir et al. [26] conducted stochastic simulations for free vibration analysis, employing the FOPT approach while considering material uncertainties. Raza et al. [27] performed stochastic simulations to investigate in-plane free vibrations. Shaker et al. [28] implemented a stochastic finite element framework to analyze stochastic free vibrations. Lal and Singh [29] conducted stochastic simulations for nonlinear free vibrations using the first-order perturbation technique. Secgin and Kara [30] applied the statistical moment method to analyze stochastic free vibrations. Bahmyari [31] conducted stochastic simulations of laminated composite plates for free vibrations, incorporating a non-intrusive chaotic radial function. Nasker et al. [32] performed stochastic simulations to determine natural frequencies by introducing a stochastic representative volume element concept. Nayak and Satapathy [33] studied stochastic analysis of damped free vibrations. Venini and Mariani [34] implemented the Rayleigh–Ritz approach to perform stochastic simulations of composite plates for free vibrations while considering uncertainties in boundary conditions, mass density, and Young’s moduli. Chakraborty et al. [35] conducted stochastic analyses of composite plates for free vibrations, employing polynomial correlated function expansion. Hien and Noh [36] performed stochastic simulations for free vibrations, considering material randomness. Raza et al. [37] employed FOPT and conducted stochastic simulations of FG plates with edge cracks to analyze free flexural vibrations.

Over the last decade, porous structures have garnered significant attention from researchers. They have extensively explored porous plates. Porosity in structure may alter the structural response, making it essential to consider during structural analysis. Xue et al. [38] simulated the vibration of plates with porosity using the isogeometric approach. Du et al. [39] examined the free vibration of porous plates, while Slimane et al. [40] also focused on simulating the free vibration of porous plates. Rjoub and Alshatnawi et al. [41] used an artificial neural network to simulate the free vibration of porous plates. Saad et al. [42] delved into the simulation of free vibration and reported on the effect of porosity in functionally graded sandwich plates on frequency. Merdaci et al. [43] performed simulations of the free vibration of functionally graded plates with porosity. In another study, [44] conducted a simulation for the vibration of functionally graded plates with porosity in a thermal environment. Farsani et al. [45] perform simulations of the free vibration of plates with porosity. Belarbi et al. [46] implemented an extended layerwise theory to simulate the free vibration of functionally graded plates with porosity. Rezai et al. [47] simulated the free vibration of plates using the Carrera unified formulation, and Kumar et al. [48] focused on simulating the free vibration of plates with porosity. Rezai et al. [49] performed free vibration simulations of functionally graded plates with porosity. Tran et al. [50] present a BCMO-ANN algorithm to optimize vibration and buckling in functionally graded porous microplates. The author integrates the higher-order shear deformation theory and modified couple stress theory to explore the material property uncertainties and their impact on natural frequencies and critical buckling loads. Nguyen et al. [51] discuss the use of a hybrid phase-field approach within isogeometric analysis to model crack propagation in functionally graded materials with porosity. The author demonstrates the impact of porosity on critical force and crack path while optimizing computational efficiency through a local refinement multi-patch algorithm based on the VUKIMS technique. Le et al. [52] introduce an isogeometric numerical solution based on nonlocal strain gradient elasticity theory to analyse the static bending, free vibration, and buckling of sigmoid functionally graded nanoplates, considering two core configurations. Pham et al. [53] employ isogeometric analysis based on higher order shear deformation theory to investigate the dynamic response of sandwich nanoplates with a porous functionally graded core. Vinh et al. [54] perform free vibration in functionally graded porous doubly curved nanoshells by considering variable nonlocal parameters. Tran et al. [55] investigate the free vibrations of functionally graded porous plates reinforced with graphene platelets and piezoelectric layers, exploring diverse configurations and their effects on vibration characteristics. Sharma et al. [56] present a free vibration analysis of porous functionally graded plates using efficient eight-noded 3D degenerated shell elements that reduce computational time while accurately accommodating material property variations through thickness.

During the manufacturing of FGM, invisible flaws and voids can exist in the domain, which may later result in crack initiation during the operation of engineering components or structures. Even a tiny crack can significantly affect the free vibration response of these structures. Variations in the crack size can lead to changes in the natural frequency of the structures, which can result in unexpected phenomena such as resonance, potentially leading to catastrophic structural failure. To address the issue of discontinuities in the plate domain, several advanced techniques are available. In this study, the XFEM method [57,58,59] has been employed to analyze cracked functionally graded plates in the context of free flexural vibration. XFEM is a well-established and efficient computational technique for modeling discontinuity problems. It offers higher convergence and more accurate solutions compared to conventional FEM. XFEM has several advantages over FEM. It allows for modeling the crack separately, eliminating the need for conformal meshing or special elements. This, in turn, eliminates the need for a time-consuming and computationally expensive remeshing process [60]. The level set method [61] is used as a mathematical tool to determine the region of the crack tip and crack face, along with their corresponding elements and nodes within the plate domain. In XFEM, tip elements, tip nodes, split elements, and split nodes are identified, and special treatment is applied to these discontinuous elements. The enrichment technique is implemented using the partition of unity method [57] to improve the approximation of primary variables. Over the past decades, numerous researchers have conducted analyses on cracked structures. For instance, Bachene et al. [62] employed XFEM to investigate the free vibration of cracked isotropic plates. Natarajan et al. [63] incorporated Mindlin’s plate theory within the XFEM framework to study the free vibration of cracked plates. Raza et al. [64] applied the XFEM framework to computationally investigate porous functionally graded plates under free flexural vibration. Raza et al. [65] conducted a simulation for the free vibration analysis of cracked functionally graded plates with porosity, considering a thermal environment. In the present study, porosity is considered as a microstructural defect. Dwivedi et al. [66] introduce a method using HOXFEM and ANN to predict the natural frequencies of cracked sandwich plates, enhancing computational efficiency and accuracy.

The introduction of cracks, porosity, and material uncertainty can significantly impact the free vibration and overall performance of FG plates. To predict the structural response while considering these parameters, the investigation of free vibration represents an interesting area of research. The main motivations for this study include understanding FGM dynamic behaviour, enhancing safety by predicting crack effects, optimizing material parameters for efficiency, advancing computational mechanics through innovative methods, contributing to academic knowledge, reducing computational cost, exploring industrial applications, and improving structural designs and materials understanding. The objectives and results of this paper encompass the following scientific interests: firstly, it involves advancing computational methods through the development and application of the stochastic extended finite element method for modal analyses. This represents a notable progression in computational approaches, addressing uncertainties in material properties. Secondly, the study delves into understanding the correlation between crack and porosity distribution with free vibration, providing critical insights into how structural irregularities and material heterogeneities influence the dynamic behaviour of FGM plates. This understanding is fundamental for predicting and managing structural integrity. Thirdly, the investigation explores the effect of material gradation within the porous FGM domain, revealing how varying material properties impact the dynamic response. Optimizing this gradation is essential for achieving enhanced structural performance. Lastly, the study analyses the effect of material randomness on frequency dispersion, offering valuable insights into how variations in material properties affect the behaviour of FGM plates. This understanding is pivotal for real-world structural design and assessment, contributing collectively to the advancement of the field of structural mechanics. To the best of the author’s knowledge based on the literature review, no prior research has been reported on the stochastic free vibration of cracked porous FG plates considering material randomness. The objectives for the current study are outlined below:

  • The stochastic extended finite element method is developed and implemented for the modal analyses of porous FGM plates with crack discontinuity.

  • The distribution of cracks and porosity was analyzed in correlation with free vibration.

  • The effect of material gradation in the porous FGM domain is analyzed and discussed.

  • The effect of material randomness is studied on the dispersion in the linear frequency of porous FGM plates.

Theoretical Formulations

Porous FGM Modelling

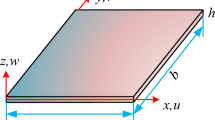
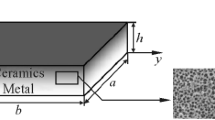
Consider a uniformly distributed porous FGM plate with a crack at the middle of the left edge whose configuration and dimensions are shown in the diagram in Fig. 1a. Ceramic and metal are the constituent materials of the considered porous FGM plate. In the considered FGM plate, the bottom of the plate is fully metal, the top is fully ceramic, and the constituent material is graded in the thickness direction, which can be seen in Fig. 1b. Porosity distribution over the thickness of the FGM plate can be seen in Fig. 1c. The dimension length, width, and thickness of the cracked porous FG plates are designated as a, b, and h in x, y, and z directions, respectively. The crack length is defined as d, as shown in Fig. 1a. The reference plane or the origin of the coordinate geometry is shown with the dotted line in shown in Fig. 1a. The material is fully metal at –h/2, whereas the material is fully ceramic at h/2. The Power-law is incorporated to model the FG plates. The Power-law for the gradation of constituent material is given as [6]:

$$V_{{\text{c}}} (z) = \left( {\frac{z}{h} + 0.5} \right)^{\gamma } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(0 \le \gamma \le \infty ),$$
(1)

where Vc is designated as the volume fraction of ceramic and γ the gradient index. Figure 2 shows the variation of material along the thickness direction.

Fig. 1
figure 1

Functionally graded plate with a edge crack in three dimensions, b material distribution over the thickness, c porosity distribution in the thickness direction, and d edge crack in two dimensions

Full size image
Fig. 2
figure 2

Variation of volume fraction for ceramic in the thickness direction of the plate

Full size image

The effective material property in the FGM domain can be evaluated using the equation written as:

$$P\left( z \right) = P_{{\text{m}}} + \left( {\frac{h + 2z}{{2h}}} \right)^{\gamma } \left( {P_{{\text{c}}} - P_{{\text{m}}} } \right) - \frac{\alpha }{2}\left( {P_{{\text{c}}} + P_{{\text{m}}} } \right),$$
(2)

where P is designated as a generalized material property, the subscript c and m represent ceramic and metal, respectively.

Plate Kinematics

Displacement Field Higher order shear deformation theory is incorporated to investigate the plate. The displacement field of plate in Fig. 3 proposed by JN Reddy [67] is written as:

$$\begin{aligned} \overline{u}_{1} (x,y,z) & = u(x,y) + \left( {z - \frac{{4z^{3} }}{{3h^{2} }}} \right)\varphi_{x} (x,y) - \frac{{4z^{3} }}{{3h^{2} }}\psi_{x} (x,y) \\ \overline{u}_{2} (x,y,z) & = v\,(x,y) + \left( {z - \frac{{4z^{3} }}{{3h^{2} }}} \right)\varphi_{y} (x,y) - \frac{{4z^{3} }}{{3h^{2} }}\psi_{y} (x,y) \\ \overline{u}_{3} (x,y,z) & = w(x,y). \\ \end{aligned}$$
(3)
Fig. 3
figure 3

Visualization of plate geometry with coordinate axis

Full size image

Strain–Displacement Relation Further strain [68] can be expressed as:

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{1}^{0} } \\ {\varepsilon_{2}^{0} } \\ {\varepsilon_{4}^{0} } \\ {\varepsilon_{5}^{0} } \\ {\varepsilon_{6}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {k_{1}^{1} } \\ {k_{2}^{1} } \\ {k_{6}^{1} } \\ 0 \\ 0 \\ \end{array} } \right\} + z^{2} \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {k_{5}^{2} } \\ {k_{4}^{2} } \\ \end{array} } \right\} + z^{3} \left\{ {\begin{array}{*{20}c} {k_{1}^{3} } \\ {k_{2}^{3} } \\ {k_{6}^{3} } \\ 0 \\ 0 \\ \end{array} } \right\}.$$
(4)

Material Constitutive Equation The constitutive equation [69] can be written as:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & 0 & 0 & 0 \\ 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\},$$
(5)

Where,

$$C_{11} = \frac{E(z)}{{1 - \nu^{2} }} = C_{22} ,\,\,C_{12} = \frac{\nu E(z)}{{1 - \nu^{2} }},C_{44} = \frac{E(z)}{{2(1 + \nu )}} = C_{55} = C_{66} .$$

XFEM Approximation

The XFEM approximation for the cracked plate by augmenting the primary variable is written as [70,71,72]:

$$\overline{\user2{u}}({\varvec{x}}) = \sum\limits_{i = 1}^{n} {N_{i} ({\varvec{x}})\left( {{\varvec{u}}_{i} + \underbrace {{(H({\varvec{x}}) - H({\varvec{x}}_{i} )){\varvec{a}}_{{\varvec{i}}} }}_{{i \in n_{s} }} + \underbrace {{\sum {(\xi_{\alpha } ({\varvec{x}}) - \xi_{\alpha } ({\varvec{x}}_{i} )){\varvec{b}}_{{\varvec{i}}} } }}_{{i \in n_{t} }}} \right)} .$$
(6)

In above equation, Heaviside enrichment (\(H({\varvec{x}})\)) is required to address the crack face discontinuity, whereas tip enrichment (\(\xi_{\alpha } ({\varvec{x}})\)) is required to take care of the crack tip singularities. ui is the displacement field that stands for the conventional FEM mesh, ai is the additional variable for Heaviside enrichment, whereas bi is the enriched variable corresponding to tip enrichment. There are two types of displacement in the plate kinematics; one is linear, and the other is due to rotation. Hence, there are two types of enrichment [62] required to model the thorough crack in the plate domain for flexural analysis of the plate using plate theory. The tip enrichment function is given below in detail. Φ and Ψ are the tip enrichment functions for linear displacement and rotation, respectively.

$$\Phi_{\alpha } (r,\theta ) = \left\{ {r^{1/2} \sin \left( {\frac{\theta }{2}} \right),\,\,r^{3/2} \sin \left( {\frac{\theta }{2}} \right),\,\,r^{3/2} \cos \left( {\frac{\theta }{2}} \right),\,\,r^{3/2} \sin \left( {\frac{3\theta }{2}} \right),\,\,r^{3/2} \cos \left( {\frac{3\theta }{2}} \right)} \right\}$$
(7)
$$\Psi_{\alpha } (r,\theta ) = \left\{ {r^{1/2} \sin \left( {\frac{\theta }{2}} \right),\,\,r^{1/2} \cos \left( {\frac{\theta }{2}} \right),\,\,r^{1/2} \sin \left( {\frac{\theta }{2}} \right)\sin (\theta ),\,\,r^{1/2} \cos \left( {\frac{\theta }{2}} \right)\sin (\theta )} \right\}.$$
(8)

The terminologies related to cracks in the discretized domain, such as split nodes, split elements, tip nodes, and tip elements, are defined in the schematic diagram shown in Fig. 4.

Fig. 4
figure 4

Domain discretization with XFEM

Full size image

Governing Equation

In this work, the origin of the coordinate geometry is in the middle of the plate. Discretization is done using a four-noded quadrilateral element. The displacement vector is given as:

$$\left\{ {\overline{\user2{u}}} \right\} = \left[ {\varvec{N}} \right]\left\{ {\varvec{q}} \right\}.$$
(9)

Here, \(\left[ {\varvec{N}} \right]\) is the shape function matrix.

Strain can be evaluated and expressed as:

$$\left\{ {\varvec{\bar{\varepsilon }}} \right\} = \left[ \varvec{B} \right]\left\{ \varvec{q} \right\},$$
(10)

where \(\left[ {\varvec{B}} \right]\) is the strain–displacement matrix.

The strain energy [73] of the plate due to the vibration is written as:

$$S = \frac{1}{2}\int\limits_{v} {\left\{ {\bar{\varvec{\varepsilon }}} \right\}^{T} \left[ \varvec{Q} \right]} \left\{ {\bar{\varvec{\varepsilon }}} \right\}{\text{d}}v.$$
(11)

The kinetic energy [74] of the plate due to vibration is given as:

$$T = \frac{1}{2}\int\limits_{v} {\left\{ {\dot{\varvec{\overline{u}}}} \right\}^{T} \rho } \left\{ {\dot{\varvec{\overline{u}}}} \right\}{\text{d}}v.$$
(12)

Using the variational principle [63], the equation can be written as:

$$\left[ {\varvec{M}} \right]\left\{ {\ddot{\user2{q}}} \right\} + \left[ {\varvec{K}} \right]\left\{ {\varvec{q}} \right\} = 0,$$
(13)

where \(\left[ {\varvec{M}} \right]\) is the global mass matrix, and \(\left[ {\varvec{K}} \right]\) is the global stiffness matrix.

First-Order Perturbation Technique (FOPT)

The first-order perturbation technique is a probabilistic method that is relatively computationally cost-effective. FOPT provides accurate solutions for input random variables of less than 20%. In a study conducted by Cha and Gu [9], they applied FOPT to compute perturbed natural frequencies and compared the results with a deterministic approach. The random variable can be expressed as the mean variable, denoted as ‘m’, and its zero-mean random variable, denoted as ‘r’.

$$\lambda_{i} = \lambda_{i}^{m} + \lambda_{i}^{r} \;{\varvec{q}}_{i} = {\varvec{q}}_{i}^{m} + {\varvec{q}}_{i}^{r} \;{\varvec{K}} = {\varvec{K}}^{m} + {\varvec{K}}^{r} .$$
(14)

Here, λ and q are eigenvalues and eigenvectors, respectively.

Solve the equation after putting Eq. (13) in Eq. (12). Zeroth-order and first-order from the derivation is segregated and written as:

$${\text{Zeroth order }} \left[ {{\varvec{K}}^{m} } \right]\left\{ {{\varvec{q}}_{i}^{m} } \right\} = \lambda_{i}^{m} \left[ {\varvec{M}} \right]\left\{ {{\varvec{q}}_{i}^{m} } \right\}$$
(15)
$${\text{The first order }} \left( {\left[ {{\varvec{K}}^{m} } \right] - \lambda^{m} \left[ {\varvec{M}} \right]} \right)\left\{ {{\varvec{q}}_{i}^{r} } \right\}{ + }\left( {\left[ {{\varvec{K}}^{r} } \right] - \lambda^{r} \left[ {\varvec{M}} \right]} \right)\left\{ {{\varvec{q}}_{i}^{m} } \right\}{ = 0}{.}$$
(16)

Taylor’s series is used to express random variables about the mean values and can be written as:

$${\varvec{\lambda}}_{i}^{r} = \sum\limits_{{i{ = 1}}}^{n} {\lambda_{i,j}^{m} b_{j}^{r} } ;\;{\varvec{q}}^{r} = \sum\limits_{{i = {1}}}^{n} {{\varvec{q}}_{i,j}^{m} b_{j}^{r} } ;\;{\varvec{K}}^{r} = \sum\limits_{{i = {1}}}^{n} {{\varvec{K}}_{i,j}^{m} b_{j}^{m} } ,$$
(17)

where br and bm are material properties.

The variance of the eigenvalues can be defined as:

$$Var\left( {\lambda _{i} } \right) = \sum\limits_{{j = 1}}^{n} {\sum\limits_{{k = 1}}^{n} {\lambda _{{i,j}}^{m} \lambda _{{ik}}^{m} } } Cov\left( {b_{j}^{r} ,b_{k}^{r} } \right).$$
(18)

Boundary Conditions

The boundary conditions implemented in the present work are expressed as follows:

  1. 1.

    For clamped (CCCC) boundary condition, the degree of freedom at all sides is zero.

  2. 2.

    For simply supported (SSSS), v = w = φy = ψy = 0 at x = 0 and a, whereas u = w = φx = ψx = 0 at y = 0 and b.

The flowchart for the deterministic simulation of cracked plate for free vibration is presented in Fig. 5. A MATLAB code based on the algorithm given in the flowchart is developed to simulate the problem.

Fig. 5
figure 5

Flowchart of deterministic approach for free vibration analysis of cracked plate

Full size image

Numerical Results and Discussion

In this section, a numerical analysis is presented using the developed formulation. An in-house MATLAB code is developed to solve the defined problem. The algorithm for the developed XFEM formulation is illustrated in Fig. 5. To check the accuracy and reliability of the developed XFEM formulation, a comparative study is conducted. This study involves solving various numerical problems, considering different parameters, such as material uncertainty, porosity, cracks, and volume fraction, with various boundary conditions. The section begins with the deterministic results for a porous FG plate with cracks, followed by a detailed stochastic analysis and discussion is performed.

Convergence and Comparative Study

In this sub-section, the developed mathematical formulation for the defined problem is validated by solving some numerical examples.

Example 1.

A problem of free flexural vibration in a non-cracked porous plate is solved for validation. The plate is assumed to be square and simply supported, with a thickness ratio (b/h) of 10. Material properties from Table 1 are utilized, and the results are compared, as presented in Table 2. The observation from the validation study lead to the conclusion of the efficacy and accuracy of the solution.

Table 1 Material properties [49] of FGM plate
Full size table
Table 2 Validation of the linear frequency under SSSS boundary condition for the porous FGM plate; a/b = 1; h/b = 0.1; Al/ Al2O3
Full size table

Example 2.

In this problem, free flexural vibration of edge cracked functionally graded plate has been solved for the comparison study. Material properties from Table 1 are utilized. The plate considered is square and simply supported, with a thickness ratio of h/b = 0.1, and it has an edge crack located at y = a/2. The results are compared, as reported in Table 3. The findings from the validation study indicate the effectiveness of the developed formulation.

Table 3 Validation of linear frequency (\(\omega^{*} = \omega (a^{2} /h)\sqrt {\rho_{c} /E_{C} }\)) for cracked FGM plate under SSSS boundary condition; a/b = 1; h/b = 0.1; Al/ Al2O3
Full size table

Example 3.

In this example, a numerical problem is solved in a stochastic medium, and the results are compared with the results available in the literature. The effect of material randomness on dispersion in the linear frequency is evaluated. The FOPT is implemented to solve the problem. The covariance of the square of natural frequency is evaluated by varying the covariance of Young’s modulus of ceramic from 0 to 20%. Functionally graded material (Al/ZrO2) is assumed for this problem. A square FG plate with simple support and a thickness ratio of 0.1 is considered. The material properties are as follows: Ec = 151 GPa; Em = 70 GPa; ρc = 3000 kg/m3; ρm = 2707 kg/m3; νc = 0.3; νm = 0.3. The value of the gradient index is 2. The results are compared and reported in Fig. 6. The validation inference confirms the accuracy of the solution.

Fig. 6
figure 6

Validation of linear frequency dispersion variation for Young’s modulus uncertainty in ceramics using the present method and a prior study

Full size image

Parametric Study

In this section, deterministic and stochastic free flexural vibrations of cracked FG plates are presented. The schematic diagram of the considered functionally graded plate is shown in Fig. 1. The material properties listed in Table 1 are utilized.

Deterministic Analysis

In this sub-section, simulation for free vibration of porous FG plate (Al/Al2O3) with a crack is performed in a deterministic environment. A simple supported square porous plate is considered with a thickness ratio of h/b = 0.1 and an edge crack located at y = a/2. The porosity index can be defined as the volume fraction of porous medium to the whole domain or in terms of percentage. The porosity index is varying from 0 to 0.3.

The non-dimensional frequency \(\omega^{*} = \omega h\sqrt {\rho_{{\text{c}}} /E_{{\text{c}}} }\) is evaluated. The results for influential parameters such as gradient and porosity indexes are obtained. The obtained results for various boundary conditions are reported in Tables 4, 5, and 6. The investigation reports the variation in frequency. The value is decreasing with the increase in the gradient index. The frequency is also decreasing with the increase in crack size. With the increase in porosity index, the value of the frequency increases for gradient index zero (fully ceramic), whereas, for gradient index rise, the value of frequency decreases.

Table 4 Variation of non-dimensional frequency (\(\overline{\omega }^{{}} = \omega h\sqrt {\rho_{{\text{c}}} /E_{{\text{c}}} }\)) with porosity of FGM plate under SSSS boundary condition; a/b = 1; h/a = 0.01; Al/Al2O3
Full size table
Table 5 Variation of non-dimensional frequency (\(\overline{\omega }^{{}} = \omega h\sqrt {\rho_{{\text{c}}} /E_{{\text{c}}} }\)) with porosity of FGM plate under CCCC boundary condition; a/b = 1; h/a = 0.01; Al/Al2O3
Full size table
Table 6 Variation of non-dimensional frequency (\(\overline{\omega }^{{}} = \omega h\sqrt {\rho_{{\text{c}}} /E_{{\text{c}}} }\)) with porosity of FGM plate under SSCC boundary condition; a/b = 1; h/a = 0.01; Al/Al2O3
Full size table

Stochastic Analysis

In this section, stochastic-free vibration in cracked porous FG plate based on HSDT plate kinematics is presented. The FG plate is assumed to be composed of ceramic and metal. One side is considered fully ceramic, while the other side is fully metal. In the region between these two sides, the material composition varies according to a power-law distribution. The First-Order Probability Theory (FOPT) is implemented for the stochastic analysis and validated with previous studies that used the Second Order Reliability Method, as illustrated in Fig. 7. This figure clearly demonstrates that the covariance (standard deviation/mean) of the natural frequency increases with an increase in the covariance of the Young's moduli (ceramic/ metal). It can also be observed that the covariance in the natural frequency of the FGM plate is higher when considering the covariance in Young's modulus of metal. The analysis is performed for various porosity indices and various gradient indexes. Material uncertainty in Young’s modulus and Poisson’s ratio, is considered an input variable. These analyses aim to explore the influence of material randomness on the dispersion in frequency. Figures 8 and 9 present the stochastic simulation of a cracked square FGM plate (a/b = 1, h/a = 0.1, d/b = 0.5) for free vibration. A square plate with a thorough edge crack is considered for the analysis. The crack is located at the edge of the plate (y = a/2). The crack is assumed to be static. The thickness ratio of the plate is assumed as h/a = 0.01. The material considered for this problem is Al/ Al2O3, whose material properties are given in Table 1. The porosity index is varying from 0 to 0.4. The porosity index can be defined as the volume fraction of porous medium to the whole domain or in terms of percentage.

Fig. 7
figure 7

Comparative analysis of covariance variation (SD/Mean) in natural frequencies of FGM plate between present and previous study

Full size image
Fig. 8
figure 8

Dispersion in linear frequency as a function of porosity index for varying Young’s modulus in ceramic (a, c, e) and metal (b, d, f) under different boundary conditions

Full size image
Fig. 9
figure 9

Illustrate the impact of Poisson’s ratio uncertainty on linear frequency dispersion of FGM plate at different porosity levels

Full size image

The covariance of linear frequency varies linearly with the covariance of Young’s modulus (SD/mean). Figure 8a, c, e shows the dispersion in linear frequency decreases with the increase in porosity index for variation in Young’s modulus of ceramic. Whereas the dispersion in linear frequency increases with the increase in porosity index for variation in Young’s modulus of metal, as shown in Fig. 8b, d, and f. From these figures, it can be observed that the dispersion of natural frequency of the plate is higher when the plate is subjected to CCCC boundary conditions, and the lowest natural frequency is obtained under SSSS boundary conditions. The effect of uncertainty in Poisson’s ratio on dispersion in linear frequency of FGM plate (a/b = 1, h/a = 0.1, d/b = 0.5) is shown in Fig. 9. From this figure, it can be observed that the covariance of natural frequency increases with an increase in the covariance of Poisson's ratio. As the porosity index increases, the dispersion in natural frequency increases with respect to the covariance of poisson’ ratio. The effect of Poisson’s ratio on dispersion in linear frequency for various porosity indices is much less with respect to Young’s modulus. Figures 10 and 11 show the influence of the coefficient of variation of material properties on the dispersion in free vibration of the cracked plate in the porous medium. Functionally graded material Al/Al2O3 is assumed for the present investigation, and material properties are given in Table 1. A square plate with a thorough edge crack is considered for the analysis. The coefficient of variation (SD/mean) of the input parameter varies from 0 to 20% to examine the dispersion in the frequency parameter. Figure 10 shows the influence of uncertainty in Young’s modulus on dispersion in linear frequency of FGM plate (a/b = 1, h/a = 0.01, d/b = 0.5) for various gradient indices. With the increase in the gradient index, the covariance of linear frequency is decreasing for Young’s modulus of ceramic. The problem is solved for various boundary conditions and various gradient indices. Figure 11 shows the influence of uncertainty in Young’s modulus on dispersion in linear frequency of FGM plate (a/b = 1, h/a = 0.01, d/b = 0.5) for various porosity indices. The covariance of linear frequency varies with the variation in Young’s modulus (SD/mean). Figure 11a, c, e shows the dispersion in linear frequency decreases with the increase in porosity index for variation in Young’s modulus of ceramic. Whereas the dispersion in linear frequency increases with the increase in porosity index for variation in Young’s modulus of metal, as shown in Fig. 11b, d, and f. From these figures, it can be observed that the dispersion of natural frequency of the plate is higher when the plate is subjected to CCCC boundary conditions, and the lowest natural frequency is obtained under SSSS boundary conditions.

Fig. 10
figure 10

Effect of Young’s modulus (ceramic) uncertainty on linear frequency dispersion of FGM plate at different gradient indices and boundaries

Full size image
Fig. 11
figure 11

Dispersion in linear frequency as a function of porosity index for varying Young’s modulus in ceramic (a, c, e) and metal (b, d, f) under different boundary conditions

Full size image

Conclusions

In this study, both deterministic and stochastic analyses for free flexural vibration of the cracked porous functionally graded plate are reported. In the deterministic analysis, extended finite element formulation based on higher order shear deformation plate kinematics is successfully implemented using in-house MATLAB code for considered problems. In stochastic analysis, FOPT is employed to anticipate the covariance of the linear frequency with the material randomness. This study is interesting because it examines how cracks, porosity, and gradient index affect the natural frequency of functionally graded materials (FGMs). Additionally, it explores how material randomness influences this behavior through stochastic analysis, informing better material design and structural integrity. These insights have significant implications for practical applications in engineering and materials science. The robustness and efficacy of the proposed computational algorithm are validated by several numerical examples presented in this paper. A further parametric study has been performed for both deterministic and stochastic problems with various influential parameters. The investigation concluded with the following observations:

  • The presence of a crack has a significant effect on the non-dimensional frequency of the plate, resulting in a reduction in the natural frequency as the crack size increases.

  • An increase in the gradient index is associated with a reduction in the non-dimensional natural frequency of the FGM plate.

  • The covariance of material properties has a notable effect on the linear frequency of the plate. Specifically, as the coefficient of variation in material properties increases, the coefficient of variation of natural frequency also increases linearly.

  • The porosity index plays a role in influencing the dispersion in the linear frequency of the plate. As the porosity index increases, the dispersion in linear frequency decreases for variations in Young’s modulus of ceramic. However, for variations in Young’s modulus of metal, the dispersion in linear frequency increases with a higher porosity index.

  • A higher gradient index reduces the variation in linear frequency for changes in Young’s modulus of ceramic.