Free vibration analysis of laminated composite porous plate

Abstract

In the present work, the free vibration response of laminated composite porous plates explored using improved cubic shear deformation theory. It is the first attempt to analyse vibration analysis of the laminate using this advanced theory. In this theory, transverse shear stress continuity incorporated at the interface of each laminate in conjunction with free surface consideration at the plate top and bottom. The different types of porosity distribution introduced in the entire thickness of the plate. A 2D finite element model developed for the present mathematical model to analyse the fundamental frequency of the porous plate. Due to the interface shear stress continuity of individual layers, the improved third-order shear deformation theory depicts better results than the first, second, and third-order theories. An in-house FORTRAN code developed for the present study by the authors. The effects of different orientation angles, boundary conditions, and material properties on the fundamental frequency were investigated with different numerical examples. The convergence study was conducted to determine the stability and accuracy of the present model. The results in comparison with the literature found to agree well.

Introduction

Recent studies have focused on the vibrations of multi-layered composite plates. Use of this research is for the marine system, laminated construction, aircraft, etc. Hence, it increased the interest of engineers while modelling such structures under the effects of dynamic behaviour, leading to an exact solution and saving computational time. Many researchers have done work related to the vibration analysis of isotropic and composite plates. It can be seen in detail in the literature. Nosier et al. (1993) performed Reddy’s research using layer-wise theory to determine natural frequency and various mode shapes and elasticity equations are explained with the help of state-space variables and transfer matrix. Qatu (1994) presented known natural frequency for different shapes of a cross-section of cantilever laminated angle ply, such as triangular, trapezoidal, and so on, and also analysed for convergence and obtained reasonably accurate results. Cheung and Zhou (2001) investigated free vibration due to static sinusoidal loading of rectangular laminated plates. In this investigation vibrating trial function is used in this study for the in-plane shear deformation of the plate. Shimpi (2002) performed a single response of bending and shear i.e., not contributed to each other by using loading bending moment and shear forces. The effectiveness of this theory is performed by numerical examples. Liew (2003) computed natural frequency due to the vibration effect of the laminated plate and compare it with the published result using moving least square deferential quadrilateral methods. Jianwei et al. (2004) analysed a simply supported curve panel with the help of higher-order shear deformation theory. A set of Fourier series function is formed for the highly coupled deferential equation and the boundary conditions. Ferreira and Fasshauer (2006) performed a numerical result and discussed different thickness-to-length ratios for the vibration analysis of the Timoshenko beam. Magnucka-Blandzi and Magnucki (2007) derived a differential equation of equilibrium on the basis of minimum potential energy for designing a sandwich beam having metal core foam. Liu et al. (2008) used the linearly interpolation method a mesh-free approach is made for the flexure analysis of the multi-layered combined beam. Seçgin and Sarigül (2008) presented the first computer algorithm then it verifies with the discrete solution convolution for the exact simply supported thin beam having simply supported end condition. Zhang et al. (2008) investigated using Bernoulli’s-Euler flexural hypothesis due to load for the dynamic responses to the double-beam connected elastically having simply supported end condition. Ferreira et al. (2011) performed using a radial-based formulation to the buckling and dynamic responses of isotropic layered plates, and a numerical approach is explained for the same. Benachour et al. (2011) presented that the refined lamina method for the transverse stress causes a parabolic distribution of shear strain without shear correction for the vibration analysis having different gradient values. Palmeri and Adhikari (2011) investigated the vibration analysis of a double-beam system with an elastically connected outer beam and an inner viscoelastic beam, and a numerical example was performed to ensure the accuracy of the results. Bîrsan et al. (2012) examined the direct approach for the deformation analysis of a functionally graded beam. It is performed in general analytical formulation and it is valid for any shape of cross-section. Qu et al. (2013) performed with different boundary conditions of vibration behaviour of a shell using the first shear deformation hypothesis. Material properties are varied to the thickness of the shell. Bhardwaj et al. (2015) developed a finite element model having eight nodded triangular cut-out and analysed it with the help of ANSYS Code. A convergence study is also conducted for available literature and then analysed for varying edge conditions, material characteristics, thickness ratio and geometry of the cut-out. Li et al. (2016) performed a semi-numerical hypothesis to determine the dynamic responses of a double-beam approach with the viscoelasticity of the inside layer of the plate. Based on frequency and mode shape, a nodal-expansion approach is further applied to analyse the response of forced vibration. Li and Sun (2016) analysed the natural frequency and mode shape with the help of a semi-analytical hypothesis for the double-beam approach having a uniformly distributed elastic layer with arbitrary boundary condition, material properties, thickness ratio and loading condition. Rezaei and Saidi (2016) observed that due to the change in porosity effect along the thickness of the plates, changes the mechanical properties of the laminated rectangular cellular plates. It follows the cosine rule for properties of the cellular plate and observes that natural frequency is decreased by the porosity effect in each discussed boundary condition. Belarbi et al. (2017) investigated with analytical approach and analysed it by higher order layered theory for the flexural analysis of the multi-layered plate. Gurjar et al. (2017) examined an orthotropic laminated plate for dynamic responses of a symmetric thick plate using an ANSYS design language for the finite element model using first-order shear deformation hypothesis. Rezaei et al. (2017) examined the dynamic behaviour of a laminated plate with two boundary layer functions. The effect of changes in porosity, thickness ratio, material properties, and aspect ratio on natural frequency appears to be investigated in depth. Ebrahimi et al. (2017) investigated dynamic responses due to magneto electric elasticity laminated plate having even and uneven porosity by analytical methods for the arbitrary boundary condition. It seems that mechanical properties vary with plate thickness, and porosity distribution approximates a power law. Muni Rami Reddy et al. (2018) investigated dynamic responses of thin and thick layered plates with the help of an analytical approach and found all possible natural frequencies of the plate. Arshid and Khorshidvand (2018) examined the dynamic behaviour of porous curved plates with piezoelectric patches. Researchers consider thin plates and transverse shear stress to be neglected. The methodology has been made with the help of classical plate theory. Wang’s et al. (2019) proposed a two-dimensional elasticity model by assuming plane stress in each layer of the laminate and edge conditions are linked with the 2D elasticity hypothesis. Saidi and Sahla (2019) presented a new deformation theory of the natural frequency with the elasticity medium of a porous plate. In this study, a new porosity distribution is introduced for the formation of porosity during the fabrication of the functionally graded plate inside. Safaei et al. (2019) examined the fundamental response of various plate models, including the higher deformation theory and plate theory of carbon nanotube-containing plates. The material properties of nanocarbon tubes are investigated using a multiscale finite element approach for different composites. It analysed the porosity effect of multi-layered plate based on higher-order theory and parabolic distribution of stress is experienced along the thickness of the plate and due to shear correction is neglected. Merdaci (2019) analysed the porosity effect of a layered plate using higher order deformation hypothesis, and a nonlinear distribution of stress is experienced to the plate thickness and due to this shear correction is neglected. With isogeometric analysis, Xue et al. (2019) investigated porosity effect of thick plates having different types of cross-section such as circular, rectangular, and square. He presented numerical examples with different porosity distribution, boundary condition and material properties for validation of results. Ghasemi and Meskini (2019) performed a circular cylindrical shell with a porosity effect with the help of Love’s shell hypothesis and found that with an increase in porosity coefficient, the non-dimensional frequency decreases. Yüksel and Akbaş (2019) considered a uniform porosity model for the laminates and material properties are orthotropic and a computer programme is used for the result computation. In the analytical approach, the porosity distribution, orientation and sequence of the laminate are investigated, and it is found that porosity is a significant change to the free vibration analysis of laminated plates. Alambeigi et al. (2020) presented three arbitrary models for porosity that were introduced for the force and free vibration of the plate. The porosity distribution is along the thickness of the core and the result is validated with different literature. A mathematical model investigated by Soleimanian et al. (2020) of the perforated composite plate for the vibrational analysis due to the temperature effect. Based on the classical plate hypothesis, a significant change in the result has been found due to perforation for the thermal buckling and vibrational frequency. Belarbi et al. (2021) investigated a layer-wise model for the vibrational analysis of sandwich plates for different boundary conditions. The advantage of this study is that when varying the number of layers on the plate, unknowns may be fixed and the results are compared for 2D, 3D quasi, and 3D convergence studies, which are beneficial for both thin and thick layered sandwich plates. Many studies have been conducted by researchers for rectangular, square, and circular laminated plates, with less attention being paid to the elliptical shape, but Balak et al. (2021) studied the vibrational behaviour of a porous-core elliptical lamina having two piezoelectric layers. Adopted theory is widely used for a variety of boundary conditions, including simple and fixed, and getting better results for frequency. Kim et al. (2021a, 2021b) performed a double beam system for vibrational analysis of functionally graded plates. The correctness and convergence of the applied methods are satisfied by having different literature using a finite element approach. A lot of new results have been found for the frequency characteristics of the plate. Zhang et al. (2021) introduced a mathematical model for double beam systems for fundamental frequency of multi-layered 3D plate. Now a combination of first-order deformation theory and classical plate theory are introduced in the governing equation. In addition to it Fourier series is also applied to the mathematical model in order to find natural frequency and mode shape with complex boundary conditions. Devarajan (2021) investigated the effects of iso-geometric vibration on the curvilinear plate using first-order shear deformation. The convergence study is carried out and the new result is analysed with numerical examples with different angles of orientation, thickness ratio, sequence of laminate, shape and boundary condition of laminate. Kim et al. (2021a, 2021b) introduced the elastic sprig technique for different boundary conditions for the dynamic responses of the double plate system plate. By using meshfree discussion, all displacement functions are considered, including boundary condition. The proposed model is validated with past literature and analytical methods. A detailed discussion of the fundamental frequency is to be done in the present study for the different shapes of boundary conditions and material properties. Kumar et al. (2021) investigated a varying depth porous functionally graded plate for normal frequency, which was resting on Pasternack’s and Winkler’s elastic foundation system. The numerical solution is presented with varying, height-to-width ratio, support conditions, and shape of the layered plate. Verma et al. (2022) investigated carbon boron-based matrixes for the normal frequency of the lamina using classical plate theory for different support conditions. Sayyad et al. (2022) analysed the circular beam for dynamic responses and static analysis with even and uneven porosity due to a lack of literature. A numerical example is discussed for the non-dimensional values of displacement stresses and fundamental frequency having different even and uneven porosity, power law index, and radius of curvature. Van Vinh and Huy (2022) presented analytical methods for the flexural, buckling, and nonlinear responses of the porous plate using the hyperbolic shear deformation hypothesis. With the help of computer code in MATLAB, he analysed the mechanical behaviour of the multi-layered plate with different porosity distributions and the significant role of porosity is discussed with a numerical problem in detail. In this research article, entire analysis is due to the porosity effect, different orientation angle and different edge condition had been analysed for the dynamic response of the multi-layered plate. Many researchers had been used methods like first, second and third-order theory in the past year. No one Researcher has used improved third-order theory as method for free vibration analysis for the laminated porous plate. All results are computed based on improved third-order theory. I analysed various example for the normalized fundamental frequency with help of In-house code with a 2D finite element model.

Methodology

Free vibration analysis and governing equation

The present study consists of free vibration analysis and governing equation for this analysis is as follows:

$$\left[ K \right]\left\{ \varphi \right\} = \omega^{2} \left[ M \right]\left\{ \varphi \right\}$$

(1)

Stress–strain relationship

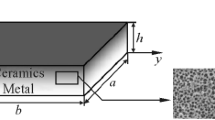
In Fig. 1 a four-layered rectangular plate has been shown which has length are ${L}_{X}$ and ${L}_{Y}$. The thickness is shown in Z direction. The plate is split into three equal sections with symmetry about the midplane. So that individual thickness of the plate is h/6 and h/3 is in the upper part and same thickness in the lower part of the plate. In the present investigation, three different lamina are opted with different orientation angle having simply supported edge condition. The whole segment of the laminate illustrated in Fig. 2, uses the porosity distribution model. This distribution approach states that the material characteristics for the laminate (E) vary depending on the young modulus, poison’s ratio, etc., and are followed as E(p) = E(1-p). Below is a detailed discussion of the relation between stress and strain:

$$\left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \tau_{xz} \hfill \\ \tau_{yz} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} (p)} & {\overline{Q}_{12} (p)} & {\overline{Q}_{16} (p)} & 0 & 0 \\ {\overline{Q}_{12} (p)} & {\overline{Q}_{22} (p)} & {\overline{Q}_{26} (p)} & 0 & 0 \\ {\overline{Q}_{16} (p)} & {\overline{Q}_{26} (p)} & {\overline{Q}_{66} (p)} & 0 & 0 \\ 0 & 0 & 0 & {\overline{Q}_{55} (p)} & {\overline{Q}_{45} (p)} \\ 0 & 0 & 0 & {\overline{Q}_{45} (p)} & {\overline{Q}_{44} (p)} \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \gamma_{xz} \hfill \\ \gamma_{yz} \hfill \\ \end{gathered} \right\}\quad {\text{or}}\quad \left\{ {\overline{\sigma } } \right\} = \left[ {Q^{ - i} } \right]\left\{ {\overline{\varepsilon } } \right\}$$

(2)

Fig. 1

Four-layered simply supported plate

Fig. 2

Distribution of porosity

Here the materials’ characteristics (${E}_{1},$ ${E}_{2}$, ${\nu }_{12}$,${G}_{13}$,${G}_{23}{,G}_{12}$) and the angle of orientation ($\theta$), Which is used to developed for the rigidity matrix $\left[ {Q^{ - i} } \right]$ in the present study.

$$\overline{Q}_{11} (p) = Q_{11} (p)\cos^{4} \theta + 2(Q_{12} (p) + 2Q_{66} (p))\sin^{2} \theta \cos^{2} \theta + Q_{22} (p)\sin^{4} \theta$$

$$\overline{Q}_{12} (p) = (Q_{11} (p) + Q_{22} (p) - 4Q_{66} (p))\sin^{2} \theta \cos^{2} \theta + Q_{12} (p)(\cos^{4} \theta + \sin^{4} \theta )$$

$$\overline{Q}_{22} (p) = (Q_{22} (p)\cos^{4} \theta + 2(Q_{12} (p) + 2Q_{66} (p))\sin^{2} \theta \cos^{2} \theta + Q_{11} (p)\sin^{4} \theta )$$

$$\overline{Q}_{16} (p) = (Q_{11} (p) - Q_{12} (p) - 2Q_{66} (p))\sin \theta \cos^{3} \theta + (Q_{12} (p) - Q_{22} (p) + 2Q_{66} (p))\sin^{3} \theta \cos \theta$$

$$\overline{Q}_{26} (p) = (Q_{11} (p) - Q_{12} (p) - 2Q_{66} (p))\sin^{3} \theta \cos \theta + (Q_{12} (p) - Q_{22} (p) + 2Q_{66} (p))\sin \theta \cos^{3} \theta$$

$$\overline{Q}_{66} (p) = (Q_{11} (p) + Q_{22} (p) - 2Q_{12} (p) - 2Q_{66} (p))\sin^{2} \theta \cos^{2} \theta + \overline{Q}_{66} (p)(\cos^{4} \theta + \sin^{4} \theta )$$

$\overline{Q}_{44} (p) = G_{13} (p)\cos^{2} \theta + G_{23} (p)\sin^{2} \theta$, $\overline{Q}_{45} (p) = (G_{13} (p) - G_{23} (p))\sin \theta \cos \theta$

$$\overline{Q}_{55} (p) = G_{23} (p)\cos^{2} \theta + G_{13} (p)\sin^{2} \theta$$

$$Q_{11} (p) = \frac{{E_{1} (p)}}{{1 - \nu_{12} (p)\nu_{21} (p)}},Q_{12} = \frac{{\nu_{12} (p)E_{2} (p)}}{{1 - \nu_{12} (p)\nu_{21} (p)}},Q_{22} = \frac{{E_{1} (p)}}{{1 - \nu_{12} (p)\nu_{21} (p)}},Q_{66} = G_{12} (p).$$

(3)

Relationship between material characteristics and displacement

In Fig. 3, the variation of in-plane displacement over the plate's thickness at the interfaces of the several laminated layers is displayed.

$$\left\{ {u_{1} } \right\} = \left\{ {u_{1}^{0} } \right\} + \sum\nolimits_{i = 0}^{nu - 1} {S_{1}^{i} } (Z - Z_{i} )\left\{ H \right\}(Z - Z_{i} ) + \sum\nolimits_{i = 1}^{nl - 1} {T_{1}^{i} } (Z - \rho_{i} )\left\{ H \right\}( - Z + \rho_{i} ) + \left\{ {\xi_{1} } \right\}Z^{2} + \left\{ {\varphi_{1} } \right\}Z^{3}$$

(4)

$$\left\{ {u_{2} } \right\} = \left\{ {u_{2}^{0} } \right\} + \sum\nolimits_{i = 0}^{nu - 1} {S_{2}^{i} } (Z - Z_{i} )\left\{ H \right\}(Z - Z_{i} ) + \sum\nolimits_{i = 1}^{nl - 1} {T_{2}^{i} } (Z - \rho_{i} )\left\{ H \right\}( - Z + \rho_{i} ) + \left\{ {\xi_{2} } \right\}Z^{2} + \left\{ {\varphi_{2} } \right\}Z^{3}$$

(5)

Fig. 3

In-plane displacement throughout the laminate’s plate thickness

where nu and nl stand for the number of the upper layer and lower layer, respectively, and $\left\{ {u_{1}^{0} } \right\}$ indicate the in-plane displacement for any point to the middle layer surface.$S_{1}^{i}$, $S_{2}^{i}$, $T_{1}^{i}$, $T_{2}^{i}$ represent the gradient of ith layer of the lower and upper layers, respectively. Unit step functions, higher-order unknown terms, and coordinate directions are represented by $\left\{ H \right\}(Z - Z_{i} )$, $(Z - \rho_{i} )$,$\left\{ {\xi_{1} } \right\}$, $\left\{ {\xi_{1} } \right\}$, $\left\{ {\varphi_{1} } \right\}$, $\left\{ {\varphi_{2} } \right\}$, and 1, 2 (i.e., $x,\;y$ in this equations), respectively.

Transverse displacement is considered to be constant over the full thickness of the plate. which is a function of x and y i.e.,

$$\left\{ {u_{3} } \right\} = \left\{ {w} \right\}$$

(6)

By excluding some terms from HZT's in-plane displacement expressions, FSDT and Third order theory were substituted for the expansion-enhanced higher-order theory. By excluding the following terms from Eqs. 4 and 5, Zig zag theory becomes the important generic hypothesis. For higher-order shear deformation theory, all not included $S_{1}^{i}$, $S_{2}^{i}$,${S}_{3}^{i},$ $T_{1}^{i}$, $T_{2}^{i}$,${T}_{3}^{i}$ except${S}_{1}^{0}$, ${T}_{1,}^{0 }{S}_{2,}^{0}$, ${T}_{2}^{0} , {S}_{3}^{0}{ ,T}_{3}^{0}$ and for FSDT expecting $\xi_{i}$, $\varphi_{i}$ and all ${S}_{\alpha }^{i}, {T}_{\alpha }^{i},$ except ${S}_{\alpha }^{0}$, ${T}_{\alpha }^{0},$ where α = 1,2 i.e., x and y direction of the laminated plate.

Using the edge condition and transverse shear stress for the top and bottom of the plate. $\sigma_{3\alpha /z = \pm h/2} = 0$ now $\xi_{\alpha }$ and $\varphi_{\alpha }$ of the advanced third-order shear deformation hypothesis may be presented, where α = 1, 2 represent x and y coordinate of the laminated plate

$$\left\{ {\varphi_{1} } \right\} = - \frac{4}{{3h^{2} }}\left\{ {w_{1} + \frac{1}{2}\left( {\sum\nolimits_{i = 0}^{nu - 1} {S_{1}^{i} } + \sum\nolimits_{i = 0}^{nl - 1} {T_{1}^{i} } } \right)} \right\}$$

(7)

$$\left\{ {\varphi_{2} } \right\} = - \frac{4}{{3h^{2} }}\left\{ {w_{2} + \frac{1}{2}\left( {\sum\nolimits_{i = 0}^{nu - 1} {S_{2}^{i} } + \sum\nolimits_{i = 0}^{nl - 1} {T_{2}^{i} } } \right)} \right\}$$

(8)

$$\left\{ {\xi_{1} } \right\} = - \frac{1}{2h}\left\{ {w_{1} + \frac{1}{2}\left( {\sum\nolimits_{i = 0}^{nu - 1} {S_{1}^{i} } - \sum\nolimits_{i = 0}^{nl - 1} {T_{1}^{i} } } \right)} \right\}$$

(9)

$$\left\{ {\xi_{2} } \right\} = - \frac{1}{2h}\left\{ {w_{2} + \frac{1}{2}\left( {\sum\nolimits_{i = 0}^{nu - 1} {S_{2}^{i} } - \sum\nolimits_{i = 0}^{nl - 1} {T_{2}^{i} } } \right)} \right\}$$

(10)

Comparatively, by substituting the continuation of the transverse stress to the inner layer of surfaces. The subsequent ${S}_{\alpha }and$ ${T}_{\alpha }$ expressions are mentioned as follows:

$$S_{1}^{i} = a_{1\gamma }^{i} \left( {w_{\gamma } + \Psi_{\gamma } } \right) + b_{1\gamma }^{i} w,_{\gamma }$$

(11)

$$S_{2}^{i} = a_{2\gamma }^{i} \left( {w_{\gamma } + \Psi_{\gamma } } \right) + b_{2\gamma }^{i} w,_{\gamma }$$

(12)

$$T_{1}^{i} = c_{1\gamma }^{i} \left( {w_{\gamma } + \Psi_{\gamma } } \right) + d_{1\gamma }^{i} w,_{\gamma }$$

(13)

$$T_{2}^{i} = c_{2\gamma }^{i} \left( {w_{\gamma } + \Psi_{\gamma } } \right) + d_{2\gamma }^{i} w,_{\gamma }$$

(14)

where $a_{1\gamma }^{i}$,$b_{1\gamma }^{i}$,$a_{2\gamma }^{i}$,$b_{2\gamma }^{i}$,$c_{1\gamma }^{i}$,$d_{1\gamma }^{i}$,$c_{2\gamma }^{i}$,$d_{2\gamma }^{i}$ are constants, which depends on the material characteristics and geometry of each layers and $w,_{\gamma }$ is a transverse displacement derivative which is assumed as constant earlier, where $\gamma$=1, 2 and ${S}_{\alpha }^{0}$= $\Psi_{\alpha }$ is angular displacement about midpoint of the axis where. Now by using Eq. (2), Eqs. (4) and (5)–Eqs. (13) and (14) we find strain field vector and it is obtained as:

$$\left\{ {\overline{\varepsilon } } \right\} = \left[ H \right]\left\{ \varepsilon \right\}$$

(15)

$\left\{ \varepsilon \right\}$ is corrected midplane strain, which has a size of 17 × 1, and $\left\{ {\overline{\varepsilon } } \right\}$ is the strain field vector of matrix size 5 × 1. $\left[ H \right]$ matrix having size of 5 × 17 comprises relevant term to material characteristics and ‘z’ containing terms

$$\left\{ \varepsilon \right\}^{T} = \left\{ \begin{gathered} \frac{{\delta u_{1} }}{\delta x}\frac{{\delta u_{2} }}{\delta y}\frac{{\delta u_{2} }}{\delta x} + \frac{{\delta u_{1} }}{\delta y}\frac{{\delta w_{1} }}{\delta x}\frac{{\delta w_{2} }}{\delta y}\frac{{\delta w_{2} }}{\delta x}\frac{{\delta w_{1} }}{\delta y}\frac{{\delta \psi_{1} }}{\delta x}\frac{{\delta \psi_{2} }}{\delta y} \hfill \\ \frac{{\delta \psi_{2} }}{\delta x}\frac{{\delta \psi_{1} }}{\delta y}\Psi_{1} \Psi_{2} \frac{\delta w}{{\delta x}}\frac{\delta w}{{\delta y}}w_{1} w_{2} \hfill \\ \end{gathered} \right\}$$

(16)

$$\left\{ \varepsilon \right\} = \left[ B \right]\left\{ \delta \right\}$$

(17)

where $\left\{ \delta \right\}$ is the unknown nodal vector having a matrix size of 63 × 1. $\left[ B \right]$ is the usual strain displacement matrix having a size of 17 × 63.

Finite element formulation

The displacement fields must have ${\mathrm{C}}^{1}$ continuity with the transverse displacement to use the finite element formulation. The derivatives of w are written as to avoid issues with ${\mathrm{C}}^{1}$ continuity with respect to x and y are written as

$$\frac{\delta w}{{\delta x}} = w_{1} \quad {\text{and}}\quad \frac{\delta w}{{\delta y}} = w_{2}$$

(18)

The aforementioned equations aid in defining all changeable terms, including $w_{1}$ and $w_{2}$ as ${\mathrm{C}}^{0}$ continuity. The nine nodded quadrilateral ${\mathrm{C}}^{0}$ continuous isoperimetric element employed in the current study has seven degrees of node freedom and is mentioned below. Figure 4 illustrate an isoparametric element with nine nodes.

$$\begin{gathered} u_{1} = \sum\limits_{i = 1}^{9} {N_{i} u_{i} } ,\;u_{2} = \sum\limits_{i = 1}^{9} {N_{i} v_{i} } ,\;u_{3} = \sum\limits_{i = 1}^{9} {N_{i} u_{i} } ,\;\psi_{1} = \sum\limits_{i = 1}^{9} {N_{i} \psi_{1i} } ,\; \hfill \\ \psi_{2} = \sum\limits_{i = 1}^{9} {N_{i} \psi_{2i} } ,\;w_{1} = \sum\limits_{i = 1}^{9} {N_{i} w_{1i} } ,\;w_{2} = \sum\limits_{i = 1}^{9} {N_{i} w_{2i} } \hfill \\ \end{gathered}$$

(19)

Fig. 4

Nine nodded isoparametric element

where ${N}_{i}$ is the shape function of the ${i}_{\mathrm{th}}$ node and shape function for analysis of the model is given below:

$$\begin{gathered} N_{1} = (1 - \xi )(1 - \eta )/4;\;N_{2} = (1 - \xi )(1 + \eta )/4;\;N_{3} = (1 + \xi )(1 + \eta )/4;\; \hfill \\ N_{4} = (1 + \xi )(1 - \eta )/4;\;N_{5} = (1 - \xi^{2} )(1 - \eta )/4;\;N_{6} = (1 - \xi )(1 - \eta^{2} )/2; \hfill \\ N_{7} = (1 - \xi^{2} )(1 + \eta )/2;\;N_{8} = (1 + \xi )(1 - \eta^{2} )/2;\;N_{9} = (1 - \xi^{2} )(1 - \eta^{2} ) \hfill \\ \end{gathered}$$

(20)

In this part, the element nodal load vector and element stiffness matrix are derived for the static analysis. The equation of equilibrium and the element stiffness matrix listed below may be created with the use of the Hamilton principle.

$$\left[ {k^{el} } \right] = \sum\limits_{i = 1}^{nu + nl} {\iiint {\left[ B \right]}^{T} } \left[ H \right]^{T} \left[ {Q^{ - i} } \right]\left[ H \right]\left[ B \right]dxdydz + \left[ {p_{0} } \right]$$

(21)

$$\left[ {k^{el} } \right] = \sum\limits_{i = 1}^{nu + nl} {\iint {\left[ B \right]^{T} }} \left[ D \right]\left[ B \right]dxdy + \left[ {p_{0} } \right]$$

(22)

where $\left[ B \right]$ is the strain matrix, $\left[ Q \right]$ is the converted material constant matrix and $\left[ H \right]$ is the matrix consists of terms containing z and material properties term.

where $\left[ D \right] = \int_{k = 1}^{n} {\int {\left[ H \right]}^{T} \left[ {Q^{ - i} } \right]} \left[ H \right]dz$.

Now, using Eq. 15, the sanction term is represented as

$$\left[ {p_{0} } \right] = \iint {\mu \left( {\left\{ {\frac{\delta w}{{\delta x}} - w_{1} } \right\}\left\{ {\frac{\delta w}{{\delta x}} - w_{1} } \right\} + \left\{ {\frac{\delta w}{{\delta y}} - w_{2} } \right\}\left\{ {\frac{\delta w}{{\delta y}} - w_{2} } \right\}} \right)}dxdy$$

(23)

where $\mu$ is the sanction parameter.

With the use of Eq. 19, the element load vector may also be obtained throughout the computation process and shown as

$$\left[ {p_{0} } \right] = \int {\left[ N \right]}^{T} qdxdy$$

(24)

where q is the magnitude of the transverse load and is $\left[ N \right]$ the matrix representing the shape function, respectively.

Element mass matrix

For free vibration problem, the acceleration at any point within the plate is can be expressed in form of reference plane parameters with the help of Eqs. (4)–(6) as

$$\left\{ {\ddot{f}} \right\} = - \omega^{2} \left\{ \begin{gathered} \overline{u}_{1} \hfill \\ \overline{u}_{2} \hfill \\ {\overline{w}} \hfill \\ \end{gathered} \right\}$$

(25)

$$\left\{ {\ddot{f}} \right\} = - \omega^{2} \left[ F \right]\left\{ f \right\}$$

(26)

where the matrix $\left[ F \right]$ is the order of 3 × 7 contains z and some constant qualities like that of $\left[ H \right]$ and

$$\left\{ f \right\} = \left[ {\begin{array}{*{20}c} {u_{1} } & {u_{2} } & {u_{3} } & {\psi_{1} } & {\psi_{2} } & {w_{1} } & {w_{2} } \\ \end{array} } \right]^{T}$$

(27)

Finally, it may be expressed in terms of nodal displacement vector $\left\{ \delta \right\}$ with the help of Eq. 19 as

$$\left\{ f \right\} = \left[ C \right]\left\{ \delta \right\}$$

(28)

where the matrix $\left[ C \right]$ is an order of 7 × 63 and $\left[ {N_{1} } \right]$, $\left[ {N_{2} } \right]$ along with its derivatives.

Now using the above Eqs. (25)–(28), the consistent mass matrix of an element can be derived as

$$\left[ {m^{e} } \right] = \sum\nolimits_{i = 1}^{nu + nl} {\int {\rho_{i} } } \left[ C \right]^{T} \left[ F \right]^{T} \left[ F \right]\left[ C \right]dxdydz = \int {\left[ C \right]^{T} \left[ L \right]\left[ C \right]} dxdy$$

(29)

where $\rho_{i}$ is the mass density of the ith layer and $\left[ C \right]$ is the shape function matrix and the matrix $\left[ L \right]$ is expressed as

$$\left[ L \right] = \int {\rho_{i} } \left[ F \right]^{T} \left[ F \right]dz$$

(30)

Free vibration analysis

In the governing Eq. (1) is solved by the simultaneous iteration technique for the calculation of eigen values and eigen vectors. In this method $\left[ K \right]$ is positive definite and can be expressed as

$$\left[ K \right] = \left[ L \right]\left[ T \right]^{T}$$

(31)

$$\left\{ {\left[ L \right]^{ - 1} \left[ M \right]\left[ L \right]^{ - T} } \right\}\left[ L \right]^{T} \left\{ \delta \right\} = \frac{1}{{\omega^{2} }}\left[ L \right]^{T} \left\{ \delta \right\}$$

(32)

In the above equation, it is solved for the exact eigen value and eigen vectors. In this Eq. 1/$\omega^{2}$ is the eigen value. Therefore, the eigen value crossholdings to the natural frequency. The non-dimensional natural frequencies are computed as

$$\overline{\omega } = \frac{{\omega a^{2} }}{h}\sqrt {\frac{\rho }{{E_{2} }}}$$

(33)

Results and discussion

In the present research article, many examples are discussed for the vibration analysis of the laminated porous plate using a finite element model. A convergence study is carried out to determine the accuracy and applicability of the finite element model. In the present analysis, improved third-order shear deformation is carried out throughout the entire discussion. I selected a 12 × 12 mesh size of the plate in the entire discussion. In addition to it, a different porosity distribution is introduced in relation to the thickness of the plate, like 0.1, 0.2, and 0.3. In the result and discussion portions, a change in the angle of orientation of the fibre is also experienced as an effect of the vibration analysis.

Example 1

This problem is solved to access the performance of the proposed finite element model for the free vibration analysis of laminated plates. The validation study of the present research is shown in Table 1, and new results have been obtained for the different porosity distributions, angles of orientation, and material properties, etc. A four-layered simply supported square (a = b) plate has an angle of orientation of $0^\circ$/$90^\circ$/$90^\circ /0^\circ$ and the material properties of each individual layer are considered as: ${E}_{1}$/${E}_{2}$=open, ${G}_{12}$=${G}_{13}$=0.6${E}_{2}$, ${G}_{23}$=0.5${E}_{2}$, $\upsilon_{12}$ = $\upsilon_{13}$ = 0.25 and $\rho = 1$. The non-dimensional natural frequencies are obtained as

$$\overline{\omega } = \frac{{\omega a^{2} }}{h}\sqrt {\frac{\rho }{{E_{2} }}} .$$

Table 1 Validation of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$

The normalised fundamental frequency parameter obtained by the present finite element model with various modulus ratios, thickness ratios, and changes in orientation angles of the laminated porous composite plate. A detailed discussion is carried out for the normalised fundamental frequency in Tables 2, 3, and 4 having different porosity distributions along the thickness of the plate with the help of improved third-order deformation theory. In Table 2, by decreasing the orientation angle of the laminated fiber, the normalised fundamental frequency increases for any modulus ratio like 10, 20, 30, or 40. In Table 2, all results have been shown without porosity distribution, like (p = 0). For a thickness ratio and modulus ratio of 10, the frequency is increased by 1.2% for the change in angle of orientation from $0^\circ$/$90^\circ$/$90^\circ 0^\circ$ to $0^\circ$/3$0^\circ$/30$^\circ 0^\circ$ and is also increases by approximately 1.4% for modulus ratio 20, 30, and 40. In Table 2, there seems to be no major change in normalised frequency by changing the angle of orientation of the laminate. But by changing the modulus ratio from 10 to 20 for a particular orientation angle, there is a major change in frequency of about 24.23%. Now in Table 3, a porosity of 0.1 is introduced in the entire thickness of the plate, and the frequency is reduced by 3.7% for the thickness and modulus ratio of 10 and orientation angle of $0^\circ$/$90^\circ$/$90^\circ /0^\circ$. In Table 3, for a modulus ratio of 30 and an orientation angle of $0^\circ$/$90^\circ$/$90^\circ 0^\circ$, the frequency increases by 16.84% due to a change in a thickness ratio of 10 to 20. In Table 4, the frequency is decreased by 8.87% compared to Table 2 for the thickness ratio, modulus ratio, and orientation angle of 20, 40 and $0^\circ$/$90^\circ$/$90^\circ /0^\circ$, respectively. In Table 4, the fundamental frequency is increased by 11%when then the thickness ratio is increased from 10 to 20 for the modulus ratio of 30 and orientation angle of $0^\circ$/$30^\circ$/$30^\circ /0^\circ$. Now a porosity distribution of 0.3 is introduced in the entire thickness of the plate and seems to be normalized frequency is decreased by 13.88% compared to the porosity of p = 0, for the thickness and modulus ratio of 20 having orientation angle of $0^\circ$/$45^\circ$/$45^\circ /0^\circ$. In Table 5, the fundamental frequency is increased to 13.67% by a change in a thickness ratio of 10–50 due to a modulus ratio of 30 and orientation angle of $0^\circ$/$60^\circ$/$60^\circ /0^\circ$.

Table 2 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$ having porosities (p = 0)

Table 3 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$ having porosities (p = 0.1)

Table 4 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$ having porosities (p = 0.2)

Table 5 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$ having porosities (p = 0.3)

Example 2

Fundamental frequencies for symmetric cross-ply laminated plates are presented in Tables 6, 7, 8, 9, and 10. In Table 6, a validation study is carried out for the accuracy and applicability of the finite element model with different boundary conditions. A three-layered symmetric cross-ply laminated simply supported square plate has an angle of orientation of $0^\circ$/$90^\circ /0^\circ$ and the material properties of each individual layer are considered as: ${E}_{1}$/${E}_{2}$=25, ${G}_{12}$=${G}_{13}$=0.5${E}_{2}$, ${G}_{23}$=0.2${E}_{2}$, $\upsilon_{12}$ = $\upsilon_{13}$ = 0.25 and $\rho = 1$. The non-dimensional natural frequencies are obtained as

$$\overline{\omega } = \frac{{\omega a^{2} }}{h}\sqrt {\frac{\rho }{{E_{2} }}} .$$

Table 6 Validation of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$/$0^\circ$ with different boundary condition

Table 7 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0)

Table 8 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0.1)

Table 9 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0.2)

Table 10 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0.3)

All layers are assumed to be the same thickness, density, and made of the same orthotropic material. The boundary condition and coordinates of the laminate are as follows: the edges $x_{1} = 0,a$ are assumed as simply supported while $x_{2} = \pm b/2$ can take any combination of clamped (C), Free (F), and simply supported (S) edge conditions.

In Table 6, the result is validated with a different boundary condition for an orientation angle of $0^\circ$/$90^\circ$/$0^\circ$ and new results are obtained in Tables 7, 8, 9, and 10 for laminated plates with different porosity, thickness ratio, orientation angle, and boundary conditions.

In Table 7, the normalised fundamental frequency is increased by decreasing the angle of orientation for different thickness ratios and boundary conditions. For the thickness ratio of 10, the fundamental frequency is increased by 8.2% by changing the orientation angle from $0^\circ$/$90^\circ$/$0^\circ$ to $0^\circ$/$30^\circ$/$0^\circ$ having edge condition SSSS. For boundary conditions of SSSC, frequency is decreased by 6.8% by changing the orientation angle from $0^\circ$/$90^\circ$/$0^\circ$ to $0^\circ$/$30^\circ$/$0^\circ$ having a thickness ratio of 20. As shown in Table 8, the fundamental frequency is reduced by 3.14% due to the porosity effect (p = 0 to p = 0.1) having SSCC boundary conditions. Now for the thickness ratio of 50 frequency is reduced by10% due to a change in orientation angle from $0^\circ$/$90^\circ$/$0^\circ$ to $0^\circ$/$45^\circ$/$0^\circ$ and having edge condition of the plate is SSFS. In Table 9, fundamental frequency is increased by 8.4% by changing the orientation angle from $0^\circ$/$90^\circ$/$0^\circ$ to $0^\circ$/$30^\circ$/$0^\circ$ for the SSCC end condition and having a thickness ratio of 20. Normalized fundamental frequency increases with decreasing orientation angle for a given thickness ratio. Now in Table 10, when the thickness ratio increases, the fundamental frequency also increases for any particular edge condition and orientation angle of the laminate. By introducing a porosity of 0.3, the frequency further decreases as compared to Table 7. For the SSFS edge condition, the frequency decreases by 9% by a change in orientation angle from $0^\circ$/$90^\circ$/$0^\circ$ to $0^\circ$/$45^\circ$/$0^\circ$ with a thickness ratio of 100.

Example 3

Two layered antisymmetric cross-ply laminated square plate having an orientation angle of $0^\circ$/$90^\circ$ is analysed for different boundary condition. Material properties are as follows: ${E}_{1}$/${E}_{2}$=25, ${G}_{12}$=${G}_{13}$=0.5${E}_{2}$, ${G}_{23}$=0.2${E}_{2}$, $\upsilon_{12}$ = $\upsilon_{13}$ = 0.25 and $\rho = 1$. Normal fundamental frequency is calculated the same as the previous example. In Table 11 result is validated and a new result has been obtained in Tables 12, 13, 14, and 15.

Table 11 Validation of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of orientation angle $0^\circ$/$90^\circ$ with different boundary condition

Table 12 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0)

Table 13 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0.1)

Table 14 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0.2)

Table 15 New result of normalized fundamental frequency ($\stackrel{-}{}$) for the simply supported square laminate of different boundary conditions having porosities (p = 0.3)

In Table 12 different angle of orientation has been applied in the anti-symmetric laminated plate with different boundary conditions. It seems to be normalized that fundamental frequency increases as decreases thickness of the plate. In most cases, boundary condition frequency is increased by a decrease in orientation angle of the laminate. Now for the edge condition, SSFC frequency decreases by 16.34% by decreasing the orientation angle from $0^\circ$/$90^\circ$ to $0^\circ$/$60^\circ$. A porosity distribution is p = 0.1 is induced in the entire thickness of the plate and the result is shown in Table 13 for the thickness ratio of 100 and orientation angle of $0^\circ$/$60^\circ$ fundamental frequency is decreased by 3.6% with edge condition SSSS. For a thickness ratio of 5 fundamental frequency is decreased by 19.8% having edge condition SSFC of the laminated plate.it seems to be frequency is decreased by 11.79% with a change in orientation angle of the anti-symmetric plate from $0^\circ$/$90^\circ$ to $0^\circ$/$45^\circ$ having thickness ratio 10 and boundary condition is SSSC. Now a porosity of 0.2 is introduced in the entire thickness of the plate and results have been shown in Table 14. For the edge condition, SSSS frequency is increased by 6.37% when the orientation angle changes from $0^\circ$/$90^\circ$ to $0^\circ$/$60^\circ$ with a thickness ratio of 5. In Table 14 fundamental frequency is increased by approximately 9% with a change in orientation angle $0^\circ$/$90^\circ$ to $0^\circ$/$45^\circ$ having a thickness ratio of 10.

For the free vibration analysis of the laminated porous plate, a porosity of 0.3 is introduced in the entire thickness of the plate and the fundamental frequency is obtained as shown in Table 15. Further decrease in fundamental frequency as compared to Tables 13 and 14 in some edge conditions such as SSSS, SSSC, SSCC and SSFF. In boundary conditions, SSFS and SSFC fundamental frequencies are decreased for the entire thickness ratio like 5, 10, 20, and 50. For the thickness ratio of 50 normalized fundamental frequency is decreased by 12.72% with a change in orientation angle from $0^\circ$/$90^\circ$ to $0^\circ$/$60^\circ$ having edge condition SSFS. Normalized fundamental frequency is also decreased by approximately 6%, while a change in orientation angle from $0^\circ$/$45^\circ$ to $0^\circ$/$30^\circ$ having a thickness ratio of 10.

Conclusion

Free vibration analysis of laminated composite porous plate analysed with improved third-order theory. It analysed different boundary conditions and porosity distributions. The main outcomes of the present research article are listed below.

• The fundamental frequency decreases with porosity distribution in the entire thickness of the plate, like p = 0.0, 0.1, 0.2, 0.3.

• The fibre orientation angle is a significant change in the normal frequency of the laminated plate.

• In most of the boundary conditions like SSSS, SSSC, SSCC, and SSFF, the fundamental frequency increases with the decrease in orientation angle, like from $0^\circ$/$90^\circ$/$0$ to $0^\circ$/$30^\circ$/$0^\circ$.

• In SSFS and SSFC edge conditions, fundamental frequency is increased with a change in orientation angle from $0^\circ$/$90^\circ$/$0$ to $0^\circ$/$30^\circ$/$0^\circ$.

• For the modulus ratio of 40 and the thickness ratio of 10, the normalised fundamental frequency is increased by 1.4% with a change in orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$ to $0^\circ$/$30^\circ$/$30^\circ /0^\circ$.

• With a porosity distribution of 0.1 in the entire thickness of the plate fundamental frequency is decreased by 3.2% for the modulus ratio of 40 and orientation angle $0^\circ$/$90^\circ$/$90^\circ /0^\circ$.

• For the thickness ratio of 100 and modulus ratio of 10, the normalised fundamental frequency is decreased by 13.4% with a porosity of 0.3 and orientation angle of $0^\circ$/$90^\circ$/$90^\circ /0^\circ$.

• For the boundary condition SSSC, fundamental frequency is decreased by 4.87% with a thickness ratio of 100 and orientation angle $0^\circ$/$90^\circ$/$0$.

• With a change in orientation angle of $0^\circ$/$90^\circ$/$0$ to $0^\circ$/$30^\circ$/$0^\circ$, the fundamental frequency is decreased by 14.36% for the boundary condition of SSFS.

• With a porosity distribution of 0.2 in the laminated plate, frequency is decreased by 7.76% with an edge condition of SSFC.

• For an antisymmetric laminated plate of $0^\circ$/$90^\circ$ and edge condition of SSSS, frequency is reduced by 3.6% due to a porosity value of 0.1.

• With boundary condition SSFF, the fundamental frequency is decreased by 8.0% due to a porosity distribution of 0.2 in the entire thickness of the laminated plate.

• As introduced porosity of 0.3 in a laminated simply supported square plate, the fundamental frequency decreases by 9.46% for the orientation angle of $0^\circ$/$45^\circ$.