Introduction

Vibrational energy harvesting (VEH) is a clean and sustainable energy source and has become popular recently due to its potential to generate continuous energy from harvesting widely available environmental vibrations in real-life application such as wind flow [1], human activities [2], ocean waves [3], machine operation [4]. It finds applications to power low-energy devices such as charging batteries of electronic devices, wireless sensors, implantable electronics for safety monitoring devices, biomedical engineering and microelectro-mechanical system applications [5,6,7,8,9]. The linear vibratory energy harvester, represented as a linear spring–mass–damper system coupled with piezoelectric [5, 10, 11] or electromagnetic [12] or electrostatic [13] transduction mechanism, operates based on the principle of resonance limiting its effectiveness only to a very narrow effective frequency bandwidth close to the resonance frequency [5]. Moreover, natural frequencies for miniaturized VEH are in order of kilohertz [14], while environmental excitations have frequency in the range of \(0-30\)Hz. To make VEH more effective over a broader frequency range, random excitations and various techniques of nonlinearities such as bistability [10, 15, 16], multistabilty [17,18,19,20], plucking frequency-up conversion [21], passive or active frequency tuning [22] have been introduced in the design of VEH [6,7,8, 11]. Due to the unique advantages of stiffness nonlinearity, the nonlinear based VEH model has a wider frequency bandwidth resulting in enhanced broadband performance of VEH. The analysis of nonlinear vibration energy harvester subjected to random excitations thus has been investigated widely in the literature [7, 8, 15, 19].

Nonlinear oscillators with different potential energy functions, such as monostable [23], bistable [7, 8] and tristable [19] potential wells have been received considerable attention recently in the design of VEH systems. Several design models such as a cantilever beam with magnetic repulsion [17, 18], ferromagnetic beam with magnetic attraction [17, 18], magnetic levitation [24], buckling beam [25] and buckling plate [26] have been proposed in the context of bistable VEH. Compared to the linear model, they are found to enhance the effectiveness of the vibration energy harvesters (VEH) over a wider frequency range due to activation of large inter-well escape mechanism.

Sebald[27] investigated the Duffing oscillator with piezoelectric electromechanical coupling and excited with sine bursts or colored noise as VEH and showed that big gain in bandwidth performance is possible when the VEH is nonlinear. They also observed that monostable VEH behaves very similar to a linear model. Daqaq [23] theoretically investigated a nonlinear monostable VEH and observed that it does not outperform the linear counterpart under broadband random excitation. To overcome these difficulties, the concept of multi-modal VEH is proposed. A significant number of theoretical and experimental investigations on bistable energy harvester under Gaussian white noise excitation [7, 8, 10, 16, 28] showed direct correlation between the power output and the noise intensity. He and Daqaq [28] used statistical linearization techniques to investigate the effect of potential function asymmetries on the performance of nonlinear VEHs under Gaussian white noise excitations and found that VEH with a symmetric bistable potential produced higher output power. Narayanan et al.[16] derived closed-form approximate solution for the mean harvested power and derived the optimal design parameters under broadband random ambient excitations such that the harvested power is maximized. Adhikari et al. [10] using the theory of random vibrations investigated a piezoelectric based VEH subjected to random base excitation and derived exact closed-form expressions for mean output power. Jiang and Chen [29] using the stochastic averaging method derived the exact stationary solution of the averaged Fokker Planck (FP) equation and observed that quadratic nonlinearity alone or combined with appropriate cubic nonlinearities can improve the performance of a nonlinear VEH under Gaussian white noise excitation. Kumar et al.[8] numerically solved the three dimensional FP equation associated with bistable VEH and obtained the optimal system parameter under ambient Gaussian white noise excitation for maximum power output. They observed a threshold value of the noise intensity for activation of desirable inter-well motion in a bistable VEH.

Recently, new class of energy harvesters with triple potential wells has been proposed to improve the broadband performance of randomly excited VEH [19]. Several design philosophies such as cantilever beam with a tip magnet [17], ferromagnetic beam [17], spring based configuration [30], magnetic levitation [31] are used in this context. Due to the shallower potential barrier, longer distance between outermost stable equilibrium points, lower potential barrier and having better stable state than the bistable VEH, tristable VEH has advantages over the bistable VEH [17]. The influence of potential well depth for a tristable energy harvesting under deterministic excitation was experimentally investigated in [19]. They found that the tristable VEH with shallower potential enhanced the broadband performance and also has smaller threshold of input energy for inter potential well motion. For stochastic excitation also relatively lower noise intensity is required to trigger the inter-well motion.

Most of the investigation of VEH systems has considered either deterministic or Gaussian white noise excitations [7, 8, 10, 16, 19, 28]. White noise with delta function correlation time is a idealized model to represent broad band excitation. However, in practice, random excitations have a finite correlation time, though small [10, 32] and hence the effect of temporal correlation has to be taken into consideration. For this reason the Gaussian colored noise (Ornstein-Uhlenbeck process) having non-zero correlation time has been attracting attention as a realistic model to approximate the ambient vibration [33, 34]. In the context of the energy harvesting problem, a piezomagnetoelastic VEH under exponentially correlated Gaussian colored noise, increases the state-space dimension of the problem involving the solution of a corresponding four-dimensional Fokker–Planck–Kolmogorov(FPK) equation, adding numerical difficulties in the solution procedure. Hence, approximate methods have been used to numerically investigate the performance of VEH under colored noise excitation. Using the stochastic averaging method, Liu et al. [35] investigated the probabilistic response of nonlinear VEH driven by exponentially correlated Gaussian colored noise. Zhang et al. [20] investigated the stochastic bifurcations and the performance of an inductive type power generator with a tristable potential function driven by colored Gaussian noise. They employed stochastic averaging method to derive the averaged FPK equation and obtained the PDF of the amplitude. Using the stochastic averaging method, Xiao et al. [11] investigated monostable duffing-type VEH with piezoelectric coupling under correlated multiplicative and additive white noise and observed that the mean output power first increases with increasing ratio of the time constant reaches a maximum and then decreases.

In this paper, the effectiveness of single, double- and triple-well potential wells on energy harvesting under exponentially correlated Gaussian colored noise is investigated. In the case of random excitation, the finite difference(FD) method is used to solve the corresponding Fokker-Planck (FP) equation giving the joint probability density functions (JPDF) of the response and the voltage generated. The electromechanical coupling coefficient, damping ratio, intensity of noise and time constant and the shape of the potential wells have significant effects on the harvested energy. For very low noise levels, the energy harvester with single potential well outperforms the harvester with multiple deep potential wells. Energy harvesters with multiple well potentials perform better with higher noise levels as the response increases and jumps from one potential well to another with inter-well dynamics operating. Hence the depth and distributed positions of potential wells are factors which directly influence the performance of multistable VEH. It is found that the probability of jumps between potential wells are enhanced with increase in the noise intensity and corresponding increase in the mean power generation. However, this enhancement is weakened with increase in correlation time of excitation. The mean output power first increases with increase in the quintic stiffness, reaches a maximum and then decreases. The conflicting interplay of the oscillator parameters including the shape of the potential wells leads to an optimization problem for maximum energy harvesting, which is also considered in this paper. The estimated PDFs as obtained using the FP solution are verified using Monte Carlo simulation (MCS) studies.

Fig. 1
figure 1

a Schematic of a tristable piezomagnetoelastic cantilever beam subjected to random base excitation, b tristable potential function

Full size image

Mathematical Model of Multistable Energy Harvester

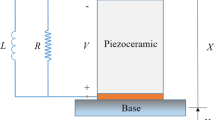
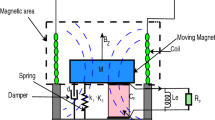
VEH with multi-potential wells can be constructed by coupling the nonlinear oscillator to an electrical circuit as shown in Fig. 1(a). The ferromagnetic cantilever beam [6] is supported between two symmetric permanent magnets with the variable inclination angles, near the free end and subjected to support random excitation. The tip of the cantilever too has a magnet which acts as proof mass and its interaction with the other two magnets produce a magnetic force. In addition to the monostable state, the multi stable configuration such as bistable and tristable states can be obtained by adjusting the design parameters of magneto-elastic interaction. Piezoelectric layers are bonded to the cantilever beam near the root and connected to an electrical load.The voltage generated from the piezoelectric layers across the load due to the random excitation contributes to the energy harvesting.

The coupled nonlinear electromechanical equations of the motion of tristable VEH, governing the system first natural mode and electric voltage generated can be written in the following form [7]

$$\begin{aligned} m\ddot{X}+c\dot{X}+\bar{U}^{'}{(X)}-\theta V = -m\ddot{X}_b, \end{aligned}$$
(1)
$$\begin{aligned} C_p\dot{V}+\frac{V}{R_l} +\theta \dot{X}=0, \end{aligned}$$
(2)

where X represents the relative transverse displacement of the beam tip with respect to support motion \(X_b\), V is the voltage output across the load resistance \(R_l\), c is a linear viscous damping coefficient, \(\theta\) is a linear piezoelectric coupling coefficient in the two equations, \(C_p\) is the capacitance of the piezoelectric material, \(\ddot{X}_b\) is the stochastic support acceleration, \(\bar{U}^{'}(X)\) is the potential energy function of the mechanical system which depends on the nonlinearity present in the harvester, \((')\) denotes differentiation with respect to X and the dot represents the derivative with respect to time t. In this work, potential energy function is chosen in the following general form

$$\begin{aligned} \bar{U}(X) = \frac{1}{2}\bar{k}_1X^2+\frac{1}{4}\bar{k}_3X^4+\frac{1}{6}\bar{k}_5X^6, \end{aligned}$$
(3)

where \(\bar{k}_1,\,\bar{k}_3\) and \(\bar{k}_5\) are respectively the linear, cubic and quintuple nonlinear stiffness coefficients.

Fig. 2
figure 2

Potential energy for (a) \(k_1=1, k_5=1\) and different values of \(k_3\); (b) \(k_1=1, k_3=-2.3\) and different values of \(k_5\)

Full size image
Fig. 3
figure 3

a Auto-correlation and b spectral densities for the Gaussian colored noise

Full size image

With the appropriate change of variables, Eqs. (1) and (2) can be rewritten in the following form as

$$\begin{aligned} \ddot{X}+2\zeta \omega _n\dot{X}+\frac{\textrm{d} U(X)}{\textrm{d} X}-\chi V=\xi (t), \end{aligned}$$
(4)
$$\begin{aligned} \dot{V}+\lambda V+\beta \dot{X}=0, \end{aligned}$$
(5)

where \(\zeta =c/{2\,m\omega _n},\, U(X) = {\frac{1}{2}}k_1X^2+{\frac{1}{4}}k_3X^4+{\frac{1}{6}}k_5X^6,\,k_1 =\bar{k}_1/m,\, k_3=\bar{k}_3/m,\, k_5=\bar{k}_5/m,\, \ddot{X}_b=\xi (t),\,\lambda =1/{R_lC_p},\,\beta =\theta /C_p,\,\chi =\theta ^2/{k_1C_p}.\)

Regardless of the coupling mechanism, chosen potential energy function permits Eqs. (4) and (5) to characterize the different kind of dynamics for the nonlinear energy harvesting system. When \(k_3^2-4k_1k_5<0\) nonlinear energy harvesting system will have only one fixed point at the origin and hence U(X) will have monostable potential. For \(k_1>0,\,k_3<0,\,k_5>0\) and \(k_3^2-4k_1k_5> 0\), system has five fixed points at \((0,0),(\sum _{j=1} ^4 X_j,0)\), where \(X_{1,2}=\pm \sqrt{\gamma _1}, X_{3,4}=\pm \sqrt{\gamma _2},\gamma _{1,2}=\frac{-k_3\pm \sqrt{k_3^2-4k_1k_5}}{2k_5}\). Out of these five fixed points \((0,0),(X_1,0)\) and \((X_2,0)\) are stable equilibrium nodes, while \((X_3,0)\) and \((X_4,0)\) are saddle nodes and U(X) will have tristable potential function as shown in Fig. 1(b). Moreover, as shown in Figs. 2(a) and (b) both depth and span of two symmetric wells depend on the stiffness parameter \(k_3\) and \(k_5\). With the decrease of either \(k_3\) or \(k_5\), the potential well barrier increases and, hence, inter-well motion between two consecutive wells will be restricted.

We assume ambient random excitation \(\xi (t)\) in Eq. (4) as Gaussian colored noise (Ornstein-Uhlenbeck process) with zero mean and an exponentially decaying correlation function as follows (Fig. 3(a))

$$\begin{aligned}{} & {} \textrm{E}[\xi (t) \xi (s)] = \frac{D}{\tau } \exp {\big [-\frac{\mid t -s \mid }{\tau }\big ]} \nonumber \\{} & {} \quad = \frac{\sigma ^2}{2\tau } \exp {\big [-\frac{\mid t -s \mid }{\tau }\big ]}, \end{aligned}$$
(6)

where \(\sigma =\sqrt{2D}\) measures the intensity of Gaussian colored noise, the characteristic time \(\tau\) denotes the correlation time of the noise. The power spectral density of \(\xi (t)\) can be expressed as (Fig. 3(b))

$$\begin{aligned} S_\xi (\omega )=\frac{2D}{1+\tau ^2\omega ^2}. \end{aligned}$$
(7)

An idealized condition when \(\tau \rightarrow 0,\) the colored noise \(\xi (t)\) tends to the white noise process W(t) which has the following statistical properties

$$\begin{aligned} \textrm{E}[W(t)] = 0,\,\,\,\,\, \textrm{E}[W(t) W(s)] = \sigma ^2 \delta (t-s),\,\,\,\sigma ^2 =2D, \end{aligned}$$
(8)

where D is the spectral density of the white noise and \(\delta (\cdot )\) is the Dirac-delta function.

The time evolution of such exponentially correlated Gaussian colored noise \(\xi (t)\) can be conveniently expressed in terms of the white noise W(t) in the following form

$$\begin{aligned} \dot{\xi }(t)=-\frac{1}{\tau } \xi + \frac{1}{\tau } W(t), \end{aligned}$$
(9)

where \(W(t) = \sigma \textrm{d} B(t)/\textrm{d}t\), is the mean zero stationary Gaussian white noise process and B(t) is the unit Wiener process.

Fokker–Planck Equation of VEH

Introducing the variables \(X_1 = X\), \(X_2 = \dot{X}\), \(X_3=V\) and \(X_4=\xi\), Eqs. (4), (5) and (9) can be expressed in terms of a set of first order It\(\hat{o}\) type stochastic differential equation (SDE) of the form

$$\begin{aligned}{} & {} \left\{ \begin{array}{c} \textrm{d} X_1(t)\\ \textrm{d} X_2(t)\\ \textrm{d} X_3(t)\\ \textrm{d} X_4(t) \end{array} \right\} =\left[ \begin{array}{c} X_2\\ -k_1 X_1-k_3 X_1^3-k_5 X_1^5-2\zeta \omega _n X_2+\chi X_3+X_4\\ -\beta X_2-\lambda X_3\\ -\frac{1}{\tau }X_4 \end{array}\right] \nonumber \\{} & {} \quad \textrm{d}t + \left\{ \begin{array}{c} 0\\ 0\\ 0\\ \frac{\sqrt{2D}}{\tau } \end{array}\right\} \textrm{d} B(t), \end{aligned}$$
(10)

where \(\textrm{d} B(t)= B(t_{n+1})-B(t_n) \sim \sqrt{t_{n+1}-t_{n}}N(0,1)\) is the unit Wiener process increment and N(0, 1) is the unit normal random variate. For Gaussian white noise excitation, the response state vector \(\mathbf{{X}} =[X_1,X_2,X_3,X_4]^T\) corresponding to Eq. (10) of the energy harvesting system is Markovian and consequently the time evolution of the joint PDF p will be governed by the following four-dimensional FP equation [36]

$$\begin{aligned}{} & {} \frac{\partial p}{\partial t} = -X_2 \frac{\partial p}{\partial X_1} + (2\zeta \omega _n X_2+k_1 X_1\nonumber \\{} & {} \quad +k_3 X_1^3+k_5 X_1^5-\chi X_3-X_4)\frac{\partial p}{\partial X_2}+ \nonumber \\{} & {} \quad (\beta X_2+\lambda X_3)\frac{\partial p}{\partial X_3}+\frac{1}{\tau }\frac{\partial p}{\partial X_4} \nonumber \\{} & {} \quad +\frac{\sigma ^2}{2 \tau ^2}\frac{\partial ^2 p}{\partial X_4^2}+(2\zeta \omega _n+\lambda )p, \end{aligned}$$
(11)

where p is the joint PDF of the state variables \(\mathbf{{X}}\). The stationary joint probability density function (PDF) of the response variables of the corresponding four-dimensional FP equation \((\frac{\partial p}{\partial t}=0)\) of VEH is numerically obtained using the FD method [37, 38]. The response statistics, the mean square voltage and the mean square displacement of the VEH are obtained from the respective joint PDFs. The time histories for the state variables associated with VEH are obtained by direct numerical integration of Eq. (10) using the Euler–Maruyama method [39].

To compare the accuracy of the FP solution, the estimated PDF for the state variables as obtained using the FD method is compared with those obtained from Monte Carlo simulation (MCS) scheme. The MCS is a direct numerical integration technique [40, 41], which involved the numerical simulation for the increments of a Wiener process \(\textrm{d} B(t)\) and numerical integration of the SDEs as in Eq. (10) to each discrete excitation using the forward Euler–Maruyama (EM) integration scheme [39, 40]. In this work, to estimate the stationary PDF for the state variables using MCS, on the average, \(2 \times 10^5\) realizations with a time step \(\textrm{d}t=0.0005\) have been used to integrate the governing set of four coupled first order SDE as in Eq. (10) using the forward EM numerical integration until the steady state is achieved.

Fig. 4
figure 4

a Mesh surface of the mean square electric voltage \(\textrm{E}[V^2]\) in \(\sigma -\tau\) plane (b) variation of \(E[V^2]\) with respect to noise intensity \(\sigma\) for different values of \(\tau\)

Full size image
Fig. 5
figure 5

Joint PDF for \(k_3=-2.3, \,k_5=1,\,\zeta =0.025,\,\tau =1\) and (a) \(\sigma =0.05\), (b) \(\sigma =0.08\), (c) \(\sigma =0.125\), (d) \(\sigma =0.25\)

Full size image
Fig. 6
figure 6

Marginal PDF of voltage corresponding to Fig. 5

Full size image
Fig. 7
figure 7

Joint PDF for \(k_3=-2.3, \,k_5=1,\,\zeta =0.05,\,\sigma =0.1\) and a \(\tau =0.025\), b \(\tau =0.8\), c \(\tau =1\), d \(\tau =2\)

Full size image
Fig. 8
figure 8

Marginal PDF of voltage corresponding to Fig. 7

Full size image

Numerical Results

The dynamics of the piezomagnetoelastic nonlinear energy harvester represented by Eqs. (4), (5) and (9) is numerically investigated. The following system parameters \(\omega _n^2=1,\,k_1=1,\,\lambda =0.05,\,\beta =0.5\) and \(\chi =0.05\) for the oscillator are kept fixed in most of the investigations. The coefficients of the nonlinear terms \(k_3\) and \(k_5\), electromechanical coupling parameter \(\lambda\), piezoelectric coupling coefficient \(\chi\), the damping ratio \(\zeta\), noise intensity \(\sigma\) and its correlation time \(\tau\) are varied.

To better understand the effect of noise intensity and its correlation time of the colored noise on the performance of the tristable VEH, the variations of mean square electric voltage with respect to noise intensity \(\sigma\) and correlation time \(\tau\) are shown in Fig. 4(a). The other parameters adopted for the oscillator are \(\zeta =0.05,\, k_3=-2.3\) and \(k_5=1\). It can be seen from Fig. 4(b) that for a given correlation time \(\tau\) of Gaussian colored noise, the mean square voltage almost increases proportionally with the excitation intensity. However, for a given noise intensity, increase of the correlation time reduces the mean output power. Hence the increase of correlation time of the colored noise will weaken the performance of the VEH. Figure 4(b) presents the mean square voltage for the case of Gaussian white noise excitation \((\tau \rightarrow 0)\). It can be seen that for the given noise intensity, \(\textrm{E}[V^2]\) increases with decrease in correlation time \(\tau\); however, this increase is not perceptible for lower values of correlation time. For the given system parameters, the mean square electric voltage for the colored noise having correlation time \(\tau =0.025\) is almost the same for white noise.

Figure 5 shows the JPDF of \(X_1\) and \(X_2\) for four values of \(\sigma\) and for \(\zeta =0.025,\,\tau =1\). For low intensity of excitation \(\sigma =0.05\) the joint PDF is unimodal at origin. For the noise intensity to \(\sigma =0.08\), the peak value at origin decreases and almost vanishes and two symmetric peaks appear in the joint PDF. For further increase in the noise intensity, the peak at the origin starts to gain strength and subsequently at \(\sigma =0.25\), the VEH has a tri-modal joint PDF. This signifies that with increase in the noise intensity there is larger probability of the system response to move between the potential wells and hence the increase in the mean power output. The marginal PDF of the voltage as obtained using the FP and MCS solutions corresponding to Fig. 5 is shown in Fig. 6, having the excellent agreement of the FP solution with the MCS results and hence validating the numerical solution of the FP equation.

Next for a given noise intensity \(\sigma =0.1\), Fig. 7 shows the JPDF of \(X_1\) and \(X_2\) for four values of noise correlation time \(\tau\), which clearly indicates that increasing the correlation time has the opposite effect to that of noise intensity. For increased \(\tau\), the center peak intensity reduces, transforming to tri-modal and then to bimodal and finally to unimodal behavior. The marginal PDF of the voltage as obtained using the FP and MCS solutions corresponding to Fig. 7 is shown in Fig. 8, once again showing the good agreement between the two.

Fig. 9
figure 9

a Mesh surface of the mean square electric voltage \(\textrm{E}[V^2]\) in \(\zeta -\tau\) plane (b) variation of \(E[V^2]\) with respect to damping coefficient \(\zeta\) for different values of \(\tau\)

Full size image
Fig. 10
figure 10

Variation of the mean square electric voltage \(E[V^2]\) with damping coefficient \(\zeta\) for different value of noise intensity \(\sigma\)

Full size image
Fig. 11
figure 11

Joint PDF for \(k_3=-2.3, \,k_5=1,\,\sigma =0.1,\,\tau =0.025\) and (a) \(\zeta =0.0125\), (b) \(\zeta =0.05\), (c) \(\zeta =0.075\)

Full size image
Fig. 12
figure 12

a Mesh surface of the mean square electric voltage \(\textrm{E}[V^2]\) in \(k_5-\tau\) plane (b) variation of \(E[V^2]\) with respect to nonlinear term \(k_5\) for different values of \(\tau\)

Full size image
Fig. 13
figure 13

Variation of the mean square electric voltage \(E[V^2]\) with \(k_5\) for different value of damping ratio \(\zeta\)

Full size image
Fig. 14
figure 14

Joint PDF for \(k_3=-2.3, \,c=0.025,\,\sigma =0.1,\,\tau =0.025\) and (a) \(k_5=0.75\), b \(k_5=1\), (c) \(k_5=1.4\)

Full size image
Fig. 15
figure 15

Mesh surface of the mean square electric voltage \(\textrm{E}[V^2]\) in (a) \(\beta -\zeta\), b \(\lambda -\zeta\), c \(\chi -\zeta\) plane

Full size image
Fig. 16
figure 16

A relative comparison of the mean square electric voltage \(\textrm{E}[V^2]\) (a) for different type of potential function (b) magnified view for low intensity; FP solution (——); MCS (\(\circ\))

Full size image
Fig. 17
figure 17

Time waveform of displacement at \(\sigma =0.1\) for Fig. 16 for (a) nonlinear monostable, (b) bistable with shallow potential, (c) tristable

Full size image
Fig. 18
figure 18

Time waveform of voltage at \(\sigma =0.1\) for Fig. 16 for (a) nonlinear monostable, (b) bistable with shallow potential, (c) tristable

Full size image

Figures 9 and 10 present the impact of viscous damping ratio \(\zeta\) on the mean square voltage for different correlation time of Gaussian colored noise and its intensity. The other parameters adopted for the oscillator are \(k_3=-2.3\) and \(k_5=1\). For a given value of the noise intensity as the damping ratio \(\zeta\) increases the mean square voltage significantly reduces. Figure 9(b) presents the mean square voltage for the case of Gaussian white noise excitation. As mentioned earlier the mean square electric voltage for the Gaussian white noise excitation is almost the same as for the case of colored noise having correlation time \(\tau =0.025\). Figure 11 shows the JPDF of \(X_1\) and \(X_2\) for three values of \(\zeta\) and for \(\sigma =0.1,\,\tau =0.025\). The three separate peaks in the JPDF tend to come closer as \(\zeta\) decreases and merges for \(\zeta =0.0125\). This signifies that there is larger probability of the system response to move between the potential wells for lower values of \(\zeta\). For higher damping, there is higher probability of the response staying in the neighborhood of the stable equilibrium points of the deterministic system and the probability of the response to move between potential wells is negligible.

Figures 12 and 13 present the effects of the quintic stiffness coefficient \(k_5\) on the mean square voltage for different correlation time of Gaussian colored noise and damping coefficient respectively. The other parameters adopted for the oscillator are \(k_3=-2.3\) and \(\sigma =0.1\). As shown in Fig. 12(b), for the given oscillator parameters as the correlation time reduces, mean square electric voltage increases and is maximum for the Gaussian white noise. Figure 13 shows the variation of mean square voltage as a function of the nonlinear stiffness parameter \(k_5\) for three damping coefficients \(\zeta =0.0125,0.025\) and 0.05. For a given value of the correlation time or the damping coefficient as \(k_5\) increases the mean square voltage initially increases, reaches a maximum for a particular \(k_5\) and decreases with further increase in \(k_5\). Thus, it may be concluded that for a given value of the damping ratio \(\zeta\) and excitation parameters, there is an optimum value of \(k_5\) for which the mean square voltage is a maximum. As seen from Fig. 14 for the given damping coefficient, at lower value of \(k_5\) the separation distance between the potential wells and depth of the potential wells increase and larger intensity of noise is required to enable the inter-well motion. As \(k_5\) increases the three peaks in the JPDF merge. This signifies that there is larger probability of the system response moving from one potential well to the other. This also signifies that there is increase in the power output. With further increase in \(k_5\) the JPDF tends to become unimodal with the JPDF peaking around the zero equilibrium point with consequent decrease in the mean square voltage. This is the reason for the mean square voltage to attain a maximum value for a particular value of \(k_5\).

Figure 15 demonstrates the effect of the system parameters \(\lambda\), the electromechanical coupling coefficient in the mechanical system \(\chi\) and the coupling coefficient in the electrical equation \(\beta\), on the mean square voltage for three different values of the damping ratio \(\zeta\) for the tristable oscillator. The other parameters adopted for the oscillator are \(k_3=-2.3,\,k_5=1\), \(\sigma =0.1\) and \(\tau =0.0.025\). The mean square voltage decreases with increase in \(\lambda\), decreases slightly with increase in \(\chi\), but increases considerably with increase in \(\beta\). Hence the energy harvesting capability of the nonlinear oscillator can be enhanced by proper tuning of the parameters of the system in addition with an optimum choice of the noise intensity.

Figure 16 presents a comparison of the mean square voltage for different types of potential wells as a function of noise intensity. Four different categories of potential functions (i) linear (\(k_1>0, k_3 =k_5=0\)),(ii) nonlinear monostable (\(k_1 \ge 0,k_3 \ne 0,k_5=0\)),(iii) nonlinear bistable (\(k_1<0,k_3 > 0,k_5=0\)) and (iv) nonlinear tristable (\(k_1> 0,k_3 <-2\sqrt{k_5},k_5>0\)) are chosen for comparison. Upto some threshold value of \(\sigma\), the mean square voltage is very low, but it increases steeply with \(\sigma\) beyond this value. This behavior is irrespective of the shape of the potential wells. It is observed that the mean square voltage and hence the harvested energy is significantly larger with bistable shallow potential well and tristable potential well than with linear, monostable potential well and bistable deep potential well. Moreover, for low excitation intensity as shown in Fig. 16(b), the linear VEH performs better than the nonlinear oscillators with monostable potential well and bistable deep potential well. Time waveforms of displacement and voltage for nonlinear monostable, bistable with shallow potential and tristable VEH at \(\sigma =0.1\) corresponding to Fig. 16 are shown in Figs. 17 and  18, respectively. It can be seen that for the given noise intensity both bistable and tristable VEH undergo frequent jumps between potential wells and produce large amplitude of response, thus generating a high output voltage, whereas for nonlinear monostable VEH, the response is restricted to a single well and the output voltage is relatively low. The mean square voltage obtained by Monte Carlo simulation (MCS) is also shown alongside which shows very good agreement with the result of the numerical solution of the FP equation solutions.

Conclusions

The relative performance of piezomagnetoelastic nonlinear energy harvester with different types of potential wells under exponentially correlated Gaussian colored noise is investigated by numerical solution of the corresponding FP equation. The influence of various types of potential well functions, coupling parameters, damping coefficient and the intensity of Gaussian colored noise on the mean square voltage is investigated. The mean output power increases with an increase in the noise intensity while it decreases with increase in the correlation time of the Gaussian colored noise which is directly linked with the stochastic transitions between the potential wells. The linear VEH outperforms a nonlinear VEH with monostable potential well and bistable deep potential well especially for low noise intensities. This may be attributed to the low probability of inter-well movement with low intensity of noise. The nonlinear VEH with bistable shallow potential well and tristable potential well outperforms the linear VEH and the nonlinear VEH with monostable potential well and bistable deep potential well significantly. In all the cases, the mean square voltage increases slowly with increase in noise intensity initially but rapidly after a threshold value of noise intensity. The higher mean square voltage of nonlinear VEH with bistable shallow potential well and tristable potential well is due to the higher probabilities of inter-well motions. The mean square voltage also varies with respect to other system parameters such as the damping coefficient c, electromagnetic coupling coefficient \(\beta\) and \(\chi\) and the load resistance capacitance parameter \(\lambda\) in a complex and conflicting way which leads to an optimization problem for maximum energy harvested in terms of mean square voltage with respect to the parameters as well as the noise intensity and shape of potential wells which can be investigated further.