Introduction

Micro/nanoelectromechanical systems (MEMS/NEMS) benefit from inimitable specifications such as diminutive size, high precision, slight energy consumption and excellent level of permanence. Consequently, the demand for using these systems in recently developed engineering tools is constantly growing. One of the most employed elements in MEMS/NEMS are circular and rectangular cross-sectional micro/nanorings. On account of their plain configuration, miniaturized rings are extensively utilized as basic constructive elements of vibrating ring gyroscopes [1, 2], rate sensors [3, 4], multi-axis angular velocity sensors [5], force sensors [6], electro-optical modulators [7], ultrasonic actuators [8], label-free sensors [9], diaphragm sensors [10], pressure and temperature sensors [11] and so on. One of the key factors in the design of these small-scaled systems is to minimize all types of energy dissipation to optimize their performance. It has been found that thermoelastic damping (TED) is one of the definite origins of energy loss in miniaturized mechanical elements [12, 13]. Therefore, its accurate modeling in such structures is of great importance to ascertain the factors affecting energy loss, perform optimal design and maximize the quality factor.

To find the responses of mechanical systems or solve their governing equations, there are various methods such as experimental, numerical and analytical methods. Experimental methods are mostly expensive and can only be used for some situations or materials. Although numerical methods can be used for a wider range of problems, they mainly suffer from some shortcomings. They only yield approximate solutions, require some initial information at any point to start iterations, and cannot clearly show the role of influencing parameters in the solution. Analytical methods could remedy the deficiencies in experimental and numerical methods so that they can be used for a wide range of conditions and the impact of key factors on the response can be clearly seen. Therefore, the mathematical modeling of mechanical structures and the analytical solution of their governing equations have gained special importance.

For the mathematical description of heat transport in solid continua, several heat conduction theories have been proposed. The Fourier model is the first and most well-known of these models, in which the heat flux is proportional to the temperature gradient at any point of the material. On the basis of several experimental observations, the Fourier model is not able to adequately explain heat transfer in small dimensions or short times. As a result, different non-Fourier models for heat conduction have been introduced to overcome the shortcomings of the Fourier model. As one of the simplest non-Fourier models, one can mention the Lord and Shulman (LS) model which includes only one relaxation time [14]. By adding a nonlocal parameter to LS model, Guyer and Krumhansl presented a more complete model for heat conduction (GK model) [15]. By accommodating an additional phase lag parameter in the constitutive relations of LS model, Tzou established the dual-phase-lag (DPL) model to account for the small-scale effect on both size and time [16].

Based on the results reported from analytical and experimental studies, thermoelastic dissipation or thermoelastic damping is known as one of the main sources of energy loss in micro/nanostructures. This mechanism of energy dissipation can limit the quality factor of MEMS/NEMS and disrupt their optimal performance. Through the calculation of wasted energy and utilization of the entropy generation (EG) approach, Zener [17] provided the first analytical model for predicting TED value in Euler–Bernoulli beams. By separating the real and imaginary parts of the frequency, which is known as the complex frequency (CF) approach, Lifshitz and Roukes [18] established a single-term expression for estimating TED value in Euler–Bernoulli beams. It is worth mentioning that in the CF approach, both equations of motion and heat conduction must be extracted, but in the EG approach, there is no need to derive the equation of motion, which can be an advantage for this approach. In recent years, many analytical investigations have been done for mathematical modeling of the thermomechanical behavior of different structural elements such as beams [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49], plates [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69], shells [70,71,72,73,74,75,76,77,78,79,80,81], rings [82,83,84,85,86,87,88,89,90] and elastic media [91,92,93,94,95,96,97,98].

One of the first theoretical studies in the field of TED in rings has been carried out by Wong et al. [82], in which by employing the CF approach, a closed-form relation in the framework of the Fourier model has been presented for the calculation of TED value in the in-plane vibrations of silicon rings with rectangular cross section. Fang and Li [83] used the entropy EG approach and the Fourier model to attain an analytical solution for TED in rectangular cross-sectional ring resonators with 2D heat conduction. In the article published by Li et al. [84], 2D and 3D cases of the Fourier model have been utilized to appraise TED in circular cross-sectional small rings. By considering mass imperfections, Kim and Kim [85] assessed TED in toroidal solid microrings based on the three-dimensional Fourier model. According to the Fourier model, Tai and Chen [86] formulated an analytical model to evaluate TED in out-of-plane oscillations of microrings with rectangular cross section. In two similar studies conducted by Zhou et al. [87], and Zhou and Li [88], 1D and 2D cases of LS and DPL models have been applied, respectively, to emphasize the momentous impact of non-Fourier models on TED in small-sized rings with rectangular cross section. By means of 2D and 3D LS model, Kim and Kim [89] surveyed the influence of phase lag parameter on the amount of TED in circular cross-sectional micro/nanoring resonators. By means of modified couple stress theory (MCST) and nonlocal version of the DPL model, Ge and Sarkar [90] established 1D and 2D models for TED in rectangular cross-sectional miniatirized rungs.

According to the contents discussed above, thermoelastic damping (TED) plays a substantial role in the performance of structures with micro and submicron dimensions. Additionally, the literature review illuminates the inevitability of using non-Fourier heat conduction theories for precise modeling of the thermoelastic behavior of small-sized structures. Given these two points, it can be concluded that the assessment of TED in micro/nanostructures should be conducted in the purview of generalized thermoelasticity theories. The literature survey demonstrates that the analytical study on TED in micro/nanorings with circular cross-section via dual-phase-lag (DPL) model has not been conducted until now. Considering the mentioned advantages of analytical methods and EG approach, the paper at hand aims to remedy this defect in the literature. To reach this goal, in the first step, the coupled heat conduction equation is extracted in the context of the DPL model. Asymmetric harmonic form is then considered for vibrations of the micro/nanoring resonator to determine temperature distribution for 2D and 3D models of heat conduction. On the basis of a definition of TED in the entropy generation (EG) approach, an analytical solution in the series form is established for predicting TED value in circular cross-sectional miniaturized rings by capturing the dual-phase-lagging effect. In the results section, a validation study is first performed to ensure the correctness of the presented model by comparing the results with existing works. Next, a convergence analysis is carried out to ascertain the sufficient number of terms of the obtained solution to arrive at a convergent result. The final step is to conduct a parametric study for highlighting the sensitivity of TED to some influencing factors like phase lag parameters of the DPL model, vibration mode, the dimensions and ring material.

Basic Relationships of Dual-Phase-Lag (DPL) Heat Conduction Model

On the basis of the DPL heat conduction model for isotropic materials, the heat flux vector \({\varvec{q}}\) and gradient of temperature increment \(\nabla \vartheta\) are related through the following relation [3]:

$${\varvec{q}} + \tau_{{\text{q}}} \frac{{\partial {\varvec{q}}}}{\partial t} = - k\nabla \vartheta - k\tau_{{\text{T}}} \frac{\partial \nabla \vartheta }{{\partial t}},$$
(1)

in which \(k\) denotes thermal conductivity. In addition, material constants \({\tau }_{\mathrm{q}}\) and \({\tau }_{\mathrm{T}}\) are called phase lag of heat flux and phase lag of temperature gradient. Moreover, symbol \(\nabla\) represents the Laplace operator. The variable \(\vartheta =T-{T}_{0}\) is also the temperature variation with \(T\) and \({T}_{0}\) as instantaneous and environmental temperatures, respectively. Note that when \({\tau }_{\mathrm{T}}\) vanishes, the heat conduction equation of the DPL model corresponds to that of the LS model. Furthermore, in the absence of phase lag parameters \({\tau }_{\mathrm{q}}\) and \({\tau }_{\mathrm{T}}\), Eq. (1) reduces to the constitutive relation of the Fourier model. For an isotropic material, the equation of conservation of energy is given by [3]:

$$- \nabla .{\varvec{q}} = \rho c_{{\text{v}}} \frac{\partial \vartheta }{{\partial t}} + T_{0} \beta \frac{\partial e}{{\partial t}},$$
(2)

where \(\rho\) and \({c}_{\mathrm{v}}\) refer to the mass density and specific heat per unit mass, respectively. Additionally, parameter \(\beta =E\alpha /(1-2\nu )\) defines thermal modulus. Variable \(e\) is also a volumetric strain. Lastly, by omitting heat flux \({\varvec{q}}\) from Eqs. (1) and (2), equation of heat conduction in the framework of DPL models is obtained as follows:

$$k\left( {1 + \tau_{{\text{T}}} \frac{\partial }{\partial t}} \right)\nabla^{2} \vartheta = \left( {1 + \tau_{{\text{q}}} \frac{\partial }{\partial t}} \right)\left( {\rho c_{{\text{v}}} \frac{\partial \vartheta }{{\partial t}} + T_{0} \beta \frac{\partial e}{{\partial t}}} \right).$$
(3)

Coupled Thermoelastic Equation of Circular Cross-Sectional Rings Based on DPL Model

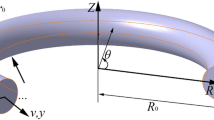
Figure 1 displays the schematic view and coordinate system of a circular cross-sectional ring with mean radius \(R_{0}\) and cross-sectional radius \(r_{0}\). The global and local coordinates are defined by \(\left( {R, \theta , Z} \right)\) and \(\left( {x, y, z} \right)\), respectively. Moreover, the parameter \(\phi\) denotes the local angle. By considering these definitions, the circumferential strain can be expressed by [84]:

$$\varepsilon_{\theta \theta } = - \frac{x}{{R_{0}^{2} }}\left( {u + \frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right),$$
(4)

in which \(u\) represents the radial displacement. Based on coupled thermoelastic constitutive relation, the following relation can be obtained:

$$\varepsilon_{\theta \theta } = \frac{{\sigma_{\theta \theta } }}{E} + \alpha \vartheta ,$$
(5)

where \(\sigma_{\theta \theta }\) indicates circumferential normal stress. Using the above relation, one can get:

$$\sigma_{\theta \theta } = E\varepsilon_{\theta \theta } - E\alpha \vartheta .$$
(6)
Fig. 1
figure 1

Schematic view and coordinate system of a circular cross-sectional ring

Full size image

Other thermoelastic constitutive relations can be expressed as follows:

$$\varepsilon_{RR} = \varepsilon_{zz} = - \nu \frac{{\sigma_{\theta \theta } }}{E} + \alpha \vartheta .$$
(7)

Substitution of Eqs. (4) and (6) in the above equation gives:

$$e = \varepsilon_{RR} + \varepsilon_{\theta \theta } + \varepsilon_{zz} = \left( {2\nu - 1} \right)\frac{x}{{R_{0}^{2} }}\left( {u + \frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right) + 2\left( {1 + \nu } \right)\alpha \vartheta .$$
(8)

By inserting Eq. (8) into Eq. (3) and simplifying the result, the equation of heat conduction becomes:

$$\chi \left( {1 + \tau_{{\text{T}}} \frac{\partial }{\partial t}} \right)\nabla^{2} \vartheta - \left[ {1 + \frac{{2\left( {1 + \nu } \right)}}{1 - 2\nu }\Delta_{{\text{E}}} } \right]\left( {1 + \tau_{{\text{q}}} \frac{\partial }{\partial t}} \right)\frac{\partial \vartheta }{{\partial t}} = - \frac{{\Delta_{{\text{E}}} }}{\alpha }\left( {1 + \tau_{{\text{q}}} \frac{\partial }{\partial t}} \right)\frac{\partial }{\partial t}\left[ {\frac{x}{{R_{0}^{2} }}\left( {u + \frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right)} \right],$$
(9)

with \(\chi = k/\rho c_{{\text{v}}}\) and \(\Delta_{{\text{E}}} = E\alpha^{2} T_{0} /\rho c_{{\text{v}}}\). Due to the small amount of parameter \(\Delta_{{\text{E}}}\) for most materials (i.e. \(\Delta_{{\text{E}}} \ll 1\)), Eq. (9) can be replaced with the following equation:

$$\chi \left( {1 + \tau_{{\text{T}}} \frac{\partial }{\partial t}} \right)\nabla^{2} \vartheta - \left( {1 + \tau_{{\text{q}}} \frac{\partial }{\partial t}} \right)\frac{\partial \vartheta }{{\partial t}} = - \frac{{\Delta_{{\text{E}}} }}{\alpha }\left( {1 + \tau_{{\text{q}}} \frac{\partial }{\partial t}} \right)\frac{\partial }{\partial t}\left[ {\frac{x}{{R_{0}^{2} }}\left( {u + \frac{{\partial^{2} u}}{{\partial \theta^{2} }}} \right)} \right].$$
(10)

Temperature increment \(\vartheta\) and radial displacement \(u\) can be expressed as follows [84]:

$$\vartheta \left( {R,\theta ,z,t} \right) = \Theta_{0} \left( {R,\theta ,z} \right)e^{{i\omega_{n} t}} , u\left( {\theta ,t} \right) = U_{n} \sin \left( {n\theta } \right)e^{{i\omega_{n} t}} ,$$
(11)

in which \(\omega_{n}\) refers to the n-th vibration frequency, which is calculated from the following relation [84]:

$$\omega_{n} = \frac{{n\left( {n^{2} - 1} \right)}}{{\sqrt {n^{2} + 1} }}\sqrt {\frac{EI}{{\rho AR_{0}^{4} }}} \left( {n \ge 2} \right),$$
(12)

with \(I = \pi r_{0}^{4} /4\) and \(A = \pi r_{0}^{2}\) as the moment of inertia and cross-sectional area, respectively. From Fig. 1, one can write:

$$x = r\sin \phi , z = r\cos \phi .$$
(13)

By substituting Eqs. (11) and (13) into Eq. (10) and sorting the result, one can achieve the following equation:

$$\chi \left( {1 + i\omega_{n} \tau_{{\text{T}}} } \right)\nabla^{2} \Theta_{0} - \left( {i\omega_{n} - \tau_{{\text{q}}} \omega_{n}^{2} } \right)\Theta_{0} = - \frac{{\Delta_{{\text{E}}} }}{\alpha }\frac{r\sin \phi }{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right)\left( {i\omega_{n} - \tau_{{\text{q}}} \omega_{n}^{2} } \right).$$
(14)

Three-dimensional form of the Laplace operator can be written as follows:

$$\nabla_{{3{\text{D}}}}^{2} \Theta_{0} = \frac{{\partial^{2} \Theta_{0} }}{{\partial R^{2} }} + \frac{1}{R}\frac{{\partial \Theta_{0} }}{\partial R} + \frac{1}{{R^{2} }}\frac{{\partial^{2} \Theta_{0} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} \Theta_{0} }}{{\partial z^{2} }}.$$
(15)

By referring to Eq. (13) and relation \(R = R_{0} + x\), and considering the fact that in thin rings \(R_{0} \gg x\), Eq. (15) takes the following form:

$$\nabla_{{3{\text{D}}}}^{2} \Theta_{0} = \frac{{\partial^{2} \Theta_{0} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \Theta_{0} }}{\partial r} + \frac{1}{{R_{0}^{2} }}\frac{{\partial^{2} \Theta_{0} }}{{\partial \theta^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} \Theta_{0} }}{{\partial \phi^{2} }}.$$
(16)

In the case of 2D heat conduction, the temperature gradient along the circumferential direction is neglected. Hence, the Laplace operator can be written as:

$$\nabla_{{2{\text{D}}}}^{2} \Theta_{0} = \frac{{\partial^{2} \Theta_{0} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \Theta_{0} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} \Theta_{0} }}{{\partial \phi^{2} }}.$$
(17)

According to the relationship between global and local coordinates, \(\Theta_{0} \left( {r,\theta ,\phi } \right)\) can be used instead of \(\Theta_{0} \left( {R,\theta ,z} \right)\). By assuming adiabatic conditions on the outer surface of the ring and continuity of temperature in all angles \(\theta\) and \(\phi\), the thermal boundary conditions can be expressed as follows:

$$\frac{{\partial \Theta_{0} }}{\partial r}\left( {r = r_{0} } \right) = 0, \Theta_{0} \left( {r,\theta ,\phi } \right) = \Theta_{0} \left( {r,\theta + 2\pi ,\phi } \right), \Theta_{0} \left( {r,\theta ,\phi } \right) = \Theta_{0} \left( {r,\theta ,\phi + 2\pi } \right).$$
(18)

By considering the above relations and inserting Eq. (16) into Eq. (14), the temperature distribution is derived as follows [84]:

$$\Theta_{0} \left( {r,\theta ,\phi } \right) = \mathop \sum \limits_{m = 0}^{\infty } \mathop \sum \limits_{j = 1}^{\infty } C_{jm} J_{1} \left( {\frac{{a_{j} }}{{r_{0} }}r} \right)\sin \left( {m\theta } \right)\sin \phi ,$$
(19)

in which \(J_{1}\) refers to the first-order Bessel function of the first kind. To attain the amount of coefficients \(a_{j}\), the first relation of Eq. (18) is employed. By substituting Eq. (19) into the mentioned relation and exploiting the properties of Bessel functions, one can get:

$$J_{0} \left( {a_{j} } \right) = J_{2} \left( {a_{j} } \right).$$
(20)

Thus, \(a_{j}\) is equal to the j-th root of the above equation. The first ten roots of this equation are listed in Table 1. To extract the coefficients \(C_{jm}\), the orthogonality property of Bessel and trigonometric functions is used. By inserting Eq. (19) into (14), multiplying the result by \(rJ_{1} \left( {\frac{{a_{k} }}{{r_{0} }}r} \right)\sin \left( {n\theta } \right)\sin \phi\), and integrating the outcome in the range of \(\left( {0,r_{0} } \right)\), \(\left( {0,2\pi } \right)\) and \(\left( {0,2\pi } \right)\), it is finally obtained that:

$$C_{kn} = \frac{{\Delta_{E} }}{\alpha }\frac{{2r_{0} }}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \frac{1}{{\left( {a_{k}^{2} - 1} \right)J_{1} \left( {a_{k} } \right)}}\frac{{\left( {i\omega_{n} - \tau_{q} \omega_{n}^{2} } \right)\tau_{k} }}{{\left( {1 + i\omega_{n} \tau_{T} } \right)\left( {1 + \delta_{kn}^{2} } \right) + \left( {i\omega_{n} - \tau_{q} \omega_{n}^{2} } \right)\tau_{k} }},$$
(21)

where

$$\delta_{kn} = \frac{{nr_{0} }}{{a_{k} R_{0} }}$$
(22a)
$$\tau_{k} = \frac{{r_{0}^{2} }}{{\chi a_{k}^{2} }}.$$
(22b)
Table 1 The first ten terms of \({a}_{k}\) and \({G}_{k}\) for the rings with circular cross-section
Full size table

Hence, the final form of temperature distribution can be expressed via the following relation:

$$\Theta_{0} \left( {r,\theta ,\phi } \right) = \frac{{\Delta_{{\text{E}}} }}{\alpha }\frac{{2r_{0} }}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right)\sin \phi \mathop \sum \limits_{k = 1}^{\infty } \frac{{J_{1} \left( {\frac{{a_{k} }}{{r_{0} }}r} \right)}}{{\left( {a_{k}^{2} - 1} \right)J_{1} \left( {a_{k} } \right)}}\frac{{\left( {i\omega_{n} - \tau_{q} \omega_{n}^{2} } \right)\tau_{k} }}{{\left( {1 + i\omega_{n} \tau_{T} } \right)\left( {1 + \delta_{kn}^{2} } \right) + \left( {i\omega_{n} - \tau_{q} \omega_{n}^{2} } \right)\tau_{k} }}.$$
(23)

By separating the real and imaginary parts of the above relation, one can obtain:

$$Re\left( {\Theta_{0} } \right) = \frac{{\Delta_{E} }}{\alpha }\frac{{2r_{0} }}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right)\sin \phi$$
$$\begin{gathered} {\text{Re}}\left( {\Theta_{0} } \right) = \frac{{\Delta_{{\text{E}}} }}{\alpha }\frac{{2r_{0} }}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right)\sin \phi \hfill \\ \mathop \sum \limits_{k = 1}^{\infty } \frac{{J_{1} \left( {\frac{{a_{k} }}{{r_{0} }}r} \right)}}{{\left( {a_{k}^{2} - 1} \right)J_{1} \left( {a_{k} } \right)}}\frac{{ - \tau_{k} \tau_{{\text{q}}} \omega_{n}^{2} \left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{{\text{q}}} \omega_{n}^{2} } \right) + \tau_{k} \omega_{n}^{2} \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{{\text{T}}} + \tau_{k} } \right]}}{{\left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{{\text{q}}} \omega_{n}^{2} } \right)^{2} + \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{{\text{T}}} + \tau_{k} } \right]^{2} \omega_{n}^{2} }} \hfill \\ \end{gathered}$$
(24a)
$$\begin{gathered} {\text{Im}}\left( {\Theta_{0} } \right) = \frac{{\Delta_{E} }}{\alpha }\frac{{2r_{0} }}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right)\sin \phi \hfill \\ \mathop \sum \limits_{k = 1}^{\infty } \frac{{J_{1} \left( {\frac{{a_{k} }}{{r_{0} }}r} \right)}}{{\left( {a_{k}^{2} - 1} \right)J_{1} \left( {a_{k} } \right)}}\frac{{\tau_{k} \omega_{n} \left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{q} \omega_{n}^{2} } \right) + \tau_{k} \tau_{{\text{q}}} \omega_{n}^{3} \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{T} + \tau_{k} } \right]}}{{\left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{q} \omega_{n}^{2} } \right)^{2} + \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{T} + \tau_{k} } \right]^{2} \omega_{n}^{2} }} \hfill \\ \end{gathered}$$
(24b)

Derivation of a Relationship to Compute the Value of TED

According to the entropy generation (EG) approach, TED value is determined by:

$${\text{TED}} = \frac{1}{2\pi }\frac{\Delta W}{W},$$
(25)

where \(\Delta W\) is the wasted energy through entropy generation per cycle of vibration and \(W\) stands for the maximum strain energy stored in the ring at the time of vibration. The wasted energy in a vibrating structure with volume \(\Omega\) during a cycle is given by [99]:

$$\Delta W = - \pi \iiint\limits_{\Omega } {\tilde{\sigma }_{ij} {\text{Im}}\left( {\tilde{\varepsilon }_{ij}^{{{\text{thermal}}}} } \right){\text{d}}\Omega },$$
(26)

where the symbol \(\sim\) refers to the maximum value of a variable per cycle of oscillation. The value of \(W\) is also given by:

$$W = \frac{1}{2}\iiint\limits_{\Omega } {\tilde{\sigma }_{ij} \tilde{\varepsilon }_{ij} {\text{d}}\Omega }.$$
(27)

In a ring, the amount of \(\Delta W\) is estimated by the following relation:

$$\Delta W = - \pi \iiint\limits_{\Omega } {\tilde{\sigma }_{\theta \theta } {\text{Im}}\left( {\alpha \Theta_{0} } \right){\text{d}}\Omega }.$$
(28)

In addition, the maximum stored energy \(W\) can be determined by:

$$W = \frac{1}{2}\iiint\limits_{\Omega } {\tilde{\sigma }_{\theta \theta } \tilde{\varepsilon }_{\theta \theta } {\text{d}}\Omega }.$$
(29)

By utilizing Eqs. (4), (6) and (11) and disregarding thermal stress, one can arrive at the following relation:

$$\tilde{\sigma }_{\theta \theta } = - \frac{Ex}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right) = - \frac{Er\sin \phi }{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right).$$
(30)

Similarly, one can obtain:

$$\tilde{\varepsilon }_{\theta \theta } = - \frac{x}{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right) = - \frac{r\sin \phi }{{R_{0}^{2} }}\left( {1 - n^{2} } \right)U_{n} \sin \left( {n\theta } \right).$$
(31)

For a toroidal ring, one can write:

$${\text{d}}\Omega = \left( {R + x} \right){\text{d}}\theta .r{\text{d}}\phi .{\text{d}}r = \left( {R + r\sin \phi } \right){\text{d}}\theta .r{\text{d}}\phi .{\text{d}}r.$$
(32)

By inserting Eqs. (30)–(32) into Eq. (29) and integrating the result over \(0 \le \theta \le 2\pi\), \(0 \le \phi \le 2\pi\) and \(0 \le r \le r_{0}\), the maximum stored energy \(W\) is obtained as:

$$W = \frac{{\pi {\text{EIR}}_{0} }}{2}\left[ {\frac{{\left( {1 - n^{2} } \right)U_{n} }}{{R_{0}^{2} }}} \right]^{2} .$$
(33)

Through a similar method, substitution of Eqs. (24b), (30) and (32) into Eq. (28) and integration over the entire ring volume gives:

$$\Delta W = 2\pi \Delta_{{\text{E}}} .W.\mathop \sum \limits_{k = 1}^{\infty } G_{k} \frac{{\tau_{k} \omega_{n} \left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{q} \omega_{n}^{2} } \right) + \tau_{k} \tau_{{\text{q}}} \omega_{n}^{3} \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{{\text{T}}} + \tau_{k} } \right]}}{{\left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{{\text{q}}} \omega_{n}^{2} } \right)^{2} + \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{T} + \tau_{k} } \right]^{2} \omega_{n}^{2} }},$$
(34)

in which \(G_{k}\) is a weight coefficient that is defined by:

$$G_{k} = \frac{8}{{a_{k}^{2} \left( {a_{k}^{2} - 1} \right)}}.$$
(35)

The values \(G_{k}\) for the first ten terms are presented in Table 1.

Finally, by inserting Eq. (34) into Eq. (25), the relation for computing TED value in circular cross-sectional micro/nanorings, which includes the phase lag parameters of the DPL model is obtained as follows:

$$TED = \Delta_{E} \mathop \sum \limits_{k = 1}^{\infty } G_{k} \frac{{\tau_{k} \omega_{n} \left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{q} \omega_{n}^{2} } \right) + \tau_{k} \tau_{q} \omega_{n}^{3} \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{T} + \tau_{k} } \right]}}{{\left( {1 + \delta_{kn}^{2} - \tau_{k} \tau_{q} \omega_{n}^{2} } \right)^{2} + \left[ {\left( {1 + \delta_{kn}^{2} } \right)\tau_{T} + \tau_{k} } \right]^{2} \omega_{n}^{2} }}$$
(36)

It is worth noting that in the absence of phase lags \(\tau_{{\text{q}}}\) and \(\tau_{{\text{T}}}\), above equation is reduced to the relation derived by Li et al. [84] by means of the Fourier model. Also, by dropping the terms including \(\tau_{{\text{T}}}\), the relationship developed in this work corresponds to that established by Kim and Kim [89] according to single-phase-lag (SPL) or LS model. These comparisons can be evidence to verify the presented formulation.

Numerical Results and Discussion

In this section, firstly, a comparison study is carried out to examine the validity and accuracy of the developed formulation in this research. For this purpose, the results of the present study for a specific case are compared with those reported by Kim and Kim [89]. It should be noted that for estimating the amount of TED in 2D model, it is enough that the terms caused by the derivatives in the circumferential direction are removed. In other words, the value of \({\delta }_{kn}\) is set equal to zero in the calculations. In the article of Kim and Kim [89], TED in rings with circular cross section has been assessed on the basis of LS model. Accordingly, the outcomes of the current article can be compared with those of [89] by setting \({\tau }_{\mathrm{T}}=0\) in the formulation presented in Eq. (36). In addition, to compare the results of this paper with the investigation of Li et al. [84], which has been done in the framework of the Fourier model, the terms including \({\tau }_{\mathrm{q}}\) and \({\tau }_{\mathrm{T}}\) in Eq. (36) should be neglected. In Fig. 2, the variation of TED in a ring made of silicon (Si) with respect to the vibration mode \(n\) is depicted. Material constants of Si are presented in Table 2. The geometric parameters of the ring are also considered as \(r_{0} = 1\) µm and \(R_{0} = 50\) µm. As can be seen, the outcomes of the present work are consistent with those of [89], which can be a sign of the integrity and veracity of the model derived in this article.

Fig. 2
figure 2

Comparison study for a ring made of silicon with geometric properties \(r_{0} = 1\) µm and \(R_{0} = 50\) µm

Full size image
Table 2 Material constants of silicon (Si) at a reference temperature \({T}_{0}=293 K\) [89]
Full size table

In the following, several numerical examples are provided to appraise the sensitivity of TED value to some key factors such as phase lag parameters of DPL model, number of vibration mode, 2D and 3D cases of heat transfer, geometrical characteristics and material. Mechanical and thermal properties of gold (Au), copper (Cu), lead (Pb) and silver (Ag) at \({T}_{0}=300 \mathrm{K}\) are presented in Table 3 [3]. Except for the cases where the effect of the material on TED is investigated, the rest of the results are given for the rings made of gold.

Table 3 Properties of gold (Au), copper (Cu), lead (Pb) and silver (Ag) at a reference temperature \({T}_{0}=300 K\) [3]
Full size table

In Fig. 3, the effect of the number of terms considered in Eq. (36) on the value of TED as a function of vibration mode number is analyzed. In this figure, the curves are plotted for 2D and 3D models and for solutions including only one term and the first ten terms. Also, the geometrical properties of the ring are assumed to be \({r}_{0}=200 \mathrm{nm}\) and \({R}_{0}=20{r}_{0}\). As it is clear, the difference of the results obtained from considering the first ten terms and only one term is insignificant and the graphs of these two cases are almost identical.

Fig. 3
figure 3

Variations of TED in terms of vibration mode number for only one term and the first ten terms of presented solution for \(r_{0} = 200 \;{\text{nm}}\) and \(R_{0} = 20r_{0}\)

Full size image

For 2D and 3D models of heat conduction, Fig. 4 indicates the ratio of TED calculated by the first ten terms to that estimated by the single term. As can be seen, the difference between the results of these two cases is less than one percent. This difference is much smaller for lower vibration modes. Based on Figs. 3 and 4, it can be concluded that considering the first ten terms is enough to achieve convergent results. Therefore, in the following figures, the results are drawn for the first ten terms of the provided solution.

Fig. 4
figure 4

The ratio of TED with the first ten terms to TED with only the first term for \(r_{0} = 200 {\text{nm}}\) and \(R_{0} = 20r_{0}\)

Full size image

Figures 5a, b illustrate the impact of the Fourier and DPL models on the variations of TED with mode number for cases \({R}_{0}=20{r}_{0}\) and \({R}_{0}=100{r}_{0}\), respectively. To achieve these figures, it is assumed that \({r}_{0}=50 \mathrm{nm}\). Based on these graphs, it can be concluded that, in general, DPL model predicts lower values for TED than the Fourier model. When the dimensions of the ring are larger (i.e. \({R}_{0}=100{r}_{0}\)), this result can be stated with more certainty and for almost all vibration modes. The physical interpretation of this result is that DPL model anticipates a wave-like characteristic for heat propagation with finite velocity, whereas the Fourier model estimates that thermal signals transfer in solids through diffusion phenomenon. Owing to finite speed of heat transfer in DPL model, heat induced by a nonuniform stress field has no adequate time to propagate during the vibration of structure, which alleviates energy loss originated by thermoelastic damping. Accordingly, TED values predicted by the DPL model are lower than those of the Fourier model. Another conclusion that can be drawn from these curves is that for a wide range of vibration modes, TED value calculated by 3D model is smaller than that determined by the 2D model. It is also observed that when the size of the ring becomes larger (i.e. \({R}_{0}=100{r}_{0}\)), the difference between the Fourier and DPL models as well as the difference between 2 and 3D cases of heat conduction lessen for a wider range of vibration mode number.

Fig. 5
figure 5

The influence of the Fourier and DPL models on the variations of TED versus vibration mode number for \(r_{0} = 50 {\text{nm}}\) a \(R_{0} = 20r_{0}\) b \(R_{0} = 100r_{0}\)

Full size image

Figures 6a, b are drawn under the same conditions as Fig. 5a, b. The only difference is that in these figures \({r}_{0}=1\) µm is considered. In other words, these diagrams are plotted for the rings with larger dimensions than the previous figure. Comparing these diagrams with the curves in the previous figure shows that the effect of the DPL model on TED is almost the same for both cases \({r}_{0}=50 \mathrm{nm}\) and \({r}_{0}=1\) µm, that is, for a large range of vibration modes, TED value calculated by the DPL model is lower than that obtained by means of the Fourier model. These graphs also illustrate that 2D and 3D models have different effects on cases \({r}_{0}=50 \mathrm{nm}\) and \({r}_{0}=1\) µm, so that unlike the case \({r}_{0}=50 \mathrm{nm}\), 3D model predicts more values for TED in case \({r}_{0}=1 \mu m\). According to what was said before, to arrive at the results of 2D model, term \({\delta }_{kn}\) in Eq. (36) should be set equal to zero. Thus, one can state that the difference between 2 and 3D models gets negligibly small as the variable \({\delta }_{kn}\) takes an insignificant value. In view of the relation \({\delta }_{kn}=\left(n/{a}_{k}\right)\left({r}_{0}/{R}_{0}\right)\), this issue happens when either the number of vibration mode \(n\) is low or the amount of ratio \({r}_{0}/{R}_{0}\) is very small. This can be readily seen in Figs. 5 and 6. In cases where \({\delta }_{kn}\) has a considerable value, given the appearance of this term in both the numerator and denominator of Eq. (36), it is problematic to extract a single pattern for TED for 2D and 3D models.

Fig. 6
figure 6

The influence of the Fourier and DPL models on the variations of TED versus vibration mode number for \(r_{0} = 1\) µm a \(R_{0} = 20r_{0}\) b \(R_{0} = 100r_{0}\)

Full size image

In Fig. 7a, b, the impact of the Fourier and DPL models on TED versus geometrical ratio \({R}_{0}/{r}_{0}\) is examined for cases \(n=10\) and \(n=100\), respectively. In these curves it is supposed that \({r}_{0}=50 nm\). By observing these curves, it is reconfirmed that TED obtained in the framework of the DPL model has a smaller value compared to that computed based on the Fourier model. It is also obvious that for case \(n=10\) where the vibration mode number is relatively small, as the value of \({R}_{0}/{r}_{0}\) ascends and the parameter \({\delta }_{kn}\) reduces, both the effect of size and the effect of using a 2D or 3D model on TED value shrink.

Fig. 7
figure 7

The impact of the Fourier and DPL models on the variations of TED with respect to the geometrical ratio \(R_{0} /r_{0}\) for \(r_{0} = 50 \;{\text{nm}}\) a \(n = 10\) b \(n = 100\)

Full size image

Figure 8a, b are drawn with the same conditions as Fig. 7a, b, with the only difference that in these figures it is assumed that \({r}_{0}=1\) µm. It can be seen again that for case \({r}_{0}=1\) µm, TED value calculated by 3D model is higher than that determined by 2D model. Besides, it is evident that by increasing the value of \({R}_{0}/{r}_{0}\), the effect of size weakens and the results of DPL model approach those of the Fourier model.

Fig. 8
figure 8

The impact of the Fourier and DPL models on the variations of TED with respect to geometrical ratio \(R_{0} /r_{0}\) for \(r_{0} = 1\) µm a \(n = 10\) b \(n = 100\)

Full size image

In Figs. 9 and 10, the dependence of TED value on the material of the ring is discussed. For this purpose, four materials gold (Au), copper (Cu), lead (Pb) and silver (Ag) at a reference temperature \({T}_{0}=300 \mathrm{K}\) are surveyed. In all these figures, the parameter \({r}_{0}\) is considered a fixed value of \(400 \;{\text{nm}}\). Figure 9a, b represent the variation of TED versus vibration mode number for 2D and 3D cases of heat conduction, respectively. In these figures, it is assumed that \({R}_{0}=20{r}_{0}\). According to these figures, in low vibration modes (i.e. \(n<20\)), TED in ascending order belongs to Au, Ag, Cu and Pb rings. In regard to the reason for this outcome one can say that the principal parameter that makes the coupling between structural and thermal domains is the thermal expansion coefficient \(\alpha\). Hence, greater amounts of \(\alpha\) lead to more intensive thermoelastic coupling and higher levels of energy dissipation. Additionally, when phase lag parameters \({\tau }_{\mathrm{q}}\) and \({\tau }_{\mathrm{T}}\) take higher values, the impact of diffusion-type heat conduction dwindles. Consequently, for larger amounts of \({\tau }_{\mathrm{q}}\) and \({\tau }_{\mathrm{T}}\), it is expected that the value of TED will be lower. In high mode numbers (i.e. almost \(n>50\)), the highest value of TED occurs in rings made of Ag, Au, Cu and Pb, respectively. In Fig. 10a, b, the variation of TED as a function of the geometrical ratio \({R}_{0}/{r}_{0}\) is displayed for 2D and 3D models, respectively. These figures are plotted for mode number \(n=20\). As it is apparent, for the range \({R}_{0}/{r}_{0}<30\), no specific rule can be mentioned for different materials, but for the range \({R}_{0}/{r}_{0}>30\), rings made of Pb, Cu, Ag and Au experience the highest amount of TED, respectively.

Fig. 9
figure 9

The effect of material on the variations of TED versus vibration mode number for \(r_{0} = 400 \;{\text{nm}}\) and \(R_{0} = 20r_{0}\) a 2D b 3D cases of heat conduction

Full size image
Fig. 10
figure 10

The effect of material on the variations of TED versus geometrical ratio \(R_{0} /r_{0}\) for \(r_{0} = 400 \;{\text{nm}}\) and \(n = 20\) a 2D b 3D cases of heat conduction

Full size image

Conclusions

In the current article, by incorporating the size effect into the thermal domain by way of a dual-phase-lag (DPL) heat conduction model, 2D and 3D models has been developed for evaluating thermoelastic damping (TED) in micro/nanorings with circular cross section. To this aim, the equation of heat conduction obtained in the context of the DPL model has been solved first. Next, the temperature distribution in the ring has been extracted in the form of infinite series for 2D and 3D models of heat transfer. Then, the definition of quality factor in entropy generation (EG) approach has been applied to establish an analytical relation containing the two-phase lag parameters of the DPL model for approximation of TED value in circular cross-sectional micro/nanorings. At the final stage, a thorough parametric study has been made to appraise the dependence of TED on some crucial factors like phase lag parameters of the DPL model, vibration mode number, geometrical parameters and material. The main concluding remarks can be stated as follows:

  • Convergence analysis demonstrates that the inclusion of the first ten terms of a developed solution is adequate for the attainment of an accurate result.

  • In general, the amount of TED estimated in the framework of the DPL model is lower than that predicted by the Fourier model. The greatest effect of the DPL model on TED can be seen in high vibration modes or smaller ring sizes (more precisely in nano dimensions).

  • According to the definition of a parameter \({\delta }_{kn}\), the difference between 2 and 3D models becomes noticeable in high vibration modes \(n\) and low geometrical ratios \({R}_{0}/{r}_{0}\).

  • In the range of low values of vibration mode number \(n\) or high values of geometrical ratio \({R}_{0}/{r}_{0}\), the sensitivity of TED to dual-phase-lagging effect and 2D or 3D cases of heat conduction gets weak. Additionally, for very thin rings vibrating in the low mode numbers, TED is affected faintly by the DPL model and two or three-dimensionality of heat conduction.

  • By the enlargement of cross-sectional radius \({r}_{0}\), the impact of size on the heat conduction field shrinks, so that the discrepancy between the predictions of the Fourier and DPL models descends.

  • Among the examined materials, the maximum and minimum amount of TED in the low vibration modes occurs in the rings made of lead (Pb) and gold (Au), respectively.