Introduction

Perturbation methods [1,2,3] had grasped the attention of many researchers throughout the past few decades to acquire the solutions for the rotatory motion of a rigid body (RB) problem [4,5,6,7,8,9,10,11]. It is reported that such a problem is regulated by six non-linear differential equations and three associated first integrals [12]. The solutions to these equations are only found in a few special cases [13], where the urgent fourth integral was discovered. There are several limitations in these circumstances regarding the location of the body's center of mass and the magnitudes of the main moments of inertia. To achieve this integral, a number of integrable scenarios have appeared, including [12, 14,15,16,17,18]. Six integrable scenarios for the RB were found in [14] when a body is being affected by an axisymmetric combination of gyroscopic and potential forces in accordance with initial circumstances. The author also looked at the generalization of Lagrange's scenario, the Kovalevskaya case, and the body's full symmetric case. In [15], a transformation rotation with position-dependent angular velocity has been used to examine the generalization of the other six integrable situations. Two new criteria are used in [16] to provide the appropriate integrable situations for the rigid body motion similar to Kovalevskaya top. Additional requirements are constructed in [17], to generalize the integrable scenario of Chaplygin and Yehia. A brand-new class of 2D integrable systems with twenty arbitrary parameters is examined in [18]. The author provided an integrable situation of a third degree in velocities to generalize certain earlier cases. When the body rotates while being affected by a gyrostatic moment, the necessary and sufficient condition for getting the fourth first integral is stated in [12].

In [19], the authors investigated the behavior of a heavy ball rolling inside a semi-spherical chamber when subjected to horizontal kinematic excitation. This ball has been designed to make an excellent contact with the hollow surface without slipping at all. Harmonic horizontal excitation was taken into consideration during the numerical analysis of this problem. However, they examined the predictable and recognizable patterns of free motion of a tuned mass damper of the ball type in [20]. The neighborhood of seven different limit solutions (or limit trajectories) has been discovered and physically explained. The movement of a big ball rolling inside a semi-spherical chamber in the presence of a kinematical excitation in a horizontal direction is simulated analytically and numerically in [21] and [22], respectively. In light of the Lagrangian governing system, an analytical approach is used to examine this movement.

There are many different approximations can be used to treat the difficulty in solving the nonlinear ordinary differential equations, such as the small parameter method (SPM), the Krylov–Bogoliubov–Mitropolski (KBM), and the averaging method (AM). The SPM is used in [4] and [5] to obtain the asymptotic solutions of the fast rotatory RB's motion when the uniform gravitational field and the Newtonian gravitational field are acted upon, respectively. On the other hand, these solutions contain singular points that are treated for ever in the works [6,7,8], when the authors thought about the action of the gyrostatic moment (GM) on the body, regardless of whether the gravitational field or the Newtonian one is applied. Furthermore, the approximate solutions of the 3D rotatory motion of a RB under the action of a Newtonian field, a magnetic one and the GM are examined in [9] using the SPM, in which the formulas of Euler’s angles are derived. Recently, this method is utilized in [23] to examine the RB motion similar to the Bobylev–Steklov conditions when the body is forced by GM, electromagnetic field, and Newtonian field. Whereas in [24], the authors considered that the body's center of mass deviates somewhat from its dynamic axis of symmetry. The body is forced by one component of the GM and the electromagnetic field.

The approach of KBM was used in [10] to provide the approximate analytical solutions of the equations of motion (EOM) for a symmetrical case of the RB in a uniform gravity field. As before, these solutions include singular points. The generalization of this issue is found in [11] and [25] when a GM and a Newtonian field, respectively, have an effect on the body. The obtained results do not have any point of singularity at all, due to the use of Amer’s frequency [6, 11, 25]. Recently, the RB problem is examined in [26] at the closeness of inertia’s ellipsoid and rotation’s ellipsoid. The authors considered the action of a uniform field only beside one component of the GM about the symmetry dynamic axis. The numerical solutions are obtained and compared with the analytical ones. Moreover, the treatment of this problem for the scenario of Euler and Poinsot is found recently in [27] using the KBM. In [28], the numerical outcomes of the EOM of a RB that is loaded with a rotating mass in the presence of a Newtonian field are discussed. The author considered that the body’s center of mass is located in one of the planes of the moments of inertia.

On another level, the AM has met with the endorsement of numerous scientists to acquire the approximate solutions for the body’s motion, whether under the influence of the gravitational field [29,30,31,32,33,34,35,36,37] or the Newtonian field [37,38,39]. In [30], the authors studied the perturbed movement of the RB near a regular precession for Lagrange’s scenario. A small parameter was introduced into the governing EOM in accordance with some initial circumstances. The rotatory problem of a dynamically spherical RB connected with a viscoelastic element was presented in [31]. This element has been represented by a moving mass that is coupled to the point on one of the main axes of inertia via a spring and damper. The motion is investigated in the context of a restoring moment, which is dependent on the nutation angle. Recently, the numerical solutions of this problem has been examined in [32] and [33], in light of the averaging system of the governing one, when the body is influenced by the moments of perturbing and restoring. In these works, it is considered that the body has a high starting angular velocity around the dynamic principal axis of inertia, in which it is subjected to the moments of perturbing at the principal axes directions. The AM is applied to gain the solutions of the EOM. Along with the previous moments, the rotational motion of this body is examined in [35] when the GM is acted in which its first components are considered to be zero. The extension of this work is included in [36] when the body is charged according to a subjected point charge on the dynamic symmetry axes and its position of mass is a bit displaced from this axis. In [37], the authors considered the action of the Newtonian field only, which is generalized in [38] and in [39] when the authors adopted the full activity of the GM and the action of the electromagnetic field, respectively. Some applications are concerned with the controlling of the angular velocity, linear dissipative moments, and the atmospheric case are considered in [34, 38, 39]. However, the numerical solutions of the symmetric body under the impact of the third projection of the GM and the Newtonian field are investigated in [40]. More contributions on the application of the AM procedure for various dynamical models can be found in [41].

This article deals with the rotational motion of a symmetric solid body around one fixed point with a fresh perspective, in which it rotates initially with a rapidly angular velocity around its dynamic symmetry axis. It is considered that the body rotates in the entity of GM and perturbing one around the inertia principal axes. The regulating system of the EOM is modulated to the averaging one applying the AM. The later system is solved analytically for some applications. The attained results are discussed and demonstrated in various plots for each application to show the effectiveness of several parameters on the body’s behavior. These results generalize the previous works [29, 30], and [34].

Description of the Problem

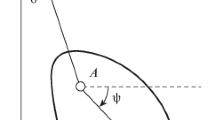
The major aim of the present section is to outline the rotational motion of a symmetric RB (having a mass \(m\)) around one fixed point \(O\). Let us consider two Cartesian orthogonal systems having the same origin point \(O\); namely a fixed system \(OXYZ\) and a moving one \(Oxyz\) which is immovable in the body but moving with it, and it is directed on the body's inertia principal axes. The body is supposed to be connected from its upper point \(N_{1}\) with a spring (of stiffness \(\nu\)), in which its second end \(N_{2}\) is positioned on the axis \(OZ\) at a distance \(d\) from \(O\). Therefore, we consider \(N_{1} N_{2} = S(\theta ),\,\,\,\,\theta \ne 0\), where \(\theta\) is the angle between \(Oz\) and \(OZ\). The investigated motion is considered under the disposal of a perturbing moment vector \(\underline{M}\) and a gyrostatic one \(\underline{\ell }\); in which their projections \(M_{j}\) and \(\ell_{j} \,\,(j = 1,2,3)\) are acted about the body’s principal axes \(Ox,Oy,\) and \(Oz\) (Fig. 1).

Fig. 1
figure 1

The dynamical model

Full size image

The governing system of EOM can be acquired using the next angular momentum equation [38]

$$\underline{{\dot{h}}}_{O} + \underline{\omega } \wedge \underline{h}_{O} = \underline{L}_{O} ,$$

where

$$\begin{aligned} & \underline {h}_{O} \equiv (I_{1} p + \ell_{1} ,I_{2} q + \ell_{2} ,I_{3} r + \ell_{3} ), \\ & \underline {L}_{O} = {\text{mg}}(\underline {\gamma } \wedge \underline{Oc} ) + \underline {M} . \\ \end{aligned}$$

Here, \(\underline{h}_{O}\) and \(\underline{L}_{O}\) are the vectors of angular momentum and the moment of all applied forces at \(O\), respectively. The dots refer to the time's differentiation,\(\underline{\omega } \equiv (p,\;q,r)\) is the vector of angular velocity, \(\underline{Oc} = \underline{l} \equiv (0,0,\,l\,)\) represents the position vector of the center of mass, \({\text{g}}\) is the gravitational acceleration, \(I_{j} \,\,(j = 1,2,3)\) are the inertia’s principal moments, and \(\underline{\gamma } \equiv (\,\sin \theta \sin \varphi ,\;\sin \theta \cos \varphi ,\;\cos \theta )\) is the unit in the direction of \(Z{\kern 1pt}\)-axis, in which \(\varphi\) is the angle of self-rotation.

It is worthy to mention that the angular velocity projections \(p,q,\) and \(r\) can be written in terms of the Euler's angles \(\theta ,\,\varphi\), and \(\psi\) in the following forms [13]

$$\begin{aligned} & p = \dot{\psi }\sin \varphi \sin \theta + \dot{\theta }\cos \varphi , \\ & q = \dot{\psi }\cos \varphi \sin \theta - \dot{\theta }\sin \varphi , \\ & r = \dot{\varphi } + \dot{\psi }\cos \theta , \\ \end{aligned}$$

in which \(\theta\) and \(\psi\) are the nutation and precession angles, respectively.

Based on the above simulation, we can conclude that the acting forces of the body are the gravity force and the spring elastic’s force \(F\), in which its modulus is directly regulated with the spring's deformation, i.e., \(F = \nu (S - S_{0} )\) where \(S_{0} = N_{1} N_{2}\) at \(\theta = 0\) is the un-deformed length of the spring. Therefore, along the body's main axis, the restoring torque is composed as follows

$$\begin{aligned} & \underline{M}_{{_{{{\text{restoring}}}} }} = (u\sin \theta \cos \varphi , - u\sin \theta \sin \varphi ,0); \\ & u = {\text{mg}}{\kern 1pt} {\kern 1pt} l \, \, + \nu {\kern 1pt} {\kern 1pt} d{\kern 1pt} {\kern 1pt} z^{ * } [1 - S_{0} (d^{2} + z^{ * 2} - 2dz^{ * } \cos \,\,\theta )^{{^{ - 1/2} }} ], \\ & z^{ * } = ON_{1} ,\quad d = ON_{2} . \\ \end{aligned}$$
(1)

After grasping the previous, the EOM with respect to the Cartesian system \(Oxyz\) can be expressed in the form

$$\begin{aligned} & I_{1} {\kern 1pt} \dot{p} + (I_{3} - I_{1} ){\kern 1pt} {\kern 1pt} qr + q\ell_{3} \,\, - r\ell_{2} \, = u\,\,\cos \varphi \sin \theta \, + M_{1} , \\ {\kern 1pt} & I_{1} \,{\kern 1pt} \dot{q} + (I_{1} - I_{3} ){\kern 1pt} {\kern 1pt} rp\, - p{\kern 1pt} \ell_{3} + r{\kern 1pt} \ell_{1} = - u\sin \varphi \sin \theta + M_{2} , \\ & I_{3} \,\dot{r} + p{\kern 1pt} \ell_{2} - q\ell_{1} = M_{3} ,\,\,\,\, \\ & \dot{\theta } = - q{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \varphi + p{\kern 1pt} {\kern 1pt} \cos \varphi , \\ & \dot{\varphi } = r - (\,q{\kern 1pt} \cos \varphi + p\sin \varphi )\cot \theta , \\ & \dot{\psi } = (\,q\cos \varphi + p\sin \varphi )\csc \theta . \\ \end{aligned}$$
(2)

Here, it is considered that \(I_{1} = I_{2}\) for the studied symmetric case. According to the above EOM, one can obtain the governing EOM of Lagrange's case at \(\underline{\ell } \equiv \underline{0} ,\,\,\underline{M} \equiv \underline{0} ,\) and \(u = {\text{const}}\). Moreover, the governing system in [29, 30], and [34] can be obtained at \(\underline{\ell } \equiv \underline{0}\), in which the same approach of these works is used in the analysis of the present work.

It is supposed that at the start of motion, the body spins around the dynamic symmetry axis with rapid angular velocity, the first two components of \(\underline{M}\) are less than \(u\) while its third component is approximately order of \(u\). Therefore, one can write

$$p^{2} + q^{2} \ll r^{2} ,I_{3} r^{2} \gg u,\left| {M_{i} } \right| \ll u,M_{3} \approx u(i = 1,2).$$
(3)

Now, we are going to introduce a small parameter \(\varepsilon\) to apply the AM. Therefore, the previous conditions (3) can be interpreted as follows

$$\begin{aligned} & p = \varepsilon P,q = \varepsilon Q,u = \varepsilon U,\quad \ell_{i} = \varepsilon \ell_{i}^{*} \\ & M_{i} = \varepsilon^{2} M_{i}^{*} (P,Q,r,\psi ,\theta ,\varphi ,\tau );\quad (i = 1,2), \\ & M_{3} = \varepsilon M_{3}^{*} (P,Q,r,\psi ,\theta ,\varphi ,\tau ),\quad \tau = \varepsilon t. \\ \end{aligned}$$
(4)

Here, the variables \(Q,P\,\), and the functions \(\,M_{i}^{*} ,U\) are considered to be limited values of unity at \(\varepsilon \to 0\) such as \(r,\,\,\psi ,\,\theta ,\) and \(I_{1} ,\,I_{3}\).

It is remembered that the goal of the present work is to achieve the solutions of the EOM (2) in the presence of conditions (3) and equalities (4) using the AM [1, 2].

The Averaging Method (AM)

Our aim in this part is to get the averaging system of the corresponding controlling one of the EOM (2). Therefore, the AM is used to achieve the desired system. To acquire this aim, making use of (4) into (2), and then cancelling \(\varepsilon\) from both sides of the resulted system to yield

$$\begin{aligned} & I_{1} \,\dot{P} + (I_{3} - I_{1} )\,Qr + Q\,\ell_{3} \, - r\ell_{2}^{*} = U\sin \theta \cos \varphi + \varepsilon M_{1}^{*} , \\ & I_{1} \dot{Q} + (I_{1} - I_{3} )\,\,rP + r\,\ell_{1}^{*} - P{\kern 1pt} \ell_{3} \, = - U\sin \theta \sin \varphi + \varepsilon M_{2}^{*} , \\ & I_{3} {\kern 1pt} \dot{r}\, = \varepsilon {\kern 1pt} \ell_{1} Q - \varepsilon {\kern 1pt} \ell_{2} P + \varepsilon \,M_{3}^{*} , \\ & \dot{\theta } = \varepsilon ( - Q{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \varphi + P{\kern 1pt} {\kern 1pt} \cos \varphi ), \\ & \dot{\varphi } = r - \varepsilon {\kern 1pt} ({\kern 1pt} Q{\kern 1pt} {\kern 1pt} \cos \varphi + P{\kern 1pt} \sin \varphi )\cot \theta , \\ & \dot{\psi } = \varepsilon (\,Q{\kern 1pt} {\kern 1pt} \cos \varphi + P\sin \varphi )\csc \theta . \\ \end{aligned}$$
(5)

To achieve the desired solutions, we begin with the approximation at \(\varepsilon = 0\). Consequently, the solutions of the final four equations in the aforementioned system are

$$r = r_{0} ,\quad \theta = \theta_{0} ,\quad \varphi = r_{0} \,t + \varphi_{0} ,\quad \psi = \psi_{0} ,\quad U_{0} = U(\theta_{0} ),$$
(6)

where \(r_{0} ,\;\theta_{0} ,\,\varphi_{0} ,\) and \(\psi_{0}\) are the constants of integration that correspond to the variables at the beginning of the motion.

Inserting (6) into the first two equations of (5) when \(\varepsilon = 0\), and then the derivatives of the resulted two equations produce

$$\begin{aligned} & \ddot{P} + y_{0}^{2} {\kern 1pt} P = U_{0} \,Z_{0} {\kern 1pt} \sin \theta_{0} \sin (r_{0} \,t + \varphi_{0} ) + y_{0} \,r_{0} \,I_{1}^{ - 1} \ell_{1}^{*} , \\ & \ddot{Q} + y_{0}^{2} {\kern 1pt} Q = U_{0} \,Z_{0} {\kern 1pt} \sin \theta_{0} \cos (r_{0} \,t + \varphi_{0} ) + y_{0} \,r_{0} \,I_{1}^{ - 1} \ell_{2}^{*} . \\ \end{aligned}$$
(7)

The nonlinear system described above has two degrees of freedom, and its integration yields

$$\begin{aligned} & P = a\cos \gamma_{0} + b\sin \gamma_{0} + E_{0} \sin \theta_{0} \sin (r_{0} \,t + \varphi_{0} ) + (I_{1} \,y_{0} )^{ - 1} r_{0} \,\ell_{1}^{*} , \\ & Q = a\sin \gamma_{0} - b\cos \gamma_{0} + E_{0} \sin \theta_{0} \cos (r_{0} \,t + \varphi_{0} ) + (I_{1} \,y_{0} )^{ - 1} r_{0} \,\ell_{2}^{*} , \\ \end{aligned}$$
(8)

where

$$\begin{aligned} & a = P_{0} - E_{0} \sin \theta_{0} \sin \varphi_{0} - (I_{1} \,y_{0} )^{ - 1} r_{0} \,\ell_{1}^{*} , \\ & b = - Q_{0} + E_{0} \sin \theta_{0} \cos \varphi_{0} + (I_{1} \,y_{0} )^{ - 1} r_{0} \,\ell_{2}^{*} , \\ & \gamma_{0} = y_{0} {\kern 1pt} {\kern 1pt} t,\,\,\,\,n_{0} = (\,I_{3} - I_{1} ){\kern 1pt} {\kern 1pt} {\kern 1pt} r_{0} \,I_{1}^{ - 1} , \\ & E_{0} = {{U_{0} \,} \mathord{\left/ {\vphantom {{U_{0} \,} {[I_{1} ({\kern 1pt} {\kern 1pt} y_{0} + r_{0} {\kern 1pt} )}}} \right. \kern-0pt} {[I_{1} ({\kern 1pt} {\kern 1pt} y_{0} + r_{0} {\kern 1pt} )}}],\quad \,\left| {{{y_{0} } \mathord{\left/ {\vphantom {{y_{0} } {r_{0} }}} \right. \kern-0pt} {r_{0} }}} \right| \le 1,\quad r_{0} \ne 0, \\ & y_{0} = \,n_{0} + I_{1}^{ - 1} \,\ell_{3} ,\quad Z_{0} {\kern 1pt} = (y_{0} - r_{0} )\,I_{1}^{ - 1} . \\ \end{aligned}$$

Here \(P_{0} = P_{t = 0} ,\,\,\,\,Q_{0} = Q_{t = 0} ,\) \(\gamma_{0}\) refer to the generating system oscillation phase, and \(a,b\) represent the van der Pol type of the osculating variables [30].

Since Eq. (5) constitute a nonlinear system, we can insert \(\gamma = \gamma (t)\) as a new variable, to transform this system to an autonomous one, according to

$$\dot{\gamma } = y,\quad \gamma (0) = 0;\quad y = I_{1}^{ - 1} [(\,I_{3} - I_{1} ){\kern 1pt} {\kern 1pt} {\kern 1pt} r + \ell_{3} ].$$
(9)

Based on (6) and (8) at \(\varepsilon = 0\), the general solutions of (5) can be estimated. The variables \(Q\) and \(P\) can be expressed in an alternative form as follows

$$\begin{aligned} & P = a\cos \gamma + b\sin \gamma + E\sin \theta \sin \varphi + (I_{1} y)^{ - 1} {\kern 1pt} r\,\ell_{1}^{*} , \\ & Q = a\sin \gamma - b\cos \gamma + E\sin \theta \cos \varphi + (I_{1} y)^{ - 1} {\kern 1pt} r\,\ell_{2}^{*} . \\ \end{aligned}$$
(10)

Therefore, in accordance with (10), \(a\) and \(b\) can be written as the next form

$$\begin{aligned} & a = Q{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \gamma + P{\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \gamma - E{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \theta {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \alpha - (I_{1} y)^{ - 1} {\kern 1pt} r{\kern 1pt} {\kern 1pt} {\kern 1pt} (\ell_{1}^{*} \cos \gamma + \ell_{2}^{*} \sin \gamma ), \\ & b = - Q{\kern 1pt} {\kern 1pt} \cos \gamma + P{\kern 1pt} {\kern 1pt} \sin \gamma + E{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \theta {\kern 1pt} {\kern 1pt} \cos \alpha - (I_{1} y)^{ - 1} r{\kern 1pt} {\kern 1pt} (\ell_{1}^{*} \sin \gamma - \ell_{2}^{*} \cos \gamma ); \\ & \alpha = \gamma + \varphi . \\ \end{aligned}$$
(11)

Let us reconsider the system of Eq. (5) at \(\varepsilon \ne 0\) beside Eq. (10) and according to the above discussion, we can alter \(P,\;Q,r,\psi ,\theta ,\varphi ,\) and \(\gamma\) in (5) and (9) to obtain the \(a,b,\,r,\psi ,\theta ,\alpha ,\) and \(\gamma\) as new variables. From (11), the following form can be obtained through various manipulations and reductions

$$\begin{aligned} \dot{a} & = \varepsilon \,I_{1}^{ - 1} (M_{1}^{0} \cos \gamma + M_{2}^{0} \sin \gamma ) - \varepsilon \,(I_{1} \,y)^{ - 2} I_{3}^{ - 1} M_{3}^{0} \,\ell_{3} \,(\ell_{1}^{*} \cos \gamma + \ell_{2}^{*} \sin \gamma ) \\ & \quad - \varepsilon {\kern 1pt} E\,\cos \theta {\kern 1pt} {\kern 1pt} [b - E\,\sin \theta \,\cos \alpha + (I_{1} y)^{ - 1} {\kern 1pt} r\,(\ell_{1}^{*} \sin \gamma - \ell_{2}^{*} \cos \gamma )] + I_{1}^{ - 1} \sin \theta \, \\ & \quad \times \,\cos \alpha [U - E{\kern 1pt} {\kern 1pt} (\,I_{3} {\kern 1pt} {\kern 1pt} r + \ell_{3} )] - \varepsilon \,U\,[I_{1} (y + {\kern 1pt} r)]^{ - 2} M_{3}^{0} \,{\kern 1pt} \sin \theta \sin \alpha \\ & \quad + \varepsilon \,\nu {\kern 1pt} {\kern 1pt} d^{2} z^{{ *^{2} }} s_{0} [I_{1} (y + {\kern 1pt} r)]^{ - 1} \sin^{2} \theta (d^{2} + z^{ * 2} - 2d{\kern 1pt} z^{ * } \cos \,\,\theta )^{ - 3/2} [a\,\cos \alpha \sin \alpha \\ & \quad + b\,\sin^{2} \alpha + (I_{1} y)^{ - 1} r\,\sin \alpha (\ell_{1}^{*} \cos \varphi - \ell_{2}^{*} \sin \varphi )], \\ \end{aligned}$$
$$\begin{aligned} \dot{b} & = \varepsilon \,I_{1}^{ - 1} (M_{1}^{0} \sin \gamma - M_{2}^{0} \cos \gamma ) - \varepsilon \,(I_{1} y)^{ - 2} I_{3}^{ - 1} M_{3}^{0} \,\ell_{3} \,(\ell_{1}^{*} \sin \gamma - \ell_{2}^{*} \cos \gamma ) \\ & \quad + \varepsilon {\kern 1pt} E\,\cos \theta [a + E\,\sin \theta \,\sin \alpha + (I_{1} y)^{ - 1} {\kern 1pt} r\,(\ell_{1}^{*} \cos \gamma + \ell_{2}^{*} \sin \gamma )] + I_{1}^{ - 1} \sin \theta \sin \alpha \\ & \quad \times [U - E{\kern 1pt} (\,I_{3} {\kern 1pt} r + \ell_{3} )] - \varepsilon \,[I_{1} (y + {\kern 1pt} r)]^{ - 2} U\,M_{3}^{0} \,\sin \,\theta \,\cos \alpha \\ & \quad + \varepsilon \,\nu {\kern 1pt} {\kern 1pt} d^{2} z^{ * 2} s_{0} [I_{1} (y + {\kern 1pt} r)]^{ - 1} \sin^{2} \theta (d^{2} + z^{ * 2} - 2d{\kern 1pt} z^{ * } \cos \,\,\theta )^{ - 3/2} [a\,\cos^{2} \alpha \\ & \quad + b\,\sin \alpha \cos \alpha + (I_{1} y)^{ - 1} {\kern 1pt} r\,\cos \alpha \,(\ell_{1}^{*} \cos \varphi - \ell_{2}^{*} \sin \varphi )], \\ \end{aligned}$$
(12)
$$\begin{aligned} {\kern 1pt} & \dot{r} = \varepsilon \,I_{3}^{ - 1} {\kern 1pt} [M_{3}^{0} + \varepsilon {\kern 1pt} I_{3} (Q\,\ell_{1}^{*} - P\,\ell_{2}^{*} )], \\ & \dot{\theta } = \varepsilon \,[\,a{\kern 1pt} {\kern 1pt} \cos \alpha + b{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \alpha \, + (I_{1} y)^{ - 1} {\kern 1pt} r\,(\ell_{1}^{*} \cos \varphi - \ell_{2}^{*} \sin \varphi )], \\ & \dot{\psi } = \varepsilon \,[\,a{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \alpha - b{\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \alpha + E\sin \theta + (I_{1} y)^{ - 1} r\,(\ell_{1}^{*} \sin \varphi + \ell_{2}^{*} \cos \varphi ){\kern 1pt} {\kern 1pt} ]\csc \,\theta {\kern 1pt} \,, \\ & \dot{\alpha } = I_{1}^{ - 1} (I_{3} {\kern 1pt} {\kern 1pt} r + \ell_{3} ) - \varepsilon [a{\kern 1pt} {\kern 1pt} \sin \alpha - b{\kern 1pt} {\kern 1pt} \cos \alpha + E{\kern 1pt} {\kern 1pt} \sin \theta \\ & \quad + (I_{1} y)^{ - 1} {\kern 1pt} r\,(\ell_{1}^{*} \sin \varphi + \ell_{2}^{*} \cos \varphi )]\cot \theta , \\ & \dot{\gamma } = I_{1}^{ - 1} [(I_{3} - I_{1} )\,{\kern 1pt} r + \ell_{3} {\kern 1pt} ], \\ \end{aligned}$$

where

$$M_{j}^{0} (a,b,{\kern 1pt} r,\psi ,\theta ,\alpha ,\gamma ,\tau ) = M_{j}^{*} (P,Q,{\kern 1pt} r,\psi ,\theta ,\varphi ,\tau ),\quad j = 1,\,2,\,3.$$

A closer look at the above system (12) reveals that this system has slow variables \(a,b,\,{\kern 1pt} r,\psi ,\theta ,\tau ,\) and the fast ones \(\alpha ,\,\gamma\). It is obvious that system (12) is considered to be more general than the systems considered in [29, 30], and [34] at \(\,\ell_{j} = 0,\,\,\,\underline{M} \ne \underline{M} (\tau )\,\,\,\,(j = 1,2,3)\).

Taking into consideration that \(M_{j} = M_{j} (t)\) and therefore it is very difficult to apply the AM which is due to that system (12) is nonlinear. Then, we consider a simple case of dependence on the variable \(\tau\). According to the periodicity of \(M_{j}\) with the period \(2\pi\) in \(\varphi\), then referring to (8) we find that \(M_{j}^{(0)}\) are also periodic function with period \(2\pi\) in \(\alpha\) and \(\gamma\). It is clear that the frequencies \(\omega_{\alpha } = I_{1}^{ - 1} (I_{3} {\kern 1pt} {\kern 1pt} r + \ell_{3} )\) and \(\omega_{\gamma } = I_{1}^{ - 1} [(I_{3} - I_{1} )\,{\kern 1pt} r + \ell_{3} {\kern 1pt} ]\) of system (12) correspond the phases \(\alpha\) and \(\gamma\). The axial projection \(r\) of \(\underline{\omega }\) and the component \(\ell_{3}\) of the GM represent the backbone of these frequencies. Consequently, two pending cases can be examined when system (12) is averaged. The first case is the non-resonance which is occurring when \(\omega_{\alpha }\) and \(\omega_{\gamma }\) are non-commensurable i.e., \({{(I_{3} {\kern 1pt} r + \ell_{3} )} \mathord{\left/ {\vphantom {{(I_{3} {\kern 1pt} r + \ell_{3} )} {I_{1} {\kern 1pt} r}}} \right. \kern-0pt} {I_{1} {\kern 1pt} r}} \ne {\hbar \mathord{\left/ {\vphantom {\hbar \Im }} \right. \kern-0pt} \Im }\) is an irrational number. The second one is the resonance which occurs for the commensurable frequencies i.e.,\({{(I_{3} \,r + \ell_{3} )} \mathord{\left/ {\vphantom {{(I_{3} \,r + \ell_{3} )} {I_{1} {\kern 1pt} r}}} \right. \kern-0pt} {I_{1} {\kern 1pt} r}} = {\hbar \mathord{\left/ {\vphantom {\hbar \Im }} \right. \kern-0pt} \Im } < 2;\,\,\,\hbar ,\Im\) are prime natural numbers.

According to the first case \({{(I_{3} \,{\kern 1pt} r + \ell_{3} )} \mathord{\left/ {\vphantom {{(I_{3} \,{\kern 1pt} r + \ell_{3} )} {I_{1} \,{\kern 1pt} r}}} \right. \kern-0pt} {I_{1} \,{\kern 1pt} r}} \ne {\hbar \mathord{\left/ {\vphantom {\hbar \Im }} \right. \kern-0pt} \Im }\), one obtains the approximate averaging system up to the first approximation by the way of averaging the right sides of (12) relative to \(\alpha\) and \(\gamma\). Considering \(\tau = \varepsilon \,t\) and omitting \(\varepsilon\) from the sides of (12) we get

$$\begin{aligned} a^{\prime} & = I_{1}^{ - 1} \mu_{1} - b{\kern 1pt} \,U\,(I_{3} {\kern 1pt} r + \ell_{3} )^{ - 1} \,\cos \theta + U[\,(I_{3} \,{\kern 1pt} r + \ell_{3} )]^{ - 2} \sin \theta \,\mu_{3}^{s} \, \\ & \quad - [(I_{3} - I_{1} )\,{\kern 1pt} r + \ell_{3} ]^{ - 2} I_{3}^{ - 1} \ell_{3} \mu_{4} + \frac{b}{2}\,(I_{3} \,{\kern 1pt} r + \ell_{3} )^{ - 1} \sin^{2} \theta {\kern 1pt} {\kern 1pt} {\kern 1pt} \nu {\kern 1pt} {\kern 1pt} d^{2} z^{ * 2} s_{0} \\ & \quad \times (d^{2} + z^{ * 2} - 2d{\kern 1pt} z^{ * } \cos \,\,\theta )^{ - 3/2} , \\ b^{\prime} & = I_{1}^{ - 1} \mu_{2} + a\,{\kern 1pt} U\,(I_{3} \,{\kern 1pt} r + \ell_{3} )^{ - 1} \,\cos \theta - U(I_{3} \,{\kern 1pt} r + \ell_{3} )^{ - 2} \sin \theta \,\mu_{3}^{c} \\ & \quad - [(I_{3} - I_{1} )\,r + \ell_{3} ]^{ - 2} I_{3}^{ - 1} \ell_{3} \mu_{5} + \frac{a}{2}(I_{3} \,r + \ell_{3} )^{ - 1} \sin^{2} \theta {\kern 1pt} {\kern 1pt} \nu {\kern 1pt} {\kern 1pt} d^{2} z^{ * 2} s_{0} \\ & \quad \times (d^{2} + z^{ * 2} - 2d{\kern 1pt} z^{ * } \cos \,\,\theta )^{ - 3/2} , \\ {\kern 1pt} r^{\prime} & = I_{3}^{ - 1} \mu_{3} ,\quad \theta^{\prime} = 0,\quad \psi^{\prime} = U\,(I_{3} \,{\kern 1pt} r + \ell_{3} )^{ - 1} , \\ \gamma^{\prime} & = I_{1}^{ - 1} [\ell_{3} + (I_{3} - I_{1} )\,\,r], \\ \alpha^{\prime} & = I_{1}^{ - 1} \,(\ell_{3} + I_{3} {\kern 1pt} r) - U\,(\ell_{3} + I_{3} {\kern 1pt} r)^{ - 1} \,\cos \theta . \\ \end{aligned}$$
(13)

The primes here, denote the differentiation with respect to \(\tau\) and

$$\begin{aligned} & \mu_{1} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {(M_{1}^{0} \cos \gamma + M_{2}^{0} \sin \gamma )\,{\text{d}}\alpha \,{\text{d}}\gamma } ,} \\ & \mu_{2} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {(M_{1}^{0} \sin \gamma - M_{2}^{0} \cos \gamma )\,{\text{d}}\alpha \,{\text{d}}\gamma } ,} \\ & \mu_{3} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {M_{3}^{0} \,{\text{d}}\alpha \,{\text{d}}\gamma } ,} \\ & \mu_{3}^{s} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {M_{3}^{0} \sin \alpha \,{\text{d}}\alpha \,{\text{d}}\gamma } ,} \\ & \mu_{3}^{c} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {M_{3}^{0} \cos \alpha \,{\text{d}}\alpha \,{\text{d}}\gamma } ,} \\ & \mu_{4} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {M_{3}^{0} (\ell_{1}^{ * } \cos \gamma + \ell_{2}^{ * } \sin \gamma )\,{\text{d}}\alpha \,{\text{d}}\gamma } ,} \\ & \mu_{5} = \frac{1}{{4\,\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{0}^{2\pi } {M_{3}^{0} (\ell_{1}^{ * } \sin \gamma - \ell_{2}^{ * } \cos \gamma )\,{\text{d}}\alpha \,{\text{d}}\gamma } .} \\ \end{aligned}$$

It is important to note that the moment \(U\) and its derivatives depend on \(\tau\). Therefore, some applications will be discussed in the next section for the gyrostatic perturbed motion.

Applications

The main goal of this part of the paper is to study some applications and to extend the results of the works [29, 30], and [34] for the considered gyrostatic motion utilizing the AM.

The Case of Linear Dissipative Moment

Here, we are going to express \(M_{j} (j = 1,2,3)\) in terms of the slow time parameter \(\tau\) according to the next forms

$$\begin{aligned} & M_{1} = - \varepsilon^{2} \,(A_{1} \,\sin^{2} \tau )\,\,P, \\ & M_{2} = - \varepsilon^{2} \,(A_{1} \,\sin^{2} \tau )\,\,Q, \\ & M_{3} = - \varepsilon \,(A_{3} \,\cos^{2} \tau )\,\,r, \\ \end{aligned}$$
(14)

where \(A_{1}\) and \(A_{3}\) are constants, in which they are depending on the properties of the body. These projections are given in terms of the small parameter \(\varepsilon\), in which their influence is focused in the direction of the third principal axis \(Oz\), while the other two components have lower values along the axes \(Ox\) and \(Oy\).

Making use of (14) into (13), and then applying some mathematical reduction to get the approximate solutions of (13) as

$$\begin{aligned} a(\tau ) & = \exp \left[ {\frac{{ - A_{1} }}{{2I_{1} }}\left( {\tau - \frac{1}{2}\sin 2\tau } \right)} \right][P_{0} \cos \beta + \,Q_{0} \sin \beta \\ & \quad - U_{0} \,(I_{3} \,{\kern 1pt} r_{0} + \ell_{3} )^{ - 1} \,\sin \theta_{0} \sin (\beta + \varphi_{0} )],{\kern 1pt} \\ b(\tau ) & = \exp \left[ {\frac{{ - A_{1} }}{{2I_{1} }}\left( {\tau - \frac{1}{2}\sin 2\tau } \right)} \right][\,P_{0} \sin \beta - \,Q_{0} \cos \beta \\ & \quad + U_{0} \,(I_{3} {\kern 1pt} r_{0} + \ell_{3} )^{ - 1} \,\sin \theta_{0} \cos (\beta + \varphi_{0} )],{\kern 1pt} \\ r(\tau ) & = \,{\kern 1pt} r_{0} \,\exp \left[ {\frac{{ - A_{3} }}{{2I_{3} }}\left( {\tau + \frac{1}{2}\sin 2\tau } \right)} \right],\quad \theta = \theta_{0} , \\ \psi & = \,\psi_{0} + Ud^{ * } , \\ \beta & = [U\cos \theta_{0} + \frac{1}{2}\sin^{2} \theta_{0} \nu {\kern 1pt} {\kern 1pt} d^{2} z^{ * 2} s_{0} (d^{2} + z^{ * 2} - 2d{\kern 1pt} z^{ * } \cos \,\,\theta_{0} )^{ - 3/2} ]d^{ * } ; \\ d^{ * } & = \frac{1}{{\ell_{3} }}\sum\limits_{n = 0}^{\infty } {\sum\limits_{m = 0}^{\infty } {( - 1)^{n + m} \left( {\frac{{I_{3} \,{\kern 1pt} r_{0} }}{{\ell_{3} }}} \right)} }^{n} \left( {\frac{{n\,A_{3} }}{{2I_{3} }}} \right)^{m} \int\limits_{0}^{\tau } {\left( {k + \frac{1}{2}\sin 2k} \right)^{m} {\text{d}}k} . \\ \end{aligned}$$
(15)

Referring to this system, we conclude that the behavior of the angle \(\theta\) has a stationary manner in which it equals the initial value. The axial velocity \(r\) has a decreasing exponentially behavior, i.e. it has a stable manner. A closer look to the expressions of \(a\) and \(b\) reveals that these expressions are dependently on the values of \(A_{1}\). Therefore, the values of \(A_{1}\) and \(\tau\) effect on their manners, in which they are exponentially vanishing according to these values. According to the value of the convergence term \(d^{ * }\), the precession angle \(\psi\) has an increasing manner.

Substituting from (15) about \(a,\,b,\) and \({\kern 1pt} r\) into (10) and (4), one can get

$$\begin{aligned} p & = \exp \left[ {\frac{{ - A_{1} }}{{2I_{1} }}\left( {\tau - \frac{1}{2}\sin 2\tau } \right)} \right]\{ - q_{0} \sin (\gamma - \beta ) + p_{0} \cos (\gamma - \beta ) + u_{0} \,(I_{3} \,r_{0} \\ & \quad + \ell_{3} )^{ - 1} \,\,\sin (\gamma - \beta - \varphi_{0} )\sin \theta_{0} \} + u\{ \sin \varphi \sin \theta_{0} \{ I_{3} r_{0} \,\exp \left[ {\frac{{ - A_{3} }}{{2I_{3} }}\left( {\tau + \frac{1}{2}\sin 2\tau } \right)} \right] \\ & \quad + \ell_{3} \}^{ - 1} \} + \left\{ {I_{3} - I_{1} + \ell_{3} r_{0}^{ - 1} \exp \left[ {\frac{{A_{3} }}{{2I_{3} }}\left( {\tau + \frac{1}{2}\sin 2\tau } \right)} \right]} \right\}^{ - 1} \ell_{1} ,{\kern 1pt} \\ q & = \exp \left[ {\frac{{ - A_{1} }}{{2I_{1} }}\left( {\tau - \frac{1}{2}\sin 2\tau } \right)} \right][q_{0} \cos (\gamma - \beta ) + p_{0} \sin (\gamma - \beta ) - u_{0} \,(I_{3} r_{0} \\ & \quad + \ell_{3} )^{ - 1} \,\cos (\gamma - \beta - \varphi_{0} )\sin \theta_{0} ] + u\{ \cos \varphi \sin \theta_{0} \{ I_{3} \,r_{0} \,\exp \left[ {\frac{{ - A_{3} }}{{2I_{3} }}\left( {\tau + \frac{1}{2}\sin 2\tau } \right)} \right] \\ & \quad + \ell_{3} \}^{ - 1} \} + \{ I_{3} - I_{1} + \ell_{3} \,r_{0}^{ - 1} \exp \left[ {\frac{{A_{3} }}{{2I_{3} }}\left( {\tau + \frac{1}{2}\sin 2\tau } \right)} \right]\}^{ - 1} \ell_{2} ,{\kern 1pt} \\ \gamma & = I_{1}^{ - 1} \left\{ {\ell_{3} \tau \, + (I_{3} - I_{1} )\,\,r_{0} \left[ {\int\limits_{0}^{\tau } {\sum\limits_{m = 0}^{\infty } {( - 1)^{m} \left( {\frac{{A_{3} }}{{2I_{3} }}} \right)^{m} } \left( {k + \frac{1}{2}\sin 2k} \right)^{m} {\text{d}}k} } \right]} \right\}. \\ \end{aligned}$$
(16)

Here, one concludes that the first two projections \(p\) and \(q\) of \(\underline{\omega }\) are expressed in terms of \(p_{0} ,q_{0} ,\theta_{0} ,\) and \(u_{0}\), in which their behaviors have an exponentially decreasing which elucidates that they have stable manners. It is noted that \((\ell_{1} ,\ell_{3} )\) and \((\ell_{2} ,\ell_{3} )\) have a good significance on the behavior of \(p\) and \(q\), respectively. Finally, it is obvious that \(\gamma\) has an increasing behavior with time.

The difference between the obtained results and the previous ones in [29, 30], and [34] can be represented by all terms that depend on components of the GM \(\ell_{j} \,(j = 1,2,3)\). As a result, the results of this work can be used to obtain some limited cases, such as in the previously mentioned works at \(\ell_{j} = 0\).

Controlling the Projections of \(\underline{\omega }\)

This subsection investigates the case of regular precession of the studied problem. As a result, we can consider the moments under the following small control constraints in the forms

$$\begin{aligned} & M_{1} = \frac{{ - \varepsilon^{2} p^{ * } }}{{(1 + \tau^{2} )(p^{ * 2} + q^{ * 2} )^{1/2} }},\,\,M_{2} = \frac{{ - \varepsilon^{2} \,q^{ * } }}{{(1 + \tau^{2} )(p^{ * 2} + q^{ * 2} )^{1/2} }},\,\,M_{3} = \varepsilon \,e^{ - \tau } , \\ & p^{ * } = P - U(I_{3} \,r + \ell_{3} )^{ - 1} \sin \theta \sin \varphi - [(I_{3} - I_{1} )\,r + \ell_{3} ]^{ - 1} r\,\ell_{1}^{*} , \\ & q^{ * } = Q - U(I_{3} \,r + \ell_{3} )^{ - 1} \sin \theta \cos \varphi - [(I_{3} - I_{1} )\,r + \ell_{3} ]^{ - 1} r\,\ell_{2}^{*} , \\ \end{aligned}$$
(17)

The above Eq. (17) describes the suppression of time-optimal for the components \(p^{ * }\) and \(q^{ * }\) of the angular velocity [42] associated with the regular precession. Referring to (4), (10), and (17) we can write

$$M_{1} = - \varepsilon^{2} \,\frac{a\,\cos \gamma + b\,\sin \gamma }{{(1 + \tau^{2} )(a^{2} + b^{2} )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }},\,\,\,\,M_{2} = - \varepsilon^{2} \,\frac{a\,\sin \gamma - b\,\cos \gamma }{{(1 + \tau^{2} )(a^{2} + b^{2} )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }},\,\,\,\,M_{3} = \varepsilon \,e^{ - \tau } .$$
(18)

Substituting (18) into (13) and integrating the resulting equations to obtain

$$\begin{aligned} & a(\tau ) = R_{1} (\tau )\,[P_{0} \cos \chi + Q_{0} \sin \chi - U_{0} \,(I_{3} \,r_{0} + \ell_{3} )^{ - 1} \,\sin \theta_{0} \sin (\chi + \varphi_{0} )],{\kern 1pt} \\ & b(\tau ) = R_{1} (\tau )[P_{0} \sin \chi - Q_{0} \cos \chi + U_{0} \,(I_{3} \,r_{0} + \ell_{3} - )^{ - 1} \,\sin \theta_{0} \cos (\chi + \varphi_{0} )],{\kern 1pt} \\ & r(\tau ) = r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } ),\,\,\theta = \theta_{0} ,\,\,\psi = \,\psi_{0} + U\,R_{2} (\tau ), \\ & \chi = \left[ {U\cos \theta_{0} + \frac{1}{2}\sin^{2} \theta {\kern 1pt} {\kern 1pt} {\kern 1pt} \nu {\kern 1pt} {\kern 1pt} d^{2} z^{ * 2} s_{0} (d^{2} + z^{ * 2} - 2d{\kern 1pt} z^{ * } \cos \,\,\theta )^{ - 3/2} } \right]\,R_{2} (\tau ),\, \\ & R_{1} (\tau ) = \left[ {1 - \frac{{I_{1}^{ - 1} \tan^{ - 1} \tau }}{{(a_{0}^{2} + b_{0}^{2} )^{1/2} }}} \right], \\ & R_{2} (\tau ) = (1 + I_{3} \,r_{0} + \ell_{3} )^{ - 1} \left[ {\tau + \sum\limits_{n = 1}^{\infty } {\left( {\frac{{1 - e^{ - n\tau } }}{{(1 + I_{3} \,r_{0} + \ell_{3} )^{n} }}} \right)} } \right]. \\ \end{aligned}$$
(19)

It is obvious that the angle \(\theta\) of nutation has a stationary value that equals its initial value. The projection \(r\) of \(\underline{\omega }\) exhibits an increasing behavior due to the excellent effect of the value of \(r_{0}\), in addition to the value of \(I_{3}\) and the slow time parameter \(\tau\). As described in the above case, the variables \(a\) and \(b\) depend upon the constants \(p_{0} ,q_{0} ,\theta_{0} ,u_{0}\) besides the component \(\ell_{3}\) of the moment \(\underline{\ell }\). Moreover, the time history of the precession angle \(\psi\) has an increasing monotonic behavior.

Utilizing (19), (10), and (4), one obtains the formulas of \(p,q,\) and \(\gamma\) as follows

$$\begin{aligned} p & = R_{1} (\tau )[ - q_{0} \sin (\gamma - \chi ) + p_{0} \cos (\gamma - \chi ) + u_{0} \,(I_{3} \,r_{0} + \ell_{3} )^{ - 1} \, \\ & \quad \times \sin \theta_{0} \sin (\gamma - \chi - \varphi_{0} )] + u\,(1 + I_{3} \,\,r_{0} \, + \ell_{3} - e^{ - \tau } )^{ - 1} \sin \theta_{0} \sin \varphi \\ & \quad + (I_{3} - I_{1} )^{ - 1} \{ 1 + \ell_{3} \,(I_{3} - I_{1} )[\,r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )]^{ - 1} \,\} \ell_{1} ,{\kern 1pt} {\kern 1pt} \\ q & = R_{1} (\tau )[q_{0} \cos (\gamma - \chi ) + p_{0} \sin (\gamma - \chi ) - u_{0} \,(I_{3} \,r_{0} + \ell_{3} )^{ - 1} \, \\ & \quad \sin \theta_{0} \cos (\gamma - \chi - \varphi_{0} )] + u(1 + I_{3} \,r_{0} \, + \ell_{3} - e^{ - \tau } )^{ - 1} \sin \theta_{0} \cos \varphi \\ & \quad + (I_{3} - I_{1} )^{ - 1} \{ 1 + \ell_{3} \,(I_{3} - I_{1} )[\,r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )]^{ - 1} \,\} \ell_{2} ,{\kern 1pt} \,\, \\ \gamma & = I_{1}^{ - 1} \{ \ell_{3} \tau + (I_{3} - I_{1} )[\,r_{0} \tau + I_{3}^{ - 1} (\tau + e^{ - \tau } - 1)\,]\} . \\ \end{aligned}$$
(20)

It is clear from (20) that \(p\) and \(q\) behave in periodic manners, and consequently they have a stationary, stable behavior. The values of \((\ell_{1} ,\ell_{3} )\) and \((\ell_{2} ,\ell_{3} )\) have good impacts on the structures of \(p\) and \(q\) as observed in (20). Moreover, the variable \(\gamma\) is impacted by the values of \(\ell_{3}\). It must be noted that all variables that depend on GM components can be used to describe the difference between the results obtained and the earlier results in [29] and [34].

The Atmospheric Case of a Symmetric Body

In this part, we examine the following form of the restoring moment on the motion of a dynamically symmetric body

$$\begin{aligned} u(\tau ,\theta ) & = \varepsilon \,U(\tau ,\theta ) \\ & = \varepsilon \,[U(\theta ) + \delta \,\sin \upsilon \tau ] = u^{*} (\theta ) + \varepsilon \,\delta \,\sin \upsilon \tau ; \\ U(\theta ) & = I_{1} (\mu \, + 2\eta \,\cos \theta ),\,\,\upsilon = {\text{const}}.,\,\,\delta > 0,\,\,\delta < 0. \\ \end{aligned}$$
(21)

Here \(\eta \,\) and \(\mu\) denote the constant coefficients. Such works are focused on the uncontrolled 3D rotational motion of the RB in the atmospheric case [43].

Making use of (18) and (21) in (13), and then using (4) and (10) to obtain the following expressions of \(\psi ,\chi ,p,\) and \(q\) in the forms

$$\begin{aligned} & \psi = \psi_{0} + U(\theta_{0} )\int\limits_{0}^{\tau } {(I_{3} r + \ell_{3} )^{ - 1} {\text{d}}\tau \, + R_{1} \,} , \\ & \chi = \int\limits_{0}^{\tau } {[U} (\theta_{0} ){\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \theta_{0} - I_{1} \,\eta {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin^{2} \theta_{0} ]\,[I_{3} \,r + \ell_{3} ]^{ - 1} {\text{d}}\tau + R_{1} \,{\kern 1pt} \cos \theta_{0} ,\, \\ & \gamma = I_{1}^{ - 1} \{ \ell_{3} \tau + (I_{3} - I_{1} )[\,r_{0} \,\tau + I_{3}^{ - 1} (\tau + e^{ - \tau } - 1)\,]\} , \\ & r = I_{3}^{ - 1} \,\int\limits_{0}^{\tau } {k\,(\tau )} \,{\text{d}}\tau = r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } );\,\,k\,(\tau ) = e^{ - \tau } \\ \end{aligned}$$
$$\begin{aligned} p & = F_{4} [p_{0} \cos (\gamma - \chi ) - q_{0} \sin (\gamma - \chi ) + u^{*} (\theta_{0} )\,(I_{3} \,r_{0} + \ell_{3} )^{ - 1} \,\sin \theta_{0} \\ & \quad \times \sin (\gamma - \chi - \varphi_{0} )] + u^{*} (\theta_{0} )\,[I_{3} \,(r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )) + \ell_{3} ]^{ - 1} \,\sin \theta_{0} \sin \varphi \\ & \quad + \{ (I_{3} - I_{1} )[r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )] + \ell_{3} \}^{ - 1} [r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )]\ell_{1} + R_{2} ,{\kern 1pt} \\ q & = F_{4} [p_{0} \sin (\gamma - \chi ) + q_{0} \cos (\gamma - \chi ) - u^{*} (\theta_{0} )(I_{3} \,r_{0} + \ell_{3} )^{ - 1} \,\sin \theta_{0} \\ & \quad \times \cos (\gamma - \chi - \varphi_{0} )] + u^{*} (\theta_{0} )[I_{3} \,(r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )) + \ell_{3} ]^{ - 1} \,\sin \theta_{0} \sin \varphi \\ & \quad + \{ (I_{3} - I_{1} )[r_{0} \, + I_{3}^{ - 1} (1 - e^{ - \tau } )] + \ell_{3} \}^{ - 1} [r_{0} + I_{3}^{ - 1} (1 - e^{ - \tau } )]\,\ell_{2} + R_{3} ,{\kern 1pt} {\kern 1pt} \\ \end{aligned}$$
(22)

where

$$\begin{aligned} & R_{1} = \delta \int\limits_{0}^{\tau } {(I_{3} r + \ell_{3} )^{ - 1} \sin (\upsilon \tau ){\text{d}}\tau ,} \\ & R_{2} = \varepsilon \delta \sin (\upsilon \tau )(I_{3} r + \ell_{3} )^{ - 1} \sin \theta_{0} \sin \varphi , \\ & R_{3} = \varepsilon \delta \sin (\upsilon \tau )(I_{3} r + \ell_{3} )^{ - 1} \sin \theta_{0} \cos \varphi , \\ & F_{4} = [1 - \frac{1}{{I_{1} (a^{2} + b^{2} )^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}\int\limits_{0}^{\tau } {h(\tau ){\text{d}}\tau } ],\,h(\tau ) = \frac{1}{{1 + \tau^{2} }}. \\ \end{aligned}$$

According to (22), we can say that \(\psi\) is time-dependent in which its manner increases with the increasing of time. The projections \(p\) and \(q\) of \(\underline{\omega }\) have a periodic behavior over the entire time interval, reflecting their stability.

Small Constant Moment Case

Here, we are going to investigate the significance of a small value of the projections \(M_{j} (j = 1,2,3)\) of \(\underline{M}\) for the analogous rotatory body’s motion of the Lagrange’s case. Therefore, we examine the responses of the body to the moment of a small constant value directed along the \(Oz\) axis. To accomplish this goal, we consider that \(M_{j}\) have the forms [29]

$$M_{1} = \varepsilon^{2} \,M_{1}^{*} = {\text{const}},M_{2} = \varepsilon^{2} \,M_{2}^{*} = {\text{const}},\,\,\,\,\,\,\,\,M_{3} = \varepsilon \,M_{3}^{*} = {\text{const}}.$$
(23)

Regarding the non-resonant case, the averaging system (13) takes the form

$$\begin{aligned} & a^{\prime} = - bU(I_{3} r + \ell_{3} )^{ - 1} \cos \theta + \frac{b}{2}\nu d^{2} z^{ * 2} s_{0} \sin^{2} \theta (d^{2} + z^{ * 2} - 2dz^{ * } \cos \theta )^{ - 3/2} (I_{3} r + \ell_{3} )^{ - 1} , \\ & b^{\prime} = aU(I_{3} r + \ell_{3} )^{ - 1} \cos \theta + \frac{a}{2}\nu d^{2} z^{ * 2} s_{0} \sin^{2} \theta (d^{2} + z^{ * 2} - 2dz^{ * } \cos \theta )^{ - 3/2} (I_{3} r + \ell_{3} )^{ - 1} , \\ & r^{\prime} = \varepsilon \,I_{3}^{ - 1} M_{3}^{*} ,\,\,\theta^{\prime} = 0,\,\,\psi^{\prime} = U(I_{3} r + \ell_{3} )^{ - 1} . \\ \end{aligned}$$
(24)

Integrating \(r^{\prime}\) and \(\theta^{\prime}\) to get

$$r = r_{0} + \varepsilon I_{3}^{ - 1} M_{3}^{*} t,\quad \theta = \theta_{0} ,$$
(25)

where \(r_{0} \,\) and \(\theta_{0}\) are integration's constants, in which \(r_{0}\) is an arbitrary initial value of \(r\) and \(\theta = \theta_{0}\) defines the constancy of the nutation angle through the motion.

Substituting (25) into the expression of \(\psi^{\prime}\) in (24), the result will be

$$\psi = \psi_{0} + \frac{U\,}{{\,M_{3}^{*} \,}}\,\ln \,\left| {(I_{3} \,r_{0} \, + \varepsilon \,\,M_{3}^{*} t + \ell_{3} )} \right|,$$
(26)

where \(\psi_{0} = \psi_{t = 0}\).

With the aid of Eq. (25), the solution of the first two equations of (24) can be written as

$$\begin{aligned} & a = P_{0} \cos \beta + Q_{0} \sin \beta - U_{0} (I_{3} r_{0} + \ell_{3} )^{ - 1} \sin \theta_{0} \sin (\beta + \varphi_{0} ), \\ & b = P_{0} \sin \beta - Q_{0} \cos \beta + U_{0} (I_{3} r_{0} + \ell_{3} )^{ - 1} \sin \theta_{0} \cos (\beta + \varphi_{0} ); \\ & \beta = \frac{1}{{M_{3}^{*} }}\left[ {U\cos \theta_{0} + \frac{1}{2}\nu d^{2} z^{ * 2} \sin^{2} \theta_{0} s_{0} (d^{2} + z^{ * 2} - 2dz^{ * } \cos \theta_{0} )^{ - 3/2} } \right]\ln \left| {\varepsilon M_{3}^{*} t + I_{3} r_{0} + \ell_{3} } \right|. \\ \end{aligned}$$
(27)

Making use of (4), (10), (25), and (27), one obtains \(p\) and \(q\) in the forms

$$\begin{aligned} p & = p_{0} \cos (\gamma - \beta ) - q_{0} \sin (\gamma - \beta ) + u_{0} \,(I_{3} \,r_{0} + \ell_{3} )^{ - 1} \, \\ & \quad \times \sin \theta_{0} \sin (\gamma - \beta - \varphi_{0} ) + u{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [I_{3} (r_{0} \, + \varepsilon \,I_{3}^{ - 1} \,M_{3}^{*} \,t)\, + \ell_{3} ]^{ - 1} \\ & \quad \times \sin \theta_{0} \sin \varphi_{0} + \{ (I_{3} - I_{1} ) + \ell_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} (r_{0} \, + \varepsilon \,I_{3}^{ - 1} \,M_{3}^{*} \,t)^{ - 1} \,\}^{ - 1} \,\ell_{1} ,\,\, \\ q & = p_{0} \sin (\gamma - \beta ) + q_{0} \cos (\gamma - \beta ) - u_{0} \,(I_{3} r_{0} + \ell_{3} )^{ - 1} \, \\ & \quad \times \sin \theta_{0} \cos (\gamma - \beta - \varphi_{0} )] + u{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [I_{3} (r_{0} \, + \varepsilon \,I_{3}^{ - 1} \,M_{3}^{*} \,t)\, + \ell_{3} ]^{ - 1} \\ & \quad \times \sin \theta_{0} \cos \varphi_{0} + \{ (I_{3} - I_{1} ) + + \ell_{3} {\kern 1pt} {\kern 1pt} {\kern 1pt} (r_{0} \, + \varepsilon \,I_{3}^{ - 1} \,M_{3}^{*} \,t)^{ - 1} \,\}^{ - 1} \ell_{2} ,\,\, \\ \gamma & = I_{1}^{ - 1} \left[ {\ell_{3} t + (I_{3} - I_{1} )\left( {r_{0} \,t + \frac{1}{2}\varepsilon \,I_{3}^{ - 1} \,M_{3}^{*} \,t^{2} } \right)} \right]. \\ \end{aligned}$$
(28)

It is obvious that \(p\) and \(q\) are expressed in terms of trigonometric functions, the components \(\ell_{1} ,\ell_{3}\) and \(\ell_{2} ,\ell_{3}\) of the GM have a good effect on the manner of the waves illustrating \(p\) and \(q\), respectively. Moreover, the gained results represent a generalization of those which were obtained in [29, 30], and [34] for the free motion of the GM.

Analysis of the Results

This section is presented to discuss the achieved results of the applications in the previous section through some graphical plots. To achieve this task, the following data are considered

$$\begin{aligned} & I_{1} = 8\;{\text{kg}}\,{\text{m}}^{2} ,\,\,\,\,\,I_{3} = 5\;{\text{kg}}\,{\text{m}}^{2} ,\,\,\,\,\varepsilon = 0.001,\,\,\,\,r_{0} = 11.5\;{\text{rad}}\,{\text{s}}^{ - 1} ,\,\,\,\,p_{0} = 0.06\,{\text{rad}}\,{\text{s}}^{ - 1} , \\ & q_{0} = 0.04\,{\text{rad}}\,{\text{s}}^{ - 1} ,\,\,\,\,\,\theta_{0} = {{(\pi } \mathord{\left/ {\vphantom {{(\pi } 6}} \right. \kern-0pt} 6})\,\,{\text{rad}},\,\,\,\,\varphi_{0} = {{(\pi } \mathord{\left/ {\vphantom {{(\pi } {18}}} \right. \kern-0pt} {18}})\,\,{\text{rad}},\,\,\,\,\psi_{0} = {{(\pi } \mathord{\left/ {\vphantom {{(\pi } 3}} \right. \kern-0pt} 3})\,\,{\text{rad}}, \\ & m = 200\;{\text{kg}},\,\,\,\,a = 1,\,\,\,\,b = 1,\,\,\,\,\ell_{1} ,\ell_{2} ,\ell_{3} ( = 100,\,\,150,\,\;200\,)\;{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1} , \\ & g = 9.81\,{\text{m}}\,{\text{s}}^{ - 2} ,\,\,\,\,s_{0} = 2.5,\,\,\,\,\nu \, = 0.05,\,\,\,\,h = 1.1,\,\,\,\,\,z^{ * } = 1.5,\,\,\,\,L = 2.5,\,\,\,\,\upsilon = 0.001, \\ & \mu = {2,}\,\,\,\,\eta = {1,}\,\,\,\,\,\delta = 3. \\ \end{aligned}$$

The principal aim of the calculations presented in Figs. 2, 3, 4, 5, 6, 7, 8 and 9 is to examine the influence of the projections \(\ell_{1} ,\ell_{2} ,\) and \(\ell_{3}\) of the GM on the body’s dynamical behavior.

Fig. 2
figure 2

Behavior of \(p(t)\) and \(q(t)\) for the first case when a at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100{\kern 1pt}\) and \(\ell_{3} ( = 100,150,200){\kern 1pt}\), b at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100\) and \(\ell_{3} ( = 100,150,200)\), c at \(\ell_{2} = \ell_{3} = 100{\kern 1pt}\) and \(\ell_{1} ( = 100,150,200)\), d at \(\ell_{1} = \ell_{3} = 100\) and \(\ell_{2} ( = 100,150,200)\)

Full size image
Fig. 3
figure 3

The time dependently of \(\gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,\) and \(r\) of the first case

Full size image
Fig. 4
figure 4

The solutions \(p(t)\) and \(q(t)\) for the second case when a at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100\) and \(\ell_{3} ( = 100,150,200){\kern 1pt}\), b at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100{\kern 1pt}\) and \(\ell_{3} ( = 100,150,200){\kern 1pt}\), c at \(\ell_{2} = \ell_{3} = 100{\kern 1pt}\) and \(\ell_{1} ( = 100,150,200)\), d at \(\ell_{1} = \ell_{3} = 100\) and \(\ell_{2} ( = 100,150,200)\)

Full size image
Fig. 5
figure 5

The time-relations of \(\gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} r,\) and \(\psi\) of the second case

Full size image
Fig. 6
figure 6

Effects of the GM on \(p\) and \(q\) for the atmospheric case of a symmetric body when a at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100\) and \(\ell_{3} ( = 100,150,200)\), b at \(\ell_{1} = \ell_{2} = 100\) and \(\ell_{3} ( = 100,150,200)\), c at \(\ell_{2} = \ell_{3} = 100{\kern 1pt}\) and \(\ell_{1} ( = 100,150,200)\), d at \(\ell_{1} = \ell_{3} = 100\) and \(\ell_{2} ( = 100,150,200)\)

Full size image
Fig. 7
figure 7

The time-dependence for \(\gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,\) and \(r\) of the third case

Full size image
Fig. 8
figure 8

Characterizes waves of \(p\) and \(q\) with \(t\) for the fourth case when a at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100\) and \(\ell_{3} ( = 100,150,200)\), b at \(\ell_{1} {\kern 1pt} = \ell_{2} = 100{\kern 1pt}\) and \(\ell_{3} ( = 100,150,200)\), c at \(\ell_{2} = \ell_{3} = 100\) and \(\ell_{1} ( = 100,150,200)\), d at \(\ell_{1} = \ell_{3} = 100\) and \(\ell_{2} ( = 100,150,200)\)

Full size image
Fig. 9
figure 9

Time history of \(\gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,\) and \(r\) against time \(t\) of the fourth case

Full size image

According to Eqs. (15) and (16) that describe the case of linear dissipative moment and based on the above data, the variations of \(p\) and \(q\) versus \(t\) are plotted graphically in Fig. 2 for different values of \(\ell_{j} (j = 1,2,3)\). Parts (a) and (b) reveal the impact of \(\ell_{3}\) on these solutions. An inspection of these parts shows periodic progressive waves are obtained, in which the waves’ amplitudes decrease and the oscillations number increases with the increase of \(\ell_{3}\) values. In contrast, the other two parts (c) and (d) of Fig. 2 explore the change of \(p\) and \(q\) when \(\ell_{1}\) and \(\ell_{2}\) have different values. It is obvious that periodic waves are graphed where their amplitudes increase with the increase of the values of \(\ell_{1}\) and \(\ell_{2}\).

Parts of Fig. 3 show the time behavior of angles \(\gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,\) and the axial angular velocity \(r\) of the first case. It is noted that the behavior of \(\gamma\) and \({\kern 1pt} {\kern 1pt} \psi\) increases gradually during the examined time interval when \(\ell_{3}\) increases as predicted before from Eqs. (15) and (16), as shown in portions (a) and (b) while, the axial component decreases with the increase of time, as displayed in part (c).

The curves indicated in Fig. 4 reveal the changes of the solutions \(p\) and \(q\) with time \(t\) for distinct values of \(\ell_{1} ,\ell_{2} ,\) and \(\ell_{3}\) of the achieved results of the second case in Sect. 4.2. Figure 4a, b are calculated when \(\ell_{3} ( = 100,150,200){\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\), while Fig. 4c, d are drawn when \(\ell_{1}\) and \(\ell_{2}\) have the values \((100,150,200)\). In this figure, periodic waves are obtained in which they obey to the formulas of (20). It's worth noting that the components \((\ell_{1} ,\ell_{3} )\) and \((\ell_{2} ,\ell_{3} )\) have significance effect on the natural of the waves of \(p\) and \(q\).

According to the graphs in Fig. 5, we can see that the behavior of angle \(\psi\) increases gradually with time, as seen in parts (c), (d), and (e) at the mentioned values of \(\ell_{3}\). The same conclusion holds true for the behavior of \(\gamma\) and \(r\) as drawn in Fig. 5a, b, respectively.

Parts of Fig. 6 show the change of the obtained results \(p\) and \(q\) for the atmospheric case versus time \(t\) when \(\ell_{j} \,\,(j = 1,2,3)\) take various values. It is evident that the variation of the third projection \(\ell_{3} ( = 100,150,200)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) of the GM \(\underline{\ell }\) at \(\ell_{1} = \ell_{2} = 100{\kern 1pt} \,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) produces periodic waves, as shown in portions (a) and (b) of the considered figure, in which the waves’ amplitudes increase with the increase of \(\ell_{3}\) values while the number of oscillations remains constant. The same concluding remarks are observed when \(\ell_{1} ( = 100,150,200)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) at \(\ell_{2} = \ell_{3} = 100\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) and \(\ell_{2} ( = 100,150,200)\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) when \(\ell_{1} = \ell_{3} = 100\,{\text{kg}}\,{\text{m}}^{2} \,{\text{s}}^{ - 1}\) as illustrated in the other two parts (c) and (d), respectively.

The inspection of the parts of Fig. 7 reveals that the behavior of the angle \(\psi\) of precession, the self-rotation angle \(\gamma\), and the axial angular velocity \(r\) with the time \(t\). It is noted that the variation of the value of the component \(\ell_{3}\) has a positive action on the behavior of the variables \(\gamma\) and \(\psi\) as shown in parts (a) and (b). Alternatively, there is no variation of the axial angular velocity with the variation of \(\ell_{3}\) due to that this component does not depend on \(\ell_{3}\). Based on the equations of (22), we can conclude that the behavior of the variables \(\gamma ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \psi ,\) and \(r\) increases gradually, which is in line with the indicated drawing.

The objective of the portions of Fig. 8 is to discuss the time histories of the variables \(p\) and \(q\) for the fourth case according to the values of the GM projections. It is observed that the represented waves in the parts of this figure behave in periodic forms to assert the stability of the achieved outcomes. The waves’ amplitudes decrease with the increasing of \(\ell_{3}\) when \(\ell_{1}\) and \(\ell_{2}\) take stationary values, as shown in parts (a) and (b) of this figure, while the amplitudes of the same results increase with the increasing of \(\ell_{1}\) and \(\ell_{2}\) when \(\ell_{3}\) unchanged as plotted in parts (c) and (d).

Looking closely at the parts of Fig. 9, we can see that the behavior of the variables \(\gamma ,\psi ,\) and \(r\) increases gradually as time goes on, in which the effect of \(\ell_{3}\) does not appear with the axial angular velocity \(r\) as indicated in Fig. 9g, while it appears clearly with the self-rotation angle \(\gamma\) and \(\psi\) as seen in Fig. 9a–f.

Based on the above simulation and the studied cases, we conclude that the motion of the body can be defined as having a stable behavior and being chaotic-free.

Conclusion

The rotational motion of a symmetric RB in 3D, attached with a string, about the principal axis of dynamic symmetry has been examined. This motion is considered to be under the influence of the moments of perturbation and gyrostat, along the inertia main axes. The small parameter is inserted based on the assumptions of high angular velocity around the axis of the body’s dynamic symmetry, and the projections of the perturbing moment are estimated to be less than or equal to the moment of restoring. The AM is used to yield the averaging system of the controlling EOM and to obtain the approximate analytic solutions for some important applications. The solutions of these applications have been discussed and represented graphically to explore the good effects of the considered moments on the body’s dynamical behavior. Moreover, the achieved results generalize the previously related works, such as in [29, 30], and [34]. The significance of this work is due to its different engineering applications, especially in devices and vehicles that are based on vibrating systems.