INTRODUCTION

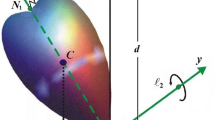
We consider a solid having a weight mg and suspended by an inextensible weightless thread of length \(\ell \). The motion of the solid is such that the velocity vectors of all its points are parallel to the fixed vertical plane \(OXY\) passing through the solid’s center of gravity \(C\) and its suspension point \(A\) (see Fig. 1). We believe that the thread is stretched during the motion.

figure 1

Fig. 1.

The material system under consideration has two degrees of freedom. We set the angle \(\theta \) that makes the direction of the thread OA with the vertical axis \(OX\) and the angle \(\psi \) between the segment \(AC\) and the horizontal axis \(OY\) as generalized coordinates.

The aim of the article is to study the evolution of motion within an infinite time interval under the following two assumptions: the distance r from point \(A\) to the center of gravity \(C\) is small, the length of the thread \(\ell \) is large. The analysis is carried out using classical and modern methods of perturbation theory [1–4].

Currently, the dynamics of a solid suspended on a weightless, ideally flexible, inextensible thread (string) is being developed rapidly. The problem on the existence, stability, and bifurcations of periodic, stationary, and precessional motions has been investigated in detail; the case of non-ideal string has also been considered [5–8]. In articles [9, 10], some problems on dynamics of solids that deal with a thread as an ideal unilateral constraint are investigated.

1 EQUATIONS OF MOTION

The kinetic and potential energies of the solid are calculated by the formulas

$$T = \frac{1}{2}m({{\dot {x}}^{2}} + {{\dot {y}}^{2}}) + \frac{1}{2}{{J}_{c}}{{\dot {\psi }}^{2}},\quad \Pi = - mg{{x}_{c}},$$
(1.1)
$${{x}_{c}} = \ell \cos \theta + r\sin \psi ,\quad {{y}_{c}} = \ell \sin \theta + r\cos \psi .$$
(1.2)

Here, the dot denotes the differentiation with respect to time t, and \({{J}_{c}}\) is the moment of inertia of the solid about the axis passing through its center of gravity perpendicular to the plane \(OXY\)

Using (1.1) and (1.2), we have an expression for the Lagrange function \(L = T - \Pi \):

$$L = \frac{1}{2}({{J}_{c}} + m{{r}^{2}}){{\dot {\psi }}^{2}} - mr\ell \sin (\theta + \psi )\dot {\psi }\dot {\theta } + \frac{1}{2}m{{\ell }^{2}}{{\dot {\theta }}^{2}} + mg(\ell \cos \theta + r\sin \psi ).$$

In what follows, we use the Hamiltonian form of the equations of motion. The Hamilton function \(\Gamma \) is given by the equality \(\Gamma = T + \Pi \), on the right-hand side of which the quantities \(\dot {\psi }\) and \(\dot {\theta }\) must be expressed in terms of generalized momenta \({{p}_{\psi }}\), \({{p}_{\theta }}\):

$${{p}_{\psi }} = \tfrac{{\partial L}}{{\partial \dot {\psi }}},\quad {{p}_{\theta }} = \tfrac{{\partial L}}{{\partial \dot {\theta }}}.$$

Having performed simple calculations, we get the Hamilton function in the following form:

$$\begin{gathered} \Gamma = \frac{1}{{2[{{J}_{c}} + m{{r}^{2}}{{{\cos }}^{2}}(\theta + \psi )]}}\left[ {p_{\psi }^{2} + 2\frac{r}{\ell }\sin (\theta + \psi ){{p}_{\psi }}{{p}_{\theta }} + \frac{{J_{c}^{2} + m{{r}^{2}}}}{{m{{\ell }^{2}}}}p_{\theta }^{2}} \right] \\ - \;mg(\ell \cos \theta + r\sin \psi ). \\ \end{gathered} $$
(1.3)

2 SMALL PARAMETER. REPRESENTATION OF THE HAMILTON FUNCTION AS A SERIES

Instead of \({{p}_{\psi }}\), \({{p}_{\theta }}\), we introduce dimensionless momenta \({{p}_{\chi }}\), \({{p}_{\delta }}\) using the canonical (with valence \({{(m\ell \sqrt {g\ell } )}^{{ - 1}}}\)) transformation of the form

$${{p}_{\psi }} = {{(m\ell \sqrt {g\ell } )}^{{ - 1}}}{{p}_{\chi }},\quad {{p}_{\theta }} = {{(m\ell \sqrt {g\ell } )}^{{ - 1}}}{{p}_{\delta }},\quad \psi = \chi ,\quad \theta = \delta $$
(2.1)

and pass to the new (dimensionless) independent variable τ:

$$\tau = (m\ell \sqrt {g\ell } {\text{/}}{{J}_{c}})t.$$
(2.2)

The new variables correspond to the function G calculated by the formula

$$G = {{{{J}_{c}}} \mathord{\left/ {\vphantom {{{{J}_{c}}} {({{m}^{2}}g{{\ell }^{3}})}}} \right. \kern-0em} {({{m}^{2}}g{{\ell }^{3}})}}\Gamma ,$$
(2.3)

where \(\Gamma \) is the function (1.3) in which the substitution (2.1) is made.

In accordance with the accepted (see Introduction section) assumptions, we introduce a small parameter \(\varepsilon \) (\(0 < \varepsilon \ll 1\)) into the equations of motion by setting

$$r = \varepsilon {\text{ a,}}\quad \ell = {{\varepsilon }^{{ - 1/2}}}\sqrt {{{{{J}_{c}}} \mathord{\left/ {\vphantom {{{{J}_{c}}} m}} \right. \kern-0em} m}} ,$$
(2.4)

where a is a quantity of the order of unity that has the dimension of length.

Hamilton function (2.3) can be represented as a series in powers of the parameter ε as follows:

$$G = {{G}_{0}} + \varepsilon {{G}_{1}} + {{\varepsilon }^{2}}{{G}_{2}} + O({{\varepsilon }^{3}}),$$
(2.5)
$${{G}_{0}} = \frac{1}{2}p_{\chi }^{2},\quad {{G}_{1}} = - \frac{1}{2}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}p_{\chi }^{2}{{\cos }^{2}}(\delta + \chi ) + \frac{a}{\ell }{{p}_{\chi }}{{p}_{\delta }}\sin (\delta + \chi ) + \frac{1}{2}p_{\delta }^{2} - \cos \delta ,$$
$$\begin{gathered} {{G}_{2}} = - \frac{a}{\ell }\sin \chi + \frac{1}{2}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}p_{\chi }^{2}{{\cos }^{4}}(\delta + \chi ) \\ - \;\frac{{{{a}^{3}}}}{{{{\ell }^{3}}}}{{p}_{\chi }}{{p}_{\delta }}\sin (\delta + \chi ){{\cos }^{2}}(\delta + \chi ) + \frac{1}{2}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}p_{\delta }^{2}{{\sin }^{2}}(\delta + \chi ). \\ \end{gathered} $$

3 SIMPLIFICATION OF THE HAMILTON FUNCTION

The system with Hamilton function (2.5) has a rapidly rotating phase χ. Using the classical perturbation theory, one can construct a canonical transformation χ, δ, pχ, \({{p}_{\delta }} \to x,y,{{p}_{x}},{{p}_{y}}\), which is close to the identity and excludes the dependence of the Hamilton function on the fast phase in any finite approximation in ε. Let us give an explicit form of the canonical substitution, which excludes the fast phase in terms up to the second power of ε inclusive. We set the generating function \(S({{p}_{x}},{{p}_{y}},\chi ,\delta )\) in the form

$$S = {{p}_{x}}\chi + {{p}_{y}}\delta + \varepsilon {{S}_{1}}({{p}_{x}},{{p}_{{y,}}}\chi ,\delta ) + {{\varepsilon }^{2}}{{S}_{2}}({{p}_{x}},{{p}_{{y,}}}\chi ,\delta ).$$
(3.1)

From (3.1) and the relations

$$x = \tfrac{{\partial S}}{{\partial {{p}_{x}}}},\quad y = \tfrac{{\partial S}}{{\partial {{p}_{y}}}},\quad {{p}_{\chi }} = \tfrac{{\partial S}}{{\partial \chi }},\quad {{p}_{\delta }} = \tfrac{{\partial S}}{{\partial \delta }}$$

it follows that

$$\begin{gathered} \chi = x - \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial {{p}_{x}}}} + O({{\varepsilon }^{2}}),\quad \delta = y - \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial {{p}_{y}}}} + O({{\varepsilon }^{2}}), \\ {{p}_{\delta }} = {{p}_{y}} + \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial y}} + O({{\varepsilon }^{2}}), \\ \end{gathered} $$
(3.2)
$${{p}_{\chi }} = {{p}_{x}} + \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial x}} + {{\varepsilon }^{2}}\left( {\frac{{\partial {{S}_{2}}}}{{\partial x}} - \frac{{{{\partial }^{2}}{{S}_{1}}}}{{\partial {{x}^{2}}}}\frac{{\partial {{S}_{1}}}}{{\partial {{p}_{x}}}} - \frac{{{{\partial }^{2}}{{S}_{1}}}}{{\partial x\partial y}}\frac{{\partial {{S}_{1}}}}{{\partial {{p}_{y}}}}} \right) + O({{\varepsilon }^{3}}),$$
(3.3)

where \({{S}_{i}} = {{S}_{i}}({{p}_{x}},{{p}_{{y,}}}x,y)\) (\(i = 1,\;2\)).

Substituting expressions (3.2) and (3.3) into the right-hand side of equality (2.5) and carrying out simple calculations, we find that to eliminate the fast phase \(x\) from the terms up to the second power inclusive in the expansion of the new Hamilton function \(F({{p}_{x}},{{p}_{y}},x,y,\varepsilon )\) in a series in \(\varepsilon \), the functions \({{S}_{1}}\) and \({{S}_{2}}\) should be set as follows:

$${{S}_{1}} = \frac{a}{\ell }{{p}_{y}}\cos (x + y) + \frac{1}{8}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{p}_{x}}\sin (2x + 2y),$$
$${{S}_{2}} = - \frac{a}{{2\ell {{p}_{x}}}}\cos x - \frac{a}{{8\ell {{p}_{x}}}}\left( {\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}p_{x}^{2} + 8p_{y}^{2}} \right)\cos (x + y) - \frac{a}{{2\ell {{p}_{x}}}}\cos (x + 2y)$$
$$\begin{gathered} + \;\frac{1}{{24}}\frac{{{{a}^{3}}}}{{{{\ell }^{3}}}}{{p}_{x}}\cos (3x + 3y) - \frac{1}{{16}}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}\left( {\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{p}_{x}} + 6{{p}_{y}}} \right)\sin (2x + 2y) \\ - \;\frac{1}{{256}}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}{{p}_{x}}\sin (4x + 4y). \\ \end{gathered} $$

New Hamilton function is written as follows:

$$F = \frac{1}{2}{{A}_{0}}p_{x}^{2} - \frac{1}{2}{{\varepsilon }^{2}}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{p}_{x}}{{p}_{y}} + \varepsilon \left( {\frac{1}{2}p_{y}^{2} - \cos y} \right) + {{\varepsilon }^{3}}{{F}_{3}}({{p}_{x}},{{p}_{y}},x,y,\varepsilon ),$$
(3.4)

where the notation is introduced

$${{A}_{0}} = 1 - \frac{1}{2}\varepsilon \frac{{{{a}^{2}}}}{{{{\ell }^{2}}}} + \frac{9}{{32}}{{\varepsilon }^{2}}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}.$$
(3.5)

The structure of the Hamilton function (3.4) can be simplified by making a univalent canonical transformation \(x,y,{{p}_{x}},{{p}_{y}} \to {{w}_{0}},q,{{I}_{0}},p\) by the formulas

$$x = {{w}_{0}} - \frac{1}{2}\varepsilon \frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}q,\quad y = q,\quad {{p}_{x}} = {{I}_{0}},\quad {{p}_{y}} = p + \frac{1}{2}\varepsilon \frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{I}_{0}}.$$
(3.6)

Transformation (3.6) suppresses the second term in function (3.4) and in terms of new variables the equations of motion are given by the Hamilton function

$$F = \frac{1}{2}{{A}_{0}}I_{0}^{2} + \varepsilon \left( {\frac{1}{2}{{p}^{2}} - \cos q} \right) + {{\varepsilon }^{3}}{{A}_{3}}({{I}_{0}},p,{{w}_{0}},q,\varepsilon ),\quad {{A}_{3}} = {{F}_{3}} - \frac{1}{8}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}I_{0}^{2}.$$
(3.7)

Here, \({{F}_{3}}\) is the function from (3.4), in which the substitution (3.6) is made.

An even greater simplification can be achieved by setting \({{\tau }_{*}} = {{A}_{0}}\tau \) as an independent variable. This leads to dividing the Hamilton function (3.7) by \({{A}_{0}}\). If instead of \(\varepsilon \)we introduce a new small parameter \(\mu \)by the formula \(\mu = \varepsilon {\text{/}}{{A}_{0}}\), then instead of the function \(F\) from (3.7) we obtain a function \(H\) of the form

$$H = {{H}^{{(0)}}}({{I}_{0}}) + \mu {{H}^{{(1)}}}(p,q) + {{\mu }^{3}}{{H}^{{(3)}}}({{I}_{0}},p,{{w}_{0}},q,\mu ),$$
(3.8)
$${{H}^{{(0)}}} = \frac{1}{2}I_{0}^{2},\quad {{H}^{{(1)}}} = \frac{1}{2}{{p}^{2}} - \cos q.$$
(3.9)

4 ANALYSIS OF THE SYSTEM WITH THE HAMILTON FUNCTION (3.8)

In an approximate system with a function \({{H}^{{(0)}}} + \mu {{H}^{{(1)}}}\), the variable I0 is a constant and the angular coordinate \({{w}_{0}}\) changes uniformly with time. Variables q, \(p\) correspond to the motion of the mathematical pendulum. We assume that the oscillatory mode of its motion is realized. The vibration amplitude is denoted by \({{q}_{{\max }}}\) \((0 < {{q}_{{\max }}} < \pi {\text{/}}2)\). To describe the oscillations, we introduce the action-angle variables I, \(w\). The variable I is calculated [11] by the formula

$$I = \frac{8}{\pi }[E(k) - (1 - {{k}^{2}})K(k)].$$
(4.1)

Hereinafter, the generally accepted notations for elliptic integrals and functions are used. In (4.1) \(k = \sin ({{q}_{{\max }}}{\text{/}}2)\) (\(0 < {{k}^{2}} < 1{\text{/}}2\)).

The canonical transformation \(q,p \to w,I\) is given by the formulas [11]:

$$q = 2\arcsin (k{\text{sn}}(u,k)),\quad p = 2k{\text{cn}}(u,k),\quad u = (2K(k){\text{/}}\pi )w,$$
(4.2)

where \(k = k(I)\) is the function inverse to function (4.1).

Now the Hamilton function (3.8) can be written in the form

$$H = {{H}^{{(0)}}}({{I}_{0}}) + \mu {{H}^{{(1)}}}(I) + {{\mu }^{3}}{{H}^{{(3)}}}({{I}_{0}},p,{{w}_{0}},q,\mu ).$$
(4.3)

Here, \({{H}^{{(1)}}} = - 1 + 2{{k}^{2}}(I)\), this function can be represented by a convergent series in powers of I. The variables p and q in the function \({{H}^{{(3)}}}\) must be replaced by formulas (4.2).

Function (4.3) is analytic in all its arguments and \(2\pi \) is periodic in w0 and w. In addition, the case of intrinsic degeneracy takes place [1], since for μ = 0 there is only one nonzero frequency in the system:

$$\tfrac{{\partial {{H}^{{(0)}}}}}{{\partial {{I}_{0}}}} = {{I}_{0}} \ne 0.$$
(4.4)

The derivatives of the function H(1) from (4.3) satisfy the inequalities

$$\tfrac{{\partial {{H}^{{(1)}}}}}{{\partial I}} \ne 0,\quad \tfrac{{{{\partial }^{2}}{{H}^{{(1)}}}}}{{\partial {{I}^{2}}}} \ne 0.$$
(4.5)

In fact,

$$\tfrac{{\partial {{H}^{{(1)}}}}}{{\partial I}} = \frac{\pi }{{2K(k)}} = 1 - \frac{1}{8}I - \frac{3}{{256}}{{I}^{2}} - \frac{5}{{2048}}{{I}^{3}} + O({{I}^{4}}) > 0,$$
$$\tfrac{{{{\partial }^{2}}{{H}^{{(1)}}}}}{{\partial {{I}^{2}}}} = - {{\pi }^{2}}\frac{{E(k) - (1 - {{k}^{2}})K(k)}}{{16{{k}^{2}}(1 - {{k}^{2}}){{K}^{3}}(k)}} = - \frac{1}{8} - \frac{3}{{128}}I - \frac{{15}}{{2048}}{{I}^{2}} + O({{I}^{3}}) < 0.$$

Since the approximate system with the Hamilton function \({{H}^{{(0)}}} + \mu {{H}^{{(1)}}}\) satisfies conditions (4.4) and (4.5), then [2] in the complete system with the Hamilton function (4.3) the action variables I0, I for all values of \(t\) remain close to their initial values and differ from them by magnitudes of the order of \(\mu \) (or order of \(\varepsilon \), which is the same). In this case, the measure of the invariant tori of the approximate system that are vanished when the perturbation \({{H}^{{(3)}}}\) in (4.3) is taken into account, is of order of \(\exp \left( { - c{\text{/}}\varepsilon } \right)\) (\(c > 0\) = const).

Main result of the analysis. Summing up the above, it follows that for small \(\varepsilon \), the motion of a solid suspended on an ideal thread in a uniform gravity field is stable with respect to perturbations of quantities \(\theta \), \(\dot {\theta }\), \(\dot {\psi }\). In particular, if the initial values of θ and \(\dot {\theta }\) have, for example, the order of \({{\varepsilon }^{{1 - \sigma }}}\) (\(0 < \sigma < 1\)), then \(\theta \) and \(\dot {\theta }\) for all \(t\) remain small quantities of the same order.

Remark. The article [12] dealing with the dynamics of the Maxwell pendulum states that “the deviation of the pendulum from the vertical has a finite swing at the corresponding arbitrarily small initial values of the coordinates and velocities of the thread. The reason for this instability is the rather fast transient motion of the pendulum when its motion changes from bottom to top”. The attempt to present an argument for this statement made in [12] contains inaccuracies and the statement itself is invalid.