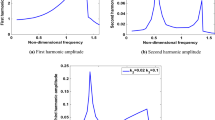
Abstract
Purpose
Response characteristics of nonlinear systems have been extensively studied for system identification. But all these studies mainly employ single tone harmonic excitation. In contrast, there are very few research literatures on the use of multi-tone harmonic excitation, obviously due to the challenges in more complicated formulation of response characteristics. This research intends to identify a polynomial type of damping nonlinearity using Higher-order Frequency Response Functions (HoFRFs) and harmonic amplitude measurement data under multi-tone harmonic excitation.
Methods
In the present study, the Volterra series is employed to demonstrate benefits of using multi- tone harmonic excitation for identification of damping nonlinearity. It is shown a large number of combination tones of higher harmonics are formed in the response spectrum. Response harmonic amplitude series are formulated for these harmonics using higher order Volterra kernel synthesis for both symmetric and asymmetric forms of damping nonlinearity.
Results and conclusion
A novel parameter estimation algorithm is presented to first estimate the nonlinear parameter and then the linear modal parameters of the system using two experiments only, whereas, for single-tone harmonic excitation, one would require at least six to eight experiments. The signal strength of higher harmonics is studied for selection of most effective frequency combinations in the multi-tone excitation. Numerical simulations with a typical two-tone excitation demonstrate that fairly accurate estimates of nonlinear damping parameters and linear modal parameters can be obtained with proper selection of frequency pair and excitation level.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Nonlinear dynamic systems and their related problems in many engineering applications have been extensively attempted and published articles by many authors in the recent past to understand insight into the system, which dominates the nonlinear response behavior. Most mechanical structures modelled through damping such as vibration isolator, absorber, energy harvester, etc., are often intrinsically nonlinear in nature. Nonlinearity in damping form exhibits undesired consequences in the system characterization which imposes constraints on the performance of the system. Nonlinear damping can be classified as polynomial and non-polynomial functions, and polynomial functions are further classified as symmetric and asymmetric.
The identification technique provides an explicit analytical relationship between the output response and the system parameters in a nonlinear system. System identification will have two parts in the literature of nonlinear and linear system identification: parametric and nonparametric identification. Nonlinearities are commonly described in mechanical and structural systems using polynomial and non-polynomial forms (Nayfeh [1]). An approach for identifying nonlinear systems is described based on multiple-input/single-output (MI/SO) linear processes used to reverse dynamic systems constructed for proposed nonlinear differential equations of motion (Duffing, Van der Pol, Mathieu, and Dead-Band) by Bendat et al. [2]. Tiwari and Vyas [3] suggested approaches for estimating nonlinear parameters of rolling element bearings based on the analysis and measurement of signals from bearing housing vibration. Balachandran et al. [4] studied nonlinear interactions between structural modes of pair of quadratically and cubically coupled oscillators with damping nonlinearity. They discovered that the frequency relationship between the two modes of oscillation for quadratically connected oscillators is two-to-one, but the frequency relationship between the two modes of oscillation for cubically coupled oscillators is one-to-one. Khan and Balachandran [5] extended their research using bispectral analysis and higher order spectra. Bikdash et al. [6] used Melnikov equivalent damping coefficients for linear plus quadratic damping and linear plus cubic damping to study the nonlinear roll dynamics of ships.
Volterra series is employed to analyze nonlinear system response behavior from input–output mapping in the field of non-parametric system identification by Volterra [7]. George [8] introduced a concept of generalized FRFs for linear study in frequency domain analysis. Boyd and Chua [9] extended their linear FRFs concept to general FRFs for nonlinear applications. Bedrosian and Rice [10] proposed a method of harmonic probing to derive higher-order FRFs, which is confined to only continuous nonlinear systems under single input harmonic excitation. Later on, Worden et al. [11] extended the Bedrosian and Rice harmonic probing method to multi-input and multi-output Volterra series through the definition of higher-order direct and cross kernels employed to depict the connection among the frequencies of multi-inputs. Marmarelis and Naka [12] studied Winer's theory of single input to multi-input and multi-output for nonlinear systems, and experimentally applied to biological systems Boaghe and Billings [13] use the single-input multi-output (SIMO) Volterra series to investigate the subharmonic region that can develop from nonlinear oscillations, bifurcation, and chaos. Higher-order FRFs are generated by the multidimensional Fourier transform of Volterra kernels (Rough [14], Schetzen [15]), which are used to forecast the response of several nonlinear effects such as higher harmonics and jump phenomena. Chatterjee and Vyas [16] devised a parameter estimation technique based on a recursive iteration using the Volterra series; convergence and error analysis for a cubic stiffness nonlinear system has been discussed.
Chatterjee [17] also studied the Volterra series for crack severity and structural degradation in nonlinear systems with a bilinear oscillator. Cheng et al. [18] investigated Volterra series-based techniques and their applicability in various nonlinear models and problem-solving methodologies. Noel and Kerschen [19] reviewed past and recent advances in nonlinear system identification and applications, highlighted their benefits and drawbacks, and suggested future research avenues in this field. The researchers discussed various nonlinear methods, such as the perturbation technique [20] and the Harmonic Balance Method [21,22,23,24], for response representation of many nonlinear system applications.
However, authors also studied response analysis of the nonlinear system in the frequency domain concept is derived from the Volterra series such as Nonlinear Output Frequency Response Functions (NOFRF) by Lang and Billings [25]; they also discussed Output Frequency Response Functions (OFRF) in [26] and its applications in mechanical systems such as isolators, energy harvesters, etc. [27,28,29,30]. Nonlinear MDOF model, cantilever beam with breathing crack modeled as bilinear stiffness, and nonlinear electric circuit models are studied using HOFRFs to estimate nonlinear parameters by Lin et al. [31].
Recently, authors are showing more interest in a system with damping nonlinearity. Adhikari and Woodhouse [32] studied the identification of a non-viscously damped system with exponentially decaying function by a perturbation method. Xiao et al. [33] analysed the vibration isolator subjected to force and base excitation with cubic damping nonlinearity to suppress the vibration at resonance. Shum [34] exploited the nonlinear viscous damping parallel to a tuned mass damper for vibration absorber application. Nonlinear damping systems with cubic and fifth power terms are studied the generation of isolated resonance curves (IRCs) in the response spectrum by Habib et al. [35]. Chatterjee and Chintha [36] studied response characteristics of the system with cubic damping nonlinearity using the Volterra series to investigate the nonlinear parameter with the concept of a measurability ratio. Further, their study extended to system identification of asymmetric damping nonlinearity [37]. Silveira et al. [38] studied the SDOF oscillator with piecewise asymmetrical damping using the harmonic balance method and explored the effect of an asymmetric ratio on over and under damping cases.
However, most of the literature mentioned above focuses on the single-input Volterra series, which only allows limited FRF measurement in a single experiment. In contrast, the multi-tone Volterra series can generate huge distinct harmonics at different combination tones in the response series (Chatterjee [39] and [41]). We have devised a systematic identification and parameter estimation approach for symmetric and asymmetric damping nonlinearity systems using two-tone excitation in this proposed work. Section 2 consists of response formulation using Volterra series and higher-order FRFs and characteristic behavior of the system in terms of response spectrum. The signal strength of higher harmonics, parameter estimation algorithm, and numerical simulation and error analysis for cubic damping nonlinearity in Sect. 3 and for square damping nonlinearity in Sect. 4 are presented.
Volterra Series Response Representation under Harmonic Excitation
Volterra series representation for a general nonlinear dynamic system with input excitation force \(f(t)\) and output response \(x(t)\) can be expressed in the following form:
where \({h}_{n}\left({\tau }_{1},{\tau }_{2},\dots ,{\tau }_{n}\right)\) are known as nth order Volterra kernels and \({x}_{1}\left(t\right)\), \({x}_{2}\left(t\right)\) are the response components given by
Fourier Transform of the Volterra kernels \({h}_{n}\left({\tau }_{1},{\tau }_{2},\dots ,{\tau }_{n}\right)\) gives the nth order frequency response functions (FRFs)
For any general nonlinear dynamic system acted upon by a single-tone harmonic excitation with \(f\left(t\right)=A\,\,\mathrm{cos}\,\,\left(\omega t\right)= \frac{A}{2}{e}^{j\omega t}+\frac{A}{2}{e}^{-j\omega t}\), the first three response components, following Eqs. (2–4), become
Total response, \(x\left(t\right)\) can be then written in the following form:
where \(H_n^{p,q}\left( \omega \right) = {H_n}(\underbrace {\omega ,\omega , \ldots }_{p\;times},\underbrace { - \omega , - \omega , \ldots )}_{q\;times}\), \({\omega }_{p,q}=(p-q)\omega\) and \({{}^{n}C}_{q}=\frac{n!}{\left(n-q\right)!q!}\)
Response amplitude of mth harmonic \(X\left(m\omega \right)\), from Eq. (8), can be obtained as
First three harmonic amplitudes, from Eq. (9), become
For a system with polynomial form of damping nonlinearity given by
The higher order FRFs, applicable for single-tone excitation, can be synthesized as given in [36]. Synthesis formulas for the second- and third-order FRFs are given below.
Nonlinear Response Representation Under Multi-Tone Excitation
A multi-tone excitation is given by
For the sake of simplicity and as a representative example, we consider a two-tone excitation, \(f\left(t\right)=A\,\,\mathrm{cos}\,\,\left({\omega }_{1}t\right)+B\,\,\mathrm{cos}\,\,\left({\omega }_{2}t\right),\) and formulate the response series. The procedure is general and can be extended to any larger multi-tone excitation. Taking
Schetzen [15] demonstrated that the kernels could be symmetric without sacrificing generality. That is if n = 2,then \({h}_{2}\left({\tau }_{1},{\tau }_{2}\right)={h}_{2}\left({\tau }_{2},{\tau }_{1}\right)\), and for n = 3, then \({h}_{3}\left({\tau }_{1},{\tau }_{2},{\tau }_{3}\right)={h}_{2}\left({\tau }_{3},{\tau }_{2},{\tau }_{1}\right)\). Similarly, it is worth noting that kernel transforms also be symmetric. If n = 2, \({H}_{2}\left({\omega }_{1},{\omega }_{2}\right)={H}_{2}\left({\omega }_{2},{\omega }_{1}\right)\) and for n = 3, then \({H}_{3}\left({\omega }_{1},{\omega }_{2},{\omega }_{3}\right)={H}_{3}\left({\omega }_{3},{\omega }_{2},{\omega }_{1}\right)\). Using this property of symmetry number of terms could be reduced to a minimum in the below equations (Eq. 17–19).
The response components under the two-tone excitation, can be obtained as
Similarly,
Thus we see that in addition to excitation frequencies, \(\omega_{1}\) and \(\omega_{2}\), there will be many higher harmonics or combination tones in the nonlinear response. Second response component, \(x_{2} \left( t \right)\) will have a dc component and four higher harmonics, \(2\omega_{1}\), \(2\omega_{2} ,\omega_{1} + \omega_{2}\hspace{0.2cm} and\hspace{0.2cm} \omega_{1} - \omega_{2}\). The third response component, \(x_{3} \left( t \right)\) will have six higher harmonics; \(3\omega_{1} , 3\omega_{2} , 2\omega_{1} + \omega_{2} ,2\omega_{1} - \omega_{2} , 2\omega_{2} + \omega_{1}\hspace{0.2cm} and\hspace{0.2cm} 2\omega_{2} - \omega_{1}\). Similarly proceeding, we can show that many more combination harmonics of higher order will be generated in the higher order response components. Response amplitude for a general higher order combination tones can be obtained as
where \(C_{{m_{1} + p,p,m_{2} + s,s}} = \frac{N!}{{\left( {m_{1} + p} \right)!\left( p \right)!\left( {m_{2} + s} \right)!s!}}\) with \(N = \left( {m_{1} + p} \right) + p + \left( {m_{2} + s} \right) + s\)
and \([H_{n + 2i - 2}^{{m_1} + p,p,{m_2} + s,s}\left( \omega \right) = {H_n}\left( {\underbrace {{\omega _1}, \ldots }_{\left( {{m_1} + p} \right)\hspace{0.1cm}{\rm{times}}},\underbrace { - {\omega _1}, \ldots }_{p\hspace{0.1cm}{\rm{times}}},\underbrace {{\omega _2}, \ldots }_{\left( {{m_2} + s} \right)\hspace{0.1cm}{\rm{times}}},\underbrace { - {\omega _2}, \ldots }_{{\rm{s\hspace{0.1cm}times}}},} \right).\)
such that \(n = \left| {m_{1} } \right| + \left| {m_{2} } \right|,\) and \(p + s = i - 1\).
Response Spectrum Characterization Of Symmetric And Asymmetric Damping Nonlinearity
The presence of various combination tones or higher harmonics will depend on whether the damping nonlinearity is symmetric or asymmetric. The simplest model of an asymmetric damping nonlinearity would be the one with the only square term given by
The nonlinear system given by Eq. (21) is excited by a two-tone harmonic force, \(f\left( t \right) = A\cos \left( {\omega_{1} t} \right) + B\cos \left( {\omega_{2} t} \right)\), and the response x(t) is computed using RK-4 numerical method and considering the following parameters: m = 1.0, \(c_{1}\) = 0.1, \(k_{1}\) = 1.0 and A = 1.0.The nonlinear parameter \(c_{2}\) is taken as 0.02, 0.05, 0.08 and 0.1 in the numerical study. The FFT spectrum of the corresponding response (Fig. 1) shows the characteristic presence of different harmonics at frequencies \(\omega_{1} ,\omega_{2} ,2\omega_{1}\), \(2\omega_{2} ,\omega_{1} + \omega_{2} \; {\text{and}}\; \omega_{1} - \omega_{2}\). Here, excitation frequencies are selected as \(\omega_{1} /\omega_{n} = 0.8\) and \(\omega_{2} /\omega_{n} = 0.6\) such that no combination tones are formed near the resonance frequency. It can be seen that the peak amplitudes of the higher harmonics are much smaller than the peak amplitudes at driving frequencies, \(\omega_{1} /\omega_{n} = 0.8\) and \(\omega_{2} /\omega_{n} = 0.6\)
Similarly, simplest model of a symmetric damping nonlinearity would be considered as cubic term given by
Here, we select the two-tone excitation frequencies at \(\omega_{1} /\omega_{n} = 0.5\) and \(\omega_{2} /\omega_{n} = 0.4\) so that no combination tones appear near the resonance frequency. Figure 2 shows the response spectrum for.
cubic damping nonlinearity (\(c_{3}\) varying between 0.05 to 0.2), where peaks can be seen at driving frequencies \(\omega_{1} , \omega_{2}\) and combination tones \(3\omega_{1} , 3\omega_{2} , 2\omega_{1} + \omega_{2} ,2\omega_{1} - \omega_{2} ,2\omega_{2} + \omega_{1} \; {\text{and}}\; 2\omega_{2} - \omega_{1}\). Here also peak amplitudes of the higher harmonics are much smaller than the peak amplitudes at driving frequencies.
The signal strength or amplitude of the higher order harmonics will be smaller and smaller as the order increases for a weakly nonlinear system and hence we will limit our response series up to third order response component, \(x_{3} \left( t \right)\) only.
All the harmonic and super harmonic amplitudes can be formulated using Eq. (20) for a general model with both cubic and square terms given by
Amplitude series for driving harmonics become
Amplitude series for second-order harmonics are
Similarly, 3-rd order harmonic amplitude series can be written as follows:
It can be noted that all these amplitude series involve a large number of higher order FRFs. These higher order FRFs can be synthesized in terms of first-order FRFs and the nonlinear parameters, \({c}_{2}\) and \({c}_{3}\), and the formulation is explained and presented in detail in Appendix-A. The synthesis formulae for second order FRFs are
Formation of third order FRFs for above equation Eq. (23) are.
Parameter Estimation Algorithm for Symmetric (Cubic) Damping Nonlinearity
For a nonlinear system with cubic damping nonlinearity only, the equation of motion under two-tone harmonic excitation becomes
The equation can be normalized into a non-dimensional form as
where
with the normalized form of nonlinear damping parameter \(\beta_{3}\) given by
The parameter estimation algorithm aims primarily to find out the nonlinear parameter, \(\beta_{3}\) and then the linear modal parameters, \(\omega_{n}\) and \(\xi\). Same excitation amplitude is considered here for both the tones such that, \(\mu = 1\). Equation (31) given above indicates that the parameter \(\beta_{3}\) not only depends on the cubic damping parameter \(c_{3}\) but it also depends on the excitation level, A. This means that even when the nonlinear parameter, \(c_{3}\) is very small, the parameter \(\beta_{3}\) can be increased to the desired value by adjusting the excitation level. The response harmonic amplitudes for a general combination tone, \(\left( {m_{1} \Omega_{1} + m_{2} \Omega_{2} } \right)\), can be written in a non-dimensional form as
The response amplitudes, for the eight harmonics that appear in the nonlinear response up to 3rd response component, then becomes
Thus we have nine unknowns, eight FRF values \(H_{1} \left( {\Omega_{1} } \right)\), \(H_{1} \left( {\Omega_{2} } \right)\), \(H_{1} \left( {3\Omega_{1} } \right)\), \(H_{1} \left( {3\Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{1} + \Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{2} + \Omega_{1} } \right)\), \(H_{1} \left( {2\Omega_{1} - \Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{2} - \Omega_{1} } \right)\) and the cubic nonlinear parameter, \(\beta_{3}\), where as we have eight equations (Eq. 33a–h). In case the last unknown \(\beta_{3}\) can be obtained along with FRFs at driving frequencies \(H_{1} \left( {\Omega_{1} } \right)\) and \(H_{1} \left( {\Omega_{2} } \right)\) then from equations (Eq. 33c–h), we can easily estimate the six unknown FRFs of higher harmonics. Thus we need one more equation, which can be obtained through measuring single-tone response amplitude at any of the six higher harmonics, i.e., \(3\Omega_{1} , 3\Omega_{2} , 2\Omega_{1} + \Omega_{2} ,2\Omega_{1} - \Omega_{2} , 2\Omega_{2} + \Omega_{1} \; {\text{and}}\; 2\Omega_{2} - \Omega_{1}\). From Figs. 1 and 2, it is to be noted that harmonic amplitude at these higher harmonics will be much smaller in comparison to the response amplitude at driving frequencies. To get a better estimate of \(\beta_{3}\), the response amplitude of the selected higher harmonic should be as large as possible to reduce the undesirable effect of noise in the measured signal.
Figure 3a, b shows the signal strength of these combination tones or higher harmonics for a range of nonlinear parameter, \(\beta_{3}\) = 0.05–0.25, respectively, for two pairs of driving frequencies. The variation pattern is almost linear, which can be justified by the Eq. (33c–h) where the harmonic amplitudes are proportional to \(\beta_{3}\), for a given pair of driving frequencies.
It can be noted that the signal strength for the combination tone, \(2\Omega_{1} - \Omega_{2}\), is highest and far greater than any other harmonic amplitude for all the pair of multi-tone excitation frequencies. Harmonic amplitudes are obtained through the Fourier filtering for different nonlinearity levels \(\beta_{3} = 0.05 \; {\text{to}}\; 0.2\) at specific harmonics and for two pairs of driving frequencies are shown in Fig. 4.
Following observations can be made from Fig. 4a–d
-
1.
One can note that signal strength of the pair of two-tone excitation frequency \({\Omega }_{1} = 0.6,{\Omega }_{2} = 0.5\) is better than the other pair of frequency \({\Omega }_{1} = 0.5,{\Omega }_{2} = 0.4\).
-
2.
It is also observed that signal strength is highest for the combination tone of \(\left( {2{\Omega }_{1} - {\Omega }_{2} } \right)\) in comparison to all other higher harmonics for both the driving frequencies.
So we focus on Eq. (33f) associated with the combination tone \(2\Omega_{1} - \Omega_{2}\). Here it is to be noted that if we can get FRF \(H_{1} \left( {2\Omega_{1} - \Omega_{2} } \right)\), we can obtain an estimate of nonlinear parameter, \(\beta_{3}\).This can be done if we make an independent measurement of \(\overline{\eta }\left( {2\Omega_{1} - \Omega_{2} } \right)\) from response under a single-,tone excitation with \(\Omega = \left( {2\Omega_{1} - \Omega_{2} } \right)\) and then approximating \(\overline{\eta }\left( {2\Omega_{1} - \Omega_{2} } \right) \approx H_{1} \left( {2\Omega_{1} - \Omega_{2} } \right)\).
Now we can get the estimate of \(\beta_{3}\) as
where \(\left| {H_{1} \left( {\Omega_{1} } \right)} \right|,\left| {H_{1} \left( {\Omega_{2} } \right)} \right|\;{\text{and}}\;\left| {H_{1} \left( {2\Omega_{1} - \Omega_{2} } \right)} \right|\) are the previously approximated values of the respective FRFs.
Now, with the estimated value of \(\beta_{3}\), we can find the remaining five FRFs, i.e., \(H_{1} \left( {3\Omega_{1} } \right)\), \(H_{1} \left( {3\Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{1} + \Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{2} + \Omega_{1} } \right)\), \(H_{1} \left( {2\Omega_{2} - \Omega_{1} } \right)\), using Eqs. (33cd, e, g, h).These series of actions can be summarized in an algorithm consisting of following steps.
Step 1: Measure response time history, \(\eta \left( t \right)\) under two-tone excitation and using Fourier Filtering, we first compute the harmonic amplitudes, \(\overline{\eta }\left( {\Omega_{1} } \right)\) and \(\overline{\eta }\left( {\Omega_{2} } \right)\). Now, approximate \(\overline{\eta }\left( {\Omega_{1} } \right) \approx H_{1} \left( {\Omega_{1} } \right)\) and \(\overline{\eta }\left( {\Omega_{2} } \right) \approx H_{1} \left( {\Omega_{2} } \right)\).
Step 2: Measure response time history, \(\eta \left( t \right)\) using single-tone excitation at \(\Omega = 2\Omega_{1} - \Omega_{2}\) and using Fourier filtering, compute harmonic amplitude, \(\overline{\eta }\left( {2\Omega_{1} - \Omega_{2} } \right)\). Then approximate to get an estimate \(H_{1} \left( {2\Omega_{1} - \Omega_{2} } \right) \approx \overline{\eta }\left( {2\Omega_{1} - \Omega_{2} } \right)\) with single-tone excitation.
Step 3: Using Eq. (34), obtain an estimate of nonlinear parameter, \(\beta_{3}\).
Step 4: Using Eq. (33c, d, e, g, h), estimates the FRF values \(H_{1} \left( {3\Omega_{1} } \right)\), \(H_{1} \left( {3\Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{1} + \Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{2} + \Omega_{1} } \right)\), \(H_{1} \left( {2\Omega_{2} - \Omega_{1} } \right)\).
Step 5: using all eight FRF values, a curve fitting procedure [42] will give an estimate of non-dimensional natural frequency \(\Omega_{n}\) and modal damping parameter, ξ.
Numerical Simulation and Error Analysis
We first consider excitation frequency pair to be \(\Omega_{1} = 0.5 \;{\text{and}}\; \Omega_{2} = 0.4\) with ξ = 0.05 and \(\beta_{3} = 0.05, \;0.1,\; 0.15\;{\text{ and}}\; 0.2\). Response is computed by numerical integration of the differential equation (Eq. 30) and harmonic amplitudes are obtained using Fourier filtering of the response time history. The values of the harmonic amplitudes are given in Table 1 below.
A sample step by step calculation for estimation of nonlinear damping parameter and linear modal parameters is demonstrated below for a typical value of \(\beta_{3} = 0.2\).
Step 1: First, we measure response time history, \(\eta \left( t \right)\) under two-tone excitation and using Fourier Filtering, and computed the harmonic amplitude, and approximated it as
Step 2:Measure response time history, \(\eta \left( t \right)\) using single-tone excitation at \(\Omega = 2\Omega_{1} - \Omega_{2}\) and using Fourier filtering, then approximate as
Step 3: This gives an estimate of \(\beta_{3}\) using Eq. (34) as \(\beta_{3} =\) 0.19648 (error in estimate = 1.75).
Step 4: Now Eqs. (33c, d, e, g, h) give \(H_{1} \left( {3\Omega_{1} } \right) = H_{1} \left( {1.5} \right) = 0.8305\)
Step 5:These five first-order FRF values with previously obtained three FRF values provide a set of total eight FRF values, which upon curve fitting (shown in Fig. 5) gives \(\Omega_{n} = 1.0078\)( error = 0.78%) and ξ = 0.0518 (error = 3.6%).
The error in estimating eight FRF values is only significant in the frequency range of 0.6–1.2, as shown in Fig. 5. As a result, no measurement is recommended in the same frequency range.
Estimated values of modal parameters for a two-tone excitation frequency pair, \(\Omega_{1} = 0.5\; {\text{and}}\; \Omega_{2} = 0.4\) at different values of \(\beta_{3}\) such as normalised natural frequency (which is \({\Omega }_{n} = 1\)) and damping ratio (which is \(\xi = 0.5\)) from curve fitting procedure [42] are listed in Table 2. Error estimation in natural frequency is insignificant. Error estimation in the linear damping ratio is little bit higher.
Proceeding in the same manner with two-tone excitation frequency pair,\(\Omega_{1} = 0.6\; {\text{and}}\; \Omega_{2} = 0.5\), harmonic amplitudes are measured and listed in Table 3 and corresponding estimates of linear and nonlinear parameters are listed in Table 4.
Error estimation in natural frequency and nonlinear parameter is fairly good. Estimation error in linear damping ratio in comparison with the excitation frequency pair \(\Omega_{1} = 0.5 \;{\text{and}}\; \Omega_{2} = 0.4\) is more.
The following observations can be made from Fig. 6:
-
1.
Fairly good estimates are obtained for a different nonlinear parameters \(\beta_{3}\) at 0.05, 0.1, 0.15, 0.2. Estimate of nonlinear parameter \(\beta_{3}\) for a pair of frequency \({\Omega }_{1} = 0.5,{\Omega }_{2} = 0.4\)(< 1.76% error) is better than the other pair of frequencies \({\Omega }_{1} = 0.6,{\Omega }_{2} = 0.5\) (< 12% error). But the signal strength of second pair (\({\Omega }_{1} = 0.6,{\Omega }_{2} = 0.5\)) of frequency is better than the first pair (\({\Omega }_{1} = 0.5,{\Omega }_{2} = 0.4)\) is shown in Fig. 4.
-
2.
Estimate of natural frequency \(\Omega_{n}\) is fairly good,the error is less than 0.8% for pair of frequency \({\Omega }_{1} = 0.5,{\Omega }_{2} = 0.4\), and for other pair of frequency \({\Omega }_{1} = 0.6,{\Omega }_{2} = 0.5\) is less than 4.2%. But for damping ratio(ξ) error is good at lower \(\beta_{3}\), and increasing at high value of \(\beta_{3}\)
Parameter Estimation Algorithm for Square Damping Nonlinearity
Similarly, for a nonlinear system with square damping nonlinearity only, the equation of motion under two-tone harmonic excitation becomes
The equation can be normalized into a non-dimensional form as
where the normalized form of nonlinear damping parameter \(\beta_{2 }\) given by
The response amplitudes, for the six harmonics that appear in the nonlinear response up to 3rd response component, then becomes
Similar to cubic nonlinear damping, but here we have seven unknowns, six FRF values \(H_{1} \left( {\Omega_{1} } \right)\), \(H_{1} \left( {\Omega_{2} } \right)\), \(H_{1} \left( {2\Omega_{1} } \right)\), \(H_{1} \left( {2\Omega_{2} } \right)\), \(H_{1} \left( {\Omega_{1} + \Omega_{2} } \right)\), \(H_{1} \left( {\Omega_{1} - \Omega_{2} } \right)\), and the square nonlinear parameter, \(\beta_{2}\), whereas we have six equations (Eq. 38a–f). Thus we need one more equation, which can be obtained through measuring single-tone response amplitude at any of the four higher harmonics, i.e., \(2\Omega_{1} , 2\Omega_{2} , \Omega_{1} + \Omega_{2} \;{\text{and}}\; \Omega_{1} - \Omega_{2}\). From Fig. 1, it is to be noted that harmonic amplitude at these higher harmonics will be much smaller in comparison to the response amplitude at driving frequencies. To get a better estimate of \(\beta_{2}\), the response amplitude of the selected higher harmonic should be as large as possible to reduce undesirable effect of noise in the measured signal.
Figure 7a–c shows the signal strength of these combination tones or higher harmonics for a range of nonlinear parameter, \(\beta_{2}\) = 0.02–0.1, respectively for three pairs of driving frequencies. The variation pattern is almost linear, which can be justified by the Eq. (38c–f) where the harmonic amplitudes are proportional to \(\beta_{2}\), for a given pair of driving frequencies. It can be seen that in Fig. 7a, c that the signal strength for the combination tone, \(\Omega_{1} - \Omega_{2}\), is highest for the first pair (\({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.6)\) and third pair (\({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.7)\) of driving frequencies, whereas in Fig. 7b, second pair (\({\Omega }_{1} = 0.7,{\Omega }_{2} = 0.6\)) of driving frequency having highest signal strength for the combination tone, \(\Omega_{1} + \Omega_{2}\) in comparison with other higher harmonic combination tones.
For a square damping nonlinearity, the harmonic amplitudes obtained through the Fourier filtering at different values of a nonlinear parameter β2, for the three pairs of two-tone excitation frequencies are shown in Fig. 8a–d Following observations can be made from Fig. 8a–d:
-
1.
One can note that the signal strength of the pair of two-tone excitation frequencies \({{ \Omega }}_{1} = 0.8,{\Omega }_{2} = 0.7\) is better than the other two pairs (\({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.6\) and \({\Omega }_{1} = 0.7,{\Omega }_{2} = 0.6\)) of frequencies.
-
2.
Thes signal strength is highest for the combination tone of \(\left( {{\Omega }_{1} - {\Omega }_{2} } \right)\) in comparison to the other higher harmonics for both the driving frequencies.
So we considered the Eq. (38f), associated with the combination tone \(\Omega_{1} - \Omega_{2}\) and first we obtain the FRF \(H_{1} \left( {\Omega_{1} - \Omega_{2} } \right)\), which is further used to an estimate of the nonlinear parameter, \(\beta_{2}\). This can be done if we make an independent measurement of \(\overline{\eta }\left( {\Omega_{1} - \Omega_{2} } \right)\) from response under a single-tone excitation with \(\Omega = \left( {\Omega_{1} - \Omega_{2} } \right)\) and then approximating \(\overline{\eta }\left( {\Omega_{1} - \Omega_{2} } \right) \approx H_{1} \left( {\Omega_{1} - \Omega_{2} } \right)\).
Now we can get the estimate of \(\beta_{2}\) as
where \(\left| {H_{1} \left( {\Omega_{1} } \right)} \right|,\left| {H_{1} \left( {\Omega_{2} } \right)} \right|and \left| {H_{1} \left( {\Omega_{1} - \Omega_{2} } \right)} \right|\) are the previously approximated values of the respective FRFs.
Now, with the estimated value of \(\beta_{2}\), we can find the remaining three FRFs, i.e., \(H_{1} \left( {2\Omega_{1} } \right)\), \(H_{1} \left( {2\Omega_{2} } \right)\), \(H_{1} \left( {\Omega_{1} + \Omega_{2} } \right)\) using Eq. (38c, d, e). These series of actions can be summarized in an algorithm consisting of following steps:
Step 1: Measure response time history, \(\eta \left( t \right)\) under two-tone excitation and using Fourier Filtering, we first compute the harmonic amplitudes, \(\overline{\eta }\left( {\Omega_{1} } \right)\) and \(\overline{\eta }\left( {\Omega_{2} } \right)\). Now, approximate \(\overline{\eta }\left( {\Omega_{1} } \right) \approx H_{1} \left( {\Omega_{1} } \right)\) and \(\overline{\eta }\left( {\Omega_{2} } \right) \approx H_{1} \left( {\Omega_{2} } \right)\).
Step 2: Measure response time history, \(\eta \left( t \right)\) using single-tone excitation at \(\Omega = \Omega_{1} - \Omega_{2}\) and using Fourier filtering, compute harmonic amplitude, \(\overline{\eta }\left( {\Omega_{1} - \Omega_{2} } \right)\). Then approximate to get an estimate \(H_{1} \left( {\Omega_{1} - \Omega_{2} } \right) \approx \overline{\eta }\left( {\Omega_{1} - \Omega_{2} } \right)\) with single-tone excitation.
Step 3: Using Eq. (39), obtain an estimate of nonlinear parameter, \(\beta_{2}\).
Step 4: Using Eqn.. (38c–e), estimate the FRF values \(H_{1} \left( {2\Omega_{1} } \right)\), \(H_{1} \left( {2\Omega_{2} } \right)\) and \(H_{1} \left( {\Omega_{1} + \Omega_{2} } \right)\),
Step 5: using all six FRF values, a curve fitting procedure [42] will give an estimate of non-dimensional natural frequency \(\Omega_{n}\) and modal damping parameter, ξ.
Following a similar step-by-step procedure for the two-tone excitation frequency pair, \(\Omega_{1} = 0.7 \;{\text{and}}\; \Omega_{2} = 0.6\), here, the signal strength is highest for the combination tone \(\left( {\Omega_{1} + \Omega_{2} } \right)\) to estimate the nonlinear parameter \(\beta_{2}\).
Numerical Simulation and Error Analysis
We first consider excitation frequency pair to be \(\Omega_{1} = 0.8 \;{\text{and}}\; \Omega_{2} = 0.6\) with ξ = 0.05 and \(\beta_{2} = 0.02, 0.055, 0.08 \;{\text{and}}\; 0.1\). Response is computed by numerical integration of the differential equation (Eq. 36) and harmonic amplitudes are obtained using Fourier filtering of the response time history. The values of the harmonic amplitudes are given in Table 5 below.
A sample step by step calculation for estimation of nonlinear damping parameter and linear modal parameters is demonstrated below for a typical value of \(\beta_{2} = 0.08\).
Step 1: First, we measured response time history, \(\eta \left( t \right)\) under two-tone excitation and using Fourier Filtering, computed the harmonic amplitude, and approximated it as
Step 2: Measured response time history, \(\eta \left( t \right)\) using single-tone excitation at \(\Omega = \Omega_{1} - \Omega_{2}\) and using Fourier filtering and then approximated as
Step 3:This gives an estimate of \(\beta_{2}\) using Eq. (39) as \(\beta_{2} = 0.99726\) (error in estimate = 0.27443%).
Step 4: Now Eq. (38c–e) gives \(H_{1} \left( {2\Omega_{1} } \right) = H_{1} \left( {1.6} \right) = 0.62877\)
Step 5: These three first-order FRF values with previously obtained three FRF values provide a set of total six FRF values, which upon curve fitting (shown in Fig. 9) gives \(\Omega_{n} = 0.99726\)(error = 0.27%) and ξ = 0.05070 (error = 1.39%) (Fig. 10).
Estimated values of nonlinear parameter \(\beta_{2}\) for a two-tone excitation frequency pair, \(\Omega_{1} = 0.8 \;{\text{and}}\; \Omega_{2} = 0.6\) at different values of \(\beta_{2}\) and model parameters, normalised natural frequency (which is \({\Omega }_{n} = 1\)) and damping ratio (which is \(\xi = 0.5\)) from curve fitting procedure are listed in Table 6.
Harmonic amplitude obtained through fourier filter for the pair of two-tone excitation frequency \(\Omega_{1} = 0.7 \;{\text{and}}\; \Omega_{2} = 0.6\) is listed in Table 7.
Estimated values of nonlinear parameter \(\beta_{2}\) at different values and modal parameters, natural frequency \(\Omega_{n}\), and damping ratio ξ for the pair of two-tone excitation frequency pair, \(\Omega_{1} = 0.7\;{\text{ and}}\; \Omega_{2} = 0.6\) is shown in Table 8.
Harmonic amplitude obtained through fourier filter for the pair of two-tone excitation frequency \(\Omega_{1} = 0.8 \;{\text{and}}\; \Omega_{2} = 0.7\) is listed in Table 9.
Proceeding the similar manner, and estimated the values of nonlinear parameter \(\beta_{2}\) at different values and modal parameters, natural frequency \(\Omega_{n}\), and damping ratio ξ for the pair of two-tone excitation frequency pair, \(\Omega_{1} = 0.8 \;{\text{and}}\; \Omega_{2} = 0.7\) is shown in Table 10.
The following observations can be made from Fig. 10.
-
1.
Fairly good estimates are obtained for a different nonlinear parameters \(\beta_{2}\) at 0.02, 0.05, 0.08, 0.1. Estimate of nonlinear parameter \(\beta_{2}\) for a pair of frequency \({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.7\) (< 1.38% error) is better than the other pair of frequencies \({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.6\) (< 1.9% error), for \({\Omega }_{1} = 0.7,{\Omega }_{2} = 0.6\) (< 3.06% error). Signal strength of third pair (\({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.7\)) of frequency is also better than the other two pairs.
-
2.
Estimate of natural frequency \(\Omega_{n}\) is fairly good, error estimates of a pair of frequencies are \({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.7\) (< 0.34% error),\({\Omega }_{1} = 0.7,{\Omega }_{2} = 0.6\) (< 0.44% error), \({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.7\) (< 0.18% error). But for damping ratio (ξ), error is optimum at \(\beta_{2}\) = 0.05 and 0.08 for pair of frequencies \({\Omega }_{1} = 0.8,{\Omega }_{2} = 0.7\) and \({\Omega }_{1} = 0.7,{\Omega }_{2} = 0.6\)
Conclusion
The present work discusses a novel method for nonlinear damping parameter estimation using multi-tone harmonic excitation for both symmetric and asymmetric form of damping nonlinearity. Response harmonic amplitudes are formulated using Volterra series and higher order kernel synthesis. A novel parameter estimation algorithm is developed to estimate nonlinear damping parameter and linear modal parameters. It is shown that multi-tone excitation generates large number of combination tones in the nonlinear response. Response amplitudes at these higher harmonics are measured and linear and nonlinear parameters are estimated by solving the set of nonlinear equations relating first order FRFs and the parameters. The main advantage of proposed method is that the number of experiments needed is only two instead of many more as required for single-tone excitation cases. Numerical simulations with a typical two-tone excitation demonstrate that fairly accurate estimates of nonlinear damping parameter and linear modal parameter can be obtained with proper selection of frequency pair and excitation level. Although the procedure is demonstrated here for polynomial forms of damping, it can be extended for some of the non-polynomial damping forms also as disused in [40]
Availability of Data and Materials
Exhaustively included in the manuscript itself.
Code Availability
May be made available from Author on specific request.
Abbreviations
- A, B:
-
Excitation force amplitudes
- \({\beta }_{2}\) :
-
Second order nonlinear damping parameter
- \({\beta }_{3}\) :
-
Third order nonlinear damping parameter
- \({c}_{1}\) :
-
Linear damping coefficient
- \({c}_{2}\) :
-
Square damping coefficient
- \({c}_{3}\) :
-
Cubic damping coefficient
- \(f(t)\) :
-
Excitation force
- ξ:
-
Damping ratio
- \({h}_{1}\left({\tau }_{1}\right)\) :
-
First order Volterra kernel
- \({h}_{2}\left({\tau }_{1},{\tau }_{2}\right)\) :
-
Second order Volterra kernel
- \({h}_{n}\left({\tau }_{1},{\tau }_{2},\dots ,{\tau }_{n}\right)\) :
-
nth order Volterra kernel
- \({H}_{1}(\omega )\) :
-
First order Volterra kernel transform
- \({H}_{2}(\omega ,\omega )\) :
-
Second order Volterra kernel transform
- \({H}_{3}\left(\omega ,\omega ,\omega \right)\) :
-
Third order Volterra kernel transform
- \({H}_{n}\left({\omega }_{1},{\omega }_{2},\dots ,{\omega }_{n}\right)\) :
-
nth Order Volterra kernel transform or Frequency Response Function
- \({k}_{1}\) :
-
Linear stiffness coefficient
- \(m\) :
-
Mass of the system
- t :
-
Time
- \(\tau\) :
-
Non-dimensional time
- \({\omega }_{1}\) :
-
Two-tone first driving frequency
- \({\omega }_{2}\) :
-
Two-tone second driving frequency
- \({\omega }_{n}\) :
-
Natural frequency
- \({\omega }_{p,q,s,u}\) :
-
General higher harmonic of \(\omega\)
- \({\Omega }_{E}\) :
-
Non-dimensional excited frequency
- \({\Omega }_{1}=\frac{{\omega }_{1}}{{\omega }_{n}}\) :
-
Non-dimensional two-tone first driving frequency
- \({\Omega }_{2}=\frac{{\omega }_{2}}{{\omega }_{n}}\) :
-
Non-dimensional two-tone secnd driving frequency
- x(t):
-
Response function
- \(\dot{x}(t)\) :
-
Velocity of system
- \(\ddot{x}\left(t\right)\) :
-
Acceleration of system
- \(X\) :
-
Amplitude of system
- \(X\left(m\omega \right)\) :
-
mth harmonic response amplitude
- \(X\left(\omega \right)\) :
-
First harmonic amplitude
- \(X\left(2\omega \right)\) :
-
Second harmonic amplitude
- \(X\left(3\omega \right)\) :
-
Third harmonic amplitude
- \(\eta \left(\tau \right)\) :
-
Non-dimensional response
- \({\eta }^{\prime}\left(\tau \right)\) :
-
Non-dimensional Velocity
- \(\eta^{\prime\prime} \left(\tau \right)\) :
-
Non-dimensional acceleration
- \(\overline{\eta }\left(\Omega \right)\) :
-
Non-dimensional first harmonic amplitude
- \(\overline{\eta }\left(2\Omega \right)\) :
-
Non-dimensional second harmonic amplitude
- \(\overline{\eta }\left(3\Omega \right)\) :
-
Non-dimensional third harmonic amplitude
- \({x}_{1}\left(t\right)\) :
-
First response component
- \({x}_{2}\left(t\right)\) :
-
Second response component
- \({x}_{3}\left(t\right)\) :
-
Third response component
- \({x}\left(t\right)\) :
-
Total response
- \(X\left({m}_{1}{\omega }_{1}+{m}_{2}{\omega }_{2}\right)\) :
-
Response harmonic amplitude for a Combination tone \(\left({m}_{1}{\omega }_{1}+{m}_{2}{\omega }_{2}\right)\)
- \(X\left({\omega }_{1}\right)\) :
-
First harmonic amplitude for a driving frequency \({\omega }_{1}\)
- \(X\left({\omega }_{2}\right)\) :
-
First harmonic amplitude for a driving frequency \({\omega }_{2}\)
- \(X\left({2\omega }_{1}\right)\) :
-
Second harmonic amplitude for a frequency \({2\omega }_{1}\)
- \(X\left(2{\omega }_{2}\right)\) :
-
Second harmonic amplitude for a frequency \({2\omega }_{2}\)
- \(X\left({\omega }_{1}+{\omega }_{2}\right)\) :
-
Second harmonic amplitude for a combination tone \({(\omega }_{1}+{\omega }_{2})\)
- \(X\left({\omega }_{1}-{\omega }_{2}\right)\) :
-
Second harmonic amplitude for a combination tone \(({\omega }_{1}-{\omega }_{2})\)
- \(X\left({3\omega }_{1}\right)\) :
-
Third harmonic amplitude for a frequency \(3{\omega }_{1}\)
- \(X\left(3{\omega }_{2}\right)\) :
-
Third harmonic amplitude for a frequency \(3{\omega }_{2}\)
- \(X\left(2{\omega }_{1}+{\omega }_{2}\right)\) :
-
Third harmonic amplitude for a combination tone \(\left(2{\omega }_{1}+{\omega }_{2}\right)\)
- \(X\left(2{\omega }_{1}-{\omega }_{2}\right)\) :
-
Third harmonic amplitude for a combination tone \(\left(2{\omega }_{1}-{\omega }_{2}\right)\)
- \(X\left(2{\omega }_{2}+{\omega }_{1}\right)\) :
-
Third harmonic amplitude for a combination tone \(\left(2{\omega }_{2}+{\omega }_{1}\right)\)
- \(X\left(2{\omega }_{2}-{\omega }_{1}\right)\) :
-
Third harmonic amplitude for a combination tone \(\left(2{\omega }_{2}-{\omega }_{1}\right)\)
- \(\overline{\eta }\left({m}_{1}{\Omega }_{1}+{m}_{2}{\Omega }_{2}\right)\) :
-
Non-dimensional response harmonic amplitude for a combination tone \(\left({m}_{1}{\Omega }_{1}+{m}_{2}{\Omega }_{2}\right)\)
- \(\overline{\eta }\left({\Omega }_{1}\right)\) :
-
Non-dimensional first harmonic amplitude for a driving frequency \({\Omega }_{1}\)
- \(\overline{\eta }\left({\Omega }_{2}\right)\) :
-
Non-dimensional first harmonic amplitude for a driving frequency \(\left({\Omega }_{2}\right)\)
- \(\overline{\eta }\left(2{\Omega }_{1}\right)\) :
-
Non-dimensional harmonic amplitude for a frequency \(2{\Omega }_{1}\)
- \(\overline{\eta }\left(2{\Omega }_{2}\right)\) :
-
Non-dimensional harmonic amplitude for a frequency \(2{\Omega }_{2}\)
- \(\overline{\eta }\left({\Omega }_{1}+{\Omega }_{2}\right)\) :
-
Non-dimensional second harmonic amplitude for a combination tone \(\left({\Omega }_{1}+{\Omega }_{2}\right)\)
- \(\overline{\eta }\left({\Omega }_{1}-{\Omega }_{2}\right)\) :
-
Non-dimensional second harmonic amplitude for a combination tone \(\left({\Omega }_{1}-{\Omega }_{2}\right)\)
- \(\overline{\eta }\left(3{\Omega }_{1}\right)\) :
-
Non-dimensional third harmonic amplitude for a frequency \(3{\Omega }_{1}\)
- \(\overline{\eta }\left(3{\Omega }_{2}\right)\) :
-
Non-dimensional third harmonic amplitude for a frequency \(\left(3{\Omega }_{2}\right)\)
- \(\overline{\eta }\left(2{\Omega }_{1}+{\Omega }_{2}\right)\) :
-
Non-dimensional third harmonic amplitude for a combination tone \(\left(2{\Omega }_{1}+{\Omega }_{2}\right)\)
- \(\overline{\eta }\left(2{\Omega }_{1}-{\Omega }_{2}\right)\) :
-
Non-dimensional third harmonic amplitude for a combination tone \(\left(2{\Omega }_{1}-{\Omega }_{2}\right)\)
- \(\overline{\eta }\left(2{\Omega }_{2}+{\Omega }_{1}\right)\) :
-
Non-dimensional third harmonic amplitude for a combination tone \(\left(2{\Omega }_{2}+{\Omega }_{1}\right)\)
- \(\overline{\eta }\left(2{\Omega }_{2}-{\Omega }_{1}\right)\) :
-
Non-dimensional third harmonic amplitude for a combination tone \(\left(2{\Omega }_{2}-{\Omega }_{1}\right)\)
References
Nayfeh AH, Mook DT (1979) Nonlinear oscillations. Willey, New York
Bendat JS, Palo PA, Coppolino RN (1992) A general identification technique for nonlinear differential equations of motion. Probab Eng Mech 7(1):43–61. https://doi.org/10.1016/0266-8920(92)90008-6
Tiwari R, Vyas NS (1995) Estimation of nonlinear stiffness parameters of rolling element bearings from random response of rotor bearing systems. J Sound Vib 187(2):229–239. https://doi.org/10.1006/jsvi.1995.0517
Balachandran B, Nayfeh AH, Smith SW, Pappa RS (1994) Identification of nonlinear interactions in structures. AIAA J Guid Control Dyn 17(2):257–262. https://doi.org/10.2514/3.21191
Khan KA, Balachandran B (1997) Bispectral analyses of interactions in quadratically and cubically coupled oscillators. Mech Res Commun 24(5):545–550. https://doi.org/10.1016/S0093-6413(97)00060-8
Bikdash M, Balachandran B, Nayfeh AH (1994) Melnikov analysis for a ship with a general roll-damping model. Nonliear Dyn 6:101–124. https://doi.org/10.1007/BF00045435
Volterra V (1958) Theory of functionals and integral integro-differential equations. Dover Publications Inc, New York
George DA (1959) Continuous nonlinear systems. MIT RLE Tech Rep 355.
Boyd S, Chua L (1985) Fading memory and the problem of approximating nonlinear operators with Volterra series. IEEE Trans Circ Syst 32(11):1150–1161. https://doi.org/10.1109/TCS.1985.1085649
Bedrosian E, Rice SO (1971) The output properties of Volterra systems (nonlinear systems with memory) driven by harmonic and Gaussian inputs. Proc IEEE 59(12):1688–1707. https://doi.org/10.1109/PROC.1971.8525
Worden K, Manson G, Tomlinson GR (1997) A harmonic probing algorithm for the multi-input Volterra series. J Sound Vib 201(1):67–84. https://doi.org/10.1006/jsvi.1996.0746
Marmarelis PZ, Naka KI (1974) Identification of multi-input biological systems. IEEE Trans Biomed Eng 21(2):88–101. https://doi.org/10.1109/TBME.1974.324293
Boaghe OM, Billings SA (2003) Subharmonic oscillation modelling MISO Volterra series. IEEE Trans Circ Syst I Fund Theory Appl 50(7):874–884. https://doi.org/10.1109/TCSI.2003.813965
Rugh WJ (1981) Nonlinear system theory—The Volterra/Wiener approach. The Johns Hopkins University Press, Baltimore
Schetzen M (1980) The Volterra and wiener theories of nonlinear systems. Wiley, New York
Chatterjee A, Vyas NS (2003) Nonlinear parameter estimation with Volterra series using the method of recursive iteration through harmonic probing. J Sound Vib 268(4):657–678. https://doi.org/10.1016/S0022-460X(02)01537-7
Chatterjee A (2010) Identification and parameter estimation of a bilinear oscillator using Volterra series with harmonic probing. Int J Non Linear Mech 45(1):12–20. https://doi.org/10.1016/j.ijnonlinmec.2009.08.007
Cheng CM, Peng MK, Zhang WM, Meng G (2017) Volterra-series-based nonlinear system modelling and its engineering applications: a state-of-the-art review. Mech Syst Signal Process 87:340–364. https://doi.org/10.1016/j.ymssp.2016.10.029
Noel JP, Kerschen G (2017) Nonlinear system identification in structural dynamics: 10 more years of progress. Mech Syst Signal Process 83:2–35. https://doi.org/10.1016/j.ymssp.2016.07.020
Cveticanin L (2011) Oscillators with nonlinear elastic and damping forces. Comput Math with Appl 62(4):1745–1757. https://doi.org/10.1016/j.camwa.2011.06.016
Detroux T, Renson L, Kerschen G (2014) The harmonic balance method for advanced analysis and design of nonlinear mechanical systems. In: Kerschen G (eds) Nonlinear Dynamics, Volume 2. Conference Proceedings of the Society for Experimental Mechanics Series. Springer, Cham. https://doi.org/10.1007/978-3-319-04522-1_3
Xu L, Lu MW, Cao Q (2002) Nonlinear vibrations of dynamical systems with a general form of piecewise-linear viscous damping by incremental Harmonic Balance Method. Phys Lett A 301(1–2):65–73. https://doi.org/10.1016/S0375-9601(02)00960-X
Peng ZK, Meng G, Lang ZQ, Zhang WM, Chu FL (2012) Study of the effects of cubic nonlinear damping on vibration isolations using Harmonic Balance Method. Int J Non Linear Mech 47(10):1073–1080. https://doi.org/10.1016/j.ijnonlinmec.2011.09.013
Elliott SJ, Tehrani MG, Langley RS (2015) Nonlinear damping and quasi-linear modelling. Philos Trans R Soc A Math Phys Eng Sci 373:20140402. https://doi.org/10.1098/rsta.2014.0402
Lang ZQ, Billings SA (2005) Energy transfer properties of non-linear systems in the frequency domain. Int J Control 78(5):345–362. https://doi.org/10.1080/00207170500095759
Lang ZQ, Billings SA, Yue R, Li J (2007) Output frequency response function of nonlinear Volterra systems. Automatica 43(5):805–816. https://doi.org/10.1016/j.automatica.2006.11.013
Peng J, Tang J, Chen Z (2004) Parameter identification of weakly nonlinear vibration system in frequency domain. Shock Vib 11(5–6):685–692. https://doi.org/10.1155/2004/634785
Ho C, Lang ZQ, Billings SA (2014) A frequency domain analysis of the effects of nonlinear damping on the Duffing equation. Mech Syst Signal Process 45(1):49–67. https://doi.org/10.1016/j.ymssp.2013.10.027
Zhang B, Billings SA (2017) Volterra series truncation and kernel estimation of nonlinear systems in the frequency domain. Mech Syst Signal Process 84(1):39–57. https://doi.org/10.1016/j.ymssp.2016.07.008
Laalej H, Lang ZQ, Daley S et al (2012) Application of non-linear damping to vibration isolation: an experimental study. Nonliear Dyn 69:409–421. https://doi.org/10.1007/s11071-011-0274-1
Lin RM, Ng TY (2018) A new method for the accurate measurement of higher-order frequency response functions of nonlinear structural systems. ISA Trans 81:270–285. https://doi.org/10.1016/j.isatra.2018.05.015
Adhikari S, Woodhouse J (2001) Identification of damping: part 2 non-viscous damping. J Sound Vib 243(1):63–88. https://doi.org/10.1006/jsvi.2000.3392
Xiao Z, Jing X, Cheng L (2013) The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitation. J Sound Vib 332(5):1335–1354. https://doi.org/10.1016/j.jsv.2012.11.001
Shum KM (2015) Tuned vibration absorbers with nonlinear viscous damping for damped structures under random load. J Sound Vib 346:70–80. https://doi.org/10.1016/j.jsv.2015.02.003
Habib G, Cirillo GI, Kerschen G (2018) Isolated resonances and nonlinear damping. Nonlinear Dyn 93:979–994. https://doi.org/10.1007/s11071-018-4240-z
Chatterjee A, Chintha HP (2020) Identification and parameter estimation of cubic nonlinear damping using harmonic probing and volterra series. Int J Non Linear Mech 125:103518. https://doi.org/10.1016/j.ijnonlinmec.2020.103518
Chatterjee A, Chintha HP (2021) Identification and parameter estimation of asymmetric nonlinear damping in a single-degree-of freedom system using volterra series. J Vib Eng Technol 9:817–843. https://doi.org/10.1007/s42417-020-00266-7
Silveira M, Wahi P, Fernandes JCM (2019) Exact and approximate analytical solutions of oscillator with piecewise linear asymmetrical damping. Int J Non Linear Mech 110:115–122. https://doi.org/10.1016/j.ijnonlinmec.2018.12.007
Chatterjee A (2010) Parameter estimation of duffing oscillator using Volterra series and multi-tone excitation. Int J Non Linear Mech 52(12):1716–1722. https://doi.org/10.1016/j.ijmecsci.2010.09.005
Chintha HP, Chatterjee A (2022) Identification and parameter estimation of non-polynomial forms of damping nonlinearity in dynamic systems. Int J Non Linear Mech 143:104017. https://doi.org/10.1016/j.ijnonlinmec.2022.104017
Chatterjee A, Vyas N (2002) Non-linear parameter estimation using Volterra series with multi-tone excitation. In: XXIMAC Proceedings of the 20th International Model Analysis Conference, Los Angeles CA (pp. 880–885)
Ewins DJ (1984) Modal testing: theory and practice. Research Studies Press, Baldock
Funding
No funding received in connection with this research work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
None.
Appendix-A: Synthesis of Higher Order FRFs
The Volterra series response representation for a general nonlinear system under multi-tone harmonic excitation is given by
Then the response series in velocity \(\dot{x}(t)\) becomes
where \(H_n^{p,q,s,u}\left( \omega \right) = {H_n}\left( {\underbrace {{\omega _1} \ldots }_{p\;times},\underbrace { - {\omega _1} \ldots }_{q\;times},\underbrace {{\omega _2} \ldots }_{s\;times},\underbrace { - {\omega _2} \ldots }_{u\;times},} \right)\)
\({C}_{p,q,s,u}=\frac{n!}{p!q!s!u!}\), where \(n=p+q+s+u\)
Now, for a general polynomial nonlinearity up to cubic term for multi-tone excitation, equation of motion becomes
Substituting Eqs. (A.1–A.3) in Eq. (A.4), one obtains
Equating coefficients of \(\frac{1}{{2}^{n}}{A}^{p+q}{B}^{s+u}{e}^{j{\omega }_{p,q,s,u}t}\) both sides in Eq. (A.5), n = 1,2,3…., one obtains
For n > 1,
Coefficient of \(\frac{1}{{2}^{n}}{A}^{p+q}{B}^{s+u}{e}^{j{\omega }_{p,q,s,u}t}\) in first line of Eq. (A.5) is
Coefficient of \(\frac{1}{{2}^{n}}{A}^{p+q}{B}^{s+u}{e}^{j{\omega }_{p,q,s,u}t}\) in second line of Eq. (A.5) is
such that, \({p}_{1}+{q}_{1}+{s}_{1}+{u}_{1}={n}_{1},\; {p}_{2}+{q}_{2}+{s}_{2}+{u}_{2}={n}_{2}\) and \({n}_{1}+{n}_{2}=n\)
Coefficient of \(\frac{1}{{2}^{n}}{A}^{p+q}{B}^{s+u}{e}^{j{\omega }_{p,q,s,u}t}\) in third line of Eq. (A.5) is
such that, \({p}_{1}+{q}_{1}+{s}_{1}+{u}_{1}={n}_{1}, {p}_{2}+{q}_{2}+{s}_{2}+{u}_{2}={n}_{2}, {p}_{3}+{q}_{3}+{s}_{3}+{u}_{3}={n}_{3}\) and \({n}_{1}+{n}_{2}+{n}_{3}=n\).
Coefficient of \(\frac{1}{{2}^{n}}{A}^{p+q}{B}^{s+u}{e}^{j{\omega }_{p,q,s,u}t}\) in fourth line of Eq. (A.5) is
such that, \({p}_{1}+{q}_{1}+{s}_{1}+{u}_{1}={n}_{1}, {p}_{2}+{q}_{2}+{s}_{2}+{u}_{2}={n}_{2}\) and \({n}_{1}+{n}_{2}=n\)
Coefficient of \(\frac{1}{{2}^{n}}{A}^{p+q}{B}^{s+u}{e}^{j{\omega }_{p,q,s,u}t}\) in fifth line of Eq. (A.5) is
such that, \({p}_{1}+{q}_{1}={n}_{1}, {p}_{2}+{q}_{2}={n}_{2}, {p}_{3}+{q}_{3}={n}_{3}\) and \({n}_{1}+{n}_{2}+{n}_{3}=n\)
Sum of all these terms coming from LHS of Eq. (A.5) will be zero as there is no such term on the RHS for n > 1. Therefore,
This gives,
Synthesis of \({H}_{2}\left(\omega ,\omega \right)\) and \({H}_{3}\left(\omega ,\omega ,\omega \right)\) for damping nonlinearity with square and cubic terms.
If coefficients of nonlinear stiffness \({k}_{2}={k}_{3}=0\) then, Eq. (A.9) becomes
Appendix-B: List of Symbols
The symbols and description listed in “List of symbols”.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Chintha, H.P., Chatterjee, A. Identification and Parameter Estimation of Nonlinear Damping Using Volterra Series and Multi-Tone Harmonic Excitation. J. Vib. Eng. Technol. 10, 2217–2239 (2022). https://doi.org/10.1007/s42417-022-00535-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42417-022-00535-7