Identification and Parameter Estimation of Asymmetric Nonlinear Damping in a Single-Degree-of-Freedom System Using Volterra Series

Abstract

Most of the dynamic systems are inherently nonlinear either with stiffness nonlinearity or with damping nonlinearity. Presence of nonlinearity often leads to characteristic behaviours in response such as jump phenomenon, limit cycle and super-harmonic resonances. Such behviours can be accurately predicted only if the nonlinearity structure and related parameters are properly known. A majority of identification works is based on a-priori knowledge of nonlinearity structure and most of them consider only stiffness nonlinearities. Not much work has been reported on identification and parameter estimation in the area of damping nonlinearities. This paper presents a systematic classification of asymmetric damping nonlinearity and develops a parameter estimation algorithm using harmonic excitation and response amplitudes in terms of higher order Frequency Response Functions. The asymmetry in damping nonlinearity is modeled as a polynomial function containing square and cubic nonlinear terms and then Volterra series is employed to derive the response amplitude formulation for different harmonics using synthesied higher order Frequency Response Functions. Detailed numerical study is carried out with different combinations of square and cubic nonlinearity parameters to investigate appropriate excitation level and frequency so as to get measurable signal strength of second and third harmonics and at the same time keeping the Volterra series approximation error low. The estimation algorithm is first presented for nonlinear parameters and then it is extended for estimation of linear parameters including damping ratio. It is demonstrated through numerical simulation that nonlinear damping parameters can be accurately estimated with proper selection of excitation level and frequency.

Introduction

Identification of dynamic systems from input–output data has gained considerable importance in the recent past. Dynamic responses can be predicted accurately only if the system model is known in terms of its mathematical structure and physical parameters. Identification procedures of a linear dynamic system are, by now, well established. However, identification problem is more involved for a non-linear system, where it requires both; identification of the non-linearity structure as well as estimation of the parameters associated with the model. Presence of nonlinearity leads to certain response characteristics such as limit cycle, jump phenomenon, super-harmonic resonances etc. and such behaviours can be predicted only if the nonlinearity structure and related parameters are properly known. Most of the nonlinear system identification research works is based on a-priori knowledge of nonlinearity structure and the most common example is Duffing’s oscillator with cubic stiffness nonlinearity. Recently, other types of nonlinearities also such as bilinear stiffness nonlinearity due to crack initiation, damping nonlinearity in a vibration absorber or p-th power stiffness nonlinearity exhibited by rolling element bearing, have been discussed by researchers highlighting specific response characteristics.

In mechanical and structural systems, nonlinearities are generally modeled through polynomial form, though non-polynomial forms such as quadratic damping, hysteretic damping, coulomb damping, bilinear stiffness etc. (Nayfeh [1]) are also observed in the physical systems. Nayfeh [2] proposed a method to identify nonlinear character of a system, investigating presence of self-oscillatory terms or hysteresis in a free vibration test; perturbing the system about equilibrium positions. Bendat et al. [3] developed a general identification technique from measured input–output stochastic data for a wide range of nonlinearities including Duffing’s oscillator, Van-der Pol oscillator, dead band and clearance nonlinearity. Tiwari and Vyas [4] discussed procedures for estimation of nonlinear elastic parameters of rolling element bearing based on the analysis of random response signals measured from bearing housing vibration. Rice and Fitzpatrick [5] presented a spectral density approach, based on ‘reverse path analysis’, for measurement of nonlinear damping in a single-degree-of-freedom system. Balachandran et al. [6] studied free oscillation of a pair of quadratically and cubically coupled oscillators with nonlinear damping and investigated nonlinear interactions between the structural modes. The study was further extended using bispectral analysis and higher order spectra by Khan and Balachandran [7]. Bikdash et al. [8] analysed nonlinear roll dynamics of ships using Melnikov equivalent damping coefficients for linear plus quadratic damping and linear plus cubic damping. Balachandran [9] obtained analytical approximations for higher order spectra and coherence functions using Method of Multiple Scales for quadratically coupled oscillators having stiffness nonlinearity. Numerical studies were carried out to validate the analytical predictions.

Above methods belong to the class of parametric identification techniques, where sufficient a-priori information about the nonlinearity class or structure is available. The identification in such cases reduces to estimation of system parameters through a search in parametric space. Non-parametric identification concerns modeling in function space by input–output mapping, for systems where sufficient information on the mathematical structure or nonlinearity class is not known. Volterra series [10, 11], which is a functional series, has recently come up as an efficient mathematical tool for non-parametric modeling and identification of nonlinear systems. Using Volterra series, response of a general nonlinear system under harmonic excitation can be expressed in terms of first and higher order frequency response functions (FRFs). Chatterjee and Vyas [12, 13] developed a parameter estimation algorithm based on recursive iteration of first and third order Volterra kernel transforms and used it for nonlinear stiffness identification of rotor bearing system. Similarly Volterra series based nonlinear output frequency response functions (NORFRs) have been employed for response analysis and kernel identification in [14,15,16,17]. Volterra series has been also used for parameter estimation in oscillators with bilinear stiffness asymmetry [18].

Some other methods used by researchers for analysis and characterisation of response under harmonic excitation are perturbation technique [19] and Harmonic Balance Method [20]. Harmonic balance method gives the harmonic amplitudes in an implicit equation form, where as Volterra series formulates the harmonic amplitudes in an explicit series form, which is easy to compute but due to error resulting from series truncation, excitation frequency and excitation level are to be selected carefully [21]. A comprehensive survey on nonlinear system identification can be found in the review paper [22] by Noel and Kerschen.

Recently, researchers have focussed in the applictions involving symmetric and asymmetric nonlinear damping. Elliot et al. [23] studied n-th power nonlinear damping using harmonic balance method and estimated the equivalent damping that can fairly represent the nonlinear attenuation in the response amplitude. Shum [24] introduced a quadratically nonlinear viscous damping in parallel to a tuned mass damper for vibration absorber application and observed that a small nonlinear damping can significantly enhance the role of viscous damping in TMD. Habib et al. [25] considered single-degree-of-freedom system with polynomial form of nonlinear damping consisting cubic and fifth power terms and studied generation of isolated resonance curves (IRC) in the frequency response spectrum. Adhikari and Woodhouse [26] studied identification of non-viscously damped system parameters, where damping force is formulated through an integral operator. They found that the system gives nonlinear Eigen value problem with additional Eigen modes. All these works mainly considered symmetric form of damping nonlinearity. Similarly, studies on asymmetric damping nonlinearity can be found in applications involving shock absorbers, energy harvestors [27,28,29].

Thus, extensive research has been done in the area of analysis and characterisation of nonlinear systems, particularly for systems involving stiffness nonlinearity. However, very few research works are available in the area of identification and parameter estimation in systems with damping nonlinearity. A recent study discussing identification and parameter estimation of symmetric cubic damping nonlinearity can be found in [30].

The proposed work in this presentation attempts to develop a well structured methodology for identification and parameter estimation in systems with asymmetric damping nonlinearity. Here, we first present identification between symmetric and asymmetric nonlinearity structures and then asymmetric damping nonlinearity is classified from asymmetric stiffness nonlinearity (Sect. 2). In Sect. 3, nonlinear response is formulated using Volterra series and higher order FRFs, which are then synthesised for the specific case of asymmetric damping nonlinearity. In Sect. 4, dependance of signal strength and measurability of second and third harmonics on excitation frequency selection and excitation level is investigated. Simultaneously, error in Volterra series approximation of these harmonic amplitudes is also studied to find most suitable excitation frequency and excitation level. In Sect. 5, parameter estimation algorithm based on single term Volterra series is developed and procedures are presented step by step. Through numerical simulation, parameter estimation errors in both linear and nonlinear damping are studied for different excitation frequency and varying excitation level. In Sect. 6, robustness of the estimation algorithm is investigated against random error and bias error in response measurement and signature analysis in practical situations.

Mathematical Models and Harmonic Response Analysis of Nonlinear Systems

A single degree of freedom system with a general form of nonlinearity can be represented by the equation of motion,

$$m\ddot{x}\left( t \right) + F_{D} \left[ {\dot{x}\left( t \right)} \right] + F_{R} \left[ {x\left( t \right)} \right] = f\left( t \right).$$

(1)

Here F_D is the dissipative or damping force, F_R is the elastic restoring force, x(t) is the system response and f(t) is the excitation force. The nonlinearity can be present in either damping force or in restoring force or in both. It can be classified as symmetric or asymmetric nonlinearity; further as a polynomial function model (such as Duffing oscillator) or a transcendental function model (i.e., quadratic damping) or a piecewise continuous function model (such as bilinear stiffness oscillator). Thus, there exists wide variety of nonlinearities, each with its own characteristic response behaviour. Identification of the particular nonlinearity type and estimation of associated linear and nonlinear parameters are important for reliable and accurate prediction of the dynamic response. In the following presentation in this section, we first define symmetric and asymmetric nonlinearity with examples and explain how one can be distinguished from the other type. We, then study response behaviour of assymetric stiffness nonlinerity and assymetric damping nonlinearity to note the distinctions which can be used to identify an assymetric damping case.

• (a) Symmetric nonlinearity

  
  

  A system with symmetric nonlinearity will satisfy the condition,

  $$F_{D} \left[ {\dot{x}\left( t \right)} \right] = - F_{D} \left[ { - \dot{x}\left( t \right)} \right]\;{\text{and}}\;F_{R} \left[ {x\left( t \right)} \right] = - F_{R} \left[ { - x\left( t \right)} \right].$$

  (2)

  Common examples are,

  • 1.
    $${\text{Duffing's}}\;{\text{oscillator}}\;{\text{with}}\;F_{R} \left[ {x\left( t \right)} \right] = k_{1} x\left( t \right) + k_{3} x^{3} \left( t \right).$$

    (3a)
  • 2.
    $${\text{Quadratic}}\;{\text{stiffness}}\;{\text{with}}\;F_{R} \left[ {x\left( t \right)} \right] = k_{2} x\left( t \right)\left| {x\left( t \right)} \right|.$$

    (3b)
  • 3.
    $${\text{Cubic}}\;{\text{damping}}\;{\text{with}}\;F_{D} \left[ {\dot{x}\left( t \right)} \right] = c_{1} \dot{x}\left( t \right) + c_{3} \dot{x}^{3} \left( t \right).$$

    (4a)
  • 4.
    $${\text{Quadratic}}\;{\text{damping}}\;{\text{with}}\;F_{D} \left[ {\dot{x}\left( t \right)} \right] = c_{2} \dot{x}\left( t \right)\left| {\dot{x}\left( t \right)} \right|.$$

    (4b)

• (b) Asymmetric nonlinearity

  A system with asymmetric nonlinearity will satisfy the condition,

  $$F_{D} \left[ {\dot{x}\left( t \right)} \right] \ne - F_{D} \left[ { - \dot{x}\left( t \right)} \right]\;\;{\text{or}}\;\;F_{R} \left[ {x\left( t \right)} \right] \ne - F_{R} \left[ { - x\left( t \right)} \right].$$

  (5)

Common examples are,

• 1.
  $${\text{Asymmetric}}\;{\text{damping}}\;{\text{with}}\;F_{D} \left[ {\dot{x}\left( t \right)} \right] = c_{1} \dot{x}\left( t \right) + c_{2} \dot{x}^{2} \left( t \right) + c_{3} \dot{x}^{3} \left( t \right).$$

  (6)
• 2.
  $${\text{Asymmetric}}\;{\text{stiffness}}\;{\text{with}}\;F_{R} \left[ {x\left( t \right)} \right] = k_{1} x\left( t \right) + k_{2} x^{2} \left( t \right) + k_{3} x^{3} \left( t \right).$$

  (7)

• 3. Bi-linear oscillator with restoring force given by,

  $$F_{R} \left[ {x\left( t \right)} \right] = kx\left( t \right) if x\left( t \right) > 0 or F_{R} \left[ {x\left( t \right)} \right] = \alpha kx\left( t \right) if x\left( t \right) < 0 , \alpha < 1$$

  (8)
• 4.
  $${\text{Coulomb}}\;{\text{damping}}\;{\text{with}}\;F_{D} \left[ {\dot{x}\left( t \right)} \right] = \pm \mu N.$$

  (9)

• 5. Piecewise linear stiffness or Piecewise linear damping such as clearance nonlinearity, backlash or dead zone and saturation nonlinearity etc.

Nonlinearity structures in both symmetric and asymmetric groups can further be of two types. First type is nonlinearity of pure polynomial form such as given in Eqs. 3a, 4a, 6 and 7. Second type includes those which are of non-polynomial forms such as given in Eqs. 3b, 4b, 9, 10 and that of piecewise linear forms as given in type v) under asymmetric group. As long as these non-polynomial functions are continuous within the range of response amplitude and it is a case of weak nonlinearity, such non-polynomial form of nonlinearity can be approximated by a polynomial form [18]. In our present discussion we will consider nonlinearities in polynomial forms only. This consideration will provide easy sysnthesis of higher order frequency response functions using Volterra series.

Under harmonic excitation, a linear system response will have only the harmonic at excitation frequency in its response spectrum, whereas a nonlinear system will have higher harmonics also. Again, a symmetric nonlinearity will have only the odd harmonics in its response spectrum, whereas an asymmetric nonlinearity will have both even and odd harmonics. This has been well discussed in [30], and using this method of response characterisation, one can identify an asymmetric nonlinearity. However, the question still remains whether the nonlinearity is in damping or it is in the stiffness.

Identification Between Asymmetric Damping and Asymmetric Stiffness Nonlinearities

In a polynomial form of nonlinearity, asymmetry comes from the even powers of displacement or velocity. The first even power comes from the square term in the asymmetric nonlinearity model. However, we consider an extended model upto cubic term as it presents more general cases of asymmetry. We first consider asymmetric stiffness nonlinearity, for which the equation of motion, under harmonic excitation force, becomes,

$$m\ddot{x}\left( t \right) + c_{1} \dot{x}\left( t \right) + k_{1} x\left( t \right) + k_{2} x^{2} \left( t \right) + k_{3} x^{3} \left( t \right) = f\left( t \right) = A\cos \left( {\omega t} \right).$$

(10)

Here, the polynomial model is considered upto cubic term just for keeping the model simple and yet general.

Characteristic variation of harmonic response amplitude over a range of excitation frequency is computed through numerical simulation with m₁ = 1.0, k₁ = 1.0 and c₁ = 0.1 (5% damping factor). These values are selected as they represent non-dimensional or normalised values (to be discussed in section “Harmonic Probing and Nonlinear Response Analysis Using Volterra Series”). Natural frequency in normalised form becomes equal to 1. Two sets of nonlinear stiffness coefficients are considered as k₂ = 0.02, k₃ = 0.1 and k₂ = 0.05, k₃ = 0.1. The first, second and third harmonic amplitudes are fourier filtered from the numerically simulated time response x(t) and are plotted in Figs. 1 and 2 as shown below.

Fig. 1

Response harmonic amplitude for asymmetric stiffness nonlinearity, ($k_{2}$ = 0.02, $k_{3}$ = 0.1)

Fig. 2

Response harmonic amplitude for asymmetric stiffness nonlinearity ($k_{2}$ = 0.05,$k_{3}$ = 0.1)

Similarly for asymmetric damping nonlinearity, the equation of motion is considered as,

$$m\ddot{x}\left( t \right) + c_{1} \dot{x}\left( t \right) + c_{2} \dot{x}^{2} \left( t \right) + c_{3} \dot{x}^{3} \left( t \right) + k_{1} x\left( t \right) = A\cos \omega t.$$

(11)

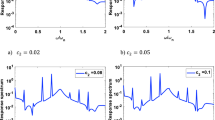
Two sets of nonlinear damping coefficients are considered as c₂ = 0.02, c₃ = 0.1 and c₂ = 0.05, c₃ = 0.1. First, second and third harmonic amplitudes, obtained from numerically simulated response, are shown in Figs. 3, 4.

Fig. 3

Response harmonic amplitudes for asymmetric damping nonlinearity, ($c_{2}$ = 0.05, $c_{3}$ = 0.1)

Fig. 4

Response harmonic amplitudes for asymmetric damping nonlinearity, ($c_{2}$ = 0.1, $c_{3}$ = 0.05)

One can clearly note that in case of stiffness nonlinearity, there occurs jump phenomenon in all the harmonics, but no such jump phenomenon is seen for damping nonlinearity. Also, the third harmonic amplitude at natural frequency is bigger than that at one-third ntural frequency for damping nonlinearity, whereas for stifness nonlinearity it is otherwise. These characteristics provide a mechanism to distinguish asymmetric damping nonlinearity from asymmetric stiffness nonlinearity.

Upto this step, we have discussed how to identify whether the system nonlinearity is an asymmetric damping nonlinearity or not. Once it is identified, next step is to estimate the nonlinear and then linear parameters in Eq. (11). Here, we use Volterra series response formulation in terms of first and higher order FRFs for approximating measured harmonic amplitudes under a single-tone harmonic excitation.

Volterra Series Based Nonlinear Response Formulation Under Harmonic Excitation

A general physical system in terms of Volterra series is represented by an input excitation force f (t) and output response x(t),

$$\begin{aligned} x\left( t \right) & = \mathop \int \limits_{ - \infty }^{\infty } h_{1} \left( {\tau_{1} } \right)f(t - \tau_{1} ){\text{d}}\tau_{1} \\ & \quad + \ldots \mathop \int \limits_{ - \infty }^{\infty } \ldots \mathop \int \limits_{ - \infty }^{\infty } h_{n} \left( {\tau_{1} ,\tau_{2} , \ldots ,\tau_{n} } \right)f\left( {t - \tau_{1} } \right) \ldots f\left( {t - \tau_{n} } \right){\text{d}}\tau_{1} \ldots {\text{d}}\tau_{n} \\ & = x_{1} \left( t \right) + x_{2} \left( t \right) + \cdots + x_{n} \left( t \right) + \cdots , \\ \end{aligned}$$

(12)

where, $h_{n} \left( {\tau_{1} ,\tau_{2} , \ldots ,\tau_{n} } \right)$ are known as nth order Volterra kernel and its Fourier Transform provides the nth order frequency response functions (FRFs) or Volterra kernel transforms as,

$$H_{n} \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right) = \mathop \int \limits_{ - \infty }^{\infty } \ldots \mathop \int \limits_{ - \infty }^{\infty } h_{n} \left( {\tau_{1} ,\tau_{2} , \ldots ,\tau_{n} } \right)\mathop \prod \limits_{i = 1}^{n} {\text{e}}^{{ - j\omega_{i} \tau_{i} }} {\text{d}}\tau_{1} \ldots {\text{d}}\tau_{n} .$$

(13)

For a harmonic excitation with $f\left( t \right) = A\cos \left( {\omega t} \right) = \frac{A}{2}{\text{e}}^{j\omega t} + \frac{A}{2}{\text{e}}^{ - j\omega t}$, the first three response components, following Eq. (11), become,

$$x_{1} \left( t \right) = \frac{A}{2}H_{1} \left( \omega \right){\text{e}}^{j\omega t} + \frac{A}{2}H_{1} \left( { - \omega } \right){\text{e}}^{ - j\omega t} ,$$

(14a)

$$x_{2} \left( t \right) = \frac{{A^{2} }}{2}H_{2} \left( {\omega , - \omega } \right) + \frac{{A^{2} }}{4}H_{2} \left( {\omega ,\omega } \right){\text{e}}^{j2\omega t} + \frac{{A^{2} }}{4}H_{2} \left( { - \omega , - \omega } \right){\text{e}}^{ - j2\omega t} ,$$

(14b)

$$\begin{aligned} x_{3} (t) & = \frac{{A^{3} }}{8}H_{3} \left( {\omega ,\omega ,\omega } \right){\text{e}}^{j3\omega t} + \frac{{3A^{3} }}{8}H_{3} \left( {\omega ,\omega , - \omega } \right){\text{e}}^{j\omega t} x\left( t \right) \\ & = x_{1} \left( t \right) + x_{2} \left( t \right) + \cdots = \mathop \sum \limits_{n = 1}^{\infty } \left( \frac{A}{2} \right)^{n} \mathop \sum \limits_{p + q = n}^{{}} {}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right){\text{e}}^{{j\omega_{p,q} t}} \\ & \quad + \frac{{3A^{3} }}{8}H_{3} \left( {\omega , - \omega , - \omega } \right){\text{e}}^{ - j\omega t} + \frac{{A^{3} }}{ 8}H_{3} \left( { - \omega , - \omega , - \omega } \right){\text{e}}^{ - j3\omega t} , \\ \end{aligned}$$

(14c)

Total response, x(t) can be then expressed as,

$$x\left( t \right) = x_{1} \left( t \right) + x_{2} \left( t \right) + \cdots = \mathop \sum \limits_{n = 1}^{\infty } \left( \frac{A}{2} \right)^{n} \mathop \sum \limits_{p + q = n}^{{}} {}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right){\text{e}}^{{j\omega_{p,q} t}} ,$$

(15)

where, $H_{n}^{p,q} \left( \omega \right) = H_{n} \left( {\underbrace {\omega ,\omega , \ldots }_{{p\;{\text{times}}}},\underbrace { - \omega , - \omega , \ldots }_{{q\;{\text{times}}}}} \right),\;\;\omega_{p,q} = \left( {p - q} \right)\omega \,\,{\text{and}}\,\,{}_{{}}^{n} C_{q} = \frac{n!}{{\left( {n - q} \right)!q!}}$.

The nonlinear response (Eq. 15) can be written in terms of various harmonic amplitudes as,

$$x\left( t \right) = X_{0} + \left| {X\left( \omega \right)} \right|\cos \left( {\omega t + \varphi_{1} } \right) + \left| {X\left( {2\omega } \right)} \right|\cos \left( {2\omega t + \varphi_{2} } \right) + \cdots ,$$

(16)

where, response amplitude of mth harmonic X(mω) can be obtained as,

$$X\left( {m\omega } \right) = \mathop \sum \limits_{i = 1}^{\infty } 2\left( \frac{A}{2} \right)^{m + 2i - 2} {}_{{}}^{m + 2i - 2} C_{i - 1} H_{m + 2i - 1}^{m + i - 1,i - 1} \left( \omega \right),$$

(17)

First, second and third harmonic amplitudes, using Eq. (17), can be expressed in a series form as,

$$X\left( \omega \right) = AH_{1} \left( \omega \right) + \frac{3}{4}A^{3} H_{3} \left( {\omega ,\omega , - \omega } \right) + \frac{5}{8}A^{5} H_{5} \left( {\omega ,\omega ,\omega , - \omega , - \omega } \right) + \cdots ,$$

(18a)

$$X\left( {2\omega } \right) = \frac{{A^{2} }}{2}H_{2} \left( {\omega ,\omega } \right) + \frac{{A^{4} }}{2}H_{4} \left( {\omega ,\omega ,\omega , - \omega } \right) + \cdots ,$$

(18b)

$$X\left( {3\omega } \right) = \frac{{A^{3} }}{4}H_{3} \left( {\omega ,\omega ,\omega } \right) + \frac{5}{16}A^{5} H_{5} \left( {\omega ,\omega ,\omega ,\omega , - \omega } \right) + \cdots .$$

(18c)

Above equations are well known already [12, 13] and presented here in brief for ease of understanding of further work, which uses Volterra series, but specific to a new nonlinearity type, i.e., asymmetric damping nonlinearity. Equations (18a–c) are general for the whole class of nonlinear systems, but become specific when we use specific sythesis of higher order FRFs in the harmonic amplitude equations. In the following section, we first derive the synthesis formula for the higher order FRFs for the specific case of asymmetric damping nonlinearity.

Synthesis of Higher Order FRFs for Asymmetric Damping Nonlinearity

Equation (15), upon differentiation, gives the series form for velocity $\dot{x}\left( t \right)$ as,

$$\dot{x}\left( t \right) = \mathop \sum \limits_{n = 1}^{\infty } \left( \frac{A}{2} \right)^{n} \mathop \sum \limits_{p + q = n}^{{}} j\omega_{p,q} {}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right){\text{e}}^{{j\omega_{p,q} t}} .$$

(19)

Substituting Eqs. (15) and (19) in Eq. (11), one obtains,

$$\begin{aligned} & \mathop \sum \limits_{n = 1}^{\infty } \left( \frac{A}{2} \right)^{n} \mathop \sum \limits_{p + q = n} {}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right){\text{e}}^{{j\omega_{p,q} t}} \left[ { - m\omega_{p,q}^{2} + k_{1} + jc_{1} \omega_{p,q} } \right] \\ & \quad + c_{2} \left[ {\mathop \sum \limits_{n = 1}^{\infty } \left( \frac{A}{2} \right)^{n} \mathop \sum \limits_{p + q = n}^{{}} j\omega_{p,q} {}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right)e^{{j\omega_{p,q} t}} } \right]^{2} \\ & \quad + c_{3} \left[ {\mathop \sum \limits_{n = 1}^{\infty } \left( \frac{A}{2} \right)^{n} \mathop \sum \limits_{p + q = n}^{{}} j\omega_{p,q} {}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right)e^{{j\omega_{p,q} t}} } \right]^{3} \\ & \quad = \frac{A}{2}{\text{e}}^{j\omega t} + \frac{A}{2}{\text{e}}^{ - j\omega t} . \\ \end{aligned}$$

(20)

Equating coefficients of $\left( \frac{A}{2} \right)^{n} {\text{e}}^{{j\omega_{p,q} t}}$ both sides in Eq. (20), n = 1, 2, 3…., one obtains,

$$H_{1} \left( \omega \right) = \frac{1}{{\left( { - m\omega^{2} + k_{1} + jc_{1} \omega } \right)}},\quad {\text{for}}\;n = {1}.$$

(21)

For n > 1,

Coefficient of $\left( \frac{A}{2} \right)^{n} {\text{e}}^{{j\omega_{p,q} t}}$ in first line of Eq. (20) gives,

$${}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right)\left[ { - m\omega_{p,q}^{2} + k_{1} + jc_{1} \omega_{p,q} } \right] = \frac{{{}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right)}}{{H_{1} \left( {\omega_{p,q} } \right)}},$$

(22)

such that, $p_{1} + q_{1} = n_{1} , p_{2} + q_{2} = n_{2} , p_{3} + q_{3} = n_{3}$ and $n_{1} + n_{2} + n_{3} = n$.

Coefficient of $\left( \frac{A}{2} \right)^{n} {\text{e}}^{{j\omega_{p,q} t}}$. in second line of Eq. (20) is

$$c_{2} \sum \left\{ {j\omega_{{p_{1} ,q_{1} }} {}_{{}}^{{n_{1} }} C_{{q_{1} }} H_{{n_{1} }}^{{p_{1} ,q_{1} }} \left( \omega \right)} \right\}\left\{ {j\omega_{{p_{2} ,q_{2} }} {}_{{}}^{{n_{2} }} C_{{q_{2} }} H_{{n_{2} }}^{{p_{2} ,q_{2} }} \left( \omega \right)} \right\},$$

(23)

such that, $p_{1} + q_{1} = n_{1} , p_{2} + q_{2} = n_{2}$ and $n_{1} + n_{2} = n$.

Coefficient of $\left( \frac{A}{2} \right)^{n} e^{{j\omega_{p,q} t}}$ in third line of Eq. (20) is,

$$c_{3} \sum \left\{ {j\omega_{{p_{1} ,q_{1} }} {}_{{}}^{{n_{1} }} C_{{q_{1} }} H_{{n_{1} }}^{{p_{1} ,q_{1} }} \left( \omega \right)} \right\}\left\{ {j\omega_{{p_{2} ,q_{2} }} {}_{{}}^{{n_{2} }} C_{{q_{2} }} H_{{n_{2} }}^{{p_{2} ,q_{2} }} \left( \omega \right)} \right\}\left\{ {j\omega_{{p_{3} ,q_{3} }} {}_{{}}^{{n_{3} }} C_{{q_{3} }} H_{{n_{3} }}^{{p_{3} ,q_{3} }} \left( \omega \right)} \right\},$$

(24)

such that, $p_{1} + q_{1} = n_{1} , p_{2} + q_{2} = n_{2} , p_{3} + q_{3} = n_{3}$ and $n_{1} + n_{2} + n_{3} = n.$

Sum of all these terms coming from LHS of Eq. (20) will be zero as there is no such term on the RHS for n > 1. Therefore,

$$\begin{aligned} & \frac{{{}_{{}}^{n} C_{q} H_{n}^{p,q} \left( \omega \right)}}{{H_{1} \left( {\omega_{p,q} } \right)}} + c_{2} \sum \left\{ {{}_{{}}^{{n_{1} }} C_{{q_{1} }} H_{{n_{1} }}^{{p_{1} ,q_{1} }} \left( \omega \right)} \right\}\left\{ {{}_{{}}^{{n_{2} }} C_{{q_{2} }} H_{{n_{2} }}^{{p_{2} ,q_{2} }} \left( \omega \right)} \right\} \\ & \quad + c_{3} \sum \left\{ {j\omega_{{p_{1} ,q_{1} }} {}_{{}}^{{n_{1} }} C_{{q_{1} }} H_{{n_{1} }}^{{p_{1} ,q_{1} }} \left( \omega \right)} \right\}\left\{ {j\omega_{{p_{2} ,q_{2} }} {}_{{}}^{{n_{2} }} C_{{q_{2} }} H_{{n_{2} }}^{{p_{2} ,q_{2} }} \left( \omega \right)} \right\}\left\{ {{}_{{}}^{{n_{3} }} C_{{q_{3} }} H_{{n_{3} }}^{{p_{3} ,q_{3} }} \left( \omega \right)} \right\} \\ \end{aligned}$$

(25)

This gives,

$$\begin{aligned} \frac{{{}_{{}}^{n} c_{q} H_{n}^{p,q} \left( \omega \right)}}{{H_{1} \left( {\omega_{p,q} } \right)}} & = - c_{2} \mathop \sum \limits_{{\begin{array}{*{20}c} {p_{i} + q_{i} = n_{i} } \\ {n_{1} + n_{2} = n} \\ \end{array} }} \left\{ {j\omega_{{p_{1} ,q_{1} }} {}_{{}}^{{n_{1} }} c_{{q_{1} }} H_{{n_{1} }}^{{p_{1} ,q_{1} }} \left( \omega \right)} \right\} \left\{ {j\omega_{{p_{2} ,q_{2} }} {}_{{}}^{{n_{2} }} c_{{q_{2} }} H_{{n_{2} }}^{{p_{2} ,q_{2} }} \left( \omega \right)} \right\} \\ & \quad - c_{3} \mathop \sum \limits_{{\begin{array}{*{20}c} {p_{i} + q_{i} = n_{i} } \\ {n_{1} + n_{2} + n_{3} = n} \\ \end{array} }} \left\{ {j\omega_{{p_{1} ,q_{1} }} {}_{{}}^{{n_{1} }} c_{{q_{1} }} H_{{n_{1} }}^{{p_{1} ,q_{1} }} \left( \omega \right)} \right\}\left\{ {j\omega_{{p_{2} ,q_{2} }} {}_{{}}^{{n_{2} }} c_{{q_{2} }} H_{{n_{2} }}^{{p_{2} ,q_{2} }} \left( \omega \right)} \right\}\left\{ {j\omega_{{p_{3} ,q_{3} }} {}_{{}}^{{n_{3} }} c_{{q_{3} }} H_{{n_{3} }}^{{p_{3} ,q_{3} }} \left( \omega \right)} \right\}. \\ \end{aligned}$$

(26)

The synthesis formulation as obtained above gives second order and third order FRFs as,

$$H_{2} \left( {\omega ,\omega } \right) = c_{2} \omega^{2} H_{1}^{2} \left( \omega \right)H_{1} \left( {2\omega } \right),$$

(27)

$$H_{3} \left( {\omega ,\omega ,\omega } \right) = H_{1}^{3} \left( \omega \right)H_{1} \left( {3\omega } \right)\left\{ {4c_{2}^{2} \omega^{4 } H_{1} \left( {2\omega } \right) + jc_{3} \omega^{3 } } \right\}.$$

(28)

Equation (27) shows that second order FRF is related to square nonlinearity parameter c₂ only and Eq. (28) shows that third order FRF is related to both c₂ and c₃. In addition they are also explicitly related to frequency ω.

Above equations simplify formulation and analysis of nonlinear response and form the basis for nonlinear parmeter estimation. In next sections, we first carry out response analysis and characterisation for systems with asymmetric damping nonlinearity, investigate the behaviours with the help of Volterra series based harmonic amplitude formulations and then study signal measurabilty and volterra series truncation error to decide appropriate excitation level and excitation frequency for estimation of nonlinear and linear parameters.

Harmonic Probing and Nonlinear Response Analysis Using Volterra Series

Equation (11) is numerically solved for a given harmonic excitation and first, second and third harmonic amplitudes are filtered out from the measured response using Fourier filtering technique. A parametric study is then carried out to investigate effect of varying nonlinear parameters on the amplitude of these harmonics. This parametric study is done with non-dimensionl form of Eq. (11) given by,

$$\eta^{\prime \prime } \left( \tau \right) + 2\xi \mathop \eta \limits \left( \tau \right) + \eta \left( \tau \right) + \beta_{2} \mathop \eta \limits^{2} \left( \tau \right) + \beta_{3} \mathop \eta \limits^{3} \left( \tau \right) = \cos \left( {\Omega \tau } \right),$$

(29)

where,

$$\begin{aligned} \eta & = \frac{x}{{X_{s} }} = \frac{x}{A/k},\;\;\Omega = \frac{\omega }{{\omega_{n} }},\;\; \tau = \omega_{n} t, \\ \frac{{\text{d}}}{{{\text{d}}t}} & = \omega_{n} \frac{{\text{d}}}{{{\text{d}}\tau }}\;\;and\;\;\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }} = \omega_{n}^{2} \frac{{{\text{d}}^{2} }}{{{\text{d}}\tau^{2} }}. \\ \end{aligned}$$

with the normalised form of nonlinear damping parameters given by,

$$\beta_{2} = \frac{{c_{2} A\omega_{n}^{2} }}{{k_{1}^{2} }}\;\;{\text{and}}\;\;\beta_{3} = \frac{{c_{3} A^{2} \omega_{n}^{3} }}{{k_{1}^{3} }}.$$

(30)

Here, all derivatives are with respect to non-dimensional time $\tau$ and frequency is represented in normalised form, $\Omega = \frac{\omega }{{\omega_{n} }}$, such that the first order FRF becomes,

$$H_{1} \left( \Omega \right) = \frac{1}{{\left( {1 - \Omega^{2} } \right) + j2\xi \Omega }}$$

(31)

Then the non-dimensional form of harmonic amplitudes given by Volterra series will be,

$$\overline{\eta }\left( \Omega \right) = H_{1} \left( \Omega \right) + \frac{3}{4}H_{3} \left( {\Omega ,\Omega , - \Omega } \right) + \frac{5}{8}H_{5} \left( {\Omega ,\Omega ,\Omega , - \Omega , - \Omega } \right) + \cdots ,$$

(32)

$$\overline{\eta }\left( {2\Omega } \right) = \frac{1}{2}H_{2} \left( {\Omega ,\Omega } \right) + \frac{1}{2}H_{4} \left( {\Omega ,\Omega ,\Omega , - \Omega } \right) + \cdots ,$$

(33)

$$\overline{\eta }\left( {3\Omega } \right) = \frac{1}{4}H_{3} \left( {\Omega ,\Omega ,\Omega } \right) + \frac{5}{16}H_{5} \left( {\Omega ,\Omega ,\Omega ,\Omega , - \Omega } \right) + \cdots .$$

(34)

Above expressions are in terms of higher order FRFs, which can be expanded in terms of first order FRF and nonlinear parameters using Synthesis formulation given in Eq. (26) to give,

$$\begin{aligned} \overline{\eta }\left( \Omega \right) & = H_{1} \left( \Omega \right)\quad + \;{\text{series}}\;{\text{first}}\;{\text{term}} \\ & \quad - \frac{1}{4}H_{1}^{3} \left( \Omega \right)H_{1} \left( { - \Omega } \right)\left\{ {\beta_{2}^{2} 4\Omega^{4 } H_{1} \left( {2\Omega } \right) + 3c_{3} j\Omega^{3 } } \right\} + \quad {\text{series}}\;{\text{second}}\;{\text{term,}} \\ \end{aligned}$$

$$\begin{aligned} & \frac{1}{{16}}\Omega ^{4} H_{1}^{4} \left( \Omega \right)H_{1}^{2} \left( { - \Omega } \right) \\ & \quad \times \left\{ {16\Omega ^{2} \beta _{2}^{4} H_{1} \left( {2\Omega } \right)\left( {2H_{1} \left( \Omega \right)H_{1} \left( {2\Omega } \right) + H_{1} \left( { - \Omega } \right)H_{1} \left( { - 2\Omega } \right) + 6H_{1} \left( {2\Omega } \right)H_{1} \left( {3\Omega } \right) - 3H_{1} \left( {3\Omega } \right)H_{1} \left( { - 2\Omega } \right)} \right)} \right. \\ & \quad + 2J\Omega \beta _{2}^{2} \beta _{3} \left( {4H_{1} \left( \Omega \right)H_{1} \left( {2\Omega } \right) - H_{1} \left( { - \omega } \right)H_{1} \left( {2\Omega } \right) + H_{1} \left( { - \Omega } \right)H_{1} \left( { - 2\Omega } \right) + 5H_{1} \left( {2\Omega } \right)H_{1} \left( {3\Omega } \right) - H_{1} \left( { - 2\Omega } \right)H_{1} \left( {3\Omega } \right)} \right. \\ & \left. {\quad + 4H_{1} \left( {2\Omega } \right)^{2} - 2H_{1} \left( {2\Omega } \right)H_{1} \left( { - 2\Omega } \right)} \right)\left. { + 9\beta _{3}^{2} ( - 2H_{1} \left( \Omega \right) + H_{1} \left( { - \Omega } \right) - H_{1} \left( {3\Omega } \right))} \right\}\quad {\text{series}}\,\,{\text{third}}\;{\text{term}} \\ \end{aligned}$$

(35)

$$\overline{\eta }\left( {2\Omega } \right) = \frac{1}{2}\beta_{2} \Omega^{2 } H_{1}^{2} \left( \Omega \right)H_{1} \left( {2\Omega } \right)\quad {\text{series}}\;{\text{first}}\;{\text{term}}$$

$$\begin{aligned} & - \frac{3}{4}\Omega^{5} \beta_{2} H_{1}^{3} \left( \Omega \right)H_{1} \left( { - \Omega } \right)H_{1} \left( {2\Omega } \right) \\ & \quad \times \left\{ {\left( {\frac{4}{3}\Omega \beta_{2}^{2} H_{1} \left( \Omega \right) + 4\Omega \beta_{2}^{2} H_{1} \left( {3\Omega } \right) + 2jc_{3} } \right)H_{1} \left( {2\Omega } \right) + j\beta_{3} \left( {H_{1} \left( \Omega \right) + H_{1} \left( {3\Omega } \right)} \right)} \right\}\quad {\text{series}}\;{\text{second}}\;{\text{term,}} \\ \end{aligned}$$

(36)

$$\begin{aligned} \overline{\eta }\left( {3\Omega } \right) & = \frac{1}{4}H_{1}^{3} \left( \Omega \right)H_{1} \left( {3\Omega } \right)\left\{ {\beta_{2}^{2} 4\Omega^{4 } H_{1} \left( {2\Omega } \right) + \beta_{3} j\Omega^{3 } } \right\}\quad {\text{series first term}} \\ & \quad - \frac{1}{16}\Omega^{6} H_{1}^{4} \left( \Omega \right)H_{1} \left( { - \Omega } \right)H_{1} \left( {3\Omega } \right) \\ & \quad \times \left\{ {16\Omega^{2} \beta_{2}^{4} H_{1} \left( {2\Omega } \right)\left( {12H_{1} \left( {4\Omega } \right)H_{1} \left( {3\Omega } \right) + 2 H_{1} \left( {4\Omega } \right)H_{1} \left( {2\Omega } \right) + 3 H_{1} \left( \Omega \right)H_{1} \left( {2\Omega } \right) + 6H_{1} \left( {3\Omega } \right)H_{1} \left( {2\Omega } \right)} \right)} \right. \\ & \quad + 12J\Omega \beta_{2}^{2} \beta_{3} \left( {4 H_{1} \left( {4\Omega } \right) H_{1} \left( {3\Omega } \right) + 4 H_{1} \left( {4\Omega } \right) H_{1} \left( {2\Omega } \right) + 4 H_{1} \left( {2\Omega } \right)H_{1} \left( \Omega \right) + 8 H_{1} \left( {3\Omega } \right)H_{1} \left( {2\Omega } \right) + 5H_{1} \left( {2\Omega } \right)^{2} } \right) \\ & \quad \left. { - 9\beta_{3}^{2} (H_{1} \left( \Omega \right) + 2H_{1} \left( {3\Omega } \right))} \right\}\quad {\text{series}}\;{\text{second}}\;{\text{term}}{.} \\ \end{aligned}$$

(37)

For weakly nonlinear system, values of nonlinear parameters, β₂ and β₃ will generally be very small and can be controlled by excitation force magnitude (Eq. 30). For small parametric values, we can simplify the series expressions given in Eqs. (35)–(37), truncating them to their first term only as given below,

$$\overline{\eta }\left( \Omega \right) \approx \overline{\eta }_{1} \left( \Omega \right) = H_{1} \left( \Omega \right),$$

(38)

$$\overline{\eta }\left( {2\Omega } \right) \approx \frac{1}{2}H_{2} \left( {\Omega ,{\Omega }} \right) = \frac{1}{2}\beta_{2} {\Omega }^{2} H_{1}^{2} \left( {\Omega } \right)H_{1} \left( {2\Omega } \right),$$

(39)

$$\overline{\eta }\left( {3\Omega } \right) \approx \frac{1}{4}H_{3} \left( {{\Omega },{\Omega },{\Omega }} \right) = \frac{1}{4}H_{1}^{3} \left( \Omega \right)H_{1} \left( {3\Omega } \right)\left\{ {\beta_{2}^{2} 4\Omega^{4 } H_{1} \left( {2\Omega } \right) + \beta_{3} j\Omega^{3 } } \right\}.$$

(40)

Single term approximation of above amplitude series expressions, help to simplify the mathematical and computational work but this introduces a truncation error which will be higher for higher parametric values. Smaller values of β₂ and β₃ will keep the error negligible but then second and third harmonic amplitudes will be much smaller than first harmonic amplitude and may not be distinctly measurable or visible in the response spectrum. This calls for a parametric response analysis to design or select proper excitation force level and excitation frequency range, so that error in Volterra series truncation is sufficiently small and yet the signal strength of second and third harmonic are good enough to be measurable.

Measurability Study and Characteristic Dependance of Harmonic Amplitudes on Nonlinear Parameters

A fundamental problem associated with experimental measurements in a nonlinear system is that the measured signal strength of higher harmonics are often much smaller and can get easily overlooked or immersed in the baseline noise spectrum. As given above, Eq. (39) shows that the signal strength of second harmonic with respect to first harmonic will be of the order of the nonlinear parameter, β₂, which will generally be very small; of the same order as nonlinear damping coefficient, c₂. Similarly Eq. (40) shows that third harmonic amplitude with respect to first harmonic will be of the order of nonlinear parameter, β₃. We can use these equations to get an approximate idea of measurability of second and third harmonics, but the approximation error will be much higher near the resonant frequency (this will be discussed through Figs. 11, 12, 13 and 14 in next Sect. 4.2). To get better quantitative values of measurability of higher harmonics, a set of numerical simulations are carried out by considering a range of nonlinear parameters over a frequency range of $\Omega$ = 0.3 to 1.6 and harmonic amplitudes, $\overline{\eta }\left( \Omega \right)$, $\overline{\eta }\left( {2\Omega } \right)$ and $\overline{\eta }\left( {3\Omega } \right)$, are filtered out from the measured response. The excitation level, A, (which indirectly controls the value of nonlinear parameter $\beta_{2} , \beta_{3}$ (Eq. 11), even if the damping nonlinearity parameters c₂ and c₃ remains same) is selected so that the second and third harmonic amplitude is measurable (the word ‘measurable’ used by us here mean that these harmonic amplitudes are at least greater than 1% of fundamental harmonic amplitude in low frequency zone). In Figs. 5, 6, and 7, variation in first, second and third harmonic amplitudes are plotted over the frequency range $\Omega$ = 0.3 to 1.6 for different levels of nonlinear parameters, $\beta_{2} , \beta_{3}$.

Fig. 5

Response harmonic amplitude for different values of, $\beta_{2}$ = 0.02, $\beta_{3}$ = 0.05, 0.1, 0.2

Fig. 6

Response harmonic amplitude for different values of, $\beta_{2}$ = 0.05, $\beta_{3}$ = 0.05,0.1,0.2

Fig. 7

Response harmonic amplitude for different values of, $\beta_{2}$ = 0.1, $\beta_{3}$ = 0.05, 0.1, 0.2

From above figures (Figs. 5, 6, 7), some important and interesting response characteristics are observed (these characteristics are then explained with the harmonic amplitude expressions given in Eqs. (38)–(40)).

• 1. Third harmonic amplitude increases as β₃ increases and the amplitude is relatively much higher around frequencies 0.33 and 1.0 (Figs. 5(iii), 6(iii), 7(iii)). This observation is very important from the point of view of measurability of third harmonic, which indicates that to measure third harmonic amplitude, excitation frequency should be around 0.33 or 1.0. However, for final decision, error due to series truncation also needs to be considerd.

• 2. First harmonic amplitude decreases as β₃ increases (Figs. 5(i), 6(i), 7(i)).

• 3. Here β₂ has been kept constant and β₃ has been varied. So second harmonic amplitude should not have changed. But it changes and rather second harmonic amplitude decreases as β₃ increases (Figs. 5(ii), 6(ii), 7(ii)). This amplitude gets higher around the frequency 0.5 and 1.0.

Now we try to provide justification/validation of the observations on the basis of Voltera series-based harmonic amplitude expressions as given in Eqs. (38)–(40).

Explanations on Observation (i)

From Eq. (40), it can be seen that third harmonic amplitude is proportional to β₃ and hence amplitude increases as β₃ increases. Also it can be seen from the equation that third hamonic amplitude is proportional to $H_{1}^{3} \left( \Omega \right)H_{1} \left( {3\Omega } \right)$. This is the reason why the amplitude is relatively higher at $\Omega$ = 1 and at 0.33.

Explanation on Observation (ii)

The variation in First harmonic amplitude with different nonlinear parameter set can be attributed to varition in equivalent linearised damping, which depends on the contribution from nonlinear damping. Energy dissipation in one cycle of a system with damping equal to c_eq will be $\pi c_{{{\text{eq}}}} \omega X^{2}$. Now, for the system with asymmetric damping with square and cubic terms, energy dissipated in one cycle (taking first order approximation of the response as $x\left( t \right) = X\sin \omega t$ and substituting, $\omega t = \theta$) can be found to be

$$\begin{aligned} \int F_{d} {\text{d}}x & = \mathop \int \limits_{0}^{T} F_{d} \dot{x}(t){\text{d}}t = \mathop \int \limits_{0}^{T} \left( {c_{1} \dot{x}\left( t \right) + c_{2 } \dot{x}^{2} \left( t \right) + c_{3} \dot{x}^{3} \left( t \right)} \right)\dot{x}{\text{d}}t \\ & = \mathop \int \limits_{0}^{2\pi } \left( {c_{1} \omega X^{2} \cos^{2} \theta + c_{2} \omega^{2} X^{3} \cos^{3} \theta + c_{3} \omega^{3} X^{4} \cos^{4} \theta } \right){\text{d}}\theta \\ & = \pi c_{1} \omega X^{2} + \frac{3}{4}\pi c_{3} \omega^{3} X^{4} \\ \end{aligned}$$

(41)

which gives,

$$\begin{aligned} \pi c_{eq} \omega X^{2} & = \pi c_{1} \omega X^{2} + \frac{3}{4}\pi c_{3} \omega^{3} X^{4} \quad {\text{such}}\;{\text{that}} \\ c_{eq} & = c_{1} + \frac{3}{4}c_{3} \omega^{2} X^{2} , \\ \end{aligned}$$

(42)

which, in normalised form, becomes

$$\xi_{eq} = \xi + \frac{3}{8}\beta_{3} \Omega^{2} \overline{\eta }^{2} .$$

(43)

Thus with increasing β₃, equivalent linearised damping value increases and hence first harmonic amplitude decreases over the complete frequency range and significantly near the natural frequency. Equation (43) is an important result as it will help us to estimte linear damping ξ from measurement of equivalent damping ξ_eq, once nonlinear parameter β₃ is estimated.

Explanation on Observation (iii)

If we look at Eq. (39), second harmonic amplitude does not depend on β₃, and yet second harmonic is found to be decreasing with increasing β₃. This is because, with increasing β₃ harmonic amplitudes $H_{1} \left( \Omega \right)$ decreases (as explained in previous point) and that makes second harmonic to decrease.

We now present figures (Figs. 8, 9, 10) where, β₃ has been kept constant and β₂ is varied.

Fig. 8

Response harmonic amplitude for different values of, $\beta_{3}$ = 0.05, $\beta_{2}$ = 0.02, 0.05, 0.1

Fig. 9

Response harmonic amplitude for different values of, $\beta_{3}$ = 0.1, $\beta_{2}$ = 0.02, 0.05, 0.1

Fig. 10

Response harmonic amplitude for different values of, $\beta_{3}$ = 0.2, $\beta_{2}$ = 0.02, 0.05, 0.1

Following observations can be made on the characteristic variation in the harmonic amplitudes, with respect to constant β₃ and varying β₂.

• 1. Third harmonic gets bigger around frequency 0.33 and 1.0 (Figs. 8(iii), 9(iii), 10(iii)) but does not change much as β₂ varies. This can be explained by square power term of β₂ in Eq. (40) for which its contribution is much smaller.

• 2. Second harmonic amplitude increases sharply at frequency 0.5 (Figs. 8(ii), 9(ii), 10(ii)) as β₂ increases. This observation is very important for measurability of second harmonic and can be explained on the basis of Eq. (39)

• 3. First harmonic amplitude has no significant change as β₂ varies (Figs. 8(i), 9(i), 10(i)). This is because equivalent linearised damping (Eq. 43) does not depend on square nonlinear parameter, β₂.

Study of Series Truncation Error in Measured Harmonic Amplitudes

Equation (29) is numerically solved for a range of nonlinear parameters and first three harmonic amplitudes are filtered out from the response. These amplitudes are then compared (Figs. 11, 12) with synthesised harmonic amplitudes as given in Eqs. (38)–(40), which are based on single-term Volterra series approximation.

Fig. 11

Comparison of measured harmonic amplitudes with single term Volterra series approximation, $\beta_{2}$ = 0.05 and $\beta_{3}$ = 0.1

Fig. 12

Comparison of measured harmonic amplitudes with single term Volterra series approximation, $\beta_{2}$ = 0.05 and $\beta_{3}$ = 0.2

From the comparison of first harmonic amplitudes in Figs. 11a, 12a, one can note that error in Volterra series approximation becomes large in frequency range 0.6 to 1.4. Hence for estimation of linear modal parameters, i.e., natural frequency and linear damping ratio, excitation frequency should be selected excluding this high error zone. For second harmonic amplitude, Volterra series approximation deviates considerably from exact value near one-half of natural frequency and natural frequency. Similarly, for third harmonic amplitude, error in Volterra series approximation grows significantly near one-third of natural frequency and natural frequency. However, these frequencies are ideal for measurement of higher harmonics as maximum measurability occurs at these frequencies as can be seen in Figs. 5, 6, 7, 8, 9 and 10. To get a better idea, error between numerically simulated value and approximated single term Volterra series value is computed in a short range of ω/ω_n = 0.3 to 0.7 in above cases and the error variations are presented in Figs. 13, 14 below.

Fig. 13

Error in single-term Volterra series approximation for second and third harmonic amplitude $\left( {\beta_{2} = { }0.05,{ }\beta_{3} = { }0.1} \right)$

Fig. 14

Error in single-term Volterra series approximation for second and third harmonic amplitude $\left( {\beta_{2} = { }0.05,{ }\beta_{3} = { }0.2} \right)$

Selection of Harmonic Excitation Level and Frequency

From Figs. 13 and 14, it can be seen that error becomes very small near the frequency ratio of 0.4 and 0.6, with 0.4 having even smaller error than 0.6. Measurability of second and third harmonics are moderately good at frequency ratio of 0.4 and 0.6, specifically 0.4 is better than 0.6 for second harmonic and 0.6 is better than 0.4 for third harmonic. Based on these factors, both 0.4 and 0.6 are recommended as the frequency ratio to be used for measurement of higher harmonic amplitudes in experimentation. The selection of excitation level can be decided from the measurability so as to get at least 1% signal strength in case of higher harmonics. We find that β₂ = 0.05 or 0.1 is good enough for second harmonic measurability and β₃ has to be preferably more than 0.05 for signal strength of third harmonic. But higher β₃ causes a serious problem of increasing effective damping in the system, which distorts both first and second harmonic amplitude values. In our proposed algorithm, we investigated estimation error for β₂ = 0.05, 0.1 and β₃ = 0.05, 0.1, 0.2 and 0.3.

Parameter Estimation Algorithm and Simulation

We first make a preliminary estimate of natural frequency, using frequency sweep test. This is the frequency at which peak amplitude occurs. This need not be exact natural frequency. Then we follow the steps one by one as given below.

Step 1: Measure first harmonic amplitude X(ω) for a series of frequencies ω/ω_n = 0.3, 0.4, 0.5, 0.6, 1.2, 1.4, 1.6 and 1.8. Frequencies close to natural frequency (except ω/ω_n = 1.2) are avoided because single-term Volterra series truncation error would be very high (Figs. 11a, 12a). For second and third harmonic measurement, excitation frequency has been selected to be 0.4 and 0.6 and since ω/ω_n = 1.2 is second harmonic for 0.6 and third harmonic for 0.4, we have to make a measurement at this frequency although it is close to natural frequency.

Step 2: Response amplitudes X(ω) are approximated as

$$\frac{X\left( \omega \right)}{A} \approx H_{1} \left( \omega \right) = \frac{1}{{\left( {k_{1} - m\omega^{2} } \right) + jc_{1} \omega }}$$

And then curve fitted [31] to obtain an initial estimate of natural frequency and linear stiffness k₁. Now excitation frequencies are adjusted with respect to estimated natural frequency to make normalised excitation frequencies $\Omega_{E} = \frac{\omega }{{\omega_{n} }}$ = 0.3, 0.4 etc. Measured first harmonic amplitudes are now converted into normalised amplitudes $\overline{\eta }\left( \Omega \right) = \frac{{k_{1} X\left( \omega \right)}}{A}$ and the fresh set of normalised amplitudes are used in curve fitting according to equation,

$$\overline{\eta }\left( \Omega \right) \approx H_{1} \left( \Omega \right) = \frac{1}{{\left( {1 - \Omega^{2} } \right) + j2\xi \Omega }}$$

which gives estimates of normalised natural frequency and equivalent damping ratio ξ_Eq. $\overline{\eta }\left( {3\Omega } \right)$.

Step 3: Measure second and third harmonic amplitudes $\overline{\eta }\left( {2\Omega } \right)$ and at the pre-decided forcing frequency ${\Omega }_{E} = \frac{\omega }{{\omega_{n} }}$ = 0.4 or 0.6.

Step 4: Make a preliminary estimate of cubic nonlinear parameter, β₃, using Eq. (40) as

$$\beta_{3} \approx \left| { - j\left( {\frac{{4 \overline{\eta }\left( {3\Omega_{E} } \right)}}{{{\Omega }^{3} H_{1}^{3} \left( {\Omega_{E} } \right)H_{1} \left( {3\Omega_{E} } \right)}}} \right)} \right|.$$

(44)

Because β₂ appears in second power in Eq. (40), its contribution in third harmonic will be very small and can be neglected. Note that we do not know linear damping ξ yet and hence can not compute the first order FRFs $H_{1} \left( {\Omega } \right) or H_{1} \left( {3{\Omega }} \right)$ at this stage. So, initially we take the help of single-term Volterra series approximation, $H_{1} \left( {\Omega } \right) \approx \overline{\eta }\left( \Omega \right)$.

Step 5: We can now estimate linear damping ξ from the estimated values of equivalent linearised damping ξ_eq and of nonlinear parameter, β₃, using Eq. (43) in the form

$$\xi = \xi_{eq} - \frac{3}{8}\beta_{3} \left( {{\Omega }_{E} } \right)^{2} \overline{\eta }^{2} ,{\text{where}}\;\overline{\eta }\;{\text{is}}\;{\text{the}}\;{\text{normalised}}\;{\text{harmonic}}\;{\text{amplitude}}\;{\text{at}}\;\Omega = \Omega_{E} .$$

Step 6: Now we compute $H_{1} \left( {\Omega } \right)\;{\text{and}}\;H_{1} \left( {3{\Omega }} \right)$ using estimated value of linear damping and substitute them back in step 4, to get refined estimate of β₃.

Step 7: Substitute back new estimate of β₃ in step 5 to get refined estimate of ξ.

This iteration in Steps 6 and 7 is continued till estimates converge to an acceptable tolerance limit. This completes estimation of ξ and β₃.

Step 8: Now we estimate square nonlinear parameter β₂, from the formula (Eq. 39)

$$\beta_{2} \approx \left| {\frac{{2\overline{\eta }\left( {2\Omega_{E} } \right)}}{{{\Omega }^{2} H_{1}^{2} \left( {\Omega_{E} } \right)H_{1} \left( {2\Omega_{E} } \right)}}} \right| = \frac{{\left| {2\overline{\eta }\left( {2\Omega_{E} } \right)} \right|}}{{{\Omega }^{2} \left| {H_{1}^{2} \left( {\Omega_{E} } \right)} \right|\left| {H_{1} \left( {2\Omega_{E} } \right)} \right|}},$$

(45)

Here $H_{1} \left( {\Omega } \right) \; \;and\;\; H_{1} \left( {2{\Omega }} \right)$. are FRF values computed using estimated linear damping ξ.

There will be error in the estimated values, which can be attributed mainly to two factors.

• 1. Error in approximation of $H_{1} \left( {\Omega } \right) \approx \overline{\eta }\left( \Omega \right)$. This error will be significantly higher for frequencies ω/ω_n in between 0.6 to 1.4 and hence we dont go for mesurement in this range except for ω/ω_n = 1.2 as explained before.

• 2. Error in single-term Volterra series approximation of second and third harmonic amplitudes. This error is relatively less around ω/ω_n = 0.4 and 0.6 and hence these two frequencies are selected here as excitation frequency for maesurement of higher harmonic amplitudes. Measurability wise 0.6 is a better frequency than 0.4, but as we will see later, estimation error is also higher at this frequency.

Estimation Results from Numerical Simulation

Numerical simulation is carried out with normalised values of modal parameters, ${\Omega }_{n}$ = 1.0 and linear damping ξ = 0.05. A range of values are considered for nonlinear parameters; β₂ = 0.05 and 0.1 and β₃ = 0.05, 0.1, 0.2 and 0.3.

For illustration, we show step by step numerical results for a typical case of β₂ = 0.05 and β₃ = 0.1 at excitation frequency ω/ω_n = 0.6. Measured harmonic amplitudes are given in Table 1 and curvefitting based on first harmonic amplitudes is shown in Fig. 15 below.

Table 1 Harmonic amplitudes (β₂ = 0.05, β₃ = 0.1 and ω/ω_n = 0.6)

Fig. 15

Curve fitting of first order FRF from measured harmonic amplitude, $\beta_{2}$ = 0.05, $\beta_{3}$ = 0.1 at ω/ω_n = 0.6

Curve fitting (shown in Fig. 15) gives ω_n = 1.0357 and ξ_eq = 0.0699,

$${\text{Step}}\;{4}\;{\text{gives}}\;\;\beta_{3} = \frac{{4X\left( {1.8} \right)}}{{\Omega_{E}^{3} H_{1}^{3} \left( {0.6} \right)H_{1} \left( {1.8} \right)}} \approx \frac{4 \times 0.00834}{{0.6^{3} \times 1.5565^{3} \times 0.4507}} = 0.0910,$$

$${\text{Step}}\;{5}\;{\text{gives}}\;\;\xi = \xi_{eq} - \frac{3}{8}\beta_{3} \left( {\frac{{\omega_{E} }}{{\omega_{n} }}} \right)^{2} \overline{\eta }^{2} = 0.0699 - \frac{3}{8} \times 0.091 \times 0.6^{2} \times 1.5565^{2} = 0.040.$$

Computation of first order FRF with this estimated linear damping gives H₁(0.6) = 1.5581 and H₁(1.8) = 0.445. Substituting in step 4 gives β₃ = 0.0917.

Step 5 gives ξ = 0.0402. Another iteration gives same value and we stop here.

To estimate β₂ now, we first find H₁(1.2) = 2.220 using ξ = 0.0402. Then Step 8 gives

$$\beta_{2} = \frac{{2X\left( {2\omega } \right)}}{{\Omega_{E}^{2} H_{1}^{2} \left( \omega \right)H_{1} \left( {2\omega } \right)}} = \frac{2 \times 0.0414}{{0.6^{2} \times 1.5581^{2} \times 2.220}} = 0.0427.$$

In the same manner, estimation is made for all combinations and results are summarized in Tables 2, 3, 4, and 5.

Table 2 Estimated values of nonlinear parameters for varying β₃ with β₂ = 0.05, $\Omega_{E}$ = 0.6

Table 3 Estimated values of nonlinear parameters for varying β₃ with β₂ = 0.1 $\Omega_{E}$, = 0.6

Table 4 Estimated values of nonlinear parameters for varying β₃ with β₂ = 0.05, $\Omega_{E}$ = 0.4

Table 5 Estimated values of nonlinear parameters for varying β₃ with β₂ = 0.1, $\Omega_{E}$ = 0.4

Analysis and Observations from Estimation Results

Figures 16, 17, 18 and 19 show comparisons both on measurability count and estimation error count.

Fig. 16

Harmonic amplitude for varying nonlinear parameters,$\beta_{2}$ and $\beta_{3}$ (${\Omega }_{E}$ = 0.4)

Fig. 17

Harmonic amplitude for varying nonlinear parameters,$\beta_{2}$ and $\beta_{3}$ (${\Omega }_{E}$ = 0.6)

Fig. 18

Estimation error in nonlinear parameters,$\beta_{2}$ and $\beta_{3}$ (${\Omega }_{E}$ = 0.4)

Fig. 19

Estimation error in nonlinear parameters,$\beta_{2}$ and $\beta_{3}$ (${\Omega }_{E}$ = 0.6)

From above figures, one can see that excitation frequency 0.4 gives better estimation (within 10%) for both the nonlinear parmeters, whereas, frequency of 0.6 gives higher estimation error, which is reasonably around 10% for β₃ = 0.1 but error increases sharply for higher β₃. So finally one has to decide between two cases. Either to set excitation frequency at 0.4 and then to set excitation level so as to make β₃ as much as 0.2, or set excitation frequency at 0.6 and then set excitation level so as to make β₃ maximum 0.1. Among these two cases, which ever gives better measurability, is to be adopted for estimation.

Robustness of the Estimation Algorithm in Presence of Random and Bias Errors

The numerical results presented so far did not consider a possible error, which can very well occur in the measurement of response amplitudes and frequency values, while doing spectrum analysis. It has been emphasised before that for weak nonlinearity, signal strength of second and third harmonic will be much less compared to overall response amplitude and therefore accurate amplitude measurement of these higher harmonics will become difficult in presence of noise, if noise magnitude is also of the same order as signal strength of these higher harmonics. To study the possible effect of measurement errors on the accuracy of parameter estimation, further numerical simulations are carried out in this section introducing two types of errors in the estimation procedure.

Case I: Presence of Random noise in measured response x(t). This error may be due to background vibration or other ambient conditions. We consider here white Gaussian noise with a noise to signal ratio of 2% (this means ratio of respective rms values).

Case II: Bias error occurring in frequency measurement of excitation as well as response harmonics in FFT spectrum.

Investigation of Effect of Random Noise in Response Measurement (Case I)

Here to simulate a random noise in MATLAB, a Gaussian random data set is first created using RAND command and the data set is adjusted in magnitude to have its mean value zero with rms value 2% of rms of the response amplitude in each case. This simulates the random noise data which is added with simulated response x(t) and then the noisy response data is submitted for signature analysis to obtain the harmonic amplitudes. Due to presence of noise, measured harmonic amplitudes at First, Second and Third harmonics will have different values now than when noise was not considered. Numerical simulation is done for a typical set of nonlinear parameters; β₂ = 0.05 and β₃ = 0.1. Figure 20a shows both of the response and noise signal on the same plot (for 2% noise to signal ratio) for excitation frequency $\frac{{\omega_{E} }}{{\omega_{n} }} = 0.6$. The resulting noisy response is plotted in Fig. 20b. One can see from Fig. 21b that presence of noise is not dominantly visible in the time history plot, but still this much of noise will affect our signature analysis. This can be seen from Table 6, where response harmonic amplitudes under ten different sets of noisy data from repeated response simulation are presented along with the mean amplitude values and harmonic amplitudes in noise free response for comparative study. It can be seen that noise has more effect on second and third harmonic amplitude values than on first harmonic amplitude. This is obvious because, first harmonic amplitude is much larger (almost 50 times noise signal), whereas second harmonic amplitude is of the same order as noise signal and third harmonic amplitude is rather smaller than the noise signal. This observation once again emphasises the importance of measurability and signal strengthening which has been discussed in Sect. 4.1.

Fig. 20

Time history plot of response without and with 2% random noise

Fig. 21

Scattering of estimation errors in nonlinear parameters under different noise samples

Table 6 Harmonic amplitudes measured in presence of 2% random noise. Ω_E = 0.6

Now with each set of measured harmonic amplitudes, nonlinear parameter estimation is carried out using the same step by step procedure and the estimates with error values are presented in Table 7 below.

Table 7 Error in estimated nonlinear parameters with and without random noise

The scattering of estimation error for different noise samples is shown in Fig. 21a, b. The scattering is less around the mean value for nonlinear parameter, β₂ but it is relatively much higher for the parameter, β₃. This can again be explained by the fact that third harmonic amplitude was a weaker signal here compared to noise level. However, the average taken over a sample size of 10 data sets for random noise, the estimate is quite close to that of noise free case for both the nonlinear parameters. The presence of noise will give slightly higher error in estimates (15.2% compared to 14.6% for β₃ and 9.1% compared to 8.3% for β₂). One may consider increasing the excitation level so as to enhance signal strength of third harmonic to reduce the impact of noise. It will reduce the scattering band but average value will be higher as noise free estimation error itself will increase at higher excitation values. Since it is a random noise, averaging is the best option that can be suggested here.

Investigation of Effect of Bias Error in Harmonic Amplitude Measurement (Case II)

Here, we will consider two sources of bias error. First, the error in excitation frequency measurement, which may be due to instrumental error in its display resolution counter. Second source of error can be attributed to frequency resolution gap in a FFT spectrum. When we do signature analysis we do not get amplitude at every frequency value as a continuous function, rather we get amplitudes at discrete frequency points which are separated by a factor which depends on sample data bloc size and number of spectral lines in the frequency window. For example with a data bloc size of 2048, number of spectral lines can be calculated as 2048/2.56 = 800. So the spectral gap or frequancy resolution in a FFT spectrum will be Full scale frequency/800. The factor 1/800 amounts to 0.00125 or 0.125%. Considering first and second factors together we carry out the simulation, where harmonic amplitudes are measured with a frequency disturbance with $\pm 0.5\%$ and $\pm 1\%$ bias errors.

We consider effect of bias error on second and third harmonics only as first harmonic amplitude will be very little affected, similar to random error as discussed earlier. The estimation errors are listed in Table 8 below.

Table 8 Harmonic amplitudes, estimates and error under different level of bias errors

Here, one can observe that no clear trend is visible in estimation error Vs bias error. In some cases estimation is even better than noise free case. It can be concluded that on average basis, the error of estimation in presence of bias error is not significantly different from noise free estimates.

Conclusion

An identification procedure for classification of asymmetrically damped nonlinear system from other types of nonlinearities is presented. Response harmonic characteristics are studied for asymmetric damping case and Volterra series based response formulation is used to explain those characteristics. It is shown that square and cubic nonlinear parameters both can be estimated from measured values of second and third harmonic amplitudes. The parameter estimation algorithm is developed and presented through a structured step by step procedure. Numerical simulation shows that the procedure can give resonably accurate estimation if excitation level and frequencies are selected properly as per the guidelines framed. The algorithm also captures fairly good estimation of linear damping ratio through estimation of equivalent linearised damping. Finally, the algorithm is also tested for its robustness against random noise and bias error.