Introduction

Contemporarily, the identification of dynamic load and its position plays a crucial role in substantial practical engineering situations including motion of vehicle or aircraft and vibration of buildings induced by earthquake, wind or waves. There are two approaches used to identify dynamic loads: the direct way and indirect way. The direct method determines the dynamic loads by measuring apparatus, however, the dynamic loads are difficult to measure directly or even cannot be measured in many complex practical engineering situations, including push force acted on the rocket, road excitation applied to vehicle, etc. Thus, the technique of load identification, a significant indirect way to obtain dynamic loads, has been rapidly developing since the early 70s. It determines dynamic loads based on the dynamic characteristics of system and the measured responses of structure.

Currently, there are two main series of load identification method: the frequency-domain technique and the time-domain technique. The frequency-domain technique converts the kinetic equation into frequency domain to identify the loads with known information. Due to the linear relationship between the loads and responses, the identification process becomes easier, which make the identification technique developed rapidly and applied to practical engineering problems successfully. Bartlett and Flannelly [1] first employed the frequency domain technique and determined hub forces in a helicopter modal successfully. Hillary et al. [2] established the systematic frequency-domain method of load identification using measured strain as the known response information to identify the dynamic loads in frequency domain, and discussed the effect of different response parameters on identification accuracy. Starkey et al. [3, 4] found that directly inverse of frequency response function was ill conditioned near the resonance zone, and the increase of identification loads number reduced the accuracy of the identification result. Yu et al. [5] used bending moment responses of bridge modal to identify the moving vehicle axle loads in frequency domain, and evaluated two solutions of the overdetermined set of equations established in the process of load identification. Liu et al. [6] used enhanced least squares schemes and a total least-squares scheme to identify forces in the frequency domain with considering the error both in the structural response signals and the frequency response function (FRF) matrix. The frequency-domain techniques often require long enough data to do Fourier transformation or other harmonic transformation, thus the applications of these frequency-domain techniques are limited. Based on these reasons, the time-domain technique was developed. The research of time-domain technique started relatively late and still has many problems need to be solved, like the convolution between loads and responses which leads to the difficulties of mathematical process. In recent years, the time-domain technique is continually improved with further studies. Desanghere et al. [7] first introduced the modal coordinate transformation in the process of identifying the excitation and established the time-domain method for dynamic load identification. Chan et al. [8, 9] studied the moving load identification and developed a series of identification methods. Because of the noise data of measured responses and the ill-conditioned characteristic of the system, dynamic load identification is generally an ill-posed inverse problem. Choi et al. [10] used Tikhonov regularization to improve the condition of the inverse problems, and compared the efficiency of several methods which were available to select the optimal regularization parameter, including ordinary cross-validation (OCV), generalized cross-validation (GCV) and L-curve method. Beside of the Tikhonov regularization method, there have been also some traditional regularization methods, such as the truncated singular value decomposition (TSVD) [11], the modified TSVD [12], the damped singular value decomposition [13], the iterative regularization methods [14] and so on. Liu et al. [15, 16] used the shape function and moving least square fitting method to approximate the load, while the Galerkin method was adopted to overcome the influences of the noise and improve the accuracy of the dynamic load identification. Since the load identification modal relates to the positions of measurement points, many researches including those mentioned above have the same premise that the position of the dynamic load is known, which is generally not the case and needs to be identified before the reconstruction of the dynamic load. To settle this problem, Gaul et al. [17] employed a wavelet transform to determine the arrival time of the waves at different frequencies, and used an optimization method to identify the impact location. Bakari et al. [18] used the particle swarm optimization algorithm to solve the localization of the distributed impact force acting on the beam structure. Li and Lu [19] adopted a complex method to determine the location of the impact and then identify the impact history by a constrained optimization scheme. Ginsberg [20] created a sample-force-dictionary as the prior knowledge to transform the impact identification into a sparse recovery task. Zhu et al. [21, 22] studied the identification methods of dynamic load position in frequency domain and in time domain, respectively, and proposed minimum determination coefficient as the criterion in the optimization problems.

However, if the dynamic loads act in more than one position, due to the permutation and combination of the different positions, the process of dynamic load position identification costs plenty of time which would cause unknown problems during researches and practical engineering situations. Considering the factors above, this paper proposes a novel algorithm of load position identification in frequency domain, which can efficiently reduce the time of dynamic load position identification. The process of identification becomes easier due to the linear correlation between the dynamic load and the response. At a certain frequency, the dynamic loads are constants and the other loads can be obtained by one load multiplying corresponding coefficients, then a linear equation set of the coefficients can be established. By solving this equation set, the relationship of load positions can be expressed as a parameter optimization problem. In the process of computing the parameter optimization problem, many load position combinations can be excluded from the possible true position combinations, as the parameter values of these load position combinations are too large. Then only few groups of load positions need to be considered, which reduces the times of matrix inversion obviously. The high accuracy and effectiveness of the novel algorithm are successfully demonstrated through numerical simulation and identification test on the simply supported beam structure. The results indicate that under the premise of satisfying the reasonable precision, the novel algorithm can reduce the time of dynamic load position identification apparently, which is greatly beneficial to the further study of the load identification problems.

Formulation of Load Position Identification

In this section, the identification of dynamic load position is formulated by referring to the multiple-degree-of-freedom system (i.e. MDOF system) as well as other systems. The degree of freedom of this system is assumed to be L. The dynamic equilibrium equation of the MDOF system can be expressed as

$${\mathbf{M\ddot{x}}}(t){\mathbf{ + C\dot{x}}}(t){\mathbf{ + Kx}}(t){\mathbf{ = f}}(t),$$
(1)

where M, C, and K represent the mass, damping and stiffness matrixes, respectively. Their dimensions are L × L and they are supposed to be constant with respect to time t. x and f are the displacement and load vector, respectively. The dot represents the derivative with respect to time t.

Based on Fourier transform, the dynamic equilibrium equation can be transformed to

$$- \omega^{2} {\mathbf{MX}} + i\omega {\mathbf{CX + KX = F}},$$
(2)

where X and F are the response and load spectrum vector, respectively. Their dimensions are L × 1. The ω is called the circle frequency.

By introducing the frequency response function matrix, Eq. (2) can be derived as

$${\mathbf{X = HF}},$$
(3)

where

$${\mathbf{H}} = ({\mathbf{K}} - \omega^{2} {\mathbf{M}} + {\text{i}}\omega {\mathbf{C}})^{ - 1} .$$
(4)

We suppose the number of dynamic loads is \(n\) (\(2n < L\)). Now, the subscripts of true dynamic loads are assumed as \(a_{1}\), \(a_{2}\), \(a_{3}\),…, \(a_{n}\). With responses of \(n\) points, the relationship between responses and dynamic loads can be written as

$${\mathbf{X}}_{\text{I}} {\mathbf{ = H}}_{\text{I}} {\mathbf{F}}_{\text{I}} ,$$
(5)

where \({\mathbf{X}}_{\text{I}} = [X_{1} ,X_{2} , \ldots ,X_{n} ]^{\text{T}}\), \({\mathbf{F}}_{\text{I}} = [F_{{a_{1} }} ,F_{{a_{2} }} , \ldots ,F_{{a_{n} }} ]^{\text{T}}\), and

$${\mathbf{H}}_{\text{I}} = \left[ {\begin{array}{*{20}c} {H_{{1,a_{1} }} } & {H_{{1,a_{2} }} } & {H_{{1,a_{3} }} } & \cdots & {H_{{1,a_{n} }} } \\ {H_{{2,a_{1} }} } & {H_{{2,a_{2} }} } & {H_{{2,a_{3} }} } & \cdots & {H_{{2,a_{n} }} } \\ {H_{{3,a_{1} }} } & {H_{{3,a_{2} }} } & {H_{{3,a_{3} }} } & \cdots & {H_{{3,a_{n} }} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {H_{{n,a_{1} }} } & {H_{{n,a_{2} }} } & {H_{{n,a_{3} }} } & \cdots & {H_{{n,a_{n} }} } \\ \end{array} } \right]$$
(6)

where \(H_{i,j}\) represents the frequency response function at the ith point when a unit simple harmonic force is applied at the jth point.

For a certain system, the frequency response function matrix is usually given, and the responses can also be measured, so the loads can be acquired by the matrix inversion as

$${\mathbf{F}}_{\text{I}} {\mathbf{ = H}}_{\text{I}}^{ - 1} {\mathbf{X}}_{\text{I}} .$$
(7)

As the true dynamic load positions are unknown, every dynamic load positions combination \(\left\{ {z_{i} } \right\},i = 1,2, \cdots n\), can lead to a group of dynamic load values. The number of the groups is \(C_{L}^{n}\) in terms of the assumption that the \(n\) positions of dynamic loads are different to each other. In these \(C_{L}^{n}\) groups, just one group is the true dynamic load positions combination. The number \(C_{L}^{n}\) can be expressed as

$$C_{L}^{n} = \frac{L*(L - 1)* \cdots (L - n + 1)}{n*(n - 1)* \cdots *2*1}.$$
(8)

To find the true dynamic load position combination, responses of other \(n\) points are measured and represented by subscripts of \(n + 1\) to \(2n\). Like Eq. (7), the load spectrum vector can also be expressed as

$${\mathbf{F}}_{\text{II}} {\mathbf{ = H}}_{\text{II}}^{ - 1} {\mathbf{X}}_{\text{II}} ,$$
(9)

where \({\mathbf{X}}_{\text{II}} = [X_{n + 1} ,X_{n + 2} , \ldots ,X_{2n} ]^{\text{T}}\), and

$${\mathbf{H}}_{\text{II}} = \left[ {\begin{array}{*{20}c} {H_{{n + 1,a_{1} }} } & {H_{{n + 1,a_{2} }} } & {H_{{n + 1,a_{3} }} } & \cdots & {H_{{n + 1,a_{n} }} } \\ {H_{{n + 2,a_{1} }} } & {H_{{n + 2,a_{2} }} } & {H_{{n + 2,a_{3} }} } & \cdots & {H_{{n + 2,a_{n} }} } \\ {H_{{n + 3,a_{1} }} } & {H_{{n + 3,a_{2} }} } & {H_{{n + 3,a_{3} }} } & \cdots & {H_{{n + 3,a_{n} }} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {H_{{2n,a_{1} }} } & {H_{{2n,a_{2} }} } & {H_{{2n,a_{3} }} } & \cdots & {H_{{2n,a_{n} }} } \\ \end{array} } \right].$$
(10)

For each dynamic load positions combination \(\left\{ {z_{i} } \right\},i = 1,2, \cdots n\), Eqs. (7) and (9) can give two groups of dynamic load values, respectively. With avoiding the influence of symmetry, these two groups of dynamic load values are equal just in the true dynamic load positions combination. Thus, the problem of dynamic load position identification can be transformed into the optimization problem of finding the minimum difference between the two groups of equivalent dynamic loads obtained by Eqs. (7) and (9). The optimization function can be expressed as follows:

$$\delta (z_{1} ,z_{2} , \ldots ,z_{n} ) = \left\| {{\mathbf{F}}_{\text{I}} - {\mathbf{F}}_{\text{II}} } \right\|_{2}^{2} .$$
(11)

The determination coefficient \(\delta\) in Eq. (11) depends on the position variables \(\left\{ {z_{i} } \right\},i = 1,2, \cdots n\). Only when the variables happens to be the actual load positions, the coefficient \(\delta\) will take the minimum value. It can be expressed as follows:

$$\delta (a_{1} ,a_{2} , \ldots ,a_{n} ) = \hbox{min} \{ \delta \} .$$
(12)

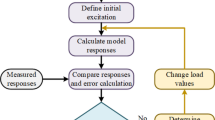
The flowchart of the traditional method to identify the load positions is shown in Fig. 1. To identify the true dynamic load position combination, the traditional method calculates \(C_{L}^{n}\) groups of the determination coefficient \(\delta\), then the minimum can be found. The position combination corresponding to the minimum determination coefficient is the true dynamic load position combination. In the whole process of identification, there are \(2C_{L}^{n}\) times of the matrix inversion which cost plenty of time and lead to much trouble in the practical operation.

Fig. 1
figure 1

The flowchart of the traditional method

Full size image

Novel Algorithm of Load Position Identification

At a certain frequency, the values of \(n\) dynamic load spectrums are constants, so the other load spectrums can be represented by the first one with corresponding scale coefficients.

$$F_{{a_{i} }} = \lambda_{i} F_{{a_{1} }} ,\;i = 2,3, \ldots ,n,$$
(13)

where \(\lambda_{2}\), \(\lambda_{3}\), \(\cdots\), \(\lambda_{n}\) are the scale coefficients corresponding to the load spectrums \(F_{{a_{2} }}\), \(F_{{a_{3} }}\),\(\cdots\),\(F_{{a_{n} }}\). Substituting Eq. (13) into Eq. (5), the relationship between responses and loads can be rewritten as

$$X_{k} = \left( {H_{{k,a_{1} }} + \sum\limits_{i = 2}^{n} {\lambda_{i} H_{{k,a_{i} }} } } \right)F_{{a_{1} }} ,k = 1,2, \ldots ,n,$$
(14)

From the first equation of the equation set (14), \(F_{{a_{1} }}\) can be expressed

$$F_{{a_{1} }} = \frac{{X_{1} }}{{(H_{{1,a_{1} }} + \sum\limits_{i = 2}^{n} {\lambda_{i} H_{{1,a_{i} }} } )}}.$$
(15)

Substituting \(F_{{a_{1} }}\) into the other equations of the equation set (14) and merging similar terms, an equation set about scale coefficients can be obtained

$${\mathbf{B = U\lambda }},$$
(16)

where \({\varvec{\uplambda}} = [\lambda_{2} ,\lambda_{3} , \ldots ,\lambda_{n} ]^{\text{T}}\), and the elements of the vector \({\mathbf{B}}\) and matrix \({\mathbf{U}}\) can be represented as follows:

$$b_{i} = X_{1} H_{{i + 1,a_{1} }} - X_{i + 1} H_{{1a_{1} }} ,i = 1,2, \ldots ,n - 1$$
(17)
$$u_{i,j} = X_{i + 1} H_{{1,a_{j + 1} }} - X_{1} H_{{i + 1,a_{j + 1} }} ,\begin{array}{*{20}c} {i = 1,2, \ldots ,n - 1} \\ {j = 1,2, \ldots ,n - 1} \\ \end{array} ,$$
(18)

As the same as Eq. (16), Eq. (9) can be expressed as

$${\mathbf{D = W\lambda }},$$
(19)

where

$$d_{i} = X_{n + 1} H_{{n + i + 1,a_{1} }} - X_{n + i + 1} H_{{n + 1a_{1} }} ,i = 1,2, \ldots ,n - 1,$$
(20)
$$w_{i,j} = X_{n + i + 1} H_{{n + 1,a_{j + 1} }} - X_{n + 1} H_{{n + i + 1,a_{j + 1} }} ,\begin{array}{*{20}c} {i = 1,2, \ldots ,n - 1} \\ {j = 1,2, \ldots ,n - 1} \\ \end{array} .$$
(21)

Through a matrix inversion of Eq. (16), the coefficient vector can be derived from

$${\mathbf{\lambda = U}}^{ - 1} {\mathbf{B}},$$
(22)

where \({\mathbf{U}}^{ - 1}\) is the inversion of the matrix \({\mathbf{U}}\), and by referring to matrix theory, the \({\mathbf{U}}^{ - 1}\) can be expressed as

$${\mathbf{U}}^{ - 1} = \frac{1}{{\left| {\mathbf{U}} \right|}}\left[ {\begin{array}{*{20}c} {U_{1,1}^{*} } & {U_{2,1}^{*} } & \cdots & {U_{n - 1,1}^{*} } \\ {U_{1,2}^{*} } & {U_{2,2}^{*} } & \cdots & {U_{n - 1,2}^{*} } \\ \vdots & \vdots & \ddots & \vdots \\ {U_{1,n - 1}^{*} } & {U_{2,n - 1}^{*} } & \cdots & {U_{n - 1,n - 1}^{*} } \\ \end{array} } \right],$$
(23)

where \(\left| {\mathbf{U}} \right|\) is the determinant of the matrix \({\mathbf{U}}\), and \(U_{i,j}^{*}\) is the algebraic complement of the element \(u_{i,j}\). \(U_{i,j}^{*}\) can be written asEquation (22) can be rewritten into an equation set form as

$$\lambda_{i + 1} = \frac{{\sum\nolimits_{j = 1}^{n - 1} {U_{j,i}^{*} b_{j} } }}{{\left| {\mathbf{U}} \right|}},\;i = 1,2, \ldots ,n - 1.$$
(24)

Through a matrix inversion of Eq. (19), the coefficients can also be expressed as

$$\lambda_{i + 1} = \frac{{\sum\nolimits_{k = 1}^{n - 1} {W_{k,i}^{*} d_{k} } }}{{\left| {\mathbf{W}} \right|}},\;\;i = 1,2, \ldots ,n - 1.$$
(25)

For Eqs. (24) and (25) with the same subscript \(i\), the right side of the two equations are equal, so a equation set reflecting the relationship of \(2n\) responses can be obtained

$$\frac{{\sum\nolimits_{j = 1}^{n - 1} {U_{j,i}^{*} b_{j} } }}{{\sum\nolimits_{k = 1}^{n - 1} {W_{k,i}^{*} d_{k} } }} = \frac{{\left| {\mathbf{U}} \right|}}{{\left| {\mathbf{W}} \right|}},\;i = 1,2, \ldots ,n - 1$$
(26)

According to the properties of the matrix, the determinant \(\left| {\mathbf{U}} \right|\) and \(\left| {\mathbf{W}} \right|\) can be expressed as

$$\left| {\mathbf{U}} \right| = \sum\limits_{j = 1}^{n - 1} {U_{j,1}^{*} u_{j,1} } ,\;\left| {\mathbf{W}} \right| = \sum\limits_{j = 1}^{n - 1} {W_{j,1}^{*} w_{j,1} } .$$
(27)

The equations of with different subscript \(i\) in the equation set (26) are similar to each other. The right side of each equation is the same function with the position variables \(a_{2}\), \(a_{3}\), \(a_{4}\),…, \(a_{n}\). The left side of each equation is the function with \(n - 1\) position variables. First, considering Eq. (26) with the subscript \(i = 1\), it can be expanded as

$$\frac{{U_{1,1}^{*} b_{1} + U_{2,1}^{*} b_{2} + \cdots + U_{n - 1,1}^{*} b_{n - 1} }}{{W_{1,1}^{*} d_{1} + W_{2,1}^{*} d_{2} + \cdots + W_{n - 1,1}^{*} d_{n - 1} }} = \frac{{U_{1,1}^{*} u_{1,1} + U_{2,1}^{*} u_{2,1} + \cdots + U_{n - 1,1}^{*} u_{n - 1,1} }}{{W_{1,1}^{*} w_{1,1} + W_{2,1}^{*} w_{2,1} + \cdots + W_{n - 1,1}^{*} w_{n - 1,1} }}.$$
(28)

From Eqs. (17) and (18), it is obvious that \(b_{i}\) and \(u_{i,1}\) (\(i = 1,2, \ldots ,n - 1\)) have the same form except that their position variables are different. \(b_{i}\) contains the position variable \(a_{1}\), while \(u_{i,1}\) contains the position variable \(a_{2}\). Thus, through replacing the position variable \(a_{1}\) with \(a_{2}\), the component \(b_{i}\) turns to \(- u_{i,1}\). The transforming situation is the same as the \(d_{i}\) and \(- w_{i,1}\).

Now a function \(S\) composed of \(n - 1\) variables is introduced. To represent the left side of Eq. (28), let the \(n - 1\) variables of \(S\) be \(a_{1}\), \(a_{3}\), \(a_{4}\),…, \(a_{n} ,\) respectively, then

$$S(a_{1} ,a_{3} ,a_{4} , \ldots ,a_{n} ) = \frac{{U_{1,1}^{*} b_{1} + U_{2,1}^{*} b_{2} + \cdots + U_{n - 1,1}^{*} b_{n - 1} }}{{W_{1,1}^{*} d_{1} + W_{2,1}^{*} d_{2} + \cdots + W_{n - 1,1}^{*} d_{n - 1} }}.$$
(29)

By transforming the position variable \(a_{1}\) in function \(S\) to \(a_{2}\), the right side of Eq. (28) can be represented by

$$S(a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} ) = \frac{{U_{1,1}^{*} u_{1,1} + U_{2,1}^{*} u_{2,1} + \cdots + U_{n - 1,1}^{*} u_{n - 1,1} }}{{W_{1,1}^{*} w_{1,1} + W_{2,1}^{*} w_{2,1} + \cdots + W_{n - 1,1}^{*} w_{n - 1,1} }}.$$
(30)

Because the left side of Eq. (28) equals to the right side, Eq. (28) can be expressed by the function \(S\) as

$$S(a_{1} ,a_{3} ,a_{4} , \ldots ,a_{n} ) = S(a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} ).$$
(31)

From Eq. (31), a relationship of the true load positions is known that the value of function \(S\) is invariable when the first variable value is transformed from \(a_{1}\) to \(a_{2} ,\) while the other \(n - 2\) variable values equal to \(a_{3}\), \(a_{4}\),…, \(a_{n} ,\) respectively.

Now, we consider Eq. (26) with the subscript \(i = 2\). By the properties of elementary matrix transformation in mathematics, it is known that the algebraic complement \(U_{i,1}^{*}\) becomes \(- U_{i,2}^{*}\) (\(i = 1,2, \ldots ,n - 1\)) by transforming the position variable \(a_{3}\) to \(a_{2}\) and at the same time \(W_{i,1}^{*}\) becomes \(- W_{i,2}^{*}\). Therefore, when the position variable \(a_{3}\) is transformed to \(a_{2}\), the left side of Eq. (28) becomes the left side of Eq. (26) with the subscript \(i = 2,\) while the right side of Eq. (26) can also be written as \(S\left( {a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} } \right)\). Like Eq. (31), Eq. (26) with the subscript \(i = 2\) can be expressed by the function \(S\) as

$$S(a_{1} ,a_{2} ,a_{4} , \ldots ,a_{n} ) = S(a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} ),\;i = 3,4, \ldots ,n - 1.$$
(32)

Similarly, Eq. (26) with the other subscripts can also be rewritten as the form of the function \(S\)

$$S(a_{1} ,a_{2} , \ldots ,a_{i} ,a_{i + 2} , \ldots ,a_{n} ) = S(a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} ),\;i = 3,4, \ldots ,n - 1.$$
(33)

Equation (31), (32) and (33) can be combined as

$$S(a_{1} ,a_{2} , \ldots ,a_{i} ,a_{i + 2} , \ldots ,a_{n} ) = S(a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} ),\;i = 1,2, \ldots ,n - 1.$$
(34)

Moving the right side to the left and taking the absolute value of the equation, Eq. (34) can be transformed to

$$\left| {S(a_{1} ,a_{2} , \ldots ,a_{i} ,a_{i + 2} , \ldots ,a_{n} ) - S(a_{2} ,a_{3} ,a_{4} , \ldots ,a_{n} )} \right| = 0,\;i = 1,2, \ldots ,n - 1.$$
(35)

The true load positions \(a_{1}\), \(a_{2}\), \(a_{3}\),…, \(a_{n}\) make Eq. (35) valid. On the contrary, the false load position combinations do not satisfy this equation generally. Therefore, the filter coefficients are introduced to determinate the true load positions from the plenty of load position combinations. The filter coefficients are expressed as follows:

$$\varepsilon_{i} (z_{1} ,z_{2} , \ldots ,z_{n} ) = \left| {S(z_{1} ,z_{2} , \ldots ,z_{i} ,z_{i + 2} , \ldots ,z_{n} ) - S(z_{2} ,z_{3} , \ldots ,z_{n} )} \right|,\;i = 1,2, \ldots ,n - 1,$$
(36)

where the \(\varepsilon_{i}\) (\(i = 1,2, \ldots ,n - 1\)) is the filter coefficient composed of the variables \(\left\{ {z_{i} } \right\},i = 1,2, \cdots n\), so they can be expressed as the form of functions like \(\varepsilon_{i} \left( {z_{1} ,z_{2} , \ldots ,z_{n} } \right)\). When the variables \(z_{1}\), \(z_{2}\), \(z_{3}\),…, \(z_{n}\) equal to true load positions \(a_{1}\), \(a_{2}\), \(a_{3}\),…, \(a_{n} ,\) respectively, the filter coefficient \(\varepsilon_{i}\) equals to zero. Therefore, we have

$$\varepsilon_{i} (a_{1} ,a_{2} ,a_{3} , \ldots ,a_{n} ) = 0,\;i = 1,2, \ldots ,n - 1.$$
(37)

Since the filter coefficient \(\varepsilon_{i}\) (\(i = 1,2, \ldots ,n - 1\)) is nonnegative, so the sum of these filter coefficients is also nonnegative. The sum can be written as

$$\varepsilon (z_{1} ,z_{2} ,z_{3} , \ldots ,z_{n} ) = \sum\limits_{i = 1}^{n - 1} {\varepsilon_{i} (z_{1} ,z_{2} ,z_{3} , \ldots ,z_{n} )}$$
(38)

The overall filter coefficient \(\varepsilon\) contains \(n\) variables. Then, Eq. (37) is equivalently expressed as

$$\varepsilon (a_{1} ,a_{2} ,a_{3} , \ldots ,a_{n} ) = 0.$$
(39)

It is known to us that the equation set has more than one set of solutions when the number of unknowns is greater than the number of equations. In view of this theory, the unique solution of Eq. (37) cannot be determined, so it is impossible to calculate the true load positions only by Eq. (36). However, Eq. (37) can help to exclude the most load position combinations which do not satisfy this equation before using the matrix inversion to identify the true load positions. Compared to all position combinations, the quantity of those combinations which satisfy Eq. (37) is so small that times of the matrix inversion can be reduced obviously. In theory, when the load position \(a_{n}\) is given, the other \(n - 1\) load positions can be determined by Eq. (37), what means that for any given \(a_{n}\), the corresponding load positions \(a_{1}\), \(a_{2}\), \(a_{3}\),…, \(a_{n - 1}\) can be found.

The novel algorithm of load position identification can be divided into four steps as follows:

Step 1. An assumption is made that the load positions satisfy \(z_{1}\) > \(z_{2}\) > \(z_{3}\) > ···> \(z_{n - 1}\) > \(z_{n}\). The values of function \(S\) about different position combinations \(\left\{ {z_{i} } \right\},i = 1,2, \ldots n\) can be obtained by the definition of \(S\) in Eq. (29). Because the function \(S\) contains \(n - 1\) variables, the function value is evaluated \(C_{L}^{n - 1}\) times.

Step 2. When a group of load positions \(z_{2}\), \(z_{3}\),…, \(z_{n}\) are assumed, the corresponding \(z_{1}\) can be determined by searching the minimum of the filter coefficient \(\varepsilon\) in the section \(\left[ {z_{2} + 1,{\text{L}}} \right]\) which means position \(z_{1}\) satisfies \(z_{2} + 1 \le z_{1} \le {\text{L}}\). Because the load position \(z_{1}\) is determined by \(z_{2}\), \(z_{3}\),…, \(z_{n}\), it can be represented as the form of function \(z_{1} (z_{2}\), \(z_{3}\),…, \(z_{n} )\). In step 2, the main operation is to compare the size of values, of which computation time is much shorter than that of matrix inversions.

Step 3. After defining the load position \(z_{1} (z_{2}\), \(z_{3}\),…, \(z_{n} )\), filter coefficient \(\varepsilon\) can be used to further filtrate the load position combinations. The second load position \(z_{2}\) can be obtained by searching the minimum of the filter coefficient \(\varepsilon\) in the section \(\left[ {z_{3} + 1,{\text{L}} - 1} \right]\). Then, \(z_{2}\) can be expressed as \(z_{2} (z_{3}\), \(z_{4}\),…, \(z_{n} )\). In a similar way, the other load positions \(z_{3}\), \(z_{4}\),…, \(z_{n - 1}\) can also be obtained by filter coefficient \(\varepsilon ,\) respectively. Due to the assumption \(z_{1}\) > \(z_{2}\) > \(z_{3}\) > ···> \(z_{n - 1}\) > \(z_{n}\), the section of \(z_{n}\) is \(\left[ {1,L - n + 1} \right]\). Thus, \(L - n + 1\) position combinations can be obtained finally.

Step 4. The \(L - n + 1\) position combinations obtained in step 3 are used to identify the true load positions by computing the corresponding determination coefficient \(\delta (z_{1}\), \(z_{2}\),…, \(z_{n} )\) and finding the minimum value. The position combination with the minimum determination coefficient \(\delta\) is the true load positions \(\left\{ {a_{i} } \right\},i = 1,2, \ldots n\).

Through the four steps mentioned above, the true dynamic load positions can be identified. The flow chart of the novel algorithm to identify the load positions is shown in Fig. 2. In process of the identification, there are many times of searching minimums which costs much short time in computer arithmetic. And a lot of position combinations are excluded by the filter coefficients. The number of position combinations which are need to compute the determination coefficients is \(\left( {L - n + 1} \right)\). This number is smaller than that of the traditional method which is \(C_{L}^{n} .\) Therefore, the true load position combination can be identified rapidly through the novel algorithm.

Fig. 2
figure 2

The flowchart of the novel algorithm

Full size image

Simulation Results

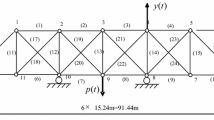
To verify the validity of the proposed algorithm, a simulation example of a beam structure is studied to illustrate the process of load position identification. The computation time and identified results of the novel algorithm are compared with those based on the traditional method. The simulation model of the Bernoulli–Euler beam with fixed ends is shown in Fig. 3.

Fig. 3
figure 3

The finite element model of a beam with fixed ends

Full size image

In this model, the length, width and height of the beam are \(l = 0.64{\text{m}}\), \(w = 0.04{\text{m}}\) and \(h = 0.01{\text{m}}\) respectively. The material of the beam has the density 7800 kg/m3, the Young’s module 210 GPa and the Poisson’s ratio 0.3. The beam is evenly divided into 640 elements and there are 641 nodes in total.

The beam is subjected to three sine loads in vertical direction with frequency \(f = 50 {\text{Hz}}\) which is shown in Fig. 4. The position of the external loads are \(x_{{a_{1} }} = 0.193 {\text{m}}\), \(x_{{a_{2} }} = 0.317 {\text{m}}\) and \(x_{{a_{3} }} = 0.409{\text{m}}\) and the corresponding amplitudes are \(F_{{a_{1} }} = 35{\text{N}}\), \(F_{{a_{2} }} = 55{\text{N}}\) and \(F_{{a_{3} }} = 75{\text{N}}\).

Fig. 4
figure 4

The load curve of the external load in \(x_{{a_{1} }}\)

Full size image

To identify the load positions, six measurement points of the response are chosen and their positions are \(x_{1} = 0.15{\text{m}}\), \(x_{2} = 0.25{\text{m}}\), \(x_{3} = 0.28{\text{m}}\), \(x_{4} = 0.31{\text{m}}\), \(x_{5} = 0.33{\text{m}}\) and \(x_{6} = 0.37{\text{m}}\). By simulation calculation, the noisy acceleration response of \(x_{1}\) in vertical direction with 5% noise levels is shown in Fig. 5, and the corresponding frequency response is shown in Fig. 6.

Fig. 5
figure 5

The acceleration of Point \(x_{1}\) in vertical direction

Full size image
Fig. 6
figure 6

The acceleration of point \(x_{1}\) in frequency domain

Full size image

To identify the load positions, the frequency–response function of the whole model is calculated. There are 641 nodes in the model and except the fixed nodes in 2 ends, the other 639 nodes all have the possibility of being an exciting point. Therefore, the degree of freedom of this system \(L\) is 639 and the number of dynamic loads \(n\) is 3.

The identified results through the traditional method and the novel algorithm are shown in Table 1 as well as the computation time of the two method. The determination coefficient curves of the two methods in the exponent are shown in Figs. 7 and 8, respectively. For ease of observation, logarithmic form of the determination coefficient is used here. The minimum determination coefficient of the traditional method is 0.8054 and its corresponding number is 28044195. The load positions represented by this number is shown in Table 1. As for the novel algorithm, the minimum determination coefficient is 0.8074, and its corresponding first load position is 0.187.

Table 1 The identified results of the simulation through two method
Full size table
Fig. 7
figure 7

The curve of determination coefficient based on the traditional method

Full size image
Fig. 8
figure 8

The curve of determination coefficient based on the novel algorithm

Full size image

From the identified results in Table 1, it is shown that both the two methods can be used to identify the effective load position from the noisy measured responses. Thus, the novel algorithm proposed in this paper is valid and steady. However, the computation time of the two methods has greater difference, and the computation time of the novel algorithm is much shorter than that of the traditional method. The time of traditional method is 248 times as long as the novel algorithm. These results demonstrate that the novel algorithm can identify the load positions more rapidly and efficiently than the traditional method and at the same time keep the identified results satisfactory.

Experimental Results

A dynamic test on a simply supported beam structure is carried out to prove the feasibility of the proposed algorithm in practical engineering situation. As shown in Fig. 9, the steel rectangular beam is simply supported at the two ends.

Fig. 9
figure 9

The experimental model of simply supported beam

Full size image

The geometric dimension of this beam is measured. The length, width and thickness are \(l = 0.695{\text{m}}\), \(w = 0.039{\text{m}}\) and \(h = 0.007{\text{m}},\) respectively. The material of this beam has the density 7800 kg/m3, the Young’s module is 210 GPa and the Poisson’s ratio is 0.3. Based on these parameters given above, the finite element model of this beam is established, evenly dividing the beam into 695 elements composed of 696 nodes.

According to the frequency response function obtained by the experiment, the finite element model of the beam is modified, and the simulation values and experiment values of the first four-order natural frequency are recorded in Table 2.

Table 2 Natural frequency of the beam (unit: Hz)
Full size table

Three sine loads are subjected on the beam structure and the frequency of the loads is \(f = 60{\text{Hz}}\). The position of the loads are \(x_{{a_{1} }} = 0.17{\text{m}}\), \(x_{{a_{2} }} = 0.38{\text{m}}\) and \(x_{{a_{3} }} = 0.56{\text{m}}\). Except the two simply supported ends, there are 694 nodes having the possible of being a load position. To identify the true load positions, the responses of six points are measured and the positions of these points are \(x_{1} = 0.204 {\text{m}}\), \(x_{2} = 0.339{\text{m}}\), \(x_{3} = 0.41{\text{m}}\), \(x_{4} = 0.485{\text{m}}\), \(x_{5} = 0.276{\text{m}}\) and \(x_{6} = 0.561{\text{m}}\). The measured response of \(x_{2}\) in time domain and in frequency domain are shown in Figs. 10 and 11, respectively.

Fig. 10
figure 10

The measured response of point \(x_{2}\) in time domain

Full size image
Fig. 11
figure 11

The measured response of point \(x_{2}\) in frequency domain

Full size image

The determination coefficient curves of the two method are shown in Figs. 12 and 13 and the corresponding identified results are recorded in Table 3. It can be seen that both the two methods can identify the load positions accurately from the measured response in the test. The minimum determination coefficient of the traditional method in the exponent is − 1.4821 and its corresponding number is 32332823. This number represents the load positions combination [0.173, 0.387, 0.556]. For the novel algorithm, the minimum value of the determination coefficient in the exponent is − 1.4375, and its corresponding first load position is 0.163 m. The other two positions are shown in Table 3.

Fig. 12
figure 12

The curve of determination coefficient of the traditional method in test

Full size image
Fig. 13
figure 13

The curve of determination coefficient of the novel algorithm in test

Full size image
Table 3 The identified results of the test through two method
Full size table

It can be found that the maximum error of the identified load positions based on the novel algorithm is 0.009 m and it exists in the second point. This error is smaller compared with the size of the sensor used in this test, so we can consider that the identified results satisfy the precision requirement of the practical engineering structure.

What are also recorded in Table 3 are the computation time of the traditional method and the novel algorithm. From Table 3, it is shown that the computation time of the novel algorithm is obviously decreased than that of the traditional method. The novel algorithm can give an approximately accurate result of identifying the load positions in a very short period of time, which brings much convenience to the load position identification in practical engineering problems. The results of this test illustrate that the novel algorithm is stable and efficient enough to identify the load positions rapidly.

Conclusion

This paper proposes a novel algorithm that can identify the multi-point dynamic load positions from measured responses in frequency domain stably and rapidly. The following main conclusions can be drawn:

  1. 1.

    The filter coefficient is introduced to filter the load position combinations before the inversion of frequency response function matrixes. In this process, many dynamic load position combinations can be found that they do not satisfy the requirement, so they can be excluded from the possible true position combinations. Compared with the traditional method, the novel algorithm only needs to sort out the true positions from a few dynamic load position combinations by searching the minimum determination coefficient.

  2. 2.

    The results of the simulation and the test both prove that the novel algorithm can identify the external loads acting on the MDOF structure accurately.

  3. 3.

    In the process of load position identification, the novel algorithm consumes much shorter computation time than that the traditional method consumes, which demonstrates that the novel algorithm is effective, accurate and rapid for solving load position identification in practical engineering problems.