1 Introduction

In engineering practice, environmental erosion or operating conditions may cause the physical properties of a system to vary over time [1]. For example, bridges with trains passing over them, rockets launching into space, and deployable and flexible aerospace structures with variable geometry are all time-varying TV structural systems [2]. The execution of dynamic load identification (DLI) on these systems is imperative for maintaining stability and safety amidst fluctuating temporal and operational conditions, thereby furnishing indispensable validation for system design. The direct quantification of dynamic loads on time-varying structural systems frequently presents challenges due to technological and measurement limitations. However, DLI methods, which utilize the analysis of structural responses, facilitate an indirect deduction of dynamic loads. These methods surmount the obstacles inherent in direct measurement and offer pragmatic solutions for tangible engineering applications. Therefore, developing a DLI method suitable for such systems is an urgent need.

DLI technology for time-invariant structural systems has been extensively developed. The main DLI methods can be classified into frequency domain method (FDM) [3, 4] and time domain method (TDM) [5, 6]. The advantage of FDM is that the input–output relationship of the system’s mathematical model in the frequency domain is linear, and the inverse operation process is easy to be handled. The advantage of TDM is that its identification result is a load time history, which can intuitively reflect the load variation over time, thus more suitable for engineering practice than FDM [7,8,9,10]. In recent years, emerging theories such as wavelet analysis, modal filter, neural network, and artificial intelligence have also provided new ideas and methods for DLI [11,12,13].

In spite of that, recent studies have rarely concerned with DLI methods for TV structural systems. The existing research only assumes that the time-varying structural parameters are constant in each micro-time unit, and identifies the load for each unit to obtain the load-time history [14, 15]. However, some drawbacks still exist in this method, which are the low computational efficiency, large computational amount, and the accuracy that is hard to guarantee. Therefore, the major task of this work is to find a DLI method for TV structural systems based on analytical solutions of differential equations.

It should be noted that ordinary differential equations with time-varying coefficients for LTV structural systems usually lack analytical solutions [16, 17]. Thus, numerical methods such as the Runge–Kutta method are often used to obtain numerical solutions to approximate the closed-form solution [18, 19]. To qualitatively analyze the solutions, the Wentzel–Kramers–Brillouin (WKB) approximation, first proposed for structural dynamics [20,21,22], provides an explicit approximation to the one-dimensional steady-state Schrödinger equation parse representation. The WKB method can solve kinetic equations with slowly varying coefficients with high accuracy and convergence [23,24,25]. To overcome the limitations of traditional numerical integration, the WKB solution and the recursive formula are derived in real functions [26, 27]. The WKB real function solution improves the computational efficiency and offers a new idea for DLI of TV structures.

This paper aims to reverse the derivation process of the recursive solution of the WKB real function and propose a novel method for dynamically identifying loads in linear time-varying (LTV) structural systems. The second section of this paper presents the fundamental process and conclusions of the recursive displacement solution using the WKB real function. In the third section, the recursive acceleration solution of the WKB real function is derived, and a relationship between acceleration response and load in time-varying structural systems is established. DLI using acceleration offers superior anti-noise performance and stability compared to displacement, which is significant in the field of DLI. The fourth section demonstrates the inverse reasoning of the recursive acceleration solution using the WKB real function, thereby obtaining the recursive load solution for time-varying structural systems. Finally, the specific steps of the inverse Wentzel–Kramers–Brillouin (IWKB) load identification method are summarized, and a comprehensive flow chart is provided. In the fifth section, the numerical simulation of the IWKB dynamic load identification method is carried out to verify the performance of the method.

2 Recursive solution of WKB real functions for LTV structural systems

Modal decomposition allows for the transformation of the vibration of a linear system, including LTV structural systems, into multiple single-degree-of-freedom (SDOF) dynamic equations expressed in modal coordinates. The dynamic equations of a SDOF LTV structural system can be represented by the following differential equations,

$$m(t)\ddot{x}(t) + c(t)\dot{x}(t) + k(t)x(t) = F(t)$$
(1)

Both sides of the upper equation are divided by \(m(t)\) at the same time, and can be obtained

$$\ddot{x}(t) + a(t)\dot{x}(t) + b(t)x(t) = f(t)$$
(2)

where \(a(t) = c(t)/m(t)\),\(b(t) = k(t)/m(t)\),\(f(t) = F(t)/m(t)\). At this point, the time-varying coefficients of the differential equations become \(a(t)\) and \(b(t)\).

In general, the rates of change of the parameters of a linear slow time-varying system are much less than that of the response solution, and the above equation can be expressed as

$$\ddot{x}(t) + a(\varepsilon t)\dot{x}(t) + b(\varepsilon t)x(t) = f(t)$$
(3)

in which \(\varepsilon (0 < \varepsilon < < 1)\) is a small coefficient that \(a(t)\) and \(b(t)\) change at the relatively slow time scale \(\tau = \varepsilon t\). Thus, the equations of motion of the above equations can be rewritten in the form of the independent time variable \(\tau\)

$$\varepsilon^{2} x^{\prime \prime } + \varepsilon a(\tau )x^{\prime } + b(\tau )x = f(\tau ,\varepsilon )$$
(4)

where \(x^{\prime} = dx/d\tau\), \(x^{\prime\prime} = d^{2} x/d\tau^{2}\), abbreviated \(x(\tau ,\varepsilon )\) as \(x\).

Since Eq. (4) has no analytical solution, an approximate solution to the real function can be obtained using the WKB method.

$$x = (e_{1} y_{1} + e_{2} y_{2} ) + \left( {y_{2} T_{1} - y_{1} T_{2} } \right)$$
(5)

Equation (5) is the form of a real function of the approximate solution of WKB, where

$$\left\{ \begin{gathered} y_{1} = \exp \left( { - \frac{1}{2}\int_{0}^{\tau } {\frac{a(\tau )}{\varepsilon }d\tau } } \right)\cos \left( {\frac{1}{\varepsilon }\int_{0}^{\tau } {h(\tau )d\tau } } \right) \hfill \\ y_{2} = \exp \left( { - \frac{1}{2}\int_{0}^{\tau } {\frac{a(\tau )}{\varepsilon }d\tau } } \right)\sin \left( {\frac{1}{\varepsilon }\int_{0}^{\tau } {h(\tau )d\tau } } \right) \hfill \\ \end{gathered} \right.$$
(6)
$$\left\{ \begin{gathered} e_{1} = x_{0} \hfill \\ e_{2} = \frac{{a(0)x_{0} + 2\varepsilon x^{\prime}_{0} }}{2h(0)} \hfill \\ \end{gathered} \right.$$
(7)
$$\left\{ \begin{gathered} T_{1} = \int_{0}^{\tau } {\frac{{y_{1} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } \hfill \\ T_{2} = \int_{0}^{\tau } {\frac{{y_{2} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } \hfill \\ \end{gathered} \right.$$
(8)

and

$$h(\tau ) = \sqrt { - \left( {\frac{{a^{2} (\tau )}}{4} + \frac{{\varepsilon a^{\prime } (\tau )}}{2} - b(\tau )} \right)}$$
(9)
$$U(\tau ) = y_{1}^{2} + y_{2}^{2} = \exp \left( { - \int_{0}^{\tau } {\frac{a(\tau )}{\varepsilon }d\tau } } \right)$$
(10)

3 Acceleration recursive solution based on approximate solution of WKB real function

3.1 Acceleration solution based on the approximate solution of the WKB real function

The pair (6) finds the first-order and second-order differentials respectively, and the obtained Eqs. (11) and (12).

$$\left\{ \begin{gathered} y^{\prime }_{1} = - \frac{a(\tau )}{{2\varepsilon }}y_{1} - \frac{h(\tau )}{\varepsilon }y_{2} \hfill \\ y^{\prime }_{2} = - \frac{a(\tau )}{{2\varepsilon }}y_{1} + \frac{h(\tau )}{\varepsilon }y_{2} \hfill \\ \end{gathered} \right.$$
(11)
$$\left\{ \begin{gathered} y^{\prime \prime }_{1} = \left( {\frac{{a^{2} (\tau )}}{{4\varepsilon^{2} }} - \frac{{a^{\prime } (\tau )}}{2\varepsilon } - \frac{{h^{2} (\tau )}}{{\varepsilon^{2} }}} \right)y_{1} + \left( {\frac{a(\tau )h(\tau )}{{\varepsilon^{2} }} - \frac{{h^{\prime } (\tau )}}{\varepsilon }} \right)y_{2} \hfill \\ y^{\prime \prime }_{2} = \left( {\frac{{a^{2} (\tau )}}{{4\varepsilon^{2} }} - \frac{{a^{\prime}(\tau )}}{2\varepsilon } - \frac{{h^{2} (\tau )}}{{\varepsilon^{2} }}} \right)y_{2} - \left( {\frac{a(\tau )h(\tau )}{{\varepsilon^{2} }} - \frac{{h^{\prime}(\tau )}}{\varepsilon }} \right)y_{1} \hfill \\ \end{gathered} \right.$$
(12)

Equation (13) can be obtained by first-order differential of Eq. (8), which reads

$$\left\{ \begin{gathered} T^{\prime }_{1} = \frac{{y_{1} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )} \hfill \\ T^{\prime }_{2} = \frac{{y_{2} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )} \hfill \\ \end{gathered} \right.$$
(13)

Similarly, Eq. (14) can be obtained by first-order differentiation of Eq. (5),

$$x^{\prime} = (e_{1} y^{\prime}_{1} + e_{2} y^{\prime}_{2} ) + \left( {y^{\prime}_{2} T_{1} + y_{2} T^{\prime}_{1} - y^{\prime}_{1} T_{2} - y_{1} T^{\prime}_{2} } \right)$$
(14)

It can be found from Eq. (13) that

$$y_{2} T^{\prime}_{1} - y_{1} T^{\prime}_{2} = 0$$
(15)

Thus, Eq. (14) can be simplified to

$$x^{\prime} = (e_{1} y^{\prime}_{1} + e_{2} y^{\prime}_{2} ) + \left( {y^{\prime}_{2} T_{1} - y^{\prime}_{1} T_{2} } \right)$$
(16)

By calculating the derivative of the Eq. (16) we can get

$$x^{\prime\prime} = (e_{1} y^{\prime\prime}_{1} + e_{2} y^{\prime\prime}_{2} ) + \left( {y^{\prime\prime}_{2} T_{1} + y^{\prime}_{2} T^{\prime}_{1} - y^{\prime\prime}_{1} T_{2} - y^{\prime}_{1} T^{\prime}_{2} } \right)$$
(17)

It is easy to deduce from Eqs. (10), (11), and (13) that

$$y^{\prime}_{2} T^{\prime}_{1} - y^{\prime}_{1} T^{\prime}_{2} = \frac{f(\tau ,\varepsilon )}{{\varepsilon^{2} }}$$
(18)

The substitution of (11), (12), (13) into the Eq. (17), and combined with the Eq. (10) is arrived at

$$x^{\prime\prime} = (e_{1} y^{\prime\prime}_{1} + e_{2} y^{\prime\prime}_{2} ) + \left( {y^{\prime\prime}_{2} T_{1} - y^{\prime\prime}_{1} T_{2} } \right) + \frac{f(\tau ,\varepsilon )}{{\varepsilon^{2} }}$$
(19)

Equation (19) is about the acceleration solution of \(\tau\).

Further, it is known from Eq. (4) that

$$\ddot{x} = \frac{{d^{2} x}}{{dt^{2} }} = \varepsilon^{2} \frac{{d^{2} \varepsilon }}{{dt^{2} }} = \varepsilon^{2} x^{\prime\prime}$$
(20)

3.2 Acceleration time recursive solution based on WKB real function approximate solution

The time step of the recurrence formula is \(\tau\), which is a small constant. It can be derived from Eq. (19) that

$$x^{\prime\prime}(\tau + \Delta \tau ) = \left( {e_{1} - T_{2} (\tau + \Delta \tau )} \right)y^{\prime\prime}_{1} (\tau + \Delta \tau ) + \left( {e_{2} + T_{1} (\tau + \Delta \tau )} \right)y^{\prime\prime}_{2} (\tau + \Delta \tau ) + \frac{f(\tau + \Delta \tau ,\varepsilon )}{{\varepsilon^{2} }}$$
(21)

It can also be derived from Eq. (12) that

$$\left\{ \begin{gathered} y^{\prime\prime}_{1} (\tau + \Delta \tau ) = \left( {\frac{{a^{2} (\tau + \Delta \tau )}}{{4\varepsilon^{2} }} - \frac{{a^{\prime}(\tau + \Delta \tau )}}{2\varepsilon } - \frac{{h^{2} (\tau + \Delta \tau )}}{{\varepsilon^{2} }}} \right)y_{1} (\tau + \Delta \tau )\\ + \left( {\frac{a(\tau + \Delta \tau )h(\tau + \Delta \tau )}{{\varepsilon^{2} }} - \frac{{h^{\prime}(\tau + \Delta \tau )}}{\varepsilon }} \right)y_{2} (\tau + \Delta \tau ) \hfill \\ y^{\prime\prime}_{2} (\tau + \Delta \tau ) = \left( {\frac{{a^{2} (\tau + \Delta \tau )}}{{4\varepsilon^{2} }} - \frac{{a^{\prime}(\tau + \Delta \tau )}}{2\varepsilon } - \frac{{h^{2} (\tau + \Delta \tau )}}{{\varepsilon^{2} }}} \right)y_{2} (\tau + \Delta \tau ) \\- \left( {\frac{a(\tau + \Delta \tau )h(\tau + \Delta \tau )}{{\varepsilon^{2} }} - \frac{{h^{\prime}(\tau + \Delta \tau )}}{\varepsilon }} \right)y_{1} (\tau + \Delta \tau ) \hfill \\ \end{gathered} \right.$$
(22)

According to Eq. (6), only \(y_{1} (\tau + \Delta \tau )\) and \(y_{2} (\tau + \Delta \tau )\) contains the integral terms in Eq. (22), such that we can get

$$\begin{aligned} y_{1} (\tau + \Delta \tau ) = & \exp \left( { - \frac{1}{2}\int_{0}^{{\tau + \Delta \tau }} {\frac{{a(\tau )}}{\varepsilon }d\tau } } \right)\cos \left( {\frac{1}{\varepsilon }\int_{0}^{{\tau + \Delta \tau }} {h(\tau )d\tau } } \right) \\ = & \exp \left( { - \frac{1}{2}\int_{0}^{\tau } {\frac{{a(\tau )}}{\varepsilon }d\tau } } \right)\exp \left( { - \frac{1}{2}\int_{{\Delta \tau }}^{{\tau + \Delta \tau }} {\frac{{a(\tau )}}{\varepsilon }d\tau } } \right)\cos \left( {\frac{1}{\varepsilon }\int_{0}^{\tau } {h(\tau )d\tau + \frac{1}{\varepsilon }\int_{{\Delta \tau }}^{{\tau + \Delta \tau }} {h(\tau )d\tau } } } \right) \\ = & \exp \left( { - \frac{1}{2}\int_{0}^{\tau } {\frac{{a(\tau )}}{\varepsilon }d\tau } } \right)\left( {\cos \left( {\int_{{\Delta \tau }}^{{\tau + \Delta \tau }} {\frac{{h(\tau )}}{\varepsilon }d\tau } } \right)y_{1} (\tau ) - \sin \left( {\int_{{\Delta \tau }}^{{\tau + \Delta \tau }} {\frac{{h(\tau )}}{\varepsilon }d\tau } } \right)y_{2} (\tau )} \right) \\ \end{aligned}$$
(23)

The variations of \(a(\tau )\) and \(h(\tau )\) in Eq. (23) falling into the interval \(\left[ {\tau ,\tau + \Delta \tau } \right]\) are relatively small, thus the above equation can be approximated as follows,

$$\begin{aligned} y_{2} (\tau + \Delta \tau ) = & \exp \left( { - \frac{{\left( {a(\tau ) + a(\tau + \Delta \tau )} \right)\Delta \tau }}{{4\varepsilon }}} \right) \\ & \left( {\cos \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{{2\varepsilon }}} \right)y_{1} (\tau ) + \sin \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{{2\varepsilon }}} \right)y_{2} (\tau )} \right) \\ \end{aligned}$$
(24)

Substituting Eq. (24) into Eq. (23), we can get

$$\begin{aligned} y_{1} (\tau + \Delta \tau ) = & \exp \left( { - \frac{{\left( {a(\tau ) + a(\tau + \Delta \tau )} \right)\Delta \tau }}{{4\varepsilon }}} \right) \\ & \left( {\cos \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{{2\varepsilon }}} \right)y_{1} (\tau ) - \sin \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{{2\varepsilon }}} \right)y_{2} (\tau )} \right) \\ \end{aligned}$$
(25)

Similarly, the expression for \(y_{2} (\tau + \Delta \tau )\) can be obtained as

$$\begin{aligned} y_{2} (\tau + \Delta \tau ) &= \exp \left( { - \frac{{\left( {a(\tau ) + a(\tau + \Delta \tau )} \right)\Delta \tau }}{{4\varepsilon }}} \right) \\ &\quad \left( \begin{gathered} \cos \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{{2\varepsilon }}} \right)y_{1} (\tau ) + \sin \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{{2\varepsilon }}} \right)y_{2} (\tau ) \hfill \\ \end{gathered} \right), \end{aligned}$$
(26)
$$\left\{ \begin{gathered} T_{1} (\tau + \Delta \tau ) = \int_{0}^{\tau } {\frac{{y_{1} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } + \int_{\tau }^{\tau + \Delta \tau } {\frac{{y_{1} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } = T_{1} (\tau ) + \int_{\tau }^{\tau + \Delta \tau } {\frac{{y_{1} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } \hfill \\ T_{2} (\tau + \Delta \tau ) = \int_{0}^{\tau } {\frac{{y_{2} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } + \int_{\tau }^{\tau + \Delta \tau } {\frac{{y_{2} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } = T_{2} (\tau ) + \int_{\tau }^{\tau + \Delta \tau } {\frac{{y_{2} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau } \hfill \\ \end{gathered} \right.$$
(27)

The integral term in Eq. (27) can also be approximated as follows,

$$\left\{ \begin{gathered} \int_{\tau }^{\tau + \Delta \tau } {\frac{{y_{1} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau \approx \frac{\Delta \tau }{{2\varepsilon }}\left( {\frac{{y_{1} (\tau )f(\tau ,\varepsilon )}}{h(\tau )U(\tau )} + \frac{{y_{1} (\tau + \Delta \tau )f(\tau + \Delta \tau ,\varepsilon )}}{h(\tau + \Delta \tau )U(\tau + \Delta \tau )}} \right)} \hfill \\ \int_{\tau }^{\tau + \Delta \tau } {\frac{{y_{2} f(\tau ,\varepsilon )}}{\varepsilon h(\tau )U(\tau )}d\tau \approx \frac{\Delta \tau }{{2\varepsilon }}\left( {\frac{{y_{2} (\tau )f(\tau ,\varepsilon )}}{h(\tau )U(\tau )} + \frac{{y_{2} (\tau + \Delta \tau )f(\tau + \Delta \tau ,\varepsilon )}}{h(\tau + \Delta \tau )U(\tau + \Delta \tau )}} \right)} \hfill \\ \end{gathered} \right.$$
(28)

where

$$\begin{aligned} U(\tau + \Delta \tau ) & = \exp \left( { - \int_{0}^{\tau + \Delta \tau } {\frac{a(\tau )}{\varepsilon }d\tau } } \right) = U(\tau )\exp \left( { - \int_{\tau }^{\tau + \Delta \tau } {\frac{a(\tau )}{\varepsilon }d\tau } } \right)\\ & = U(\tau )\exp \left( { - \frac{{\left( {a(\tau ) + a(\tau + \Delta \tau )} \right)\Delta \tau }}{2\varepsilon }} \right) \end{aligned}$$
(29)

Substituting Eqs. (22) to (29) into Eq. (21), the recursive expression of the acceleration response can be obtained.

$$\begin{aligned} x^{\prime\prime}(\tau + \Delta \tau ) = & \left( {e_{1} y^{\prime\prime}_{1} (\tau + \Delta \tau ) + e_{2} y^{\prime\prime}_{2} (\tau + \Delta \tau )} \right) + \left( {y^{\prime\prime}_{2} (\tau + \Delta \tau )T_{1} (\tau ) - y^{\prime\prime}_{1} (\tau + \Delta \tau )T_{2} (\tau )} \right) \\ & \; + \frac{{\Delta \tau }}{{2\varepsilon }}\frac{{y^{\prime\prime}_{2} (\tau + \Delta \tau )y_{1} (\tau ) - y^{\prime\prime}_{1} (\tau + \Delta \tau )y_{2} (\tau )}}{{h(\tau )U(\tau )}}f(\tau ,\varepsilon ) \\ & \; + \left( {\frac{{\Delta \tau }}{{2\varepsilon }}\frac{{y^{\prime\prime}_{2} (\tau + \Delta \tau )y_{1} (\tau + \Delta \tau ) - y^{\prime\prime}_{1} (\tau + \Delta \tau )y_{2} (\tau + \Delta \tau )}}{{h(\tau + \Delta \tau )U(\tau + \Delta \tau )}} + \frac{1}{{\varepsilon ^{2} }}} \right)f(\tau + \Delta \tau ,\varepsilon ) \\ \end{aligned}$$
(30)

In addition, the application of this recursive formula also requires the initial values of \(y_{1}\), \(y_{2}\), \(U\), \(T_{1}\) and \(T_{2}\) at \(\tau = 0\), and these values can be directly given according to their respective expressions

$$\begin{gathered} y_{1} (0) = 1 \hfill \\ y_{2} (0) = 0 \hfill \\ U(0) = 1 \hfill \\ T_{1} (0) = T_{2} (0) = 0 \hfill \\ \end{gathered}$$
(31)

4 IWKB dynamic load identification method using acceleration response

It can be seen from the above analysis that only \(T_{1}\), \(T_{2}\), and \(f\) in Eq. (19) are related to the load. By expanding Eq. (21) and merging similar terms, we can get

$$f(\tau + \Delta \tau ,\varepsilon ) = \frac{\begin{gathered} x^{\prime\prime}(\tau + \Delta \tau ) - (e_{1} y^{\prime\prime}_{1} (\tau + \Delta \tau ) + e_{2} y^{\prime\prime}_{2} (\tau + \Delta \tau )) - \left( {y^{\prime\prime}_{2} (\tau + \Delta \tau )T_{1} (\tau ) - y^{\prime\prime}_{1} (\tau + \Delta \tau )T_{2} (\tau )} \right) \hfill \\ - \frac{\Delta \tau }{{2\varepsilon }}\frac{{y^{\prime\prime}_{2} (\tau + \Delta \tau )y_{1} (\tau ) - y^{\prime\prime}_{1} (\tau + \Delta \tau )y_{2} (\tau )}}{h(\tau )U(\tau )}f(\tau ,\varepsilon ) \hfill \\ \end{gathered} }{{\frac{\Delta \tau }{{2\varepsilon }}\frac{{y^{\prime\prime}_{2} (\tau + \Delta \tau )y_{1} (\tau + \Delta \tau ) - y^{\prime\prime}_{1} (\tau + \Delta \tau )y_{2} (\tau + \Delta \tau )}}{h(\tau + \Delta \tau )U(\tau + \Delta \tau )} + \frac{1}{{\varepsilon^{2} }}}}$$
(32)

Equation (32) is the time recursive formula of the load.

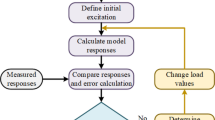
So far, we have deduced a DLI method based on WKB accelerated recursion. Since this method is obtained by inversion based on the recursive solution of the WKB real function, we can call it an inverse WKB (IWKB) method. The specific steps are described below. Figure 1 shows a flow chart of the specific steps.

Fig. 1
figure 1

Flow chart of IWKB dynamic load identification method

Full size image

Step 1 Initial calculation.

\(x(0) = x_{0}\),\(\dot{x}(0) = \dot{x}_{0}\),\(\ddot{x}(0) = \ddot{x}_{0}\);

\(y_{1} (0) = 1\),\(y_{2} (0) = 0\),\(U(0) = 1\),\(T_{1} (0) = T_{2} (0) = 0\);

\(f(0) = m(0)\ddot{x}(0) + c(0)\dot{x}(0) + k(0)x(0)\).

Step 2 The acceleration is correspondingly converted into the space related to \(\tau\), and the time step \(\Delta \tau\) and the tiny parameter \(\varepsilon\) are determined;

Step 3 Derivation for each time step.

(1) Determine \(y_{1} (\tau + \Delta \tau )\),\(y_{2} (\tau + \Delta \tau )\),\(y^{\prime\prime}_{1} (\tau + \Delta \tau )\),\(y^{\prime\prime}_{2} (\tau + \Delta \tau )\).

$$\left[ {\begin{array}{*{20}c} {y_{1} (\tau + \Delta \tau )} \\ {y_{2} (\tau + \Delta \tau )} \\ \end{array} } \right] = \exp \left( { - \frac{{\left( {a(\tau ) + a(\tau + \Delta \tau )} \right)\Delta \tau }}{4\varepsilon }} \right)\left[ {\begin{array}{*{20}c} {\cos \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{2\varepsilon }} \right)} & { - \sin \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{2\varepsilon }} \right)} \\ {\cos \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{2\varepsilon }} \right)} & {\sin \left( {\frac{{\left( {h(\tau ) + h(\tau + \Delta \tau )} \right)\Delta \tau }}{2\varepsilon }} \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{1} (\tau )} \\ {y_{2} (\tau )} \\ \end{array} } \right]$$
$$\left[ {\begin{array}{*{20}c} {y^{\prime\prime}_{1} (\tau + \Delta \tau )} \\ {y^{\prime\prime}_{2} (\tau + \Delta \tau )} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{a^{2} (\tau + \Delta \tau )}}{{4\varepsilon^{2} }} - \frac{{a^{\prime}(\tau + \Delta \tau )}}{2\varepsilon } - \frac{{h^{2} (\tau + \Delta \tau )}}{{\varepsilon^{2} }}} & {\frac{a(\tau + \Delta \tau )h(\tau + \Delta \tau )}{{\varepsilon^{2} }} - \frac{{h^{\prime}(\tau + \Delta \tau )}}{\varepsilon }} \\ { - \left( {\frac{a(\tau + \Delta \tau )h(\tau + \Delta \tau )}{{\varepsilon^{2} }} - \frac{{h^{\prime}(\tau + \Delta \tau )}}{\varepsilon }} \right)} & {\frac{{a^{2} (\tau + \Delta \tau )}}{{4\varepsilon^{2} }} - \frac{{a^{\prime}(\tau + \Delta \tau )}}{2\varepsilon } - \frac{{h^{2} (\tau + \Delta \tau )}}{{\varepsilon^{2} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {y_{1} (\tau + \Delta \tau )} \\ {y_{2} (\tau + \Delta \tau )} \\ \end{array} } \right]$$

(2) Confirm \(f(\tau + \Delta \tau ,\varepsilon )\).

$$f(\tau + \Delta \tau ,\varepsilon ) = \frac{{x^{\prime\prime}(\tau + \Delta \tau ) - \left[ {\begin{array}{*{20}c} {e_{1} - T_{2} (\tau )} \\ {e_{2} + T_{1} (\tau )} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {y^{\prime\prime}_{1} (\tau + \Delta \tau )} \\ {y^{\prime\prime}_{2} (\tau + \Delta \tau )} \\ \end{array} } \right] - \frac{\Delta \tau }{{2\varepsilon }}\frac{1}{h(\tau )U(\tau )}\left[ {\begin{array}{*{20}c} {y_{2} (\tau )} \\ { - y_{1} (\tau )} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {y^{\prime\prime}_{1} (\tau + \Delta \tau )} \\ {y^{\prime\prime}_{2} (\tau + \Delta \tau )} \\ \end{array} } \right]f(\tau ,\varepsilon )}}{{\frac{\Delta \tau }{{2\varepsilon }}\frac{1}{h(\tau )U(\tau )}\left[ {\begin{array}{*{20}c} { - y_{2} (\tau + \Delta \tau )} \\ {y_{1} (\tau + \Delta \tau )} \\ \end{array} } \right]^{T} \left[ {\begin{array}{*{20}c} {y^{\prime\prime}_{1} (\tau + \Delta \tau )} \\ {y^{\prime\prime}_{2} (\tau + \Delta \tau )} \\ \end{array} } \right] + \frac{1}{{\varepsilon^{2} }}}}$$

(3) Determine \(T_{1} (\tau + \Delta \tau )\),\(T_{2} (\tau + \Delta \tau )\).

$$U(\tau + \Delta \tau ) = U(\tau )\exp \left( { - \frac{{\left( {a(\tau ) + a(\tau + \Delta \tau )} \right)\Delta \tau }}{2\varepsilon }} \right)$$
$$\left\{ \begin{gathered} T_{1} (\tau + \Delta \tau ) = T_{1} (\tau ) + \frac{\Delta \tau }{{2\varepsilon }}\left( {\frac{{y_{1} (\tau )f(\tau ,\varepsilon )}}{h(\tau )U(\tau )} + \frac{{y_{1} (\tau + \Delta \tau )f(\tau + \Delta \tau ,\varepsilon )}}{h(\tau + \Delta \tau )U(\tau + \Delta \tau )}} \right) \hfill \\ T_{2} (\tau + \Delta \tau ) = T_{2} (\tau ) + \frac{\Delta \tau }{{2\varepsilon }}\left( {\frac{{y_{2} (\tau )f(\tau ,\varepsilon )}}{h(\tau )U(\tau )} + \frac{{y_{2} (\tau + \Delta \tau )f(\tau + \Delta \tau ,\varepsilon )}}{h(\tau + \Delta \tau )U(\tau + \Delta \tau )}} \right) \hfill \\ \end{gathered} \right.$$

Step 4 Transform the identified loads into space relative to time t.

$$f(t) = f(\tau ,\varepsilon )$$

5 Numerical examples of LTV dynamic systems

5.1 Noiseless acceleration response

An LTV system is examined based on Matlab, and the proposed DLI method is verified based on the approximate solution of WKB. The differential equation for vibration in a structural system with a SODF that varies with time can be formulated as \(\ddot{x}(t) + a(t)\dot{x}(t) + b(t)x(t) = F(t)\). System parameters are designated \(a(t) = 10 + 0.1\varepsilon t\sin (0.1\pi \varepsilon t)\), \(b(t) = 36 + 0.2\varepsilon t\sin (0.3\pi \varepsilon t)\), where \(\varepsilon = 0.1\); system initial conditions are \(x_{0} = 0\) m, \(\dot{x}_{0} = 0\) m/s. The displacement response of this system cannot be solved analytically, so the Runge–Kutta method is employed to solve the system response within 0 to 1s numerically, and the numerical solution of the system acceleration response is obtained. The acceleration response is then incorporated into the DLI method developed in this paper to solve, and the obtained data is resampled at a sampling rate of 100 Hz.

  1. (1)

    The external excitation is set to sinusoidal excitation with TV amplitude: \(f(t) = (1 + 0.08\varepsilon t)\sin (60\pi \varepsilon t)\) N.

  2. (2)

    The external excitation is set to an impact excitation with an amplitude of 15N, and the action time is 0.1s.

  3. (3)

    Load a random load with amplitude of − 5N ~ 5N on the system, and set the sampling frequency of the acceleration response to 1000Hz.

As depicted in Figs. 2 and 3, the DLI method grounded on WKB exhibits a good identification effect on the sinusoidal load and impact load of the LTV structural system, and the identified load time history is remarkably proximate to the actual load. Figure 4 illustrates that the IWKB load identification method is effective in identifying random loads. Upon detailed examination of the interval between 0.60 and 0.65 s, we noted that the IWKB method accurately identified the load and confirmed our previous conclusion.

Fig. 2
figure 2

Load identification time history for sinusoidal loads

Full size image
Fig. 3
figure 3

Load identification time history for shock loads

Full size image
Fig. 4
figure 4

Load identification time history for random loads

Full size image

To conduct a quantitative analysis of the error level throughout the entire time history, we designate the relative average error \(E\) as a parameter to measure the accuracy of load identification.

$$E = \frac{{\frac{1}{N}\sum {\left| {p(t) - F(t)} \right|} }}{{\frac{1}{N}\sum {\left| {F(t)} \right|} }} \times 100\%$$
(33)

Among them, \(p(t)\) represents the identified load, \(F(t)\) represents the real load loaded by the system, and \(N\) represents the number of time steps.

Table 1 shows that the IWKB load identification method has high identification accuracy without noise. When we use the acceleration response obtained from the WKB real function recursive solution to identify the load, the relative error is reduced to the order of 1e-14. Therefore, we can conclude that the error is due to the difference between the Runge–Kutta numerical solution and the recursive solution of the WKB real function itself.

Table 1 IWKB Load Identification Error
Full size table

5.2 Acceleration response polluted by noise

A sinusoidal load with TV amplitude is applied to the TV structural system in Numerical Example 5.1, i.e.,\(f(t) = (1 + 0.08\varepsilon t)\sin (400\pi \varepsilon t)\). The sampling frequency is set to 1000 Hz. We use the acceleration response polluted by Gaussian white noise for DLI. The signal-to-noise ratios (SNR) of the noise are 30 dB, 25 dB, 20 dB, and 10 dB, respectively.

Figures 5, 6, 7 and 8 show the identification results of sinusoidal loads under different noise conditions. The figures demonstrate that both the inverse Wilson-θ method and the IWKB method are effective in accurately determining the time histories of the unknown loads. Under 30 dB SNR input, the load time histories identified by the two methods perfectly align with the real load. In comparison, the load time histories under 25 dB SNR identified by the two methods align with the real load; under 20 dB noise, the load time histories identified by the two methods align with the real load with a good degree of alignment and slight deviation; under 10 dB noise, although there is a certain deviation between the time history of the load identified by the two methods and the real load, it can depict the change law of the load over time.

Fig. 5
figure 5

Time history of load identification at SNR = 30dB

Full size image
Fig. 6
figure 6

Time history of load identification at SNR = 25dB

Full size image
Fig. 7
figure 7

Time history of load identification at SNR = 20dB

Full size image
Fig. 8
figure 8

Time history of load identification at SNR = 10dB

Full size image

Table 2 demonstrates that as the signal-to-noise ratio decreases and noise increases, the recognition result worsens. Furthermore, under the same noise conditions, the IWKB method has slightly higher recognition accuracy than the Inverse Wilson-θ method.

Table 2 Error comparison of two load identification methods
Full size table

5.3 Comparison between IWKB method and inverse Wilson-θ method

Now we calculate the numerical example again by employing the LTV structural system with load \(f(t) = (1 + 0.08\varepsilon t)\sin (60\pi \varepsilon t)\) and an acceleration response sampling frequency of 100 Hz.

For the long-term identification of sinusoidal excitations with TV amplitudes, we employ the IWKB method and the inverse Wilson-θ method. Figure 9 Loads identified by the IWKB method in 0 ~ 15s and Fig. 10 Loads identified by Inverse Wilson-θ method in 0 ~ 15s depict the temporal evolution of DLI. These figures demonstrate that both algorithms are effective in long-term DLI when the acceleration response is free from noise interference. To facilitate a comprehensive comparison of the two methods, we computed their recognition error and time consumption. The IWKB method exhibits a relative error of 0.1710% for the 0–15 s identification, whereas the inverse Wilson-θ method yields a relative error of 0.1856% for the same identification period. The IWKB method demonstrates a 7.87% reduction in recognition error compared to the inverse Wilson-θ method, resulting in a slightly higher recognition accuracy. Furthermore, the IWKB method requires 0.0439s to perform identification over the 0–15 s duration, while the inverse Wilson-θ method takes 0.1636s for the same identification interval. Hence, the IWKB method achieves a 73.17% reduction in calculation time, resulting in significantly improved calculation efficiency.

Fig. 9
figure 9

Loads identified by the IWKB method in 0 ~ 15s

Full size image
Fig. 10
figure 10

Loads identified by Inverse Wilson-θ method in 0 ~ 15s

Full size image

To further compare the Inverse Wilson-θ method with the IWKB load identification method, we perform the DLI process from 0 to 2s on the above system and analyze the identification accuracy and efficiency of the two methods under different time steps.

From Fig. 11, it is evident that the IWKB method takes slightly longer than the Inverse Wilson-θ method when time step \(\Delta t\) is greater than 2e-3s. When \(\Delta t\) equals 2e-3s, both methods take a similar amount of time. However, when \(\Delta t\) is less than 2e-3s, the IWKB method is significantly less time-consuming than the Inverse Wilson-θ method. The smaller \(\Delta t\) is, the more obvious the time-saving of the IWKB method becomes. In general, the smaller the time step, the longer it takes for the two methods to identify the load from 0 to 2 s. This is attributed to the fact that the smaller the time step, the more time steps are needed to identify the load for the same duration.

Fig. 11
figure 11

Time-consuming comparison of DLI at different time steps of 0 ~ 2s

Full size image

As shown in Fig. 12, when is less than or equal to 2e-4s, the recognition error of the IWKB method is comparable to that of the Inverse Wilson-θ method. The error fluctuates between 0.0083 and 0.0103%, indicating that when is less than or equal to 2e-4s, the accuracy of DLI will not be further improved. When is greater than 2e-4s and less than or equal to 1e-3s, the recognition error of the IWKB method is slightly smaller than that of the Inverse Wilson-θ method. When is greater than 1e-3s, compared with the Inverse Wilson-θ method, the IWKB method has a significantly reduced recognition error and improved recognition accuracy. In general, the smaller the time step, the greater the load identification accuracy of the two methods. This is attributed to the fact that the smaller the time step, the superior the fit for the time-varying parameters, and the higher the accuracy of the identified load.

Fig. 12
figure 12

Error comparison of DLI at different time steps of 0 ~ 2s

Full size image

When the DLI time is fixed, within a certain range, the larger the time step \(\Delta t\), the fewer the number of time steps and thus less time-consuming both DLI methods become. However, this also leads to a greater identification error and lower identification accuracy. For higher recognition accuracy, we should choose a smaller \(\Delta t\); for higher computational efficiency, we should choose a larger \(\Delta t\). Considering efficiency and error comprehensively and compared with the Inverse Wilson-θ method, we recommend using a value of \(\Delta t\) between 1e-3s and 2e-3s for the IWKB method.

5.4 The influence of TV parameters on recognition accuracy and efficiency

The system parameters are designated as: \(m(t) = 1 - 0.05\sin \alpha \pi t\) kg, \(c(t) = 0.1 + 0.1\sin (\beta \pi t)\) Ns/m, \(k(t) = 5 + 1.5\sin (\gamma \pi \varepsilon t)\) N/m. The initial conditions of the system are set to: \(x_{0} = 0\) m, \(\dot{x}_{0} = 0\) m/s. The sampling frequency is established at 1000Hz.

Initially, we employ the Runge–Kutta method to solve the acceleration response of this system, and then incorporate the acceleration response into the IWKB method to identify the load of the TV system. The values of α, β, and γ individually represent the rate of change of parameters m(t), c(t), and k(t). Table 3 presents the scenario when β = γ = 0, that is, c(t) and k(t) are constants, and the influence of the rate of change of m(t) on the accuracy and efficiency of DLI by the IWKB method. Table 4 depicts the situation when α = γ = 0, and the effect of the rate of change of c(t) on the accuracy and efficiency of DLI by the IWKB method. Table 5 illustrates the case when α = β = 0, and the impact of the rate of change of k(t) on the accuracy and efficiency of DLI by the IWKB method.

Table 3 E and time-consuming under different α values
Full size table
Table 4 E and time-consuming under different β values
Full size table
Table 5 E and time-consuming under different γ values
Full size table

Upon observation of the simulation results, it becomes evident that the accuracy of DLI by IWKB is affected by the values of α, β, and γ. Specifically, the larger the rate of change of each parameter of the system over time, or in other words, the more drastic the parameter changes, the greater the relative error of DLI, and the lower the recognition accuracy, which is consistent with the assumptions in the previous text. Nevertheless, the accuracy of DLI using the IWKB method falls within an acceptable range. For instance, for γ = 10, the change period of k(t) is 0.2s, and E is within 1% at 0.60%. The efficiency of IWKB in DLI is essentially unaffected by the values of α, β, and γ, and the time consumed in DLI varies between 0.0185 and 0.022s.

5.5 DLI of an LTV mass beam model simply supported at both ends

As shown in Fig. 13, the simply supported beam has a length of 1 m and a cross-section of 0.04 m × 0.01 m. It has an elastic modulus of 2.1 × 1011 N/m2, and a TV density of \(\rho (t) = 7800(1 - 30t^{2} )\) kg/m3. The damping of the system is set to proportional damping, and the damping ratio of each order is 0.02. The x-axis is taken as its axis, and the left end of the beam is taken as the origin. The beam is only subjected to lateral forces, and the load is applied at a distance of 0.335 m from the far point. Sampling points are set at 0.2 m, 0.4 m, 0.6 m, and 0.8 m from the origin, and the acquisition frequency of the acceleration response is 4000 Hz. The IWKB method is used to identify the loaded dynamic load in time domain.

Fig. 13
figure 13

Schematic diagram of a simply supported beam

Full size image

(1) Working condition 1: an amplitude of 100 N and an impact time of 0.005 s.

The acceleration response of measuring point 1 is shown in Fig. 14 for the collected acceleration signal of 0 to 0.12 s. The collected signal is subjected to FFT transformation to obtain the frequency response of the acceleration response of measuring point 1 as shown in Fig. 15.

Fig. 14
figure 14

Time-domain acceleration response of measuring point 1

Full size image
Fig. 15
figure 15

Frequency domain acceleration response of measuring point 1

Full size image

It can be observed from Fig. 15 that in the frequency response diagram of the LTV structure system, the resonance peak is wider than that of the time-invariant system because the natural frequency of the LTV structure system varies with time. Three distinct peaks appear between 0 and 500 Hz, indicating that the mode at 0 and 500 Hz makes the main contribution.

To help us determine the modal order between 0 and 500 Hz and analyze the change of natural frequency with time, we calculated the first seven natural frequencies of the system. Figure 16 shows that the first four natural frequencies are in the range of 0 to 500 Hz, so it is reasonable for us to arrange four measuring points. The natural frequency of each order increases with time, following a quadratic function relationship. The LTV law of the natural frequency can be calculated from the LTV structural parameters. Since the system only involves the LTV mass and the time-varying mass is a quadratic function, the time-varying law of natural frequency is the same as that of mass.

Fig. 16
figure 16

Variation law of the first 7 natural frequencies

Full size image

The measured acceleration response was resampled with a sampling frequency of 2000 Hz. The resampled natural frequency was then used to identify the load and the time history of the impact load under the condition of no noise, as shown in Fig. 17.

Fig. 17
figure 17

Time history of identified impact loads

Full size image

(2) Working condition 2: a sinusoidal load \(f(t) = 50\sin 200\pi t\).

We treated the acceleration response in the same way as working condition 1, and the time history of identifying the sinusoidal load is shown in Fig. 19.

The IWKB load identification method has been shown to have high identification accuracy for both the impact load and sinusoidal load of the time-varying simply supported beam model as demonstrated in Figs. 17, 18, 19, 20. Additionally, Table 6 shows that the IWKB load identification method is highly accurate and efficient in time-varying simply supported beam structures.

Fig. 18
figure 18

Time history of identified impact loads at SNR = 30db

Full size image
Fig. 19
figure 19

Time history of identified sinusoidal loads

Full size image
Fig. 20
figure 20

Time history of identified sinusoidal loads at SNR = 30db

Full size image
Table 6 Comparison of DLI for Simply Supported Beams
Full size table

5.6 IDL of multi-degree-of-freedom (MODF) discrete LTV cantilever beam systems

The geometric and physical parameters of the beam mirror the simply supported beam in 5.4, with the boundary conditions altered to a fixed left end and a free right end. As shown in Fig. 21, the beam is partitioned into 20 elements and 21 nodes. The load f is applied in the vertical direction at the 7th node, and the acceleration measurement points are positioned at the 5th, 10th, 15th, and 20th nodes, with a designated sampling frequency of 4000Hz. DLI is conducted using the IWKB method.

Fig. 21
figure 21

Schematic diagram of a discrete cantilever beam with MODF

Full size image

Working condition 1: f is an impact load with a loading duration of 0.005 s and an amplitude of 50N.

As depicted in Fig. 22, Variation law of the first 7 natural frequencies, the first 7 modal frequencies of this system escalate with time, mirroring the change in natural frequencies of the system in 5.4. The temporal characteristics of the modal frequency exhibit a strong correlation with the temporal characteristics of the mass. Owing to different boundary conditions, the first 7 natural frequencies of the discrete cantilever beam fall below the first 7 natural frequencies of the simply supported beam.

Fig. 22
figure 22

Variation law of the first 7 natural frequencies

Full size image

In a similar vein, we resample the measured acceleration response at a sampling frequency of 2000 Hz. Subsequently, using the resampled acceleration response, we identify the time history of the impact load. Figure 23 Time history of identified impact loads depicts the load time history identified by the IWKB method when the acceleration response is unpolluted. Figure 24 Time history of identified impact loads at SNR = 30dbillustrates the load time history identified by the IWKB method when the acceleration response contains Gaussian white noise with SNR = 30db.

Fig. 23
figure 23

Time history of identified impact loads

Full size image
Fig. 24
figure 24

Time history of identified impact loads at SNR = 30db

Full size image

Working condition 2: a sinusoidal load \(f(t) = 60\sin 170\pi t\).

We employ the same method as in working condition 1 to process the acceleration response and identify the time history of the sinusoidal load. Figure 25 Time history of identified sinusoidal loads depicts the load time history identified by the IWKB method when the acceleration response is unpolluted. Figure 26 Time history of identified sinusoidal loads at SNR = 30db illustrates the load time history identified by the IWKB method when the acceleration response contains Gaussian white noise with SNR = 30db.

Fig. 25
figure 25

Time history of identified sinusoidal loads

Full size image
Fig. 26
figure 26

Time history of identified sinusoidal loads at SNR = 30db

Full size image

As observed from Figs. 23, 24, 25, 26, the IWKB method exhibits good recognition accuracy for the parameter-varying discrete cantilever beam system, and the load identified maintains relative accuracy even in the presence of noise. Table 7 presents a comparison of the DLI errors using the IWKB method under different noise conditions. With the escalation of noise, the error of DLI correspondingly escalates, but the identified load retains a certain level of accuracy and offers practical reference value.

Table 7 Comparison of DLI for Cantilever Beam
Full size table

6 Conclusions

This paper derives the IWKB dynamic load identification method for the LTV structural system from the approximate solution of the WKB real function. The step-by-step derivation process of the DLI method is summarized, and the influence of the time step on accuracy and efficiency of DLI is investigated. The simulation results show that this method has high recognition accuracy for impact load, harmonic load, and random load of LTV structural systems. When selecting an appropriate time step, compared with Wilson-θ back analysis methods, IWKB methods can not only improve recognition accuracy but also significantly improve calculation efficiency and greatly save program running time. The rate of change of TV parameters significantly influences the accuracy of load identification, but it does not affect efficiency. Furthermore, whether the method proposed in this article can achieve DLI for SDOF nonlinear systems remains an area worthy of further exploration. However, for complex nonlinear systems, such as MDOF systems or continuous structural systems, due to their high complexity and non-compliance with the principle of linear superposition, modal decomposition cannot be performed, rendering the IWKB method inapplicable.