Thinking about spiking neural P systems: some theories, tools, and research topics

Abstract

The present work focuses on three notions about spiking neural P systems (SN P systems), namely normal forms, homogeneous systems, and software tools for easy access and visual simulation of such systems. The three notions are presented in general and specific ways: their backgrounds and motivations, with detailed and up to date results. The aim of the work is to outline many results on these notions, mainly for research and pedagogy. SN P systems with normal or homogeneous forms, having many biological and computing inspirations, have much to contribute in the opinion of the author to membrane computing at least. The software we here mention aims to support both learning and research of such systems. We provide a brief survey of results in chronological order, using a unified notation to aid in more detailed comparisons of results. Lastly, we provide a list of open problems or research topics on the three notions and related areas, with the hope to further extend the theory and applications of SN P systems.

1 Introduction

Membrane computing is an active area of investigation under the more general field of natural computing, being part of a four-volume handbook in [89]. P systems, the models in membrane computing started in [78] (earlier as a technical report in [77]), are investigated both for their theory and practice. Some evidence for the enthusiasm in the investigations of P systems includes a recent survey in [90], a bibliometric analysis in [87], and the acceptance of the Journal of Membrane Computing (established in 2019) in the ESCI and SCOPUS indexing.¹

A P system variant known as spiking neural P systems (in short, SN P systems) introduced in 2006 [55] is one of many P system variants with vigorous research activity. One of the main reasons for the great interest in spiking neuron models such as SN P systems, according to [82], is that, while nature proves to be a rich source of ideas for computing, the human brain is a “gold mine” of such idea source. Furthermore, the human brain consumes only about 20 watts of power, but it is capable of parallel and distributed processing of images, speech, consciousness, and so on. For these reasons and more, the research on SN P systems is quite active. For instance in the bibliometric analysis in [87], we see the following numbers: 10 of the top 20 papers are about SN P systems or variants; SN P systems, together with membrane algorithms, are the top in the 9 largest co-citation clusters.

SN P systems and their variants, whether biologically or mathematically inspired, have been used to solve many computational problems. Further details can be found in [55, 82] and the SN P systems chapter in the membrane computing handbook [84]. Some works on the computing power of SN P systems and variants include [55, 69, 75] with recent works such as [5, 67, 74]. Such works mainly look at the effects or requirements of certain features with respect to classes of languages or problems that can or cannot be solved. Such features, with some given more details in the sections below, include delays in sending the spike signals, amount of spikes produced, the types of rules or neurons in the system. The classes of languages or problems are often with regards to classical models such as automata, grammars, Turing machines.

Some works on computing efficiency include [27, 62, 73, 100] with recent works in [7, 19, 108]. These works on efficiency are mainly concerned with how much space or time is required to solve certain, usually computationally hard, (classes of) problems. In the case of SN P systems, space usually refers to the total number of neurons, rules, synapses, and so on, while time usually refers to (non)deterministic “clock steps” to halting after a solution (or lack thereof) is reached. Besides these theoretical results, much advancements in applications of SN P systems and variants appear in the last decade such as [95, 96, 109] with earlier surveys in [28, 34, 36]. Further details, especially when contributing to the three main notions of this present and brief survey, are provided in their respective sections in the following sections.

Several PhD theses have also been done on SN P systems and their variants listed in [86] and the International Membrane Computing Society [54]. The present work is a largely revised and extended version of the abstract and talk given by the author in [12], with many references taken from a bibliography, as of March 2022, in [20]. The revisions and extensions include some up to date results as of March 2024 by the groups of the authors on the three main notions focused by this present work.

The organization of this work is as follows: Sect. 2 begins with some very brief preliminaries, followed by three general notions; Sect. 2.1 defines the basic or standard model of SN P systems, with an illustrative example in Sect. 2.2. Sect. 2.3 and Sect. 2.4 provide a chronological view of the results on normal forms and homogeneous systems, respectively, for SN P systems and variants; Besides the chronological order of results, Sect. 2.3 and Sect. 2.4 provide a more unified notation to compare many results on their respective ideas; For instance, a convention for providing results is to focus on a normal form of some variant with a certain feature, with less or no focus on comparable features of a normal form for another variant. Section 2.5 introduces pedagogical software for the improved ease of access, visualization, and interaction of SN P systems and variants. Section 3 provides a long list of open problems and research topics based on, but not limited to, the previous sections.

2 SN P stories: definitions and main notions

We consider two theoretical notions (Sects. 2.3 and 2.4) and one practical notion (Sect. 2.5) also in the hopes of furthering both theory and practice of SN P systems. Both theoretical notions have some biological inspiration: bio-neurons can be seen as rather “simple” or restricted compared to other types of cells; bio-neurons also seem rather “similar” or homogeneous at least for certain parts of the brain. The practical notion is an easy to access and visual tool for pedagogical purposes, not just for experts but also for students or new researchers. Definitions of SN P systems, their syntax and semantics, are only mentioned in brief below to be able to focus more on three main notions in the present section. Excellent introductions to and definitions of SN P systems include the seminal work in [55], the dedicated chapter in the handbook in [89], with open access tutorials in [61] and [80].

2.1 SN P systems: the basic model

Very briefly, an SN P system includes spike processors (the neurons) as nodes in a directed graph, where edges are called synapses. The neurons communicate using signals known as spikes which are sent to other neurons using synapses. Specifically, an SN P system is a tuple or construct $\Pi = ( \{ a\}, \sigma _1, \sigma _2, \ldots , \sigma _m, syn, in, out)$ which uses a single symbol a as the spike symbol, each $\sigma _i$ is a neuron, $syn \subset \{ 1, 2 \ldots , m\} \times \{ 1, 2, \ldots , m \}$ is the set of synapses between the m neurons (a reflexive synapse (i, i) is not allowed in this basic model), with in and out as the labels of the input and output neurons, respectively.

Each neuron $\sigma _i = (n_i, R_i)$ includes the number $n_i$ of spikes contained in $\sigma _i$, and a rule set $R_i$. Rules in $R_i$ include spiking rules of the form $E/a^c \rightarrow a;d$ where E is a regular expression over $\{a\},$ with natural numbers $c \ge 1, d \ge 0.$ A spiking rule is enabled if neuron $\sigma _i$ contains $n_i$ spikes written as string $a^{n_i},$ such that $a^{n_i} \in L(E),$ that is, there is a regular set L(E) to “check” if all $a^{n_i}$ spikes are “covered” in the language L(E). The application or firing of a spiking rule consumes c spikes, so only $n_i - c$ spikes remain in $\sigma _i$, followed by sending of one spike to each $\sigma _j$ such that $(i, j) \in syn.$

Checking, consuming, and firing of spikes are performed in a single step t, except when the delay $d \ge 1$ in which the spike is received by “neighbor” neurons at step $t+d$. From step t until $t+d-1$ the neuron is closed, inspired by refractory periods of bio-neurons: a closed neuron is waiting to release or fire its spike at step $t+d$, it cannot apply other rules, and it cannot accept new spikes. Spikes sent to a closed neuron are considered lost or removed from the system. The neuron becomes open at step $t+d$ when new spikes can be received. A rule can be applied next by the open neuron at step $t+d+1.$

The other rule form in rule set $R_i$ is a forgetting rule of the form $a^s \rightarrow \lambda .$ The meaning is that if neuron $\sigma _i$ contains exactly s spikes these spikes are erased or removed from $\sigma _i$. Note that in the basic model, the enabling of forgetting rules and spiking rules are mutually exclusive, that is, we can have all spikes in $\sigma _i$ as $a^{n_i}$ enabling either forgetting rules only, or spiking rules only. More specifically, if $\sigma _i$ has a forgetting rule $a^s \rightarrow \lambda$ then $a^s \notin L(E)$ for any E of any spiking rule of $\sigma _i$.

It is possible to have more than one rule in a neuron $\sigma _i$ that can be applied, that is, there exist at least two rules with expressions $E_1$ and $E_2$ where $L(E_1) \cap L(E_2) \ne \emptyset .$ In this case, the rule to be applied is chosen nondeterministically. The system $\Pi$ is globally parallel, that is, all neurons can fire at each step, but $\Pi$ is locally sequential, that is, at most one rule in each neuron is applied. $\Pi$ has a global clock to synchronize all neurons, that is, at each step if a neuron can apply a rule then it must do so. A system can have an out (in, respectively) neuron only if acting as a generator (acceptor, respectively), or both in and out neurons as a transducer or device for computing functions.

Even with the basic or standard definition of an SN P system in this present section, there are various ways to interpret or obtain the output. Here we mention for now one common way to obtain the output, using a time interval between the first two spikes of the output neuron out to the environment. Visually, the out neuron has a synapse going out of the system given by an arrow that does not point to any neuron. Specifically, if neuron out fires its first and second spikes at steps t and $t'$, respectively, the output is said to be the number $n = t' - t.$ Thus, the basic model computes or generates numbers, or sets of numbers in the case of nondeterministic systems. This way of obtaining the output applies whether the system halts or not. A system halts if no more rules can be enabled.

2.2 An example: generating numbers

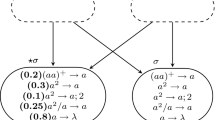
Consider a small example as follows, labeled as SN P system $\Pi _1$.

Let $\Pi _1 = (\{ a \}, \sigma _1, \sigma _2, \sigma _3, syn, 3),$ where

• 1. $\sigma _1 = (2, \{ a^2 /a \rightarrow a;0, a \rightarrow \lambda \}),$ that is, neuron 1 initially contains 2 spikes and its rule set $R_1$ contains two rules.

• 2. $\sigma _2 = ( 1, a \rightarrow a;0, a \rightarrow a;1),$ here neuron 2 is the only nondeterministic neuron in $\Pi _1:$ both of its rules require exactly one spike a, but one rule has no delay while the other rule has a delay of 1 step when firing its spike. A writing convention is seen here: if $E = a^c$ then $E/a^c \rightarrow a;d$ is written simply as $a^c \rightarrow a;d.$

• 3. $\sigma _3 = (3, a^3 \rightarrow a;0, a \rightarrow a;1, a^2 \rightarrow \lambda ),$ with neuron 3 as the output neuron.

• 4. $syn = \{ (1,2), (2,1), (1,3), (2,3) \}$ are synapses of $\Pi _1$.

We briefly describe the computation of $\Pi _1$ as follows:

Step 1: all 3 neurons can fire, but only neuron 2 has a nondeterministic choice. Neuron 1 must apply its rule $a^2 / a \rightarrow a;0$ which consumes one spike (only one spike remains in $\sigma _1$) and sends one spike each to $\sigma _2$ and $\sigma _3$. Assume for now that neuron $\sigma _2$ applies rule $a \rightarrow a;0,$ no spikes remain in $\sigma _2$ and one spike each is sent to $\sigma _1$ and $\sigma _3$. Neuron 3 applies rule $a^3 \rightarrow a;0$ so at step $t = 1$ the output neuron fires its first spike to the environment, consuming all of its spikes.

Step 2: $\sigma _1$ has two spikes in total from step 1, so it must apply the same rule from step 1. At this step, as long as neuron $\sigma _2$ decides to apply its first rule $a \rightarrow a;0$ then $\sigma _1$ always behaves as in step 1, while $\sigma _3$ always contains two spikes so it must always apply its forgetting rule $a^2 \rightarrow \lambda .$ The output is obtained soon after $\sigma _2$ decides to apply its second rule. Assume here at step 2 that $\sigma _2$ applies its second rule instead: it is closed from step 2 until step $2 + 1 - 1 = 2,$ that is, closed for only one step.

Step 3: The spike from $\sigma _1$ to $\sigma _2$ in step 2 is lost since $\sigma _2$ was closed in step 2. Only the forgetting rule $a \rightarrow \lambda$ of $\sigma _1$ can be used so it contains no more spikes. Note that the spike from the opening of $\sigma _2$ here at step 3 can only be used by $\sigma _1$ at the next step 4. Neuron 2 is now open and sends one spike each to $\sigma _1$ and $\sigma _3$. Neuron 3 has only one spike from $\sigma _1$ in step 2 so $a \rightarrow a;1$ is applied and $\sigma _3$ closes.

Step 4: neuron 1 applies its forgetting rule, so here both $\sigma _1$ and $\sigma _2$ contain no spikes. Neuron 3 fires its second spike to the environment at step $t' = 4.$ $\Pi _1$ halts since no more rules can be applied, with the output of this nondeterministic branch of computation as $t' - t = 4 - 1 = 3.$

The reader can easily verify that $\Pi _1$ can generate smaller or larger numbers depending on the step when $\sigma _2$ decides to apply its second rule. In this way, we say $\Pi _1$ computes or generates all natural numbers starting from 2, that is, $L(\Pi _1) = \{ k \mid k \ge 2 \}.$ From the definition in Sect. 2.1 and the seminal work in [55], we make a quick note: a minor “bug” in [61] where $\Pi _1$ appears as Fig. 1 to compute the set $\{ k' \mid k' \ge 1 \}$, that is, all natural numbers starting from 1. A visual representation of $\Pi _1$ appears later in Fig. 5 of Sect. 2.5.

2.3 Normal forms

In short, a normal form is a simplifying set of restrictions for a given machine, model, or system. In language theory, a well-known normal form is the Chomsky normal form (in short, CNF) for context-free sets from [29] which says that instead of writing context-free rules in a large number of forms, it is enough to use two forms to describe all such sets. In other words, we maintain the computing power of context-free grammars to generate context-free sets while restricting the forms of rules of such grammars. The CNF is of theoretical and practical use, allowing less complicated proofs and further results. It is thus of interest to apply normal forms to other models, certainly to SN P systems.

We set up some basic notations for use in the following sections, although a few more are introduced later when they are more relevant. We note that in the cited works there is not a standard convention, though there are many intersections, for the notations that follow. Further details of the following notations, including the preliminaries of computations in SN P systems, can be found in tutorials, monographs, surveys as in [61, 80, 84]. We write as $Spik_i P_j ( rule_k, cons_l, forg_m, dley_n)$ the set of numbers computed by the basic model of SN P systems as defined in Sect. 2.1. The parameter $i \in \{ 2, acc\}$ depends on how the result is obtained: as a number generator the result is the interval between the first two spikes from the output neuron, hence the subscript 2; as a number acceptor, the result is halting the system, given an input as the interval between the first two spikes to the input neuron. The parameters j, k, l, m, and n give the upper bounds for the number neurons, rules, consumed spikes, forgetting rules, and rules with delay, respectively. If the bound is finite but arbitrary we replace the parameter with the $*$ symbol. A D is appended at the start of the set of numbers to emphasize deterministic computation since we assume by default that computations are nondeterministic.

Even in the seminal paper of SN P systems in [55], we already have some results on normal forms, though such results were not labeled as “normal form” in the paper. For instance, the set of all finite sets of numbers NFIN can be generated by an SN P system with at most 2 neurons, each neuron with an unbounded number of rules, each rule consuming at most one spike, and without forgetting rules. We can summarize this result as follows:

Theorem 1

(Ionescu et al 2006 [82] )

$$\begin{aligned} Spik_{2} P_1 (rule_*, cons_1, forg_0) = Spik_2 P_2 (rule_*, cons_*, forg_*) = NFIN. \end{aligned}$$

We use parameters $ind_i$ and $outd_j$ to mean a neuron has an indegree at most i and an outdegree at most j, respectively. For the indegree of SN P systems, Theorem 2 is one result from [81] which limits the indegree of each neuron to at most two incoming synapses. In the sections that follow, we omit from writing some parameters such as ind and outd if such parameters are not the main focus of a work or result.

Theorem 2

(Păun et al 2006 [81])

$$\begin{aligned} Spik_2P_*(rule_2, cons_3, forg_1, dley_1, ind_2, outd_2) = NRE \end{aligned}$$

An early and explicit work on normal forms for SN P systems is [48]. Results from [48] are about Turing completeness or the characterization of the set of all Turing computable sets of numbers NRE, as follows:

Theorem 3

(Ibarra et al 2007 [48]) The following sets of numbers are equivalent to NRE:

• 1. $Spik_2P_*(rule_3, cons_4, forg_5, dley_0, outd_*).$

• 2. $DSpik_{\{2,acc\}}P_*(rule_2, cons_3, forg_2, dley_0, outd_*).$

• 3. $Spik_2 P_* (rule_3, cons_4, forg_4, dley_0, outd_2)$.

• 4. $Spik_2P_*(rule_2, cons_3, forg_0, dley_1, outd_2).$

• 5. $Spik_2P_*(rule_2, cons_2, forg_1, dley_2, outd_2), a^i$ for $i \ge 1$ or $a^+.$

Some interesting results in Theorem 3 from [48] include: removal of delay, for both the nondeterministic (item 1) and deterministic case (item 2); restricting the outdegree of each neuron (item 3); removal of forgetting rules (item 4); lastly, restricting the type of regular expression (item 5).

Notice that results in Theorem 3 allow only the removal in a mutually exclusive way for features such as delays, forgetting rules, or simplified regular expressions. In [40], some of these features are combined while maintaining the computing power of SN P systems. For instance, Theorem 4 combines simplified regular expressions and removal of delays.

Theorem 4

(García-Arnau et al 2009 [40])

$$\begin{aligned} Spik_2P_*(rule_3, cons_3, forg_3, dley_0, outd_2) = NRE \end{aligned}$$

using rules of the form $a^*/a \rightarrow a$ or $a^r \rightarrow a,$ and $a^s \rightarrow \lambda$ for $r,s \le 3.$

An open problem from [40] asks if more than two features of the system can be removed simultaneously while maintain Turing completeness. A positive answer to this open problem was provided in [71] as Theorem 5.

Theorem 5

(Pan, Păun 2010 [71])

$$\begin{aligned} Spik_2 P_* (rule^1_2, cons_3, forg_0, dley_0, outd_4) = NRE \end{aligned}$$

using only the following types of regular expressions: $a(aa)^*, a(aaa)^*,$ or $(a^2 \cup a).$

What is surprising about Theorem 5 is how restricted an SN P system is where $rule^e_k$ means that each neuron uses at most k rules and at most e types of regular expressions. Theorem 5 not only answers an open problem from [40] but also shows how “simple” the neurons can be to be Turing complete: a neuron only needs at most two rules using exactly one of three types of regular expressions, and without delays and forgetting rules. An open problem from [71] is if the system can maintain its computing power with fewer types of regular expressions.

Before we proceed to further normal forms for SN P systems, we make a short digression for some variants of SN P systems. SN P systems with anti-spikes or ASN P systems are SN P systems that allow for a second type of spike known as an anti-spike [72]. The idea of an anti-spike in [72] is inspired from the inhibitory features of biological neurons. Using $\overline{a}$ as the anti-spike symbol, a normal form for ASN P systems include Theorem 6 (Theorem 1 in [94]).

Theorem 6

(Song et al 2013 [94])

$$\begin{aligned} Spik_2ASNP_*( cat_2, prule_2, forg_0, dley_0) = NRE \end{aligned}$$

using categories $(a,a), (a, \overline{a}).$

The feature $prule_k$ means each neuron uses at most k “pure” spiking rules of the form $E/b^c \rightarrow b',$ and the regular expression E has $L(E) = b^c$ for $b,b' \in \{a, \overline{a}\}.$ That is, we simply write pure spiking rules as $b^c \rightarrow b'.$ The feature $cat_l$ means there are at most l categories in each neuron, from a total of four possible categories: $(a,a), (a, \overline{a}), ( \overline{a}, a), ( \overline{a}, \overline{a}).$ For instance, category $( \overline{a}, a)$ means rules can only consume anti-spikes and produce spikes.

Another normal form was introduced in [92] for sequential SN P systems. Sequential SN P systems, as introduced in [49], are systems where neurons cannot operate in parallel. For instance, in the case of max-sequential mode, only the neuron with the most number of spikes can apply a rule: if more than one such neuron exists then one neuron is nondeterministically chosen to apply its rule. A normal form (Theorem 3.1) from [92] improves a result in [49] by proving systems in max-sequential mode are Turing complete without forgetting rules, each neuron has exactly one rule, but with the use of delays.

The last variant we consider for now are SN P systems with (structural) plasticity or SNPSP systems from [17]. SNPSP systems are inspired by the ability of biological neurons to create new or remove existing synapses. A parameter introduced in [17] was $\alpha \in \{ +, -, \pm , \mp \}$ where $\alpha$ is used in a new type of rule known as a plasticity rule. For $\alpha = +$, this means that a rule can only create new synapse, up to some number k, while $\alpha = \pm$ means a rule can create new synapses in the present step and delete synapses in the next step. A normal form from [91] is Theorem 7.

Theorem 7

(Song, Pan 2015 [91])

$$\begin{aligned} Spik_2 SNPSP_*( \alpha \in \{ +, - \}, rule^4_4, cons_4, forg_1, dley_0, outd_3) = NRE. \end{aligned}$$

Theorem 7 has $rule^4_4$ which means each neuron uses at most 4 types of regular expressions and at most 4 rules. Another normal form for SNPSP systems is Theorem 8 from [66]. Normal forms for SNPSP systems under max- and min-sequential modes, as in [49], are given in [16].

Theorem 8

(Macababayao et al 2019 [66])

$$\begin{aligned} Spik_2SNPSP_*( \alpha \in \{ \pm \}, rule^3_3, cons_4, forg_0, dley_0, outd_R) = NRE \end{aligned}$$

where R is the maximum number of subtraction instructions associated with any register of the simulated register machine.

Explicit in the results of Theorem 8 and later results is the idea of a register machine: actually all the results on Turing completeness in this work since the seminal paper in [55] are shown by simulating register machines. In short, register machines are Turing complete models which have finite and rudimentary instructions or programs. Further details on register machines and how SN P systems and variants simulate them are from [61, 84]. Theorem 8 uses a single yet “compound” type for $\alpha$, unlike the “simple” types in Theorem 7, with the trade-off that Theorem 8 has smaller values for other ingredients, including the lack of delays and forgetting rules.

Now we return to an open problem from [71]: can fewer than three types of regular expressions allow SN P systems to be Turing complete? That is, can we improve on Theorem 5? The belief in [71] was in the negative. An early and positive answer to this open problem comes from improving Theorem 8 for SNPSP systems and attempting to apply it to SN P systems, resulting in Theorem 9 from [21].

Theorem 9

(Macababayao et al 2019 [21]) Using only regular expressions $a(aa)^*$ or $(a^2 \cup a),$ the following sets of numbers are equivalent to NRE : 

$$\begin{aligned} Spik_2 P_* (rule^1_2, cons_3, forg_0, dley_0, outd_4), \end{aligned}$$

and

$$\begin{aligned} Spik_2SNPSP_*( \alpha \in \{ \pm \}, rule^1_1, cons_4, forg_0, dley_0, outd_4). \end{aligned}$$

Even more interesting are improvements from [67] which lowered the values from [21].

Theorem 10

(Macababayao et al 2022 [67]) Using only the regular expression $a(aa)^*,$ the following sets of numbers are equivalent to NRE : 

$$\begin{aligned}{} & {} Spik_2 P_* (rule^1_2, cons_3, forg_0, dley_0, outd_3),\\{} & {} DSpik_{acc}P_*(rule^1_1, cons_3, forg_0, dley_0, outd_3), \end{aligned}$$

and

$$\begin{aligned} Spik_2SNPSP_*( \alpha \in \{ \pm \}, rule^1_1, cons_3, forg_0, dley_0, outd_{2R}) \end{aligned}$$

where R is the maximum number of subtraction instructions associated with any register of the simulated register machine.

2.4 Homogeneous systems

Next we look at a notion not too dissimilar to a normal form: the idea of a homogeneous system. At least in the context of SN P systems, such a system is homogeneous if every neuron has the same set of rules. The idea of homogeneous SN P system was first introduced in [114]. In some sense a homogeneous system is a “restricted” system, hence the similarity of the notions of normal forms and homogeneous systems. From the perspective of computing, a homogeneous system is where processors, or neurons in the case of SN P systems, are not distinct from each other. In terms of engineering for instance, this can mean that replacing a malfunctioning or damaged processor can be easily done: we simply swap the old processor with a new processor, since both processors are identical. Not only in engineering, such homogeneous systems may also reduce other necessary resources, such as during the design, manufacture, and maintenance of a single kind of processor.

From the perspective of the human brain, the neocortex or “new brain” is visually uniform. A natural question for the study of the brain is how various functions, such as perception, language, vision, and so on, arise from such uniformity. A common answer to this question, though much details still elude us, is how neurons are connected: the “size” of each connection, number of connections, "distance” between connections, and so on. Thus, both from the computing and biological perspectives, the idea of homogeneous SN P systems is well-motivated.

An early result is that SN P systems as number generators can be Turing machines with the same set of seven rules in every neuron, given by Theorem 11 (Theorem 4.1 from [114]). Since every neuron or processor in the SN P system has the same set of rules, the “programming” of the system is focused on the topology or connection of the system using synapses, rather than the “details” of each neuron.

Theorem 11

(Zeng et al 2009 [114]) The following sets of numbers are equivalent to NRE : 

$$\begin{aligned} Spik_2 HSNP_* (rule^6_7, cons_7, forg_1, dley_1, outd_3, weight_5), \end{aligned}$$

and

$$\begin{aligned} DSpik_{acc} HSNP_* (rule^6_7, cons_7, forg_1, dley_1, outd_3, weight_6). \end{aligned}$$

The $weight_5$ feature in Theorem 11 refers to synapses having integer weights of at most 5, to multiply the number of spikes sent to specific neurons. A way to remove the weight feature, resulting in “standard” synapses of weight of 1, is also included in [114]. As expected, removing the synapse weight increases the number of synapses and outdegree of the system.

Further results on homogeneous SN P systems combine ideas from results on normal forms, such as removing delays. In [58] the max-sequential mode is applied to HSN P systems, resulting in Theorem 12.

Theorem 12

(Jiang et al 2013 [58]) The following sets of numbers are equivalent to NRE : 

$$\begin{aligned} Spik^{ms}_2 HSNP_* (rule^8_8, cons_{11}, forg_1, dley_0, outd_3, weight_5), \end{aligned}$$

and

$$\begin{aligned} DSpik^{ms}_{acc} HSNP_* (rule^8_8, cons_7, forg_1, dley_0, outd_3, weight_6). \end{aligned}$$

An interesting result from Theorem 12 using max-sequential mode, hence the superscript ms, the delay is removed but values of other ingredients are increased, such as number of rules. An improvement on another computing parameter is given in [76] where they improve on [114] by giving “small” universal systems. We return later to small universal systems, where the main goal of such works is to reduce the number of neurons while maintaining Turing completeness.

An interesting extension of Theorem 11 is in [64] where the entire system is heterogeneous, but parts of the system are homogeneous. That is, the system is locally homogeneous. Specifically, neurons in modules are homogeneous, where such modules simulate operations of a register machine. Since there are three such operations, there are three sets of rules in [64] summarized in Theorem 13. We note in Theorem 13 that some of their modules now use negative weights, unlike previous results where the minimum weight is one: $weight^{-2}_5$ means the minimum weight is -2 while maximum is 5.

Theorem 13

(Liu, Qi 2016 [64])

$$\begin{aligned} Spik_2 LocHSNP_* (rule^3_4, cons_5, forg_0, dley_0, outd_3, weight^{-2}_5) = NRE. \end{aligned}$$

Before we end this section, we mention more recent works on homogeneous variants of SN P systems. In [31], homogeneous SNPSP systems were investigated. Each of the neurons in the homogeneous SNPSP systems in [31] uses the same set of 9 rules. In [117], the asynchronous mode is applied to homogeneous SN P systems. In asynchronous mode, a second level of nondeterminism is applied: if a neuron can apply a rule the neuron nondeterministically decides to apply the rule or not. Specifically, local synchronization is used where the entire system is asynchronous but sets of neurons operate in a synchronous manner, similar to the idea of locally homogeneous systems in [64]. Local synchronization is used since the lack of synchronization makes programming the system more difficult, see for instance details in [24]. Using local synchronization, at most 5 rules are required to characterize NRE, with trade-offs including an increase in the outdegree of neurons.

An interesting and recent work on homogeneous SN P systems is in [33] which introduces H, a homogenization algorithm for an arbitrary SN P system $\Pi$, such that $H(\Pi ) = \Pi '$ where $\Pi '$ is a homogeneous SN P system computing the same set as $\Pi$. Algorithm H requires some reasonable constraints, such as the lack of delay which is known to not affect their computational completeness, see for instance [67]. Using operations such as neuron translation and subsystem scaling, H introduces modifications in the number of spikes, rule sets, synapses, and neurons of $\Pi$ to produce $\Pi '$.

2.5 Visual- and web-based simulators

The practical notion is that of a visual simulator, for now at least, of SN P systems and some variants. At least one way to better engage or increase enthusiasm of new and old researchers is to have tools to allow easy and visual creation and experimentation of theoretical models. One such pedagogical tool for use in automata and grammar models is a well-known tool Java Formal Languages and Automata Package (in short, JFLAP) see for instance [42]. With JFLAP, novice and experts can easily and visually interact with notions from automata and formal languages, such as a step-by-step transformation of a nondeterministic finite automaton to a deterministic one or a regular grammar.

Fig. 1

A screen of Snapse, showing the software interface, four neurons (boxes labeled with 8, 9, 10, 12), synapses (arrows), a spike (yellow circle between neurons 9 and 10)

For SN P systems, in a similar way, it is useful to have some examples of solutions to problems: applying notions such as normal forms from Sect. 2.3 or homogeneous systems in Sect. 2.4 can improve appreciation and increase engagement. For instance, an easy access and visual tool to create or interact with SN P systems generating certain languages, accepting numbers, or solving small instances of hard problems. An early attempt for such an easy access and visual tool is Snapse, see Fig. 1, in [37] which includes a download link to the tool. Snapse allows a visual and (quite) easy to access tool to experiment with SN P systems, with features such as: animations for the sending of spikes between neurons, pseudorandom mode to simulate nondeterministic application of rules or guided mode to allow users to select which rules to apply, some examples such as a natural number generator, a bit comparator, and a bit adder. While Snapse was tested in a few platforms, such as Windows and Linux computers, it’s ease of access (among other features) can still be improved. Thus, WebSnapse was introduced in [35], see Fig. 2, with links in [110]. WebSnapse is mainly a web browser version of Snapse.

Fig. 2

A screen of WebSnapse version 1, showing the software interface, eight neurons, synapses, firing of spikes (arrows with broken lines)

WebSnapse allows an improved ease of access since its access is not limited to computers running Windows or Linux. Most modern web browsers, including those found in laptops, tablets, or mobile phones can be used to access WebSnapse. Besides the improved ease of access, WebSnapse includes new features such as the viewing of a computation history of an SN P system: for each time step, WebSnapse records the rules applied for each neuron, and the output of the system. WebSnapse also supports an XML file format, inspired by one of the formats of the well-known tool P-Lingua [68].

Fig. 3

A screen of WebSnapse V2, with some new features: improved access to edit parts (e.g., nodes or neurons, synapses) of the system; a slider at the top right, to change the simulation and animation speed; support for weights on synapse, such as weight of 1 for both synapses in the screen

An improvement is in WebSnapse V2 (that is, version 2) from [30], also shown in Fig. 3. In WebSnapse V2, all features of version 1 are included, together with further variants or ingredients, such as multiple input and output neurons, weights on synapses. WebSnapse V2 also includes new simulator features, such as increasing or decreasing the speed of the simulation and animation, improving the ways to create, remove, or edit parts of the system.

More recently, a significant improvement is WebSnapse CS (that is, client–server) from [43] and shown in Fig. 4. Together with another contemporary variant known as WebSnapse V3 from [39], WebSnapse CS includes all features of WebSnapse V2 but with improved efficiency from the perspective of the user and from the software developer. For the user: the screen interface can be more intuitive or aligned toward recent software applications especially for mobile devices such as phones and tablets; improved ways to add, edit, or delete neurons, rules, spikes, and synapses using context-aware gestures or clicks of the computer mouse; support for LaTeX-like input of rules and regular expressions; support for improved representation of input or output trains of spikes, such as by writing the string 1$0^8$10 in the output neuron out in Fig. 4 instead of the explicit string 10000000010 from previous versions; support for light and dark themes or modes to improve visibility depending on the screen or device used.

Fig. 4

A screen of WebSnapse CS using dark theme or mode; at the bottom right is a minimap, a small directed graph to represent the simulated system and its placement in the software canvas; support for LaTeX-like inputs and outputs; support for client–server architecture or style of simulation

For the developer, WebSnapse CS allows easier extension for future variants by improving the separation of the code for the user interface and the “logic” and simulations of the computation. Also, the CS or client–server part of WebSnapse CS allows the logic to be computed in a separate machine from the machine for the user interface (i.e., the computer for viewing the screen): in previous versions both the simulation and user interface can only be done in the same machine or computer; with WebSnapse CS it is possible to use a more powerful computer (e.g., server or workstation computer) to perform the computations of the simulation, while a less powerful computer (e.g., laptop or tablet computer) can be used to view the animations, results. In this way, larger systems can be simulated compared to previous versions of WebSnapse, while maintaining ease of access and visual simulations.

WebSnapse is currently used not only for research but also for pedagogy in the research group of the author. For instance, at least in the undergraduate classes CS198 and CS199 for two semesters at the University of the Philippines Diliman, WebSnapse has been used since 2021 for some students to learn about SN P systems or variants. In both classes, undergraduate students are expected to prepare a technical or research project for the degree. The author and some colleagues use WebSnapse, as well as require the software for students focusing on SN P systems or related systems. Our experience is similar with the JFLAP tool for automata and formal languages, where WebSnapse allows improved understanding of SN P systems and their computations.

Recalling the example $\Pi _1$ from Sect. 2.2, we see the system depicted in WebSnapse in Fig. 5.

Fig. 5

The SN P system $\Pi _1$ from Sect. 2.2, shown with output $1001 = 10^21$ in the environment node with label $env_{out}$: spikes represented as symbol “1” are released by neuron 3 at clock tick or step 1 and step 4; in this way the generated output is 4 - 1 = $3 \in \{ k \mid k \ge 2 \}$

A few more examples of SN P systems in WebSnapse are the bit adder in Fig. 6 with more details in [30, 45], and a comparator or sorting “module” in Fig. 7 with more details in [25, 30]. We do not go here in the details, only to mention other examples for WebSnapse include addition (increment), subtraction (decrement) modules simulating instructions of register machines, and a system solving an instance of the NP-complete problem Subset Sum from [62]. The group aims to keep adding more examples to the list in the WebSnapse page [110], and we welcome the contributions of other users and researchers.

Fig. 6

An SN P system included in the list of examples in WebSnapse: a bit adder which adds the binary numbers $0^21 = 001$ and $0^31 = 0001,$ which are the binary strings in reverse for the numbers $4_{10} = 100_2$ and $8_{10} = 1000_2;$ the expected output is the string $0^3 1^2 0$ = 0 0011 0 with only the digits in bold considered part of the output in reverse, that is, $1100_{2} = 12_{10}$

Fig. 7

An SN P system included in the list of examples in WebSnapse: a comparator which compares two inputs numbers written in unary, that is, comparing the numbers $2_{10} = 11 = 1^2$ and $4_{10} = 1^4$; the smaller and larger numbers are stored in neurons min and max, respectively

Recently, we provide a tutorial or step-by-step guide in using WebSnapse and its extensions to learn and work with SN P systems and some variants: the shorter and online version in [110] with revision and extension at [59]. The group has also prepared some test cases or benchmarks for use by novices or experts, found in the main WebSnapse page at [110]. The WebSnapse page also includes links to all main versions of the software, including the simulators and their source codes.

3 Some open problems and research topics

What follows is a list of problems or topics which is of course not meant to be exhaustive. Unlike the previous sections there is less structure in the next list, for instance, there is no ordering according to significance, interest, or time with the membrane computing community. The topics are presented in varying depth, some more formal, some more informal or preliminary.

• 1. An early and explicit work restricting SN P systems is [51], though their work is mainly focused on Turing complete systems or otherwise, with two types of neurons: bounded neurons consist of only bounded or finite rules of the form $a^i / a^j \rightarrow a; d$ where the language $L(a^i)$ is finite; unbounded neurons consist of only unbounded rules of the form $E/a^j \rightarrow a;d$ where language L(E) is an infinite and unary regular set of expression E. The extension of such neuron and rule types to systems is a natural one: a bounded (resp., unbounded) SN P system is one that consists only of bounded (resp., unbounded) neurons. The third type, for instance from [52], are general neurons which can have bounded and unbounded rules. Most of the results from Sect. 2.3 and Sect. 2.4, except perhaps [67], do not focus or even ignore such types of neurons. How are results from [51, 52] affected, such as trade-offs, when considering the earlier normal forms such as Theorem 3 or the more recent and restrictive forms from Theorem 10?

  Extending results from [51, 52], Sects. 2.3, and 2.4 to other classes of numbers or languages, between the capabilities of finite automata and the Turing machine is of interest, not just for theory but for practical applications also. Such extensions are also suggested in problems L and K in [82]. A recent attempt on other classes in the Chomsky hierarchy is [32], but several problems remain open: what are the effects of applying normal forms or homogeneous systems on the SNPSP systems and other variants to “simplify” the construction? How about a characterization (the work in [32] was only in one direction) with normal or homogeneous forms for context-free and other language classes, including infinite sequences such as in [38] ?

• 2. Some rather “general” issues or interests from, but not limited to, Sects. 2.3 and 2.4: most if not all results here mentioned are about generating or accepting sets of numbers. How about languages applying such notions to systems accepting or generating languages? One early work on SN P systems generating languages is [26], with a recent work in [74] using homogeneous SNPSP systems to generate label languages. The case of computing strings is interesting: certain “easy” functions and languages cannot be computed by SN P systems as transducers [83] and language generators [26] over a binary alphabet. Can normal forms or homogeneous systems maintain or reduce further the power of such systems? SN P systems as various transducers are given in [50] with recent results in [2, 15]. From the view of theory and applications, it is interesting to provide trade-offs, normal and homogeneous forms for such transducers.

• 3. For WebSnapse and similar software for SN P systems, the following are some natural topics. Since WebSnapse is open source it is interesting to extend it to other types of P systems, including P systems with active membranes: not just for experts but also for novice researchers, the author suspects it is of interest to have the user define a “small” P system with active membrane $\Pi _{AM}$. Details of P systems with active membranes is in [79] and the corresponding chapter in the [84]. The user can then view the animation of $\Pi _{AM}$ similar to animations in WebSnapse, such that the polynomial number of cells (with respect to a “small” instance of a problem) produce an exponential number of cells. An animation feature, among other features, perhaps can be used to attract not only researchers but even more funding: at the least, such features can perhaps make our work more accessible to laypersons or researchers of other scientific fields.

  A visual suggestion is provided in Fig. 8. WebSnapse and similar software can be used by novice or experts to easily create, share, and experiment with their P systems of choice, using laptop computers, workstations, tablet computers, mobile phones and other devices. Common file formats can be shared between simulation software, or even specific formats for certain applications. For instance in [10], they mention more than one decade of using P systems for controlling robots: perhaps WebSnapse and similar software can be extended to design and visualize P systems for robot controls. Aside from robots, WebSnapse can be extended to include the use of evolutionary computing such as genetic algorithms to automatically design P systems. A survey of evolutionary membrane computing is in [115] with recent works on SN P system from [23, 44]. For the inclusion of evolutionary SN P systems in WebSnapse, the animation feature can be extended so that users can see the changes made by the genetic algorithm on the neurons, rules, synapses etc of the system. Perhaps even view the evolution of populations of SN P systems, from an initial population.

  Other theories on SN P systems and variants, including those from Sects. 2.3 and  2.4, can be included in WebSnapse and other software to make “more tangible” the theories especially for novice researchers. For instance, a preliminary work on implementing the homogenization algorithm in [33] is given in [65]. In this preliminary work, using WebSnapse V2, a user can click or tap a button which transforms an input system $\Pi$ to an equivalent and homogeneous $\Pi '$. Our group also aims to support, among other output formats, to output LaTeX code such that the created system in WebSnapse can be exported to a format for use in preparing LaTeX documents. It is also convenient if outputs can be produced in matrix or vector forms, for ease of use with parallel simulators such as those in [22, 44, 70].

  Using WebSnapse or similar tools, an interesting problem is how to setup an easy to access, use, and “integrated” workflow for researchers and users? An integrated workflow between users and developers, including their hardware and software, can perhaps allow better access to practical applications. That is, domain and software (hardware) experts working together in WebSnapse to achieve domain specific goals. For instance, designing and visualizing the problem (which may include checking for model errors), perhaps downloading to specialized circuits, robots, “wet laboratory”, parallel hardware or software, and so on, then back to WebSnapse for further evaluations and analyses. Such integrated workflows can perhaps make SN P systems and membrane computing accessible to many more researchers, for practical applications, see for instance [103]: WebSnapse or other software tools can (and perhaps must) be extended to work with hardware tools including parallel accelerators such as GPUs, FPGAs, robots, and so on.

  For instance, WebSnapse or similar tools can be used or integrated in the workflow regarding the real world or practical problem of pattern recognition. For instance, the first work to use SN P systems with Hebbian learning to recognize English letters is [95]. Systems such as those from [95] help in automating tasks such as image to text or image to speech.

  Another practical problem where tools such as WebSnapse can further help developers, domain experts and other users include skeletonizing images. Skeletonizing images helps reduce the amount of stored information by removing less useful or important parts of the images. Work in [96] uses SN P systems with weights to improve the skeletonizing method of images.

• 4. Several ways to study the properties and computations of SN P systems and variants include their matrix representation [3, 113] and formal framework [104, 105]. Similar to other normal forms in informatics, a usual trade-off for restrictions such as a normal form or homogeneous system is the increase in the number of other parameters, such as rules and computation time. How can we use the matrix representations or formal framework for SN P systems to compare and contrast results on Turing completeness, to transfer results, and so on? Related to this question is how to use such representation or framework to investigate further properties of systems under normal forms, prior to transferring results. A related idea to matrix representation (even energy efficiency, more on this later) is reversibility in the computations of SN P systems as in [97]. In short, a reversible SN P system is one where earlier configurations of the system can be obtained by reversing the order of rules applied in the system. It is of interest to design normal or homogeneous and reversible SN P systems, analyzed with matrix representation or formal frameworks.

  For instance in [69], it is shown that the lower bound for a universal SN P system is 4 neurons, using extended spiking rules which are rules allowing a neuron to fire more than one spike each step. Systems in [69] require more details than given here, such as a different way to encode inputs, outputs, and instructions of register machines compared to results from Sects. 2.3 and 2.4. As expected, one trade-off from the lower bound results in [69] is the larger number of rules for each neuron. Mentioned in [18] is the idea of Korec simulation technique which assumes “simpler neurons”, that is with much fewer or simpler types of rules, compared to “super neurons” such as in [69] and elsewhere. How can we use results on normal forms, together with matrix representations, formal frameworks, to further compare and transfer results on “small” systems with “super neurons” and systems using Korec simulation technique from Sects. 2.3 and 2.4?

  Related to the use of normal forms or homogeneous systems is that resulting systems have a sparse adjacency matrix, that is, we have more processors or neurons than links or synapses. A recent work in [9] shares some details on the effects of using a “dense” representation of SN P systems and variants, on the time and memory performance of parallel processors. Preliminary experiments of some ideas from [9] is in [46] with extensions in [47], providing significant improvements of the dense representation over well-known representations in GPU computing. On the one hand, normal forms and homogeneous systems provide “simple” systems for theoretical investigations. On the other hand, we may need to modify our existing approaches for such systems in parallel computing, circuits, robots, and so on to gain improvements on real world applications.

• 5. Specifically for results on “small” universal systems such as [18, 69], starting from [75] is to find small universal systems under normal forms or that are homogeneous. The search for such SN P systems and variants is quite active, for instance the bibliography on SNP systems as of June 2016 in [63] lists at least 17 citations dedicated to such small systems. Related to the Korec simulation technique mentioned in [18] are the following notions: for small universal systems to use the $rule_k$ parameter in Sect. 2.3 where each neuron has at most k rules; for comparison or transfer of results (see again item 3 in this list) a notion such as rule density, that is, the ratio of the total number rules over the total number of neurons. Again we go back to the idea of bio-neurons seemingly “simple” or not “too complex”. Hence, such a ratio can be a metric to use in new normal or homogeneous forms, among other results.

• 6. An open problem in [24] is whether asynchronous SN P systems using only standard spiking rules (that is, at any step a neuron can fire at most one spike) are Turing complete. The difficulty in answering this problem led to features to work around the removal of a global clock or synchronization, such as local synchronization in [117]. Perhaps one way to approach an answer to this problem is to use normal forms or homogeneous systems, to restrict the ways the system can perform its computations.

  Besides the asynchronous feature, another feature is polarization to remove regular expressions in SN P systems. SN P systems with polarizations or PSN P systems were introduced in [111], since even a “regular oracle” can be too powerful in the following sense: that is, the ability to evaluate in one time step if a string of arbitrary length is described by a regular expression. Thus, PSN P systems only use at most three kinds of polarizations: positive, negative, and neutral. Together with the feature to send spikes is the feature to send such polarities, so that neurons have an additional information (the polarity) besides the contained spikes. A normal form for PSN P systems is in [5] which says that at most 2 polarizations is enough to achieve Turing completeness. In [111] it is asked how to “transfer” some of their results to SN P systems with regular expressions, to further find restricted types of regular expressions while maintaining the computing power. In Theorem 10, a single type of regular expression is the optimal lower bound, with [67] giving some ideas on some optimizations for “bounded rules”. That is, certain neurons in the system only serve as “relay neurons”. Hence, a bounded rule such as $a \rightarrow a$ is sufficient, instead of an unbounded rule.

• 7. Since WebSnapse and similar tools are mainly pedagogical tools, they can be integrated or connected to more performance-specific simulators such as those in GPUs which are massively parallel processors. For instance, the CuSNP simulators of SN P systems in GPUs from [1, 22, 44]. Normal forms and homogeneous systems can support such simulators, by perhaps using a “preprocessing” phase to convert (at least parts) of an input system to a more restricted system prior to simulation. A preliminary work to combine benefits of web-based simulations with GPUs is in [102] with improvements in [70]. Again, some hardware details such as those investigated in [9] and item 4 in this list may be considered. When using evolutionary approaches such as those from [23, 44, 115], restricted forms of SN P systems can be considered to decrease the size of the search space for such approaches in order to find “optimal” populations or chromosomes.

  For pedagogical tools, perhaps the inclusion of “game playing” or “gamification” can be another dimension to consider. That is, the inclusion of game or play elements including, but not limited to: cooperation, adversaries, ranking based on a reward system such as points or scores. In automata and language theory, a well-known way to prove certain languages are not regular or context-free is using an adversarial style of proving, such as pumping lemmas. Similarly, from results now or in future for normal or homogeneous forms, including ideas from small systems such as those from [75], how can we apply them to allow users to “play” with SN P systems or similar systems? The slider feature in WebSnapse (see Sect. 3 and [43]) allows the increase or decrease of the simulation speed: combining this feature for instance with evolutionary approaches such as in [23, 115] can be a form of play between humans with or versus humans (or machines).

• 8. In this work, we mention only a few variants of SN P systems, but in fact there are many variants so here we mention a few more. SN P systems with rules on synapses (RSSN P systems) are an interesting variant which takes inspiration from the fact that synapses in brains perform processing instead of simply acting as a communication channel, more details in [93]. In fact, a similar and optimal lower bound normal form for RSSN P systems is also given in [67]. At least for computing numbers or strings, much can still be investigated for normal or homogeneous forms for RSSN P systems.

  A less explored but still interesting variant is spiking neural distributed P systems (SN dP systems) from [53]. An SN dP system $\Delta$ consists of a finite number of components $\Pi _1, \Pi _2, \ldots$ where each component $\Pi _i$ is an SN P system. Each $\Pi _i$ are independent in most parts of their computations, except when they need to communicate through special external synapses: the idea is that the input to system $\Delta$ is partitioned and distributed among its components, so that not one component has the entire input. Thus, components must communicate and cooperate to recognize certain languages using their external synapses. A recent work on SN dP systems involves homogeneous components, but not neurons in such components, from [11]. Of interest is to investigate normal or homogeneous components or neurons of SN dP systems. For instance, component $\Pi _i$ may have a normal or homogeneous form different from $\Pi _j$ for $i \ne j.$ For such normal or homogeneous systems, it is interesting to show what are their capabilities or limitations.

  A related yet distinct variant of ASN P systems from [94] are SN P systems with inhibitory synapse (ISN P systems) with homogeneous results in [98]. Besides the results in [98], many problems still remain for ASN P systems, such as: lower or optimal bounds in the normal or homogeneous forms; can the bounds be lowered using other features such as other derivation modes, or using a trade-off such as increase in one parameter (for instance the number of neurons or rules in the system) but decrease in another? For RSSN P systems, [57] provides results on homogeneous synapses. As with other variants, much work remains open for such systems such as: how to remove delay and/or forgetting rules; decrease other bounds in the system, since synapses which are processors in [57] each use 8 rules; identify trade-offs when decreasing other parameters, such as number of rules, neurons, types of regular expressions. Further results similar to those in Sects. 2.3 and 2.4 applied to ISN P systems, RSSN P systems, SN dP systems and other variants are of interest.

  Another variant related to SNPSP systems from [17] are SN P systems with scheduled synapses (in short, SSN P systems) in [14]. SNPSP and SSN P systems are variants focusing mainly on dynamism of synapses, instead of mainly dynamism of neurons as in most related works. That is, systems with a dynamic topologies, inspired not only by dynamism in biological and spiking neurons, but also by dynamic or time-varying graphs, networks from maths and computing. Some normal forms are provided for SSN P systems in [14] involving features, such as number of rules, delays, and consumed spikes. In SSN P systems, certain synapses appear or disappear depending on a schedule: a system with local schedules defines disjoint sets of neurons, each with a reference neuron which defines the schedules for a specific set; a system with a global schedule has only one set of reference neurons. Further details, topics, and problems on topologically dynamic systems such as SSN P systems are provided in [14].

• 9. Much of the present work and items on this list are about computing power, but certainly of theoretical and practical interest is computing efficiency. That is, the amount of time, space, and other resources is required to solve problems. For instance, a variant of SN P systems inspired by neurogenesis in the brain, that is, the creation of new neurons, are SN P systems with neuron division and budding from [73]. Division rules allow creation of neurons in parallel: if a division rule is applied in neuron $\sigma _i,$ then $\sigma _i$ is replaced with two neurons $\sigma '_i$ and $\sigma ''_i$ such that the incoming and outgoing synapses of $\sigma _i$ are inherited by $\sigma '_i$ and $\sigma ''_i$. Budding rules allow creation of neurons in sequence: if a budding rule is applied to $\sigma _j$ a new neuron $\sigma '_j$ is created with a new synapse from $\sigma _j$ to $\sigma '_j$ and all outgoing synapses of $\sigma _j$ are transferred to $\sigma '_j$. Systems from [73] were used to solve the SAT problem in time polynomial in terms of the input size of the problem.

  A sort of normal form is given in [107] where it is shown that neuron division suffices to efficiently solve SAT: that is, neuron budding is not required. Some interesting problems from or related to [73, 107] are the following: identification of trade-offs, normal or homogeneous forms for solving problems; for instance, division rules can be considered “wasteful” in the sense that such rules create two neurons instead of one, so how about trade-offs for using budding rules only? What are the computing efficiency of systems from Sect. 2? As in automata and formal language theory, we usually expect that systems under a normal or homogeneous form incur a “slowdown”, but it remains interesting to show how much is the slowdown; Aside from sequential or asynchronous modes from Sect. 2, further results on restricting SN P systems and variants using other derivation modes or semantics are interesting. Some of these semantics include: maximally parallel mode, exhaustive mode, generalized use of rules, time or clock-free systems, with more details from [61] and [6].

  The human brain, as with many examples in biology at least, seems to be quite “wasteful” in the sense that from childhood to adulthood some billions of neurons are created only to be pruned later. Such phenomenon may be an inspiration for pre-computed resources in [27] and emphasized again in [82] and elsewhere: an arbitrarily large number of resources (mainly, neurons and synapses) exists at the start of the computation, with some of these neurons later “activated” to efficiently solve problems. Perhaps to make such systems can become “closer” to biology for instance, by applying some normal or homogeneous form to them. For instance, in [56] the PSPACE-complete problem QSAT is solved in linear time. In [100] a normal form for regular expressions provides systems which characterize the class P, while a polynomial amount of time is upper bounded by the class PSPACE.

• 10. Lastly, we mention some “nearby” areas of similar inspiration with SN P systems. For instance, in the area of machine learning, it is of interest to use and extend SN P systems to recognize images, perform natural language processing, and more. A recent survey of efforts to combine machine learning with SN P systems and variants is [28]. In recent years, advances in computer vision and natural language processing are in part due to parallel processors such as GPUs, and recent variants of artificial neural networks known as transformers. However, it seems that only exceptionally large companies or organizations can afford the training and maintenance of “large” models of natural languages using transformers and GPUs: the cost of training and maintaining such models, even with a large number of expensive GPUs, can be very prohibitive. Such costs are usually in terms of processor hours, in joules or watts of energy. While many approaches are considered to reduce the costs of training and maintenance of such models, perhaps ideas based on normal or homogeneous forms, certainly the human brain, can further reduce the costs.

  Besides such issues on software and hardware, much of the modern computers today including parallel processors are based on the von Neumann architecture. Creating hardware and software inspired by the brain is known as neuromorphic computing: unlike the von Neumann architectures which is inspired by the Turing machine, a neuromorphic processor can be analog instead of digital, or use circuit elements other than silicon transistors. Again we ask how ideas on normal or homogeneous forms can aid in the design of such neuromorphic computers, since as late as around the first half of the twentieth century we know how similar and different human brains and digital computers can be [106].

  Other models bearing many similarities to SN P systems, certainly in the structural or visual sense, include Boolean circuits and Petri nets. Ideas for Petri nets and SN P systems are mentioned in problem N in [82], with latter works such as [13]. Some recent works involving similar analyses and properties between Petri nets and SN P systems include [3, 4] including formal verification in [41]. Petri nets and Boolean circuits seem to represent many interesting ideas related to normal or homogeneous forms, also similar to SN P systems in [111]. Thus, work between such nets, circuits, SN P systems and variants, are likely to lead to interesting or useful ideas. For instance, the feature of probabilistic or stochastic computation is well-known in Petri nets, but can still be further investigated for SN P systems, with some results in [8, 60, 112]. It is interesting to include a feature in WebSnapse to convert certain classes of SN P systems to Petri nets and vice-versa, including the support of colored spikes inspired by colored tokens [99].

  In relating SN P systems to Boolean circuits or similar models, we are likely to have or even require some normal or homogeneous form, to obtain further results on topology of SN P systems. What kinds of languages are computed by such systems with (non)planar and other types (for instance, kite or hammock, simple, acyclic) of graphs? How much time and space are required to solve hard problems using such systems? Further topics for investigations on SN P systems are in [85], with a recent book on applications, software, and hardware of P systems in [116].

Fig. 8

A visual suggestion for extending WebSnapse or similar software, for improved ease of access and integration of workflows, features, tools

4 Final remarks

A survey of results with the length of the present work, even confined on notions such as those in Sect. 2 is expected to be incomplete: at least a few previous works on such notions are likely to be missing in this work. For instance, at the time of writing the present work, it is likely that at least some of those mentioned in the list in Sect. 3 are already being investigated even if in preliminary form. Besides the results in Sect. 2, the problems and topics in Sect. 3 are mainly informed with the experience of the author working with SN P systems since around 2011, together with excellent and earlier lists such as [61, 82, 85, 88]. The present work is a brief survey on specific aspects of theory and pedagogy of SN P systems, with some recent surveys including more comprehensive details on theory (see [61]) and applications (see [36]). It is thus recommended to complement ideas from such recent and comprehensive surveys with problems and topics mentioned in Sect. 3 of the present work. While the research on SN P systems and variants is quite active, the author and many others, suspect much is still to come in both theory and applications of such systems. We end the present work with the provocative and hopeful last line from [101] by Alan Turing: “We can only see a short distance ahead, but we can see plenty there that needs to be done.”