1 Introduction

Membrane computing is a branch of natural computing inspired by the structure and the functioning of living cells (Păun 2000; Pan et al. 2019). Its models, called P systems, can be considered as distributed multiset rewriting, from a theoretical point of view (Valencia-Cabrera et al. 2020; Orellana-Martín and Riscos-Núñez 2020; Zhang et al. 2020). Beside many theoretical results and relations to other multiset-based models (like chemical reaction networks, Petri nets, register machines etc.), P systems have numerous applications in different fields ranging from biological modelling to robotic control and machine learning, we refer to Csuhaj-Varjú et al. (2021), Zhang et al. (2021a) for a recent overview. An SNP system is a variant of P systems that is particularly suitable for this last field and there are numerous results showing that it can provide highly competitive algorithms for different real-world problems, see a recent overview in Rong et al. (2018), Zhang et al. (2017).

P systems, as well as the related models, are mostly based on the multiset data structure (Dong et al. 2022; Zhang et al. 2021b). While a multiset can be seen as a set whose elements have multiplicity that can be greater than one, it is also possible to consider a multiset to be a vector of non-negative integer numbers (since its support/alphabet is finite). There are numerous models using a multiset or a vector of numbers as a data structure, e.g., P systems, Petri nets, vector addition systems, register machines, population protocols, Boolean networks etc. (this list is far from being exclusive) (Battyányi and Vaszil 2020; Adorna 2020). In order to be able to analyse and compare different P systems and also multiset-based models in general, the formal framework (FF) for P systems was developed (Freund and Verlan 2007; Verlan et al. 2020).

The core of FF is the family of models called Network of Cells (NC). This family corresponds to a very generic computing model that abstracts many computing models using multisets/vectors of numbers as a data structure. The data structure of NC is composed from distributed (spatially distinct) locations called cells each containing a multiset (of objects). Hence, as a whole, it can be seen as a vector of multisets. Because of the equivalence between a multiset and a vector of (non-negative) integers, the above representation can also be seen as a vector of vectors of integers. Obviously, a vector of vectors can be seen as a big vector obtained as a concatenation of individual components, the corresponding procedure being called flattening. However, doing so the location information might be lost and also the complexity of rules needed to handle the flattened model might increase.

The computation is performed by rules updating the contents of multisets and guarded by different context conditions verifying if the vector contents belongs to some (semilinear) sets. This allows to define the applicability of a rule and also of a group of rules, yielding the set of applicable multisets (groups) of rules. Also, an implicit secondary structure can be deduced by considering all cells involved in a single rule to be part of a connection. In the general case, this induces a hypergraph, however, in most of the situations a graph or even a tree structure is obtained.

The important point of the definition of NC is that it does not specify a default semantics and, in particular, how the data are input, output and processed. The definition is given in terms of abstract functions that produce the input, restrict the rule set to be applied and provide the output. These details are completed using the formal framework, which provides ready concrete specifications for common cases and mechanisms for more complex definitions. Thus, a concrete instance of a model from the family is obtained.

From the description above it looks clear that most of models that have a multiset (or a vector of multisets) as a data structure and that update this structure based on some kind of rewriting rules can be directly rewritten in terms of network of cells. This implies that there is trivial strong bisimulation between corresponding models and the matching instance of NC. We recall that in such case most properties valid for the NC are also valid for the target model. Hence, the model of network of cells combined with the formal framework gives a powerful tool for the specification, the analysis and the comparison of most models using multiset as a data structure.

In this paper we present the functioning of the model of network of cells and list some important bricks provided by the formal framework, especially in the context of SNP systems. The presentation is not focused on definitions, but rather aims to help in the understanding how to use the model. We present a series of examples and use cases showing how to use network of cells and the formal framework to understand, compare and extend models from the area of SNP systems.

The structure of the paper is organized as follows. Section 2 gives an introduction to the formal framework and SNP systems model. It also discusses the particularities of the representation of SNP systems in the formal framework. Section 3 considers some existing models from the area of SNP systems. It shows how they can be translated to NC using FF and explains how to analyse the obtained results. Section 4 gives examples of bisimulation between different variants of SNP and P systems using NC as intermediate. Section 5 explains how to extend existing systems with new features based on their NC descriptions. Finally, Sect. 6 summarizes the main points discussed in the paper and gives further research ideas.

2 Network of cells, formal framework and SNP systems

This section recalls the ideas behind the model of NC and the FF. We will not present the definitions and we refer to Verlan et al. (2020), Freund and Verlan (2007) for the formal details. This section also quickly presents SNP systems and the restrictions that can be considered in the formal framework when using SNP systems.

We start with a discussion on the links between multisets, vectors of numbers and vectors of multisets. For an alphabet V (of objects), a multiset over V is a mapping \(M:V\rightarrow \mathbb {N}\), where \(\mathbb {N}\) is the set of non-negative integers. It is custom to denote a multiset using a string w over V, where the multiplicity of each symbol corresponds to the value of M: \(\vert w\vert _a=M(a)\), for all \(a\in V\). It should be clear that there might be several strings denoting the same multiset. By numbering the symbols from V (\(V=\{a_1,\ldots ,a_n\}\)) it is possible to associate a vector v with M, where the component i (\(1\le i\le n\)) of v is equal to \(M(a_i)\). Hence, for a given finite alphabet V, there is a straight link between a multiset over V, a (commutative) string over V and a vector from \(\mathbb {N}^{\vert V\vert }\).

Example 1

Consider the alphabet \(V=\{a,b,c\}\) and the multiset M defined by \(M(a)=3\), \(M(b)=0\), \(M(c)=1\). Then M can be written as a string as aaac, aaca, acaa or caaa. Also, M can be written as a 3-dimensional integer vector as (3, 0, 1).

Remark 1

We would like to note that in the model of register machines (Minsky 1967), the configuration is described in terms of a vector of non-negative numbers. So, it is quite clear that the corresponding data structure is a multiset.

A vector of multisets (or a vector of vectors) can be seen as a single multiset over a bigger alphabet. This can be simply observed by taking the vector representation of the multiset. Then, by concatenating the corresponding vectors, a vector of higher dimension is obtained, that corresponds to a bigger multiset. We call this procedure flattening. We remark that while a vector of multisets is equivalent to its flattened version, it is still interesting to consider it in this manner, as it allows to spot the positional information easier.

Example 2

Consider the alphabet \(V=\{a,b,c\}\) and the vector of multisets \(v=(aab,abc,abbcc)\). In the vector representation this corresponds to the following vector of vectors of integers: ((2, 1, 0), (1, 1, 1), (1, 2, 2)). By concatenating each component a vector \(v1=(2,1,0,1,1,1,1,2,2)\) is obtained. This corresponds to the multiset \(a_1a_1b_1a_2b_2c_2a_3b_3b_3c_3c_3\) over the alphabet \(V'=\{a_1,b_1,c_1,a_2,b_2,c_2,a_3,b_3,c_3\}\). We observe that the first representation looks simpler and allows to better understand the structure of the multiset.

2.1 Network of cells and the formal framework

We start with the general schema depicting the relation between NC and FF. As shown on Fig. 1, the definition of NC specifies the notions of configuration and rule. More precisely, a configuration is a vector of multisets, each component being called a cell. Rules are defined as vector of multisets rewriting, guarded by context conditions. A context condition is defined via a vector of control languages, allowing the application of a rule only if each component of the current configuration belongs to the corresponding language. Hence, the definition of network of cells defines the applicability of a rule, the computation of the set of multisets of applicable rules (for a given configuration) and how a group (multiset) of rules is applied altogether, we refer to Verlan et al. (2020) for more details. The computation follows the algorithm below (also depicted on Fig. 2):

  1. 1.

    At each discrete time \(t\ge 0\), for a configuration C(t) (initially fixed, given by the definition) a configuration \(C'(t)\) is computed by combining C(t) and the input at time t.

  2. 2.

    Based on \(C'(t)\) and the set of rules \({\mathcal {R}}\), the set of multisets of applicable rules \(Appl({\mathcal {R}},C'(t))\) is computed.

  3. 3.

    This set is restricted according to the derivation mode (strategy) \(\delta\), yielding the set \(Appl({\mathcal {R}},C'(t),\delta )\).

  4. 4.

    If the size of \(Appl({\mathcal {R}},C'(t),\delta )\) is greater than one, a non-deterministic choice is performed in order to obtain the multiset of rules to be applied R (if the size is one, then the corresponding multiset is directly taken).

  5. 5.

    The multiset of rules R is applied to the configuration \(C'(t)\) yielding the next configuration \(C(t+1)\).

  6. 6.

    The above process is repeated for \(t+1\). The result is collected at each time step using an output function. It is possible to consider a halting mechanism and a single result.

Fig. 1
figure 1

An instance of a network of cells is obtained by specifying ingredients (input, output and derivation mode) from the formal framework

Full size image
Fig. 2
figure 2

A computational step is performed in following steps: (1) based on the current configuration, current input and the set of rules, the set of multisets of applicable rules is computed; (2) a derivation mode restricts the obtained set; (3) a non-deterministic choice is performed (if there are more than 1 variant); (4) the chosen multiset of rules is applied yielding the next configuration. The output of the system is obtained from each configuration

Full size image

Derivation mode One of the most important ingredients provided by the formal framework are the derivation modes. They concretize the semantics of the corresponding NC model, allowing it to be further considered in proofs or implementations. Technically, derivation modes are defined as set restrictions of the set of multisets of applicable rules computed for some configuration \(Appl({\mathcal {R}},C)\). This allows to extract from \(Appl({\mathcal {R}},C)\) the multiset(s) of rules satisfying the derivation mode property. We give below the informal description of some common derivation modes, see Freund and Verlan (2007) for more formal details.

  • Asynchronous (asyn): there is no additional restriction.

  • Sequential (seq): allows the application of only one rule at each time step.

  • Maximally parallel (max): at each step only maximally parallel multisets of rules from \(Appl({\mathcal {R}},C)\) can be used. A multiset (group) of rules R is maximally parallel, if there is no other multiset of applicable rules in \(Appl({\mathcal {R}},C)\) that strictly includes R.

  • Set-maximally parallel (also called flat) (smax): this variant corresponds to those maximally parallel multisets of rules, where each rule has the multiplicity at most one. It can also be seen as a set of rules that cannot be extended by a different rule and still be applicable.

  • Minimally parallel of size 1 (\(min_1\)): in this mode the rule set is additionally partitioned in subsets and from each subset at most one rule might be chosen such that the final result is not extensible by some rule (from a not yet considered subset).

We remark that set-maximally parallel derivation mode can be seen as \(min_1\) mode, where each partition is composed from exactly one rule. Usually partions correspond to cells, so it is then possible to say that a rule is “located” in the corresponding cell. In the area of Petri nets or register machines, generally, the sequential derivation mode is considered, while in the area of P systems the most common mode is the maximally parallel. However, this is different for spiking neural P systems, whose semantics is driven by the \(min_1\) mode.

Example 3

Consider a network of cells with a single cell and whose rules do not have context conditions. In this case, the configuration of the system is a multiset and the rules are plain multiset rewriting rules. Let the set of rules be defined as follows: \({\mathcal {R}}=\{r_1: a\rightarrow bc, r_2: abc\rightarrow cc, r_3: c\rightarrow ab\}\). Consider the configuration \(C=aabc\). Then, Table 1 gives the set of applicable multisets of rules for different derivation modes (for the \(min_1\) mode we consider the partition \(\{r_1,r_2\}\cup \{r_3\}\)).

Table 1 Applicable multisets of rules from Example 3 for different derivation modes
Full size table

Input Among different types of input described in the FF, we would like to mention 3 variants. The first one, initial input, corresponds to the input handling common in P systems or Petri nets—at the beginning of the computation input values (an input multiset) are added to the first configuration. The second variant, spike train input, inputs a value in the system by considering the time difference between two apparitions of some specific symbol in a specific location. The corresponding time difference is taken as the input data. Such input handling is common to the area of spiking neural P systems.

In both cases above, the input is single and it is added to the configuration (at some time step). The third variant, transient input, allows a recurrent insertion of data at some specific point of the configuration. E.g., some input value can be specified by a number of symbols a in the first cell, updated at each time step by an external entity. Such kind of input is interesting for the cases when the computation consists in continuously updating the output based on varying inputs, e.g., in the case of numerical P systems used for robot controllers.

Output As for the previous cases we shall focus on some common types of output described in FF. The most used one, called total halting, corresponds to the strategy when one waits until the system has no more applicable rules (i.e. it halts) and then the output of the computation is considered to be the contents of some predefined cell. A different strategy is a spike train output, which as in the case of the corresponding input would encode the result in the time difference between two apparitions of some value in some predefined cell. We remark that in this case there is no requirement for the system to reach a halting state, so there might be applicable rules, but they would never allow an apparition of the signal symbol in the output cell. Another strategy, the direct output, just collects a projection of the configuration of each step, and is particularly useful for transducer-like computation, e.g., for robot control applications. Finally, we would like to mention the decision output that returns a Boolean result: true if the system halts and false otherwise. This strategy is commonly used in the acceptor variants of NC.

The generic data structure and powerful rules allow a reasonable simple construction of an NC model for most variants of P systems, Petri nets and other multiset-based computing models.

2.2 Spiking neural P systems case

We recall here the definition of SNP systems given in Păun et al. (2010) and Ionescu et al. (2006).

A spiking neural P system of degree m is the following tuple:

$$\begin{aligned} \Pi = (O,\sigma _1,\ldots ,\sigma _m,syn,in,out), \end{aligned}$$

where

  • \(O=\{a\}\) is the singleton alphabet (a is called spike);

  • \(\sigma _i\), \(1\le i\le m\) are neurons of the form \((n_i,R_i)\), where \(n_i\ge 0\) is the initial number of spikes contained in \(\sigma _i\) and \(R_i\) if a finite set of rules of following two forms:

    • (spiking rules) \(E/a^c\rightarrow a;d\), where E is a regular expression over O (we also call it a context condition), \(c\ge 1\) and \(d\ge 0\). If \(E=a^c\), or \(d=0\) corresponding parts are omitted from the writing, e.g., \(a^c\rightarrow a\);

    • (forgetting rules) \(a^s\rightarrow \lambda\), \(s\ge 1\), with the restriction that for any rule of type \(E/a^c\rightarrow a;d\) from \(R_i\) we have \(a^s\not \in L(E)\);

  • \(syn\subseteq \{1,\ldots ,m\}^2\) with \((i,i)\not \in syn\), for all \(1\le i\le m\), are the synapses between neurons. The tuple \((\{1,\ldots ,m\},syn)\) forms a directed graph;

  • \(in,out\in \{1,\ldots ,m\}\) indicate the input and the output neurons of \(\Pi\).

A firing rule \(E/a^c\rightarrow a;d\in R_i\) is applicable in neuron \(\sigma _i\) if it contains \(k\ge c\) spikes and \(a^k\in L(E)\). The application of such a rule removes c spikes from \(\sigma _i\) and delivers a spike to each connected (via a synapse) neuron after d computational steps (at the same step if \(d=0\)). In the period after the spikes were removed and before they were emitted (at steps 1 to \(d-1\)), the neuron remains closed. Any spike arriving to a closed neuron is lost and also no rule can be applied (even selected) in the meanwhile. A forgetting rule just removes the corresponding number of spikes.

During each step of the computation, all applicable rules are selected for the application, with the condition of selecting at most one rule per neuron. The computation starts with the initial configuration given by the initial contents of neurons and continues by applying at each step rules as described above. The input and the output are done using a spike train, as described earlier in this section.

Informally, an SNP system is a set of neurons (cells) containing an integer number of spikes (denoted by a power of symbol a) arranged in a directed graph structure. Each neuron contains rules that remove a number of spikes from it and add one spike to each interconnected neuron (in the case of non-forgetting rules). Rules are guarded by regular expressions and may have a delay. They are executed in parallel, but at most one rule per neuron is executed.

The NC model corresponding to SNP systems has some particularities that we would like to present below. First, since the alphabet of the system is composed of a single symbol, a, the dimension of each vector corresponding to a cell is 1. Hence, in this case it becomes interesting to flatten the system and consider as configuration a vector of dimension n corresponding to the number of cells in the system. To facilitate the description, we assume that all the delays are equal to zero. As shown in Ibarra et al. (2007) such model has the same computational power. In Sect. 5.1 we will show how it is possible to simulate the notion of delay in systems without delay.

Next, a spiking rule \(E/a^n\rightarrow a\) corresponds to the subtraction of n from the current neuron and addition of 1 to each connected neuron, if the current number of spikes belongs to L(E). Because of a single-letter alphabet, L(E) corresponds to a semilinear set of numbers \(S_E\). So, the regular test for the contents of neuron i, \(1\le i\le n\), can be replaced by the test \(C_i\in S_E\), where \(C_i\) is the i-th component of the current configuration C.

So, for an SNP system with m neurons, each rule \(E/a^n\rightarrow a\) can be written as \(K/V\), where V is a vector of integers (so \(V\in \mathbb {Z}^m\)) and K is a vector of semilinear sets such that \(n\in K_i\) and \(S_E\subseteq K_i\) (where \(S_E\) is the semilinear set associated to E). Such rule is not linked to a neuron/cell — it describes the rule action at the global level. To apply a rule r : \(K/V\) one has to check that for the current configuration C and every i that \(C_i\in K_i\) and then the result of the application of r is \(C+V\), similar to a vector addition system.

Since, in most of the cases, a spiking rule verifies only the contents of a single cell, it becomes possible to simplify the notation by omitting semilinear checking sets for other cells (and that are always equal to \(\mathbb {N}\) in this case). Using the convention from above, such a rule is then written as \(i: K_i/V\). A further simplification might be done by observing that if the number of cells n is big, there is a high probability for vectors V from rules to be sparse. Hence, it is possible to use any sparse vector notation to simplify the writing of rules for such cases. In what follows we have chosen to indicate the component the value belongs to as an index enclosed in a circle (e.g., \(1_{\textcircled {3}}\) means value 1 in the third component).

Fig. 3
figure 3

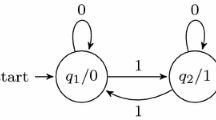
The spiking neural P system considered in Example 4

Full size image

Example 4

Consider the SNP system depicted on Fig. 3. In Table 2 we give the different notations for the rules. We also note that the configuration is a vector of size 4 and that the depicted configuration corresponds to the vector (2, 1, 3, 0). Finally, we would like to observe that the system functions in \(min_1\) mode (like most of SNP systems) and uses an initial input and a spiking train output.

Table 2 Different notations for rules from Example 4
Full size table

We give below first 4 steps of the evolution of the system.

Step

\(C_1\)

\(C_2\)

\(C_3\)

\(C_4\)

0

2

1

3

0

1

2

2

2

1

2

1

1

1

1

3

1

1

1

2

4

1

1

1

3

The exclusive normal form As shown in Verlan et al. (2020), any SNP system (and most of its variants) can be rewritten in the following form (the definition in the paper is stated in terms of NC).

Definition 1

A spiking neural P system is said to be in the exclusive normal form (ENF), if for any neuron i, all rules from that neuron have their corresponding regular expressions either disjoint or equal, i.e., if rules \(E_1/a^k\rightarrow a\) and \(E_2/a^m\rightarrow a\) belong to the same neuron, then either \(L(E_1)\cap L(E_2)=\emptyset\), or \(E_1=E_2\). Additionally, the exclusive normal form states that if the regular expression holds, then there are enough spikes to apply the corresponding rule, i.e., for any \(x\in L(E_1)\), we have \(\vert x\vert \ge k\).

An important property of a system in the exclusive normal form is that for any neuron it is possible to partition its rules into several disjoint groups such that at each time moment, if there are applicable rules, then all of them are from the same group. We call rules belonging to groups of size 1 independent rules and the other ones choice rules. Thus, the application of independent rules is always exclusive—no other rule can be applied in the same neuron, while the application of choice rules is always subject to a non-deterministic choice. Moreover, the partition of rules into groups is done based on the syntactic equality of corresponding regular expressions: two rules in the same neuron \(E_1/a^k\rightarrow a\) and \(E_2/a^m\rightarrow a\) will belong to the same group if and only if \(E_1=E_2\), which can be very easily checked. We note that the equality of expressions is checked (\(E_1=E_2\)) and not of their languages (\(L(E_1)=L(E_2)\)), which is a bit longer to verify.

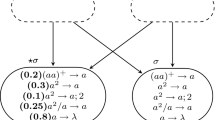
Example 5

Consider an SNP system having in some neuron the following two rules:

$$\begin{aligned} (a^2+a^3) / a\rightarrow a\quad (a^2)^* / a^2\rightarrow a \end{aligned}$$

The intersection of the two regular expressions is \(a^2\), also there is no sense to match \(\lambda\). Hence, these two rules can be rewritten to be in ENF as follows.

$$\begin{aligned} a^2 / a\rightarrow a\quad a^2 / a^2\rightarrow a \\ a^3 / a\rightarrow a\quad a^4(a^2)^* / a^2\rightarrow a \end{aligned}$$

Finally, we recall that this result is stated in terms of NC and in this case the regular expressions are replaced by their numerical counterpart—semilinear sets.

Bisimulation with NC and other P system models We recall an important consequence of the representation of SNP systems using network of cells. There is a one-to-one correspondence between the configurations of each model and also a one-to-one correspondence between rules from SNP and NC (which are of a particular type). This combined with \(min_1\) derivation mode semantics results in a strong bisimulation between SNP systems and (a variant of) NC. Consequently, any statement that can be shown in terms of an SNP system, also holds for the corresponding NC system and conversely.

The above remark is the strong point of NC and FF, allowing to use a single model/language for the analysis and comparison of different variants of SNP and even P systems. Subsequent sections show several examples of the benefits of such translation.

Moreover, the representation of SNP systems in terms of NC allows to draw links with other types of models, e.g., with ordinary P systems. For example, SNP systems where the regular expression for each rule is equal to its left-hand side (\(a^k/a^k\rightarrow a\)) and using initial input and total halting are identical to a subset of purely catalytic P systems (using a single letter different from the catalyst in the left-hand side of rules). This is obvious, because the NC representation of both models is the same. We refer to Sect. 4 for more details.

Another important point highlighted in Verlan et al. (2020) is that any SNP system corresponds to some specific NC working in sequential mode. Hence, somehow an SNP system corresponds to a sequential device able to perform semilinear checks on vectors of integers. This might be interesting for the implementation of such models, as there is no need to handle the parallelism.

3 Understand and analyze models

In this section we give several translations of different variants of SNP to NC and we show how the usage of NC and FF can help in their understanding and analysis.

3.1 Extended rules

In the standard model of SNP systems, when a rule is applied, one spike is sent to each connected neuron. Several extensions allow to modify this behavior and allow to send more spikes over a connection. Here we concentrate on 3 variants of such extension. In the first variant more than one spike can be sent over all connections exiting a neuron. The second variant allows to send different numbers of spikes over the exiting connections, but this number is fixed in advance. The third variant is the most flexible, as it allows to describe on a per rule basis the number of spikes sent over each connection.

The first variant, spiking neural P systems with extended rules, was introduced in Chen et al. (2008). Its definition differs from SNP systems only by the form and semantics of rules, which are of the form \(E/a^m\rightarrow a^n\). The difference with an SNP rule \(E/a^m\rightarrow a\) is that as a result of its execution n spikes are sent to each connected neuron, see Fig. 4a. This can obviously be written in terms of NC by using n instead of 1 in corresponding vector components. More precisely, a rule \(E/a^m\rightarrow a^n\) from a neuron i can be written using the simplified sparse notation as , where \((i,i_j)\), \(1\le j\le k\) is an edge in the synapse graph and \(S_E\) is the semilinear set corresponding to the regular expression E.

The second variant, spiking neural P systems with weighted synapses, is considered in Pan et al. (2012). The difference with SNP systems is the following: to each synapse (edge) there is a positive integer associated, the weight. When a rule is executed, each connected neuron receives the number of spikes equal to the weight of the corresponding synapse, see Fig. 4b. The translation of such rules to NC is not difficult: the value 1 should be replaced by the synapse weight for corresponding components. So, a rule \(E/a^m\rightarrow a\) becomes , where where \((i,i_j)\), \(1\le j\le k\) is an edge in the synapse graph having the weight \(n_j\).

The third variant, called extended spiking neural P systems, was considered in Alhazov et al. (2006). It features rules of form \(E/a^m\rightarrow (i_1,w_1)\dots {}(i_k,w_k)\). When such a rule is applied, each neuron \(i_j\), \(1\le j\le k\) receives \(w_k\) spikes. Even if such rule looks complex, it corresponds directly to the NC rule , see the example depicted on Fig. 4c.

Fig. 4
figure 4

Different extended spiking rules and their translation to the simplified network of cells notation: a extended rules (sending \(a^n\) over all synapses); b weights on synapses (sending \(a^k\) over the synapse with weight k); c extended SNP (allow for choosing different amounts of spikes to be sent over specified synapses, may even depend on the applied rule). In all cases \(S_E\) is the semilinear set of numbers corresponding to E

Full size image

3.2 Multiple type of spikes/colors

Several papers, e.g. (Ionescu et al. 2011; Song et al. 2017), consider SNP systems that can have multiple types of spikes, by using symbols different from a. Sometimes, these different types are referred as colors as it is custom to do in the area of Petri nets. In this case the simplification of the notation operated in Sect. 2 cannot be performed anymore: the configuration should be treated as a vector of multisets and the rules should be considered in the generic form as two vectors of multisets and a vector of semilinear sets. The translation to NC still remains straightforward, as spiking rules (even with several symbols) correspond to a subset of arbitrary NC rules (that verifies the context condition only in a single cell).

We would like to notice that the obtained NC translation is extremely close to a translation of transitional or tissue P systems. If the regular expression check is not taken into account, then corresponding spiking model is just a tissue P system where the result of a rule is sent to all connected membranes (this can be expressed in terms of rules of tissue P systems). Hence, by using several types of spikes very powerful models, generalizing tissue P systems, can be obtained. Therefore, it is important to add additional restrictions to such models, otherwise there is no point of introducing them in the SNP framework. For example, in Ionescu et al. (2011) only a single spike of some type can be obtained. However, in our opinion it is more logical to study such models directly in P systems framework.

3.3 Communication on request

In this section we analyse the model called spiking neural P systems with communication on request introduced in Pan et al. (2017). In this model the rules do not produce spikes to be distributed among neurons, but rather request a number of spikes from some other neuron. Such rules are written as E/Qw, where \(w=(a^{n_1},i_1),\ldots ,(a^{n_k},i_k)\). We remark that the original paper considers several types of spikes, but here we use a single one in order to simplify the presentation. A rule as above has the following semantics: if the contents of neuron i belongs to E, then request \(a^{n_j}\) spikes from neuron \(i_j\), \(1\le j\le k\). It is clear that corresponding neurons shall contain at least the requested number of spikes for the rule to be applicable. If \(n_j=\infty\), then all spikes from the corresponding neuron are requested. A particular semantic condition is also checked when several rules are applied. In fact, the request values for each neuron should match: it is not possible for a rule to request 4 spikes from neuron 2 and for another rule to request 3 spikes from the same neuron. Also, if several rules request the same amount of spikes n from a neuron j, then the neuron j loses only n spikes, while the other neurons get n spikes each. This is called spike replication and it is necessary in order to increase the number of spikes in the system.

Let us first discuss the case when there are no rules that request all spikes and we also suppose that any pair of applicable rules does not contain requests for the same neuron. In such case a rule \(E/Q(a^{n_1},j_1),\ldots ,(a^{n_k},j_k)\) from neuron i (for a system of m neurons) can be written in NC as the following general rule (we denote by \(S_E\) the semilinear set corresponding to E):

$$\begin{aligned}&(S_1,\ldots ,S_m) / (V_1,\ldots ,V_m), \mathrm{ where}\\&S_l={\left\{ \begin{array}{ll} \{n\in \mathbb {N}\mid n\ge n_j\} &\quad \mathrm{if }\, l=j_k,\\ S_E &{} \quad \mathrm{if }\, l=i,\\ \mathbb {N}&{} \quad \mathrm{otherwise.} \end{array}\right. }\quad \\&V_l={\left\{ \begin{array}{ll} -n_j &\quad \mathrm{if }\, l=j_k,\\ n_1+\dots +n_k &\quad \mathrm{if }\, l=i,\\ 0 &\quad \mathrm{otherwise.} \end{array}\right. } \end{aligned}$$

Now consider the case when the replication is allowed. This means that several rules can contain requests to the same neuron. It is not difficult to see that the above construction does not work anymore. The only way to handle such a condition is to adapt the method used to transform any SNP system to a sequential NC model as described in Verlan et al. (2020). This means to consider all combinations of rules (taking a single rule from a neuron) and to associate to each combination of matching rules (those that request same value from a neuron) a single rule that will perform the regular expression check for every neuron and that will compute the overall effect taking into account the replication. For example, rules \(E_1/Q(a^2,3)\), \(E_2/Q(a^2,3)\) \(E_3/Q(a,1)\) in neurons 1, 2 and 3 respectively (in a system having 3 neurons) become the rule

$$\begin{aligned} (E_1\cup \{x\in \mathbb {N}\mid x\ge 1\},E_2,E_3\cup \{x\in \mathbb {N}\mid x\ge 2\}) / (1,2,-1) \end{aligned}$$

Hence, when the replication is used, the corresponding system is checking conditions in several neurons at the same time and then adds a vector whose sum of values is strictly positive.

In the case of the “all” request, the situation cannot be modeled in a simple manner, as rules such as above can only take into account a fixed amount of spikes. In order to simulate the unbounded transfer, either an unbounded derivation mode should be used (e.g., maximally parallel), or a sequential simulation should be performed, but this would require an unbounded number of steps, which does not allow to construct a bisimulation.

So, we can deduce that the analyzed model can be seen as a collection of 3 different models. The first one (without replication), corresponds to a standard NC where it is possible to check context conditions in several neurons at a time. The second variant (with replication), cannot be directly described by an NC. Instead, it can be simulated by an appropriate NC step by step. The third model either changes the derivation mode to an unbounded one, or requires a potentially unbounded simulation by NC. So, the overall definition corresponds to a hybrid model that at each step functions in one of the ways described above.

4 Relate models by bisimulation

In this section we consider two models of SNP systems and we show that their translation to NC is the same, which implies that these two models can be related using a bisimulation.

The first model, called Spiking neural P systems with multiple channels (SNPSMC), was introduced in Peng et al. (2017). The second model, called Spiking neural P systems with target indications (SNPSTI), was considered in Wu et al. (2021). Both models have definitions very close to SNP, the only difference being the form and the semantics of their rules. In both cases the computation follows \(min_1\) derivation mode, an initial input and a spike train output are considered.

The definition of the first model has the following differences with the standard model of SNP:

  • Synapses (graph edges) are labelled by labels from a fixed set of labels L (we assume also the existence of the function lab that returns a label for an edge).

  • Each non-forgetting rule of neuron i is of form \(E/a^c\rightarrow a^p(l)\), with \(l\in L\) and \(c\ge p\ge 0\).

The semantics of the above rule is that if the contents of the corresponding neuron satisfies E, then c spikes would be removed from the current neuron (i) and p spikes will be added to all neurons connected by synapses (edges) whose label is equal to l. So, in terms of NC such rule can be written as, where \(\{(i,i_j)=l\mid 1\le j\le k\}\) is the set of all outgoing egdes from i labelled by the label l.

The definition of the second model has the following difference with the standard model of SNP:

  • Each non-forgetting rule of neuron i is of form \(E/a^c\rightarrow a^p(tar)\), where \(tar\subseteq \{1,\ldots ,m\}\) (m is the number of neurons) and \(c\ge p\ge 0\).

The semantics of the above rule is that if the contents of the corresponding neuron satisfies E, then c spikes would be removed from the current neuron (i) and p spikes will be added to all neurons listed in the set tar. So, in terms of NC such rule can be written as , where \(tar=\{i_1,\ldots ,i_k\}\).

We observe that the representation of both types of rules is very similar. We shall argue now that it is possible to transform a rule of one type to the other one. For a neuron i let \(tar_l=\{i_k\mid lab(i,i_k)=l\}\). Then a rule \(E/a^c\rightarrow a^p(l)\) of SNPSMC is equivalent a rule \(E/a^c\rightarrow a^p(tar_l)\) in SNPSTI (their NC representation is the same). Conversely, for \(1\le i\le m\) let \(s^i_1,\ldots ,s^i_{2^{m-1}-1}\) be the set of non-empty subsets of \(\{1,\ldots ,m\}\setminus \{i\}\). Consider the set of labels \(l_{i,j}\), \(1\le i\le m\), \(1\le j\le 2^{m-1}-1\). To each set \(s^i_j\) we associate the label \(l_{i,j}\). Then, a rule \(E/a^c\rightarrow a^p(tar)\) of SNPSTI is equivalent to a rule \(E/a^c\rightarrow a^p(l_{i,j})\), \(tar=s^i_j\), in SNPSMC (as again, their NC representation is the same).

Hence, for any SNPSMC \(\Pi\) it is possible to construct SNPSTI \(\Pi '\) such that they have the same configurations and any step in \(\Pi\) corresponds to a step in \(\Pi '\) and conversely. Hence, there exists a bisimulation relation between the above two models and that they are equivalent, see Fig. 5. This means that in some sense the models are “the same”—any affirmation about the computation in one model is also true for the other one. There is also a direct link between the descriptional complexity parameters of both models.

Fig. 5
figure 5

The bisimulation relation between spiking neural P systems with multiple channels and spiking neural P systems with target indications is obtained via a translation to NC where it can be seen that corresponding rules yield the same translation

Full size image

4.1 Catalytic P systems

Consider a SNP system \(\Pi\) where the regular expression for any rule is equal to its left-hand side: \(a^n / a^n\rightarrow a\) (in such case the rule is simply written \(a^n\rightarrow a\)). In this case, the regular expression check is not necessary in order to apply the rule, it suffices to verify that there are enough copies of a. Hence, such a rule translates to NC as m-dimensional vector having \(-n\) in position i and 1 for each position \(j_1,\ldots ,j_k\), corresponding to a connected neuron: . Now let’s interpret the configuration of \(\Pi\) as a multiset over some alphabet \(O=\{a_1,\ldots ,a_m\}\) of cardinality m. In this case, the NC rule above corresponds to a multiset rewriting rule \(a_i^n\rightarrow a_{j_1}\dots {}a_{j_k}\).

Hence, an SNP system as above corresponds to a context-free multiset rewriting. We remark that in order to obtain a bisimulation the multiset rewriting (as well as the NC model) should use the same semantics as SNP systems, i.e., they should be executed in \(min_1\) derivation mode, where each partition groups all rules with same \(a_i\) in the left-hand side. As shown in Verlan (2013) such systems correspond to purely catalytic P systems (Păun 2002) with m catalysts working in maximally parallel derivation mode and having rules of form \(c_ia_i^n\rightarrow w\), \(w\in O^*\), \(\vert w\vert _{a_i}=0\) and \(\vert w\vert _{a}\le 1\), for all \(a\in O\).

So, we obtain that any SNP system with rules of type \(a^n\rightarrow a\) (and of course \(a^n\rightarrow \lambda\)) is equivalent to a purely catalytic P system with m catalysts having rules of form \(c_ia_i^n\rightarrow w\), \(w\in O^*\).

5 Extend models

In this section we discuss how the representation using networks of cells can give ideas and help in the extension of spiking-based models.

5.1 Delays

First, we show how to implement delays. Of course, the delays are a part of the definition of the basic model of SNP systems. However, there is an important question: for a given SNP system with delays \(\Pi\) how to construct an equivalent system without delays, or at least a system that simulates \(\Pi\) (i.e., yields same results for the same inputs). Since systems without delays are computationally complete (Ibarra et al. 2007), it is always possible to construct a simulating system, but this affirmation is non-constructive. So, for a given SNP system with delays it might be not trivial to construct a system without delays and having the same behavior.

In what follows, we will try to make a simple construction in order to simulate the delays at the expense of using a different type of rules. First, we recall the semantics of the model when a rule with a delay is applied. Let \(r=E/a^n\rightarrow a;d\) be such a rule, located in neuron i. If r is applied, then n spikes are removed from neuron i and the neuron emits 1 spike to each connected neurons after d computational steps (if \(d=0\) then the spike is emitted immediately). During this time the neuron is “closed”, i.e., any spike sent to it during this period is lost. In order to simulate such a behavior we will implement the notion of the state of a neuron. For SNP we will use only two states: open and closed. However, the proposed construction is also applicable for more states, e.g., corresponding to neuron polarisations. In order to do this, we will adapt the method used to add the state notion to a membrane in P systems, described in Verlan (2013). First, we associate to every neuron i a new neuron \(state_i\). Now, a single spike in neuron \(state_i\) encodes that the neuron i is open and two spikes in neuron \(state_i\) mean that neuron i is closed.

Next, for any rule (the NC equivalent of \(E/a^n\rightarrow a;d\)) using a delay \(d>0\) we consider an additional neuron \(counter_{i,r}\) that will contain the delay counter for the corresponding rule. Consider now following rules (see also Fig. 6). Since the labels of neurons become large, in what follows, we use a different sparse notation: instead of we will write (i, m).

$$\begin{aligned}&\mathrm{Neuron i:}\\&\quad \quad \quad i: S_E/(i,-n), (state_i,1), (counter_{i,r}, d), \quad \mathrm{ if }\, d>1\\&\quad \quad \quad i: S_E/(i,-n), (state_i,2), (counter_{i,r}, 1), \quad \mathrm{ if }\, d=1\\&\mathrm{Neuron state}_i:\\&\quad \quad \quad state_i: \{2\} / (state_i, -1)\\&\mathrm{Neuron counter}_{i,r}:\\&\quad \quad \quad counter_{i,r}: \{3,\ldots ,d\} / (counter_{i,r}, -1)\\&\quad \quad \quad counter_{i,r}: \{2\} / (counter_{i,r}, -1) (state_i, 1)\\&\quad \quad \quad counter_{i,r}: \{1\} / (counter_{i,r}, -1) (i_1,1),\ldots ,(i_k,1) \end{aligned}$$
Fig. 6
figure 6

The simulation of delays by rules without delays. The part of the system allowing to simulate an NC rule \(i:S_E/(i,-n),(i_1,1),\ldots ,(i_k,1);d\) corresponding to a spiking rule \(i: E/a^n\rightarrow a;d\). The used sparse vector notation represents a value v in the i-th component of the vector by (i, v)

Full size image

Finally, all existing rules (including the rules we added above) should be adapted to take into account the fact that the neuron can be closed. To simplify the writing we will consider as example the rule . We replace this rule by two rules that check cells j and \(state_i\) at the same time. The first rule will verify that the contents of \(state_j\) is equal to one, and then will act as r. The second rule will check if \(state_j\) is equal to two and if this is the case, it will just decrease the value from cell j. More formally, this can be rewritten as follows (where p is the total number of neurons in the system after the addition of the abovementioned ones).

$$\begin{aligned}&(E_1,\ldots ,E_p) / (v_1,\ldots ,v_p),&(E_1',\ldots ,E_p') / (v_1',\ldots ,v_p')\\ \mathrm{where}\\&E_l = {\left\{ \begin{array}{ll}S &{} \mathrm{if }\, l=j\\ \{1\} &{} \mathrm{if }\, l=state_i\\ \mathbb {N}&{} \mathrm{otherwise} \end{array}\right. }&\quad E_l' = {\left\{ \begin{array}{ll}S &{} \mathrm{if }\, l=j\\ \{2\} &{}\quad \mathrm{if }\, l=state_i\\ \mathbb {N}&{}\quad \mathrm{otherwise} \end{array}\right. }\\&v_l = {\left\{ \begin{array}{ll}-n &{} \mathrm{if }\, l=j\\ 1 &{} \quad \mathrm{if }\, l=i\\ 0 &\quad \mathrm{otherwise} \end{array}\right. }&\quad v_l = {\left\{ \begin{array}{ll}-n &{}\quad \mathrm{if }\, l=j\\ 0 &{} \quad \mathrm{otherwise} \end{array}\right. } \end{aligned}$$

It is clear that any rule can be replaced in this manner by several rules that add additional checks for the state corresponding target neurons. This can lead to a combinatorial explosion as the number of introduced rules depends exponentially on the number of target neurons.

Now we would like to conclude by the remark that the above transformation is rather complex and needs several strong ingredients like extended rules and checking for regular expressions in several neurons at the same time. This suggests that the delay feature is a very complex contextual mechanism that potentially needs to verify the contents of all neurons before making a decision. This is “hidden” in the definition of SNP systems by the sentence explaining that a closed neuron does not accept any spike. So, in our opinion, there is a huge difference in the functioning between SNP systems with and without delays and we suggest to consider them as completely different models (although having the same computational power).

5.2 Derivation modes and probabilities

Another possible extension is to consider different derivation modes. We recall that, by definition, SNP systems work in \(min_1\) mode. Using NC and FF it becomes trivial to investigate the functioning of SNP in other modes, e.g., the maximally parallel or set-maximal (thus allowing to apply several rules in the same neuron at the same time).

Another interesting topic is the integration of the probabilistic evolution for SNP systems. The first idea is to associate probability values or stochastic/kinetic constants to each rule and to chose a rule from each neuron based on the corresponding normalized probability. More precisely, if in a neuron i containing n spikes at some time t there are k applicable rules \(r_1,\ldots ,r_k\) having probabilities \(p_1,\ldots ,p_k\), then the probability to chose a rule j is defined by:

$$\begin{aligned} p(r_j,n) = \frac{p_j}{\sum _{l=1}^n p_l},\qquad r_l \mathrm{ is\,applicable\,to }\, n. \end{aligned}$$

In this case each neuron behaves independently from the other ones and the rule probability depends only on the contents of each neuron.

Another possibility is to explore the idea of the groupwide probability as developed in Verlan (2013) for NC models. The main idea is to assign different probabilities for groups of applicable rules (from the set \(Appl({\mathcal {R}},C)\)). In order to compute the probability of joint application of a set of rules R for a configuration C, p(R, C), we rely on the propensity function \(f:2^{\mathcal {R}}\times \mathbb {N}^m\rightarrow \mathbb {R}\), where \({\mathcal {R}}\) is the set of rules of the system having m neurons. This function associates a real value for a set of rules with respect to a configuration. Hence the value f(R, C) depends not only on the set of rules R, but also on the configuration C. We remark that the construction from (Verlan 2013) considered multisets of rules, which are reduced here to sets because of the functioning in \(min_1\) derivation mode.

Then, the probability to choose a set \(R\in Appl({\mathcal {R}},C)\) is defined as the normalization of corresponding probabilities:

$$\begin{aligned} p(R,C)=\frac{f(R,C)}{\sum _{R'\in Appl({\mathcal {R}},C)}f(R',C)} \end{aligned}$$
(1)

Among different propensity functions discussed in Verlan (2013) we cite those adapted to the case of SNP systems.

  • Constant strategy: each rule r from R has a constant contribution to f and equal to \(c_r\):

    $$\begin{aligned} f(R,C)=\prod _{r\in R}c_r \end{aligned}$$
    (2)

  • Concentration-dependent strategy: this strategy originating from the mass-action law states that each rule r from R has a contribution to f proportional to a stochastic constant \(c_r\) that only depends on r and \(h_r(C)\), the number of ways it is possible to pick up the needed number of spikes from C by considering them as distinct objects (by \(\left( {\begin{array}{c}a\\ b\end{array}}\right)\) we denote the binomial function):

    $$\begin{aligned} h_r(C)&=\left( {\begin{array}{c}C_i\\ n\end{array}}\right) , \mathrm{ where }\, r=i: E/a^n\rightarrow a\\ f(R,C)&=\prod _{r\in R}c_r h_r(C) \end{aligned}$$

  • Gillespie strategy: each rule r from R has a contribution to f that depends on the order in which it was chosen and it is equal to \(c_r\cdot h_r(C')\), where \(C'\) is the configuration obtained by applying all rules that were chosen before r.

We remark that the concentration-dependent strategy is not equal to Gillespie strategy. More precisely, in a Gillespie run the probability to choose a new rule depends on the objects consumed and produced by previously chosen rules. We can consider a Gillespie run as a sequence of sequential (single-rule) applications using the concentration-dependent strategy.

We would like to remark that in the area of SNP systems, often stochastic evolution is considered. In this case, the time needed for the rule execution is determined by some probability distribution. When considering a discrete time, this can be somehow rephrased as follows: instead of a single rule, there are copies of this rule, but using different delays. Each such copy has a probability, whose value is driven by the desired probability distribution. E.g., if the uniform distribution is considered and the rule can fire the spike on steps 0 to 4 after it was executed, then this corresponds to having 5 copies of the original rule, with delays from 0 to 4 and where the probability of each rule is the same. Thus, in the discrete time case it is somehow possible to reduce a stochastic evolution to a probabilistic one.

5.3 Non-integer values

Another interesting extension idea comes from the observation that the configuration of SNP systems can be represented as vectors of integer numbers (over \(\mathbb {N}\)) and rules as semilinear sets (which are also over \(\mathbb {N}\)) combined with vectors over \(\mathbb {Z}\). The computation can be seen as a membership query followed by an addition.

So, a natural idea is to replace \(\mathbb {N}\) by a different set allowing the above operations, e.g., \(\mathbb {Z}\), \(\mathbb {R}\) or even an arbitrary group. The paper (Freund et al. 2015) investigated such replacements in the framework of NC with finite context conditions. We discuss below what are the particularities of such approach for SNP-like systems.

First we recall that SNP systems evolve in \(min_1\) derivation mode. As discussed in the aforementioned paper, bounded derivation modes allow to define a consistent semantics for an arbitrary abelian group. As for the context conditions, it is possible to use group operations to define a similar notion.

Let A be an abelian group. Consider \(v,v_1,\ldots {},v_m\in A\). We define a linear combination of \(v,v_1,\ldots {},v_m\) the set

$$\begin{aligned} S = v + \sum _{i=1}^m\lambda _i v_i,\qquad \mathrm{ where }\ \lambda _i\in \mathbb {N}\end{aligned}$$

We observe that since A is a vector space, the formula above can be seen as the set of linear combination of vectors \(v,v_1,\ldots ,v_m\).

A semilinear combination is a finite union of linear combinations. We will denote by SL(A) the set of all semilinear combinations of elements from an abelian group A.

Now, by taking an abelian group A, it is possible to extend an SNP system by considering that its configuration is the vector \(A^n\) and its rules are of type S/V, where \(S\in SL(A)^n\) and \(V\in A^n\).

In the area of SNP systems several models using supports other than \(\mathbb {N}\) were considered. For example, the model with anti-spikes (Song et al. 2018) considers \(\mathbb {Z}\) and the model from Wang et al. (2010) uses \(\mathbb {R}\) as a support. However, while the above papers concentrated on the replacement of the configuration and value vector, the extension of the context condition was minimal (none in the case of anti-spikes and only by threshold sets \(\mathbb {R}_{<T}=\{x\in \mathbb {R}\mid x<T\}\) in the second case).

In our opinion, a particular attention deserves the variant using real-numbers as support, which is interesting for many real-world applications. The interesting point is that any Boolean combination of (real) intervals is a semilinear combination, hence it is possible to use complex rules using any Presburger arithmetic-like syntax. For example, one can have the following rule.

$$\begin{aligned}&(P,P,Q)/(-1.5,1,-0.5),\quad \mathrm{where }\\&P=\{x\in \mathbb {R}\mid x<10\} \mathrm{ and }\\&Q=\{x\in \mathbb {R}\mid (x\ge 5.5 \vee x<10) \wedge (x>0 \vee x\le 1.1)\}. \end{aligned}$$

A next step can be done by considering that the base of the configuration and rules is defined by a Boolean fuzzy set, so corresponding elements become fuzzy truth values. The paper (Wang et al. 2013) implicitly considers such a variant. As context conditions fuzzy cuts are used. By applying the same reasoning as above for \(\mathbb {R}\) it is possible to have richer conditions that can be useful for different practical applications.

6 Conclusion

In this paper we presented a tutorial aiming to help persons willing to better understand the model of network of cells and the formal framework in the context of SNP systems. We would like to highlight that the presented tools do not aim to replace the existing (and future) syntax and definitions of models related to SNP systems. The main idea is to use the description provided by NC and FF as a complement to already existing research. We stress that NC and FF provide a powerful tool allowing to better analyse, compare and extend existing models and, in our opinion, it should be considered only with this goal. At the same time, we suggest to use this tool on a regularly basis as our experience shows that this might provide important insight about the existing research and suggest future research ideas.

Beside topics discussed in this tutorial it might be interesting to consider the adaptation of the FF to the case of dynamical structures, i.e., when the number of neurons/cells can also evolve during the computation. Such demand is regularly observed in applications related to machine learning. The paper (Freund et al. 2013) gives some ideas how to handle such cases, however corresponding constructions are much more complex than for the case of a static structure.

Another interesting topic is to consider non-semilinear conditions and vector operations. As shown in Alhazov et al. (2015), Shang et al. (2021) more powerful conditions allow to express in a simpler (and shorter) way a desired complex behavior.