1 Introduction

Composite structures and panels are modern structures possessing a considerably high strength-to-weight ratio due to their unique properties (Pekbey et al. 2012; Maleki and Toygar 2019; Hoseinzadeh et al. 2023; Maleki et al. 2022; Niu et al. 2022; Li et al. 2022). In general, low weight, resistance to a specific load, and multi-purpose ability have increased the usage of these panels (Vinyas 2020). A sandwich structure comprises two thin yet strong layers that coat a flexible, soft, and moderately thick core. The layers are frequently made of thin and strong metal or multi-layered panels. The core of these structures is typically composed of light polymers, foams, or honeycomb structures (Makweche and Dundu 2022; San Ha and Lu 2020; Khosravi 2022; Toygar et al. 2019).

Overall, fluids whose characteristics change with the alteration of the magnetic field are called magnetorheological fluids. These materials are widely utilized to control structures owing to their swift time response (Kolekar et al. 2019). Moreover, there is a significant change in the hardness and loss properties of these fluids. Also, these fluids are ideal for controlling large-amplitude vibrations (Nagiredla et al. 2022; Joladarashi et al. 2022; Momeni and Zabihollah 2023). Among the recent studies on MR fluid is the work of Selvaraj et al. (Selvaraj et al. 2023). They investigated the optimum placement of the MR layers to maximize the loss factor of a sandwich beam. In addition, Lotfan et al. (2021) have introduced a general framework for the formulation and calculations of the dynamic analysis of the shell and the multilayered doubly-curve sheet with a medium thickness. Optimizing is an important and decisive part of the structural design process. Optimizing methods allows designers to produce better designs and save time and money. Boddeti et al. (2020) analyzed the optimal design with discrete variables stiffness of sandwich sheets. Gao et al. (2019) also optimized corrugated-core sandwich panels by minimizing two objective functions, including weight and structure deviation. Cai et al. (2021) examined a general procedure for optimizing sandwich sheets to minimize the impacts of explosive loading. Ly et al. (2022a) developed a neural network-nondominated sorting genetic algorithm II approach to optimize laminated carbon nanotube-reinforced composite quadrilateral panels.

Using magneto-electro-elastic panels combined with active damping, Nguyen-Thoi et al. (2022) examined vibration analysis and optimal control. Their study examines the influence of porous distribution and boundary conditions on the dynamic response of the plate as well as the optimal control solution. For hybrid damping vibration control of laminated composite plates, Ly et al. (2022b) utilized the zig-zag theory. The influence of magnetic field and materials on the vibrations of MR-laminated beams was studied by Ly et al. (2022c) and Momeni and Zabihollah (2023). To construct the sandwich MR-laminated beam, materials, including carbon fiber, E-glass, and Kevlar, have been used as base materials. For different boundary conditions of MR fluid sandwich beams, Nagiredla et al. (2023) determined the influence of magnetic field strength, length, and thickness on loss factor, deflection, and frequencies. Sharif et al. (2022) manufactured and experimentally analyzed beams with a metal face plate and an elastomer in a honeycomb core. Based on the results of the experiment, it was established that frequencies, amplitudes, and damping ratios of panels with MR honeycomb cores shifted with an increase in an induced magnetic field. Under high-temperature conditions, Mirzavand Borojeni et al. (2022) investigated the influence of magnetoelastic load and temperature on the dynamics of an elastomer beam. Based on elastic foundations and corrugated composite sandwich plates filled with MR elastomer, Zhao et al. (2023) investigated their dynamic behavior. A comparison of numerical results indicates that the performance of the structure is improved when the magnetic field intensity, boundary stiffness, and elastic foundation are increased. Based on the study by Zheng et al. (2023), predictions of nth-order derivatives of dynamics and loss factors for a shell composed of an MR core and composite face layers. Sahu et al. (2022) investigated the dynamics of the MR sandwich plate and found increasing modal loss factors and frequencies when the magnetic field is applied.

The main objective of this work is to obtain optimal values of effective parameters on the free vibrations of the panel for single- and multi-objective optimization of doubly-curved panels with laminated faces and MR core to minimize the mass and maximize the loss factor by the bee algorithm. Sandwich panel studies in this research have simple support conditions. Using the high-order theory of sandwich panels for the first time, the equations of motion governing the doubly-curved sandwich panel with MR core and Hamilton’s principle were extracted to determine the objective optimization functions for the system based on the IHOT of sandwich panels. Following the extraction of the equations of motion that govern the system, comparing them to similar results, and ensuring that the extracted equations are correct and reliable, a single-objective and multi-objective optimization of the panel has been performed utilizing this valid model. As a next step, the layer thickness, the thickness of the core, the fiber angle, and the magnetic field intensity were considered optimization variables. Single-objective optimization involves finding the intensity of the magnetic field and the optimal thickness for the layers to improve the panel’s vibrations. Furthermore, minimizing the sheet’s mass is considered in multi-objective optimization in addition to the vibration behavior criterion.

2 Formulation

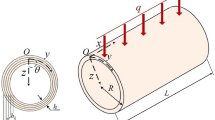
Considering that the face layers thickness is usually thin, therefore the theory of first-order shear deformation theory will be accurate. On the other hand, due to the greater thickness of the core, it is better to use high-order theories. Based on this, in the present research, to improve the accuracy of the mathematical model, surface layers are modeled using the FSDT, and the thick core is modeled using the high-order theory. The IHOT of the sandwich panel was utilized to obtain the motion equations of the system. Based on this theory, the FSDT theory has been used for the layers’ composite panel. Furthermore, for the core, the polynomial expression of the displacements based on the displacements of the high-order model presented by Frostig et al. (Frostig and Thomsen 2004) is used. Subsequently, using the minimum potential energy principle, governing equations have been extracted. The geometry of a doubly-curved sandwich panel with MR core and composite (laminated) layers is shown in Fig. 1. Based on FSDT, v, u, and w displacements of layers in the y, x, and z directions, assuming linear displacements, are as:

$$\begin{gathered} u_{i} \left( {x,y,z,t} \right) = u_{0}^{i} \left( {x,y,t} \right) + z\psi_{x} \left( {x,y,t} \right) \hfill \\ v_{i} \left( {x,y,z,t} \right) = v_{0}^{i} \left( {x,y,t} \right) + z\psi_{y} \left( {x,y,t} \right) \hfill \\ w_{i} \left( {x,y,z,t} \right) = w_{0}^{i} \left( {x,y,t} \right),\,\,\,\,i = T,B \hfill \\ \end{gathered}$$
(1)

where t represents time, \(\psi_{x}\) is the normal rotation components around the x axes, and \(\psi_{y}\) is the normal rotation components around the y axes. \(u_{0}^{i}\)،\(v_{0}^{i}\) and \(w_{0}^{i}\) are displacements in the direction of the x- and y-axes and the vertical deformation of the layers. T and B represent the top and bottom surfaces of the panel, respectively.

Fig. 1
figure 1

Doubly-curved sandwich panel geometry with composite layers and MR core

Full size image

Based on the Frostig model (Frostig and Thomsen 2004), displacement for the core are as:

$$u_{c} \left( {x,y,z,t} \right) = \left( {1 + \frac{z}{{R_{x} }}} \right)u_{0}^{c} \left( {x,y,t} \right) + z_{c}^{3} u_{3}^{c} \left( {x,y,t} \right) + z_{c}^{2} u_{2}^{c} \left( {x,y,t} \right) + z_{c} u_{1}^{c} \left( {x,y,t} \right)$$
(2)
$$v_{c} \left( {x,y,z,t} \right) = \left( {1 + \frac{z}{{R_{y} }}} \right)v_{0}^{c} \left( {x,y,t} \right) + z_{c}^{3} v_{3}^{c} \left( {x,y,t} \right) + z_{c}^{2} v_{2}^{c} \left( {x,y,t} \right) + z_{c} v_{1}^{c} \left( {x,y,t} \right)$$
(3)
$$w_{c} \left( {x,y,z,t} \right) = z_{c}^{2} w_{2}^{c} \left( {x,y,t} \right) + z_{c} w_{1}^{c} \left( {x,y,t} \right) + w_{0}^{c} \left( {x,y,t} \right)$$
(4)

where \(u_{k}^{c}\) and \(v_{k}^{c}\) stand in-plane displacements and \(w_{k}^{c} \,(k = 0,1,2)\) is the vertical displacements. \(R_{x}\) and \(R_{y}\) represent the curvature of the panel in the y- and x- plane, respectively. This research assumes that the layers are ideally attached to the core. As a result, all of the upper layer and the core displacement components are equal at the interface. So, assuming full bending among the layers and the core, the compatibility equation in the bottom and top connection of layers and core is obtained as:

$$\begin{gathered} u_{c} \left( {z = z_{c} } \right) = u_{0}^{i} + \frac{1}{2}\left( { - 1} \right)^{k} h_{i} \psi_{x}^{i} \hfill \\ v_{c} \left( {z = z_{c} } \right) = v_{0}^{i} + \frac{1}{2}\left( { - 1} \right)^{k} h_{i} \psi_{y}^{i} \hfill \\ w_{c} \left( {z = z_{c} } \right) = w_{0}^{i} \hfill \\ \end{gathered}$$
(5)

where hi is the thickness of the ith layer.

MR has linear viscoelastic properties before yielding, so its shear modulus is mixed and depends on its magnetic field intensity. In this research, the relationship proposed for the connection between MR magnetic field intensity and mixed shear modulus is employed (Srinivasa et al. 2020). The mixed shear modulus for viscoelastic materials is defined as (Rajamohan et al. 2010):

$$Q = Q^{\prime} + iQ^{\prime\prime}$$
(6)

where \(Q^{\prime}\) and \(Q^{\prime\prime}\) represent storage modulus and loss modulus, respectively, and for MR, it is a polynomial function of the intensity of the magnetic field B as:

$$Q^{\prime} = - 3.3691B^{2} + 4.9675 \times 10^{3} B + 0.873 \times 10^{6}$$
(7)
$$Q^{\prime\prime} = - 0.9B^{2} + 0.8134 \times 10^{3} B + 0.1865 \times 10^{6}$$
(8)

Finally, by replacing the displacement fields and also the relations of the layers’ stress in the relations of the potential and kinetic energy variation using Hamilton’s principle (Fallah and Arab Maleki 2021; Pourreza et al. 2022, 2021; Nasrabadi et al. 2022) and the basic principle of the calculus of variations, the motion equations for the doubly-curved sandwich panel with the MR core are acquired. Therefore, after some algebraic manipulation, the motion equations obtained as:

$$\left( {\frac{1}{3}\frac{{\partial^{2} u_{0}^{T} }}{{\partial t^{2} }} + \frac{1}{6}\frac{{\partial^{2} u_{0}^{B} }}{{\partial t^{2} }} + \frac{1}{12}\frac{{\partial^{2} w_{0}^{B} }}{{\partial x\partial t^{2} }} - \frac{1}{6}\frac{{\partial^{2} w_{0}^{T} }}{{\partial x\partial t^{2} }}} \right)M_{c} - \frac{{\partial N_{xx} }}{\partial x} - \frac{{\partial N_{xy} }}{\partial y} + \frac{{\partial^{2} u_{0}^{T} }}{{\partial t^{2} }}M_{t} - \left( {\psi_{x}^{T} + \psi_{x}^{B} } \right) = 0$$
(9)
$$\begin{aligned} & \left( {\frac{1}{3}\frac{{\partial^{2} v_{0}^{T} }}{{\partial t^{2} }} + \frac{1}{6}\frac{{\partial^{2} v_{0}^{B} }}{{\partial t^{2} }} + \frac{1}{12}\frac{{\partial^{2} w_{0}^{B} }}{{\partial y\partial t^{2} }} - \frac{1}{6}\frac{{\partial^{2} w_{0}^{T} }}{{\partial y\partial t^{2} }}} \right)M_{c}\\ &\quad - \frac{{\partial N_{yy} }}{\partial y} - \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial^{2} v_{0}^{T} }}{{\partial t^{2} }}M_{t} - \left( {\psi_{y}^{T} + \psi_{y}^{B} } \right) = 0 \end{aligned}$$
(10)
$$\begin{aligned} &\left( { - \frac{1}{12}\frac{{\partial^{4} w_{0}^{T} }}{{\partial y^{2} \partial t^{2} }} + \frac{1}{12}\frac{{\partial^{3} u_{0}^{B} }}{{\partial x\partial t^{2} }} + \frac{1}{24}\frac{{\partial^{4} w_{0}^{B} }}{{\partial x^{2} \partial t^{2} }} + \frac{1}{6}\frac{{\partial^{3} u_{0}^{T} }}{{\partial x\partial t^{2} }} } \right. \hfill \\ &\quad\left. {+ \frac{1}{6}\frac{{\partial^{2} w_{0}^{B} }}{{\partial t^{2} }} - \frac{1}{12}\frac{{\partial^{4} w_{0}^{T} }}{{\partial x^{2} \partial t^{2} }} + \frac{1}{6}\frac{{\partial^{3} v_{0}^{T} }}{{\partial y\partial t^{2} }}} \right. \hfill \\ &\quad\left. { + \frac{1}{24}\frac{{\partial^{4} w_{0}^{B} }}{{\partial y^{2} \partial t^{2} }} + \frac{1}{12}\frac{{\partial^{3} v_{0}^{B} }}{{\partial y\partial t^{2} }} + \frac{1}{3}\frac{{\partial^{2} w_{0}^{T} }}{{\partial t^{2} }}} \right)M_{c} \hfill \\ &\quad- \left( {\frac{{\partial^{4} w_{0}^{T} }}{{\partial x^{2} \partial t^{2} }} + \frac{{\partial^{4} w_{0}^{T} }}{{\partial y^{2} \partial t^{2} }}} \right)I_{mt} \frac{1}{2}\,\,\left( {\frac{{\partial \psi_{x}^{T} }}{\partial y} + \frac{{\partial \psi_{y}^{T} }}{\partial x}} \right) \\ &\quad- 2\frac{{\partial^{2} M_{xy}^{{}} }}{\partial x\partial y} - \frac{{\partial^{2} M_{yy}^{{}} }}{{\partial y^{2} }} - \frac{{\partial^{2} M_{xx}^{{}} }}{{\partial x^{2} }}\\ &\quad - Q\left( {\frac{{\partial^{2} N_{xx}^{{}} }}{{\partial x^{2} }} + \frac{{\partial^{2} N_{yy}^{{}} }}{{\partial y^{2} }}} \right) = 0 \hfill \\ \end{aligned}$$
(11)
$$\left( {\frac{1}{3}\frac{{\partial^{2} u_{0}^{B} }}{{\partial t^{2} }} + \frac{1}{6}\frac{{\partial^{2} u_{0}^{T} }}{{\partial t^{2} }} + \frac{1}{12}\frac{{\partial^{2} w_{0}^{T} }}{{\partial y\partial t^{2} }} - \frac{1}{6}\frac{{\partial^{2} w_{0}^{B} }}{{\partial y\partial t^{2} }}} \right)M_{c} - \frac{{\partial N_{yy} }}{\partial y} - \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial^{2} u_{0}^{B} }}{{\partial t^{2} }}M_{t} - \left( {\psi_{y}^{T} + \psi_{y}^{B} } \right) = 0$$
(12)
$$\left( {\frac{1}{3}\frac{{\partial^{2} v_{0}^{B} }}{{\partial t^{2} }} + \frac{1}{6}\frac{{\partial^{2} v_{0}^{T} }}{{\partial t^{2} }} + \frac{1}{12}\frac{{\partial^{3} w_{0}^{T} }}{{\partial x\partial t^{2} }} - \frac{1}{6}\frac{{\partial^{3} w_{0}^{B} }}{{\partial x\partial t^{2} }}} \right)M_{c} - \frac{{\partial N_{xx} }}{\partial x} - \frac{{\partial N_{xy} }}{\partial y} + \frac{{\partial^{2} v_{0}^{B} }}{{\partial t^{2} }}M_{t} - \left( {\psi_{x}^{T} + \psi_{x}^{B} } \right) = 0$$
(13)

in which Nyyj, Nxxj and Nxyj remain stress resultants in the transverse and longitudinal directions, and the in-plane shear stress resultant; Myyj, Mxxj and Mxyj stand bending moment in transverse and longitudinal directions and the torsion moment, respectively. These parameters are obtained as:

$$\left[ {\begin{array}{*{20}c} {N_{xx}^{j} } & {M_{xx}^{j} } \\ {N_{yy}^{j} } & {M_{yy}^{j} } \\ {N_{xy}^{j} } & {M_{xy}^{j} } \\ \end{array} } \right] = \sum\limits_{i = 1}^{3} {\int\limits_{{z_{i} }}^{{z_{i + 1} }} {\left\{ {\begin{array}{*{20}c} {\sigma_{x}^{j} } \\ {\sigma_{y}^{j} } \\ {\sigma_{xy}^{j} } \\ \end{array} } \right\}\left( {1,z} \right){\text{d}}z} }$$
(14)

It can be observed that the following answers can meet the simple support boundary conditions.

$$\left[ {\begin{array}{*{20}c} {u_{0}^{j} } \\ {v_{0}^{j} } \\ {w_{0}^{j} } \\ {\psi_{x}^{j} } \\ {\psi_{y}^{j} } \\ {u_{k}^{c} } \\ {v_{k}^{c} } \\ {w_{k}^{c} } \\ \end{array} } \right] = \sum\limits_{n = 1}^{\infty } {\sum\limits_{m = 1}^{\infty } {\left[ {\begin{array}{*{20}c} {\cos (\alpha_{m} x)\sin (\beta_{n} y)U_{0mn}^{j} (t)} \\ {\sin (\alpha_{m} x)\cos (\beta_{n} y)V_{0mn}^{j} (t)} \\ {\sin (\alpha_{m} x)\sin (\beta_{n} y)W_{0mn}^{j} (t)} \\ {\cos (\alpha_{m} x)\sin (\beta_{n} y)\psi_{xmn}^{j} (t)} \\ {\sin (\alpha_{m} x)\sin (\beta_{n} y)\psi_{ymn}^{j} (t)} \\ {\cos (\alpha_{m} x)\sin (\beta_{n} y)U_{kmn}^{c} (t)} \\ {\sin (\alpha_{m} x)\cos (\beta_{n} y)V_{kmn}^{c} (t)} \\ {\sin (\alpha_{m} x)\sin (\beta_{n} y)W_{kmn}^{c} (t)} \\ \end{array} } \right]} } ,\,\,\alpha_{m} = \frac{m\pi }{{L_{x} }},\,\,\beta_{n} = \frac{n\pi }{{L_{y} }}$$
(15)

where m and n are the wave numbers. Substituting Eq. (15) in the motion equations of and then using the weighted residual method, and Galerkin method (Maleki and Mohammadi 2017; Rezaee and Maleki 2015; Rezaee and Arab Maleki 2019), the governing equations are obtained as a system of coupled ODE as:

$$\left[ {\mathbf{M}} \right]\left\{ {{{\ddot{\mathbf{d}}}}} \right\} + \left[ {\mathbf{K}} \right]\left\{ {\mathbf{d}} \right\} = \left\{ {\mathbf{0}} \right\}$$
(16)

where \(\{ {\mathbf{d}}\} = \{U_{0mn}^{j} ,V_{0mn}^{j} ,W_{0mn}^{j} ,\psi_{xmn}^{j} ,\psi_{ymn}^{j} ,U_{0mn}^{c}, V_{0mn}^{c} ,W_{0mn}^{c} \}^{T}\). Instead of a set of differential equations, Eq. (16) produces a set of homogeneous algebraic equations. As a result, PDEs are substituted by an eigenvalue problem, stiffness and mass matrix, in which eigenvalue equals the square of eigenfrequency, and eigenvectors are the series constants for each m and n. Consequently, the last two equations of motion, which describe the compatibility conditions in the longitudinal and transverse directions at the lower face–core interface, do not contain any inertial terms. So, the stiffness matrix can be reduced to the same dimension as the mass matrix by a factor of 6. Therefore, for specified values of m and n, the eigenvalue problem yields only six eigenfrequencies. Eventually, supposing free vibrations, and also considering that the MR shear modulus is mixed and is in terms of the magnetic field intensity, an eigenvalue problem with complex eigenvalues will be acquired from which the system frequencies, ω, and the loss factor, η, for different vibration modes, can be obtained as:

$$\omega = \sqrt {{\text{Re}} \left( {\overline{\omega }^{2} } \right)} ,\,\,\,\,\,\,\,\eta = \frac{{{\text{Im}} \left( {\overline{\omega }^{2} } \right)}}{{{\text{Re}} \left( {\overline{\omega }^{2} } \right)}}$$
(17)

3 Optimization

The bee optimization algorithm is a collective intelligent search algorithm for solving optimization problems initially developed in 2006 (Pham et al. 2006). This algorithm simulates the behavior of bee groups searching for food in nature. This algorithm can optimize single or multi-objective problems. The special features of this method make it impossible to consider it a simple, random, and conventional searcher or nature imitation without any reason. The flow chart of the main stages of the bee algorithm is summarized in Fig. 2. The sources (Kamaruddin and Abd Latif 2019) provide more details about this algorithm. This algorithm depends on several parameters the user must specify before starting the algorithm (Table 1).

Fig. 2
figure 2

The proposed flowchart for the basic bee algorithm

Full size image
Table 1 Parameters in the bee algorithm
Full size table

The objective function in this research is the loss factor (\(f\left( X \right) = \eta\)) for the single-objective mode and the modal loss factor and the weight (\(f\left( X \right) = \eta ,\,\,m\left( X \right)\)) for the two-objective mode. The design parameters include the magnetic field intensity (B), the fibers angles, the composite layers’ thickness, and the core’s thickness. The loss factor is a function of layers and core thickness, the angles of the fibers, and the magnetic field intensity. The structure’s mass is also affected by the thickness and density of layers and core. Therefore, the following relationships represent the mathematical expression of design variables and objective functions:

$${\text{Modal}}\,\,{\text{loss}}\,{\text{factor}} = f\left( {\theta_{t1} ,\theta_{t2} ,\theta_{t3} ,h_{t} ,h_{c} ,B} \right)$$
(18)
$${\text{mass}} = f\left( {h_{t} ,h_{c} ,\rho_{t} ,\rho_{c} } \right)$$
(19)

The range of changes related to the thickness (thickness of the whole panel) is consistently between 2 and 10 mm.

The angles of the fibers can also be changed between -90 and + 90 degrees with a value of 2 degrees discretely. The intensity of the magnetic field can also vary between 0 and 500 gausses with an increase of 10 G. discretely. For multi-objective optimization, the population size used in the proposed method and particle swarm optimization algorithm is 150.

4 Results

The aim of this section is to associate the numerical results obtained in this study with those obtained in other studies of a similar nature. According to Table 2, the results of the present research using the IHOT of sandwich panels have been matched with those obtained via the high-order theory of sandwich panels (Biglari and Jafari 2010). Similarly, in Table 3, the optimization results obtained from this research using the bee algorithm method are compared with those acquired from particle swarm (Asgari 2010) and genetic algorithms. Table 2 demonstrates a respectable agreement between the results, which indicates the certainty and accuracy of the equations extracted in the present research. The lack of complete compatibility is due to the difference in the solution method. In addition, in the high-order theory of sandwich panels, the classical theory of multi-layered panels is used for the layers, and the vertical and transverse shear strains of the layers are omitted. In Table 3, the energy loss factor was compared with the existing results of ref. (Asgari 2010). The results show that the accuracy of the current study is around 8%, and one of the factors of this error is related to the different theories used and the solution method.

Table 2 Values of natural frequencies for the sandwich panel
Full size table
Table 3 Optimum values for the sandwich panel with MR core
Full size table

Subsequently, two single-objective and two-objective optimization problems have been investigated.

4.1 Maximization of the first loss factor of the sandwich panel considering the mass constraint

In this example, a symmetrical doubly-curved composite panel with composite layers consisting of three layers with a thickness equal to hl and an MR core with a thickness of hc is designed to maximize the loss factor by considering the mass constraint. The maximum weight of the panel is considered 500 g. This problem is also solved by the bee algorithm, and Fig. 3 illustrates the most optimal values of the modal loss factor in terms of generations. As shown in Fig. 3, from generation 45 onwards, the optimal value of the objective function has not changed. In other words, convergence has begun, and the average and best points have coincided. And finally, it has reached an end in the 55th generation of the algorithm. Figure 4 illustrates the average distance between generations. The distance is greater in the first generations and decreases as we approach the last generations. Finally, the optimal values for the variables and the objective function for this problem are presented in Table 4.

Fig. 3
figure 3

Convergence diagram of a modal mass factor in terms of generations for the single-objective mode of doubly-curved sandwich panel

Full size image
Fig. 4
figure 4

The average distance in each generation in the single-objective mode of the doubly-curved sandwich panel

Full size image
Table 4 Optimal parameters and the objective function for a single-objective mode of the doubly-curved panel
Full size table

4.2 Optimization of the doubly-curved sandwich panel for maximum modal loss factor and minimum mass

In this case, the aim is to obtain optimal solutions of the Pareto front for the maximum loss factor and the minimum mass for the doubly-curved sandwich panel. The design parameters, like the previous problems, include magnetic field intensity, fiber angles, the thickness of composite layers, and core thickness. Figure 5 shows the average distance between individuals in each generation. In this case, as can be observed, the distance is greater in the first generations and decreases as we approach the last generations. Figure 6 depicts the Pareto front. As mentioned earlier, it is observable that the optimal solutions are obtained as a set of points that form a front. One can choose among the optimal answers based on the need since none of the answers is optimal in the absolute sense.

Fig. 5
figure 5

Convergence diagram of structural mass and modal loss factor in the two-objective mode of doubly-curved sandwich panel

Full size image
Fig. 6
figure 6

Pareto front for the two-objective mode of a doubly-curved sandwich panel

Full size image

In this problem, the TOPSIS method has been utilized to select a design point among the Pareto front points (Shih and Olson 2022). Based on this, point number 10 was selected as the design point, and the optimal values of the parameters and the objective function at this point are provided in Table 5. Figure 7 shows the convergence diagram. Also, the convergence results of the proposed method, and the particle swarm optimization algorithms are given for comparison. As can be detected, the proposed algorithm achieved the optimal design in less than 150 iterations. However, the computational time needed to achieve the optimal results of the proposed method is much less than that of particle swarm optimization.

Table 5 Optimal values of parameters and objective function for two-objective optimization
Full size table
Fig. 7
figure 7

Convergence diagram of modal loss factor of the proposed method, and the particle swarm optimization

Full size image

5 Conclusion

Overall, in the current research, the thickness layers, angles of the fibers, and the magnetic field intensity are deliberated as optimization variables. Additionally, the maximum modal loss factor in the single-objective mode and the maximum modal loss factor, and the minimum mass in the dual-objective mode (with the functions of the mass objective and the modal loss factor) for sandwich panel with composite layers and MR core were analyzed. In the single-objective mode, the optimal values have been acquired, and in the multi-objective mode of the Pareto front, the optimal solutions have been presented. Regarding the single-objective mode, the results indicate the tendency of the structure to have thin layers and a thick core, which appears correct and feasible from a physical point of view, as MR fluid is placed in the core and contributes significantly to the increase in the modal loss factor. In the two-objective mode, the optimal solutions are obtained as a set of points that form a front. In fact, none of the resulting answers is optimal, and one of these optimal answers can be chosen depending on the need. Ultimately, in the case of the two-objective mode, TOPSIS was utilized to select a design point from the points of the Pareto front and to determine optimal values of parameters and objective functions.

The proposed approach may be extended in future research to identify optimal designs of curved sandwich panels by taking dynamic failure mechanisms into consideration in the optimization process. Moreover, further research will be conducted to increase the strength of sandwich panels. The proposed optimization algorithms still have a great deal of potential for speeding up. Additionally, artificial intelligence or machine learning methods may also play an important role in optimizing the performance of doubly-curved sandwich panels. Further work should focus on these meaningful topics.