1 Introduction

The high strength and stiffness of composite sandwich panels along with their lightweight has made them a popular choice for manufacturing structural components in aerospace applications (Arunkumar et al. 2016, 2018; Redmann et al. 2021). Excellent impact and energy absorption capability (Golestanipour et al. 2015; Novak et al. 2019; Wang et al. 2019a; Guo et al. 2019), great sound attenuation characteristics ([CSL STYLE ERROR: reference with no printed form.]), high thermal isolation capacity (Sun et al. 2019; Li et al. 2020), and favorable stealth characteristics (Li et al. 2019) are some other remarkable features of composite sandwich panels to be mentioned. These structures are usually comprised of two thin face sheets separated by a cellular core, and their mechanical properties mainly depend on the material and geometry of these face sheets and core (Taghizadeh et al. 2019; Lei et al. 2019). The face sheets may be made from various metals such as aluminum and steel, or fiber-reinforced polymer (FRP) composites. The core, on the other hand, is generally made of polymeric foams, honeycombs and corrugated panels, metallic foams, wood-based materials such as balsa or cork, and functionally graded materials (Gholami et al. 2021, 2022).

Many investigations have been performed on the design and manufacture of composite sandwich panels. Gholami et al. (2016) used the NMPSO algorithm for the weight minimization of a composite sandwich panel with a circular cell honeycomb core structure. Montemurro et al. (2016) dealt with the problem of the optimum design of a sandwich panel made of carbon-epoxy skins and a metallic cellular core by a multi-scale numerical optimization procedure and a genetic algorithm. The proposed strategy was applied to the least-weight design of a sandwich plate subject to different constraints. By extending the concept of ground structure in topology optimizations, An et al. (2019) introduced a two-level approximation method for simultaneous optimization of laminated stacking sequences and stiffener layout of composite stiffened panels. Two types of stiffeners were employed and the structural mass of the composite panel was minimized considering both mechanical and manufacturing constraints. Inspired by the tree leaves with fractal distributed veins that are larger and stiffer than grass leaves, Sun et al. (2017) conducted a topological optimization on the sandwich panel core. They proposed a biomimetic hybrid core, similar to the fractal distribution of tree veins, with high specific compression stiffness and peak load. Chu et al. (2019) proposed a novel approach under moving morphable components-based topology optimization for the design of sandwich panels with truss cores. This novel approach was proved to be capable of effectively improving the panel stiffness performance only by optimizing the sectional radius and ends’ coordinates of different beams in the truss core. Karen et al. (2016) used a hybrid evolutionary optimization technique based on the multi-island genetic algorithm and Hooke-Jeeves algorithm to develop sandwich structures with high energy absorption capability for shock loading applications. Wang et al. (2018) proposed a novel sandwich panel with a three-dimensional double-V auxetic structure core for air blast protection purposes. The optimization of the panel core was conducted based on Latin hypercube sampling, Gaussian process metamodel, and multi-objective particle swarm optimization methods to reduce the dynamic response under air blast loading. Cai et al. (2019) used the finite element analysis, surrogate modeling, and nondominated sorting genetic algorithm (NSGA-II) techniques to optimize the energy absorption response and the blast performance of trapezoidal corrugated core sandwich panel under air blast loading. Martin and Thrall (2014) presented a multi-objective optimization procedure to design material properties of honeycomb core sandwich panels for a minimum weight and maximum thermal resistance within the context of origami-inspired shelters. Xu et al. (2017) provided a solution algorithm based on the non-dominated sorting genetic algorithm II (NSGA-II) for simultaneously minimizing the mass and maximizing the sound insulation performance of sandwich panels. Yang et al. (2017) presented a genetic algorithm-based multi-parameter optimization method for minimizing the transmitted sound power in sandwich plates with corrugated cores, considering the manufacturability of the structure and constraints on the structural weight and fundamental frequency. Studzinski (2019) used an evolutionary optimization algorithm to find optimal solutions of a sandwich panel with a hybrid core subjected to mechanical and thermal loads. The economical aspect was investigated by minimizing the weight and maximizing the allowable span length. The thermal insulation criterion was also included in the analysis. Garrido et al. (2019) employed the Direct Multi-Search (DMS) method for the optimization of a composite sandwich panel system for building floor rehabilitation. They studied the influence of core material density, the number of ribs/webs, the type of fiber reinforcement and its respective layup on the different objective functions related to aspects such as structural serviceability and resistance, thermal insulation, acoustic performance, cost minimization, and environmental performance.

Out-of-plane pressure is a common loading mode in many aerospace structures such as aircraft rudder and wings (Wang et al. 2019b; Pan et al. 2020; Nadkarni and Satpute 2021). This pressure may lead to failure of the sandwich panel due to buckling of the cellular core or excessive stresses of face sheets (Alaei et al. 2020). In this paper, the optimal design of a hexagonal honeycomb core composite sandwich panel is investigated under out-of-plane pressure load. The buckling of honeycomb cells and the stress developed in the composite laminate face sheets are considered in the optimization process. The first-order shear deformation laminate theory is utilized to account for the effect of transverse shear loads which are among the most important parameters in the failure of sandwich structures (Anish et al. 2019). The orthotropic constitutive model is used for the face sheets and the core, independently, and the Tsai-Hill criterion, proven to be more accurate for failure prediction of composite sheets, is employed.

The following features in the proposed method have made it advantageous:

  • The solution accuracy is increased owing to the use of the first order deformation theory for modeling the panel deformation,

  • the effect of shear loads is considered in the panel failure, and it is observed that these loads have substantial impact on the panel failure,

  • the optimization accuracy has increased and the computational time and cost have reduced due to employ of NMPSO which is a relatively novel and efficient approach.

The paper is organized as follows. The details of the analysis performed on the composite sandwich panel are presented in Sect. 2. The objective function and the constraints governing the optimization process are described in Sect. 3. An overview of the optimization algorithm is provided in Sect. 4. The results of the analysis are discussed in Sect. 5, and the concluding remarks are given in Sect. 6.

2 Analysis of the Composite Sandwich Panel

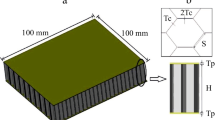
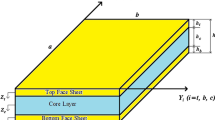
The geometry of the sandwich panel is presented in Fig. 1. The panel is assumed to be simply supported along its four edges and to be subjected to a uniform out-of-plane pressure. According to Fig. 1, each unit cell has a hexagonal cross-section with the side length of l (\(1\,{\text{mm}} \le l \le 10\,{\text{mm}}\)) and wall thickness of t (\(1\,{\text{mm}} \le t \le 10\,{\text{mm}}\)). The height of the cells is denoted by C (\(10\,{\text{mm}} \le C \le 100\,{\text{mm}}\)). The top and bottom face sheets are made of two composite layers with the area of \(L_{x} \times L_{y}\), and same thickness \({H \mathord{\left/ {\vphantom {H 2}} \right. \kern-\nulldelimiterspace} 2}\), so that their total thickness is \(H\) (\(1\,{\text{mm}} \le H \le 10\,{\text{mm}}\)). The fibers are oriented along the x-axis (\(\theta = 0^{ \circ }\)) in the outer layers, and along the y-axis (\(\theta = 90^{ \circ }\)) in the inner ones. For each layer, a local coordinate system is also defined such that the local x-axis is along the direction of the fibers.

Fig. 1
figure 1

The geometry of the composite sandwich panel

Full size image

Since face sheets are much thinner than the core, it is common practice to neglect the shear displacement of the face sheets and assume that only the core withstands the shear stresses in the sandwich panel analysis. The face sheets, on the other hand, are assumed to be responsible for tolerating the normal stresses. Consequently, in the following analysis, the shear stresses in the core, and the normal stresses in the face sheets are determined.

2.1 Laminate and Core Constitutive Equations

The constitutive stress–strain relationship for each composite layer by assuming orthotropic behavior for composite sheets is given by the following relation in the local coordinate system [30–32]:

$$\left[ \begin{gathered} \sigma_{1} \hfill \\ \sigma_{2} \hfill \\ \tau_{12} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon_{1} \hfill \\ \varepsilon_{2} \hfill \\ \gamma_{12} \hfill \\ \end{gathered} \right]$$
(1)
$$Q_{11} = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }}\,\,,\,\,\,Q_{12} = \frac{{\nu_{12} E_{1} }}{{1 - \nu_{12} \nu_{21} }}\,\,,\,\,\,Q_{22} = \frac{{E_{2} }}{{1 - \nu_{21} \nu_{12} }}\,\,,\,\,\,Q_{66} = G_{12}$$
(2)

where \({E}_{1}\), \({E}_{2}\), \({G}_{12}\), \({\nu }_{12}\) and \({\nu }_{21}\) are Young’s modulus in parallel and transverse to the fiber direction, shear modulus, and Poisson’s ratio of composite materials, respectively. The stress components in the face sheets are obtained by the stress–strain relation in the global coordinate system:

$$\begin{aligned} & \left[ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } \\ {\overline{Q}_{12} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } \\ {\overline{Q}_{16} } & {\overline{Q}_{26} } & {\overline{Q}_{66} } \\ \end{array} } \right]\left[ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right], \\ & \left\{ {\begin{array}{*{20}c} {\tau_{xz} } \\ {\tau_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{55} } & {\overline{Q}_{45} } \\ {\overline{Q}_{45} } & {\overline{Q}_{44} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} \\ \end{aligned}$$
(3)
$$\begin{aligned} & \varepsilon_{x} = \frac{\partial u}{{\partial x}} = \frac{{\partial u^{0} }}{\partial x} - Z\frac{{\partial \chi_{xz} }}{\partial x} \\ & \varepsilon_{y} = \frac{\partial v}{{\partial y}} = \frac{{\partial v^{0} }}{\partial y} - Z\frac{{\partial \chi_{yz} }}{\partial y} \\ & \gamma_{xy} = \frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}} = \frac{{\partial u^{0} }}{\partial y} + \frac{{\partial v^{0} }}{\partial x} - Z\left( {\frac{{\partial \chi_{xz} }}{\partial y} + \frac{{\partial \chi_{yz} }}{\partial x}} \right) \\ & \gamma_{xz} = \frac{{\partial w^{0} }}{\partial x} - \chi_{xz} ,\gamma_{yz} = \frac{{\partial w^{0} }}{\partial y} - \chi_{yz} \\ \end{aligned}$$
(4)

where \(\overline{Q}_{ij}\) is called the transformed reduced stiffness matrix [30–32]. In this equation, \(u^{0}\),\(v^{0}\) and \(\omega^{0}\) are the plate displacement in the middle section and \(\chi_{xz}\), \(\chi_{yz}\) are the rotation of the normal line in x–z and y–z planes, respectively.

The stress–strain relationship of core material can be calculated as follows [31]:

$$\left\{ {\begin{array}{*{20}c} {\tau_{xz}^{c} } \\ {\tau_{yz}^{c} } \\ \end{array} } \right\} = \frac{d}{C}\left[ {\begin{array}{*{20}c} {\tilde{C}^{c}_{55} } & {\tilde{C}^{c}_{45} } \\ {\tilde{C}^{c}_{45} } & {\tilde{C}^{c}_{44} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\}$$
(5)

where \(\left[ {\tilde{C}^{c} } \right]\) is the shear stiffness matrix of the honeycomb core.

2.2 The Stiffness of the Composite Panel

For a sandwich panel symmetrical with respect to its midplane, the extensional, coupling, and bending stiffness matrices (\(\left[A\right]\), \(\left[B\right]\) and \(\left[D\right]\)) are determined by:

$$\begin{aligned} & \left[ A \right] = 2\left[ A \right]^{L} ,\left[ B \right] = 0 \\ & \left[ D \right] = \frac{1}{2}d^{2} \left[ A \right]^{L} + 2\left[ D \right]^{L} + 2d\left[ B \right]^{L} \\ & \left[ {\begin{array}{*{20}c} {\left[ {A_{ij} } \right]^{L} } \\ {\left[ {B_{ij} } \right]^{L} } \\ {\left[ {D_{ij} } \right]^{L} } \\ \end{array} } \right] = \sum\limits_{k = 1}^{k} {\left( {\overline{{Q_{ij} }} } \right)}_{k} \left\{ {\begin{array}{*{20}c} {\left( {z_{k} - z_{k - 1} } \right)} \\ {\left( {z_{k}^{2} - z_{k - 1}^{2} } \right)/2} \\ {\left( {z_{k}^{3} - z_{k - 1}^{3} } \right)/3} \\ \end{array} } \right\},i,j = 1,2,6 \\ \end{aligned}$$
(6)

where \(\left[ A \right]^{L}\), \(\left[ B \right]^{L}\), and \(\left[ D \right]^{L}\) matrices are the extensional, coupling, and bending stiffness matrices of the face sheet laminate, respectively (Kaw 2005). Furthermore, the parameters \({z}_{k}\), \({z}_{k-1}\) are kth ply distances from the reference plane. In addition, the shear stiffness matrix of the sandwich panel, \(\left[ {\tilde{S}} \right]\) can be determined as (Kollár and Springer 2003):

$$\left[ {\tilde{S}} \right] = \frac{{d^{2} }}{C}\left[ {\tilde{C}^{c} } \right]\quad {\text{or}}\quad \left[ {\begin{array}{*{20}c} {\widetilde{S}_{11} } & {\tilde{S}_{12} } \\ {\tilde{S}_{12} } & {\tilde{S}_{22} } \\ \end{array} } \right] = \frac{{d^{2} }}{C}\left[ {\begin{array}{*{20}c} {\tilde{C}^{c}_{55} } & {\tilde{C}^{c}_{45} } \\ {\tilde{C}^{c}_{45} } & {\tilde{C}^{c}_{44} } \\ \end{array} } \right]$$
(7)

Since the honeycomb core shows orthotropic behavior, the components of its shear stiffness matrix are:

$$C_{55}^{c} = G_{xz}^{c} \,\,,\,\,\,\,C_{44}^{c} = G_{yz}^{c} \,\,,\,\,\,\,C_{45}^{c} = 0$$
(8)

where \(G_{xz}^{c}\) and \(G_{yz}^{c}\) are the shear modulus of the core in xz and yz direction. Ashby and Gibson (1999) proved that the core shear stiffness is proportional to the cell dimensions and geometry. For the regular hexagonal cell studied in this paper, the shear stiffness in terms of the shear modulus of the cell material, \(G_{s}\), is given by:

$$G_{xz}^{c} = G_{yz}^{c} = 0.5774\frac{t}{l}G_{s}$$
(9)

2.3 Deflection, Rotations and Strains of Composite Panel

The potential of the external forces for a sandwich plate under out of the plane and in-plane loads can be obtained as follows [31]:

$$U = - \int\limits_{0}^{{L_{x} }} {\int\limits_{0}^{{L_{y} }} { - pw^{0} {\text{d}}y{\text{d}}x} }$$
(10)

The strain energy for the symmetric composite panel is:

$$U = \frac{1}{2}\int\limits_{0}^{{L_{x} }} {\int\limits_{0}^{{L_{y} }} {\int\limits_{{ - t_{p/2} }}^{{t_{p/2} }} {\left( {\sigma_{x} \varepsilon_{x} + \sigma_{y} \varepsilon_{y} + \tau_{xy} \gamma_{xy} + \tau_{xz} \gamma_{xz} + \tau_{yz} \gamma_{yz} } \right)\,} {\text{d}}z{\text{d}}y{\text{d}}x} }$$
(11)

where \(t_{P} = C + 2H\) is the thickness of the panel. For a simply supported symmetrical orthotropic composite panel, \(\epsilon_{x}^{0} = \epsilon_{y}^{0} = \gamma_{xy}^{0} = 0\), \(B_{ij} = 0\) and \(D_{16} = D_{26} = \tilde{S}_{12} = 0\). Therefore, by substituting Eqs. (3) and (5) into Eq. (11), the strain energy takes the form [31]:

$$\begin{aligned} U & = \frac{1}{2}\int\limits_{0}^{{L_{x} }} \int\limits_{0}^{{L_{y} }} \left[ {D_{11} \left( {\frac{{\partial \chi_{xz} }}{\partial x}} \right)^{2} + D_{22} \left( {\frac{{\partial \chi_{yz} }}{\partial y}} \right)^{2} } \right. \\ & \quad + 2D_{12} \frac{{\partial \chi_{xz} \partial \chi_{yz} }}{\partial x\partial y} + D_{66} \left( {\frac{{\partial \chi_{xz} }}{\partial y} + \frac{{\partial \chi_{yz} }}{\partial x}} \right)^{2} \\ &\left. \quad + \widetilde{S}_{11} \left( {\frac{{\partial w^{0} }}{\partial x} - \chi_{xz} } \right)^{2} + \widetilde{S}_{22} \left( {\frac{{\partial w^{0} }}{\partial y} - \chi_{yz} } \right)^{2} \right]{\text{d}}y{\text{d}}x \\ \end{aligned}$$
(12)

Considering the simply supported boundary conditions at each panel edge, the following relations are obtained for the panel displacement and rotation (Kollár and Springer 2003):

$$\begin{aligned} & \omega^{0} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\omega_{ij} \sin \frac{i\pi x}{{L_{x} }}\sin \frac{j\pi y}{{L_{y} }}} } \\ & \chi_{xz} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\chi_{xz} } \right)_{ij} \cos \frac{i\pi x}{{L_{x} }}\sin \frac{j\pi y}{{L_{y} }}} } \\ & \chi_{yz} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\chi_{yz} } \right)_{ij} \sin \frac{i\pi x}{{L_{x} }}\cos \frac{j\pi y}{{L_{y} }}} } \\ \end{aligned}$$
(13)

where \(I\) and \(J\) are the number of terms chosen arbitrarily. Based on the principle of stationary potential energy \(\frac{{\partial \left( {U + {\Omega }} \right)}}{{\partial w_{ij} }} = 0\), \(\frac{{\partial \left( {U + {\Omega }} \right)}}{{\partial \left( {\phi_{xz} } \right)_{ij} }} = 0\), \(\frac{{\partial \left( {U + {\Omega }} \right)}}{{\partial \left( {\phi_{yz} } \right)_{ij} }} = 0\), the parameters \(\omega_{ij}\), \(\left( {\chi_{xz} } \right)_{ij}\) and \(\left( {\chi_{yz} } \right)_{ij}\) in Eq. (6) are determined by the following matrix equation (Kollár and Springer 2003):

$$\left\{ {\begin{array}{*{20}c} {\omega_{ij} } \\ {\left( {\chi_{xz} } \right)_{ij} } \\ {\left( {\chi_{yz} } \right)_{ij} } \\ \end{array} } \right\} = \frac{16P}{{\pi^{2} ij}}\left[ {\begin{array}{*{20}c} {F_{33} } & {F_{34} } & {F_{35} } \\ {F_{34} } & {F_{44} } & {F_{45} } \\ {F_{35} } & {F_{45} } & {F_{55} } \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ \end{array} } \right\}$$
(14)

where:

$$\begin{aligned} & F_{33} = D_{11} \left( {\frac{i\pi }{{L_{x} }}} \right)^{4} + 2(D_{12} + 2D_{66} )\left( {\frac{i\pi }{{L_{x} }}} \right)^{2} \left( {\frac{j\pi }{{L_{y} }}} \right)^{2} + D_{22} \left( {\frac{j\pi }{{L_{y} }}} \right)^{4} \\ & F_{34} = - D_{11} \left( {\frac{i\pi }{{L_{x} }}} \right)^{3} - (D_{12} + 2D_{66} )\frac{i\pi }{{L_{x} }}\left( {\frac{j\pi }{{L_{y} }}} \right)^{2} \\ & F_{35} = - D_{22} \left( {\frac{j\pi }{{L_{y} }}} \right)^{3} - (D_{12} + 2D_{66} )\frac{j\pi }{{L_{y} }}\left( {\frac{i\pi }{{L_{x} }}} \right)^{2} \\ & F_{44} = D_{11} \left( {\frac{i\pi }{{L_{x} }}} \right)^{2} + D_{66} \left( {\frac{j\pi }{{L_{y} }}} \right)^{2} + \tilde{S}_{11} \\ & F_{45} = (D_{12} + 2D_{66} )\left( {\frac{j\pi }{{L_{y} }}} \right)\left( {\frac{i\pi }{{L_{x} }}} \right)\, \\ F_{55} = D_{22} \left( {\frac{j\pi }{{Ly}}} \right)^{2} + D_{66} \left( {\frac{i\pi }{{L_{x} }}} \right)^{2} + \tilde{S}_{22} \\ \end{aligned}$$
(15)

In these equations, P is the uniform out-of-plane pressure applied on the top face sheet of the panel and S denotes the shear stiffness matrix of the sandwich panel given in Eq. (5). Only odd values of i and j (i.e. \(i,j = 1,3,5, \ldots\)) are present in the above equations, since \(\omega_{ij}\), \(\left( {\chi_{xz} } \right)_{ij}\), and \(\left( {\chi_{yz} } \right)_{ij}\) vanish for even values. In the next step, the parameters calculated from Eq. (14), can be used to determine the components of the panel in-plane and out-of-plane strain by the following relations:

$$\begin{aligned} & \varepsilon_{x} = Z\frac{i\pi }{{L_{x} }}\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\chi_{xz} } \right)_{ij} \sin \frac{i\pi x}{{L_{x} }}\sin \frac{j\pi y}{{L_{y} }}} } \\ & \varepsilon_{y} = Z\frac{j\pi }{{L_{y} }}\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\chi_{yz} } \right)_{ij} \sin \frac{i\pi x}{{L_{x} }}\sin \frac{j\pi y}{{L_{y} }}} } \\ & \gamma_{xy} = - Z\left( {\frac{j\pi }{{L_{y} }}\left( {\chi_{xz} } \right)_{ij} + \frac{i\pi }{{L_{x} }}\left( {\chi_{yz} } \right)_{ij} } \right)\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\cos \frac{i\pi x}{{L_{x} }}\cos \frac{j\pi y}{{L_{y} }}} } \\ \end{aligned}$$
(17)
$$\begin{aligned} & \gamma_{xz} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\gamma_{xz} } \right)_{ij} \cos \frac{i\pi x}{{L_{x} }}\sin \frac{j\pi y}{{L_{y} }}} } \\ & \gamma_{yz} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\gamma_{yz} } \right)_{ij} \sin \frac{i\pi x}{{L_{x} }}\cos \frac{j\pi y}{{L_{y} }}} } \\ \end{aligned}$$
(18)

where:

$$\begin{aligned} & \left( {\gamma_{xz} } \right)_{ij} = \frac{i\pi }{{L_{x} }}\omega_{ij} - \left( {\chi_{xz} } \right)_{ij} \\ & \left( {\gamma_{yz} } \right)_{ij} = \frac{i\pi }{{L_{x} }}\omega_{ij} - \left( {\chi_{xz} } \right)_{ij} \\ \end{aligned}$$
(19)

3 Objective Functions and Constraints

3.1 Objective Function

In this section, an optimization process is performed to design a sandwich panel, with two composite face sheets and a hexagonal honeycomb core, capable of withstanding allowable stresses and displacements with minimum possible weight. Accordingly, one of the objective functions is to minimize the total weight of the panel. The following relation may be used to calculate the weight of the composite panel:

$$\begin{aligned} & W_{P} = 2W_{L} + W_{{{\text{core}}}} = 2\rho_{L} \,H\,L_{x} L_{y} + n_{{\text{w}}} \rho_{c} \,l\,t\,C \\ & \quad = \sqrt 3 n_{{\text{h}}} \left( {3n_{{\text{v}}} + 1} \right)\rho_{L} \,H\,l^{2} + \left( {\left( {3n_{{\text{v}}} + 2} \right)n_{{\text{h}}} + n_{{\text{v}}} } \right)\rho_{c} \,l\,t\,C \\ \end{aligned}$$
(20)

where \(n_{{\,{\text{h}}}}\) and \(n_{{\text{v}}}\) are the number of cells in the horizontal and vertical directions and \(n_{{\text{w}}}\) denotes the total number of the side walls in the core. Furthermore, \(\rho_{L}\) and \(\rho_{c}\) are the density of the laminate and core.

3.2 Constraints

  • Excessive deflection can generate internal forces between layers leading to the failure of the interlayer adhesive and consequently, the separation of layers. In this study, the maximum deflection (occurring at \(x = \frac{{L_{x} }}{2}\,,\,\,y = \frac{{L_{y} }}{2}\)) is limited to be at most equal to 10% of the height of the cells (Gholami et al. 2016):

    $$g_{1} = \omega_{\max } - 0.1\,C \le 0$$
    (21)

  • The failure caused by shear stresses in the core is one of the potential modes of failure in the sandwich panels. Banerjee et al. (2010) demonstrated that the relative density of the honeycomb core affects its macroscopic shear strength. The relative density (\(\Phi\)) is defined to be the ratio of the effective density of the honeycomb core (\(\rho^{*}\)) to the density of the core material (\(\rho_{c}\)). For a honeycomb core with regular hexagonal cells, the maximum out-of-plane shear strengths (\(\tau_{xz}^{*} ,\,\,\tau_{yz}^{*}\)) are also calculated by (Banerjee et al. 2010):

    $$\begin{array}{*{20}c} {\tau_{xz}^{*} = 0.503\,\Phi \tau_{\max } } \\ {\tau_{yz}^{*} = 0.577\,\Phi \tau_{\max } } \\ \end{array} \quad {\text{where}}\,\,\,\,\Phi = \frac{{\rho^{*} }}{{\rho_{s} }} = \frac{2}{\sqrt 3 }\frac{t}{l}$$
    (22)

In these relations, \(\tau_{\max }\) is the shear strength of the core material. Assuming a safety factor of two, the following constraints must be satisfied to keep the core shear stress lower than its allowable shear strength:

$$\begin{aligned} & g_{2} = \left| {\left. {\left( {\tau_{xz} } \right)_{\max } } \right| - 0.5\tau_{xz}^{*} } \right. \le 0 \\ & g_{3} = \left| {\left. {\left( {\tau_{yz} } \right)_{\max } } \right| - 0.5\tau_{yz}^{*} } \right. \le 0 \\ \end{aligned}$$
(23)

  • The failure of the composite face sheets is another breakdown mode of the sandwich panels. The Tsai-Hill criterion is used in this study to predict the failure of the face sheets (Kaw 2005):

    $$\left( {\frac{{\sigma_{1} }}{{\sigma_{{{\text{1ut}}}} }}} \right)^{2} - \frac{{\sigma_{1} \sigma_{2} }}{{\sigma_{{{\text{1ut}}}}^{2} }} + \left( {\frac{{\sigma_{2} }}{{\sigma_{{{\text{2ut}}}} }}} \right)^{2} + \left( {\frac{{\tau_{12} }}{{\tau_{{{\text{12ut}}}} }}} \right)^{2} < 1$$
    (24)

In this equation, \(\sigma_{1}\) is the stress parallel to the fibers, \(\sigma_{2}\) denotes the stress orthogonal to the fibers, and \(\tau_{12}\) is the shear stress in the local plane. \(\sigma_{{{\text{1ut}}}}\), \(\sigma_{{{\text{2ut}}}}\) and \(\tau_{{{\text{12ut}}}}\) denote the ultimate strengths of the material. The Tsai-Hill criterion should be satisfied for both layers with \(\theta = 0^{ \circ }\) and \(\theta = 90^{ \circ }\):

$$\begin{aligned} & g_{4} = \left[ {\left( {\frac{{\sigma_{1} }}{{\sigma_{{{\text{1ut}}}} }}} \right)^{2} - \frac{{\sigma_{1} \sigma_{2} }}{{\sigma_{{{\text{1ut}}}}^{2} }} + \left( {\frac{{\sigma_{2} }}{{\sigma_{{{\text{2ut}}}} }}} \right)^{2} + \left( {\frac{{\tau_{12} }}{{\tau_{{{\text{12ut}}}} }}} \right)^{2} } \right]_{{0^{{\text{o}}} }} - 1 < 0 \\ & g_{5} = \left[ {\left( {\frac{{\sigma_{1} }}{{\sigma_{{{\text{1ut}}}} }}} \right)^{2} - \frac{{\sigma_{1} \sigma_{2} }}{{\sigma_{{{\text{1ut}}}}^{2} }} + \left( {\frac{{\sigma_{2} }}{{\sigma_{{{\text{2ut}}}} }}} \right)^{2} + \left( {\frac{{\tau_{12} }}{{\tau_{{{\text{12ut}}}} }}} \right)^{2} } \right]_{{90^{{\text{o}}} }} - 1 < 0 \\ \end{aligned}$$
(25)

  • The failure of the composite panel may occur due to the buckling of the cells walls. Therefore, the force applied to each wall must be lower than the critical force to avoid the buckling of the cells. Assuming a uniform distribution of the compressive force on the core surface, and Zhang and Ashby (1992) derived relation for determining the buckling critical force in walls of hexagonal cells, we have:

    $$g_{6} = F_{{{\text{wall}}}} - P_{{{\text{cr}}}} = \frac{{PL_{x} L_{y} }}{{\left( {3n_{{\text{v}}} + 2} \right)n_{{\text{h}}} + n_{{\text{v}}} }} - \frac{{5.73E_{c} }}{{\left( {1 - \upsilon_{c} } \right)^{2} }}\frac{{t^{3} }}{l} \le 0$$
    (26)

In this relation, \(E_{c}\) and \(\upsilon_{c}\) are the elasticity modulus and Poisson’s ratio of the core material, respectively.

  • The height of the cells, C, is assumed to be at most 10% of their length in other directions (Gholami et al. 2016) (due to thin plate assumption):

    $$g_{7} = C - 0.1\min \left( {L_{x} ,L_{y} } \right) \le 0$$
    (27)

4 Optimization Algorithm

4.1 NMPSO Algorithm

Owing to its high solving speed, simplicity, and ease of implementation, the particle swarm optimization algorithm (PSO) is widely used for solving many optimization problems in science and engineering applications (Jahandideh-Tehrani et al. 2021; Koessler and Almomani 2021). The idea of this method is inspired by the social and cooperative behavior of the animal species such as flocks of birds and schools of fish. The possible positions of points (particles) in the population (swarm) define the space of potential solutions in the optimization problem. In each generation, each particle updates its location iteratively to move toward its previous best location and the swarm’s best position. The velocity and position of particles are updated based on the following formula:

$$x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{k + 1}$$
(28)
$$v_{i}^{k + 1} = \omega \,v_{i}^{k} + c_{1} R_{1} \left( {P_{i}^{k} - x_{i}^{k} } \right) + c_{2} R_{2} \left( {G_{i}^{k} - x_{i}^{k} } \right),\quad i = 1,2, \ldots ,N$$
(29)

In these equations, \(x_{i}^{k}\) and \(v_{i}^{k}\) are the position and velocity of the ith particle in the kth generation, respectively. \(\omega\) is the inertia weighting factor, \(P_{i}^{k}\) denotes the best position visited by the ith particle, and \(G_{i}^{k}\) represents the entire swarm’s (global) best position, in the kth generation. \(c_{1}\) and \(c_{2}\) are learning factors,\(R_{1}\) and \(R_{2}\) are two random numbers uniformly distributed in the interval [0,1].

While PSO is a robust and efficient optimization technique, it suffers from several drawbacks. Consequently, many modified forms of this algorithm have been suggested to enhance its performance. The Memetic PSO is one of these improved versions that tries to overcome one of the main weaknesses of PSO, i.e., the inability to focus on local optima, by combining PSO with local search techniques. The local search technique performs a more refine search around the solution particles or particles with the potential of being the solution to the problem. In this study, the random walk algorithm is adopted as the local search technique.

Another deficiency of the classical PSO is its proneness to be trapped into local optima which may result in a low optimizing precision or even failure (Jia et al. 2011). Niching PSO is a technique to overcome the premature convergence of PSO by dividing the whole swarm into several sub-swarms and finding the optimal solution in each of these sub-swarms.

In this study, a combination of Memetic and Niching methods is implemented in the PSO to obtain a Niching–Memetic particle swarm optimization (NMPSO) algorithm for overcoming the PSO aforementioned shortcomings.

The developed NMPSO algorithm is schematically presented in Fig. 2. According to this figure, the swarm is partitioned into several sub-swarms. The particles of each subswarm have information sharing with all the particles inside the sub-swarm not with all the population. Therefore, each particle converges to its local sub-swarm Gbest instead of the global best particle. This kind of information sharing strategy overcomes the premature convergence difficulty. Since each sub-swarm searches individually, some sub-swarms may approach each other. In this case, the sub-swarms merge into each other and the near particles are eliminated. The pseudo code of the proposed algorithm is shown in Fig. 3.

Fig. 2
figure 2

A schematic representation of the NMPSO procedure

Full size image
Fig. 3
figure 3

The pseudo code of the developed NMPSO procedure

Full size image

4.2 Handling the Constraints

PSO algorithm is not capable of handling the problem constraints by itself. Consequently, here, a general function (\(\phi\)) containing the objective function (\(f\)) and all constraints (\(g\)) is defined using the penalty method (Rao 2009):

$$\begin{aligned} & \phi \left( {X,r_{k} } \right) = f(X) + r_{k} \sum\limits_{j = 1}^{m} {G_{j} [g_{j} (X)]} \\ & G_{j} \left[ {g_{j} \left( X \right)} \right] = \left\{ {\max \left[ {0,g_{j} \left( X \right)} \right]} \right\}^{2} \\ \end{aligned}$$
(30)

where \(r_{k}\) is the penalty factor and \(m\) is the number of constraints. The PSO algorithm is now applied to this general function.

5 Results and Discussion

The sandwich panel studied here is a square of unit area, i.e., \(L_{x} = L_{y} = 1\,{\text{m}}\). Variation of span lengths \(L_{x}\) and \(L_{y}\) leads to variation of the cells number carrying the applied pressure and therefore gives rise to variation of the stresses developed in the panel. In this study, the span lengths are assumed to be constant and instead, the applied pressure is considered varying in different cases. The face sheets are composed of two composite layers made of glass–epoxy with fibers oriented along 0° and 90° directions. The honeycomb core is a regular hexagon made of NOMEX. The mechanical properties of the face sheets and the honeycomb core are presented in Tables 1 and 2, respectively. In these tables \(E\), \(G\) and \(S\) are all in GPa and \(\rho\) is in \({{{\text{kg}}} \mathord{\left/ {\vphantom {{{\text{kg}}} {{\text{cm}}^{{3}} }}} \right. \kern-\nulldelimiterspace} {{\text{cm}}^{{3}} }}\).

Table 1 Mechanical properties of the face sheets (Kaw 2005)
Full size table
Table 2 Mechanical properties of the honeycomb core (Banerjee et al. 2010)
Full size table

5.1 Verification of the Optimization Approach

The results of the convergence test for several different pressures are presented in Table 3. Based on this table, the results are converged for penalty coefficients higher than 1000, i.e., \(r_{k} \ge 1000\). Moreover, since \(f\) and \(\phi\) values are equal, it can be deduced that all constraints are met.

Table 3 The results of the convergence test for the penalty function method
Full size table

In order to assess the validity of the proposed NMPSO approach, the genetic algorithm was also used to solve the present optimization problem. The results of these approaches are compared in Table 4, in different values of the out-of-plane pressure, P. It can be seen from this table that the results of both approaches are in excellent agreement. However, it should be noted that the genetic algorithm required an initial population of around 100,000 particles and CPU-time of about 7-h for solving each case in the Table 4. While the maximum population of around 300 particles and CPU-time of less than 1-h was enough for determining the NMPSO solution.

Table 4 Comparison of optimized results obtained by NMPSO and genetic algorithms
Full size table

5.2 Optimization Results

The optimal values for the design parameters are illustrated in Fig. 4.

Fig. 4
figure 4

The variation of design parameters with pressure

Full size image

Based on data presented in Fig. 4, the following conclusions can be drawn:

  • The height and the side length of the cells (C and l) are the most important design parameters in low pressures, i.e., \(50\,{\text{kPa}} \le P \le 100\,{\text{kPa}}\). When the pressure rises in this range, decrease of l (using a higher number of cells with smaller cross-section) and increase of C lead to the reduction of the panel deformation and the buckling probability.

  • When C reaches its maximum value, for the pressure in the range \(100\, - 215\,{\text{kPa}}\), the face sheet thickness, H, emerges as the most influential optimization parameter. Increasing H will reduce the panel deformation and the face sheets’ normal stresses. But the increase rate is low due to the substantial effect of H on the panel weight.

  • At \(P = 215\,{\text{kPa}}\), the height and side length of the cell have already reached their final values. Consequently, from this point onward, the wall thickness t and the face sheet thickness H remain as the only effective parameters. Increase in t and H reduces the cell's shear stress, deflection, and buckling probability, simultaneously. However, since H is less effective than t on the panel weight, a higher rate of increase is observed for H until \(P = 840\,{\text{kPa}}\). At \(P = 840\,{\text{kPa}}\), H reaches its final value, and from now on the cell thickness, t, is the only parameter that varies with pressure. Accordingly, its rate of increase with pressure is higher than before, and it reaches its maximum value at \(P = 1328\,{\text{kPa}}\).

The variation of the normalized design parameter with the out-of-plane pressure is presented in Fig. 5. The values of important constraints, i.e., the constraint for the core shear stress (g2), the constraint for the face sheet yield based on the Tsai-Hill criterion (g4), and the constraint for the core buckling (g6) are also shown in this figure.

Fig. 5
figure 5

The variation of design parameters with pressure

Full size image

Every point in diagrams presented in this figure corresponds to the value of a design parameter for which the panel can tolerate the specified pressure with minimum weight. Consequently, these diagrams can provide useful information for optimal design of composite sandwich panels in different regimes of out-of-plane pressure. For instance, by selecting \(t = 1\,{\text{mm}}\), \(l = 23\,{\text{mm}}\), \(C = 81.2\,{\text{mm}}\), and \(H = 1\,{\text{mm}}\) for the panel, it can effectively bear the pressure of \(P = 50\,{\text{kPa}}\) while maintaining the minimum weight. The following results can also be extracted from this figure:

  • For pressures less than \(100\,\,{\text{kPa}}\), the core buckling is critical, i.e., g6 is approximately zero. Consequently, the core buckling is the active constraint in the low-pressure regime. The core shear stress is also important in this regime, especially for cores made of materials with small shear strength,\(\tau_{\max }\).

  • Increasing the pressure leads to parameter variations that raise the buckling capacity and the shear resistance of the core. As the pressure approaches its ultimate value, the constraint regarding the face sheet strength becomes the active constraint until the face sheet yields at \(P = 1328\,{\text{kPa}}\)(\(g_{4} = 0\)).

  • The increase of t improves the core buckling (g6) and shear stress (g2) constraints, but its effect on the face sheet resistance is unfavorable. For pressures less than \(840\,\,{\text{kPa}}\), increase of H can compensate for the adverse effect of t. But, during the pressure increase from 840 to \(1320\,\,{\text{kPa}}\), where t is the only varying parameter, the constraint for the yield of the face sheets (g4) becomes the critical constraint until it approaches zero at \(P = 1328\,{\text{kPa}}\).

  • Due to restrictions applied in the problem, C reaches its maximum value in the low-pressure interval. If the sandwich panel is assumed to be analogous to an I-beam, the core and face sheets will play the role of the web and flanges of the beam, respectively. Consequently, panels made of a tall core (big C) are recommended for lowering the maximum deflection and the stress induced in the face sheets.

An important point to be discussed is the difference between the study performed here and previous similar studies. In fact, in this paper, the optimal design of composite sandwich panels with honeycomb core presented in Gholami et al. (2016) is improved and extended. The most significant enhancements and modifications are:

  • The first-order shear deformation laminate theory is used to more accurately model the sandwich panel deformation (classical theory was used in Gholami et al. 2016),

  • The core shear stress in the out of plane direction is considered in the analysis (this shear stress was neglected in Gholami et al. 2016),

  • The relations considering the composite sheets and their layout are included in the analysis (these relations were ignored in Gholami et al. 2016),

  • The orthotropic constitutive model is used for the face sheets and the core, independently (the face sheets and the core was assumed to be a single orthotropic plate in Gholami et al. 2016),

  • The Tsai-Hill criterion, proven to be more accurate for failure prediction of composite sheets, is employed (von Mises criterion was used in Gholami et al. 2016),

  • A buckling constraint is included for the cell structure of the core. This constraint is especially important for the panel design in low pressures (the buckling phenomenon was ignored in Gholami et al. 2016),

  • The cells of the honeycomb structure are assumed to have hexagonal shape (circular cells were considered in Gholami et al. 2016).

As a final note, it should be mentioned that the most notable shortcoming of this study is that only the panel weight is considered as the optimization objective function. While the panel wight is of major importance, other parameters such as the panel production cost can also be the object of the optimization. Considering such parameters requires to solve a multi-object optimization problem and can be the subject of an upcoming study.

6 Conclusions

In this paper, the optimal design of a sandwich panel with honeycomb core under an out-of-plane pressure was investigated by the NMPSO method. Minimizing the panel weight was defined as the optimization objective function and the deformation of the panel, the shear stress induced in the core, the normal stress produced in the face sheets, and the buckling of the core were the problem constraints. The side length of the hexagonal cell (l), the thickness of the cell wall (t), the height of the core (C), and the thickness of the face sheets (H) were considered as the design parameters. Comparison of the results of the proposed approach with those of the genetic algorithm demonstrated that NMPSO required considerably less computation time for finding the solution of the optimization problem. The most important results of this study for a sandwich panel comprised of mentioned materials can be summed up as follows:

  • In low pressures,\(50\,{\text{kPa}} \le P \le 100\,{\text{kPa}}\), C and l are the most important design parameters and the core buckling is the most critical constraint. When the pressure rises in this regime, decrease of l and increase of C lead to the reduction of the panel deformation and the buckling probability.

  • For pressures in the range \(100\,{\text{kPa}} \le P \le 215\,{\text{kPa}}\), H is the most influential optimization parameter. Increasing H reduces the panel deformation and the face-sheets normal stresses. But the increase rate is low due to the substantial effect of H on the panel weight.

  • For pressures higher than \(P = 215\,{\text{kPa}}\), t and H remain as the only effective parameters. Increase in t and H reduces the cell's shear stress, deformation, and buckling probability, simultaneously.

  • t is the only parameter that varies in the high-pressure regime, this time with a higher rate than before. In this regime, the constraint for the yield of the face sheets (g4) becomes the critical constraint until the face sheets yield at \(P = 1328\,{\text{kPa}}\).