1 Introduction

Electricity is one of the primary drivers of development, influencing all aspects of our socioeconomic lives. It can be found in residential, educational, commercial, and industrial structures. Educational sectors, residential buildings, commercial buildings, and so on rely on the National grid as their primary sources of electricity for the majority of Nigerian residential buildings. The primary goal of an electrical utility is to provide its customers with affordable, dependable, and high-quality electricity. The demand for electrical energy has risen rapidly over the decades and continues to rise to this day. Power outages have serious socioeconomic ramifications for utilities and their customers. While much emphasis is placed on supply availability and dependability, which drives businesses and critical utilities such as schools and telecommunication networks, power grid disruption is unpredictable and at times difficult to manage. Failure may not only result in revenue losses for utilities and supply disruptions for customers, but it may also have an indirect impact on society and the nation.

The advancement of science and technology is linked to the advancement of manufacturing, and studies on the evaluation or assessment of the reliability and performance of some serial industrial and manufacturing systems under various operating conditions have been conducted. Gulati et al. (2016) presented the performance analysis of the complex system in the series configuration under different failure and repair discipline using copula. Yang and Tsao (2019) have studied reliability and availability analysis of standby systems with working vacations and retrial of failed components. Abubakar and Singh et al. (2019) gave the study of performance assessment of an industrial system through copula linguistic approach. Gahlot et al. (2018) presented a performance assessment of repairable system in the series configuration under different types of failure and repair policies using copula linguistics. Ram and Kumar (2015) have presented the performability analysis of a system under 1-out-of-2: G scheme with perfect reworking.

2 Literature review

Numerous researchers have previously presented methods in the field of reliability analysis of solar photovoltaic systems by examining system performance under various conditions. To name a few, Ahadi et al. (2016) proposed a mathematical model for improving photovoltaic system reliability through component reliability improvement. Baschel et al. (2018) discussed the effect of unit reliability on the performance of large-scale photovoltaic systems. The effect of reliability and availability for two inverter configurations is demonstrated using fault tree analysis. Gupta et al. (2020) discussed the operational availability of power plant. Belaout et al. (2018) presented a multiclass adaptive neuro-fuzzy classifier for detecting fault and classification in a photovoltaic array. Benkercha and Moulahourn (2018) proposed an approach using a decision tree algorithm to detect and diagnose the faults in a grid-connected photovoltaic system. Kumar and Saini (2014) studied the profit of solar photovoltaic system incorporating preventive maintenance. Kumar and Saini (2018a) analyzed the availability of marine power plant using the fuzzy method. Kumar and Saini (2018b) discuss the impact of preventive maintenance and repair priority on the profit of a computer system. Kumar et al. (2018) presented stochastic modelling of a non-identical system following Weibull distribution with priority and preventive maintenance. Saini et al. (2021) investigate the reliability of the power generating unit of the sewage treatment plant. Wang et al. (2021) investigate the reliability and performance of the warm standby system. Cai et al. (2015) dealt with the reliability evaluation of photovoltaic systems with intermittent faults using dynamic Bayesian networks. Three-state Markov model which represents the state transition relationship of no faults, intermittent faults, and permanent faults for the system components is obtained. Chen et al. (2017) proposed a methodology for detecting and diagnosis fault in photovoltaic systems using extreme machine learning. Chiacchio et al. (2018) discuss the performance evaluation of photovoltaic power plant through stochastic hybrid fault tree automation mode. Colli (2015) studied failure mode and effect analysis for photovoltaic systems. Cristaldi et al. (2017) discuss the root cause and risk analysis of photovoltaic balance system failure. Das et al. (2018) focus on metaheuristic optimization-based diagnosis of fault for a photovoltaic system with nonuniform irradiance. Garoudja et al. (2017) proposed a fault-detection approach for detecting of shading of a photovoltaic system based on the direct current by combining the flexibility, and simplicity of a one-diode model.

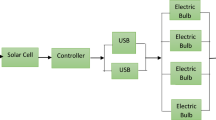
Because of the non-availability of data of the PV system, the present paper introduced a reliability modelling approach to study the overall performance of the PV system. In this paper, we have introduced a new model of the photovoltaic system consisting of four subsystems namely, panel, inverter, battery bank and control charger. Following Ismail et al. (2021), the units in each subsystem are assumed to have exponential failure and repair time.

The paper is organized into different parts. The introduction portion that focuses on the relevant literature reviewed for the study of the proposed model is defined in Sect. 2. The state description and notation used for the analysis of the proposed model are covered in Sect. 3. Section 4 presents reliability models of the system in which some particular cases are discussed. The paper is concluded with results in Sect. 5.

3 State description and assumptions

3.1 Assumptions

The following are taken throughout the discussion of the model.

  1. 1.

    Initially, both subsystems are in good working condition.

  2. 2.

    Three units from subsystem 1 and two units from subsystem 3 in consecutive are necessary for operational mode.

  3. 3.

    The one unit in subsystem 2 is necessary for operational mode. Also the one units out of one in subsystem 4 are necessary for operational mode.

  4. 4.

    The system will be inoperative if three units from subsystem 1 failed. In addition, if two units from subsystem 3 failed.

  5. 5.

    The system will also be inoperative if one unit failed from either of subsystem 2 and 4, respectively.

  6. 6.

    Failed unit of the system can be repaired when it is inoperative or failed state.

  7. 7.

    Copula repair follows a total failure of a unit in the subsystem.

  8. 8.

    It is assumed that a repaired system by copula works like a new system and no damage appears during the repair.

  9. 9.

    As soon as the failed unit gets repaired, it is ready to perform the task.

4 Reliability modelling

4.1 Formulation and solution of a mathematical model

By the probability of considerations and continuity of arguments, through Table 1, Figs. 1 and 2 the following set of difference-differential equations are associated with the above mathematical model.

$$\left[\frac{\partial }{\partial t}+3{\beta }_{1}+{\beta }_{2}+2{\beta }_{3}+{\beta }_{4}\right]{P}_{0}\left(t\right)={\int }_{0}^{\infty }\phi (x){P}_{1}(x,t)\mathrm{d}x+{\int }_{0}^{\infty }{\mu }_{0}(x){P}_{3}(x,t)\mathrm{d}x+{\int }_{0}^{\infty }{\mu }_{0}(y){P}_{4}(y,t)\mathrm{d}y+{\int }_{0}^{\infty }{\mu }_{0}(x){P}_{6}(z,t)\mathrm{d}z+{\int }_{0}^{\infty }{\mu }_{0}(k){P}_{7}(k,t)\mathrm{d}k$$
(1)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+3{\beta }_{1}+2{\beta }_{3}+\phi \left(x\right)\right]{P}_{1}\left(x,t\right)=0$$
(2)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+3{\beta }_{1}+\phi \left(x\right)\right]{P}_{2}\left(x,t\right)=0$$
(3)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{P}_{3}\left(x,t\right)=0$$
(4)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial y}+{\mu }_{0}\left(y\right)\right]{P}_{4}\left(y,t\right)=0$$
(5)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial z}+2{\beta }_{3}+\phi \left(z\right)\right]{P}_{5}\left(z,t\right)=0$$
(6)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial z}+{\mu }_{0}\left(z\right)\right]{P}_{6}\left(z,t\right)=0$$
(7)
$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial k}+{\mu }_{0}\left(k\right)\right]{P}_{7}\left(k,t\right)=0$$
(8)
Table 1 Description of the states of the system
Full size table
Fig. 1
figure 1

Block diagram for the system

Full size image
Fig. 2
figure 2

Transition diagram of the system. Complete failure Reduced capacity Perfect state

Full size image

4.2 Boundary conditions

$$ P_{1} \left( {0,t} \right) = 3\beta_{1} P_{0} \left( t \right) $$
(9)
$${P}_{2}\left(0,t\right)=9{\beta }_{1}^{2}{P}_{0}(t)$$
(10)
$${P}_{3}\left(0,t\right)=27{\beta }_{1}^{3}{P}_{0}(t)$$
(11)
$${P}_{4}\left(0,t\right)=3{\beta }_{2}{P}_{0}(t)$$
(12)
$${P}_{5}\left(0,t\right)=2{\beta }_{3}{P}_{0}(t)$$
(13)
$${P}_{6}\left(0,t\right)=4{\beta }_{3}^{2}{P}_{0}(t)$$
(14)
$${P}_{6}\left(0,t\right)={\beta }_{4}{P}_{0}(t)$$
(15)
$$ {\text{Initial}}\;{\text{condition}}\;P_{0} \left( t \right) = 1\;{\text{and}}\;{\text{other}}\;{\text{transition}}\;{\text{probability}}\;{\text{at}}\;t = 0\;{\text{are}}\;{\text{zero}} $$
(16)

Taking Laplace transformation of Eqs. (1)–(15) and using the equation with the help of (16), one can obtain

$$\left[S+3{\beta }_{1}+{\beta }_{2}+2{\beta }_{3}+{\beta }_{4}\right]{\overline{P} }_{0}\left(s\right)=1+{\int }_{0}^{\infty }\phi (x){\overline{P} }_{1}(x,s)\mathrm{d}x+{\int }_{0}^{\infty }{\mu }_{0}(x){\overline{P} }_{3}(x,s)\mathrm{d}x+{\int }_{0}^{\infty }{\mu }_{0}(y){\overline{P} }_{4}(y,s)\mathrm{d}y+{\int }_{0}^{\infty }{\mu }_{0}(x){\overline{P} }_{6}(z,s)\mathrm{d}z+{\int }_{0}^{\infty }{\mu }_{0}(k){\overline{P} }_{7}(k,s)\mathrm{d}k$$
(17)
$$\left[S+\frac{\partial }{\partial x}+3{\beta }_{1}+2{\beta }_{3}+\phi \left(x\right)\right]{\overline{P} }_{1}\left(x,s\right)=0$$
(18)
$$\left[S+\frac{\partial }{\partial x}+3{\beta }_{1}+\phi \left(x\right)\right]{\overline{P} }_{2}\left(x,s\right)=0$$
(19)
$$\left[S+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{\overline{P} }_{3}\left(x,s\right)=0$$
(20)
$$\left[S+\frac{\partial }{\partial y}+{\mu }_{0}\left(y\right)\right]{\overline{P} }_{4}\left(y,s\right)=0$$
(21)
$$\left[S+\frac{\partial }{\partial z}+2{\beta }_{3}+\phi \left(z\right)\right]{\overline{P} }_{5}\left(z,s\right)=0$$
(22)
$$\left[S+\frac{\partial }{\partial z}+{\mu }_{0}\left(z\right)\right]{\overline{P} }_{6}\left(z,s\right)=0$$
(23)
$$\left[S+\frac{\partial }{\partial k}+{\mu }_{0}\left(k\right)\right]{\overline{P} }_{7}\left(k,s\right)=0$$
(24)

4.3 Laplace of the boundary condition

$${\overline{P} }_{1}\left(0,t\right)=3{\beta }_{1}{\overline{P} }_{0}(s)$$
(25)
$${\overline{P} }_{2}\left(0,t\right)=9{\beta }_{1}^{2}{\overline{P} }_{0}(s)$$
(26)
$${\overline{P} }_{3}\left(0,t\right)=27{\beta }_{1}^{3}{\overline{P} }_{0}(s)$$
(27)
$${\overline{P} }_{4}\left(0,t\right)=3{\beta }_{2}{\overline{P} }_{0}(s)$$
(28)
$${\overline{P} }_{5}\left(0,t\right)=2{\beta }_{3}{\overline{P} }_{0}(s)$$
(29)
$${\overline{P} }_{6}\left(0,t\right)=4{\beta }_{3}^{2}{\overline{P} }_{0}(s)$$
(30)
$${\overline{P} }_{7}\left(0,t\right)={\beta }_{4}{\overline{P} }_{0}(s)$$
(31)

Solving Eqs. (18)–(24) with the help of boundary condition (25)–(31) and applying the below-shifting properties of Laplace:

$${\int }_{0}^{\infty }{[e}^{-sx}\cdot {e}^{-{\int }_{0}^{x}f(x)dx}]\mathrm{d}x=L\left\{\frac{1-{\overline{S} }_{f}(x)}{S}\right\}=\frac{1-{\overline{S} }_{f}(x)}{S}$$
(32)
$${\int }_{0}^{\infty }{[e}^{-sx}\cdot f(x) {e}^{-{\int }_{0}^{x}f\left(x\right)dx}]\mathrm{d}x=L\left\{{\overline{S} }_{f}\left(x\right)\right\}={\overline{S} }_{f}(s)$$
(33)
$${\overline{P} }_{1}\left(S\right)={\overline{P} }_{1}(0,S)\left\{\frac{1-{\overline{S} }_{\phi }(S+3{\beta }_{1}+2{\beta }_{3})}{S+3{\beta }_{1}+2{\beta }_{3}}\right\}$$
(34)
$${\overline{P} }_{2}\left(S\right)= {\overline{P} }_{2}(0,S)\left\{\frac{1-{\overline{S} }_{\phi }(S+3{\beta }_{1})}{S+3{\beta }_{1}}\right\}$$
(35)
$${\overline{P} }_{3}\left(S\right)= {\overline{P} }_{3}(0,S)\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}$$
(36)
$${\overline{P} }_{4}\left(S\right)= {\overline{P} }_{4}(0,S)\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}$$
(37)
$${\overline{P} }_{5}\left(S\right)= {\overline{P} }_{5}(0,S)\left\{\frac{1-{\overline{S} }_{\phi }(S+2{\beta }_{3})}{S+2{\beta }_{3}}\right\}$$
(38)
$${\overline{P} }_{6}\left(S\right)={\overline{P} }_{6}(0,S)\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}$$
(39)
$${\overline{P} }_{7}\left(S\right)={\overline{P} }_{7}(0,S)\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}$$
(40)

Substituting (25)–(31) in the Eqs. (34)–(40) we have

$${\overline{P} }_{1}\left(S\right)=3{\beta }_{1}\left\{\frac{1-{\overline{S} }_{\phi }(S+3{\beta }_{1}+2{\beta }_{3})}{S+3{\beta }_{1}+2{\beta }_{3}}\right\}{P}_{0}(t)$$
(41)
$${\overline{P} }_{2}\left(S\right)=9{\beta }_{1}^{2}\left\{\frac{1-{\overline{S} }_{\phi }(S+3{\beta }_{1})}{S+3{\beta }_{1}}\right\}{P}_{0}(t)$$
(42)
$${\overline{P} }_{3}\left(S\right)=27{\beta }_{1}^{3}\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}{P}_{0}(t)$$
(43)
$${\overline{P} }_{4}\left(S\right)=3{\beta }_{2}\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}{P}_{0}(t)$$
(44)
$${\overline{P} }_{5}\left(S\right)=2{\beta }_{3}\left\{\frac{1-{\overline{S} }_{\phi }(S+2{\beta }_{3})}{S+2{\beta }_{3}}\right\} {P}_{0}(t)$$
(45)
$${\overline{P} }_{6}\left(S\right)= 4{\beta }_{3}^{2}\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}{P}_{0}(t)$$
(46)
$${\overline{P} }_{7}\left(S\right)= {\beta }_{4}\left\{\frac{1-{\overline{S} }_{\mu }(S)}{S}\right\}{P}_{0}(t)$$
(47)
$$ \begin{aligned} & \overline{P}_{0} \left( S \right) = \frac{1}{D\left( S \right)} \\ & \quad {\text{where}}\;D\left( s \right) = \left[ {\left[ {S + 3\beta_{1} + \beta_{2} + 2\beta_{3} + \beta_{4} } \right] - \left( {3\beta_{1} \overline{S}_{\phi } \left( {S + 3\beta_{1} + 2\beta_{3} } \right)} \right.} \right. \\ & \quad \left. {\left. { + 27\beta_{1}^{3} \overline{S}_{\mu } \left( S \right) + 3\beta_{2} \overline{S}_{\mu } \left( S \right) + 4\beta_{3}^{2} \overline{S}_{\mu } \left( S \right) + \beta_{4} \overline{S}_{\mu } \left( S \right)} \right)} \right] \\ \end{aligned} $$
(48)
$$\mathrm{But }{D(S)\cdot \overline{P} }_{0}\left(S\right)=1$$
(49)
$$\Rightarrow {\overline{P} }_{0}\left(S\right)=\frac{1}{D\left(S\right)}$$
(50)
$${\overline{P} }_{\mathrm{up}}\left(S\right)= {\overline{P} }_{0}\left(S\right)+{\overline{P} }_{1}\left(S\right)+ {\overline{P} }_{2}\left(S\right)+ {\overline{P} }_{5}\left(S\right)$$
(51)
$${\overline{P} }_{\mathrm{down}}\left(S\right)=1-{\overline{P} }_{\mathrm{up}}\left(S\right)$$
(52)

5 Analytical study of a model for particular cases

Setting all repairs to 1. i.e. \(\phi \left(x\right)={\mu }_{0}\left(x\right)= {\mu }_{0}\left(y\right)=1\)

Taking the values of different parameters as \({\beta }_{1}=0.001\), \({\beta }_{2}=0.002,\) \({\beta }_{3}=0.003\) and \({\beta }_{4}=0.004\). In (51) then taking the inverse Laplace transform, we can obtain, the expression for availability as:

$$ \begin{aligned} & 0.0007500000000e^{ - 0.003000000000t} + 0.6666666667e^{ - 0.006000000000t} \\ & \quad + 0.3725833333e^{ - 0.01500000000t} - 0.04000000000e^{ - 0.09000000000t} \\ \end{aligned} $$
(53)

For different values of time t = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100.

Unit of time, we may get different of \({\overline{P} }_{\mathrm{up}}\left(t\right)\) with the help of (53) as shown in Table 1 and corresponding figure.

6 Reliability analysis

Taking all repair rate \(\phi \left(x\right)={\mu }_{0}\left(x\right)={\mu }_{0}\left(y\right)=0\) in Eq. (53) and for the same values of failure rate as \({\beta }_{1}=0.001\), \({\beta }_{2}=0.002\), \({\beta }_{3}=0.003\) and \({\beta }_{4}=0.004\).

And then taking inverse Laplace transform, one may have the expression for reliability for the system. Expression for the reliability of the system is given as;

$$ \begin{aligned} R\left( t \right) & = 0.0007500000000e^{ - 0.003000000000t} + 0.6666666667e^{ - 0.006000000000t} \\ & \quad + 0.3725833333e^{ - 0.01500000000t} - 0.04000000000e^{ - 0.09000000000t} \\ \end{aligned} $$

For different values of time t = 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, and 100.

Unit of time, we may get different values of Reliability that shown in the table.

7 Analysis and concluding remark

Through Table 2, Figs. 3 and 4, the results show that the energy availability of the test system is as high as 99.02% in contrast to a time availability of only 90.68%. The rationale behind the results is that any derated states or partial failures of the PV system are counted in the time unavailability. On the other hand, the PV system is still able to generate electricity during derated hours, resulting in relatively higher energy availability.

Table 2 Variation of availability with respect to time
Full size table
Fig. 3
figure 3

Availabilities as a function of time

Full size image
Fig. 4
figure 4

Availabilities as a function of time

Full size image

System’s reliability is much more sensitive with respect to simultaneous failure rate of one unit of the solar panel and one unit of Battery as elaborated in Table 3 and Fig. 5. Model investigated the reliability measures and sensitivity analysis for a system of solar installation work. The result reveals that system reliability is more sensitive with respect to failure rates of the system and MTTF of the system is more sensitive with respect to failure rate of subsystem 1. The Model which consists of n unit in parallel configuration with a standby unit considered system can fail due to unit failure, catastrophic failure, and the failure of standby unit and resulted in that system’s reliability is more sensitive with respect to battery and charge controller failure. It is concluded that the MTTF of the system is equally sensitive with respect to the failure rate charge controller and distributor of the system as demonstrated in Table 4, Fig. 6 and Table 5, Fig. 7 respectively.

Table 3 Computation of reliability for different values of time
Full size table
Fig. 5
figure 5

Reliability as a function of time (t)

Full size image
Table 4 MTTF as a function of failure rate
Full size table
Fig. 6
figure 6

MTTF as a function of failure rate

Full size image
Table 5 MTTF sensitivity as a function of failure rate
Full size table
Fig. 7
figure 7

Sensitivity analysis of the system as a function of failure rate

Full size image

In future, reliability and performance analysis of multi-unit photovoltaic system for consumption of small- and large-scale enterprises is going to be using fuzzy method.