Introduction

It is vital to identify alternative energy sources to replace the current ones due to the issues of global warming that are facilitated by the emissions from the use of conventional energy sources including fossil fuels, hydroelectricity, thermal electricity, and others. However, extensive researches are conducted worldwide which eventually led to the existing of solar energy. Since then, simple and sophisticated solar-powered devices have been created in order to overcome the challenges of safety hazards and high cost of outdated energy sources. Solar energy as user-friendly, affordable, reliable, dependable, simple, low maintenance cost and efficiency made it popular renewable energy resource and recognizes by society over the world. These peculiarities made it possible for everyone to quickly switched to the use of solar energy for better performance of their gadgets and generate mega profit. Nevertheless, this made available provisions for individuals, groups, industrial and manufacturing companies, governments, non-governmental organizations (NGOs), business enterprises, etc. Even though, there are issues linked to the usage of solar energy, such as geographical location, timing (day and night), season, and so on. Yet, society accepted it. However, advanced researches are currently ongoing in an effort to overcome the aforementioned obstacles. The present advancements in science and technology have made it possible to eliminate the limitations placed on the usage of solar energy using backup systems, energy storage devices, and more complicated gadgets.

Considering the advantages of solar-power over the obsolete sources of energy like fossil fuels, hydroelectricity, thermal electricity, and others, these necessitated researchers from all over the world to double their effort in making simulations. Many systems were investigated using various procedures, different assumptions of parameters, different systems designed and configurations all in line to produce simple and strong solar-power systems that will satisfy the need of the society in general. The impact of discrete multi-arc rib roughness on the effective efficiency of a solar air heater was studied by Arwa et al. [1]. An analysis of the performance and economic feasibility of a hybrid solar cooling system that combines an ejector with vapor compression cycle powered by a photovoltaic thermal (PV/T) unit was examined by Ghassan and Mohammad [2] Molamohamadi and Talaei [3] focused on the analysis of a proper strategy for solar energy deployment in Iran using SWOT matrix. Mohamad et al. [4] carried out the performance analysis of solar absorption ice maker driven by parabolic trough collector. Assessment of the performance of solar water heater: an experimental and theoretical investigation was inquired by Naseer et al. [5]. Shateri et al. [6] investigated the optimization of heat transfer in an enclosure with a Trombe wall and solar chimney. Al-Widyana et al. [7] investigated the effect of alkaline nitrates and operating temperature on the performance of dye sensitized solar cells. An experimental and theoretical analysis of thermal losses in a flat plate solar heater with multi risers and headers was inquired by Al-Saiydee [8]. Harrabi et al. [9] examined the assessment of uncertainties in energetic and energetic performances of a flat plate solar water heater. Energy and economic analysis of curved and spiral flow flat-plate solar water collector was reported by Muthuraman et al. [10]. Shamshirgaran et al. [11] investigated the state of the art of techno-economics of nanofluid-laden flat-plate solar collectors for sustainable accomplishment. The energy and exergy evaluation of the evacuated tube solar collector using Cu2O/water nanofluid utilizing ANN methods was conducted by Sadeghi et al. [12].

However, advanced studies were carried out on sophisticated repairable systems where authors involved the use of copula procedures and assuming different failures and repairs to assessed the reliability elements. Reliability analysis of multi-workstation computer network configured as series–parallel system via Gumbel—Hougaard family copula was inquired by Isa et al. [13]. Ismail. [14] investigated the reliability and cost analysis of sachet water plant using Copula approach. Gupta et al. [15] focused on the behavioral analysis of cooling tower in steam turbine power plant using reliability, availability, maintainability and dependability investigation. Kumar et al. [16] conducted the analysis of a redundant system with priority and Weibull distribution for failure and repair. Singh et al. [17] focused on a performance analysis of a complex repairable system with two subsystems in series configuration with imperfect switch. Rawal et al. [18, 19] examined the reliability assessment of multi-computer system consisting n clients and k-out-of-n: g operational scheme with copula repair policy. Mathematical modeling of sugar plant: a fuzzy approach was reported by Kumar and Saini [20]. Performance analysis of a computer system with imperfect fault detection of hardware was examined by Kumar et al. [21]. Yusuf et al. [22] investigated the use of copula approach to performance evaluation of manufacturing system. Saini et al. [23] carried out the availability optimization of biological and chemical processing unit using genetic algorithm and particle swarm optimization. Reliability and performance analysis of a series–parallel photovoltaic system with human operators using Gumbel-Hougaard family copula was examined by Maihulla et al. [24]. Yusuf et al. [22] reported on a Copula approach to performance evaluation of manufacturing system. Beside, many works similar to this study were previously presented by authors, nonetheless, no single author focused accurately on a multi-purpose solar system made up of four separate subsystems: a solar panel, a controller, two USB charge points, and four electric bulb points that were all merged together in a series–parallel conformation and studied using Gumbel–Hougaard family copula approach. Components/units failure is constant and in line with exponential function, copula and general repairs are available for the repair of partial and entire system failure. The transition outline of the system was used to derived the partial differential equations of order one, and solved using supplementary variable and Laplace transformation procedures. Maple software package was used to generate expressions for availability, reliability, MTTF, sensitivity and cost. Results were justified using particular examples as presented in Tables and Figures.

Notations, Assumptions, System Description, State Description

Notations

N Represent time.

\(u_{j}\) Represnt failures of subsystems, and j = 1, 2, 3 and 4.

\(g_{1} \left( {h_{1} } \right)/g_{2} \left( {h_{2} } \right)\) Represent repairs of subsystem 3 and 4.

\(r_{0} \left( {h_{j} } \right)\) Represent repairs of whole system failure, and j = 1, 2, 3 and 4.

\(Z_{i} \left( n \right)\) Represent the states of the system, and i = 0, 1, …, 8.

\(\overline{Z} (s)\) Represent the Laplace conversion of \(Z\left( n \right)\).

\(Z_{i} \left( {h_{j} ,n} \right)\) Represent states probability, repair variable and time for repair, where.

i = 0, 1…, 8, and j = 1, 2, 3 and 4.

\(E_{g} \left( n \right)\) Represent the expected gain within the range [0, n].

G1, G2 Cost essentials.

\(S_{g} \left( h \right)\) Represent function such as \(S_{g} \left( h \right)\)\(= g\left( h \right)e^{{ - \int\limits_{o}^{h} {g\left( h \right)dh} }}\).

\(\overline{S}_{h} \left( s \right)\) Represent Laplace conversion of \(S_{g} \left( h \right)\) as \(\overline{S}_{g} \left( s \right) = \int\limits_{0}^{\infty } {e^{ - sh} g\left( h \right)e^{{ - \int\limits_{0}^{h} {g\left( h \right)dh} }} } dh\).

\(r_{0} \left( h \right)\) = Cθ (\(r_{1} \left( h \right)\), \(r_{2} \left( h \right)\)) \(c_{\theta } \left( {r_{1} \left( h \right),r_{2} \left( h \right)} \right) = \exp \left( {h^{\theta } + \left\{ {\log g\left( h \right)^{\theta } } \right\}^{{\frac{1}{\theta }}} } \right)\), \(1 \le \theta \le \infty\).

Represent copula repair facility, where \(r_{1} = g\left( h \right)\), and \(r_{2} = e^{h}\).

Assumptions

In the process of authenticating the model these were taken into consideration:

Normaly, everything in the system are satisfactory.

For the system to fucntion the four subsystems are required.

There should be sunlight.

Failure of components is inevitable, though it can be addresses operating or otherwise.

Partial and whole system failure are tackled by mean of general and copula repairs.

System function satisfactory after been repaired.

System Description

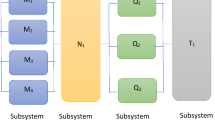
Conventionally, the solar system consisting of four subsystems: a solar panel, a controller, two USB charge points and four electric bulb points all merged together in a series–parallel conformation. Initially, the system is performing satisfactory, instantly one unit of system 3 and 4 failed, the backup unit turned to function for the replacement of the failed unit, and the failed unit has undergone repair path, system operate, and the second unit of these subsystems failed, so the subsystems failed, and this led the entire system to stopped working. Similar to this, subsystem 1 and 2 failed, therefore, the whole system breaks down. Therefore, subsystem 1 and 2 are presumed to be delicate, and for that extra cares are required for system better performance. Eventually, partial failure is resolved using general repair, and system failure is fixed by mean of copula repair (Table 1; Figs. 1, 2).

Table 1 States description
Full size table
Fig. 1
figure 1

Solar system block diagram

Full size image
Fig. 2
figure 2

Solar system transition plan

Full size image

States Description

Origination of Mathematical Model of the Solar System

The incoming set of partial differential equations are generated from the transition plan of the solar system.

$$ \begin{aligned} \left( {\frac{\partial }{\partial n} + 3u_{1} + u_{2} + u_{3} + u_{4} } \right)Z_{0} \left( n \right) & = \int_{0}^{\infty } {g_{1} \left( {h_{1} } \right)Z_{1} \left( {h_{1} ,n} \right)dh_{1} } + \int_{0}^{\infty } {g_{2} \left( {h_{2} } \right)Z_{2} \left( {h_{2} ,n} \right)dh_{2} } \\ & \quad + \int_{0}^{\infty } {r_{0} \left( {h_{1} } \right)Z_{5} \left( {h_{1} ,n} \right)dh_{1} } + \int_{0}^{\infty } {r_{0} \left( {h_{2} } \right)Z_{6} \left( {h_{2} ,n} \right)dh_{2} } \\ & \quad + \int_{0}^{\infty } {r_{0} \left( {h_{3} } \right)Z_{7} \left( {h_{3} ,n} \right)dh_{3} } + \int_{0}^{\infty } {r_{0} \left( {h_{4} } \right)Z_{8} \left( {h_{4} ,n} \right)dh_{4} } \\ \end{aligned} $$
(1)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{1} }} + 3u_{1} + u_{2} + u_{3} + u_{4} + g_{1} \left( {h_{1} } \right)} \right)Z_{1} \left( {h_{1} ,n} \right) = 0 $$
(2)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{2} }} + 3u_{1} + u_{2} + u_{3} + u_{4} + g_{2} \left( {h_{2} } \right)} \right)Z_{2} \left( {h_{2} ,n} \right) = 0 $$
(3)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{2} }} + u_{2} + g_{2} \left( {h_{2} } \right)} \right)Z_{3} \left( {h_{2} ,n} \right) = 0 $$
(4)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{1} }} + 3u_{1} + g_{1} \left( {h_{1} } \right)} \right)Z_{4} \left( {h_{1} ,n} \right) = 0 $$
(5)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{1} }} + r_{0} \left( {h_{1} } \right)} \right)Z_{5} \left( {h_{1} ,n} \right) = 0 $$
(6)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{2} }} + r_{0} \left( {h_{2} } \right)} \right)Z_{6} \left( {h_{2} ,n} \right) = 0 $$
(7)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{3} }} + r_{0} \left( {h_{3} } \right)} \right)Z_{7} \left( {h_{3} ,n} \right) = 0 $$
(8)
$$ \left( {\frac{\partial }{\partial n} + \frac{\partial }{{\partial h_{4} }} + r_{0} \left( {h_{4} } \right)} \right)Z_{8} \left( {h_{4} ,n} \right) = 0 $$
(9)

Boundary Conditions

$$ Z_{1} \left( {0,n} \right) = 3u_{1} Z_{0} \left( n \right) $$
(10)
$$ Z_{2} \left( {0,n} \right) = u_{2} Z_{0} \left( n \right) $$
(11)
$$ Z_{3} \left( {0,n} \right) = u_{2} Z_{1} \left( {0,n} \right) $$
(12)
$$ Z_{4} \left( {0,n} \right) = 3u_{1} Z_{2} \left( {0,n} \right) $$
(13)
$$ Z_{5} \left( {0,n} \right) = 3u_{1} \left( {Z_{1} \left( {0,n} \right) + Z_{4} \left( {0,n} \right)} \right) $$
(14)
$$ Z_{6} \left( {0,n} \right) = u_{2} \left( {Z_{2} \left( {0,n} \right) + Z_{3} \left( {0,n} \right)} \right) $$
(15)
$$ Z_{7} \left( {0,n} \right) = u_{3} \left( {Z_{0} \left( n \right) + Z_{1} \left( {0,n} \right) + Z_{2} \left( {0,n} \right)} \right) $$
(16)
$$ Z_{8} \left( {0,n} \right) = u_{4} \left( {Z_{0} \left( n \right) + Z_{1} \left( {0,n} \right) + Z_{2} \left( {0,n} \right)} \right) $$
(17)

Initial Conditions

$$ Z_{0} (0) = 1,\,{\text{the}}\,{\text{ remaining }}\,{\text{state }}\,{\text{probabilities }}\,{\text{at}}\,{\text{ n }} = \, 0, \, \,{\text{are}}\,{\text{ zero}}, $$
(18)

Solution of Mathematical Model of Solar System

The incoming equations are generated by mean of Laplace conversion of Eqs. (1) to (17) with assist of initial conditions.

$$ \begin{aligned} &\left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right)\overline{Z}_{0} (s)\\ &\quad = 1 + \int\limits_{0}^{\infty } {g_{1} \left( {h_{1} } \right)\overline{Z}_{1} \left( {h_{1} ,s} \right)dh_{1} } + \int\limits_{0}^{\infty } {g_{2} \left( {h_{2} } \right)\overline{Z}_{2} \left( {h_{2} ,s} \right)dh_{2} } + \int\limits_{0}^{\infty } {r_{0} \left( {h_{1} } \right)\overline{Z}_{5} \left( {h_{1} ,s} \right)dh_{1} } + \int\limits_{0}^{\infty } {r_{0} \left( {h_{2} } \right)\overline{Z}_{6} \left( {h_{2} ,s} \right)dh_{2} } \\ & + \int\limits_{0}^{\infty } {r_{0} \left( {h_{3} } \right)\overline{Z}_{7} \left( {h_{3} ,s} \right)dh_{3} } + \int\limits_{0}^{\infty } {r_{0} \left( {h_{4} } \right)\overline{Z}_{8} \left( {h_{4} ,s} \right)dh_{4} } \\ \end{aligned} $$
(19)
$$ \left( {s + \frac{\partial }{{\partial h_{1} }} + 3u_{1} + u_{2} + u_{3} + u_{4} + g_{1} \left( {h_{1} } \right)} \right)\overline{Z}_{1} \left( {h_{1} ,s} \right) = 0 $$
(20)
$$ \left( {s + \frac{\partial }{{\partial h_{2} }} + 3u_{1} + u_{2} + u_{3} + u_{4} + g_{2} \left( {h_{2} } \right)} \right)\overline{Z}_{2} \left( {h_{2} ,s} \right) = 0 $$
(21)
$$ \left( {s + \frac{\partial }{{\partial h_{2} }} + u_{2} + g_{2} \left( {h_{2} } \right)} \right)\overline{Z}_{3} \left( {h_{2} ,s} \right) = 0 $$
(22)
$$ \left( {s + \frac{\partial }{{\partial h_{1} }} + 3u_{1} + g_{1} \left( {h_{1} } \right)} \right)\overline{Z}_{4} \left( {h_{1} ,s} \right) = 0 $$
(23)
$$ \left( {s + \frac{\partial }{{\partial h_{1} }} + r_{0} \left( {h_{1} } \right)} \right)\overline{Z}_{5} \left( {h_{1} ,s} \right) = 0 $$
(24)
$$ \left( {s + \frac{\partial }{{\partial h_{2} }} + r_{0} \left( {h_{2} } \right)} \right)\overline{Z}_{6} \left( {h_{2} ,s} \right) = 0 $$
(25)
$$ \left( {s + \frac{\partial }{{\partial h_{3} }} + r_{0} \left( {h_{3} } \right)} \right)\overline{Z}_{7} \left( {h_{3} ,s} \right) = 0 $$
(26)
$$ \left( {s + \frac{\partial }{{\partial h_{4} }} + r_{0} \left( {h_{4} } \right)} \right)\overline{Z}_{8} \left( {h_{4} ,s} \right) = 0 $$
(27)

Boundary conditions

$$ \overline{Z}_{1} \left( {0,s} \right) = 3u_{1} \overline{Z}_{0} \left( s \right) $$
(28)
$$ \overline{Z}_{2} \left( {0,s} \right) = u_{2} \overline{Z}_{0} \left( s \right) $$
(29)
$$ \overline{Z}_{3} \left( {0,s} \right) = u_{2} \overline{Z}_{1} \left( {0,s} \right) $$
(30)
$$ \overline{Z}_{4} \left( {0,s} \right) = 3u_{1} \overline{Z}_{2} \left( {0,s} \right) $$
(31)
$$ \overline{Z}_{5} \left( {0,s} \right) = 3u_{1} \left( {\overline{Z}_{1} \left( {0,s} \right) + \overline{Z}_{4} \left( {0,s} \right)} \right) $$
(32)
$$ \overline{Z}_{6} \left( {0,s} \right) = u_{2} \left( {\overline{Z}_{2} \left( {0,s} \right) + \overline{Z}_{3} \left( {0,s} \right)} \right) $$
(33)
$$ \overline{Z}_{7} \left( {0,s} \right) = u_{3} \left( {\overline{Z}_{0} \left( s \right) + \overline{Z}_{1} \left( {0,s} \right) + \overline{Z}_{2} \left( {0,s} \right)} \right) $$
(34)
$$ \overline{Z}_{8} \left( {0,s} \right) = u_{4} \left( {\overline{Z}_{0} \left( s \right) + \overline{Z}_{1} \left( {0,s} \right) + \overline{Z}_{2} \left( {0,s} \right)} \right) $$
(35)

The incoming equations are generated with aid of boundary conditions

$$ \overline{Z}_{0} \left( s \right) = \frac{1}{F\left( s \right)} $$
(36)
$$ \overline{Z}_{1} \left( s \right) = \frac{{3u_{1} }}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{g_{{_{1} }} }} }} \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right)}}{{s + 3u_{1} + u_{2} + u_{3} + u_{4} }}} \right) $$
(37)
$$ \overline{Z}_{2} \left( s \right) = \frac{{u_{2} }}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{g_{{_{2} }} }} }} \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right)}}{{s + 3u_{1} + u_{2} + u_{3} + u_{4} }}} \right) $$
(38)
$$ \overline{Z}_{3} \left( s \right) = \frac{{3u_{1} u_{2} }}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{g_{{_{2} }} }} }} \left( {s + u_{2} } \right)}}{{s + u_{2} }}} \right) $$
(39)
$$ \overline{Z}_{4} \left( s \right) = \frac{{3u_{1} u_{2} }}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{g_{{_{1} }} }} }} \left( {s + 3u_{1} } \right)}}{{s + 3u_{1} }}} \right) $$
(40)
$$ \overline{Z}_{5} \left( s \right) = \frac{{\left( {9u_{1}^{2} + 9u_{1}^{2} u_{2} } \right)}}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{r_{{_{0} }} }} }} \left( s \right)}}{s}} \right) $$
(41)
$$ \overline{Z}_{6} \left( s \right) = \frac{{\left( {u_{2}^{2} + 3u_{2}^{2} u_{1} } \right)}}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{r_{{_{0} }} }} }} \left( s \right)}}{s}} \right) $$
(42)
$$ \overline{Z}_{7} \left( s \right) = \frac{{\left( {u_{3} + 3u_{1} u_{3} + u_{2} u_{3} } \right)}}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{r_{{_{0} }} }} }} \left( s \right)}}{s}} \right) $$
(43)
$$ \overline{Z}_{8} \left( s \right) = \frac{{\left( {u_{4} + 3u_{1} u_{4} + u_{2} u_{4} } \right)}}{F\left( s \right)}\left( {\frac{{1 - \overline{s}_{{_{{r_{{_{0} }} }} }} \left( s \right)}}{s}} \right) $$
(44)

where \(F\left( s \right)\) is generated as:

$$ F\left( s \right) = \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} - \left( \begin{gathered} 3u_{1} \overline{S}_{{g_{{_{1} }} }} \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right) \hfill \\ + u_{2} \overline{S}_{{g_{2} }} \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right) \hfill \\ + \left( \begin{gathered} 9u_{1}^{2} + 9u_{1}^{2} u_{2} + u_{2}^{2} + 3u_{1} u_{2}^{2} + u_{3} + 3u_{1} u_{3} \hfill \\ + u_{2} u_{3} + u_{4} + 3u_{1} u_{4} + u_{2} u_{4} \hfill \\ \end{gathered} \right)\overline{S}_{{r_{0} }} \left( s \right) \hfill \\ \end{gathered} \right)} \right) $$
(45)

The working time of the solar system is obtained as;

$$ \overline{Z}_{up} \left( s \right) = \frac{1}{F\left( s \right)}\left( \begin{gathered} 1 + 3u_{1} \left( {\frac{{1 - \overline{s}_{{_{{g_{{_{1} }} }} }} \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right)}}{{s + 3u_{1} + u_{2} + u_{3} + u_{4} }}} \right) \hfill \\ + u_{2} \left( {\frac{{1 - \overline{s}_{{_{{g_{{_{2} }} }} }} \left( {s + 3u_{1} + u_{2} + u_{3} + u_{4} } \right)}}{{s + 3u_{1} + u_{2} + u_{3} + u_{4} }}} \right) + \hfill \\ 3u_{1} u_{2} \left( {\frac{{1 - \overline{s}_{{_{{g_{{_{2} }} }} }} \left( {s + u_{2} } \right)}}{{s + u_{2} }}} \right) + 3u_{1} u_{2} \left( {\frac{{1 - \overline{s}_{{_{{g_{{_{1} }} }} }} \left( {s + 3u_{1} } \right)}}{{s + 3u_{1} }}} \right) \hfill \\ \end{gathered} \right) $$
(46)

Similar to this, the off time of the solar system was generated as:

$$\overline{Z}_{off} \left( s \right) = 1 - \overline{Z}_{up} \left( s \right)$$
(47)

Assessment of the Mathematical Model of Solar System for Copious States

Availability Analysis of the Solar System via General and Copula Repair Facilities

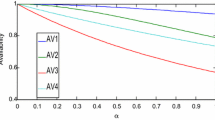
Allowing the copula repair facility as: \(c_{\theta } \left( {r_{1} \left( h \right),r_{2} \left( h \right)} \right) = \exp \left( {h^{\theta } + \left\{ {\log g\left( h \right)^{\theta } } \right\}^{{\frac{1}{\theta }}} } \right)\), \(\overline{s}_{{_{g} }} \left( s \right) = \frac{g}{s + g}\), failure rates as: \(u_{1} = 0.0123,u_{2} = 0.0213,u_{3} = 0.0031,u_{4} = 0.0045\), and all repairs are taken to one, however, these values were used in Eq. (46), the consequences were converted using the inverse Laplace transformation to obtained availability expressions for copula and general repair facilities as:

$$ \overline{Z}_{up} \left( n \right) = \left( \begin{gathered} - 0.000344e^{ - 1.02130n} - 0.000261e^{ - 1.03690n} \hfill \\ + 0.003743e^{ - 2.72854n} - 0.004273e^{ - 1.12013n} \hfill \\ + 1.001136e^{ - 0.00122n} \hfill \\ \end{gathered} \right) $$
(48)
$$ \overline{Z}_{up} \left( n \right) = \left( \begin{gathered} - 0.000180e^{ - 1.12517n} + 0.005333e^{ - 1.00521n} \hfill \\ + 0.995211e^{ - 0.00121n} - 0.000470e^{ - 1.02130n} \hfill \\ - 0.000289e^{ - 0.03690n} \hfill \\ \end{gathered} \right) $$
(49)

By means of Eqs. (48) and (49), the availability of the system was determined as presented in Table 2 (Fig. 3).

Table 2 The availability of the solar system with esteem to time
Full size table
Fig. 3
figure 3

shows availabilities of the solar system against time

Full size image

Reliability Analysis of the Solar System

Supposing the failure rates as; \(u_{1} = 0.0123,u_{2} = 0.0213,u_{3} = 0.0031,u_{4} = 0.0045\), repairs to zero, and these were used in Eq. (46), the consequences were converted using inverse Laplace transformation to produce reliability expression as:

$$ R\left( n \right) = \left( \begin{gathered} 0.017662e^{ - 0.02130n} \hfill \\ + 0.027196e^{ - 0.03690n} \hfill \\ + 1.555149e^{ - 0.06580n} \hfill \\ \end{gathered} \right) $$
(50)

Via Eqs. (50), the reliability of the system was determined as shown in Table 3 (Fig. 4).

Table 3 The reliability of the solar system with esteem to time
Full size table
Fig. 4
figure 4

depicted the reliability of the solar system against time

Full size image

MTTF Analysis of the Solar System

Repairs were assumed to zero and s approaches 0, these values were used in Eq. (46), the consequence is MTTF expression as:

$$ MTTF = \mathop {\lim }\limits_{s \to 0} \overline{Z}_{up} \left( s \right) = \frac{1}{{3u_{1} + u_{2} + u_{3} + u_{4} }}\left( \begin{gathered} 1 + \frac{{3u_{1} }}{{3u_{1} + u_{2} + u_{3} + u_{4} }} \hfill \\ + \frac{{u_{2} }}{{3u_{1} + u_{2} + u_{3} + u_{4} }} \hfill \\ + 3u_{1} + u_{2} \hfill \\ \end{gathered} \right) $$
(51)

Via Eq. (51), MTTF of each failure rate was determined and presented in Table 4 (Fig. 5).

Table 4 The MTTF of the solar system with esteem to failure rate
Full size table
Fig. 5
figure 5

displays MTTF of the solar system against failure rate

Full size image

Sensitivity Analysis of the Solar System

Sensitivity expression of the system was obtained as a result of differentiating the MTTF expression partially with esteem to failure rate. Therefore, the sensitivity of each failure rate was calculated and depicted in Table 5 (Fig. 6).

Table 5 The sensitivity of the solar system with esteem to failure rate
Full size table
Fig. 6
figure 6

shows sensitivity of the solar system against failure rate

Full size image

Cost Analysis of the Solar System

Cost Analysis of the Solar System Using Copula Repair

$$ E_{g} (n) = G_{1} \int\limits_{0}^{n} {Z_{up} (n)} dn - G_{2} n $$
(52)
$$ E_{g} \left( n \right) = G_{1} \left\{ \begin{gathered} 0.000337e^{ - 1.02130n} + 0.000252e^{ - 1.03690n} \hfill \\ - 0.001372e^{ - 2.72854n} + 0.003815e^{ - 1.12013n} \hfill \\ - 818.858878e^{ - 0.00122n} + 818.855852 \hfill \\ \end{gathered} \right\} - G_{2} \left( n \right) $$
(53)

Using Eq. (53), revenue was fixed to a unit while service cost and time were varied, therefore, the expected gain was computed and presented in Table 6 (Fig. 7).

Table 6 The expected gain of the solar system with esteem to time
Full size table
Fig. 7
figure 7

depicted expected gain of the solar system against time

Full size image

Similar to this, using Eq. (53) such that the service cost was fixed to a unit while revenue and time were varied, expected gain was calculated as shown in Table 7 (Fig. 8).

Table 7 The expected gain of the solar system with esteem to time
Full size table
Fig. 8
figure 8

shows expected gain of the solar system against time

Full size image

Cost Analysis of the Solar System Using General Repair

$$ E_{g} (n) = G_{1} \int\limits_{0}^{n} {Z_{up} (n)} dn - G_{2} n $$
(54)
$$ E_{g} \left( n \right) = G_{1} \left\{ \begin{gathered} - 0.000160e^{ - 1.12517n} - 0.005306e^{ - 1.00521n} \hfill \\ - 818.851084e^{ - 0.00121n} + 0.000479e^{ - 1.02130n} \hfill \\ + 0.000279e^{ - 1.03690n} + 818.8558443 \hfill \\ \end{gathered} \right\} - G_{2} \left( n \right) $$
(55)

By the mean of Eq. (55) and fixing the revenue to one, however, service cost and time were varied, and the expected gain was generated as displayed in Table 8 (Fig. 9).

Table 8 The expected gain of the solar system with esteem to time
Full size table
Fig. 9
figure 9

depicted the expected gain of the solar system against time

Full size image

Conversely, using Eq. (55) and fixing the service cost to one, therefor, revenue and time were varied, the expected gain was obtained and presented in Table 9 (Fig. 10).

Table 9 The expected gain of the solar system with esteem to time
Full size table
Fig. 10
figure 10

shows the expected gain of the solar against time

Full size image

Results Discussion

A thorough analysis of the solar system was conducted, and the following results were obtained. Firstly, the availability or readiness of the system was determined and presented in Tables and Figures, and the findings indicated that the availability is sufficient to performs the mission or purpose it was designed for. And from the side of managers, the availability of the solar system is encouraging as big returns are anticipated. Secondly, the reliability of the system, since the rate at which it varies with time is very slow, this shows that it is going to last for long period of time. However, managers expect mega incomes mobilization. Thirdly, MTTF of the system, as a maintenance metric which estimate the amount of time system works to failure was determined and from the findings it is very interesting to note that spontaneous change of failure rate reduces MTTF, and each failure rate coincided to its MTTF. Fourthly, the sensitivity of the system, it is another maintenance measures which describe the level of failure rate, such that if the failure is strong enough implies the strong of its sensitivity, and the system performance capacity is reduces to certain level, and the consequences lead to malfunction of the system or low incomes generation to the management. Fifthly, the cost analysis, it is studied and the results is presented in Tables and Figures, and from the findings it is carefully observed that the gain increases. In general overview, the results obtained using general repair is less than that of copula repair, therefore, copula repair is suggested for system optimal performance.

As observed from the study, subsystems such as the solar cell, the controller are seeming to be delicate, therefore, adequate care need to be provide in order to avert their failure, because failure of one may cause the failure of the entire system. Nevertheless, those subsystems could be improving by cooperating more backups units.

Conclusion

This study presents a multi-purpose solar system consisting of four subsystems: a solar panel, a controller, two USB charge points and four electric bulb points all merged together in a series–parallel conformation. The transition diagram of the system was used to derived the partial differential equations of order one, and solved using supplementary variable and Laplace transformation procedures. Maple software package was used to generate expressions for availability, reliability, MTTF, sensitivity and cost. The findings were justified using particular examples and presented in Tables and Figures.

The results of study are forecasted to be of beneficial to system managers, as it provides adequate maintenance strategies for improving reliability, profitability, and efficiency of their devices and generate mega incomes mobilization. The credit also goes to maintenance managers, designing engineers and so on.

This study future direction could be feature using other reliability optimization approaches, such as PSO, generic algorithms, genetic algorithms, grey wolf and so on.