1 Introduction

Power system stability is the ability of a system to return to its original state after being subjected to a physical disturbance [1]. The dynamic behaviour of conventional power systems are being changed due to the integration of renewable sources [2]. In order to address the increasing load demand, long transmission lines are added to the network, and power systems are operated near their maximum capacities [3]. Thus, maintaining the safe operation of power systems during numerous small or large disturbances is a challenge to be addressed [4]. In power systems that include the exchange of power among generators in various areas, low-frequency inter-area oscillation is a potentially hazardous phenomena as it can be harmful to generator rotor shaft [5, 6]. The oscillations in the coherent generators of several regions connected by extensive tie lines are known as inter-area modes of oscillation. Long cycle oscillations with low frequency between 0.2 and 0.7 Hz are the inter-area modes of oscillation [7]. Heavy power transfer across weak tie lines, which can be the source of inter-area oscillations. Inter-area mode transmits vibrations that impact the generators of neighbouring regions. Inter-area oscillations are therefore regarded as the most disastrous occurrence in the stability of the power system [8]. Employment of damping controllers is necessary to address the inter-area power oscillation problems. An Eigen value based damping controllers for single machine infinite is systems is discussed by Yildirim B et.al. [9]. The synchronous generator rotor oscillations can be damped by an auxiliary controller known as the power system stabilizer (PSS) by varying the generator excitation [10, 11]. PSSs are unquestionably effective in damping small-signal oscillations when properly tuned. However due to model errors and system variations, the PSSs constituent filters are frequently set to damp frequencies that are different from the actual frequencies seen in real system conditions. Robust PSSs are needed to address this problem [12]. Multiband PSS based PSDC using model reference adaptive control is discussed by Obaid et.al. [13]. Fuzzy based PSS is proposed for IEEE 11 bus, by Miguel Ramirez-Gonzalez et.al. The speed deviation of each machine is estimated based on the error indices such as IAE, ISE and ITAE [14, 15]. In large-scale power systems with a large number of controllers that are coordinated, conventional linear model based PSS may not be able to provide enough system damping [16].

When line loads are growing across long distances and there are inter-area power swings, PSS alone may not be able to damp the oscillations in the power system effectively. In these cases, alternative viable methods must be considered. By utilizing power oscillation dampening controllers using FACTS devices already existing PSS, the system performance can be enhanced [17]. However, the complexity of the optimization problem dramatically rises along with the number of optimal parameters for damping controllers. Multimodal optimization technique need to be used to build damping controllers, since the performance of multimodal optimization problem declines with increase in problem dimension, conventional algorithms do not work well in this situation. Additionally, one of the biggest problem with conventional heuristic algorithms is their propensity to get stuck in local minima [18,19,20,21]. Based on the voltage stability index real power loss reduction using perheron optimization, a multimodal optimization technique for IEEE 30 bus is discussed by Kanagasabai, L et.al [22]. IEEE 33 Bus power system network based on power loss index optimal location and sizing of DG is identified using genetic algorithm [23]. In power system damping, find the ideal solutions, which makes it impossible for the used damping schemes to provide robust damping with interline power flow controller [24]. Artificial intelligence based grey wolf optimization for solving multi-objective function optimization problem to damp local and inter-area oscillation in power system is proposed in this research article. This optimization results are used for tuning the controlled parameter of PODC in an 11 bus power system network.

2 Problem formulation

Poorly damped low frequency oscillation is a major threat to bulk power transmission through a weak tie-line in an interconnected power system. The inter-area oscillations can be observed in the multiple regions in the system. A controller designed by the wide-area signal is more effective to improve the damping of inter-area mode. An inter-area mode is observable from one area and controllable from another area in the power system, hence it is effective to damp out the inter-area oscillation by using a local area signal as well as a remote area signal as a feedback to the controller.

The Multiobjective function can be defined as given in (1),

F = minimization (\(Local area \& Interarea oscillation)\)

$${F=min ({F}_{1}+F}_{2})$$
(1)

F1 = Local area oscillation.

F2 = Inter area oscillation.with respect to performance indices as shown in (2), (3) & (4)

$$IAE = \int {\sum {\left\lceil {\Delta \omega_{L} } \right\rceil } } dt + \int {\sum {\left\lceil {\Delta \omega_{I} } \right\rceil } } dt$$
(2)
$$ISE=\int \sum {\lceil\Delta {\omega }_{L}\rceil}^{2}dt+\int \sum {\lceil{\Delta \omega }_{I}\rceil}^{2}dt$$
(3)
$$ITAE=\int \sum \lceil\Delta {\omega }_{L}\rceil*tdt+\int \sum \lceil\Delta {\omega }_{I}\rceil*tdt$$
(4)

where \(\sum \lceil\Delta {\omega }_{L}\rceil\) & \(\sum \lceil\Delta {\omega }_{I}\rceil\) are given by (5) & (6)

$$\sum \lceil\Delta {\omega }_{L}\rceil={(\omega }_{1}-{\omega }_{2})+({\omega }_{3}-{\omega }_{4})$$
(5)
$$\sum \lceil\Delta {\omega }_{I}\rceil={(\omega }_{1}-{\omega }_{3})+({\omega }_{1}-{\omega }_{4})+{(\omega }_{2}-{\omega }_{3})+\left({\omega }_{2}-{\omega }_{4}\right)$$
(6)

The Multiobjective optimization problem can be solved using.

Grew wolf algorithm. The methodology is discussed in the following section.

3 Methodology

3.1 Grey-wolf algorithm

Grey Wolf optimization is a stochastic algorithm. It avoids local optima and therefore higher chance of finding the global optimum solution. Low dependency on the initial solution and the non-necessity of calculation of gradient are the major advantages of the algorithm Inspiration of GWO is from social hierarchy and hunting mechanism as represented in Fig. 1, which are discussed in following subsections.

Fig. 1
figure 1

Inspiration of GWO

Full size image

3.1.1 Social hierarchy

Grey wolves have a very strict social dominate hierarchy; they are alpha, beta, delta and omega, in the form of a power pyramid as shown in Fig. 2. α-Wolves: The leader are a male & a female, called alpha wolves. The alpha wolves are most responsible for making decisions about hunting the prey. β- Wolves: The second level in the hierarchy of grey wolves is beta. The beta are subordinate wolves that help the alpha in decision making, these are the best candidates selected by alpha. δ- Wolves: The third level in the hierarchy of grey wolves is delta. Scouts, sentinels, elders, hunting & caretakers belong to this category. Scouts gives the boundary limits, sentinels protect & grant the safety of the pack. Elders are the experience wolves who are used to be alpha or beta. Hunter helps the alphas & betas when hunting prey and provide the food for the pack ω- Wolves: The lowest ranking grey wolf is omega. The omega plays the role of scapegoat. Omega wolves have to submit the preys to all the other dominant wolves. Omega is not an important individual in the pack.

Fig. 2
figure 2

Power Pyramid of Social Hierarchy

Full size image

The hunting mechanism is explained in the following subsection.

3.1.2 Hunting mechanism

Hunting mechanism is represented in cubic form which shows the positions of grey wolves while attacking prey will attack prey which is show in Fig. 3.

Fig. 3
figure 3

Hunting mechanism represented in three dimensions space

Full size image

As we can observe the grey wolves are shown as black dots encircling the prey, shown in red dot. Hunting mechanism is based on the distance reduction between the wolves and the prey. Once this distance is equal to zero then the prey is attacked by the wolves which means we obtain the solution for the given task.

3.2 Grey-wolf algorithm flow chart

Grey wolf algorithm detailed flow chart is as shown in Fig. 4. Basic idea is to find the optimal solution for the any multimodular optimization problem [25]. The power system local area and inter area oscillation damping is the objective function considered here, and the mathematical modeling are given below:

Fig. 4
figure 4

Grey-Wolf Algorithm Flow chart for power system problem

Full size image

The encircling the prey are modelled using the Eqs. (7 and 8).

$$\overrightarrow{D}=\left|\overrightarrow{C}.\overrightarrow{{X}_{P}(t)}-\overrightarrow{X\left(t\right)}\right|$$
(7)
$$\overrightarrow{X\left(t+1\right)}=\overrightarrow{X(t)} -\overrightarrow{A.}\overrightarrow{D}$$
(8)

where \(\vec{D}\) is the distance between Grey and Prey

\(\vec{A} \& \vec{C}\) are Coefficient Vector.

\(\overrightarrow {{X_{P} \left( t \right)}}\) is the position vector of prey.

\(\overrightarrow {X\left( t \right)}\) is the position vector of Grey Wolf.

\(\overrightarrow {{X\left( {t + 1} \right)}}\) is the position of next iteration.where \(\vec{A} \& \vec{C}\) defined by(9) & (10)

$$\overrightarrow{A} =2\overrightarrow{a}. \overrightarrow{{r}_{1}}-\overrightarrow{a}$$
(9)
$$\overrightarrow{C }=2\overrightarrow{a}. \overrightarrow{{r}_{2}}$$
(10)

where \(\overrightarrow{{r}_{1}}\), \(\overrightarrow{{r}_{2}}\) are random vectors\(\overrightarrow{a}\) is linearly decreased from 2 to 0.

For ‘\(\alpha\)’ grey wolves, the distance \(\overrightarrow{{D}_{\alpha }}\) is given by (11)

$$\overrightarrow{{D}_{\alpha }}=\left|\overrightarrow{C}.\overrightarrow{{X}_{\alpha }(t)}-\overrightarrow{X(t)}\right|$$
(11)

Position vector \(\overrightarrow{{X}_{1}(t)}\) is given by (12)

$$\overrightarrow{{X}_{1}(t)}=\overrightarrow{{X}_{\alpha }(t)}-\overrightarrow{a}. \overrightarrow{{D}_{\alpha }}$$
(12)

For ‘\(\beta\)’ grey wolves, the distance \(\overrightarrow{{D}_{\beta }}\) is given by (13)

$$\overrightarrow{{D}_{\beta }}=\left|\overrightarrow{C}.\overrightarrow{{X}_{\beta }(t)}-\overrightarrow{X(t)}\right|$$
(13)

Position vector \(\overrightarrow{{X}_{1}(t)}\) is given by (14)

$$\overrightarrow{{X}_{2}(t)}=\overrightarrow{{X}_{\beta }(t)}-\overrightarrow{a}. \overrightarrow{{D}_{\beta }}$$
(14)

For ‘\(\Upsilon\)’ grey wolves, the distance \(\overrightarrow{{D}_{\Upsilon}}\) is given by (15)

$$\overrightarrow{{D}_{\Upsilon \, }}=\left|\overrightarrow{C}.\overrightarrow{{X}_{\Upsilon \, }(t)}-\overrightarrow{X(t)}\right|$$
(15)

Position vector \(\overrightarrow{{X}_{3}(t)}\) is given by (16)

$$\overrightarrow{{X}_{3}(t)}=\overrightarrow{{X}_{\Upsilon }(t)}\overrightarrow{a}. \overrightarrow{{D}_{\Upsilon}}$$
(16)

Position vector \(\overrightarrow{X\left(t+1\right)}\) for the next iteration is given by (17)

$$\overrightarrow{X\left(t+1\right)}= Average (\overrightarrow{{X}_{1}(t)},\overrightarrow{{X}_{2}(t)},\overrightarrow{{X}_{3}(t)})$$
(17)

Design steps are in finding optimal value of control parameter are.

Step 1: As referred from Fig. 4, Initialization the parameters within the limits.

Step 2: Initialize the a, A and C and start the iteration count by one.

Step 3: Read the machines speed and calculate the fitness function for the Xkk.

Subscript KK is the no. variable need to optimize.

Xkk is a vector.

In our optimization problem we use nine variable.

Xkk = [Xkk(1), Xkk(2), Xkk(3), Xkk(4), Xkk(5), Xkk(6), Xkk(7), Xkk(8), Xkk(9)].

Xkk = [T1, T2, T3, T4, KP, KI, λ, KD, μ].

Step 4: Update a, A and C,

Step 5: If objective function is minimized store the value in workspace.

If it is not minimized they check for fitness function for different value of Xkk.

Step 6: Update the value of Xkk and chose the three best Xkk.which are \({X}_{kk\alpha }, {X}_{kk\beta }{ \& X}_{kk\delta }\).

\({X}_{kk\alpha }\) = [\(X_{kk\alpha } \left( 1 \right)\), \(X_{kk\alpha } \left( 2 \right)\), \(X_{kk\alpha } \left( 3 \right)\), \(X_{kk\alpha } \left( 4 \right)\), \(X_{kk\alpha } \left( 5 \right)\), \(X_{kk\alpha } \left( 6 \right)\), \(X_{kk\alpha } \left( 7 \right)\), \(X_{kk\alpha } \left( 8 \right)\), \(X_{kk\alpha } \left( 9 \right)\),]

\(X_{kk\beta }\) = [\(X_{kk\beta } \left( 1 \right)\), \(X_{kk\beta } \left( 2 \right)\), \(X_{kk\beta } \left( 3 \right)\), \(X_{kk\beta } \left( 4 \right)\), \(X_{kk\beta } \left( 5 \right)\), \(X_{kk\beta } \left( 6 \right)\), \(X_{kk\beta } \left( 7 \right)\), \(X_{kk\beta } \left( 8 \right)\), \(X_{kk\beta } \left( 9 \right)\),]

\(X_{kk\delta }\) = [\(X_{kk\delta } \left( 1 \right)\), \(X_{kk\delta } \left( 2 \right)\), \(X_{kk\delta } \left( 3 \right)\), \(X_{kk\delta } \left( 4 \right)\), \(X_{kk\delta } \left( 5 \right)\), \(X_{kk\delta } \left( 6 \right)\), \(X_{kk\delta } \left( 7 \right)\), \(X_{kk\delta } \left( 8 \right)\), \(X_{kk\delta } \left( 9 \right)\),]

Step 7: For first iteration best solution is the average of \({X}_{kk\alpha }, {X}_{kk\beta }{ \& X}_{kk\delta }\).

Step 8: If iteration is maximum.if ‘No’ go to the next iterationif ‘Yes’ display \({X}_{kk}\) i.e., the best solution.

4 Modeling and Simulation

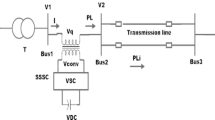
Two area IEEE 11 bus test system is considered for the simulation, which consists of four 900MVA generators with a voltage level of 20 kV, four step up transformers of 900MVA at a voltage level of 20 kV/230 kV and a long transmission line of 220 km line. Loads are connected at bus 7 and bus 9. A capacitor of 200MVAr is connected at bus 7 and a capacitor of 350MVAr is connected at bus 9 as shown in Fig. 5. Detailed test system data of generators is given in appendix [21]. The Generator is equipped with excitation system.

Fig. 5
figure 5

Single line diagram of two are 4-machine 11 bus system

Full size image

PODC for the system is implemented with a SSSC connected between bus 8 & bus 9. GWO-FOPID Controller for the SSSC is implemented, the details are discussed in detail below.

The constraints for the optimization are based on machines speeds \({\upomega }_{1}\), \({\upomega }_{2}{,\upomega }_{3}\) and \({\upomega }_{4}\). Inter-area oscillation exists between the two areas which are \({\upomega }_{1}\)-\({\upomega }_{3}\), \({\upomega }_{1}\)-\({\upomega }_{4}\), \({\upomega }_{2}\)-\({\upomega }_{3}\), \({\upomega }_{2}\)-\({\upomega }_{4}\). The local area oscillation are \({\upomega }_{1}\)-\({\upomega }_{2}\).\({\upomega }_{2}\)-\({\upomega }_{4}\).

The objective function is formulated by summing the inter-area & local area oscillations, in terms of error index Integral Time Absolute Error (ITAE) as shown in Fig. 6. Corresponding Error indices modeling as shown in Fig. 7.

Fig. 6
figure 6

GWO-FOPID Based SSSC-Controller

Full size image
Fig. 7
figure 7

Modelling of performance indices

Full size image

In fractional gain order PID controller is used as a controller for SSSC before that two stage lead lag network is used in the system. Input for FOPID is given one of the inter-area speed i.e. \({\upomega }_{1}\)-\({\upomega }_{3}\).Lead lag network is used to improve the response of the system by feeding optimal value of time constant response of the system is improved.

$${\Delta \mathrm{Y}}_{sssc}= (\Delta \omega ) {(K}_{P}+\frac{{K}_{I}}{{S}^{\lambda }}+{K}_{D}{S}^{\mu })\left(\frac{{1+ST}_{I}}{{1+ST}_{2}}\right)\left(\frac{{1+ST}_{3}}{{1+ST}_{4}}\right)$$
(18)

The change in reference input to the SSSC is quadrature axis voltage which is denote as \({\Delta \mathrm{V}}_{qref}\).

$$\Delta {\mathrm{V}}_{qref}= ({\upomega }_{1}-{\upomega }_{3}){(K}_{P}+\frac{{K}_{I}}{{S}^{\lambda }}+{K}_{D}{S}^{\mu })\left(\frac{{1+ST}_{I}}{{1+ST}_{2}}\right)\left(\frac{{1+ST}_{3}}{{1+ST}_{4}}\right)$$
(19)

The GWO-FOPID Controller is Subject to the constraints.

\({K}_{P}^{min}\)≤\({K}_{P}{\le K}_{P}^{max}\), \({K}_{I}^{min}\)≤\({K}_{I}{\le K}_{I}^{max}\), \({K}_{D}^{min} \le {K}_{D}{\le K}_{D}^{max}\)

\({T}_{1}^{min}\)≤\({T}_{1}{\le T}_{1}^{max}\),\({T}_{2}^{min}\)≤\({T}_{2}{\le T}_{2}^{max}\),\({T}_{3}^{min}\)≤\({T}_{3}{\le T}_{3}^{max}\)

,\({T}_{4}^{min}\)≤\({T}_{4}{\le T}_{4}^{max}\),\({\lambda }^{min}\le\uplambda \le {\lambda }^{max}\), \({\mu }^{min}\le\upmu \le {\mu }^{max}\)

Actual signal from the controller is the sum of change in reference quadrature voltage and reference quadrature voltage which is given by

$${{V}_{qref}^{*}=\mathrm{V}}_{qref}+\Delta {\mathrm{V}}_{qref}$$
(20)

Optimal value of Control parameter is obtained by GWO algorithm which is fed to the controller in each iteration based on the minimal ITAE i.e., Robust control parameter of the WOA-FOPID is given in Table 1.

Table 1 Optimal value of control parameters
Full size table

5 Result analysis

The test system is simulated under different cases such as (i) without PSS, (ii) with PSS & (iii) with PSDC having GWO based FOPID Controller. The GWO algorithm is test on standard CEC-2010 unimodal and multimodal test function and corresponding results are tabulated in Table 2 and 3.The Simulation results under the above mentioned cases are explained in detail in the following subsections.

Table 2 Unimodal bench mark function
Full size table
Table 3 Multimodal bench mark function
Full size table

5.1 Case 1

In this case PSS is absent in the test system. No Control signal is given to the stabilizer. So each generator gain values is are zero, and no generator is equipped with PSS. A three phase fault of 5-cycle is initiate at t = 1 s, when the fault is cleared the load angle of the machine increases beyond 180° as show in Fig. 8a. If it is increased beyond 180 degree angle is 175.691754809464 degree machine is near to motoring mode hence simulation have been stopped. Figure 8b show the machines speed, the machine is synchronized before the initiation of fault, once the fault is initiated the machine loses it synchronism. Once the machines comes of synchronism means machine acts as synchronous motor to avoid this at t = 7 s load angle is 175.691754809464 degree machine is near to motoring mode hence simulation have been stopped. Machine is synchronized before the initiation of fault, once the fault is initiated the machine loses it synchronism. Once the machines comes of synchronism means its speed deviation are more w.r.t zero reference, corresponding speed deviation of machines is shown in Fig. 8c. The terminal voltage of machines are violating the limits by going beyond 1.05 even the fault is cleared which is shown in Fig. 8d.

Fig. 8
figure 8

a Machines load angle without PSS.b Machines Speed without PSS. c Machines Speed Deviation without PSS. d Machines Terminal Voltage PSS

Full size image

5.2 Case 2

In this case PSS is present in the exciter.The control input is given to the excitation it means that there is a PSS control signal is given to stabilizer. So generator is equipped with PSS (Fig. 9). The three phase fault of 5-cycle is initiate at t = 1 s, when the fault is cleared the load angle of the machine try to damp out at t = 8 s, as shown in Fig. 10a. As soon as fault is cleared after 5-cycle due to the presence of PSS all machines will synchronized when the settling time of 8 s each machine speed will reach to its steady state value of 1.0p.u as show in Fig. 10b. Corresponding speed deviation of machines will reaches to steady state of 0.pu reference shown in Fig. 10c. The terminal voltage of each generator swing once the fault is cleared the machines try to regain its original steady state voltage of 1.0 p.u show in Fig. 10d.

Fig. 9
figure 9

Single line diagram of two are 4-machine 11 bus system with GWO-FOPID based SSSC

Full size image
Fig. 10
figure 10

a Machines load angle witH PSS. b Machines Speed with PSS. c Machines Speed Deviation with PSS. d Machines Terminal Voltage with PSS

Full size image

5.3 Case3: In this case PSS and GWO based FOPID controller are equipped in model as shown in Fig. 9. The generator is equipped with PSS, in addition to the PSS, SSSC of 100MVA rating is connected in test system and GWO-FOPID controller are included. Three phase fault of 5-cycle is initiate at t = 1 s, when the fault is cleared the load angle of the machine damps out at settling time of t = 4 s of 5% error band and the system regain its equilibrium point as shown in Fig. 11a. As soon as fault is cleared, all machines are synchronized and machines speed reaches to steady state value as shown in Fig. 11b. As the machine is synchronized the corresponding speed deviation.Will reaches to its zero reference value which is shown in Fig. 11c. Maximum terminal voltage of generators reaches to 1.077209345 p.u, at t = 4 s the generator terminal voltage reaches to steady state of 1.0 p.u as shown in Fig. 11d.

Fig. 11
figure 11

a Machines load angle with PSS & GWO-FOPID based SSSC Controller. b Machines Speed with PSS & GWO-FOPID based SSSC Controller. c Machines Speed Deviation with PSS & GWO-FOPID based SSSC Controller. d Machines Terminal Voltage with PSS & GWO-FOPID based SSSC Controller

Full size image

Testing of algorithm play a vital role in optimization problem, before solving real world problem it must be tested on different function which are unimodal and multimodal, CEC 2010 standard test function is taken for our research work In this Unimodal test function shown in the Table 2 and multimodal test function are tabulated in Table 3. Obtain solution are mean and standard deviation and it is within the acceptable limits of CEC 2010.

As from the Table 4 it is observed the objective function minimised for the case three case study. The objective function w.r.t error indices ITAE, ISE & IAE is found to be minimum for GWO-FOPID based SSSC controller which means the optimal system parameter is obtained is for FOPID controller from the GWO-algorithm. The corresponding 3-D bar graph is shown in Fig. 12.

Table 4 Objective function minimization comparison for three cases
Full size table
Fig. 12
figure 12

Objective function minimization w.r.t Error indices

Full size image

The results are compared with existing literature and tabulated in Table 5 here the main contribution of work is compared with the existing Fuzzy rules matrix[14] Fuzzy rules matrix [15] w.r.t settling time from the Table 5 the results of FRM [14] settling time is 12.28 s whereas FRM [15] settling time is 11.11 s. In our case 2 with Del Omega PSS settling time is 7.3 s, whereas with PSS & GWO-FOPID SSSC controller settling time is 3.1 s which gives better response, and steady state error of machine speed deviation also minimized w.r.t performance indices which are tabulated in Table 6.

Table 5 Comparison results from the literature
Full size table
Table 6 Generator Performance indices w.r.t to speed deviation for this three case studies considered
Full size table

Table 7 shows the results of error indices of generator speed deviation which compared with the existing literature GWO-FOPID based SSSC controller gives best results which reduces the machine speed deviation with reference to error indices which is compare with the FRM [14]& FRM [15] Corresponding 3-D bar graph of IAE,ISE & ITAE Show in Fig. 13a–c.

Table 7 Error Indices in comparison with existing techniques
Full size table
Fig. 13
figure 13

a Comparison of IAE of machine speed deviation. b Comparison of ISE of machine speed deviation. c Comparison of ITAE of machine speed deviation

Full size image

6 Conclusion

A power Oscillation Damping Controller with a static Synchronous Series Compensator using a robust Fractional Order PID Controller has been designed & simulated, whose parameters are optimized using Grey Wolf Algorithm. The proposed PODC has been tested in a 11 bus power system under 3-ϕ fault condition, and compared the results for different existing technologies. The performance of the systems under faults condition tabulated for each cases. The settling time and other error indices clearly shows that the proposed PODC with GWO-FOPID controller has enhanced performance in comparison with other existing techniques.

7 Future scope

The proposed algorithm based optimal controller parameter tuning can be applied to other FACTS controllers such as STATCOM, UPFC etc., for enhanced performance in different power system applications such as power quality enhancement, stability enhancement etc.