NSGA-II Based Analysis of Fuzzy Multi-objective Reliability–Redundancy Allocation Problem Using Various Membership Functions

Abstract

In the broadest sense, reliability is a measure of performance of the system under the stated conditions. The reliability–redundancy allocation problem gives a highly reliable system in the presence of optimal redundant components. This design is the most preferred by the design engineer. During the designing phase of the system, all the design data involved in the system are not very precise. Various types of uncertainties such as expert’s information character, qualitative statements, vagueness, incompleteness, unclear system boundaries, inability to evaluate the relative importance of the objectives, etc., are typical for many practical problems. Fuzzy set theory is an efficient technique to tackle such types of uncertainties in the system design problem. In this paper, the goals of the fuzzy multi-objective reliability–redundancy allocation problem are specified by various membership functions such as linear, quadratic, parabolic, and hyperbolic. An efficient multi-objective evolutionary algorithm, namely, NSGA-II is employed to solve it. The Pareto-optimal fronts for the various membership functions are shown in both the membership and objective spaces. Fuzzy ranking method then finds the best compromise solution for each membership function. Finally, the performance of membership functions is ranked by the data envelopment analysis by taking cost criteria (cost, weight, and volume) as inputs and benefit criteria (reliability and maximum satisfaction level) as outputs of the system. The effectiveness of the proposed approach is illustrated by a numerical example of the over-speed protection system for a gas turbine. A comparative analysis of the proposed approach is given with the existing approach.

Introduction

The reliability–redundancy allocation problem (RRAP) is a mixed-integer non-linear programming problem and NP-hard (Chern 1992) for which only approximate solutions have been proposed (Tillman et al. 1977; Sakawa 1978; Dhingra 1992). The increment of redundancies adds more cost, weight, volume, etc., in the system. Therefore, a set of trade-offs is required in multi-objective reliability–redundancy allocation problem (MORRAP) where the number of redundancies is an important decision variable. Heuristic approaches to MORRAP can be viewed in Huang et al. (2006), Tavakkoli et al. (2008), Huang et al. (2009), Garg and Sharma (2013), Sheikhalishahi et al. (2013), Damghani et al. (2013), Liu (2013), Zhang et al. (2014), Kim and Kim (2017) etc.

Multi-objective evolutionary algorithms (MOEAs) (Deb et al. 2002) are popular techniques to handle different types of multi-objective optimization problems (MOOPs) for the purpose of finding multiple solutions (popularly known as Pareto-optimal solutions) in a single simulation run. This group of algorithms conjugates the basic concepts of dominance. MOEAs are able to deal with non-continuous, non-convex, and/or non-linear as well as problems whose objective functions are not explicitly known (Salazar et al. 2006). Taboada et al. (2007) presented a practical solution for multi-objective reliability-based system design using the MOEA and clustering technique. A number of different MOEAs such as MOGA (Fonseca and Fleming 1993), NPGA (Horn et al. 1994), NSGA (Srinivas and Deb 1994), SPEA (Zitzler and Thiele 1998), PAES (Knowles and Corne 1999), MOMGA (Veldhuizen and Lamont 2000), SPEA2 (Zitzler et al. 2001), PESA-II (Corne at al. 2001), NSGA-II (Deb et al. 2002), MOEA/D (Zhang and Li 2007), AGE-II (Wagner and Neumann 2013), etc., have been developed. An ideal multi-objective optimization needs:

• 1. to get a group of solutions as close as possible to the true Pareto-optimal front, and

• 2. to maintain these solutions as diverse homogeneous as possible.

The first goal is responsible for the convergence, while the second is for diversity in the solutions set. Many MOEAs and their solution techniques to the MOOP can be viewed in Deb (2001), Konak et al. (2006), Coello et al. (2007), and Zhou et al. (2011).

Elitist non-dominated sorting genetic algorithm (NSGA-II) is one of the popular MOEAs. It comprises a second-generation MOEA which gives much better spread and good convergence near the true Pareto-optimal front compared to other elitist MOEAs such as SPEA and PAES. Simulation results of the constrained NSGA-II give better performance on several non-linear problems (Deb et al. 2002). It has some special property that makes it different from other MOEAs such as elitist strategy, parameter-less sharing approach, crowding distance, classifying the solutions into the fronts, efficient handling constraints, and low computational requirements. Salazar et al. (2006) demonstrated NSGA-II in identifying a set of optimal solutions known as Pareto-optimal front by solving constrained redundancy problems. Wang et al. (2009) solved the MORRAP using NSGA-II and compared their results with single-objective approaches. Safari (2012) proposed a variant of NSGA-II in solving MORRAP. Sharifi et al. (2016) used the NSGA-II algorithm in solving MORRAP for a series–parallel problem and k-out-of-n subsystems with three objectives. Recently, Muhuri et al. (2018) used NSGA-II to solve the MORRAP with interval type-2 fuzzy environment which considers higher order uncertainties in the component. Practically, various types of uncertainties are involved in system design. During the designing phase of the system, the designer does not have a clear idea about the design parameters such as reliability, cost, and weight of the constituent components. As a result, approximate values are considered by guessing. The environmental factors such as improper storage, adverse operating conditions, age etc., affect the reliability of the system. Therefore, all the design data involved in the system are hardly precise. In general, redundant components are found in the different models which contain less information regarding their critical parameters, e.g., failure operating time which is used to evaluate the component’s reliability. To cope up these issues, fuzzy optimization techniques (Zimmermann 1996) can be useful during the initial stages of the conceptual design of a system. In the fuzzy decision-making process, the linear membership function is often used by fixing two points as the upper and lower levels of acceptability. In real-world situations, models are built more flexible and adaptable to the human decision-making process. It needs some kind of empirical justification or assumption. Keeping these views in mind, several other (non-linear) shapes for membership functions such as concave, convex shapes need to be analyzed in determining their impact on the overall system design process. The membership function of a fuzzy goal has also been viewed as “a kind of utility function representing the degree of satisfaction or acceptance” (Dhingra and Moskowitz 1991). To choose the best compromise solution in the fuzzy MOOP is another challenge. Liu (2013) proposed an approach with fuzzy programming and DEA method to choose the efficient solution in MORRAP. Recently, Kumar and Yadav (2019) presented NSGA-II based decision-making approach to determine the optimal value of MORRAP.

In this paper, MORRAP is considered under several design constraints. The goals of the problem are specified by the various membership functions to look into the impact on the overall system design process. The best compromise solution in each membership function is obtained by the fuzzy ranking method (Pandiarajan and Babulal 2014) and the overall performance of the various membership functions is then measured by the CCR model (Charnes et al. 1978) by taking three inputs as cost, weight, and volume, and two outputs as reliability and maximum satisfaction level of the system obtained by fuzzy ranking method.

Multi-objective Optimization

This section describes some important facts of the MOOP.

Formulation of the MOOP

In general, an MOOP is defined as follows:

$$\begin{aligned} {\text{Minimize}}\;F\left( X \right) = \left[ {f_{1} \left( X \right), f_{2} \left( X \right), \ldots ,f_{k} \left( X \right)} \right]^{T} \hfill \\ {\text{subject}}\;{\text{to}}\;g_{i} \left( X \right) = 0,\;i = 1,2, \ldots ,m_{\text{e}} ; \hfill \\ g_{i} \left( X \right) \ge 0,\;i = m_{\text{e}} + 1,\;m_{\text{e}} + 2, \ldots ,M; \hfill \\ x_{j}^{l} \le x_{j} \le x_{j}^{u} ,j = 1,2, \ldots ,n, \hfill \\ \end{aligned}$$

(1)

where $k \ge 2$ is the number of objectives; $m_{\text{e}}$ is the number of equality constraints; $M$ is the total number of constraints; $X = \left[ {x_{1} ,x_{2} , \ldots ,x_{n} } \right]^{T}$ is $n$ dimensional decision vector from the feasible region or decision space $\varOmega$ defined by the following:

$$\varOmega = \left\{ {X \in {\mathbb{R}}^{n} \left| {\begin{array}{*{20}l} {g_{i} \left( X \right) \ge 0,\;g_{i} \left( X \right) = 0,\;x_{j}^{l} \le x_{j} \le x_{j}^{u} } \hfill \\ {j = 1,2, \ldots ,n} \hfill \\ \end{array} } \right.} \right\},$$

the feasible region $\varOmega \subset {\mathbb{R}}^{n}$; objective functions $f_{p} \left( X \right)$, $p = 1, 2, \ldots ,k$, where $f_{p} :\varOmega \to {\mathbb{R}}$ and the constrained functions $g_{i} \left( X \right)$, where $g_{i} :\varOmega \to {\mathbb{R}}$; the image of the feasible region denoted by $Z \subset {\mathbb{R}}^{k}$ and it is called a feasible objective region or objective space which is defined by $Z = \left\{ {F\left( X \right) \in {\mathbb{R}}^{k}| X \in \varOmega } \right\}$. The elements of $Z$ are called objective vectors or criterion vector denoted by $F\left( X \right) = \left[ {f_{1} \left( X \right), f_{2} \left( X \right), \ldots ,f_{k} \left( X \right)} \right]^{T}$; $x_{j}^{l}$ and $x_{j}^{u}$ are the lower and upper bounds of the decision variable $x_{j}$, respectively. For every point $X$ in the decision space Ω, there exists a point $F\left( X \right)$ in the objective space $Z$. Therefore, it is a mapping between n-dimensional solution vector and k-dimensional objective vector (see Fig. 1).

Fig. 1

Multi-objective evaluation mapping

If all $f_{p}$s and $g_{i}$s are linear, then the problem is called a multi-objective linear programming problem (MOLPP); otherwise, it is called a multi-objective non-linear programming problem (MONLPP).

Basic definitions

The concept of optimality in an MOOP depends on Pareto optimality. Therefore, the following definitions are defined in terms of Pareto terminology.

Definition 1

Pareto dominance (Coello et al. 2007) A vector $X \in \varOmega$ is said to dominate another $Y \in \varOmega$ denoted by $X\,\underline{ \prec } \,Y$ iff $f_{i} \left( X \right) \le f_{i} \left( Y \right) \forall i = 1, 2, \ldots ,k,$ and there exists at least one $f_{j} \left( X \right) < f_{j} \left( Y \right), j \in \left\{ {1, 2, \ldots ,k} \right\}, j \ne i$.

Definition 2

Pareto-optimal solution (Coello et al. 2007) A solution vector $X \in \varOmega$ is said to be Pareto-optimal solution (Pareto-optimal) iff there does not exist another vector $X^{\prime} \in \varOmega$ which dominates $X \in \varOmega$.

Definition 3

Pareto-optimal set (Coello et al. 2007) The Pareto-optimal set is defined as ${\text{PS}}: = \left\{ {X \in \varOmega |\neg \exists X^{\prime} \in \varOmega :\;X^{\prime}\,\underline{ \prec } \,X} \right\}$.

Definition 4

Pareto-optimal front (Coello et al. 2007) The Pareto-optimal front is defined as ${\text{PF}}: = \left\{ {F\left( X \right) = \left[ {f_{1} \left( X \right),f_{2} \left( X \right), \ldots ,f_{k} \left( X \right)} \right]^{T} {\mid }X \in {\text{PS}}} \right\}$.

Definition 5

Ideal objective vector (Coello et al. 2007) If a decision vector $X^{*} = \left[ {x_{1}^{*} ,x_{2}^{*} , \ldots ,x_{n}^{*} } \right]^{T} \in \varOmega$ is such that $f_{i} \left( {X^{*} } \right) = \mathop {{\text{min}} }\nolimits_{X \in \varOmega } f_{i} \left( X \right)$, $i \in \left\{ {1, 2, \ldots ,k} \right\}$; then the vector $F\left( {X^{*} } \right) = \left[ {f_{1} \left( {X^{*} } \right),f_{2} \left( {X^{*} } \right), \ldots ,f_{k} \left( {X^{*} } \right)} \right]^{T} \in Z$ is called an ideal objective vector for an MOOP given by (1) and $X^{*} = \left[ {x_{1}^{*} ,x_{2}^{*} , \ldots ,x_{n}^{*} } \right]^{T} \in \varOmega$ is called an ideal vector.

Definition 6

Utopian objective vector (Deb 2001) A utopian objective vector $F\left( {X^{**} } \right)$ has each of its components marginally smaller than the ideal objective vector, or $F\left( {X^{**} } \right) = F\left( {X^{*} } \right) - \in_{i}$ with $\in_{i} > 0 \, \forall i = 1, 2, \ldots ,k$.

Definition 7

Nadir (anti-ideal) objective vector (Deb 2001) Unlike the ideal objective vector which represents the lower bound of each objective, the nadir objective vector $F^{\text{nad}}$ represents the upper bound of each objective in the entire objective space ${\mathbb{R}}^{k}$.

Definition 8

Fuzzy set (Zimmermann 1996) Let $X$ be a collection of objects generically denoted by $x$. A fuzzy set $\widetilde{A}$ in $X$ is a set of ordered pair defined in the form as follows:

$$\widetilde{A} = \left\{ {\left( {x, \mu_{{\widetilde{A}}} \left( x \right)} \right)x \in X} \right\},$$

where $\mu_{{\widetilde{A}}} :\;X \to \left[ {0, 1} \right]$ is called the membership function and its function value is known as the grade of membership of $x$ in $\widetilde{A}$.

Mathematical Model of the Problem

RRAP can be understood by a series–parallel system configuration. The general configuration of the series–parallel system is shown in Fig. 2. This system contains several parallels and identical components arrayed in each stage. Generally, redundancy is applied for increasing the system reliability, but this technique gives more complexity in terms of cost, weight, volume, etc., to the system design. Therefore, it is better to solve the multi-objective programming model based problem. Here, twofold design variables are required to determine the optimal design of the system. One is the reliability of each component and other is to select a number of redundant components in each stage. Mathematically, MORRAP is given as follows:

$$\begin{aligned} & {\text{Max}}.\;R_{\text{S}} \left( {r, n} \right) = \mathop \prod \limits_{j = 1}^{m} \left[ {1 - \left( {1 - r_{j} } \right)^{{n_{j} }} } \right] \\ & {\text{Min}}.\;C_{\text{S}} \left( {r,n} \right) = \mathop \sum \limits_{j = 1}^{m} C_{j} \left( {r_{j} } \right)\left[ {n_{j} + \exp \left( {n_{j} /m} \right)} \right] \\ & {\text{subject}}\;{\text{to}}\;g_{i} \left( {r, n} \right) \le 0,i = 1,2, \ldots ,M \\ & 0 \le r_{j,{\text{min}} } \le r_{j} \le r_{j,{\text{max}} } \le 1, \\ & 1 \le n_{j,{\text{min}} } \le n_{j} \le n_{j,{\text{max}} } \quad n_{j} \in {\mathbb{Z}}^{ + } \\ & j = 1, 2, \ldots ,m. \\ \end{aligned}$$

(2)

Fig. 2

Series–parallel system configuration

Elitist Non-dominated Sorting Genetic Algorithm (NSGA-II)

Srinivas and Deb (1994) proposed the NSGA which is an early dominance-based MOEA. The purpose of developing NSGA is to find better solutions according to their non-domination levels. NSGA uses the naive and slow (Deb 2001) sorting approach to distribute a population into different non-domination levels, and a sharing function method to maintain the diversity of the population. However, it has high computational complexity $O(kN^{3} )$, where k is the number of objectives and N is the population size in the non-dominated sorting. Therefore, NSGA is computationally expensive for large population sizes. Moreover, NSGA is a non-elitist approach which affects its convergence rates compared to other MOEAs and it also requires a sharing parameter to calculate the sharing fitness, which ensures the diversity of the population.

Deb et al. (2002) proposed NSGA-II to overcome the drawbacks of NSGA. Specifically, NSGA-II presents a fast non-dominated sorting approach with the worst-case computational complexity $O\left( {k\left( {2N} \right)^{2} } \right)$. This approach searches iteratively non-dominated solutions into different fronts.

First, for each solution $X$ in the population, the algorithm calculates two entities:

• 1. $n_{X}$, the number of solutions dominating $X$,

• 2. $S_{X}$, a set of solutions dominated by $X$.

The solutions for which $n_{X} = 0$ belong to the first front. Second, for each member $Y$ in the set $S_{X}$, the value of $n_{Y}$ is reduced by one. If any $n_{Y}$ is reduced to zero during this stage, the corresponding member $Y$ is put in the second front. The above process is continued with each member in the second front to identify the third front and so on. Furthermore, NSGA-II applies the concept of crowding distance with the worst-case computational complexity $O\left( {k\left( {2N} \right)\log \left( {2N} \right)} \right)$. The introduction of crowding distance replaces the fitness sharing approach that requires a sharing parameter to be set by the user.

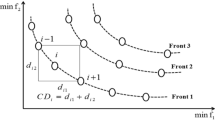
The crowding-distance value $( {\text{CD}}_{X} )$ (see Fig. 3) of the $X^{th}$ solution is calculated as follows:

$$d_{Xp} = \frac{{f_{p}^{X + 1} - f_{p}^{X - 1} }}{{f_{p}^{{\text{max}} } - f_{p}^{{\text{min}} } }}$$

(3)

$${\text{CD}}_{X} = \mathop \sum \limits_{p = 1}^{k} d_{Xp} ,$$

(4)

where $f_{p}^{X + 1}$ and $f_{p}^{X - 1}$ denote the $p{\text{th}}$ objective function of the $\left( {X + 1} \right){\text{th}}$ and $\left( {X - 1} \right){\text{th}}$ individual (solution), respectively, and $f_{p}^{{\text{max}} }$ and $f_{p}^{{\text{min}} }$ represent the maximum and minimum values of the $p{\text{th}}$ objective function.

Fig. 3

Fitness evaluation and individual crowding distance estimation

A higher value of crowding-distance gives the lesser crowded region and vice versa (Deb et al. 2002). Therefore, the crowding distance selects solutions located in less-crowded regions after the fast non-dominated sorting procedure, which is extended to an entire POF to maintain the diversity in the solution set. Finally, NSGA-II uses an elitist strategy with the worst-case computational complexity $O\left( {2N\log \left( {2N} \right)} \right)$. The elitist strategy (Zitzler et al. 2000; Laumanns et al. 2002) is used to enhance the convergence of an MOEA and avoid the loss of optimal solutions after getting it.

Deb et al. (2002) proposed constraint dominance-based binary tournament selection method in constraint handling procedure. A search space (decision space) is divided by the constraints in two regions—feasible and infeasible. Accordingly, a solution $X$ is called a constrained-dominate to a solution $Y$ if

• $X$ is feasible and $Y$ is infeasible.

• $X$ and $Y$ are infeasible, but $X$ contains a smaller overall constraint violation.

• $X$ and $Y$ are feasible, but $X$ dominates $Y$.

In Fig. 4, an evaluation cycle of the NSGA-II is shown. First, an offspring $Q_{t}$ of size N is obtained using the genetic operators such as selection, recombination, and mutation. A combined population $R_{t}$ of size 2 N is then formed which consists of the current population $P_{t}$ and the offspring population $Q_{t}$. Using fast non-dominated sorting, $R_{t}$ is divided into different fronts ${\text{PF}}_{1} ,{\text{PF}}_{2} , \ldots ,{\text{PF}}_{n}$. Let the number of solutions in each front ${\text{PF}}_{i}$ be $N_{i}$. Next, we choose members for the new population $P_{t + 1}$ from the front ${\text{PF}}_{1}$ to ${\text{PF}}_{t - 1}$, noting that $N_{1} + N_{2} + \cdots + N_{t} > N$ and $N_{1} + N_{2} + \cdots + N_{t - 1} \le N$. Afterwards, to get the exactly $N$ population members in $P_{t + 1}$, we sort the solutions in front ${\text{PF}}_{t}$ using the crowding distance sorting procedure and choose the best solutions to fill empty slot in the new population $P_{t + 1}$. This process is continued until the termination condition is satisfied.

Fig. 4

An evaluation cycle of the NSGA-II algorithm

Data Envelopment Analysis (DEA)

DEA is a data-oriented approach for evaluating the performance of decision-making units (DMUs). A complete ranking system is developed for evaluating the best DMU. An efficient design indicator $E_{k}$ is defined for the $k{\text{th}}$ DMU as follows:

$$E_{k} = \frac{{v_{1} y_{1k} + v_{2} y_{2k} + \cdots + v_{s} y_{sk} }}{{u_{1} x_{1k} + u_{2} x_{2k} + \cdots + u_{m} x_{mj} }}.$$

(5)

Let us consider $n$ DMUs to evaluate the performance of $k{\text{th}}$ DMU. Each DMU has $m$ inputs and $s$ outputs. Then, the CCR model (Charnes et al. 1978) is given in fractional form as follows:

$$\begin{aligned} & {\text{Max}}.\;E_{k} \\ & {\text{subject}}\;{\text{to}}\;0 \le \frac{{v_{1} y_{1j} + v_{2} y_{2j} + \cdots + v_{s} y_{sj} }}{{u_{1} x_{1j} + u_{2} x_{2j} + \cdots + u_{m} x_{mj} }} \le 1; \\ & j = 1,2, \ldots ,n;\;u_{1} ,u_{2} , \ldots ,u_{s} \ge 0;\;v_{1} ,v_{2} , \ldots ,v_{m} \ge 0, \\ \end{aligned}$$

(6)

where $u_{i}$s and $v_{i}$s are weights corresponding to inputs $x_{i}$s and $y_{i}$s, respectively. $x_{ij}$ is the observed amount of the $i$ th input of the $j$ th DMU and $y_{rj}$ is the observed amount of the $r$ th output of the $j$ th DMU. The general form of CCR Model can be written in linear form as follows:

$$\begin{aligned} & {\text{Max}}.\;E_{k} = \mathop \sum \limits_{r = 1}^{s} v_{r} y_{rk} \\ & {\text{subject}}\;{\text{to}} \\ & \mathop \sum \limits_{i = 1}^{m} u_{i} x_{ik} = 1; \\ & \mathop \sum \limits_{r = 1}^{s} v_{r} y_{rj} \le \mathop \sum \limits_{i = 1}^{m} u_{i} x_{ij} ,\;j = 1,2, \ldots ,n; \\ & u_{i} \ge 0, \;v_{r} \ge 0,\;i = 1,2, \ldots ,m;\;r = 1,2, \ldots ,s. \\ \end{aligned}$$

(7)

The dual form of the linear model is given as follows:

$$\begin{aligned} & {\text{Min}}.\;\theta_{k} \\ & {\text{subject}}\;{\text{to}}\;s^{ - } _{ik}= \theta_{k}x_{ik}-\sum_{j=1}^{n}x_{ij}\lambda_{jk}\geq 0,i=1,2, \ldots ,m; \\& s_{rk}^{+}= \sum_{j=1}^{n}y_{rj}\lambda_{jk}-y_{rk}\geq 0, r=1,2, \ldots ,s; \\& \lambda_{jk} \geq 0, j=1,2, \ldots, n. \end{aligned}$$

(8)

$\theta_{k}$ is unrestricted in sign, $s^{ - }_{ik}$ is called the ith input excesses and $s^{ + }_{rk}$ is called the rth output shortfalls.

To discover the possible input excesses and output shortfalls, the following two phases are considered.

• 1. The efficiency of the CCR model is the optimal value of dual form denoted by $\theta^{* }_{k}$.

• 2. The value of $\theta^{* }_{k}$ is used in the following problem:

  $$\begin{aligned} & {\text{Max}}.\;w = es^{ - } + es^{ + } \\ & {\text{subject}}\;{\text{to}} \\& s^{ - } _{ik}= \theta_{k}x_{ik}-\sum_{j=1}^{n}x_{ij}\lambda_{jk}\geq 0,i=1,2, \ldots ,m; \\& s_{rk}^{+}= \sum_{j=1}^{n}y_{rj}\lambda_{jk}-y_{rk}\geq 0, r=1,2, \ldots ,s; \\& \lambda_{jk} \geq 0, j=1,2, \ldots, n; \\&e = \left( {1, 1, \ldots , 1} \right). \\ \end{aligned}$$

  (9)

Any DMU is said to be fully efficient if $\theta^{ *}_{k} = 1$. There are possibilities to have more than one DMUs with efficiency score 1. To tackle this issue, super-efficiency model (Noura et al. 2011) in DEA can be effective. The following steps are given in this context:

• 1. Choose upper and lower limits for each input and output among efficient DMUs as follows:

  $$\begin{aligned} & E = \left\{ { j |E_{j}^{*} = 1} \right\}. \\ & x_{i}^{*u} = \underbrace {\text{Max}}_{j \in E}\left| {x_{ij} } \right|,\quad i = 1,2, \ldots ,m; \\ & x_{i}^{*l} = \underbrace {\text{Min}}_{j \in E}\left| {x_{ij} } \right|,\quad i = 1,2, \ldots ,m; \\ & y_{r}^{*u} = \underbrace {\text{Max}}_{j \in E}\left| {y_{rj} } \right|,\quad r = 1,2, \ldots ,s; \\ & y_{r}^{*l} = \underbrace {\text{Min}}_{j \in E}\left| {y_{rj} } \right|,\quad r = 1,2, \ldots ,s. \\ \end{aligned}$$

• 2. Indicate aspiration levels for each input and output. The utility inputs–outputs regarding the definition of sets as $D_{i}^{ - } ,D_{i}^{ + } , D_{o}^{ - } , D_{o}^{ + }$

  $$\begin{aligned} \overline{x} & = x_{i}^{*l } ,\quad \forall i\left( {i \in D_{i}^{ - } } \right); \\ \overline{x} & = x_{i}^{*u } ,\quad \forall i\left( {i \in D_{i}^{ + } } \right); \\ \overline{y} & = y_{r}^{*l } ,\quad \forall i\left( {i \in D_{o}^{ - } } \right); \\ \overline{y} & = y_{r}^{*u } ,\quad \forall i\left( {i \in D_{o}^{ + } } \right). \\ \end{aligned}$$

• 3. In this step, we calculate ($d_{ij} , d_{rj}$) for each ${\text{DMU}}_{j}$ s.t. $j \in E$ as follows:

  $$\begin{aligned} \quad d_{ij} = \frac{{x_{ij} }}{{\overline{x}_{i} + \gamma }}\forall i \in D_{i}^{ + } ; \hfill \\ \quad d_{ij} = \frac{{\overline{x}_{i} }}{{x_{ij} + \gamma }}\forall i \in D_{i}^{ - } ; \hfill \\ \quad d_{rj} = \frac{{y_{rj} }}{{\overline{y}_{r} + \gamma }} \forall i \in D_{r}^{ + } ;\hfill \\ \quad d_{rj} = \frac{{\overline{y}_{r} }}{{y_{rj} + \gamma }}\forall i \in D_{r}^{ - }. \hfill \\ \end{aligned}$$

Here, $\gamma$ is a small and non-zero number which prevents division by zero. So, $D_{j}$ can be defined as: $D_{j} = \mathop \sum \nolimits_{i \in I} d_{ij} + \mathop \sum \nolimits_{r \in R} d_{rj}$; $I = D_{i}^{ + } \cup D_{i}^{ - }$; $R = D_{r}^{ + } \cup D_{r}^{ - }$. It is noticed that the larger $D_{j}$ is more successful ${\text{DMU}}_{j}$ in given proposed objectives for input–output. Thus, it is possible to rank efficient DMUs with higher $D_{j}$.

Proposed Methodology

The proposed methodology is given step by step as follows.

Step 1 Find the upper and lower limits on $R_{\text{S}}$ and $C_{\text{S}}$.

The upper and lower limits on $R_{\text{S}}$ and $C_{\text{S}}$ are obtained by solving each objective one by one as follows:

$$\begin{aligned} & {\text{Max}}. / {\text{Min}}.\;R_{\text{S}} \left( {r, n} \right) \\ & {\text{subject}}\;{\text{to}}\;g_{i} \left( {r, n} \right) \le 0,\;i = 1, 2, \ldots ,M \\ & 0 \le r_{j,{\text{min}} } \le r_{j} \le r_{j,{\text{max}} } \le 1, \\ & 1 \le n_{j,{\text{min}} } \le n_{j} \le n_{j,{\text{max}} } ,\;n_{j} \in {\mathbb{Z}}^{ + } ,\;j = 1, 2, \ldots ,m \\ \end{aligned}$$

(10)

$$\begin{aligned} & {\text{Max}}. / {\text{Min}}.\;C_{\text{S}} \left( {r, n} \right) \\ & {\text{subject}}\;{\text{to}}\;g_{i} \left( {r, n} \right) \le 0,\;i = 1,2, \ldots ,M \\ & 0 \le r_{j,{\text{min}} } \le r_{j} \le r_{j,{\text{max}} } \le 1, \\ & 1 \le n_{j,{\text{min}} } \le n_{j} \le n_{j,{\text{max}} } ,\;n_{j} \in {\mathbb{Z}}^{ + } ,\;j = 1, 2, \ldots ,m. \\ \end{aligned}$$

(11)

Step 2 Construct the membership functions.

Figure 5 shows various membership functions such as linear, quadratic, parabolic, and hyperbolic to the objective functions $R_{\text{S}}$ and $C_{\text{S}}$. These membership functions are defined as follows.

Fig. 5

a Monotonically increasing membership functions for system reliability; b monotonically decreasing membership functions for system cost

• 1. Linear membership function (Kumar and Yadav 2017, 2019)

  This function is a strictly decreasing concave and convex function. It is defined as follows:

  $$\mu_{{\widetilde{R}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill &\quad {R_{\text{S}} \le R_{\text{S}}^{\text{l}} } \hfill \\ {{{\left( {R_{\text{S}} - R_{\text{S}}^{\text{l}} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{\text{S}} - R_{\text{S}}^{\text{l}} } \right)} {\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} } \right)}}} \right. \kern-0pt} {\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} } \right)}},} \hfill &\quad {R_{\text{S}}^{\text{l}} \le R_{\text{S}} \le R_{\text{S}}^{\text{u}} } \hfill \\ {1,} \hfill &\quad {R_{\text{S}} \ge R_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right.$$

  (12)
  $$\mu_{{\widetilde{C}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill &\quad {C_{\text{S}} \le C_{\text{S}}^{\text{l}} } \hfill \\ {{{\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}} } \right)} {\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} } \right),}}} \right. \kern-0pt} {\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} } \right),}}} \hfill &\quad {C_{\text{S}}^{\text{l}} \le C_{\text{S}} \le C_{\text{S}}^{\text{u}} } \hfill \\ {0,} \hfill &\quad {C_{\text{S}} \ge C_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right..$$

  (13)

• 2. Quadratic membership function (Garg et al. 2014b)

  This function is a convex function and it is defined as follows:

  $$\mu_{{\widetilde{R}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill &\quad {R_{\text{S}} \le R_{\text{S}}^{\text{l}} } \hfill \\ {\left( {{{\left( {R_{\text{S}} - R_{\text{S}}^{\text{l}} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{\text{S}} - R_{\text{S}}^{\text{l}} } \right)} {\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} } \right)}}} \right. \kern-0pt} {\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} } \right)}}} \right)^{2} ,} \hfill &\quad {R_{\text{S}}^{\text{l}} \le R_{\text{S}} \le R_{\text{S}}^{\text{u}} } \hfill \\ {1,} \hfill &\quad {R_{\text{S}} \ge R_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right.$$

  (14)
  $$\mu_{{\widetilde{C}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill &\quad {C_{\text{S}} \le C_{\text{S}}^{\text{l}} } \hfill \\ {\left( {{{\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}} } \right)} {\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} } \right)}}} \right. \kern-0pt} {\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} } \right)}}} \right)^{2} ,} \hfill &\quad {C_{\text{S}}^{\text{l}} \le C_{\text{S}} \le C_{\text{S}}^{\text{u}} } \hfill \\ {0,} \hfill &\quad {C_{\text{S}} \ge C_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right.$$

  (15)

• 3. Parabolic membership function (Singh and Yadav 2017).

  This function is a concave function and it is defined as follows:

  $$\mu_{{\widetilde{R}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill &\quad {R_{\text{S}} \le R_{\text{S}}^{\text{l}} } \hfill \\ {1 - \left( {{{\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}} } \right)} \mathord{\left/ {\vphantom {{\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}} } \right)} {\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} } \right)}}} \right. \kern-0pt} {\left( {R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} } \right)}}} \right)^{2} ,} \hfill &\quad {R_{\text{S}}^{\text{l}} \le R_{\text{S}} \le R_{\text{S}}^{\text{u}} } \hfill \\ {1,} \hfill &\quad {R_{\text{S}} \ge R_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right.$$

  (16)
  $$\mu_{{\widetilde{C}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill &\quad {C_{\text{S}} \le C_{\text{S}}^{\text{l}} } \hfill \\ {1 - \left( {{{\left( {C_{\text{S}} - C_{\text{S}}^{\text{l}} } \right)} \mathord{\left/ {\vphantom {{\left( {C_{\text{S}} - C_{\text{S}}^{\text{l}} } \right)} {\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} } \right)}}} \right. \kern-0pt} {\left( {C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} } \right)}}} \right)}^{2}, \hfill &\quad {C_{\text{S}}^{\text{l}} \le C_{\text{S}} \le C_{\text{S}}^{\text{u}} } \hfill \\ {0,} \hfill &\quad {C_{\text{S}} \ge C_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right..$$

  (17)

• 4. Hyperbolic membership function (Dhingra and Moskowitz 1991; Singh and Yadav 2017).

  This function is a convex in one part of the objective function and concave in the remaining part. “If the decision-maker is worse off with respect to a goal, then he/she tends to have a higher marginal rate of satisfaction with respect to that goal. A convex shape captures that behavior in the membership function. Similarly, if the decision-maker is better-off with respect to a goal, then he/she tends to have a smaller marginal rate of satisfaction. This type of behavior is modeled using the concave shape of the membership function” (Singh and Yadav 2017). It is defined as follows:

  $$\mu_{{\widetilde{R}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill &\quad {R_{\text{S}} \le R_{\text{S}}^{\text{l}} } \hfill \\ {\frac{1}{2 }\tanh \left( {\left( {R_{\text{S}} - \frac{{R_{\text{S}}^{\text{l}} + R_{\text{S}}^{\text{u}} }}{2}} \right)\alpha_{1} } \right) + \frac{1}{2}, } \hfill &\quad {R_{\text{S}}^{\text{l}} \le R_{\text{S}} \le R_{\text{S}}^{\text{u}} } \hfill \\ {1,} \hfill &\quad {R_{\text{S}} \ge R_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right.;\quad \alpha_{1} = \frac{6}{{R_{\text{S}}^{\text{u}} - R_{\text{S}}^{\text{l}} }}$$

  (18)
  $$\mu_{{\widetilde{C}_{\text{S}} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill &\quad {C_{\text{S}} \le C_{\text{S}}^{\text{l}} } \hfill \\ {\frac{1}{2 }\tanh \left( {\left( {\frac{{C_{\text{S}}^{\text{l}} + C_{\text{S}}^{\text{u}} }}{2} - C_{\text{S}} } \right)\alpha_{2} } \right) + \frac{1}{2},} \hfill &\quad {C_{\text{S}}^{\text{l}} \le C_{\text{S}} \le C_{\text{S}}^{\text{u}} } \hfill \\ {0,} \hfill &\quad {C_{\text{S}} \ge C_{\text{S}}^{\text{u}} } \hfill \\ \end{array} } \right.;\quad \alpha_{2} = \frac{6}{{C_{\text{S}}^{\text{u}} - C_{\text{S}}^{\text{l}} }}.$$

  (19)

Step 3 Reformulate the problem as a fuzzy MOOP.

The mathematical model of the problem is reformulated as follows:

$$\begin{aligned} &\quad {\text{Maximize}}\left( {\mu_{{\widetilde{R}_{\text{S}} }} ,\mu_{{\widetilde{C}_{\text{S}} }} } \right){\text{or}} \\ &\quad {\text{Minimize}}\left( { - \mu_{{\widetilde{R}_{\text{S}} }} , - \mu_{{\widetilde{C}_{\text{S}} }} } \right) \\ &\quad {\text{subject to}}\;g_{i} \left( {r, n} \right) \le 0,\;i = 1, 2, \ldots ,M \\ &\quad 0 \le r_{j,{\text{min}} } \le r_{j} \le r_{j,{\text{max}} } \le 1, \\ &\quad 1 \le n_{j,{\text{min}} } \le n_{j} \le n_{j,{\text{max}} } ,\;n_{j} \in {\mathbb{Z}}^{ + } ,\;j = 1, 2, \ldots ,m. \\ \end{aligned}$$

(20)

Theorem 1

The Pareto-optimal solution of the fuzzy MOOP (20) satisfies the MOOP (2).

Proof

Let $R^{*}$ be a Pareto-optimal solution of the fuzzy MOOP (20). Then, by definition of Pareto-optimal solution, we get

${\nexists } R \in \varOmega$ (feasible region), such that $- \mu_{{\widetilde{R}_{\text{S}} }} \left( R \right) \le - \mu_{{\widetilde{R}_{\text{S}} }} \left( {R^{*} } \right)$ and $- \mu_{{\widetilde{C}_{\text{S}} }} \left( R \right) < - \mu_{{\widetilde{C}_{\text{S}} }} \left( {R^{*} } \right)\,$

$\Leftrightarrow {\nexists } R \in \varOmega$, such that $- h_{1} \left[ {R_{\text{S}} \left( R \right)} \right] \le - h_{1} \left[ {R_{\text{S}} \left( {R^{*} } \right)} \right]$ and $- h_{2} \left[ {C_{\text{S }} \left( R \right)} \right] < - h_{2} \left[ {C_{\text{S}} \left( {R^{*} } \right)} \right]$

$\Leftrightarrow {\nexists } R \in \varOmega$, such that $h_{1} \left[ {R_{\text{S}} \left( R \right)} \right] \ge h_{1} \left[ {R_{\text{S}} \left( {R^{*} } \right)} \right]$ and $h_{2} \left[ {C_{\text{S}} \left( R \right)} \right] > h_{2} \left[ {C_{\text{S}} \left( {R^{*} } \right)} \right]$

$\Leftrightarrow {\nexists } R \in \varOmega$, such that $R_{\text{S}} \left( R \right) \ge R_{\text{S}} \left( {R^{*} } \right)$ and $C_{\text{S}} \left( R \right) < C_{\text{S}} \left( {R^{*} } \right)$ (since $h_{1}$ is monotonically increasing and $h_{2}$ is monotonically decreasing function).

$\Leftrightarrow {\nexists } R \in \varOmega$, such that $- R_{\text{S}} \left( R \right) \le - R_{\text{S}} \left( {R^{*} } \right)$ and $C_{\text{S}} \left( R \right) < C_{\text{S}} \left( {R^{*} } \right)$

$\Leftrightarrow R^{*} \in \varOmega$ is a Pareto-optimal solution of the MOOP given by (2).

Similarly, we can prove by taking the second objective $C_{\text{S}}$ first.

Step 4 Find the Pareto-optimal solutions (Pareto-optimal front).

In this step, the given model of the problem is encoded in MATLAB. All information about optimization part such as no. of objectives, design variables, design constraints, and the NSGA-II parameters such as population size ($N$), maximum no. of generation $(t_{{\text{max}} } )$, crossover probability $(p_{\text{c}} )$, mutation probability $(p_{\text{m}} )$, and distribution indices (Deb 2001) for SBX crossover ($\eta_{\text{c}}$) and polynomial mutation ($\eta_{\text{m}}$) are collected. To find a well-spread and well-converged set of solutions, a rigorous experimentation and tuning of parameters need to be exercised. After getting the Pareto-optimal fronts in terms of membership values of the objective functions, we are able to find the Pareto-optimal fronts in terms of the objective values.

Step 5 Find the best compromise solution.

Fuzzy ranking method (Pandiarajan and Babulal 2014) ranks the multiple solutions as per their degree of satisfaction. The best compromise solution achieves the maximum satisfaction level as follows:

$$\mu_{\text{best}} = \mathop {{\text{max}} }\limits_{P} \left[ {{\text{min}} \left\{ {\mu_{{\widetilde{R}_{\text{S}} }} ,\mu_{{\widetilde{C}_{\text{S}} }} } \right\}} \right],$$

(21)

where P is the number of obtained Pareto-optimal solutions.

Step 6 Rank the DMUs obtained by the various membership functions.

In this step, DEA is implemented to rank the efficiency of the optimal results given by the various membership functions in the form of DMUs. The CCR model (Charnes et al. 1978) is applied for efficiency and then the super-efficiency model (Noura et al. 2011) for resolving the issue of more than one DMUs having equal efficiencies. There are four DMUs as follows:

$$\begin{aligned} &\quad {\text{DMU}}_{1}\;{\text{Linear:}}\;\mu_{\text{best}}^{\text{L}} = \mathop {{\text{max}} }\limits_{P} \left[ {{\text{min}} \left\{ {\mu_{{\widetilde{R}_{\text{S}} }} ,\mu_{{\widetilde{C}_{\text{S}} }} } \right\}} \right] \\ &\quad {\text{DMU}}_{2}\;{\text{Quadratic:}}\;\mu_{\text{best}}^{\text{Q}} = \mathop {{\text{max}} }\limits_{P} \left[ {{\text{min}} \left\{ {\mu_{{\widetilde{R}_{\text{S}} }} ,\mu_{{\widetilde{C}_{\text{S}} }} } \right\}} \right] \\ &\quad {\text{DMU}}_{3}\;{\text{Parabolic:}}\;\mu_{\text{best}}^{\text{P}} = \mathop {{\text{max}} }\limits_{P} \left[ {{\text{min}} \left\{ {\mu_{{\widetilde{R}_{\text{S}} }} ,\mu_{{\widetilde{C}_{\text{S}} }} } \right\}} \right] \\ &\quad {\text{DMU}}_{4}\;{\text{Hyperbolic:}}\;\mu_{\text{best}}^{\text{H}} = \mathop {{\text{max}} }\limits_{P} \left[ {{\text{min}} \left\{ {\mu_{{\widetilde{R}_{\text{S}} }} ,\mu_{{\widetilde{C}_{\text{S}} }} } \right\}} \right]. \\ \end{aligned}$$

An Illustrative Example

Let us consider a four-stage over-speed protection system (see Fig. 6) for a gas turbine (Dhingra 1992). The over-speed detection is continuously provided by the electrical and mechanical systems. When an over-speed occurs, it is necessary to cut off the fuel supply by closing the four control valves (V1–V4). The control system is modeled as a four-stage series system. All components have a constant failure rate in the system. The objective is to determine the optimal design variables $r_{j}$ (component reliability) and $n_{j}$ (no. of the redundant components) at stage $j$, such that maximization of the system reliability ($R_{\text{S}}$) and minimization of the system cost ($C_{\text{S}}$) are achieved simultaneously. In addition, several design constraints such as minimum requirements for reliability of the system, the overall cost of the system, the total permissible volume of the system, and maximum allowable weight of the system are considered in this example. The mathematical formulation of the over-speed protection system is given as follows:

$${\text{Max}}.\;R_{\text{S}} \left( {r, n} \right) = \mathop \prod \limits_{j = 1}^{4} \left[ {1 - \left( {1 - r_{j} } \right)^{{n_{j} }} } \right]$$

(22)

$${\text{Min}}.\;C_{\text{S}} \left( {r,n} \right) = \mathop \sum \limits_{j = 1}^{4} c_{j} \left( {r_{j} } \right)\left[ {n_{j} + \exp \left( {n_{j} /4} \right)} \right]$$

(23)

$${\text{subject}}\;{\text{to}}\;V_{\text{S}} = \mathop \sum \limits_{j = 1}^{4} v_{j} n_{j}^{2} \le V$$

(24)

$$W_{\text{S}} = \mathop \sum \limits_{j = 1}^{4} w_{j} n_{j} { \exp }\left( {n_{j} /4} \right) \le W$$

(25)

$$\mathop \prod \limits_{j = 1}^{4} \left[ {1 - \left( {1 - r_{j} } \right)^{{n_{j} }} } \right] \ge R$$

(26)

$$\mathop \sum \limits_{j = 1}^{4} c_{j} \left( {r_{j} } \right)\left[ {n_{j} + \exp \left( {n_{j} /4} \right)} \right] \le C$$

(27)

$$0.5 \le r_{j} \le 1 - 10^{ - 6} , \;1 \le n_{j} \le 10, \;n_{j} \in {\mathbb{Z}}^{ + } ,\;j = \, 1,2,3,4.$$

(28)

Fig. 6

A schematic diagram of the over-speed protection system

The cost of the $j$ th component $c_{j} \left( {r_{j} } \right)$ is assumed to be an increasing function of $r_{j}$ (conversely, a decreasing function of the component failure rate) in the form:

$$c_{j} \left( {r_{j} } \right) = \gamma_{j} /\lambda_{j}^{{\delta_{j} }} ,$$

(29)

where $\gamma_{j}$ and $\delta_{j}$ are constants of characteristics factors for each component at the $j$ th stage or subsystem. This formula can be found in Kumar et al. (2009).

Each component of the system has a constant failure rate $\lambda_{j}$ that follows an exponential distribution. The reliability of each component is given by the following:

$$r_{j} \left( T \right) = \mathop \int \limits_{T}^{\infty } \lambda_{j} e^{{ - \lambda_{j} T}} {\text{d}}T = e^{{ - \lambda_{j} T}} .$$

(30)

From (29) and (30), we have

$$c_{j} \left( {r_{j} } \right) = \gamma_{j} \left[ { - T/\ln \left( {r_{j} } \right)} \right]^{{\delta_{j} }} .$$

(31)

The parameters $\delta_{j}$ and $\gamma_{j}$ give the physical features (shaping and scaling factor) of the cost–reliability curve of each component in the $j$ th subsystem and the factor $\exp \left( {n_{j} /4} \right)$ accounts for the additional cost due to the interconnection between the parallel components (Kuo and Prasad 2000; Wang et al. 2009).

Computational Results and Discussion

This section describes and analyzes the results obtained by the proposed approach.

Parameter Settings

The overall process is implemented in the MATLAB (R2017a) on Intel(R) Core(TM) i3-2370M CPU @ 2.40 GHz with 4 GB RAM. The integer variables $n_{j}$ are initially treated as real variables, but during the evaluation of the objective functions, the real values are transformed to the nearest integer values. MATLAB optimization tool-box function namely “fmincon” (Coleman et al. 1999) is used to determine the optimal values to each of the objective functions with given constraints. The design data for the given example are listed in Table 1. The optimal results for the single-objective optimization problem (SOOP) are given in Table 2 and compared it with other heuristic approaches. The parameters settings of the NSGA-II and other MOEAs such as PESA-II and SPEA2 are given as follows:

Table 1 Design data for the given example

Table 2 Optimum solutions for the SOOP

NSGA-II: $N$ = 40, $t_{{\text{max}} }$ = 100, $p_{\text{c}}$ = 0.9, $p_{\text{m}}$ = 0.1, $\eta_{\text{c}}$ = 10, $\eta_{\text{m}}$ = 100.

PESA-II (Corne et al. 2001): hyper-grid size = 10 × 10; $p_{\text{c}} = 0.8$, $p_{\text{m}} = 0.2$, $\eta_{\text{c}} = 10$, $\eta_{\text{m}} = 100$, archive size = 40; $t_{{\text{max}} } = 100$.

SPEA2 (Zitzler et al. 2001): N = 40; $p_{\text{c}} = 0.9$, $p_{\text{m}} = 0.1$; and $\eta_{\text{c}} = 10$, $\eta_{\text{m}} = 100$, archive size = 40; $t_{{\text{max}} } = 100$.

Simulation Results

After setting the parameters, a simulation run for the given problem is shown to non-fuzzy approach fuzzy approach in Fig. 7. In Figs. 8 and 9, the simulation results of the proposed approach have been shown to both the membership and objective spaces respectively. NSGA-II is shown comparatively with other elitist MOEAs such as PESA-II and SPEA2. Figure 10 shows a box-plot comparison of $R_{\text{S}}$ and $C_{\text{S}}$ between non-fuzzy and fuzzy approach.

Fig. 7

The POFs based on the non-fuzzy approach in a single simulation run

Fig. 8

The POFs in the membership grades space using the various membership functions

Fig. 9

The POFs in the objective space on the basis of the various membership functions

Fig. 10

Box-plot comparison between the fuzzy and non-fuzzy approach

The Best DMU

The best trade-off of optimal solutions for each of the membership functions is obtained by the fuzzy ranking method in Table 3. Figure 11 shows the optimal values obtained by the various membership functions in $R_{\text{S}}$ and $C_{\text{S}}$. In Fig. 12, the maximum satisfaction levels achieved by the various membership functions are compared. After that, DEA is implemented to rank the DMUs obtained by the various membership functions. Table 4 gives the ranking to each DMU. It is based on the CCR model that is implemented in DEAP solver software (Coelli 1996). The efficiencies are obtained in this model as DMU₁  = 1, DMU₂  = 0.988, DMU₃  = 1, and DMU₄  = 1. To resolve it, super-efficiency model concept (Noura et al. 2011) is used, and finally, it is ranked as DMU₄  > DMU₃  > DMU₁  > DMU₂.

Table 3 The best compromise solution for each membership function

Fig. 11

The optimal values of $R_{\text{S}}$ and $C_{\text{S}}$ on the basis of the various membership functions

Fig. 12

Maximum satisfaction level achieved by the various membership functions

Table 4 Ranking from the DEA model

A Comparative Study with Existing Approach

The proposed approach is compared with other approaches applied to the same problem. Liu (2013) solved this problem by converting into a single-objective fuzzy non-linear programming problem. A heuristic method is developed to get a set of satisfactory solutions. To rank the satisfactory solutions, DEA model is used by considering criteria of reliability, cost, volume, and weight. However, an MOOP is preferred to obtain a set of optimal solutions popularly known as Pareto-optimal solutions and the best Pareto-optimal solution is then chosen by some higher level information involved in the problem. The proposed approach simultaneously optimizes the membership functions instead of objective functions and gets multiple solutions in a single simulation run. Figure 13 shows the box-plot comparison of the proposed approach and Liu (2013) by taking the same range of limits in the linear membership function. The proposed approach gives well-distributive solutions in the same conditions.

Fig. 13

The box-plot comparison with Liu (2013)

Garg et al. (2014a) solved this problem by developing a model in fuzzy environment with the assumption that the reliability of each component is a triangular fuzzy number. To solve the problem, the developed fuzzy model is converted into crisp model using expected values of fuzzy numbers and taking into account the preference of decision-maker regarding cost and reliability goals. However, the proposed approach does not require any kind of aggregate operators and various membership functions give the desirability functions to the decision-maker in choosing the best compromise solution according to his/her own’s interest. Figure 14 shows the box-plot comparison between linear and non-linear (sigmoidal shape) membership functions. The proposed approach uses MOEA technique rather than heuristic approaches such as GA (Goldberg 1989), and PSO (Kennedy and Eberhart 1995), so it covers a larger search space where multiple solutions are generated in a single simulation run. It gives more information about the characteristics of the solutions.

Fig. 14

The box-plot comparison with Garg et al. (2014a)

Wang et al. (2009) solved the MORRAP using NSGA-II in the crisp environment. In a similar environment, Damghani et al. (2013) used multi-objective particle swarm optimization (MOPSO). Both these approaches do not reflect the real-life situations where uncertainty is an inherent character in the system design problem. Recently, Muhuri et al. (2018) solved the MORRAP with interval type-2 fuzzy set which considers higher order uncertainties in the component parameters and addressed it using NSGA-II. The comparison between the Muhuri et al. (2018) and the proposed approach is given as follows.

Muhuri et al. (2018)	Proposed approach
This type of modeling is suitable for those situations where the end points of the component or objective are ambiguous	The present approach finds the end points of each objective first and then models the given problem as a fuzzy MOOP
It does not show the POF in the membership space. In fact, this type of modeling creates difficulty to show the POF in the membership space	The present approach finds the POF in the objective space as well as its membership space
Only linear membership function is considered	However, a real-world situation demands models to be more flexible and adaptable to the human decision-making process as well as some kind of empirical justification or assumption. Keeping these views in mind, various membership functions are considered
It does not give the best solution	It finds the best “trade-off” or compromise solution

Conclusions

In this piece of work, MOEA approach is used to solve MORRAP in a fuzzy environment where the goals of the objectives are specified by various membership functions such as linear, quadratic, parabolic, and hyperbolic. A numerical example of over-speed protection system with conflicting objectives such as maximization of system reliability and minimization of system cost is considered simultaneously under several design constraints such as minimum requirements for reliability of the system, the overall cost of the system, the total permissible volume of the system, and maximum allowable weight of the system. Fuzzy ranking method is used to obtain the best compromise solution. Finally, DEA model is used to rank the results for the various membership functions in the form of DMUs.

The experiments performed by the proposed approach are concluded as follows:

• MOEA technique namely NSGA-II is shown with other MOEAs which are capable in finding a complete picture of Pareto-optimal solutions in a single simulation run, where a decision-maker gets more information such as non-dominated and their characteristics.

• The proposed approach is free from any kind of aggregation. It deals with purely multi-objective manner.

• The trade-offs between the system reliability and system cost are shown in both membership space and objective space.

• Simulation results of fuzzy and non-fuzzy approach are comparatively analyzed. It shows a fuzzy approach gives the flexibility to the decision-maker in setting the desired goals.

• The best compromise solutions are obtained for the various membership functions.

• DEA ranks the DMUs as Hyperbolic > Parabolic > Linear > Quadratic.

• Hyperbolic membership function gives the best result to the decision-maker.

• The proposed approach gives flexibility to the decision-maker in choosing the membership function to his/her’s own interests.