NSGA-II Based Decision-Making in Fuzzy Multi-objective Optimization of System Reliability

Abstract

This paper presents an approach to determine the optimal value of multi-objective optimization of a reliability-based system design problem. For this purpose, an over-speed protection system for a gas turbine is designed with mutually conflicting objectives such as the system reliability and system cost. This is a multi-objective nonlinear mixed integer programming problem subject to the upper limits on design constraints such as weight and volume. To solve the problem, a fuzzy approach is adopted to specify the goals in terms of the membership functions. This approach is effective in modeling the vague and imprecise information involved in the system. NSGA-II is employed to obtain the Pareto solutions efficiently. Finally, one out of these solutions is obtained by the decision-making methods such as TOPSIS and Shannon’s entropy approach. The efficiency of the proposed approach is compared with the existing approach.

1 Introduction

Reliability is characterized by the performance of a system under some specified conditions. It is a necessary aspect of an engineering system design. In many practical situations, a design engineer needs to improve the reliability with reduction of other resource consumptions such as cost, weight, and volume. Formulation of system design in multi-objective programming problem is a better adaptation in such situations. Many multi-objective approaches in reliability-based system design can be seen in [1,2,3,4]. Ideally, a multi-objective optimization presents a group of non-dominated solutions in the form of trade-offs, where the desired solution is then selected by some high-level information involved in the problem [5]. Classical optimization methods [6] are not able to fulfill such demands. Evolutionary algorithms [7] are useful alternatives in a multi-objective optimization problem, where a collective Pareto solutions is obtained simultaneously. The basic concepts and approaches of multi-objective evolutionary algorithms (MOEAs) can be viewed in Coello et al. [7]. Elitist non-dominated sorting genetic algorithm (NSGA-II) [6] is one of the second-generation MOEAs. It finds a much better convergence and spread of solutions near the true Pareto front [6] compared to two other elitist MOEAs such as PAES [8] and SPEA [9]. The applications of NSGA-II have now increased due to its elitism, parameter-less sharing approach, and low computational requirements [6]. Salazar et al. [10] showed the competency of NSGA-II to classify a set of optimal solutions (Pareto front) in solving constrained reliability problems. Wang et al. [11] used NSGA-II to solve multi-objective redundancy allocation problem (RAP) and compared their results with single-objective approaches. Kishore et al. [12] proposed an interactive approach to fuzzy multi-objective reliability optimization problem using NSGA-II. Safari [13] proposed a variant of NSGA-II in solving a multi-objective RAP. Khalili-Damghani et al. [14] proposed a decision-support system for multi-objective RAPs. Fuzzy-based multi-objective reliability problems are solved by Garg and Sharma [15] and Garg et al. [16] using PSO and GA. Recently, Sharifi et al. [17] present NSGA-II algorithm for solving multi-objective RAP for series–parallel and k-out-of-n subsystems with three objectives.

In this paper, a methodology is developed to achieve the optimal value of multi-objective reliability-based system design problem. First, the multi-objective problem of system design is formulated in the fuzzy environment and then solved by using NSGA-II. In order to find a concrete solution, decision-making methods such as TOPSIS [20] and Shannon’s entropy [21] are implemented on the basis of the ideal and anti-ideal points (solutions) specified by the decision-maker. The optimal values are shown graphically in the objective space. The proposed method is compared with one of the existing approaches [15]. The rest of the paper is organized as follows. In Sect. 2, a mathematical model of the problem is constructed. Section 3 presents a concise depiction of the NSGA-II algorithm. In Sect. 4, the proposed methodology is described. Section 5 gives the results and with its discussion and Sect. 6 gives the conclusion.

2 Mathematical Model of the Problem

In this work, a four-stage over-speed protection system model [1] for a gas turbine is considered. The system diagram is shown in Fig. 1.

Fig. 1

A symbolic diagram of the over-speed protection system

Over-speed detection is constantly arranged by the electrical and mechanical systems. When an over-speed occurs, the fuel supply goes cut off. In this way, four control valves (V1–V4) get locked. The control system is formed as a 4-stage series system. A constant failure rate occurs for all components in the system. The goal is to determine the optimal design variables $R_{j}$ and $\left| {X_{j} } \right|$ at each stage j such that the minimization of the system cost and the maximization of the system reliability can be achieved simultaneously.

Notation:

$R_{S}$ :

System reliability;

$C_{S}$ :

cost of the total system;

$R_{j}$ :

reliability of a component at stage j;

$\left| {X_{j} } \right|$ :

number of the redundant component at stage j;

$W_{S}$ :

total system weight;

$V_{S}$ :

total system volume;

$W_{ \lim }$ :

upper limit on the system weight;

$V_{ \lim }$ :

upper limit on the system volume;

$W_{j}$ :

weight of each component at stage j;

$V_{j}$ :

volume of each component at stage j;

$\gamma_{j}$, $\delta_{j}$:

physical quantities representing characteristics of each component at stage j;

M :

number of stages;

τ :

operating time

The mathematical model of the problem is given as follows:

$$ \text{Max}\,R_{S} = \prod\limits_{j = 1}^{M} {\left[ {1 - \left( {1 - R_{j} } \right)^{{\left| {X_{j} } \right|}} } \right]} , $$

(1)

$$ \text{Min}\,C_{S} = \sum\limits_{j = 1}^{M} {\gamma_{j} \left( {\frac{ - \tau }{{\ln \,(R_{j} )}}} \right)}^{{\delta_{j} }} \left[ {\left| {X_{j} } \right| + \exp \left( {\left| {X_{j} } \right|/4} \right)} \right], $$

(2)

subject to

$$ W_{S} = \sum\limits_{j = 1}^{M} {W_{j} \left| {X_{j} } \right|} \,\exp \left( {\left| {X_{j} } \right|/4} \right) \le W_{\lim } , $$

(3)

$$ V_{S} = \sum\limits_{j = 1}^{M} {V_{j} \left( {\left| {X_{j} } \right|} \right)^{2} } \le V_{\lim } , $$

(4)

$$ 1 \le \left| {X_{j} } \right| \le \left| {X_{\hbox{max} } } \right|,R_{\hbox{min} } \le R_{j} \le R_{\hbox{max} } ,j = 1,2, \ldots ,M;\left| {X_{j} } \right| \in {\mathbb{Z}}^{ + } ,R_{j} \in {\mathbf{\mathbb{R}}}^{ + } , $$

(5)

where $\exp \left( {\left| {X_{j} } \right|/4} \right)$ represents the interconnecting hardware, $\left| {X_{ \hbox{max} } } \right|$ denotes the maximum number of components given at each stage, $R_{ \hbox{min} }$ and $R_{ \hbox{max} }$ denote the minimum and maximum values on the reliability of each component.

Assumptions:

• (i) The cost–reliability relation is

  $$ C(R_{j} ) = \gamma_{j} \lambda_{j}^{{ - \delta_{j} }} $$

  (6)

• (ii) Each component of the system has a constant failure rate $\lambda_{j}$ that follows an exponential distribution. The reliability of each component is obtained by

  $$ R_{j} (\tau ) = \int\limits_{\tau }^{\infty } {\lambda_{j} {\text{e}}^{{ - \lambda_{j} \tau }} {\text{d}}\tau = {\text{e}}^{{ - \lambda_{j} \tau }} } $$

  (7)

From (6) and (7), the cost of each component is

$$ C(R_{j} ) = \gamma_{j} \left[ { - \tau /\ln \,(R_{j} )} \right]^{{\delta_{j} }} $$

(8)

3 NSGA-II

Non-dominated sorting genetic algorithm (NSGA) was initially suggested by Srinivas and Deb [18]. It uses Goldberg’s domination criterion [19] to assign ranks for the solutions and utilization of fitness sharing for maintaining the diversity in the solution set. It has some difficulty in regarding computational complexity, non-elitist approach, and highly dependent on the parameters of fitness sharing. Deb et al. [6] extended this algorithm in the form of NSGA-II by giving some new features like fast non-dominated sorting, crowding distance, and comparison operator.

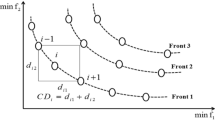
NSGA-II assigns a rank for solutions employing non-dominated sorting procedure and emphasizes good solutions throughout this algorithm. The overall complexity governed by this process is O(kN²), where k and N denote the number of objectives and population size, respectively [6]. See Fig. 2a.

Fig. 2

a Sorting procedure of a population. b Crowding distance estimation of a solution. c Evaluation cycle of the NSGA-II algorithm

For maintaining the diversity in the solution set, NSGA-II calculates the crowding distance of each solution. It is basically defined as those solutions that contain the same rank. A partial order comparison operator is applied to determine a better solution between two solutions. According to this operator, if both the solutions belong to the same rank, then preference is given to the solution that contains a higher crowding distance value. A higher crowding distance value gives the lesser crowded region and vice versa [6]. See Fig. 2b.

Deb et al. [6] proposed constraint-dominance based binary tournament selection method in constraint handling procedure. A search space is divided by the constraints into two regions—feasible and infeasible. Accordingly, a solution α is defined as a constrained-dominate to a solution β if

• (i) α is feasible and β is infeasible.

• (ii) α and β are infeasible, but α contains a lower overall constraint violation.

• (iii) α and β are feasible, but α dominates β.

The pseudocode of NSGA-II algorithm (See Fig. 2c) is given as follows:

• Step 1. Initializing randomly a parent population $P_{0}$ of size N. Setting k = 0.

• Step 2. Assigning fitness (rank) according to non-domination level and crowded-comparison operator.

• Step 3. while k < number of maximum generation do

  • (i) Creating an offspring population $Q_{k}$ of size N applying reproduction, crossover, and mutation.

  • (ii) Combining via $R_{k} = P_{k} {\cup }Q_{k}$.

  • (iii) Sorting on $R_{k}$ and classifying them into non-dominated fronts (Pareto fronts) $PF_{i} ,i = 1,2, \ldots ,$ etc.

  • (iv) Setting a new population $P_{k + 1} = {\emptyset }$ and $i = 1$.

    while the parent population size $\left| {P_{k + 1} } \right| + \left| {PF_{i} } \right| < N$ do

    • (i) Calculating the crowding distance of $PF_{i}$.

    • (ii) Adding the $i{\text{th}}$ non-dominated front $PF_{i}$ to the parent population $P_{k + 1}$.

    • (iii) $i = i + 1$.

      end while

  • (v) Sorting the $PF_{i}$ using the crowding distance-based comparison operator.

  • (vi) Filling the parent population $P_{k + 1}$ with the first $N - \left| {P_{k + 1} } \right|$ solutions of $PF_{i}$.

  • (vii) Generating the offspring population $Q_{k + 1}$.

  • (viii) Setting $k = k + 1$.

    end while

• Step 4. Collecting the non-dominated solutions in the vector P.

4 Proposed Methodology

The problem given in Sect. 2 is solved by the following steps:

• Step 1. Constructing the membership functions of fuzzy objectives (Fig. 3).

  Fig. 3

  

  Linear membership function for a system reliability b system cost

$$ \mu_{{\widetilde{R}_{S} }} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {R_{S} \le R_{S}^{\hbox{min} } ,} \hfill \\ {\frac{{R_{S} - R_{S}^{\hbox{min} } }}{{R_{S}^{\hbox{max} } - R_{S}^{\hbox{max} } }},} \hfill & {R_{S}^{\hbox{min} } < R_{S} < R_{S}^{\hbox{max} } ,} \hfill \\ {1,} \hfill & {R_{S} \ge R_{S}^{\hbox{max} } ,} \hfill \\ \end{array} } \right. $$

(9)

where $R_{S}^{ \hbox{min} }$ and $R_{S}^{ \hbox{max} }$ are the minimum and maximum values on the system reliability, respectively. This range is fixed by the decision-maker according to his/her requirements.

$$ \mu_{{\widetilde{C}_{S} }} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {C_{S} \le C_{S}^{\hbox{min} } ,} \hfill \\ {\frac{{C_{S}^{\hbox{max} } - C_{S} }}{{C_{S}^{\hbox{max} } - C_{S}^{\hbox{min} } }},} \hfill & {C_{S}^{\hbox{min} } < C_{S} < C_{S}^{\hbox{max} } ,} \hfill \\ {0,} \hfill & {C_{S} \ge C_{S}^{\hbox{max} } ,} \hfill \\ \end{array} } \right. $$

(10)

similarly, $C_{S}^{ \hbox{min} }$ and $C_{S}^{ \hbox{max} }$ are the minimum and maximum values on the system cost, respectively. This range is decided by the decision-maker according to his/her investment capacity.

• Step 2. Formulating the problem in the form of fuzzy objectives.

$$ \left. {{\text{Maximize}}\quad \left( {\mu_{{\widetilde{R}_{S} }} ,\mu_{{\widetilde{C}_{S} }} } \right)} \right\} $$

(11)

subject to the constraints given in (3)–(5).

• Step 3. Setting the parameters as given in Tables 1 and 2, and then applying the NSGA-II algorithm to get the Pareto front in (11).

• Step 4. Constructing the decision matrix of objectives (criteria) as follows:

$$ D = \left[ {\begin{array}{*{20}l} {\mu_{{\tilde{R}_{S} }}^{11} } \hfill & {\mu_{{\tilde{R}_{S} }}^{21} } \hfill & \ldots \hfill & {\mu_{{\tilde{R}_{S} }}^{m1} } \hfill \\ {\mu_{{\tilde{C}_{S} }}^{12} } \hfill & {\mu_{{\tilde{C}_{S} }}^{22} } \hfill & \ldots \hfill & {\mu_{{\tilde{C}_{S} }}^{m2} } \hfill \\ \end{array} } \right]^{\text{T}} = \left[ {\mu_{{\tilde{R}_{S} ,\tilde{C}_{S} }}^{ij} } \right];\quad i = 1,2, \ldots ,m;\quad j = 1,2. $$

(12)

Table 1 Designing data for the problem

Table 2 The parameter settings for the given problem

• Step 5. Finding the best alternative in the decision matrix given by (12).

To determine the best alternative, we apply the decision-making method as follows:

4.1 TOPSIS Approach

In the present work, we applied the TOPSIS method [20] on membership values of the objective functions. The ideal membership value is taken as 1 for the upper limit of each objective and the anti-ideal membership value is taken as 0 for the lower limit of each objective. The Euclidean distances of each membership value of the objective function from the anti-ideal and ideal points are calculated, respectively, as follows:

$$ D_{i}^{ - } = \sqrt {\sum\limits_{j = 1}^{2} {\left( {\mu_{{R_{S} ,C_{S} }}^{ij} - 0} \right)^{2} } } ,\quad i = 1,2, \ldots ,m $$

(13)

$$ D_{i}^{ + } = \sqrt {\sum\limits_{j = 1}^{2} {\left( {\mu_{{R_{S} ,C_{S} }}^{ij} - 1} \right)^{2} } } ,\quad i = 1,2, \ldots ,m $$

(14)

In this method, $D_{i}$ (relative closeness of ith alternative) is calculated as

$$ D_{i} = \frac{{D_{i}^{ - } }}{{D_{i}^{ - } + D_{i}^{ + } }} $$

(15)

Therefore,

$$ A_{i}^{\text{best}} = \hbox{max} (D_{i} ). $$

(16)

4.2 Shannon’s Entropy Approach

Entropy [21] is calculated to measure the disorder in the given discrete probability distribution of the system. It is observed that a broad distribution gives a more uncertainty than a sharply packed distribution. Consider $H_{ij}$ in the decision matrix D as follows:

$$ H_{ij} = \frac{{\mu_{{R_{S} ,C_{S} }}^{ij} }}{{\sum\limits_{i = 1}^{m} {\mu_{{R_{S} ,C_{S} }}^{ij} } }},\quad i = 1,2, \ldots ,m;\quad j = 1,2. $$

(17)

Shannon’s entropy is calculated by

$$ E_{j} = - M\sum\limits_{i = 1}^{m} {H_{ij} } \ln H_{ij} ,M = 1/\ln (m) $$

(18)

The degree of deviation is obtained by

$$ DV_{j} = 1 - E_{j} $$

(19)

The weight of jth fuzzy objective is calculated by

$$ W_{j} = \frac{{DV_{j} }}{{\sum\nolimits_{j = 1}^{2} {DV_{j} } }} $$

(20)

Finally,

$$ Y_{i} = \sum\limits_{j = 1}^{2} {H_{ij} W_{j} } ;\quad i = 1,2, \ldots ,m $$

(21)

Therefore,

$$ A_{i}^{\text{best}} = \hbox{max} (Y_{i} ). $$

(22)

Formulation of the problem for the genetic algorithm (GA) [19]-based decision-making

$$ \text{Maximize}\,\left( {1 \wedge \frac{{\alpha_{1} }}{{W_{1} }}} \right) \wedge \left( {1 \wedge \frac{{\alpha_{2} }}{{W_{2} }}} \right) $$

(23)

subject to

$$ \alpha_{1} = \mu_{{\widetilde{R}_{S} }} ,\alpha_{2} = \mu_{{\widetilde{C}_{S} }} ,W_{1} ,W_{2} \in \left( {0,1} \right] $$

(24)

$$ W_{S} = \sum\limits_{j = 1}^{M} {W_{j} \left| {X_{j} } \right|\exp \left( {\left| {X_{j} } \right|/4} \right) \le W_{\lim } } , $$

(25)

$$ V_{S} = \sum\limits_{j = 1}^{M} {V_{j} \left( {\left| {X_{j} } \right|} \right)^{2} } \le V_{\lim } , $$

(26)

$$ 1 \le \left| {X_{j} } \right| \le 10,0.5 \le R_{j} \le 1 - 10^{ - 6} ,j = 1,2,3,4;\left| {X_{j} } \right| \in {\mathbb{Z}}^{ + } ,R_{j} \in {\mathbf{\mathbb{R}}}^{ + } $$

(27)

where $\wedge$ represents min operator as the aggregate operator, $W_{1}$ and $W_{2}$ are the weights of the objectives suggested by the decision-maker, $\alpha_{1}$ and $\alpha_{2}$ are the degree of satisfaction of the objectives.

5 Results and Discussion

The problem presented in Sect. 2 is a RAP problem. A real number of encoding is used in a vector of design variables $\left[ {\left( {R_{1} ,\left| {X_{1} } \right|} \right),\left( {R_{2} ,\left| {X_{2} } \right|} \right),\left( {R_{3} ,\left| {X_{3} } \right|} \right),\left( {R_{4} ,\left| {X_{4} } \right|} \right)} \right]$. The SBX and polynomial operators [5] are used for crossover and mutation, respectively. Based on rigorous experimentation, results are obtained in Table 3. In Table 3, the proposed approach is compared with heuristic method GA where the problem is converted to single objective using aggregation operator. To make a fair comparison, same parameters are used and equal weight given to each objective. One of the best solutions is chosen from 10 independent runs in GA. In Fig. 4, the results are displayed on the basis of membership functions. There are 29 solutions found by NSGA-II in the first front. The decision-making methods are applied on the basis of the Euclidean distances from the ideal and anti-ideal points. Figure 5 shows the Pareto front and the best results obtained by the decision-making methods such as TOPSIS and Shannon’s entropy.

Table 3 Comparison of optimal solutions with the existing method

Fig. 4

The optimal values based on membership functions

Fig. 5

The optimal values based on objective functions

6 Conclusion

In this piece of work, an approach is developed to determine the optimal value of fuzzy multi-objective reliability-based system design. A mathematical model of real-world problem of the over-speed protection system is presented. To avoid any kind of aggregator operators, NSGA-II is employed to solve the problem. At the decision-making stage, we modify the decision-making methods in terms of membership function and find the best optimal value according to the Euclidean distances from the ideal and anti-ideal points (solutions) in the objective space. In order to show the efficiency of the proposed approach, it is compared with the existing approach. The obtained results are found encouraging. Thus, the proposed methodology can be a better adaptation in finding the concrete solution in multi-objective reliability-based system design problem.