On A New Extended Log-Normal Distribution: Properties, Regression, Bayesian Regression, and Data Analysis

Abstract

This article introduces and investigates the Marshall-Olkin Topp-Leone log-normal (MOTLLN) distribution, a novel extension of the log-normal distribution. It can be presented as a new four-parameter continuous distribution designed to analyze a wide range of versatile positive-valued data. In a brief first part, we explore its main aspects, including the quantile function and the hazard rate function. We then focus on its applied aspect from a statistical perspective. Parameter estimation is performed using both maximum likelihood and Bayesian methods. Furthermore, we employ the MOTLLN distribution to develop a parametric regression model and a Bayesian regression model, demonstrating its versatility. A simulation study supports the practical performance of the maximum likelihood estimation procedure. Real datasets are used to demonstrate the applicability of our methodology. The effectiveness of the additional parameter in the MOTLLN model is assessed by a likelihood ratio test. In addition, the parametric bootstrap method is used to evaluate the suitability of the MOTLLN model for the datasets. All the results obtained confirm the great potential of the proposed model in all aspects.

1 Introduction

Various fields of lifetime data analysis, including survival analysis, astronomical observations, financial modelling, risk assessment, insurance, rare event analysis and biology, require the introduction of novel distributions with different hazard rate characteristics. In fact, the effectiveness of statistical analysis depends largely on the selection of an appropriate distribution adapted to the dataset under consideration, highlighting the importance of model adaptability. However, traditional distributions often prove inadequate to accurately capture the complexity of real-world datasets arising from concrete scenarios. For this reason, there has been a notable resurgence of interest in refining established distributions through the addition of parameter(s), resulting in a number of hazard rate functions (hrfs) suitable for the analysis of skewed data with varying kurtosis. A review of some of these extended models is given in Pham and Lai (2007).

As a fundamental concept, the log-normal (LN) distribution describes the distribution of a continuous random variable whose logarithm follows a normal distribution. It has significant implications for the analysis of lifetime data, particularly when dealing with asymmetric datasets. This is the case in many disciplines within the life sciences, such as biology, geology, ecology and meteorology, as well as economics, finance and risk analysis (see Jobe et al. (1989)). It is also gaining attention in environmental sciences, physics, astrophysics and cosmology (see Bernardeau and Kofman (1994), Blasi et al. (1999), Parravano et al. (2012)). As a key mathematical point, the probability density function (pdf) of the LN distribution is given by

$$\begin{aligned} q(x) = \frac{1}{\sqrt{2\pi } \sigma x} \exp \left[ -\frac{(\log (x) - \mu )^2}{2 \sigma ^{2}} \right] , \end{aligned}$$

(1.1)

where $x>0$, $\mu \in {\mathbb {R}}$ and $\sigma >0$. The generalizations of the LN distribution have been extensively explored in the statistical literature by various authors, enhancing flexibility (see Chen (1995), Singh et al. (2012), Gui (2013), Kleiber (2014), and Toulias and Kitsos (2013)). In this article, we propose a new generalized version of the LN distribution, achieved through a flexible generalization technique.

The subsequent sections of this article are organized as follows: Sect. 2 elucidates the construction method of this generalization. Section 3 presents its main mathematical definition. Section 4 provides the quantile function (qf) and related measures. Section 5 explores the hrf and its graphical point of view via some examples of plots. Section 6 introduces the maximum likelihood (ML) and Bayesian methods for estimating the unknown parameters of the model. In addition, Sect. 7 outlines a parametric bootstrap method using the ML estimation in a simulation context. Section 8 defines a parametric regression model associated with the new distribution, while Sect. 9 introduces a Bayesian regression method. Section 10 presents a simulation study evaluating the performance of the ML estimates of the parameters involved. Finally, to demonstrate the effectiveness of the new distribution compared to other distributions, Sect. 11 analyzes three univariate uncensored real datasets and one censored real dataset for regression analysis. Section 12 provides concluding remarks.

2 Construction

To understand the construction of the new distribution, a retrospective analysis of various distributions and generator distribution schemes is essential. The Topp-Leone (TL) distribution, first introduced by Topp and Leone (1955), provides a precisely bounded J-shaped distribution that serves as an alternative to the uniform(0,1) and beta distributions. It has gained particular attention among statisticians in recent years. The cumulative distribution function (cdf) of the TL distribution is

$$\begin{aligned} F_{TL}(x) = \{x(2-x)\}^\alpha , \end{aligned}$$

(2.1)

where $0<x<1$ and $\alpha >0$. From this simple expression we can immediately derive the corresponding pdf and hrf. It is important to note that the TL distribution has a bathtub shaped hrf for all $\alpha <1$. A notable study in the literature using the TL distribution as a generator was the TL generalized exponential (TLGE) distribution introduced by Sangsanit and Bodhisuwan (2016). Convincing applications to datasets in materials science and engineering have been obtained.

On the other hand, Marshall and Olkin (1997) proposed a new scheme for generalizing distributions by introducing an additional parameter to a family of distributions called the Marshall-Olkin-G family. The authors demonstrate its applicability by comparing it with the famous exponential and Weibull families. Later, Al-Shomrani et al. (2016) developed another family of distributions, the so-called TL-G family, and discussed the inferential aspects of certain important members. By combining the Marshall-Olkin-G and TL-G families, Khaleel et al. (2020) established the Marshall-Olkin TL-G (MOTL-G) family and studied some of its general properties. The cdf of the MOTL-G family is given by

$$\begin{aligned} F_{MOTL-G}(x) = \frac{\left\{ F(x)\left[ 2 - F(x)\right] \right\} ^{\alpha }}{\beta + (1-\beta ) \left\{ F(x)\left[ 2 - F(x)\right] \right\} ^{\alpha }}, \end{aligned}$$

(2.2)

which is defined for any fixed baseline cdf F(x) and $\beta >0$.

The usefulness of the proposed family is also emphasised by an important member of this family, the so-called Marshall-Olkin TL Weibull (MOTLWe) distribution. The flexibility of the corresponding model compared to various competitors is very convincing and inspires more work in this direction. It is to be hoped that other members of this family will also perform well relative to their respective sub-models. So far, there hasn’t been much work done on other members of this family in the literature, which can be seen as a research gap.

Therefore, in this article, we consider an important member of this family by selecting the LN distribution as the baseline distribution, motivated in part by a high potential for applicability. We call the resulting distribution the Marshall-Olkin TL log-normal (MOTLLN) distribution. Our aim is to uncover various statistical properties of this distribution and to use them in reliability analysis. Our motivations are as follows:

• (i) To introduce a novel and versatile continuous distribution capable of effectively modelling lifetime data across a wider range of reliability challenges.

• (ii) To extend both LN and TL distributions.

• (iii) To include additional forms of hrfs.

3 Definition

This part introduces the definition and key features of the MOTLLN distribution.

Definition 3.1

Let X be a continuous random variable. Then we say that X follows the MOTLLN distribution with parameters $\alpha$, $\beta$, $\mu$ and $\sigma$, if its cdf is expressed as follows:

$$\begin{aligned} F(x) = \frac{ \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha }}{ \beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha } }, \end{aligned}$$

(3.1)

where $x>0$, $\mu \in \mathbb {R}$, $\alpha$, $\beta$, $\sigma >0$, and $\Phi (x)$ and $\phi (x)$ are the cdf and pdf of the standard normal distribution, respectively.

Under this setting, the corresponding pdf is indicated as

$$\begin{aligned} f(x) = \frac{2\alpha \beta \ \phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 1 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha -1}}{\sigma x \left( \beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha } \right) ^{2} }. \end{aligned}$$

(3.2)

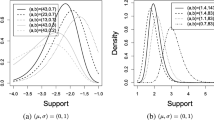
To get a visual idea of the functional possibilities of the MOTLLN distribution, Figs. 1 and 2 show some examples of plots of the corresponding cdf and pdf, respectively. The pdf may show a decreasing trend or a single peak characterising unimodality. Some flexibility is observed both in the mode and in the tails. However, it tends to be right-skewed or nearly symmetric.

Fig. 1

Examples of plots of the cdf of the MOTLLN distribution

Fig. 2

Examples of plots of the pdf of the MOTLLN distribution

Remark 3.1

For $\beta = 1$, the cdf of the MOTLLN distribution in Eq. (3.1) reduces to the cdf of the Topp-Leone log-normal (TLLN) distribution, which was developed by Chesneau et al. (2022).

Remark 3.2

The cdf of the MOTLLN distribution reduces to that of the LN distribution if x is fixed, $\beta = 1$ and

$$\begin{aligned} \alpha = \frac{ \log \left[ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] }{ \log \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} }. \end{aligned}$$

The proof is straightforward and omitted for the sake of brevity.

4 Quantile Function and Measures

In this part, we develop an explicit equation for the qf of the MOTLLN distribution, as well as several of its associated measures.

Theorem 4.1

Let $p \in (0,1)$. The $p^{th}$ quantile of the MOTLLN distribution is given by

$$\begin{aligned} Q_{p} =F^{-1}(p) = \exp \left[ {\mu + \sigma \ \Phi ^{-1} \left\{ 1 - \sqrt{ 1 - \left( \frac{p \beta }{1-p(1-\beta )} \right) ^{1/\alpha } } \right\} } \right] \end{aligned},$$

(4.1)

where F(x) is cdf specified in Eq. (3.1) and $\Phi ^{-1}(x)$ is the qf associated with the standard normal distribution.

Proof

By the definition, the $p^{th}$ quantile $Q_{p}$ is the solution of the equation $F(Q_p)=p$, so

$$\begin{aligned} \frac{ \left\{ 1 - \left[ 1 - \Phi \left( \frac{\log (Q_{p})-\mu }{\sigma } \right) \right] ^{2} \right\} ^\alpha }{ 1 - (1-\beta ) \left[ 1 - \left\{ 1 - \left[ 1 - \Phi \left( \frac{\log (Q_{p})-\mu }{\sigma } \right) \right] ^{2} \right\} ^\alpha \right] } = p. \end{aligned}$$

(4.2)

Let us solve it with a step-by-step approach. On simplification, Eq. (4.2) reduces to

$$\begin{aligned}{} & {} \left\{ 1 - \left[ 1 - \Phi \left( \frac{\log (Q_{p})-\mu }{\sigma } \right) \right] ^{2} \right\} ^{\alpha } \left( 1 - p(1-\beta ) \right) = p \beta \\{} & {} \Rightarrow \Phi \left( \frac{\log (Q_{p})-\mu }{\sigma } \right) = 1 - \left[ 1 - \left( \frac{p \beta }{1-p(1-\beta )} \right) ^{1/\alpha } \right] ^{1/2} \\{} & {} \Rightarrow \frac{\log (Q_{p})-\mu }{\sigma } = \Phi ^{-1} \left\{ 1 - \left[ 1 - \left( \frac{p \beta }{1-p(1-\beta )} \right) ^{1/\alpha } \right] ^{1/2} \right\} \\{} & {} \Rightarrow Q_{p} = \exp \left[ {\mu + \sigma \ \Phi ^{-1} \left\{ 1 - \sqrt{ 1 - \left( \frac{p \beta }{1-p(1-\beta )} \right) ^{1/\alpha } } \right\} } \right] . \end{aligned}$$

The desired expression is obtained, ending the proof. $\square$

The comprehensive analytical expression of the qf is an advantage of the MOTLLN distribution.

Remark 4.1

An alternative expression of $Q_{p}$ in Eq. (4.1) is

$$\begin{aligned} {} Q_{p} = \exp { \left[ \mu + \sigma \sqrt{2} \ \text {erf}^{-1}{ \left\{ 1- 2 \sqrt{ 1 - \left( \frac{p \beta }{1-p(1-\beta )} \right) ^{1/\alpha } } \right\} } \right] }, \end{aligned}$$

(4.3)

where $\text {erf}^{-1}(x)$ is the standard inverse error function.

The median of the MOTLLN distribution is calculated as

$$\begin{aligned} {} \text {M} = Q_{0.5} = \exp { \left[ \mu + \sigma \sqrt{2} \ \text {erf}^{-1}{ \left\{ 1- 2 \sqrt{ 1 - \left( \frac{\beta }{1+\beta } \right) ^{1/\alpha } } \right\} } \right] }. \end{aligned}$$

(4.4)

Similarly, we derive the first and third quartiles of the distribution by taking $p = 1/4$ and $p = 3/4$ into $Q_p$, respectively.

5 Hazard Rate Function

The hrf of the MOTLLN distribution is given by the following ratio:

$$\begin{aligned} h(x) = \frac{f(x)}{S(x)}, \end{aligned}$$

where $S(x) = 1 - F(x)$ is the survival function (sf) of the MOTLLN distribution. Since

$$\begin{aligned} S(x) = \frac{\beta \left[ 1 - \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha } \right] }{\beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha }}, \end{aligned}$$

the desired hrf gets the form

$$\begin{aligned} h(x) =&\frac{2 \alpha \phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 1 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] }{\sigma x \left[ 1 - \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^\alpha \right] } \times \\&\frac{\left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^ {\alpha -1}}{\beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^{\alpha }}. \end{aligned}$$

We examine this from a graphical point of view with some sample plots in Fig. 3.

Fig. 3

Examples of plots of the hrf of the MOTLLN distribution

We can also see from this figure that the MOTLLN distribution has increasing, decreasing, bathtub and upside-down bathtub shapes for its hrf. It is therefore complete in terms of hrf modelling.

6 Parametric Estimation

In this part, we examine the MOTLLN distribution from a statistical perspective, focusing on the estimation of its parameters. We explore two famous methods known for their efficiency: ML and Bayesian methods.

6.1 Maximum Likelihood Estimation

First, we consider the ML estimation for the parameters $\alpha$, $\beta$, $\mu$, and $\sigma$. Let $n$ be a positive integer, $X_1, X_2,\ldots ,X_n$ denote a random sample drawn from the MOTLLN distribution with these unknown parameters, and $x_1, x_2,\ldots ,x_n$ represent the corresponding observed values, constituting the data. The log-likelihood function is then be formulated as follows:

$$\begin{aligned} \mathcal {L}_n =&\ n \log (2) + n \log (\alpha ) + n \log (\beta ) - n \log (\sigma ) \nonumber \\ {}&- \sum _{i=1}^{n} \log (x_i) + \sum _{i=1}^{n} \log \left[ \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] + \sum _{i=1}^{n} \log \left[ 1 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] \nonumber \\ {}&+ (\alpha -1) \sum _{i=1}^{n} \log \left[ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] + (\alpha -1) \sum _{i=1}^{n} \log \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] \nonumber \\ {}&- 2 \sum _{i=1}^{n} \log \left( \beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] \right\} \right) . \end{aligned}$$

(6.1)

Ideally, we obtain the ML estimates (MLEs) ($\widehat{\alpha }, \widehat{\beta }, \widehat{\mu }, \widehat{\sigma }$) of ($\alpha , \beta , \mu , \sigma$) by maximizing this function. From a mathematical point of view, a differentiation can be made. For this purpose, the score function associated with the log-likelihood function is

$$\begin{aligned} \textbf{U} = \left( \frac{\partial \mathcal {L}_n}{\partial \alpha }, \frac{\partial \mathcal {L}_n}{\partial \beta }, \frac{\partial \mathcal {L}_n}{\partial \mu }, \frac{\partial \mathcal {L}_n}{\partial \sigma } \right) ^T. \end{aligned}$$

We now investigate the nonlinear equations $\partial \mathcal {L}_{n}/\partial \alpha = 0$, $\partial \mathcal {L}_{n}/\partial \beta = 0$, $\partial \mathcal {L}_{n}/\partial \mu = 0$, and $\partial \mathcal {L}_{n}/\partial \sigma = 0$, which are equivalent to

$$\begin{aligned}{} & {} \frac{n}{\alpha } + \sum _{i=1}^{n} \log \left[ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] + \sum _{i=1}^{n} \log \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] = 0, \end{aligned}$$

(6.2)

$$\begin{aligned}{} & {} \frac{n}{\beta } + 2 \ \sum _{i=1}^{n} \ \frac{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] }{ \beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] \right\} } = 0, \end{aligned}$$

(6.3)

$$\begin{aligned}{} & {} \sum _{i=1}^{n} \frac{\log (x_i) - \mu }{\sigma ^2} + \frac{1}{\sigma } \sum _{i=1}^{n} \left[ \frac{ \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) }{ 1 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) } \right] \nonumber \\{} & {} - \frac{\alpha -1}{\sigma } \sum _{i=1}^{n} \left[ \frac{ \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) }{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) } \right] + \frac{\alpha -1}{\sigma } \sum _{i=1}^{n} \left[ \frac{ \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) }{ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) } \right] \nonumber \\{} & {} + \frac{4(1-\beta )}{\sigma } \sum _{i=1}^{n} \left[ \frac{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] }{ \beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] \right\} } \right] = 0, \end{aligned}$$

(6.4)

and

$$\begin{aligned}&\frac{-n}{\sigma } + \sum _{i=1}^{n} \frac{(\log (x_i)-\mu )^2}{\sigma ^3} + \sum _{i=1}^{n} \left[ \frac{ \left( \frac{\log (x_i)-\mu }{\sigma ^2} \right) \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) }{1 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) } \right] \nonumber \\&- \frac{\alpha -1}{\sigma ^2} \sum _{i=1}^{n} \left[ \frac{ (\log (x_i)-\mu ) \ \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) }{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) } \right] + \frac{\alpha -1}{\sigma ^2} \sum _{i=1}^{n} \left[ \frac{ (\log (x_i)-\mu ) \ \phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) }{2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) } \right] \nonumber \\&+ \frac{4(1-\beta )}{\sigma ^{2}} \sum _{i=1}^{n} \left[ \frac{ (\log (x_i)-\mu ) \ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] }{ \beta +(1-\beta ) \left\{ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] \right\} } \right] = 0, \end{aligned}$$

(6.5)

respectively. Solving the nonlinear equations given in Eqs. (6.2), (6.3), (6.4) and (6.5) synergistically, we obtain the MLEs $\widehat{\alpha }$, $\widehat{\beta }$, $\widehat{\mu }$ and $\widehat{\sigma }$. Let us notice that, for known $\mu$ and $\sigma$, the MLE of $\alpha$ is simply calculated as

$$\begin{aligned} \widehat{\alpha } = \frac{-n}{ \sum _{i=1}^{n} \log \left[ \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] + \sum _{i=1}^{n} \log \left[ 2 - \Phi \left( \frac{\log (x_i)-\mu }{\sigma } \right) \right] }. \end{aligned}$$

Asymptotic confidence intervals (CIs) for the parameters can be determined. By computing the second partial derivatives of $\mathcal {L}_n$, we can obtain the Hessian matrix for the MOTLLN distribution, which is expressed as

$$\begin{aligned} H(\Theta ) = \begin{pmatrix} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \alpha ^{2}} &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \alpha \ \partial \beta } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \alpha \ \partial \mu } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \alpha \ \partial \sigma } \\ \\ \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \beta \ \partial \alpha } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \beta ^{2}} &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \beta \ \partial \mu } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \beta \ \partial \sigma } \\ \\ \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \mu \ \partial \alpha } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \mu \ \partial \beta } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \mu ^{2}} &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \mu \ \partial \sigma } \\ \\ \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \sigma \ \partial \alpha } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \sigma \ \partial \beta } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \sigma \ \partial \mu } &{} \dfrac{\partial ^{2} \mathcal {L}_n}{\partial \sigma ^{2}} \end{pmatrix}, \end{aligned}$$

where $\Theta = ( \alpha , \beta , \mu , \sigma )$. The observed Fisher’s information matrix is given by $J(\Theta ) = - H(\Theta )$. The inverse of this matrix yields the variance-covariance matrix of the MLEs. We define it via general matrix coefficients as

$$\begin{aligned} \Sigma = J^{-1}(\Theta ) = \begin{pmatrix} \Sigma _{11} &{} \Sigma _{12} &{} \Sigma _{13} &{} \Sigma _{14} \\ \Sigma _{21} &{} \Sigma _{22} &{} \Sigma _{23} &{} \Sigma _{24} \\ \Sigma _{31} &{} \Sigma _{32} &{} \Sigma _{33} &{} \Sigma _{34} \\ \Sigma _{41} &{} \Sigma _{42} &{} \Sigma _{43} &{} \Sigma _{44} \end{pmatrix} \end{aligned}$$

and $\Sigma _{ij} = \Sigma _{ji}$ for $i \ne j = 1,2,3,4$. Furthermore, it is widely acknowledged that the MLEs exhibit asymptotic normality. That is, $\sqrt{n} (\Theta - \widehat{\Theta })$ $\sim$ $N_{4}(0,\Sigma )$, where n is the sample size, $\sim$ means distribution approximation, and $\widehat{\Theta }=( \widehat{\alpha }, \widehat{\beta }, \widehat{\mu }, \widehat{\sigma } )$ is the ML vector estimate of $\Theta$.

For a fixed $\delta \in (0,1)$, we determine $100 \times (1-\delta ) \%$ asymptotic CIs of the parameters by

$$\begin{aligned}&\alpha \in \left[\widehat{\alpha } \mp u_{\delta /2} \sqrt{\Sigma _{11}} \right], \ \beta \in \left[\widehat{\beta } \mp u_{\delta /2} \sqrt{\Sigma _{22}} \right],\\&\mu \in \left[\widehat{\mu } \mp u_{\delta /2} \sqrt{\Sigma _{33}} \right]\ \text {and} \ \sigma \in \left[\widehat{\sigma } \mp u_{\delta /2} \sqrt{\Sigma _{44}} \right], \end{aligned}$$

where $u_{\delta }$ is the upper $\delta ^{\text {th}}$ percentile of the standard normal distribution.

6.2 Bayesian Estimation

We now perform a Bayesian analysis on the parameters involved in the MOTLLN model. To do this, we need to adopt a prior distribution for each parameter. For this purpose, we use two types of priors, the half-Cauchy (HC) prior and the normal (N) prior. Specifically, the pdf of the HC distribution with scale parameter a is defined as

$$\begin{aligned} f_{HC}(x_{*}) = \frac{2a}{\pi (x_{*}^{2} + a^{2})}, \end{aligned}$$

(6.6)

where $x_{*}>0$ and $a>0$. As is well known, the HC distribution lacks a defined mean and variance, while its mode is 0. Although its pdf is almost flat, with $a= 25$, it provides sufficient information for the numerical approximation algorithm to continue exploring the target posterior pdf. The HC distribution thus configured is recommended as a non-informative prior. We also refer to the study by Gelman and Hill (2006), where the HC distribution is shown to be a superior alternative to the uniform distribution and other informative priors. With this in mind, we specify the prior distributions of the parameters as follows:

$$\begin{aligned}&\mu \mathrm{\ is \ assumed \ to \ follow \ the \ distribution:} \ N(0, 1000), \nonumber \\ \textrm{and} \quad&\alpha , \beta , \sigma \mathrm{\ are \ assumed \ to \ follow \ the \ distribution:} \ HC(25). \end{aligned}$$

(6.7)

Now, using Eqs (6.7), the joint posterior pdf is obtained as

$$\begin{aligned} d(\mu , \alpha , \beta , \sigma ) \propto {\ell }_n d(\mu ) d(\alpha ) d(\beta ) d(\sigma ), \end{aligned}$$

(6.8)

where ${\ell }_n=\exp (\mathcal {L}_n)$ is the likelihood function of the MOTLLN distribution and $\propto$ means "directly proportional to". From Eq. (6.8), it is clear that the Bayesian estimates have no analytical expression. Therefore, we employ the Metropolis-Hastings algorithm, a notable simulation method within the framework of Markov Chain Monte Carlo (MCMC) techniques. The detailed description of the MCMC method can be found in Upadhyay et al. (2001).

7 Bootstrap CIs

In this part, we apply the parametric bootstrap method to approximate the distribution of the MLEs for the parameters of the MOTLLN model. We then use the bootstrap distribution to estimate the CIs for each parameter of the fitted MOTLLN distribution. Let $\widehat{\nu }$ be an ML estimate of $\nu \in \{ \alpha , \beta , \mu , \sigma \}$ using data, say $x_{1}, x_{2},\ldots , x_{n}$. In short, the bootstrap is a method of estimating the distribution of the underlying distribution of $\widehat{\nu }$ by taking a random sample for $\nu$ based on B random samples $\nu _{1}^{*}, \nu _{2}^{*},\ldots , \nu _{B}^{*}$, which are drawn with replacement from the original data. Further details can be found in Wasserman (2006). The resulting bootstrap sample $\nu _{1}^{*}, \nu _{2}^{*},\ldots , \nu _{B}^{*}$ can then be used to construct bootstrap CIs for $\nu$.

Thus, we obtain $100 \times (1-\delta ) \%$ bootstrap CIs of the parameters using the following formulas:

$$\begin{aligned}&\alpha \in \left[\widehat{\alpha } \mp v_{\delta /2} \ \widehat{se}_{\alpha ,boot} \right], \ \beta \in \left[\widehat{\beta } \mp v_{\delta /2} \ \widehat{se}_{\beta ,boot} \right], \nonumber \\ {}&\mu \in \left[\widehat{\mu } \mp v_{\delta /2} \ \widehat{se}_{\mu ,boot} \right]\ \text {and} \ \sigma \in \left[\widehat{\sigma } \mp v_{\delta /2} \ \widehat{se}_{\sigma ,boot} \right], \end{aligned}$$

where $v_{\delta }$ denotes the $\delta ^{\text {th}}$ percentile of the bootstrap sample and, for $\nu \in \{ \alpha , \beta , \mu , \sigma \}$,

$$\begin{aligned} \widehat{se}_{\nu ,boot} = \sqrt{\frac{1}{B} \sum \limits _{b=1}^{B}\left( \nu _{b}^{*} - \frac{1}{B} \sum \limits _{b=1}^{B} \nu _{b}^{*} \right) ^{2}}. \end{aligned}$$

8 MOTLLN Regression Model

This part develops a regression model based on the MOTLLN distribution. To do this, let X be a random variable following the MOTLLN distribution. We recall that the corresponding pdf is specified in Eq. (3.2). Then the random variable $Y = \log (X)$ has the following pdf:

$$\begin{aligned} f_{Y}(y) = \frac{2\alpha \beta \ \phi \left( \frac{y-\mu }{\sigma } \right) \left[ 1 - \Phi \left( \frac{y-\mu }{\sigma } \right) \right] \left\{ \Phi \left( \frac{y-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{y-\mu }{\sigma } \right) \right] \right\} ^{\alpha -1}}{\sigma \left( \beta +(1-\beta ) \left\{ \Phi \left( \frac{y-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{y-\mu }{\sigma } \right) \right] \right\} ^{\alpha } \right) ^{2} }, \end{aligned}$$

(8.1)

where $y \in \mathbb {R}$, $\alpha$, $\beta >0$ are the shape parameters, $\mu \in \mathbb {R}$ is the location parameter, and $\sigma >0$ is the scale parameter. We refer to the distribution defined by the pdf in Eq. (8.1) as the log-MOTLLN distribution. In this setting, the standardized random variable $Z = (Y - \mu )/\sigma$ has the pdf indicated as

$$\begin{aligned} f_{Z}(z) = \frac{2\alpha \beta \ \phi (z) \left[ 1 - \Phi (z) \right] \left\{ \Phi (z) \left[ 2 - \Phi (z) \right] \right\} ^{\alpha -1}}{\left( \beta +(1-\beta ) \left\{ \Phi (z) \left[ 2 - \Phi (z) \right] \right\} ^{\alpha } \right) ^{2} }, \end{aligned}$$

(8.2)

where $z\in \mathbb {R}$. Now, from n independent observations, for any $i=1,\ldots ,n$, the linear location-scale regression model linking the $i^{th}$ value of the response variable Y, say $y_{i}$, and the explanatory variable vector $\text {v}_{i}^{T} = (v_{i1}, v_{i2},\ldots , v_{ip})$ is given by

$$\begin{aligned} y_{i} = \mu _{i} + \sigma z_{i}, \end{aligned}$$

(8.3)

where $z_{i}$ is the random error component that has the pdf in Eq. (8.2), $\mu _{i} = \text {v}_{i}^{T} \tau$ is the location parameter of $y_{i}$, where $\tau = (\tau _{1}, \tau _{2},\ldots ,\tau _{p})^{T}$, and $\alpha , \beta$ and $\sigma$ are unknown parameters. Thus, the location parameter vector $\mu = (\mu _{1}, \mu _{2},\ldots ,\mu _{n})^{T}$ is represented by a linear model $\mu = V \tau$, where $V = (V_{1}, V_{2},\ldots , V_{n})^{T}$ is a known model matrix.

In this setting, we propose the MOTLLN regression model from Eq. (8.3). It is governed by the following formula:

$$\begin{aligned} x_{i} = \exp (y_{i}) = \exp (\mu _{i} + \sigma z_{i}), \qquad i = 1,2,\ldots ,n \end{aligned}.$$

(8.4)

Let us consider a sample $(x_{1},\text {v}_{1}), (x_{2},\text {v}_{2}),\ldots , (x_{n},\text {v}_{n})$ of n independent observations and the vector of parameters $\varvec{\psi } = (\tau ^{T}, \alpha , \beta , \sigma )^{T}$ from model Eq. (8.4). Then the total log-likelihood function for right censored data has the form

$$\begin{aligned} l(\varvec{\psi }) =&\log \left\{ \prod _{i=1}^{n} \left[ f(x_i) \right] ^{\delta _i} \left[ S(x_i) \right] ^{1 - \delta _i} \right\} \nonumber \\ =&\sum _{i=1}^{n} \delta _i \log \left[ f(x_i) \right] + \sum _{i=1}^{n} (1 - \delta _i) \left[ \log[S(x_i)] \right] , \end{aligned}$$

(8.5)

where, for $i=1,\ldots ,n$, $\delta _i = 1$ if survival (uncensored), and $\delta _i = 0$ otherwise (censored), and f(x) and S(x) are the pdf and sf of the MOTLLN distribution, respectively.

9 Bayesian Regression Model

The Bayesian analysis technique is known to be efficient for analyzing survival patterns in various real-world scenarios. In this study, we investigate its usefulness for fitting a regression model based on the MOTLLN distribution while incorporating information on prior parameters. We then use a simulation approach to facilitate Bayesian analysis of the model.

To perform a Bayesian analysis, it is essential to specify prior probability distributions for the model parameters. In this context, similarly to Subsection 6.2, we use two different priors: HC and N priors. We recall that the pdf of the HC distribution with scale parameter a is described in Eq. (6.6). Now, we can write the likelihood function for right censored data as

$$\begin{aligned} L = \prod _{i=1}^{n} \left[ f(x_i) \right] ^{\delta _i} \left[ S(x_i) \right] ^{1 - \delta _i}, \end{aligned}$$

(9.1)

where, for $i=1,\ldots ,n$, $\delta _i = 1$, if survival (uncensored) and $\delta _i = 0$ otherwise (censored), and f(x) and S(x) are the pdf and sf of the MOTLLN distribution, respectively. We use the following link function:

$$\begin{aligned} \mu = V \tau \end{aligned},$$

(9.2)

which operates a linear combination of explanatory variables. Here,

$$\begin{aligned}&\tau _j \mathrm{\ is \ assumed \ to \ follow \ the \ distribution:} \ N(0, 1000); \qquad j = 1,2,\ldots ,J \nonumber \\ \textrm{and} \quad&\alpha , \beta , \sigma \mathrm{\ are \ assumed \ to \ follow \ the \ distribution:} \ HC(25). \end{aligned}$$

(9.3)

Now, using Equations (9.1), (9.2) and (9.3), the joint posterior pdf is obtained as

$$\begin{aligned} d(\tau , \alpha , \beta , \sigma ) \propto L(V, \tau , \alpha , \beta , \sigma ) d(\tau ) d(\alpha ) d(\beta ) d(\sigma ). \end{aligned}$$

(9.4)

From Equation (9.4), it is evident that obtaining analytical solutions for the Bayesian estimates is not feasible. Hence, we employ the simulation approach, specifically the Metropolis Hastings algorithm of the MCMC method, as discussed in Subsection 6.2.

10 Performance of the Estimates Using Simulation Study

This part presents simulation experiments aimed at evaluating the performance of the MLEs for the parameters of the MOTLLN distribution across various finite sample sizes. We have simulated datasets of sizes $n = 50, 250, 500,$ and 1000 from the MOTLLN distribution for the parameter values $\alpha = 0.5, \beta = 5.5, \mu = 0.9, \sigma = 0.6$ and iterated each sample 500 times. The average absolute biases, mean squared errors (MSEs), coverage probabilities (CPs) and average lengths (ALs) are then calculated over all replications within the respective sample sizes. The analysis computes their values using the following formulas:

• Average absolute bias of the simulated estimates = $\dfrac{1}{500} \sum \limits _{i=1}^{500} | \widehat{\nu }_{i} - \nu |$,

• Average MSE of the simulated estimates = $\dfrac{1}{500} \sum \limits _{i=1}^{500} ( \widehat{\nu }_{i} - \nu )^2$,

where $\widehat{\nu } \in \{ \widehat{\alpha }, \widehat{\beta }, \widehat{\mu }, \widehat{\sigma } \}$ is the estimate of the corresponding parameter $\nu \in \{ \alpha , \beta , \mu , \sigma \}$. Table 1 contains the results. We draw the conclusion that as sample size increases, the MSE and AL of each estimate decrease. Also, the average absolute bias often appears to decrease as sample size increases. Also, the CPs of the confidence intervals (CIs) for each parameter are relatively close to the nominal 95 percent level. This demonstrates how consistent the subjacent estimators are.

Table 1 The MLE simulation results

11 Applications and Empirical Study

In this part, we illustrate the empirical relevance of the MOTLLN distribution. In order to highlight its data modelling ability over several competing distributions, we study four real datasets. The first is a dataset related to astronomy, while the second and third are datasets based on the strength of glass fibers of two different lengths. In the fourth, we use a real censored dataset based on the prognosis of women with breast cancer for the regression study. To analyze these datasets numerically, we use the R software.

11.1 Real Illustration on Univariate Real Datasets

The astronomy dataset (Dataset 1) consists of the near-infrared K-band magnitudes of the 360 globular clusters in Messier 31 (M31), our neighbouring Andromeda galaxy, taken from Nantais et al. (2006). It is given in Appendix C.3 of Feigelson and Babu (2012), as well as in the R  package astrodatR. A first statistical analysis of this dataset, focusing on a specific distribution, was carried out by Chesneau et al. (2022). The K-band represents a crucial atmospheric transmission window in infrared astronomy, indicating a region within the infrared spectrum where terrestrial heat radiation is minimally absorbed by atmospheric gases. Globular clusters, characterized by densely packed groups of old stars ranging from $10^4$ to $10^6$, have a distinctly dense, roughly spherical structure that sets them apart from the wider stellar population. Astronomers use these clusters to deduce the age of the Universe or to pinpoint the Galactic Centre through meticulous study.

In addition, the second and third datasets (Datasets 2 and 3) represent the experimental data on the strength of glass fibers of two lengths, 1.5 cm and 15 cm, from the National Physical Laboratory in England. Both of them are available in Smith and Naylor (1987).

By using standard measures, the descriptive statistics of these three datasets are given in Table 2.

Table 2 Descriptive statistics of the three datasets

We also investigate the corresponding empirical hrf using the idea of a total time on test (TTT) plot. This plot is a graph formed by the points $(i/n, w_{i,n})$, $i=1,2,\ldots , n$, where

$$\begin{aligned} w_{i,n}= \frac{ (n-i) x_{i:n}+ \sum \limits _{r=1}^{i} x_{r:n}}{\sum \limits _{r=1}^{n} x_{r:n}}, \end{aligned}$$

where $x_{r:n}$, $r = 1, 2,\ldots , n$ are the data ordered in an increasing order. It is used as a visual indicator to distinguish between several types of ageing as displayed by the hrf shapes. For more about the construction and interpretation of the TTT plot, see Aarset (1987).

Fig. 4

The TTT plots of the three data sets

Thus, based on the TTT plot approach, Fig. 4 indicates that the datasets have an increasing shape for their empirical hrf. Therefore, the MOTLLN distribution provides a credible model for analyzing these data.

The following distributions are taken into consideration for comparison purposes and highlight the tangible benefits of the MOTLLN distribution.

• The two-parameter log-normal (LN) distribution with the pdf indicated as

  $$\begin{aligned} f(x) = \frac{1}{\sqrt{2\pi } \ \sigma x} \exp \left[ -\frac{(\log (x) - \mu )^2}{2 \sigma ^{2}} \right] , \end{aligned}$$

  where $x>0$, $\mu \in {\mathbb {R}}$ and $\sigma >0$.

• The TLLN distribution already mentioned with the pdf given by

  $$\begin{aligned} f(x) = \frac{2\alpha }{\sigma x} ~ \phi \left( \frac{\log (x)-\mu }{\sigma } \right)&\left[ 1 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \times \\ {}&\left\{ \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \left[ 2 - \Phi \left( \frac{\log (x)-\mu }{\sigma } \right) \right] \right\} ^ {\alpha -1}, \end{aligned}$$

  where $x>0$, $\mu \in \mathbb {R}$ and $\sigma$, $\alpha >0$. See Chesneau et al. (2022).

• The exponentiated log-normal distribution (ELN) with the pdf specified by

  $$\begin{aligned} f(x) = \frac{\alpha }{x \sigma } \phi \left( \frac{\log (x) - \mu }{\sigma } \right) \left[ \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) \right] ^{\alpha - 1}, \end{aligned}$$

  where $x>0$, $\mu \in {\mathbb {R}}$ and $\alpha$, $\sigma >0$.

• The odd log-logistic log-normal (OLL-LN) distribution with the pdf indicated by

  $$\begin{aligned} f(x) = \frac{\alpha \phi \left( \frac{\log (x) - \mu }{\sigma } \right) \left\{ \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) \left[ 1 - \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) \right] \right\} ^{\alpha - 1}}{\sigma x \left\{ \left[ \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) \right] ^{\alpha } + \left[ 1 - \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) \right] ^{\alpha } \right\} ^{2}}, \end{aligned}$$

  where $x>0$, $\mu \in {\mathbb {R}}$, and $\alpha$, $\sigma >0$. See Ozel Kadilar et al. (2018).

• The beta log-normal distribution (BLN) with the pdf given by

  $$\begin{aligned} f(x) = \frac{\exp \left\{ -\frac{1}{2} \left( \frac{\log (x) - \mu }{\sigma } \right) ^{2} \right\} }{x \sigma \sqrt{2 \pi } \ B(\alpha , \beta )} \ \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) ^{\alpha -1} \ \left\{ 1 - \Phi \left( \frac{\log (x) - \mu }{\sigma } \right) \right\} ^{\beta -1}, \end{aligned}$$

  where $x>0$, $\mu \in {\mathbb {R}}$, $\alpha$, $\beta , \sigma >0$ and $B(\alpha , \beta )$ is the standard beta function. See Castellares et al. (2011).

• The exponentiated exponential (EE) distribution with the pdf indicated as

  $$\begin{aligned} f(x) = \alpha \sigma \left( 1 - e^{-\sigma x} \right) ^{\alpha - 1} e^{-\sigma x}, \end{aligned}$$

  where x, $\alpha$, $\sigma >0$.

• The standard gamma distribution with the pdf specified by

  $$\begin{aligned} f(x) = \frac{1}{\sigma ^{\alpha } \Gamma (\alpha )} x^{\alpha -1} \exp \left( -\frac{x}{\sigma }\right) , \end{aligned}$$

  where x, $\alpha$, $\sigma >0$ and $\Gamma (\alpha )$ is the standard gamma function.

We use a variety of statistical techniques to assess the goodness-of-fit of distributions to real datasets, including the log-likelihood (LL), Kolmogorov-Smirnov (KS), Cramér-von Mises (W$^{*}$), Anderson-Darling (A$^{*}$) statistics, alongside the Akaike information criterion (AIC) and Bayesian information criterion (BIC) values.

Furthermore, Tables 3, 4, and 5 provide the MLEs and goodness-of-fit statistics for the corresponding three datasets, respectively. Notably, the values of KS, W$^{*}$, A$^{*}$, AIC, and BIC associated with the MOTLLN distribution are consistently smaller compared to other distributions. Addition, we present essential graphical representations, including empirical pdf plots, empirical cdf plots, quantile-quantile (Q-Q) and probability-probability (P-P) plots for the three datasets in Figs. 5, 6, and 7, respectively. These plots show superimposed curves of the fitted and empirical functions. Thus, based on these comprehensive analyses, we assert that the MOTLLN distribution emerges as the most appropriate choice for all three given datasets when compared to alternative distributions.

Table 3 Dataset 1: MLEs and goodness-of-fit statistics results

Table 4 Dataset 2: MLEs and goodness-of-fit statistics results

Table 5 Dataset 3: MLEs and goodness-of-fit statistics results

Fig. 5

Various empirical plots of Dataset 1

Fig. 6

Various empirical plots of Dataset 2

Fig. 7

Various empirical plots of Dataset 3

To consolidate the previous analyses, we utilize the likelihood ratio (LR) test to compare the adequacy of the MOTLLN distribution with that of the TLLN, LN, and ELN distributions. Thus, we test the null hypotheses $H_{0}$ : TLLN distribution, $H_{0}$ : LN distribution and $H_{0}$ : ELN distribution against $H_{1}$ : MOTLLN distribution.

Tables 6, 7, and 8 show the LR statistics and corresponding p-values for all three datasets, respectively. Given the values of the test statistics and their associated p-values, we reject the null hypotheses in all cases. Therefore, we conclude that the MOTLLN distribution provides a significantly better representation than the compared distributions.

Table 6 The LR test results for Dataset 1 ($\sim$ means “follows the distribution”)

Table 7 The LR test results for Dataset 2

Table 8 The LR test results for Dataset 3

Now, the Hessian matrix corresponding to Datasets 1, 2, and 3 are, respectively, obtained as

$$\begin{aligned} H_{1}(\Theta )= & {} \begin{pmatrix} 240.1912 &{} 22.0588 &{} 3419.8414 &{} 441.0525 \\ 22.0588 &{} 2.2954 &{} 363.4472 &{} 125.6094 \\ 3419.8414 &{} 363.4472 &{} 63104.8204 &{} 36568.9384 \\ 441.0525 &{} 125.6094 &{} 36568.9384 &{} 69063.4630 \\ \end{pmatrix},\\ H_{2}(\Theta )= & {} \begin{pmatrix} 3241.6238 &{} 22.8931 &{} 2627.8527 &{} -2301.7318 \\ 22.8931 &{} 0.1841 &{} 19.8020 &{} -12.2441 \\ 2627.8527 &{} 19.8020 &{} 158784.2252 &{} -92225.4781 \\ -2301.7318 &{} -12.2441 &{} -92225.4781 &{} 325745.0176 \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} H_{3}(\Theta ) = \begin{pmatrix} 3211.0658 &{} 22.4359 &{} 1772.6019 &{} -1893.3673 \\ 22.4359 &{} 0.1917 &{} 13.2660 &{} -11.1864 \\ 1772.6019 &{} 13.2660 &{} 163236.1780 &{} -303.3624 \\ -1893.3673 &{} -11.1864 &{} -303.3624 &{} 263621.1053 \end{pmatrix}. \end{aligned}$$

The 95% asymptotic CIs of the unknown parameters of the MOTLLN distribution for the three datasets are given in Table 9.

Table 9 The 95% asymptotic CIs of the parameters of the MOTLLN distribution for the three datasets

We then focus on the application of the Bayesian procedure to estimate the parameters of the MOTLLN distribution. The analysis was carried out using the Metropolis-Hastings algorithm of the MCMC method with 1000 iterations in the context of Bayesian estimation. Table 10 shows the MLEs and Bayes estimates of the parameters of the MOTLLN model for each of the three datasets. The Bayesian estimation calculations were also performed in the R software.

Table 10 MLEs and Bayes estimates of the parameters of the MOTLLN distribution for the three datasets

We now calculate the 95% bootstrap CIs for the parameters $\alpha$, $\beta$, $\mu$, and $\sigma$ using the obtained MLEs. Based on the MOTLLN distribution, we simulate 1001 samples of the corresponding sizes found in Datasets 1, 2, and 3. The true values of the parameters are assumed to be the MLEs of the parameters. The MLEs $\widehat{\alpha }_{b}^{*}$, $\widehat{\beta }_{b}^{*}$, $\widehat{\mu }_{b}^{*}$, and $\widehat{\sigma }_{b}^{*}$ were estimated for each sample that was obtained, with $b \in \{ 1,2,\ldots ,1001 \}$. Table 11 displays the median and 95% bootstrap CIs for the parameters $\alpha$, $\beta$, $\mu$, and $\sigma$ for the three datasets.

Table 11 The median and 95% bootstrap CIs for the parameters of the MOTLLN distribution for the three datasets

11.2 Real Illustration on Censored Dataset Using Regression

In this part, we use an actual censored dataset derived from the prognosis of breast cancer patients in women. As described by Collett (2015) and documented in Leathem and Brooks (1987), it contains the number of months that women who underwent either a simple or radical mastectomy to treat a grade II, III or IV tumour between January 1969 and December 1971 survived.

The MOTLLN regression model summary resulting from the censored dataset is shown in Table 12. It includes the estimates of all parameters, the negative log-likelihood, and the value of the AIC.

Table 12 Summaries for the MOTLLN regression model for the breast cancer dataset

When using the Metropolis-Hastings algorithm of the MCMC method to solve the Bayesian regression problem, Table 13 provides a summary of 1000 times the iterated simulated results due to the censored dataset. This summary includes the posterior mean, standard deviation (SD), Monte Carlo standard error (MCSE), 95% CIs, and posterior median.

Table 13 Summaries for the MOTLLN Bayesian regression model for the breast cancer dataset

12 Concluding Remarks

We propose a new distribution that is a generalization of the LN distribution, which we call the Marshall-Olkin Topp-Leone log-normal (MOTLLN) distribution. In the first part, we study its mathematical and statistical aspects. In particular, the associated quantile function and the hazard rate function are given as explicit formulations. In terms of applicability, maximum likelihood and Bayesian estimation are used to estimate the model parameters. The parametric bootstrap technique is applied to obtain confidence intervals for the model parameters. More importantly, based on the new distribution, we offer a parametric regression model and a Bayesian regression approach. In this study, four applications of the new model to real datasets using goodness-of-fit tests demonstrate its utility. In particular, it consistently outperforms previous models in the literature on valuable goodness-of-fit criteria. We expect that the proposed model will be used to analyze positive real datasets in a variety of fields, including physics, astronomy, engineering, survival analysis, hydrology, economics, and others.