Double Inverse-Gaussian Distributions and Associated Inference

Abstract

In order to have more flexibility, several double distributions have been studied in the literature. In this paper, we propose a double inverse Gaussian distribution using random sign mixture transform and study its associated inferences. The maximum likelihood estimation is performed to estimate the parameters. Extensive simulation studies are carried out to examine the performance of the estimators and the corresponding confidence intervals of the parameters. A real data set example is presented to illustrate the procedure.

1 Introduction

In the last 40 years, there has been a considerable literature on the double continuous distributions on the real line, some of which explain the word double and some do not. Several of them use the word double as the distribution of the absolute value and some of them use the word reflection. Balakrishnan and Kocherlakota (1985) and Rao and Narasimham (1989) presented the double Weibull distribution and studied its order statistics and linear estimation. Bindu and Sangita (2015) studied the double Lomax distribution as the distribution of the absolute value of the ratio of two independent Laplace distributed variables. Govindarajulu (1966) studied the reflected version of the exponential distribution. The reflected version of the generalized Gamma was studied by Plucinska (1965, 1966, 1967) and the reflected version of the gamma distribution was studied by Kantam and Narasimham (1991). Kumar and Jose (2019) called the distribution of the absolute value of the Lindley variable as the double Lindley distribution, see also Ibrahim et al. (2020). Nadarajah et al. (2013) presented a double generalized Pareto distribution and Halvarsson (2020) studied double Pareto type II distribution. Armagan et al. (2013) presented a generalized double Pareto shrinkage distribution and used it as a prior for Bayesian shrinkage estimation and inferences in linear models.

Most of the above cited double continuous distributions have some limitations such as (i) non-existence of moments for some values of the parameters, see for example Nadarajah et al. (2013) and, (ii) non-existence of some MLEs of the parameters, see for example de Zea Bermudez and Kotz (2010a) and de Zea Bermudez and Kotz (2010b).

Recently, Aly (2018) presented a unified approach for developing double continuous/discrete distributions using two well known transforms (representations), namely

(i) random sign transform (RST):

$$\begin{aligned} Z_1 = (2 Y-1) X, \end{aligned}$$

where Y is a Bernoulli r.v. with parameter $\beta$ and X is a non-negative r.v. independent of Y. The probability density function (p.d.f.) of $Z_1$ is given by

$$\begin{aligned} f_{Z_1}(z;\,\beta , {\varvec{\theta }} )= & {} {\left\{ \begin{array}{ll} {\overline{\beta }} \ f_{X} (|z|; \,{\varvec{\theta }}), &{} z< 0, \\ \beta \ f_{X} (z; \,{\varvec{\theta }}), &{} z\ge 0, \\ \end{array}\right. } \end{aligned}$$

(1)

where $f_{X}(\cdot ;\, {\varvec{\theta }})$ is the p.d.f. of a non-negative r.v. X with (vector) parameter ${\varvec{\theta }}$ and ${\overline{\beta }}=1-\beta .$

(ii) random sign mixture transform (RSMT):

$$\begin{aligned} Z_2 = Y X_1- (1-Y) X_2, \end{aligned}$$

where Y is a Bernoulli r.v. with parameter $\beta$ while $X_1, X_2$ are independent non-negative r.v.’s independent of Y.

The p.d.f. of $Z_2$ is given by

$$\begin{aligned} f_{Z_2}(z;\,\beta , {\varvec{\theta }}_1, {\varvec{\theta }}_2 )= & {} {\left\{ \begin{array}{ll} {\overline{\beta }} \ f_{X_2} (|z|;\, {\varvec{\theta }}_2), &{} z< 0, \\ \beta \ f_{X_1} (z;\, {\varvec{\theta }}_1), &{} z\ge 0, \\ \end{array}\right. } \end{aligned}$$

(2)

where $f_{X_j}(\cdot ; \,{\varvec{\theta }}_j), \ j=1,2,$ are the p.d.f.’s of a non-negative r.v.’s $X_1, X_2$ with (vector) parameters ${\varvec{\theta }}_1, \ j=1,2.$

If $X_1$ and $X_2$ are from the same family of distributions ${{\mathcal {F}}}$, we say that $Z_2$ has a double ${{\mathcal {F}}}$ distribution.

Note that RST is a special case of RSMT when $X_1, X_2$ are independent and identically distributed (i.i.d.), i.e. $X_1 \overset{d}{=}X_2 \overset{d}{=}X.$ Moreover, all the above cited double distributions considered only the case $\beta ={1\over 2}.$

The inverse Gaussian distribution, denoted by $IG (\mu , \lambda ),$ has a p.d.f.

$$\begin{aligned} f_X(x;\,\,\mu , \lambda )= \sqrt{{\lambda \over 2 \pi }} \ x^{-3/2} \ \exp \left[ - {\lambda (x-\mu )^2\over 2 \mu ^2 x}\right] , \qquad x>0, \quad \mu , \lambda >0, \end{aligned}$$

where $\mu$ is the mean and $\lambda$ is the shape parameter. This distribution is a very versatile life distribution and its various modifications and transformations have been extensively studied in the literature. We refer the reader to Gupta and Akman (1995, 1996, 1997, 1998), Gupta and Kundu (2011) and the references therein. The inverse Gaussian distribution has also been studied under the umbrella of Birnbaum Saunders distribution. For a survey article on Birnbaum Saunders distribution, we refer to Balakrishnan and Kundu (2019).

We follow the procedure presented by Aly (2018) and study the double inverse Gaussian distribution. Specifically, we consider four double inverse-Gaussian distributions:

• 1. Double inverse Gaussian 1, DIG-1$(\beta , \mu _1, \lambda _1, \mu _2, \lambda _2),$

• 2. Double inverse Gaussian 2, DIG-2$(\beta , \mu _1, \mu _2, \lambda ) \equiv$ DIG-1$(\beta , \mu _1, \lambda , \mu _2, \lambda ),$

• 3. Double inverse Gaussian 3, DIG-3$(\beta , \mu , \lambda _1, \lambda _2)\equiv$ DIG-1$(\beta , \mu , \lambda _1, \mu , \lambda _2),$

• 4. Double inverse Gaussian 4, DIG-4$(\beta , \mu , \lambda )\equiv$ DIG-1$(\beta , \mu , \lambda , \mu , \lambda ).$

These distributions are bimodal with one mode on each side of the origin.

The contents of this paper are organized as follows. In Sect. 2, we present the statistical properties of the double inverse Gaussian distributions, including the probability density function, cumulative distribution function (c.d.f.), modes, moment generating function (m.g.f.), raw moments, variance, skewness, kurtosis, Tsallis entropy, Shannon entropy and extropy. The maximum likelihood estimation of the parameters and their asymptotic distributions are studied in Sect. 3. Extensive simulation studies are carried out in Sect. 4 to study the performance of the estimators. In Sect. 5, a real data set application is presented to illustrate the procedure. Finally, some conclusion and comments are presented in Sect. 6.

2 Statistical Properties

In this section, we present a comprehensive summary of the basic properties of the DIG-1 $(\beta , \mu _1, \lambda _1, \mu _2, \lambda _2)$ distribution. These properties include, the p.d.f., c.d.f., modes, m.g.f., raw moments and associated measures, Tsallis entropy, Shannon entropy and extropy. Corresponding properties for the nested distributions DIG-2, DIG-3 and DIG-4 are obtained as special cases when $(\lambda _1= \lambda _2=\lambda ),$ $(\mu _1= \mu _2=\mu )$ and $(\mu _1= \mu _2=\mu , \lambda _1= \lambda _2=\lambda )$, respectively.

2.1 Probability Density Function

The p.d.f of DIG-1 distribution is given by

$$\begin{aligned} f_{Z_2}(z)= & {} {\left\{ \begin{array}{ll} {\overline{\beta }} \ f_{X_2} (|z|; \,\mu _2, \lambda _2), &{} \qquad z< 0, \\ \beta \ \ f_{X_1} (z;\, \mu _1, \lambda _1), &{} \qquad z\ge 0, \end{array}\right. } \end{aligned}$$

(3)

where

$$\begin{aligned}{} & {} f_{X_j}(x;\, \mu _j, \lambda _j) = \sqrt{{\lambda _j\over 2 \pi }} \ x^{-3/2} \ \exp \left[ - {\lambda _j (x-\mu _j)^2\over 2 \mu _j^2 x}\right] ,\nonumber \\{} & {} \quad \quad x>0, \quad \mu _j, \lambda _j>0, \quad j=1,2, \end{aligned}$$

(4)

are the p.d.f.’s of inverse Gaussian distributions.

Figure 1 shows the bimodality of the p.d.f. of DIG distributions as a function in $\beta$. Also, this figure shows that the left (right) peak gets smaller (larger) as $\beta$ increases.

Fig. 1

P.d.f. of DIG-1 distribution

The DIG-1 distribution has two modes given by

$$\begin{aligned} {\textrm{Mode}}(Z_2)= - \;{\textrm{Mode}}(X_2) \ \ {\textrm{and}} \ \ {\textrm{Mode}}(X_1), \end{aligned}$$

(5)

where

$$\begin{aligned} \textrm{Mode}(X_j)= \mu _j \left[ \sqrt{1+ \left( {3 \mu _j\over 2 \lambda _j}\right) ^2} - {3 \mu _j\over 2 \lambda _j} \right] , \quad j=1,2, \end{aligned}$$

(6)

are the modes of inverse Gaussian distributions.

2.2 Cumulative Distribution Function

The c.d.f of DIG-1 distribution is given by

$$\begin{aligned} F_{Z_2}(z)= & {} {\left\{ \begin{array}{ll} {\overline{\beta }} \ \left[ 1- F_{X_2}(|z|;\, \mu _2, \lambda _2) \right] &{}\quad z< 0, \\ {\overline{\beta }}+ \beta \ F_{X_1}(z;\, \mu _1, \lambda _1) &{}\quad z\ge 0, \end{array}\right. } \end{aligned}$$

(7)

where

$$\begin{aligned}{} & {} F_{X_j}(x;\, \mu _j, \lambda _j) = \Phi \left( \sqrt{{\lambda _j\over x}} \left( {x\over \mu _j}-1\right) \right) + e^{2 \lambda _j/\mu _j} \ \Phi \left( - \sqrt{{\lambda _j\over x}} \left( {x\over \mu _j}+1\right) \right) ,\nonumber \\{} & {} \quad \ x>0, \quad j=1,2, \end{aligned}$$

(8)

are the c.d.f.’s of inverse Gaussian distributions and

$$\begin{aligned} \Phi (a)= P(Z\le a)= \int _{-\infty }^a {1\over \sqrt{2\pi }} \ e^{- z^2/2} \ dz, \qquad -\infty<a<\infty , \end{aligned}$$

(9)

is the c.d.f. of the standard normal distribution.

Figure 2 shows the c.d.f. of the DIG-1 distribution as a function in $\beta$. Also, this figure shows that $F_{Z_2}(0)={\overline{\beta }}$ and hence $F_{Z_2}(0)$ decreases as $\beta$ increases.

Fig. 2

C.d.f. of DIG-1 distribution

2.3 Moment Generating Function

The m.g.f. of DIG-1 distribution is given by

$$\begin{aligned} M_{Z_2}(t)=\beta \ M_{X_1}(t) + {\overline{\beta }} \ M_{X_2}(- t), \qquad -\infty<t<\infty , \end{aligned}$$

(10)

where

$$\begin{aligned} M_{X_j}(t)=\exp \left[ {\lambda _j\over \mu _j} \left( 1 - \sqrt{1- {2 \mu _j^2 t\over \lambda _j}}\right) \right] , \qquad |t|<{\lambda _j \over 2 \mu _j^2}, \quad j=1,2, \end{aligned}$$

(11)

are the m.g.f.’s of inverse Gaussian distributions.

2.4 Moments and Associated Measures

The rth moment of DIG-1 distribution is given by

$$\begin{aligned} E(Z_2^r)=\beta \ E(X_1^r) + (-1)^r \ {\overline{\beta }} \ E(X_2^r), \qquad r\ge 1, \end{aligned}$$

(12)

where, using the result of Sato and Inoue (1994),

$$\begin{aligned} E(X_j^r) = \mu _j^r \ \sum _{i=0}^{r-1} {(r-1+i)! \over r! \ (r-1-i)! \ 2^i} \ \left( {\mu _j\over \lambda _j}\right) ^i, \qquad j=1,2, \end{aligned}$$

(13)

are the rth moments of inverse Gaussian distributions.

Using the last expressions of $E(Z_2^r)$, the mean, variance, skewness, and kurtosis of DIG-1 distribution are easily obtained. Note that $E(Z_2)$ does not depend on $\lambda _1$ and $\lambda _2$.

Figure 3 shows the mean, variance, skewness, and kurtosis of the DIG-1 distribution as a function in $\beta$. Also, this figure shows that the skewness can be negative/positive, i.e. the DIG-1 distribution can be skewed to the left/right.

Fig. 3

Mean, variance, skewness and kurtosis of DIG-1 distribution

2.5 Tsallis Entropy

Entropies are measures of a system’s variation, instability, or unpredictability. The Tsallis entropy, Tsallis (1988), is an important measure in statistics as index of diversity. It has many applications in areas such as physics, chemistry, biology and economics.

For a continuous r.v. V with p.d.f. $f_V(v)$, the Tsallis entropy of V is defined as

$$\begin{aligned} \mathcal {T}_\alpha (V)= {1\over \alpha -1} \left[ 1- \int _S f_V^\alpha (v) dv \right] = {1\over \alpha -1} E[1- f_{V}^{\alpha -1} (V)], \quad 0<\alpha \ne 1, \end{aligned}$$

where S is the support of V.

First, we derive the Tsallis entropy of RSMT $Z_2$.

$$\begin{aligned} \mathcal {T}_\alpha (Z_2)= & {} {1\over \alpha -1} \left\{ 1- \int _{-\infty }^\infty f_{Z_2}^\alpha (z) dz \right\} \nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \int _0^\infty \beta ^\alpha f_{X_1}^\alpha (z) dz-\int _{-\infty }^0 {\overline{\beta }}^{\;\alpha } f_{X_2}^\alpha (-z) dz \right\} \nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \beta ^\alpha \int _0^\infty f_{X_1}^\alpha (z) dz-{\overline{\beta }}^{\;\alpha } \int _0^\infty f_{X_2}^\alpha (x) dx \right\} \nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \beta ^\alpha E[ f_{X_1}^{\alpha -1} (X_1)] -{\overline{\beta }}^{\;\alpha } E[ f_{X_2}^{\alpha -1} (X_2)] \right\} \nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \beta ^\alpha [1-(\alpha -1) \mathcal {T}_\alpha (X_1)] -{\overline{\beta }}^{\;\alpha } [1-(\alpha -1) \mathcal {T}_\alpha (X_2)] \right\} \nonumber \\= & {} {1\over \alpha -1} (1-\beta ^\alpha - {\overline{\beta }}^{\;\alpha } ) + \beta ^\alpha \ \mathcal {T}_\alpha (X_1) + {\overline{\beta }}^{\;\alpha } \ \mathcal {T}_\alpha (X_2), \nonumber \\= & {} \mathcal {T}_\alpha (Y) + \beta ^\alpha \ \mathcal {T}_\alpha (X_1) + {\overline{\beta }}^{\;\alpha } \ \mathcal {T}_\alpha (X_2), \end{aligned}$$

(14)

where

$$\begin{aligned} \mathcal {T}_\alpha (Y) = {1\over \alpha -1} E[1- f_{Y}^{\alpha -1} (Y)]={1\over \alpha -1} (1-\beta ^\alpha - {\overline{\beta }}^{\;\alpha } ). \end{aligned}$$

(15)

Note that Tsallis entropy of RSMT $\mathcal {T}(Z_2)$ is a non-linear function in $\beta$.

Second, we find the Tsallis entropy of $X\sim IG(\mu , \lambda )$.

$$\begin{aligned} \mathcal {T}_\alpha (X)= & {} {1\over \alpha -1} \left\{ 1- \int _0^\infty f_{X}^\alpha (x) dx \right\} \nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \int _0^\infty \left( {\lambda \over 2 \pi }\right) ^{\alpha /2} {1\over x^{3 \alpha /2}} \exp \left[ - {\alpha \lambda \over 2\mu ^2 x} (x-\mu )^2 \right] dx \right\} \nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \left( {\lambda \over 2 \pi }\right) ^{\alpha /2}\ e^{\alpha \lambda /\mu } \int _0^\infty {1\over x^{3 \alpha /2}} \exp \left[ - \left( {\alpha \lambda \over 2 \mu ^2 }\;x +{\alpha \lambda \over 2 x}\right) \right] dx\right\} \nonumber \\= & {} {1\over \alpha -1} \Bigg \{ 1- \left( {\lambda \over 2 \pi }\right) ^{\alpha /2}\ \left( {2\mu ^2\over \alpha \lambda } \right) ^{-(3 \alpha /2-1)} \ e^{\alpha \lambda /\mu } \nonumber \\{} & {} \qquad \qquad \qquad \qquad \qquad \qquad \int _0^\infty {1\over t^{3 \alpha /2}} \exp \left[ - \left( t +{(\alpha \lambda /\mu )^2\over 4 t}\right) \right] dt \Bigg \}\nonumber \\= & {} {1\over \alpha -1} \left\{ 1- \left( {\lambda /\mu \over 2 \pi }\right) ^{\alpha /2}\ {2 e^{\alpha \lambda /\mu } \over \mu ^{\alpha -1}} \ K_{3 \alpha /2-1}\; (\alpha \lambda /\mu ) \right\} . \end{aligned}$$

(16)

where

$$\begin{aligned} K_\nu (s)= {1\over 2} (s/2)^\nu \int _0^\infty {1\over t^{\nu +1}} \exp \left[ - \left( t +{s^2\over 4 t}\right) \right] dt, \quad -\infty< \nu < \infty , \quad s>0, \end{aligned}$$

(17)

is the modified Bessel function of the second kind.

Therefore, Tsallis entropy of DIG-1 distribution is explicitly given by

$$\begin{aligned} \mathcal {T}_\alpha (Z_2)=\mathcal {T}_\alpha (Y) + \beta ^\alpha \ \mathcal {T}_\alpha (X_1) + {\overline{\beta }}^{\;\alpha } \ \mathcal {T}_\alpha (X_2), \end{aligned}$$

(18)

where $\mathcal {T}_\alpha (Y)$ is given by (15) and

$$\begin{aligned} \mathcal {T}_\alpha (X_j) = {1\over \alpha -1} \left\{ 1- \left( {\lambda _j/\mu _j\over 2 \pi }\right) ^{\alpha /2}\ {2 e^{\alpha \lambda _j/\mu _j} \over \mu _j^{\alpha -1}} \ K_{3 \alpha /2-1}\; (\alpha \lambda _j/\mu _j) \right\} , \qquad j=1,2. \end{aligned}$$

(19)

2.6 Shannon Entropy

Using L’Hospital rule, we have

$$\begin{aligned} \lim _{\alpha \rightarrow 1} \mathcal {T}_\alpha (V)= - \int _S \ln (f_V (v)) f_V(v) dv = E[- \ln f_{V} (V)] = \mathcal {H}(V), \end{aligned}$$

which is the Shannon entropy of V, Shannon (1948).

As $\alpha \rightarrow 1$, (14) and (15), are simplified to

$$\begin{aligned} \mathcal {H}(Z_2)=\mathcal {H}(Y)+\beta \ \mathcal {H}(X_1)+ {\overline{\beta }}\ \mathcal {H}(X_2), \end{aligned}$$

(20)

where

$$\begin{aligned} \mathcal {H}(Y)=- \beta \ \ln \beta - {\overline{\beta }}\ \ln {\overline{\beta }}, \end{aligned}$$

(21)

which agrees with the result obtained by Aly (2018). Note that Shannon entropy of RSMT $\mathcal {H}(Z_2)$ is a non-linear function in $\beta$.

Using (16), the Shannon entropy of $X\sim \textrm{IG}(\mu , \lambda )$ is given by

$$\begin{aligned} \mathcal {H} (X)= & {} \lim _{\alpha \rightarrow 1} \mathcal {T}_\alpha (X)\nonumber \\= & {} {1\over 2} - {1\over 2} \ln \left({\lambda \over 2 \pi \mu ^3}\right) - {3\over 2} \sqrt{{2 \lambda \over \pi \mu }} \ e^{\lambda /\mu } \ {\partial \over \partial \nu } \ K_{\nu }(\lambda /\mu ) {|}_{\nu =1/2}, \end{aligned}$$

(22)

where $K_\nu (s), s>0,$ is given by (17). The proof follows by using L’HÔpital’s rule.

The last expression can be calculated using the Mathematica function $\textrm{BesselK}^{(1,0)}[1/2, \lambda /\mu ]= {\partial \over \partial \nu } K_\nu (\lambda /\mu ) {|}_{\nu =1/2}.$

Using (20), the Shannon entropy of DIG-1 distribution is given by

$$\begin{aligned} \mathcal {H}(Z_2) = \mathcal {H} (Y) +\beta \ \mathcal {H} (X_1) + {\overline{\beta }} \ \mathcal {H} (X_2), \end{aligned}$$

(23)

where $\mathcal {H} (Y)$ is given by (21) and

$$\begin{aligned} \mathcal {H} (X_j) = {1\over 2} - {1\over 2} \ln \left({\lambda _j \over 2 \pi \mu _j^3}\right) - {3\over 2} \sqrt{{2 \lambda _j\over \pi \mu _j}} \ e^{\lambda _j/\mu _j} \ {\partial \over \partial \nu _j} K_{\nu _j}(\lambda _j/\mu _j) {|}_{\nu _j=1/2}, \quad j=1,2. \end{aligned}$$

(24)

2.7 Extropy

The following relation

$$\begin{aligned} {1\over 2} [\mathcal {T}_2(V)-1]= - {1\over 2} \int _S f_V^2 (v) dv = E\left[- {1\over 2} f_{V} (V)\right] = \mathcal {J}(V), \end{aligned}$$

(25)

is known as the extropy of V (Lad et al. 2015).

Using (14) and (15), with $\alpha =2$, the extropy of RSMT is given by

$$\begin{aligned} \mathcal {J}(Z_2) = {1\over 2} [\mathcal {T}_2(Z_2)-1]=\beta ^{2} \ \mathcal {J} (X_1) + {\overline{\beta }}^{\;2} \ \mathcal {J}(X_2). \end{aligned}$$

(26)

Note that extropy of RSMT $\mathcal {H}(Z_2)$ is a quadratic function in $\beta$.

Using (16), with $\alpha =2$, the extropy of $X\sim \textrm{IG}(\mu , \lambda )$ is given by

$$\begin{aligned} \mathcal {J}(X) = {1\over 2} [\mathcal {T}_2(X)-1]=- \; {\lambda \over 2 \pi \mu ^2} \ e^{2\lambda /\mu } \ K_2(2\lambda /\mu ), \end{aligned}$$

(27)

where $K_\nu (z)$ is given by (17).

The extropy of DIG-1 distribution is given by

$$\begin{aligned} \mathcal {J}(Z_2) = \beta ^{2} \ \mathcal {J} (X_1) + {\overline{\beta }}^{\;2} \ \mathcal {J}(X_2), \end{aligned}$$

(28)

where

$$\begin{aligned} \mathcal {J} (X_j)=- \; {\lambda _j\over 2 \pi \mu _j^2} \ e^{2\lambda _j/\mu _j} \ K_2(2\lambda _j/\mu _j), \qquad j=1,2, \end{aligned}$$

(29)

where $K_\nu (z)$ is given by (17).

Figure 4 shows Tsallis entropy, Shannon entropy and extropy of DIG-1 distribution as a function in $\beta$ for selected values of the parameters. This figure also shows that Tsallis entropy of DIG-1 distribution decreases as $\alpha$ increases.

Fig. 4

Tsallis entropy, Shannon entropy and extropy of DIG-1 distribution

3 Maximum Likelihood Estimation

In this section, we derive the MLEs of the parameters of DIG distributions and their asymptotic distributions. These asymptotic distributions turned out to be multivariate normal which can be used to make statistical inference (confidence intervals and hypothesis testing) about the parameters of DIG distributions.

3.1 DIG-1: Maximum Likelihood Estimation

Let $z_{2,1}, z_{2,2}, \ldots , z_{2,n}$ be a r.s. from DIG-1$(\beta ,\mu _1, \lambda _1,\mu _2, \lambda _2)$ distribution. The log-likelihood function is given by

$$\begin{aligned} \ln L_1 = \sum _{i=1}^n \ln [\beta \; f_{X_1}(z_{2,i};\, \mu _1, \lambda _1)] \; \textbf{1}_{\{z_{2,i}>0\}}+ \sum _{i=1}^n \ln [{\overline{\beta }} \; f_{X_2}(|z_{2,i}|;\, \mu _2, \lambda _2)] \; \textbf{1}_{\{z_{2,i}<0\}}, \end{aligned}$$

(30)

where $\textbf{1}_{A}= 1 (0)$ if A is true (false) is the indicator function.

The MLEs of $(\beta ,\mu _1, \lambda _1,\mu _2, \lambda _2)$ are:

$$\begin{aligned} {\widehat{\beta }} = {n_1\over n}, \qquad {\widehat{\mu }}_1 ={a_1\over n_1}, \qquad {\widehat{\lambda }}_1 = {n_1\over c_1 - {n_1^2\over a_1}}, \qquad {\widehat{\mu }}_2 ={a_2\over n_2}, \qquad {\widehat{\lambda }}_2 = {n_2\over c_2 - {n_2^2\over a_2}}, \end{aligned}$$

(31)

where

$$\begin{aligned}{} & {} n_1=\sum _{i=1}^n \textbf{1}_{\{z_{2,i} > 0\}}, \qquad n_2=\sum _{i=1}^n \textbf{1}_{\{z_{2,i} < 0\}}, \qquad n_1+n_2=n, \end{aligned}$$

(32)

$$\begin{aligned}{} & {} a_1=\sum _{i=1}^n z_{2,i} \ \textbf{1}_{\{z_{2,i} > 0\}}, \qquad a_2=\sum _{i=1}^n |z_{2,i}| \ \textbf{1}_{\{z_{2,i} < 0\}}, \end{aligned}$$

(33)

$$\begin{aligned}{} & {} c_1=\sum _{i=1}^n {1\over z_{2,i}} \ \textbf{1}_{\{z_{2,i} > 0\}}, \qquad c_2=\sum _{i=1}^n {1\over |z_{2,i}|} \ \textbf{1}_{\{z_{2,i} < 0\}}. \end{aligned}$$

(34)

Moreover, the asymptotic distribution of the MLEs is given by:

as $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \begin{bmatrix} {\widehat{\beta }} - \beta \\ {\widehat{\mu }}_1 - \mu _1 \\ {\widehat{\lambda }}_1 - \lambda _1 \\ {\widehat{\mu }}_2 - \mu _2 \\ {\widehat{\lambda }}_2 - \lambda _2 \end{bmatrix} \ \overset{d}{\longrightarrow }\ \ MVN \left( \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \beta \ {\overline{\beta }} &{} \ 0 &{} \ 0 &{} \ 0 &{} \ 0\\ 0 &{}\ {\mu _1^3 \over \beta \lambda _1} &{} \ 0 &{} \ 0 &{} \ 0\\ 0 &{}\ 0 &{} \ {2 \lambda _1^2\over \beta } &{} \ 0 &{} \ 0\\ 0 &{} \ 0 &{} \ 0 &{}\ {\mu _2^3 \over {\overline{\beta }} \lambda _2} &{} \ 0 \\ 0 &{}\ 0 &{} \ 0 &{} \ 0 &{} \ {2 \lambda _2^2\over {\overline{\beta }}} \\ \end{bmatrix} \right) . \end{aligned}$$

(35)

where $\overset{d}{\longrightarrow }$ denotes convergence in distribution and MVN stands for multivariate normal distribution.

3.2 DIG-2: Maximum Likelihood Estimation

Let $z_{2,1}, z_{2,2}, \ldots , z_{2,n}$ be a r.s. from DIG-2$(\beta ,\mu _1, \mu _2, \lambda )$ distribution. The log-likelihood function is given by

$$\begin{aligned} \ln L_2 = \sum _{i=1}^n \ln [\beta \; f_{X_1}\{z_{2,i};\, \mu _1, \lambda )] \; \textbf{1}_{\{z_{2,i}>0\}}+ \sum _{i=1}^n \ln [{\overline{\beta }} \; f_{X_2}(|z_{2,i}|;\, \mu _2, \lambda )] \; \textbf{1}_{\{z_{2,i}<0)}. \end{aligned}$$

(36)

The MLE of $\beta$ is

$$\begin{aligned} {\widehat{\beta }} = {n_1\over n}, \end{aligned}$$

(37)

and the MLEs of $(\mu _1,\mu _2, \lambda )$ are the solutions of the normal equations:

$$\begin{aligned} {n\over {\widehat{\lambda }}} - \sum _{i=1}^n {1\over {\widehat{\mu }}_1^2 z_{2,i}} \{z_{2,i}-{\widehat{\mu }}_1)^2 \ \textbf{1}_{\{z_{2,i}>0\}} - \sum _{i=1}^n {1\over {\widehat{\mu }}_2^2 |z_{2,i}|} (|z_{2,i}|-{\widehat{\mu }}_2)^2 \ \textbf{1}_{\{z_{2,i}<0)}= & {} 0, \\ \sum _{i=1}^n \{z_{2,i}- {\widehat{\mu }}_1) \ \textbf{1}_{\{z_{2,i} >0\}}= & {} 0, \\ \sum _{i=1}^n (|z_{2,i}|- {\widehat{\mu }}_2)\ \textbf{1}_{\{z_{2,i} < 0\}}= & {} 0. \end{aligned}$$

It follows that

$$\begin{aligned} {\widehat{\mu }}_1 ={a_1\over n_1}, \qquad {\widehat{\mu }}_2 ={a_2\over n_2}, \qquad {\widehat{\lambda }}={n\over c_1 - {n_1^2\over a_1} +c_2 - {n_2^2\over a_2} }. \end{aligned}$$

(38)

Moreover, the asymptotic distribution of the MLEs is given by: as $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \begin{bmatrix} {\widehat{\beta }}- \beta \\ {\widehat{\lambda }}-\lambda \\ {\widehat{\mu }}_1-\mu _1 \\ {\widehat{\mu }}_2-\mu _2 \end{bmatrix} \ \overset{d}{\longrightarrow }\ \ MVN \left( \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \beta {\overline{\beta }} &{} \ 0 &{} \ 0 &{} \ 0 \\ 0 &{}\ 2 \lambda ^2 &{} \ 0 &{} \ 0 \\ 0 &{}\ 0 &{} \ {\mu _1^3\over \beta \lambda } &{} \ 0 \\ 0 &{}\ 0 &{} \ 0 &{} \ {\mu _2^3\over {\overline{\beta }} \lambda }\\ \end{bmatrix} \right) . \end{aligned}$$

(39)

3.3 DIG-3: Maximum Likelihood Estimation

Let $z_{2,1}, z_{2,2}, \ldots , z_{2,n}$ be a r.s. from DIG-3$(\beta , \mu , \lambda _1, \lambda _2)$ distribution. The log-likelihood function is given by

$$\begin{aligned} \ln L_3 = \sum _{i=1}^n \ln [\beta \; f_{X_1}\{z_{2,i}; \mu , \lambda _1)] \; \textbf{1}_{\{z_{2,i}>0\}}+ \sum _{i=1}^n \ln [{\overline{\beta }} \; f_{X_2}(|z_{2,i}|; \mu , \lambda _2)] \; \textbf{1}_{\{z_{2,i}<0)}. \end{aligned}$$

(40)

The MLE of $\beta$ is

$$\begin{aligned} {\widehat{\beta }} = {n_1\over n}, \end{aligned}$$

(41)

and the MLEs of $(\mu , \lambda _1, \lambda _2)$ are the solutions of the normal equations:

$$\begin{aligned} {\widehat{\lambda }}_1 \sum _{i=1}^n \{z_{2,i}-{\widehat{\mu }}_1) \ \textbf{1}_{\{z_{2,i}>0\}} +{\widehat{\lambda }}_2 \sum _{i=1}^n (|z_{2,i}|-{\widehat{\mu }}_1) \ \textbf{1}_{\{z_{2,i}<0)}= & {} 0, \\ {n_1\over {\widehat{\lambda }}_1} - \sum _{i=1}^n {1\over {\widehat{\mu }}^2 z_i} \{z_{2,i}-{\widehat{\mu }})^2 \ \textbf{1}_{\{z_{2,i}>0\}}= & {} 0, \\ {n_2\over {\widehat{\lambda }}_2} - \sum _{i=1}^n {1\over {\widehat{\mu }}^2 z_{2,i}} \{z_i-{\widehat{\mu }})^2 \ \textbf{1}_{\{z_{2,i}<0)}= & {} 0. \end{aligned}$$

It follows that

$$\begin{aligned} {\widehat{\lambda }}_1 = {n_1\over {a_1\over {\widehat{\mu }}^2} - {2 n_1\over {\widehat{\mu }}} +c_1 }, \qquad {\widehat{\lambda }}_2 = {n_2\over {a_2\over {\widehat{\mu }}^2} - {2 n_2\over {\widehat{\mu }}} +c_2 }, \end{aligned}$$

(42)

where ${\widehat{\mu }}$ is the solution in $\mu$ of the cubic equation:

$$\begin{aligned} A \mu ^3+B \mu ^2 + C \mu + D=\,0, \end{aligned}$$

(43)

where

$$\begin{aligned} A=\,\, & {} n_1^2 c_2 + n_2^2 c_1, \\ B=\,\, & {} - (n_1 c_2 a_1 + n_2 c_1 a_2 + 2 n_1 n_2 n), \\ C=\, \,& {} n_1^2 a_2 + n_2^2 a_1 + 2 n_1 n_2 (a_1+a_2), \\ D=\, \,& {} - n a_1 a_2. \end{aligned}$$

The discriminant of the above cubic equation is given by

$$\begin{aligned} \Delta =18 A B C D - 4 B^3 D + B^2 C^2 - 4 A C^3 -27 A^2 D^2 \end{aligned}$$

and it is well known that if this is negative, the cubic equation has a unique real root. This will imply that the MLEs ${\widehat{\lambda }}_1$ and ${\widehat{\lambda }}_2$ are also unique.

Moreover, the asymptotic distribution of the MLEs is given by:

as $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \begin{bmatrix} {\widehat{\beta }}- \beta \\ {\widehat{\mu }}-\mu \\ {\widehat{\lambda }}_1-\lambda _1\\ {\widehat{\lambda }}_2-\lambda _2 \end{bmatrix} \ \overset{d}{\longrightarrow }\ \ MVN \left( \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \beta {\overline{\beta }} &{} \ 0 &{} \ 0 &{} \ 0 \\ 0 &{}\ {\mu ^3 \over \beta \lambda _1 + {\overline{\beta }} \ \lambda _2} &{} \ 0 &{} \ 0 \\ 0 &{}\ 0 &{} \ {2 \lambda _1^2\over \beta } &{} \ 0 \\ 0 &{}\ 0 &{} \ 0 &{} \ {2 \lambda _2^2\over {\overline{\beta }}}\\ \end{bmatrix} \right) . \end{aligned}$$

(44)

3.4 DIG-4: Maximum Likelihood Estimation

Let $z_{1,1}, z_{1,2}, \ldots , z_{1,n}$ be a r.s. from DIG-4$(\beta ,\mu , \lambda )$ distribution. The log-likelihood function is given by

$$\begin{aligned} \ln L_4= \,\,& {} \sum _{i=1}^n \ln [\beta \; f_{X}\{z_{1,i}; \mu , \lambda )] \; \textbf{1}_{\{z_{1,i}>0\}}+ \sum _{i=1}^n \ln [{\overline{\beta }} \; f_{X}(|z_{1,i}|; \mu , \lambda )] \; \textbf{1}_{\{z_{1,i}<0\}} \nonumber \\=\,\, & {} n_1 \ln \beta + n_2 \ln {\overline{\beta }} + \sum _{i=1}^n \ln f_X(|z_{1,i}|; \mu , \lambda ). \end{aligned}$$

(45)

The MLEs of $(\beta ,\mu , \lambda )$ are:

$$\begin{aligned} {\widehat{\beta }} ={1\over n} \sum _{i=1}^n \textbf{1}_{\{z_{1,i} > 0\}},\qquad {\widehat{\mu }} = {1\over n} \sum _{i=1}^n |z_{1,i}|, \qquad {\widehat{\lambda }} = {n\over \sum _{i=1}^n {1\over |z_{1,i}|} - {n\over {\widehat{\mu }}}}. \end{aligned}$$

(46)

Moreover, the asymptotic distribution of the MLEs is given by:

as $n\rightarrow \infty$,

$$\begin{aligned} \sqrt{n} \begin{bmatrix} {\widehat{\beta }} - \beta \\ {\widehat{\mu }} - \mu \\ {\widehat{\lambda }} - \lambda \end{bmatrix} \ \overset{d}{\longrightarrow }\ \ MVN \left( \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \beta \ {\overline{\beta }} &{} \ 0 &{} \ 0 \\ 0 &{}\ {\mu ^3 \over \lambda } &{} \ 0 \\ 0 &{}\ 0 &{} \ 2 \lambda ^2 \\ \end{bmatrix} \right) . \end{aligned}$$

(47)

4 Simulations

The purpose of this section is to perform simulation studies to evaluate the behaviour of the MLEs of the parameters of the proposed four DIG distributions. Such behaviour will be evaluated in terms of the bias, mean-square error of the MLEs and the coverage probability of the 95% confidence intervals of the parameters. All computations in the simulation studies were done using the R language Version 4.0.5 for Windows.

To generate a random sample of size n,  $Z_{2,1}, Z_{2,2}, \ldots , Z_{2,n}$, from DIG-1, DIG-2 and DIG-3 distributions, we use the following algorithms:

• 1. Generate $Y_i \sim Bernoulli (\beta ), \ i=1, 2,\ldots ,n;$

• 2. Generate $X_{1,i} \sim IG (\mu _1, \lambda _1), \ i=1, 2,\ldots ,n;$

• 3. Generate $X_{2,i} \sim IG (\mu _2, \lambda _2), \ i=1, 2,\ldots ,n;$

• 4. Set $Z_{2,i}=Y_i\; X_{1,i}- (1-Y_i) \;X_{2,i}, \ i=1, 2,\ldots ,n.$

To generate a random sample of size n,  $Z_{1,1}, Z_{1,2}, \ldots , Z_{1,n}$, from DIG-4 distribution, we use the following algorithm:

• 1. Generate $Y_i \sim Bernoulli (\beta ), \ i=1, 2,\ldots ,n;$

• 2. Generate $X_{i} \sim IG (\mu , \lambda ), \ i=1, 2,\ldots ,n;$

• 3. Set $Z_{1,i}= (2 Y_i-1) \; X_{i}, \ i=1, 2,\ldots ,n.$

The sample sizes considered in the simulation studies are $n=50, 100, \ldots , 500.$

The above process of generating random data from DIG distributions is repeated $M=10,000$ times. In each of the M repetitions, the MLEs of the parameters and their standard errors (S.E.) were calculated using the expressions given in Subsections 3.1 to 3.4.

Measures examined in these simulation studies are:

• (1) Bias of the MLE ${\widehat{\nu }}$ of the parameter $\nu =\beta , \mu _1, \lambda _1, \mu _2, \lambda _2$:

  $$\begin{aligned} \textrm{Bias} ({\widehat{\nu }})= {1\over M} \sum _{i=1}^M ({\widehat{\nu }}_i-\nu ), \end{aligned}$$

  where ${\widehat{\nu }}_i$ is the MLE of the parameter $\nu$ in the ith simulation repetition.

• (2) Mean square error (MSE) of the MLE ${\widehat{\nu }}$ of the parameter $\nu$:

  $$\begin{aligned} \textrm{MSE} ({\widehat{\nu }})= {1\over M} \sum _{i=1}^M ({\widehat{\nu }}_i-\nu )^2. \end{aligned}$$

• (3) Coverage probability (CP) of 95% confidence intervals of the parameter $\nu$:

  $$\begin{aligned} \textrm{CP}(\nu )= {1\over M} \sum _{i=1}^M \textbf{1}_{\{\nu \in (L_i, U_i)\}}, \end{aligned}$$

  where $L_i= {\widehat{\nu }}_i - 1.96 \; S.E.({\widehat{\nu }}_i), \qquad U_i= {\widehat{\nu }}_i + 1.96 \; S.E.({\widehat{\nu }}_i), \qquad i=1,2, \ldots , M.$

The reported figures of the simulation studies support the following conclusions:

• 1. Figures 5, 6, 7,  8 show that the absolute biases of the MLEs of the parameters are small and tend to zero for large n.

• 2. Figures 9, 10, 11,  12 show that the MSE of the MLEs of the parameters are small and decrease as n increases.

• 3. Figures 13, 14, 15,  16 show that the coverage probability of 95% confidence intervals of the parameters is close to the nominal level of 95%.

The above conclusions show that the MLEs of the parameters of the DIG distributions are well behaved for point estimation and confidence intervals.

Fig. 5

Bias of the MLEs of the parameters of DIG-1 distribution

Fig. 6

Bias of the MLEs of the parameters of DIG-2 distribution

Fig. 7

Bias of the MLEs of the parameters of DIG-3 distribution

Fig. 8

Bias of the MLEs of the parameters of DIG-4 distribution

Fig. 9

MSE of the MLEs of the parameters of DIG-1 distribution

Fig. 10

MSE of the MLEs of the parameters of DIG-2 distribution

Fig. 11

MSE of the MLEs of the parameters of DIG-3 distribution

Fig. 12

MSE of the MLEs of the parameters of DIG-4 distribution

Fig. 13

Coverage probability of the parameters of DIG-1 distribution

Fig. 14

Coverage probability of the parameters of DIG-2 distribution

Fig. 15

Coverage probability of the parameters of DIG-3 distribution

Fig. 16

Coverage probability of the parameters of DIG-4 distribution

5 Application

In this section, we apply the proposed DIG models to a real data set for illustration. The description of the data is as follows.

In an online final exam at Kuwait university during Covid-19 shut down, students are requested to write down their solutions on paper sheets, scan these sheets as a “pdf” file and send such file to the instructor via Teams Chat. The time of submitting the solution file of each student is recorded automatically on the Teams system. Here, we are interested in modelling the difference between the time (in minutes) spent to submitting the solution file $t_i$ and the two hours exam period of 38 students, i.e. $z_i= t_i -120, \ i=1,2, \ldots , 38.$

The data set is given below.

− 18.06, −17.45, −9.90, −8.62, −6.14, −3.47, −2.57, −2.43, − 1.56, 0.84, 1.14, 1.26, 1.34, 1.58, 1.81, 1.82, 1.89, 2.11, 2.23, 2.26, 2.33, 2.36, 2.40, 2.43, 2.52, 2.89, 2.92, 3.25, 3.30, 3.30, 3.47, 3.71, 3.77, 4.02, 4.41, 4.85, 5.20, 7.94 where negative (positive) value means the student submitted the solution file earlier (later) than the two hours exam time.

Table 1 shows the MLE’s of the parameters, their standard errors (S.E.’s) and the maximized log-likelihood of the DIG models. Note that for DIG-3, the discriminant $\Delta = -1.08345\times 10^{17}$, showing that the MLE ${\widehat{\mu }}$ is unique.

Table 1 Summary of fitted DIG distributions

Table 2 Goodness-of-fit tests of DIG distributions

Table 2 shows two goodness-of-fit tests, Anderson-Darling (AD) and Cramer von-Misses (CvM) tests. Clearly, this table shows that all DIG models pass the two tests, i.e., we accept the null hypothesis that the data are drawn from each of the DIG models. However, the test statistics (p-value) for DIG-1 and DIG-2 are much smaller (larger) than those for DIG-3 and DIG-4.

Since DIG-2, DIG-3 and DIG-4 models are nested in DIG-1 model, we can use the likelihood ratio test (LRT) to test each of the following hypotheses:

• (i) $H_0: \lambda _1=\lambda _2$ (DIG-2 model) versus $H_1: \lambda _1\ne \lambda _2$ (DIG-1 model)

• (ii) $H_0: \mu _1=\mu _2$ (DIG-3 model) versus $H_1: \mu _1\ne \mu _2$ (DIG-1 model)

• (iii) $H_0: \mu _1=\mu _2, \lambda _1=\lambda _2$ (DIG-4 model) versus $H_1: \mu _1\ne \mu _2, \lambda _1\ne \lambda _2$ (DIG-1 model)

Table 3 shows that DIG-2 model cannot be rejected for the given data.

Table 3 Likelihood ratio tests for nested DIG distributions

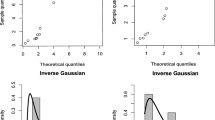
We have seen above that LR test favour the DIG-2 model to be suitable for the given data. This conclusion is also supported by the Probability-Probability (P-P) plots presented in Fig. 17 and the Quantile-Quantile (Q-Q) plots presented in Fig. 18.

Fig. 17

P-P plots of fitted DIG distributions

Fig. 18

Q-Q plots of fitted DIG distributions

6 Conclusion and Comments

Double inverse Gaussian distribution, presented here, has been formed by a procedure proposed by Aly (2018). This procedure is completely different from the procedures adopted in the literature. The unified approach, adopted here, is quite general and can be used to formulate double distributions for various classes of distributions. A natural extension of such double distributions is to include possible covariates to allow more flexibility for modelling purposes. We hope that the model presented here will be found useful for data analysts.