Generalized X-Exponential Bathtub Shaped Failure Rate Distribution

Abstract

Generalized Lindley, Generalized Gamma, Exponentiated Weibull and X-Exponential distributions are proposed for modelling lifetime data having bathtub shaped failure rate model. These distributions have several desirable properties. In this paper, we introduce a new distribution which generalizes the X-Exponential distribution. Several properties of the distribution are derived including the hazard rate function, moments, moment generating function etc. Moreover, we discussed the maximum likelihood estimation of this distribution. The usefulness of the new distribution is illustrated by means of two real data set. We hope that the new distribution will serve as an alternative model to bathtub models available in the literature.

1 Introduction

In many applied sciences such as medicine, engineering and finance, amongst others, modeling and analyzing lifetime data are crucial. Several lifetime distributions have been used to model such kinds of data. For instance, the Exponential, Weibull, Gamma, Rayleigh distributions and their generalizations (Gupta and Kundu 1999; Nadarajah and Gupta 2007; Pal et al. 2006; Sarhana and Kundu 2009). Each distribution has its own characteristics due specifically to the shape of the failure rate function which may be only monotonically decreasing or increasing or constant in its behavior (Lai et al. 2001). The Weibull distribution is more popular than Gamma and Lognormal distribution because the survival function of the latter cannot be expressed in closed forms. The Weibull distribution has closed form survival and hazard rate functions (Murthy et al. 2004). Generalized Lindley distribution has many properties, which exhibit bathtub shape for its failure rate function. Nadarajah et al. (2011) introduced Generalized Lindley distribution and discussed its various properties and applications.

Here we consider a new distribution having bathtub shaped failure rate function, which generalizes the X-Exponential distribution. The X-Exponential distribution was introduced by Chacko (2016). In order to get more flexibility in its failure rate, a small change in exponential part of X-Exponential distribution is made, the resulting distribution is named as Generalized X-Exponential. The distribution can be considered as distribution of a series system having distribution $F(x) = 1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} ,\;\;x > 0,\lambda > 0,$ for its components in which, a parabolic function $ax^{2} + bx + c$ is used as exponent with ${\text{a}} = {\text{b}} = \lambda , \;c = 0$ whereas in X-Exponential distribution, the parameter values were $a = \lambda , \;b = 0,\;c = 0$.

In this paper, we introduce a new distribution which generalizes the X-Exponential distribution. Section 2 discussed the definition of the Generalization of X-Exponential distribution. Section 3 discussed the statistical behaviors of the distribution. Section 4 discussed the distribution of maximum and minimum. The maximum likelihood estimation of the parameters is determined in Sect. 5. Real data sets are analyzed in Sect. 6 and the results are compared with existing distributions. Conclusions are given in Sect. 7.

2 Generalized X-Exponential Distribution

Consider a life time random variable X has a cumulative distribution function (cdf) with parameter $\alpha$ and $\lambda$,

$$ F(x) = \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } , \quad x > 0,\;\lambda > 0,\; \alpha > 0. $$

(2.1)

Clearly F(0) = 0, F$(\infty )$ = 1, F is non-decreasing and right continuous. More over F is absolutely continuous. Then the probability density function (pdf) with scale parameter λ is given by

$$ \begin{aligned} f(x) &= \alpha e^{{ - \lambda \left( {x^{2} + x} \right)}} \left( {\lambda \left( {1 + \lambda x^{2} } \right)\left( {2x + 1} \right) - 2\lambda x} \right)\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha - 1} ,\quad \\ &\quad x > 0,\;\alpha > 0,\;\lambda > 0. \end{aligned} $$

(2.2)

Here $\alpha$ and $\lambda$ are shape and scale parameters. It is positively skewed distribution. The distribution with pdf of the form (2.2) is named as Generalized X-Exponential distribution with parameters $\alpha$ and $\lambda$ and will be denoted by ${\text{GXED(}}\alpha ,\lambda )$.

Failure rate function of GXED distribution is

$$ \begin{aligned} h(x) &= \frac{{\alpha e^{{ - \lambda \left( {x^{2} + x} \right)}} \left( {\lambda \left( {1 + \lambda x^{2} } \right)\left( {2x + 1} \right) - 2\lambda x} \right)\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha - 1} }}{{1 - \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } }}, \quad \\ & \quad x > 0,\; \alpha > 0,\;\lambda > 0. \end{aligned} $$

(2.3)

Considering the behavior near the change point $x_{0}$, $0 < x_{0}$ and if $\frac{d}{dx}h(x_{0} ) = 0$

• (i) If $0 < \alpha < \frac{1}{2},$ and $0 < \lambda < 1,$ then $\frac{d}{dx}h(x) < 0$ when $0 < x < x_{0}$ and $\frac{d}{dx}h(x) > 0$ when $x > x_{0} ,$$\frac{{d^{2} }}{{dx^{2} }}h(x) > 0$ for $x = x_{0} .$

• (ii) If $0 < \alpha < \frac{1}{2},$ and $\lambda > 1,$ then $\frac{d}{dx}h(x) < 0$ when $0 < x < x_{0}$, $\frac{d}{dx}h(x) > 0$ when $x > x_{0} ,$$\frac{{d^{2} }}{{dx^{2} }}h(x) > 0$ for $x = x_{0} .$

• (iii) If $\frac{1}{2} < \alpha < 1,$ and $0 < \lambda < 1,$ then $\frac{d}{dx}h(x) < 0$ when $0 < x < x_{0}$ and $\frac{d}{dx}h(x) > 0$ when $x > x_{0} ,$$\frac{{d^{2} }}{{dx^{2} }}h(x) > 0$ for $x = x_{0} .$

• (iv) If $\frac{1}{2} < \alpha < 1,$ and $\lambda > 1,$ then $\frac{d}{dx}h(x) < 0$ when $0 < x < x_{0}$ and $\frac{d}{dx}h(x) > 0$ when $x > x_{0} ,$$\frac{{d^{2} }}{{dx^{2} }}h(x) > 0$ for $x = x_{0} .$

• (v) If $\alpha > 1,$ and $\lambda > 1,$ then $\frac{d}{dx}h(x) > 0$ for $x > 0$

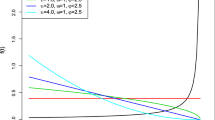
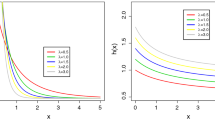
The shape of Eq. (2.3) appears monotonically decreasing or to initially decrease and then increase, a bathtub shape if $\alpha < 1$. The proposed distribution allows for monotonically decreasing, monotonically increasing and bathtub shapes for its hazard rate function. As $\alpha$ decreases from 1 to 0, the graph shift above whereas if $\lambda$ increases from 1 to $\infty$ the shape of the graph concentrate near to 0. It is the distribution of the failure of a series system with independent components (Figs. 1, 2, 3).

Fig. 1

Probability density function of GXED for values of parameters $\alpha$ = 0.5, 2, 3, 3.5, 4, 2.5, 5 and $\lambda$ = 1.5, 3, 4, 5, 6, 7, 7.5 with color shapes purple, blue, plum, green, red, black and dark cyan, respectively

Fig. 2

Cumulative distribution function of GXED for values of parameters $\alpha$ = 1.5, 2, 3.5, 4.5, 5 and $\lambda$ = 2.5, 3, 4, 5, 6 with color shapes red, green, plum, dark cyan and orange respectively

Fig. 3

Failure rate function GXED for values of parameters $\alpha$ = 0.0001, 0.1, 0.5, 2.5, 0.475 and $\lambda$ = 0.75, 5, 1.5, 7, 8 with color shapes orange, red, grey, plum and green, respectively

3 Moments

Calculating moments of X requires the following lemma.

Lemma 2.1

For $\alpha ,\;\lambda > 0,\;x > 0,\;{\text{K(}}\alpha ,\lambda ,c )= \mathop \smallint \limits_{0}^{\infty } x^{c} \Big( 1 - \Big( {1 + \lambda x^{2} } \Big)e^{{ - \lambda \Big( {x^{2} + x} \Big)}} \Big)^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx$ Then,

$$ {\text{K(}}\alpha ,\lambda ,c )= \mathop \sum \limits_{i = 0}^{\alpha - 1} \mathop \sum \limits_{j = 0}^{i} \left( {\begin{array}{*{20}c} {\alpha - 1} \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} i \\ j \\ \end{array} } \right)( - 1)^{i} \lambda^{j} \mathop \int \limits_{0}^{\infty } x^{2j + c} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx $$

Proof

We know that $(1 - z)^{\alpha - 1} = \mathop \sum \limits_{i = 0}^{\alpha - 1} \left( {\begin{array}{*{20}c} {\alpha - 1} \\ i \\ \end{array} } \right)( - 1)^{i} z^{i}$

Therefore

$$ \begin{aligned} {\text{K(}}\alpha ,\lambda ,c )& = \mathop \int \limits_{0}^{\infty } x^{c} \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx \\ & = \mathop \int \limits_{0}^{\infty } x^{c} \mathop \sum \limits_{i = 0}^{\alpha - 1} \left( {\begin{array}{*{20}c} {\alpha - 1} \\ i \\ \end{array} } \right)( - 1)^{i} \left[ {\left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right]^{i} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx \\ & = \mathop \sum \limits_{i = 0}^{\alpha - 1} \left( {\begin{array}{*{20}c} {\alpha - 1} \\ i \\ \end{array} } \right)( - 1)^{i} \mathop \int \limits_{0}^{\infty } x^{c} \left[ {\left( {1 + \lambda x^{2} } \right)} \right]^{i} e^{{ - (i + 1)\lambda \left( {x^{2} + x} \right)}} dx \\ & = \mathop \sum \limits_{i = 0}^{\alpha - 1} \left( {\begin{array}{*{20}c} {\alpha - 1} \\ i \\ \end{array} } \right)( - 1)^{i} \mathop \int \limits_{0}^{\infty } x^{c} \mathop \sum \limits_{j = 0}^{i} \left( {\begin{array}{*{20}c} i \\ j \\ \end{array} } \right)\left( {\lambda x^{2} } \right)^{j} e^{{ - (i + 1)\lambda \left( {x^{2} + x} \right)}} dx \\ {\text{K(}}\alpha ,\lambda ,c )& = \mathop \sum \limits_{i = 0}^{\alpha - 1} \mathop \sum \limits_{j = 0}^{i} \left( {\begin{array}{*{20}c} {\alpha - 1} \\ i \\ \end{array} } \right)\left( {\begin{array}{*{20}c} i \\ j \\ \end{array} } \right)( - 1)^{i} \lambda^{j} \mathop \int \limits_{0}^{\infty } x^{2j + c} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx \\ \end{aligned} $$

The result of the Lemma follows by the definition of the gamma function.

The moments are

$$ \begin{aligned} E({\text{X}}) & = \alpha\uplambda{\text{K(}}\upalpha,\uplambda,1 )+ 2\upalpha \uplambda ^{2} {\text{K(}}\upalpha,\uplambda,4 )+ \alpha\uplambda^{2} {\text{K(}}\upalpha,\uplambda,3 )\\ E(X^{n} ) & = \upalpha \uplambda {\text{K(}}\upalpha,\uplambda,{\text{n)}} + 2\alpha \lambda^{2} {\text{K(}}\upalpha,\uplambda,{\text{n}} + 3 )+ \alpha \lambda^{2} {\text{K(}}\upalpha,\uplambda,{\text{n}} + 2 )\\ \end{aligned} $$

□

3.1 Moment Generating Function

Moment generating function can be obtained from following formula

$$ \begin{aligned} M_{X} (t) & = \mathop \int \limits_{0}^{\infty } e^{tx} \alpha \left( {\lambda + \lambda x^{2} + 2\lambda^{2} x^{3} } \right)\left[ {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right]^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx \\ M_{X} (t) & = \mathop \int \limits_{0}^{\infty } \alpha \left( {\lambda + \lambda x^{2} + 2\lambda^{2} x^{3} } \right)\left[ {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right]^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right) + tx}} dx \\ \end{aligned} $$

3.2 Characteristic Function

Characteristic function can be obtained from following formula

$$ \begin{aligned} \varphi_{X} (t) & = \mathop \int \limits_{0}^{\infty } e^{itx} \alpha \left( {\lambda + \lambda x^{2} + 2\lambda^{2} x^{3} } \right)\left[ {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right]^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx \\ \varphi_{X} (t) & = \mathop \int \limits_{0}^{\infty } \alpha \left( {\lambda + \lambda x^{2} + 2\lambda^{2} x^{3} } \right)\left[ {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right]^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right) + itx}} dx \\ \end{aligned} $$

3.3 Mean Deviation About Mean

The amount of scatter in a population is evidently measured to some extent by the totality of deviations from the mean and median. Mean deviation about the mean defined by

$$ \begin{aligned} {\text{MD(Mean)}} & = 2\upmu F(\upmu) - 2\upmu + 2\mathop \int \limits_{\upmu}^{\infty } xf(x)dx \\ MD(Mean) & = 2\;\upmu F(\upmu) - 2\upmu + 2\left( {2\alpha \lambda^{2} {\text{L(}}\upalpha,\uplambda,4,\upmu )+\upalpha\lambda^{2} {\text{L(}}\upalpha,\uplambda,3,\upmu )+\upalpha \uplambda {\text{L(}}\upalpha,\uplambda,2,\upmu )} \right) \\ \end{aligned} $$

where

$$ \begin{aligned} L(\alpha ,\lambda ,c,\upmu) & = \mathop \int \limits_{\upmu}^{\infty } x^{c} \left[ {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right]^{\alpha - 1} e^{{ - \lambda \left( {x^{2} + x} \right)}} dx \\ & = \mathop \sum \limits_{i = 0}^{\alpha - 1} C_{i}^{\alpha - 1} ( - 1)^{i} \lambda^{j} \left( {\mathop \int \limits_{\upmu}^{\infty } x^{2j + c + 1} e^{{ - (j + 1)\lambda \left( {x^{2} + x} \right)}} dx} \right). \\ \end{aligned} $$

Mean deviation about the Median defined by

$$ \begin{aligned} {\text{MD(Median)}} & = - M + 2\mathop \int \limits_{M}^{\infty } xf(x)dx \\ MD(Mean) & = - M + 2\left( {2\alpha \lambda^{2} {\text{L(}}\upalpha,\uplambda,4,{\text{M)}} + \alpha \lambda^{2} {\text{L(}}\upalpha,\uplambda,3,{\text{M)}} +\upalpha \uplambda {\text{L(}}\upalpha,\uplambda,2,{\text{M)}}} \right) \\ \end{aligned} $$

4 Distribution of Maximum and Minimum

Series, Parallel, Series–Parallel and Parallel–Series systems are general system structure of many engineering systems. The theory of order statistics provides a use-full tool for analysing life time data of such systems. Let $X_{1} ,X_{2} , \ldots ,X_{n}$ be a simple random sample from Generalized X-Exponential with cdf and pdf as in (2.1) and (2.2), respectively. Let $X_{(1)} ,X_{(2)} , \ldots ,X_{(n)}$ denote the order statistics obtained from this sample. The pdf of rth order statistics $X_{(r)}$ is given by,

$$ f_{r:n} (x) = \frac{1}{B(r,n - r + 1)}[F(x;\alpha ,\uplambda)]^{r - 1} [1 - F(x;\alpha ,\uplambda)]^{n - r} f(x;\alpha ,\uplambda) $$

where $F(x;\alpha ,\uplambda)$ and $f(x;\alpha ,\uplambda)$ are the cdf and pdf given by (2.1) and (2.2), respectively.

$$ \begin{aligned} f_{r:n} (x) &= \frac{1}{{B\left( {r,n - r + 1} \right)}}\left[ {\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{r - 1} \left[ {1 - \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{n - r} \\ & \quad \alpha e^{{ - \lambda \left( {x^{2} + x} \right)}} \left( {\lambda \left( {1 + \lambda x^{2} } \right)\left( {2x + 1} \right) - 2\lambda x} \right)\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha - 1} \\ \end{aligned} $$

(4.1)

Then the pdf of the smallest and largest order statistics $X_{(1)}$ and $X_{(n)}$ are respectively given by:

$$ \begin{aligned} f_{1} (x) & = \frac{1}{{{\text{B(}}1,{\text{n)}}}}\left[ {1 - \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{n - 1}\\ & \alpha e^{{ - \lambda \left( {x^{2} + x} \right)}} \left( {\lambda \left( {1 + \lambda x^{2} } \right)(2x + 1) - 2\lambda x} \right)\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha - 1} \\ f_{n} (x) & = \frac{1}{B(n,1)}\left[ {\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{n - 1}\\ & \alpha e^{{ - \lambda \left( {x^{2} + x} \right)}} \left( {\lambda \left( {1 + \lambda x^{2} } \right)(2x + 1) - 2\lambda x} \right)\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha - 1} \\ \end{aligned} $$

The cdf of $X_{(r)}$ is given by,

$$ \begin{aligned} F_{r:n} (x) & = \mathop \sum \limits_{j = r}^{n} \left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right)F^{j} (x)\left[ {1 - F(x)} \right]^{n - j} \\ F_{r:n} (x) & = \mathop \sum \limits_{j = r}^{n} \left( {\begin{array}{*{20}c} n \\ j \\ \end{array} } \right)\left[ {\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{j} \left[ {1 - \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{n - j} \\ \end{aligned} $$

(4.2)

Then the cdf of the smallest and largest order statistics $X_{(1)}$ and $X_{(n)}$ is respectively given by:

$$ \begin{aligned} F_{1} (x) & = 1 - \left[ {1 - \left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{n} \\ F_{n} (x) & = \left[ {\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right]^{n} . \\ \end{aligned} $$

Reliability of a series system having n components with independent and identically distributed (iid) GXED distribution is

$$ R(x) = \left( {\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right)^{n} $$

Reliability of a parallel system having n components with iid GXED distribution is

$$ R(x) = 1 - \left( {\left( {1 - \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} } \right)^{\alpha } } \right)^{n} $$

Both the reliability functions can be used in various reliability calculations.

5 Estimation

In this section, point estimation of the unknown parameters of the GXED by using the method of moments and method of maximum likelihood based on a complete sample data, is explained.

Let $X_{1} ,X_{2} , \ldots ,X_{n}$ are random sample taken from GXED. Let $m_{1} = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} x_{i} ,m_{2} = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} x_{i}^{2}$. Equating sample moments to population moments we get moment estimators for parameters.

$$ \begin{aligned} m_{1} & = 2\alpha \lambda^{2} {\text{K(}}\upalpha,\uplambda,4 )+\upalpha \uplambda ^{2} {\text{K}}(\upalpha,\uplambda,3) +\upalpha \uplambda {\text{K(}}\upalpha,\uplambda,1 )\\ m_{2} & = 2\alpha \lambda^{2} {\text{K(}}\upalpha,\uplambda,5 )+\upalpha \uplambda ^{2} {\text{K(}}\upalpha,\uplambda,4 )+\upalpha \uplambda {\text{K(}}\upalpha,\uplambda,2 )\\ \end{aligned} $$

The solution of these equations are moment estimators.

To find maximum likelihood estimator, consider likelihood function as,

$$ \begin{aligned} L(\alpha ,\lambda ) & = \mathop \prod \limits_{i = 1}^{n} f\left( {x_{i} } \right) \\ L(\alpha ,\lambda ) & = \mathop \prod \limits_{i = 1}^{n} \alpha e^{{ - \lambda ( x^{2}_{i} + x_{i} )}} \left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right)\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{\left( { - \lambda ( x^{2}_{i} + x_{i} } \right)}} } \right)^{\alpha - 1} \\ L(\alpha ,\lambda ) & = (\alpha )^{n} e^{{ - \lambda \mathop \sum \limits_{i = 1}^{n} ( x^{2}_{i} + x_{i} )}} \mathop \prod \limits_{i = 1}^{n} \left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right)\mathop \prod \limits_{i = 1}^{n} \left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x^{2}_{i} + x_{i} } \right)}} } \right)^{\alpha - 1} \\ { \log }\;L(\alpha ,\lambda ) & = n{ \log }\alpha - \lambda \mathop \sum \limits_{i = 1}^{n} \left( {x_{i}^{2} + x_{i} } \right) + \mathop \sum \limits_{i = 1}^{n} \log \left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right) \\ &\quad+ \left( {\alpha - 1} \right)\mathop \sum \limits_{i = 1}^{n} { \log }\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( { x^{2}_{i} + x_{i} } \right)}} } \right) \\ \end{aligned} $$

The first partial derivatives of the log-likelihood function with respect to the two-parameters are

$$ \begin{aligned} \frac{\partial }{{\partial\upalpha}}{ \log }\;L(\alpha ,\lambda ) & = \frac{n}{\alpha } + \mathop \sum \limits_{i = 1}^{n} { \log }\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x^{2}_{i} + x_{i} } \right)}} } \right) \\ \frac{\partial }{{\partial\upalpha}}{ \log }\;L(\alpha ,\lambda ) & = 0\;{\text{implies}}\;\hat{\alpha } = - \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} { \log }\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x^{2}_{i} + x_{i} } \right)}} } \right) \\ \end{aligned} $$

(5.1)

and

$$ \begin{aligned} \frac{\partial }{{\partial\uplambda}}{ \log }\;L(\alpha ,\lambda ) & = - \mathop \sum \limits_{i = 1}^{n} \left( { x^{2}_{i} + x_{i} } \right) + \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\left( {2x_{i} + 1} \right)\left( {1 + 2\lambda x_{i}^{2} } \right) - 2x_{i} } \right)}}{{\left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right)}} \\ & \quad + (\alpha - 1)\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} \left( {x_{i}^{2} + x_{i} } \right) - e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} x_{i}^{2} }}{{\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} } \right)}} \\ \frac{\partial }{{\partial\uplambda}}{ \log }\;L(\alpha ,\lambda ) & = 0\;{\text{implies}} \\ \mathop \sum \limits_{i = 1}^{n} \left( {x^{2}_{i} + x_{i} } \right) & = \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\left( {2x_{i} + 1} \right)\left( {1 + 2\lambda x_{i}^{2} } \right) - 2x_{i} } \right)}}{{\left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right)}} \\ & \quad + (\alpha - 1)\mathop \sum \limits_{i = 1}^{n} \frac{{\left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} \left( {x_{i}^{2} + x_{i} } \right) - e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} x_{i}^{2} }}{{\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} } \right)}} \\ \end{aligned} $$

(5.2)

Solving this system in $\alpha$ and $\lambda$ gives the maximum likelihood estimates (MLE) of $\alpha$ and $\lambda$. It can be obtain estimates using R software by numerical methods. The initial values have been chosen arbitrarily. Parameter estimation is done using the non-linear method in R software.

6 Asymptotic Confidence bounds

In this section, we derive the asymptotic confidence intervals of these parameters when $\alpha > 0$ and $\lambda > 0,$ since the MLEs of the unknown parameters $\alpha > 0$ and $\lambda > 0$ cannot be obtained in closed forms, by using variance covariance matrix $I^{ - 1}$, where $I^{ - 1}$ is the inverse of the observed information matrix which is defined as follows

$$ \begin{aligned} I^{ - 1} & = \left( {\begin{array}{*{20}c} { - \frac{{\partial^{2} L}}{{\partial \alpha^{2} }}} & { - \frac{{\partial^{2} L}}{\partial \alpha \partial \lambda }} \\ { - \frac{{\partial^{2} L}}{\partial \lambda \partial \alpha }} & { - \frac{{\partial^{2} L}}{{\partial \lambda^{2} }}} \\ \end{array} } \right) \\ & = \left( {\begin{array}{*{20}c} {var(\hat{\alpha })} & {cov(\hat{\alpha },\hat{\lambda })} \\ {cov(\hat{\lambda },\hat{\alpha })} & {var(\hat{\lambda })} \\ \end{array} } \right) \\ \end{aligned} $$

The second partial derivatives are as follows

$$ \begin{aligned} \frac{{\partial^{2} L}}{{\partial \alpha^{2} }} & = - \frac{n}{{\alpha^{2} }} \\ \frac{{\partial^{2} L}}{{\partial \lambda^{2} }} & = \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right)\left[ {2x_{i}^{2} \left( {2x_{i} + 1} \right)} \right] - \left( {\left( {2x_{i} + 1} \right)\left( {1 + 2\lambda x_{i}^{2} } \right) - 2x_{i} } \right)^{2} }}{{\left( {\lambda \left( {1 + \lambda x_{i}^{2} } \right)\left( {2x_{i} + 1} \right) - 2\lambda x_{i} } \right)^{2} }} \\ & \quad + \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} } \right)\left[ {\left( {e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} x_{i}^{2} - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} \left( {x_{i}^{2} + x_{i} } \right)} \right) + e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} \left( {x_{i}^{2} + x_{i} } \right)} \right]}}{{\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} } \right)^{2} }} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {\left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} \left( {x_{i}^{2} + x_{i} } \right) - e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} x_{i}^{2} } \right)^{2} }}{{\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} } \right)^{2} }} \\ \frac{{\partial^{2} L}}{\partial \alpha \partial \lambda } & = \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} \left( {x_{i}^{2} + x_{i} } \right) - e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} x_{i}^{2} }}{{\left( {1 - \left( {1 + \lambda x_{i}^{2} } \right)e^{{ - \lambda \left( {x_{i}^{2} + x_{i} } \right)}} } \right)}} \\ \end{aligned} $$

We can derive the $(1 - \delta )100\%$ confidence intervals of the parameters $\alpha$ and $\lambda$ by using variance matrix as in the following forms

$$ \hat{\alpha } \pm Z_{{\frac{\delta }{2}}} \sqrt {var(\hat{\alpha }) } \;{\text{and}}\;\hat{\lambda } \pm Z_{{\frac{\delta }{2}}} \sqrt {var(\hat{\lambda })} $$

where $Z_{{\frac{\delta }{2}}}$ is the upper $\left( {\frac{\delta }{2}} \right){\text{th}}$ percentile of the standard normal distribution.

7 Simulation

We assess the performance of the maximum likelihood estimators given by (5.1) and (5.2) with respect to sample size n. The assessment was based on a simulation study:

• (i) Generate hundred samples of size n from (2.2). The inversion method was used to generate samples, i.e., values of the GXED distribution random variable are generated using

  $$ \left( {1 + \lambda x^{2} } \right)e^{{ - \lambda \left( {x^{2} + x} \right)}} = 1 - U^{{\frac{1}{\alpha }}} $$

  where $U \sim U(0,1)$ is a uniform variate on the unit interval.

• (ii) Compute the maximum likelihood estimates for the hundred samples, say $(\alpha_{i,} \lambda_{i} )$ for $i = 1,2, \ldots , 100$.

• (iii) Compute the biases and mean squared errors using $bias_{h} (n) = \frac{1}{100}\mathop \sum \limits_{i = 1}^{100} \left( {\hat{h}_{i} - h} \right)$ and $MSE_{h} (n) = \frac{1}{100}\mathop \sum \limits_{i = 1}^{100} \left( {\hat{h}_{i} - h} \right)^{2}$ for $h = (\alpha ,\lambda )$. We repeated these steps for n = 10, 20, …, 100 with different values of parameters, for computing $bias_{h} (n)$ and $MSE_{h} (n)$ for n = 10, 20, …, 100.

	$\alpha$		$\lambda$
	Bias	MSE	Bias	MSE
$(\alpha = 0.5,$$\lambda = 0.001$)N
10	0.022574	0.005095843	0.0001423755	2.027078 × 10−07
50	0.0028631	0.0004098582	3.40494 × 10−06	5.796808 × 10−10
100	0.0017267	0.0002981372	1.29409 × 10−06	1.674669 × 10−10
$(\alpha = 1,\lambda = 0.5$) N
10	− 0.00351507	0.0001235572	− 0.00721473	0.0005205233
50	0.001504456	0.0001131694	0.001179188	6.952422 × 10−05
100	0.001201623	0.0001443898	0.000886022	7.85035 × 10−05
$(\alpha = 1.5,\lambda = 1$) N
10	0.03376	0.011398	− 0.00575	0.000331
50	0.002923	0.000427	− 0.000568	1.61136 × 10−05
100	0.0005311	2.820577 × 10−05	0.0001264	1.59848 × 10−06

8 Application

In this section, we present the analysis of a real data set using the ${\text{GXED(}}\alpha ,\lambda )$ model and compare it with the other fitted model Generalized Lindley distribution (GLD) (Nadarajah et al. 2011) using Akaike information criterion (AIC), Bayesian information criterion (BIC) and Kolmogorov–Smirnov (K–S) statistic. We considered the Survival data for psychiatric inpatients (Klein and Moesch Berger 1997) to estimate the parameter values. The data are given below.

1

1

2

22

30

28

32

11

14

36

31

33

33

37

35

25

31

22

26

24

35

34

30

35

40

39

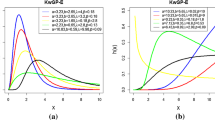
Table 1 provides the parameter estimates, standard errors obtained by inverting the observed information matrix and log-likelihood values. Table 2 provides values of AIC, BIC, and p values based on the KS statistic. The corresponding probability plots are shown in Fig. 4. We can see that the GXED distribution gives the smallest AIC value, the smallest BIC value, the largest p value based on the KS statistic. Hence, the GXED distribution provides the best fit based on the AIC values, BIC values, p values based on the KS statistic. The Failure rate and probability plots again show that the GXED distribution provides the best fit.

Table 1 MLEs of parameters, SE and Log-likelihood

Table 2 AIC, BIC, KS Statistic and p value of the model

Fig. 4

Probability plot for GXED and GLD (Data set 1)

The variance covariance matrix $I^{ - 1}$ of the MLEs under the Generalized X-Exponential distribution for the data set 1 is computed as $\left( {\begin{array}{*{20}c} {2.853228 \times 10^{ - 2} } & {3.981029 \times 10^{ - 5} } \\ {3.981029 \times 10^{ - 5} } & {1.603055 \times 10^{ - 7} } \\ \end{array} } \right)$

Thus, the variances of the MLE of $\alpha$ and $\lambda$ is $var(\hat{\alpha })$ = $2.853228 \times 10^{ - 2}$ and $var(\hat{\lambda })$ = $1.603055 \times 10^{ - 7}$. Therefore, 95% confidence intervals for $\alpha$ and $\lambda$ are [0.64168, 0.750658] and [0.001710366, 0.001968678] respectively.

8.1 Data Set 2

The data consist of the lifetimes of 50 devices, Aarset (1987) and it is provided below.

0.1

0.2

1

1

1

1

1

2

3

6

7

11

12

18

18

18

18

18

21

32

36

40

45

46

47

50

55

60

63

63

67

67

67

67

72

75

79

82

82

83

84

84

84

85

85

85

85

85

86

86

The parameter estimates, standard errors and the various measures are given in Table 3. The corresponding probability plots are shown in Fig. 5. We can see again that the GXED distribution gives the smallest AIC value, the smallest BIC value, and largest p value based on the KS statistic, see Table 4. Hence, the GXED distribution again provides the best fit based on the AIC values, BIC values, p values based on the KS statistic. The Failure rate and probability plots again show that the GXED distribution provides the better fit.

Table 3 MLEs of parameters, SE and Log-likelihood

Fig. 5

Probability plot for GXED and GLD (Data set 2)

Table 4 AIC, BIC, KS Statistic and p value of the model

The variance covariance matrix $I^{ - 1}$ of the MLEs under the Generalized X-Exponential distribution for the data set 2 is computed as $\left( {\begin{array}{*{20}c} {2.559555 \times 10^{ - 3} } & {1.707983 \times 10^{ - 6} } \\ {1.707983 \times 10^{ - 6} } & {5.462464 \times 10^{ - 9} } \\ \end{array} } \right)$.

Thus, the variances of the MLE of $\alpha$ and $\lambda$ is $var\left( {\hat{\alpha }} \right)$ = $2.559555 \times 10^{ - 3}$ and $var\left( {\hat{\lambda }} \right)$ = $5.462464 \times 10^{ - 9}$. Therefore, 95% confidence intervals for $\alpha$ and $\lambda$ are [0.3063695, 0.3299066] and [0.0002845985, 0.0003189833] respectively.

9 Conclusion

Here we introduced a new distribution having bathtub shaped failure rate, which generalizes the X-Exponential distribution. Several properties of the distribution are derived including the hazard rate function, moments, moment generating function etc. Also we studied the maximum likelihood estimation of this distribution. The usefulness of the new distribution is illustrated by means of two real data set. The first data set provides GXED distribution has smallest AIC value, the smallest BIC value, the largest p value based on the KS statistic, compared to GLD distribution. And also the second data set provides GXED distribution has smallest AIC value, the smallest BIC value, the largest p value based on the KS statistic, compared to GLD distribution. It shows that the proposed distribution is a better alternative among bathtub shaped failure rate models.