A novel Pythagorean fuzzy PERT approach to measure criticality with multi-criteria in project management problems

Abstract

In this research article, the credibility distribution is defined as a Pythagorean fuzzy restriction, which serves as an elastic constraint on the possible input states of a variable. This definition relates the credibility theory to the theory of Pythagorean fuzzy sets. The current study first defines Cauchy Pythagorean fuzzy numbers and offers a novel method for precise and analytic determination of the inverse credibility distribution. Examples with various degrees of credibility are shown numerically and graphically. Afterwards, we focus on the identification of critical paths in project networks. For this purpose, Pythagorean fuzzy Logic and Multi-Criteria Decision-Making (MCDM) methodologies are combined in a novel structure that is provided to expand the applications of the project scheduling systems. The development of the Pythagorean Fuzzy Program Evaluation and Review Technique (PFPERT), however, was motivated by the vagueness of the time and cost parameters. The primary objective is to find the critical route while considering some decision criteria such as length, duration, cost, resources, and risk factors. All of the criteria are evaluated mathematically based on Pythagorean fuzzy logic and integrated using the VIKOR approach to obtain the resulting critical route. To further clarify the potentials and capabilities of the suggested strategy, the proposed algorithm is successfully examined for a case study related to a greenhouse construction project.

1 Introduction

The Pythagorean fuzzy PERT approach is an extension of the classical PERT, incorporating Pythagorean fuzzy numbers to handle uncertainties and imprecise information in project management problems. It allows for a more comprehensive and flexible representation of the uncertainty associated with activity durations and criticality measurements. This approach is particularly useful when dealing with multi-criteria decision-making problems in project management, where there are multiple factors to consider in determining criticality. Considering various criteria simultaneously, the work enables project managers to make more informed and well-balanced decisions when prioritizing activities and allocating resources. The method aims to assist project managers in concentrating their attention on the most time-sensitive tasks and managing risks by identifying critical activities and quantifying their criticality ratings. Thus, it offers a powerful tool to handle uncertainties and complexities in project planning and execution, ultimately leading to more successful project outcomes.

Numerous problems are characterized as mathematical relationships with ambiguous information in several research domains, including optimal control and operations research. The Fuzzy Set (FS) theory, established in 1965 by Zadeh (1965), can be used to represent the imprecision in such problems. In this theory, several kinds of fuzzy numbers (FNs) and their arithmetic are required in the modeling course. In 1975, Zadeh (1975) introduced these FNs to deal with imprecise numerical quantities. In order to extend standard algebraic operations to FNs, Dubois and Prade (1987) proposed a fuzzification principle. The extension theory for fuzzy fundamental operations was first introduced by Zadeh (1975) in 1975. Alternate initializations for an interval approach were based on the $\alpha$-cut for triangular and trapezoidal FNs. This method is simple to use and has low complexity for routine operations. However, when there are more terms being multiplied, their approach could result in greater powers of $\alpha$. Researchers have also proposed various defuzzification techniques for FNs that do not rely on the $\alpha$-cut in order to avoid these problems Lee-Kwang and Lee (1999).

Possibility theory was suggested by Zadeh (1978) in 1965. It is believed that the possibility measure is an effective way to cope with uncertainty, particularly in situations where there are few data points. Various researchers have examined possibility theory, including Dubois and Prade (1987) and Klir (1999). The necessity measure is the dual component of the possibility measure, nevertheless, neither the possibility measure nor the necessity measure are self-dual. Li and Liu (2008) created the self-dual measure known as the credibility measure, which is described as the average of possibility and necessity measures. In brief, credibility measures are used to estimate the approximate probability that a fuzzy event will take place. Possibility, necessity, and credibility measures have practical implications in a wide range of applications, including risk assessment, decision-making, safety analysis, system reliability, quality control, expert systems, and data fusion. By quantifying uncertainty and degrees of belief, these measures provide valuable insights and support for making informed and robust decisions in various domains. In the context of PERT network analysis in project management, the terms ‘possibility,’ ‘necessity,’ and ‘credibility’ refer to different aspects of the estimated durations and scheduling of project activities. Possibility, in PERT analysis, refers to the likelihood or probability that a particular activity will be completed within a certain duration. It is often associated with optimistic, most likely, and pessimistic estimates for each activity. Necessity in PERT analysis relates to the idea that certain activities must be completed before others can start. It reflects the logical dependencies between activities in a project. Credibility in PERT analysis refers to the degree of confidence or trust in the project duration estimates for each activity. It helps project managers assess the reliability of the estimated durations. Activities with low credibility may require more detailed analysis or additional expert input to ensure the accuracy of their estimates. A higher level of credibility instills confidence in the project schedule and can lead to better decision-making. By considering these factors within the PERT network, project managers can develop more robust schedules, identify critical paths, and effectively manage project risks and uncertainties.

After being used successfully in a number of domains, FS theory is being extended by numerous academics. Readers are strongly encouraged to consult the sources (Chen and Lee (2010), Chen and Wang (1995), Chen and Wang (2010), Chen et al. (2009), Chen and Jian (2017), Chen et al. (2019), Liu et al. (2020), Lin et al. (2006), Meng et al. (2020)) for more comprehensive explanation of fuzziness in practical applications. The theory of Pythagorean fuzzy set (PFS), introduced by Yager and Abbasov (2013), Yager (2013) in 2013 as a continuation of intuitionistic fuzzy set (IFS) theory, which was originally developed in 1986 by Atanassov (1983), has caught the interest of academic researchers over the past decade. Even if an additional degree of membership has been provided in IFS to reflect hesitation, this restriction still prevents pairs from being chosen from a triangular zone. PFS expands the selection space of eligible pairs while taking into account the two degrees of membership, i.e., acceptance and rejection, with the restriction that their square sums must not be greater than 1. As a result, it is better equipped than FSs and IFSs to deal with uncertainty in real-world situations. The importance of Cauchy FNs in FN systems cannot be denied. The Cauchy FNs are based on an $\alpha$-stable distribution, which can be defined by a probability distribution function. This idea can be used to model many real-life situations more realistically. Pythagorean fuzzy numbers (PFNs) are superior to FNs and intuitionistic fuzzy numbers (IFNs) in several ways. In fuzzy logic systems, PFNs allow modeling and mitigation of the impacts of uncertainty. Triangular PFNs were defined by Luqman et al. (2021) with applications in risk assessments. Akram et al. (2021) defined LR-type PFNs and applied them to PF linear programming problems. A robust theory for generalized PFNs was recently established with application to the hierarchical clustering process by Akram et al. (2021a, 2023a), Habib et al. (2022). Trapezoidal PFNs were defined by Akram et al. (2022) and used as network parameters to assess maximal flow. Readers are encouraged to consult Akram and Habib (2023), Habib and Akram (2024), Nawaz and Akram (2023), Zahid and Akram (2023) for additional notations and applications.

The practice of project management is expanding as businesses become quicker and faster because more work is allocated to groups of individuals. Two of the most influential information areas in project management are project time management and project risk management. The Critical Path Method (CPM) and Program Evaluation and Review Technique (PERT) are project management techniques used to identify the most critical tasks in a project and also estimate the minimum amount of time required to complete the project. These are oriented towards activity. It is a tool that helps project managers plan, schedule, and control projects effectively. The term ‘critical’ in the context of projects refers to the activities or tasks that have a significant impact on the overall project duration. These activities are crucial to the successful completion of the project within the desired timeframe. Defining project criticality involves identifying the critical path and critical success factors, which play a crucial role in project management. Project managers need to focus on these critical elements and allocate resources and attention accordingly to ensure the project’s successful and timely completion. Regular monitoring, risk management, and contingency planning are essential to address potential challenges and uncertainties associated with critical tasks and factors. Indeed, a critical path is the longest sequence of tasks that must be completed in a specific order to ensure that the project is completed on time. PERT is particularly useful for projects with a high level of uncertainty and complexity, where accurate estimation of activity durations is challenging. In PERT, each activity is assigned three time estimates: optimistic, most likely, and pessimistic. These time estimates represent the best-case, most likely, and worst-case scenarios for the activity’s duration.

In project management, risk analysis aims to identify, assess and prioritize several types of risks. These risks can be categorized into various types, including schedule risks, cost risks, technical risks, resource risks, market risks, environmental risks, quality risks and security risks. Project managers then develop risk response strategies to mitigate, transfer or accept risks based on their significance and potential impact on the project’s objectives. FNs play a significant role in various fields and have several important applications due to their ability to represent and handle uncertainties, vagueness and imprecise information. The application of FNs in project network and risk analysis has helped project managers and decision-makers to cope with uncertainties and vagueness, resulting in more reliable and effective project planning and scheduling. Dealing with uncertainty in project networks, especially in the context of risk analysis, presents several specific challenges for researchers. These challenges can impact the accuracy, reliability and effectiveness of risk assessment strategies. Some of the key challenges include limited data availability, subjectivity and expert opinion, uncertain interdependencies, modeling complexity, etc. Researchers in project management continually strive to develop innovative methods and approaches to address these challenges. Literature has a number of attempts to apply FNs to evaluate critical path. To summarize, a brief comparison of previous works is presented in Table 1.

Table 1 Various project management techniques in existing literature

Project risk analysis is a crucial process in project management which involves identifying, assessing, and managing potential risks that could impact the successful completion of a project. It aims to actively address uncertainties and threats while also capitalizing on opportunities to improve project outcomes. The ultimate goal of project risk analysis is to increase the likelihood of project success by anticipating and managing potential challenges effectively. Nieto-Morote and Ruz-Vila (2011) discussed fuzzy approach to construction project risk assessment. Carr and Tah (2001) illustrated construction project risk management system and utilized an hierarchical risk breakdown structure with fuzzy assessments. Project teams should be prepared to adapt and adjust their strategies as new risks emerge or existing risks evolve. In this regard, Zeng et al. (2009) proposed an application of fuzzy based decision making technique to construction project risk assessment. One of the main strategies for reducing the schedule risk is the PERT. Similar to schedule risk analysis, PERT also emphasizes the diversity of the activity periods. Malcolm et al. (1959) initially presented a statistical approach to take into account the effects of variability in their renowned study on the PERT. In actuality, a large quantity of information is needed to model an unknown duration by a probability distribution, however, in most practical situations, only a small amount of information is available regarding the processing time of each activity of the project. As a result, PF techniques appeared to be significantly more suitable than those that are only probabilistic Fargier et al. (2000), Mazlum and Guneri (2015). In fact, addressing both variability and path interdependencies is made simple by the use of FNs (to model durations). Using FNs in project network and risk analysis enhances the accuracy and completeness of the analysis while providing decision-makers with a comprehensive view of the project’s uncertainties. This supports effective risk management, better resource utilization, and informed decision-making, ultimately increasing the chances of project success. Early in the 1980 s, the first paper on fuzzy PERT was released Chanas and Kamburowski (1981). Later, Chen and Chang (2001) found multiple possible critical paths using fuzzy PERT. There is a large body of related research, some approaches can be seen in Agyei (2015), Dubois et al. (2003).

MCDM is a vital approach used in various fields to support decision-making processes when multiple criteria or objectives need to be considered simultaneously. Its importance stems from the fact that many real-world decisions are complex and involve multiple conflicting factors. Opricovic and Tzeng (2004) created an MCDM technique known as VIKOR method. VIKOR stands for ‘VIekriterijumsko KOmpromisno Rangiranje’ which translates to ‘multi-criteria compromise ranking. The VIKOR approach is based on the concept of compromise programming, in which the decision-maker looks for the best possible compromise among competing criteria Mishra et al. (2022), Zahid and Akram (2023). Multi-criteria project management problems are those that involve the management of projects with multiple objectives or criteria to be met. Such problems can arise in many different contexts, including engineering, construction, software development, and organizational management. Through a weighted decision matrix, one can compare various options or criteria based on their relative importance. In literature, determination of critical path involving multi-criteria are short listed. Zammori et al. (2009) discussed a fuzzy multi-criteria approach for critical path definition. They used TOPSIS method to define resulting critical path. A few more researchers Amiri and Golozari (2011), Dorfeshan et al. (2018) used time, cost, quality and risk criteria and applied some MCDM methods to select project-critical path.

Even though fuzzy PERT is a well-established method for project scheduling and management, there is always potential for improvement. Because PFSs have naturally ambiguous membership functions, they have a variety of benefits over FSs and IFSs. Through IFSs, certain real networks have been optimized. However, in a number of real-world instances, the sum of the truthness and falseness values of time durations may be higher than 1. Moreover, since the project managers can gain a variety of advantages from applying several criteria to problem-solving in project management, therefore, we use PERT with multi-criteria. Thus, the objective of this work is to offer more room for grading, and to cope with such kind of data by combining PFS theory and MCDM techniques to expand the applications of project scheduling systems.

The main contributions of this study are as follows:

• 1. The paper focuses on the concept of credibility distribution within the context of PFNs. A new definition of credibility for PF variables is presented in this regard.

• 2. Cauchy PFNs along with its arithmetic operations and graphical representation are proposed. To axiomatize their credibility measure, we concentrate on a few more distinct forms of PFNs, such as triangular, trapezoidal, and LR-type PFNs.

• 3. The paper introduces a novel method for determining the inverse credibility distribution and proposes a new ranking technique by extending existing theories or introducing innovative concepts related to Cauchy PFNs and their use in project management.

• 4. To broaden the applicability of project scheduling systems, the paper likely introduces a mathematical framework that combines MCDM techniques and the PF Logic in PERT approach.

• 5. The paper explores the application of the proposed approach to multi-criteria decision-making in project management. Finding the critical route is the main goal while taking certain decision criteria into account, such as the length, time, cost, resources, and risk considerations. All of the criteria are mathematically analyzed based on PF logic and combined using the VIKOR technique.

• 6. Additionally, the research provides practical insights into how the developed framework can be applied to real-world project management problems. For this purpose, we examine a case study in project management related to greenhouse construction project plan with multi-criteria. We have applied the suggested approach to identify the most critical route using PF data in the project network.

• 7. The paper demonstrates the superiority of the proposed solution by showing how it can yield meaningful insights into route criticality by demonstrating its effectiveness in real cases.

The current research content is structured in the following way: Sect. 2 reviews some fundamental ideas and provides the definitions of a few specific PFNs. In Sect. 3, we define Cauchy PFNs, their $\alpha$ and $\beta$-cuts and arithmetic operations. Section 4 gives the concept of possibility, necessity and credibility measures for PFSs. Moreover, the credibility distribution functions of Cauchy PFNs as well as of other PFNs are developed along with their graphical interpretation. We illustrate the defuzzification index based on expected values of PFNs. Section 5 concerns the ranking methodology for PFNs. Section 6 presents the project planning through PFPERT in detail. Section 7 provides formulas of all decision criteria to measure criticality. Section 8 discusses VIKOR method for critical route detection. Section 9 covers the implementation of the suggested methodology on a case study in project management related to greenhouse construction project plan. Section 10 concerns results and discussion related to this case study. Section 11 describes the advantages of proposed method and its future scope. Conclusions and upcoming research are covered in the last section.

2 Fundamental concepts

This section reviews the fundamental notions related to Cauchy distribution; possibility, necessity, and credibility measures; and several types of PFNs.

2.1 Cauchy distribution

A specific subclass of the $\alpha$-stable distributions for $\alpha =1$ is the Cauchy distribution. But unlike most $\alpha$-stable distributions, it has a probability density function which is mathematically stated in Eq. 1.

$$\begin{aligned} P_{C}(x)=\frac{\gamma }{\pi ((x-\mu )^2+ \gamma ^2)}, \end{aligned}$$

(1)

where the parameters $\mu$ and $\gamma ~(>0)$ determine the peak position and the $\frac{1}{2}$ width at $\frac{1}{2}$ maximum, respectively. Here, the Cauchy distribution is depicted by the symbol $C(\mu , \gamma )$. The mean, variance, and higher moments are unquantifiable, while the mode and median are both $\mu$. A few other probability distributions have a tight relationship with the Cauchy distribution. The scale factor $\gamma$ determines how hefty the Cauchy distribution’s tail will be.

2.2 Possibility, necessity and credibility measures

Consider a fuzzy subset P of universe U which is characterized by a membership function $\mu _P,$ where $\mu _P(p)$ indicates the compatibility of p with the concept labeled P. Let X be a variable belongs to U. Then, the formulas for possibility (Pos) and necessity (Nec) measures, defined by Zadeh (1978), are given in Eqs. 2 and 3.

$$\begin{aligned} Pos\{X ~is ~P\}\equiv & {} \sup _{p\in P} \pi _X\{p\} \in [0,1], \end{aligned}$$

(2)

$$\begin{aligned} Nec\{X ~is ~P\}\equiv & {} 1- \sup _{p\in P^c} \pi _X\{p\}. \end{aligned}$$

(3)

Here, $\pi _X\{p\}$ is the possibility distribution function of $\prod _X$ (a possibility distribution associated with variable X).

The more general definition of possibility measure which extends the previous definition to FSs is expressed in Eq. 4.

$$\begin{aligned} Pos\{X ~is ~P\} \equiv \pi (P) \equiv \sup _{p\in P} \mu _{P}(p) \bigwedge \pi _X(p). \end{aligned}$$

(4)

For a fuzzy variable $\xi$ with membership function $\mu ,$ the credibility of $\xi \in \beta \subset R,$ defined by Liu and Liu (2002) in Eq. 6.

$$\begin{aligned} Cr\{\xi \in \beta \}= & {} \frac{1}{2}(Pos\{\xi \in \beta \} + Nec\{\xi \in \beta \}) \end{aligned}$$

(5)

$$\begin{aligned}= & {} \frac{1}{2}\left( \sup _{x\in \beta } \mu (x) + 1- \sup _{x\in \beta ^c} \mu (x)\right) . \end{aligned}$$

(6)

This formula was extended by Mandal et al. (2010) in the following form given in Eq. 7.

$$\begin{aligned} Cr\{\xi \in \beta \} = \rho ~Pos\{\xi \in \beta \} + (1-\rho ) ~Nec\{\xi \in \beta \},~~0\le \rho \le 1. \end{aligned}$$

(7)

A nonempty set $\varTheta$ representing sample space, a set$\mathcal {P}$ showing the power set of $\varTheta$ and Cr,  which is credibility measure on $\mathcal {P}$ constitute for a credibility space $(\varTheta , \mathcal {P}(\varTheta ),Cr).$ Li and Liu (2008) defined credibility distribution $\varPhi$ for fuzzy variable $\xi$ (a function from credibility space $(\varTheta , \mathcal {P}(\varTheta ),Cr)$ to set of real numbers) as in Eq. 8.

$$\begin{aligned} \varPhi (x) = Cr \{\theta \in \varTheta ~|~ \xi (\theta ) \le x \}. \end{aligned}$$

(8)

Here, $\varPhi (x)$ (where $\varPhi : R \rightarrow [0,1]$) is the credibility that fuzzy variable $\xi$ takes a value which is smaller than or equal to x. Liu proved that $\varPhi$ is nondecreasing function on R in addition with $\varPhi (-\infty )=0$ and $\varPhi (+\infty )=1.$

Based on credibility function, the expected value of fuzzy variable $\xi$ is also defined by Liu and Liu (2002) and given in Eq. 9.

$$\begin{aligned} E[\xi ] = \int _0^{+\infty } Cr\{\xi \ge r\} dr - \int _{-\infty }^0 Cr\{\xi \le r\} dr. \end{aligned}$$

(9)

2.3 Pythagorean fuzzy numbers

A PFN $\tilde{N}=(n_1,n_2;~l,r;~l',r')_{LR}$ is defined by Habib et al. (2022) is an LR-type PFN, if its membership function (MF) and non-membership function (non-MF) are, respectively, defined as follow.

$$\begin{aligned} \mu _{\tilde{N}}(a)= & {} {\left\{ \begin{array}{ll} L\left( \frac{n_1-a}{l}\right) , &{} a \le n_1,~l> 0 \\ 1, &{} n_1 \le a \le n_2\\ R\left( \frac{a-n_2}{r}\right) , &{} a \ge n_2,~r> 0 \end{array}\right. },\\ \nu _{\tilde{N}}(a)= & {} {\left\{ \begin{array}{ll} L'\left( \frac{n_1-a}{l'}\right) , &{} a \le n_1,~l'> 0\\ 0, &{} n_1 \le a \le n_2 \\ R'\left( \frac{a-n_2}{r'}\right) , &{} a \ge n_2,~r' > 0 \end{array}\right. }, \end{aligned}$$

such that ${\mu _{\tilde{N}}}^2 + {\nu _{\tilde{N}}}^2 \le 1,$ where, $l \le l',~r \le r';~L$ and $R'$ are monotone, continuous, increasing functions; and $L'$ and R are monotone, continuous, decreasing functions from $[0.\infty )$ to [0, 1] such that $L(0)=R(0)=1,~\lim _{a\rightarrow \infty } R(a)=\lim _{a\rightarrow \infty } L(a)=0,~L'(0)=R'(0)=0,~\lim _{a\rightarrow \infty } R'(a)=\lim _{a\rightarrow \infty } L'(a)=1.$ The real interval $[n_1,n_2]$ is called set of mean values of $\tilde{N}.$ l and r are left and right spreads of $\mu _{\tilde{N}};$ $l'$ and $r'$ are left and right spreads of $\nu _{\tilde{N}},$ respectively.

A PFN $\tilde{N}=\langle [n_1,n_2,n_3,n_4];\xi _{\tilde{N}},\eta _{\tilde{N}}\rangle$ defined by Akram et al. (2022) is said to be trapezoidal if its MF and non-MF are respectively given as

$$\begin{aligned} \mu _{\tilde{N}}(a)= & {} \left\{ \begin{array}{cc} \dfrac{a-n_1}{n_2-n_1} \xi _{\tilde{N}},~~~ n_1 \le a< n_2 \\ \xi _{\tilde{N}},~~~~~~~~~~~~~~ n_2 \le a \le n_3 \\ \dfrac{n_4-a}{n_4-n_3} \xi _{\tilde{N}},~~~ n_3< a \le n_4 \\ 0,~~~~~~~~ \textrm{otherwise} \end{array}\right. ,\\ \nu _{\tilde{N}}(a)= & {} \left\{ \begin{array}{cc} \dfrac{n_2-a+\eta _{\tilde{N}}(a-n_1)}{n_2-n_1},~~~ n_1 \le a< n_2 \\ \eta _{\tilde{N}},~~~~~~~~~~~~~~~~~~~~~~~~~~ n_2 \le a \le n_3 \\ \dfrac{a-n_3+\eta _{\tilde{N}}(n_4-a)}{n_4-n_3},~~~ n_3 < a \le n_4 \\ 1,~~~~~~~~ \textrm{otherwise } \end{array}\right. . \end{aligned}$$

Similarly, a PFN $\tilde{N}=\langle [n_1,n_2,n_3];\xi _{\tilde{N}},\eta _{\tilde{N}}\rangle$ defined by Luqman et al. (2021) is said to be triangular if its MF and non-MF are respectively given as

$$\begin{aligned} \mu _{\tilde{N}}(a)= & {} \left\{ \begin{array}{cc} \dfrac{a-n_1}{n_2-n_1} \xi _{\tilde{N}},~~~ n_1 \le a< n_2 \\ \dfrac{n_3-a}{n_3-n_2} \xi _{\tilde{N}},~~~ n_2 \le a \le n_3 \\ 0,~~~~~~~~ \textrm{otherwise} \end{array}\right. ,\\ \nu _{\tilde{N}}(a)= & {} \left\{ \begin{array}{cc} \dfrac{n_2-a+\eta _{\tilde{N}}(a-n_1)}{n_2-n_1},~~~ n_1 \le a < n_2 \\ \dfrac{a-n_2+\eta _{\tilde{N}}(n_3-a)}{n_3-n_2},~~~ n_2 \le a \le n_3 \\ 1,~~~~~~~~ \textrm{otherwise} \end{array}\right. . \end{aligned}$$

The terms $\xi _{\tilde{N}}$ and $\eta _{\tilde{N}}$ are confidence and non-confidence levels of expert, and indicate the maximum and minimum values of $\mu _{\tilde{N}}$ and $\nu _{\tilde{N}},$ respectively, such that $0\le \xi _{\tilde{N}},\eta _{\tilde{N}} \le 1$ satisfying $\xi _{\tilde{N}}^2+\eta _{\tilde{N}}^2\le 1.$

3 Cauchy Pythagorean fuzzy numbers

Cauchy fuzzy number, which is based on probability density function of Cauchy distribution, is widely used FN in engineering. In this section, we define Cauchy PFNs, their $\alpha$ and $\beta$-cuts, some arithmetic operations and a ranking technique based on their credibility distribution.

Definition 1

A PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ is called a Cauchy PFN, if its MF and non-MF are defined, respectively, as:

$$\begin{aligned} \mu _{\tilde{N}}(x)= & {} {\left\{ \begin{array}{ll} \frac{1}{ {1+\big (\dfrac{p-x}{{q_1}^L }\big )^2}}, &{} x \le p,~ {q_1}^L> 0 \\ \frac{1}{ {1+\big (\dfrac{x-p}{{q_1}^R }\big )^2}}, &{} x> p,~ {q_1}^R> 0 \end{array}\right. },\\ \nu _{\tilde{N}}(x)= & {} {\left\{ \begin{array}{ll} 1-\frac{1}{ \big [{1+\big (\dfrac{p-x}{{q_2}^L }\big )^2}\big ]^2}, &{} x \le p,~ {q_2}^L> 0 \\ 1-\frac{1}{ \big [{1+\big (\dfrac{x-p}{{q_2}^R }\big )^2}\big ]^2},&{} x> p,~ {q_2}^R > 0 \end{array}\right. }, \end{aligned}$$

such that ${\mu _{\tilde{N}}}^2 + {\nu _{\tilde{N}}}^2 \le 1.$ Here, p determines the peak location, ${q_1}^L$ and ${q_1}^R$ respectively denote the left and right-hand width of $\mu _{\tilde{N}},$ ${q_2}^L$ and ${q_2}^R$ respectively denote the left and right-hand width of $\nu _{\tilde{N}},$ and ${q_1}^L \le {q_2}^L$ and ${q_1}^R \le {q_2}^R.$

Definition 2

A Cauchy PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ is called symmetric (or bell-shaped), if ${q_1}^L={q_1}^R$ and ${q_2}^L={q_2}^R.$

Example 1

Let $\tilde{N}=(11;~5,6;~7,9)$ be a Cauchy PFN. Then, the MF and non-MF of $\tilde{N}$ can be defined as:

$$\begin{aligned} \mu _{\tilde{N}}(x)= & {} {\left\{ \begin{array}{ll} \frac{1}{ {1+\big (\frac{11-x}{5 }\big )^2}}, &{} x \le 11\\ \frac{1}{ {1+\big (\frac{x-11}{6 }\big )^2}}, &{} x> 11 \end{array}\right. },\\ \nu _{\tilde{N}}(x)= & {} {\left\{ \begin{array}{ll} 1-\frac{1}{ \big [{1+\big (\frac{11-x}{7 }\big )^2}\big ]^2}, &{} x \le 11 \\ 1-\frac{1}{ \big [{1+\big (\frac{x-11}{9 }\big )^2}\big ]^2},&{} x > 11 \end{array}\right. }. \end{aligned}$$

It is easy to observe that $\tilde{N}$ satisfies the condition ${\mu _{\tilde{N}}}(x)^2 + {\nu _{\tilde{N}}}(x)^2 \le 1.$ Figure 1 provides graphical representation of $\tilde{N}.$

Fig. 1

A Cauchy PFN $\tilde{N}=((11;~5,6;~7,9)$

3.1 $\alpha$-cut and $\beta$-cut of Cauchy PFNs

PFNs may be uniquely determined by specifying their $\alpha$ and $\beta$-cuts.

Definition 3

An $\alpha$-cut set of a Cauchy PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ is contained in $\mathbb {R}$ and defined in Eq. 10.

$$\begin{aligned} \tilde{N}_\alpha =\{x|~\mu _{\tilde{N}}(x)\ge \alpha \}=[L_{\tilde{N}}(\alpha ), R_{\tilde{N}}(\alpha )]=\bigg [p- {q_1}^L\sqrt{\frac{1-\alpha }{\alpha }}, p+ {q_1}^R\sqrt{\frac{1-\alpha }{\alpha }}\bigg ], \end{aligned}$$

(10)

where $0 < \alpha \le 1.$

Definition 4

A $\beta$ -cut set of a Cauchy PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ is contained in $\mathbb {R}$ and defined in Eq. 11.

$$\begin{aligned} \tilde{N}_\beta= & {} \{x|~\nu _{\tilde{N}}(x)\le \beta \}=[L_{\tilde{N}}(\beta ), R_{\tilde{N}}(\beta )]\nonumber \\= & {} \bigg [p- {q_2}^L\sqrt{\frac{ 1- \sqrt{1-\beta }}{\sqrt{1-\beta }}}, p+ {q_2}^R\sqrt{\frac{ 1- \sqrt{1-\beta }}{ \sqrt{1-\beta }}}\bigg ], \end{aligned}$$

(11)

where $0 \le \beta < 1.$

Definition 5

An $(\alpha , \beta )$ -cut set of a Cauchy PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ is contained in $\mathbb {R}$ and defined in Eq. 12.

$$\begin{aligned} \tilde{N}_{\alpha , \beta }=\, & {} \{x|~\mu _{\tilde{N}}(x)\ge \alpha ,~\nu _{\tilde{N}}(x)\le \beta \}\nonumber \\=\, & {} \big \{[L_{\tilde{N}}(\alpha ), R_{\tilde{N}}(\alpha )];[L_{\tilde{N}}(\beta ), R_{\tilde{N}}(\beta )]\big \}, \end{aligned}$$

(12)

where $0 < \alpha \le 1$ and $0 \le \beta < 1$ such that $\alpha ^2 + \beta ^2 \le 1.$

Example 2

Consider a Cauchy PFN $\tilde{N}=(11;5,6;7,9).$ Take $\alpha = 0.6$ and $\beta = 0.8.$ The $\alpha$ and $\beta$-cut sets of Cauchy PFN $\tilde{N}$ are [6.9, 15.9] and [2.4, 22.1],  respectively. Figure 2 describes an example of (0.6, 0.8)-cut set of given Cauchy PFN.

Fig. 2

A (0.6, 0.8)-cut set of Cauchy PFN

3.2 Cauchy Pythagorean fuzzy arithmetic

Based on $\alpha$ and $\beta$-cuts of Cauchy PFNs we define some arithmetic operations.

Definition 6

Let $\tilde{N}_1=(p_1;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ and $\tilde{N}_2=(p_2;~{q_1'}^L,{q_1'}^R;~{q_2'}^L,{q_2'}^R)$ be two Cauchy PFNs. Their $\alpha$ and $\beta$-cuts are respectively defined according to Definitions 3 and 4 as follows: $\tilde{N_1}_\alpha =[p_{1}- {q_{1}}^L\sqrt{\frac{1-\alpha }{\alpha }}, p_{1} + {q_{1}}^R\sqrt{\frac{1-\alpha }{\alpha }}],$ $\tilde{N_2}_\alpha =[p_{2}- {q_{1}^{'}}^L\sqrt{\frac{1-\alpha }{\alpha }}, p_{2} + {q_{1}^{'}}^R\sqrt{\frac{1-\alpha }{\alpha }}];$ $\tilde{N_1}_\beta = [p_{1}- {q_2}^L\sqrt{\frac{1- \sqrt{1-\beta }}{ \sqrt{1-\beta }}}, p_{1} + {q_2}^R \sqrt{\frac{1- \sqrt{1-\beta }}{ \sqrt{1-\beta }}}],$ $\tilde{N_2}_\beta =[p_{2}- {q_2^{'}}^L \sqrt{\frac{1- \sqrt{1-\beta }}{ \sqrt{1-\beta }}}, p_{2} + {q_2^{'}}^R\sqrt{\frac{ 1-\sqrt{1-\beta }}{ \sqrt{1-\beta }}}].$ The addition and subtraction of Cauchy PFNs $\tilde{N}_1$ and $\tilde{N}_2$ on the basis of their $\alpha$ and $\beta$-cuts are respectively defined as:

• 1.
  $$\begin{aligned} \tilde{N_1}_\alpha + \tilde{N_2}_\alpha= & {} \bigg [(p_{1}+ p_{2})-({q_{1}}^L + {q_{1}^{'}}^L )\sqrt{\frac{1-\alpha }{\alpha }},~ (p_{1}+ p_{2})+( {q_{1}}^R + {q_{1}^{'}}^R )\sqrt{\frac{1-\alpha }{\alpha }} \bigg ],\\ \tilde{N_1}_\beta + \tilde{N_2}_\beta= & {} \bigg [(p_{1}+ p_{2})- ({q_2}^L + {q_2^{'}}^L )\sqrt{\frac{1- \sqrt{1-\beta }}{ \sqrt{1-\beta }}}, (p_{1}+ p_{2})+ ( {q_2}^R + {q_2^{'}}^R )\sqrt{\frac{ 1-\sqrt{1-\beta }}{ \sqrt{1-\beta }}} \bigg ]. \end{aligned}$$

  The MF and non-MF of addition of Cauchy PFNs $\tilde{N_1}$ and $\tilde{N_2}$ are as follows:

  $$\begin{aligned} \mu _{\tilde{N}_1 + \tilde{N}_2}(x)= & {} {\left\{ \begin{array}{ll} \frac{1}{ {1+\bigg (\dfrac{(p_{1}+ p_{2})-x}{{q_{1}}^L + {q_{1}^{'}}^L }\bigg )^2}}, &{} x \le p_{1}+ p_{2} \\ \frac{1}{ {1+\bigg (\dfrac{x-(p_{1}+ p_{2})}{ {q_{1}}^R + {q_{1}^{'}}^R }\bigg )^2}}, &{} x> p_{1}+ p_{2} \end{array}\right. },\\ \nu _{\tilde{N}_1 + \tilde{N}_2}(x)= & {} {\left\{ \begin{array}{ll} 1-\frac{1}{ \bigg [{1+\bigg (\dfrac{(p_{1}+ p_{2})-x}{{q_2}^L + {q_2^{'}}^L }\bigg )^2}\bigg ]^2}, &{} x \le p_{1}+ p_{2} \\ 1-\frac{1}{ \bigg [{1+\bigg (\dfrac{x-(p_{1}+ p_{2})}{ {q_2}^R + {q_2^{'}}^R }\bigg )^2}\bigg ]^2},&{} x > p_{1}+ p_{2} \end{array}\right. }. \end{aligned}$$
• 2.
  $$\begin{aligned} \tilde{N_1}_\alpha - \tilde{N_2}_\alpha= & {} \bigg [(p_{1}- p_{2})-({q_{1}}^L - {q_{1}^{'}}^L )\sqrt{\frac{1-\alpha }{\alpha }},~ (p_{1}- p_{2})+( {q_{1}}^R - {q_{1}^{'}}^R)\sqrt{\frac{1-\alpha }{\alpha }} \bigg ],\\ \tilde{N_1}_\beta + \tilde{N_2}_\beta= & {} \bigg [(p_{1}- p_{2})- ({q_2}^L - {q_2^{'}}^L )\sqrt{\frac{1- \sqrt{1-\beta }}{ \sqrt{1-\beta }}}, (p_{1}- p_{2})+ ( {q_2}^R - {q_2^{'}}^R)\sqrt{\frac{ 1-\sqrt{1-\beta }}{ \sqrt{1-\beta }}} \bigg ]. \end{aligned}$$

  The MF and non-MF of addition of Cauchy PFNs $\tilde{N_1}$ and $\tilde{N_2}$ are as follows:

  $$\begin{aligned} \mu _{\tilde{N}_1 - \tilde{N}_2}(x)= & {} {\left\{ \begin{array}{ll} \frac{1}{ {1+\bigg (\dfrac{(p_{1}- p_{2})-x}{{q_{1}}^L - {q_{1}^{'}}^L }\bigg )^2}}, &{} x \le p_{1}- p_{2} \\ \frac{1}{ {1+\bigg (\dfrac{x-(p_{1}- p_{2})}{ {q_{1}}^R - {q_{1}^{'}}^R }\bigg )^2}}, &{} x> p_{1}- p_{2} \end{array}\right. },\\ \nu _{\tilde{N}_1 - \tilde{N}_2}(x)= & {} {\left\{ \begin{array}{ll} 1-\frac{1}{ \bigg [{1+\bigg (\dfrac{(p_{1}- p_{2})-x}{{q_2}^L - {q_2^{'}}^L }\bigg )^2}\bigg ]^2}, &{} x \le p_{1}- p_{2} \\ 1-\frac{1}{ \bigg [{1+\bigg (\dfrac{x-(p_{1}- p_{2})}{ {q_2}^R - {q_2^{'}}^R }\bigg )^2}\bigg ]^2},&{} x > p_{1}- p_{2} \end{array}\right. }. \end{aligned}$$

4 Possibility, necessity and credibility measures for Pythagorean fuzzy sets

This section provides the definitions of credibility measure in comparison with possibility and necessity measures. Subsequently, we develop the formulas for credibility distribution and inverse credibility distribution, respectively, for different PFNs.

Definition 7

Let $\tilde{N}$ be a PFN with MF $\mu _{\tilde{N}}$ and non-MF $\nu _{\tilde{N}}$ such that $\mu _{\tilde{N}}^2+\nu _{\tilde{N}}^2\le 1$ and t be a real value. Then, in the PF event, when the PF variable $\tilde{N}$ assumes a value below or equal to r ($\tilde{N} \le t$), the $\mu$-possibility $(Pos_{\mu })$ and $\nu$- possibility $(Pos_{\nu })$ are defined in Eqs. 13 and 14.

$$\begin{aligned} Pos_{\mu }\{\tilde{N} \le t\}= & {} \sup \{\mu _{\tilde{N}}(w) \wedge \mu _{\tilde{N}}(t) ~|~ w \in R \}, \ \end{aligned}$$

(13)

$$\begin{aligned} Pos_{\nu }\{\tilde{N} \le t\}= & {} \sup \{\nu _{\tilde{N}}(w) \wedge \nu _{\tilde{N}}(t) ~|~ w \in R \}. \end{aligned}$$

(14)

Definition 8

Let $\tilde{N}$ be a PFN with MF $\mu _{\tilde{N}}$ and non-MF $\nu _{\tilde{N}}$ such that $\mu _{\tilde{N}}^2+\nu _{\tilde{N}}^2\le 1$ and t be a real value. Then in the PF event, when the PF variable $\tilde{N}$ assumes a value below or equal to r ($\tilde{N} \le t$), the $\mu$-necessity $(Nec_{\mu })$ and $\nu$- necessity $(Nec_{\nu })$ are defined in Eqs. 15 and 16.

$$\begin{aligned} Nec_{\mu }\{\tilde{N} \le t\}= & {} \varTheta _\mu - Pos_{\mu }\{\tilde{N} > t\}, \end{aligned}$$

(15)

$$\begin{aligned} Nec_{\nu }\{\tilde{N} \le t\}= & {} \varTheta _\nu - Pos_{\nu }\{\tilde{N} > t\}, \end{aligned}$$

(16)

where, $Pos_{\mu }\{\tilde{N}> t\} = \inf \{\mu _{\tilde{N}}(w) \vee \mu _{\tilde{N}}(t) ~|~ w \in R \},~Pos_{\nu }\{\tilde{N} > t\} = \inf \{\nu _{\tilde{N}}(w) \vee \nu _{\tilde{N}}(t) ~|~ w \in R \}$ and the values of $\varTheta _\mu$ and $\varTheta _\nu$ depend on the type of PFN.

• For trapezoidal and triangular PFNs, $\varTheta _\mu =\xi _{\tilde{N}}$ and $\varTheta _\nu =1 + \eta _{\tilde{N}}.$

• For Cauchy and LR-type PFNs, $\varTheta _\mu =\varTheta _\nu =1.$

Since the necessity and possibility measurements lack the self-duality characteristic, therefore, to measure a PF event in decision making system these are not suitable to use. The credibility measure was suggested as a way to address this shortcoming. The generalized form of credibility measure is expressed along the following lines.

Definition 9

Let $\tilde{N}$ be a PFN with MF $\mu _{\tilde{N}}$ and non-MF $\nu _{\tilde{N}}$. Then, in the PF event, when the PF variable $\tilde{N}$ assumes a value below or equal to t ($\tilde{N} \le t$), the generalized $\mu$-credibility $(GCr_{\mu })$ and generalized $\nu$-credibility $(GCr_{\nu })$ are defined in Eqs. 17 and 18.

$$\begin{aligned} GCr_{\mu } \{\tilde{N} \le t\}= & {} \kappa Pos_{\mu }\{\tilde{N} \le t\} + (1-\kappa ) Nec_{\mu }\{\tilde{N} \le t\}, \end{aligned}$$

(17)

$$\begin{aligned} GCr_{\nu } \{\tilde{N} \le t\}= & {} \kappa Pos_{\nu }\{\tilde{N} \le t\} + (1-\kappa ) Nec_{\nu }\{\tilde{N} \le t\}, \end{aligned}$$

(18)

where $\kappa ~(0 \le \kappa \le 1)$ is a parameter which helps to evaluate the decision body’s overall attitude and is optimistic-pessimistic in nature.

• If $\kappa =1,$ then $GCr_{\mu }=Pos_{\mu },$ $GCr_{\nu }=Pos_{\nu },$ which shows that decision-body is optimistic and there is maximum chance of occurrence of the PF event.

• If $\kappa =0,$ then $GCr_{\mu }=Nec_{\nu },$ $GCr_{\nu }=Nec_{\nu },$ which shows that decision-body is pessimistic and there is minimum chance of occurrence of the PF event.

• If $\kappa =\frac{1}{2},$ then $GCr_{\mu }=Cr_{\mu },$ $GCr_{\nu }=Cr_{\nu },$ where, Cr is credibility measure which shows that the decision maker adopts compromise attitude.

Equations 19 and 20 provide the definition of credibility measure of PF event.

$$\begin{aligned} Cr_{\mu }\{\tilde{N} \le t\}= & {} \frac{ Pos_{\mu }\{\tilde{N} \le t\} + Nec_{\mu }\{\tilde{N} \le t\}}{2}, \end{aligned}$$

(19)

$$\begin{aligned} Cr_{\nu }\{\tilde{N} \le t\}= & {} \frac{ Pos_{\nu }\{\tilde{N} \le t\} + Nec_{\nu }\{\tilde{N} \le t\}}{2}. \end{aligned}$$

(20)

4.1 Credibility distribution

In this section, we define the credibility distribution functions for different PFNs.

4.1.1 Credibility distribution of trapezoidal PFNs

Let $\tilde{N}=\langle [n_1,n_2,n_3,n_4]: \xi _{\tilde{N}}, \eta _{\tilde{N}} \rangle$ be a trapezoidal PFN. The possibility of $\tilde{N} \le t$ for MF and non-MF, calculated according to Eqs. 13 and 14, has the following expressions.

$$\begin{aligned} Pos_{\mu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 0, &{} w \le n_1 \\ \dfrac{w-n_1}{n_2-n_1} \xi _{\tilde{N}}, &{} n_1 \le w \le n_2 \\ \xi _{\tilde{N}}, &{} w \ge n_2 \end{array}\right. },\\ Pos_{\nu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 1, &{} w \le n_1 \\ \dfrac{n_2 -w + \eta _{\tilde{N}}(w-n_1)}{n_2-n_1}, &{} n_1 \le w \le n_2 \\ \eta _{\tilde{N}}, &{} w \ge n_2 \end{array}\right. }. \end{aligned}$$

The necessity of $\tilde{N} \le t$ for MF and non-MF, calculated according to Eqs. 15 and 16, has the following expressions.

$$\begin{aligned} Nec_{\mu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 0, &{} w \le n_3 \\ \dfrac{w-n_3}{n_4-n_3} \xi _{\tilde{N}}, &{} n_3 \le w \le n_4 \\ \xi _{\tilde{N}}, &{} w \ge n_4 \end{array}\right. },\\ Nec_{\nu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 1, &{} w \le n_3 \\ \dfrac{n_4 -w + \eta _{\tilde{N}}(w-n_3)}{n_4-n_3}, &{} n_3 \le w \le n_4 \\ \eta _{\tilde{N}}, &{} w \ge n_4 \end{array}\right. }. \end{aligned}$$

The credibility distribution for MF and non-MF is constructed according to Eqs. 19, 20 and have the following expressions.

$$\begin{aligned} Cr_{\mu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 0, &{} w< n_1 \\ \dfrac{w-n_1}{2(n_2-n_1)} \xi _{\tilde{N}}, &{} n_1 \le w< n_2 \\ \dfrac{\xi _{\tilde{N}}}{2}, &{} n_2 \le w \le n_3 \\ \dfrac{w+n_4-2n_3}{2(n_4-n_3)} \xi _{\tilde{N}}, &{} n_3< w \le n_4 \\ \xi _{\tilde{N}}, &{} w > n_4 \end{array}\right. },\\ Cr_{\nu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 1, &{} w \le n_1 \\ \dfrac{2n_2-n_1-w+\eta _{\tilde{N}}(w-n_1)}{2(n_2-n_1)}, &{} n_1 \le w< n_2 \\ \dfrac{1+\eta _{\tilde{N}}}{2}, &{} n_2 \le w \le n_3 \\ \dfrac{n_4-w+\eta _{\tilde{N}}(w-2n_3+n_4)}{2(n_4-n_3)}, &{} n_3 < w \le n_4 \\ \eta _{\tilde{N}}, &{} w \ge n_4 \end{array}\right. }. \end{aligned}$$

On the basis of above functions, the credibility distribution of Trapezoidal PFN $\langle [5,9,17,23]: 0.77,0.59 \rangle$ is displayed in Fig. 3.

Fig. 3

Credibility distribution of trapezoidal PFN

4.1.2 Credibility distribution of triangular PFNs

Let $\tilde{N}=\langle [n_1,n_2,n_3]: \xi _{\tilde{N}}, \eta _{\tilde{N}} \rangle$ be a triangular PFN. The credibility distribution for MF and non-MF is described as being the average of their possibility and necessity measures, provided as follows.

$$\begin{aligned} Cr_{\mu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 0, &{} w< n_1 \\ \dfrac{w-n_1}{2(n_2-n_1)} \xi _{\tilde{N}}, &{} n_1 \le w< n_2 \\ \dfrac{w+n_3-2n_2}{2(n_3-n_2)} \xi _{\tilde{N}}, &{} n_2 \le w< n_3 \\ \xi _{\tilde{N}}, &{} w \ge n_3 \end{array}\right. },\\ Cr_{\nu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 1, &{} w< n_1 \\ \dfrac{2n_2-n_1-w+\eta _{\tilde{N}}(w-n_1)}{2(n_2-n_1)}, &{} n_1 \le w< n_2 \\ \dfrac{n_3-w+\eta _{\tilde{N}}(w-2n_2+n_3)}{2(n_3-n_2)}, &{} n_2 \le w < n_3 \\ \eta _{\tilde{N}}, &{} w \ge n_3 \end{array}\right. }. \end{aligned}$$

On the basis of above functions, the credibility distribution of triangular PFN $\langle [0,15,50]: 0.9,0.3 \rangle$ is displayed in Fig. 4.

Fig. 4

Credibility distribution of triangular PFN

4.1.3 Credibility distribution of LR-Type PFNs

Let $\tilde{N}=(n_1,n_2;~l,r;~l',r')_{LR}$ be an LR-Type PFN with $L(w)=1-\sqrt{w},~R(w)=e^{-w}$ and $L'(w)=R'(w)=\sqrt{w}.$. The credibility distribution for MF and non-MF is defined as average of their possibility and necessity measures, provided as follows.

$$\begin{aligned} Cr_{\mu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 0, &{} w< n_1-l \\ 1-\sqrt{\dfrac{n_1-w}{l}}, &{} n_1 -l \le w< n_1 \\ 1, &{} n_1 \le w \le n_2 \\ e^{\dfrac{n_2-w}{r}}, &{} w> n_2 \end{array}\right. },\\ Cr_{\nu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 1, &{} w< n_1 - l' \\ \sqrt{\dfrac{n_1-w}{l'}}, &{} n_1 - l' \le w < n_1 \\ 0, &{} n_1 \le w \le n_2 \\ \sqrt{\dfrac{w-n_2}{r'}}, &{} n_2 \le w \le n_2 + r' \\ 1, &{} w > n_2 + r' \end{array}\right. }. \end{aligned}$$

Example 3

Let $\tilde{N}=(7,8;~2,3;~3,5)_{LR}$ be an LR-type PFN with $L(w)=1-\sqrt{w},~R(w)=e^{-w}$ and $L'(w)=R'(w)=\sqrt{w}.$ Then, the MF and non-MF of $\tilde{N}$ has the following expressions:

$$\begin{aligned} \mu _{\tilde{N}}(w)= & {} {\left\{ \begin{array}{ll} 0, &{} w \le 5 \\ 1-\sqrt{\dfrac{7-w}{2}}, &{} 5 \le w< 7 \\ 1, &{} 7 \le w \le 8 \\ e^{\frac{8-w}{3}}, &{} w> 8 \end{array}\right. },\\ \nu _{\tilde{N}}(w)= & {} {\left\{ \begin{array}{ll} 1, &{} w< 4 \\ \sqrt{\dfrac{7-w}{3}}, &{} 4 \le w< 7 \\ 0, &{} 7 \le w \le 8 \\ \sqrt{\dfrac{w-8}{5}}, &{} 8 < w \le 13\\ 1, &{} w > 13 \end{array}\right. }. \end{aligned}$$

Figure 5 provides the graphical representation of credibility distribution of LR-Type PFN $\tilde{N}=(7,8;~2,3;~3,5)_{LR}.$

Fig. 5

Credibility distribution of LR-Type PFN

4.1.4 Credibility distribution of Cauchy PFNs

Let $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ be a Cauchy PFN. The credibility distribution for MF and non-MF is constructed according to Eqs. 19, 20 and given as follows.

$$\begin{aligned} Cr_{\mu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} \frac{1}{ {2+2\big (\dfrac{p-x}{{q_1}^L }\big )^2}}, &{} x \le p \\ 1- \frac{1}{ {2+2\big (\dfrac{x-p}{{q_1}^R }\big )^2}}, &{} x> p \end{array}\right. },\\ Cr_{\nu }\{\tilde{N} \le t\}= & {} {\left\{ \begin{array}{ll} 1-\frac{1}{ 2\big [{1+\big (\dfrac{p-x}{{q_2}^L }\big )^2}\big ]^2}, &{} x \le p \\ \frac{1}{ 2\big [{1+\big (\dfrac{x-p}{{q_2}^R }\big )^2}\big ]^2},&{} x > p \end{array}\right. }. \end{aligned}$$

Example 4

Let $\tilde{N}=(11;~5,6;~7,9)$ be a Cauchy PFN. Then the MF and non-MF of $\tilde{N}$ are defined in Example 1. The graphical representation of credibility distribution of Cauchy PFN $\tilde{N}=(11;~5,6;~7,9)$ is displayed in Fig. 6.

Fig. 6

Credibility distribution of Cauchy PFN

4.2 Regular Pythagorean fuzzy numbers

If a credibility distribution is monotone and continuous with respect to r,  it is considered to be regular (i.e., $\mu$-credibility distribution is strictly increasing and $\nu$-credibility distribution is strictly decreasing) such that $0< Cr_{\mu }, Cr_{\nu } <1$ and

$$\begin{aligned}{} & {} \lim _{r \rightarrow - \infty } Cr_{\mu }(t)=0,~~~\lim _{r \rightarrow + \infty } Cr_{\mu }(t) =1,\\{} & {} \lim _{r \rightarrow - \infty }Cr_{\nu }(t)=1,~~~\lim _{r \rightarrow + \infty }Cr_{\nu }(t) =0. \end{aligned}$$

Definition 10

A PFN is said to be regular PFN, if its credibility distribution is regular.

It is easy to observe that triangular PFNs and Cauchy PFNs in Definitions 4 and 1 are regular, while trapezoidal PFNs and LR type PFNs in Definitions 3 and 5 are not regular due to non-strictly monotonic behavior of $\mu$ and $\nu$-credibility distribution functions.

Regarding the regular PFNs, the idea of the inverse credibility distribution is created. This idea will be crucial to the content that follows.

Definition 11

Let $\tilde{N}$ be a PFN with regular $\mu$ and $\nu$-credibility distributions, $Cr_{\mu }$ and $Cr_{\nu },$ respectively. Then, their inverse functions $Cr_{\mu }^{-1}$ and $Cr_{\nu }^{-1}$ are called $\mu$-inverse credibility and $\nu$-inverse credibility distributions of $\tilde{N},$ respectively.

On the open interval (0, 1),  the $\mu$ and $\nu$-inverse credibility distributions are clearly specified. If necessary, we may expand their domain by

$$\begin{aligned} Cr_{\mu }^{-1}(0)= & {} \lim _{\alpha \rightarrow 0} Cr_{\mu }^{-1}(\alpha ), Cr_{\mu }^{-1}(1)=\lim _{\alpha \rightarrow 1} Cr_{\mu }^{-1}(\alpha ),~\\ Cr_{\nu }^{-1}(0)= & {} \lim _{\alpha \rightarrow 0} Cr_{\nu }^{-1}(\alpha ), Cr_{\nu }^{-1}(1)=\lim _{\alpha \rightarrow 1} Cr_{\nu }^{-1}(\alpha ). \end{aligned}$$

4.2.1 Inverse credibility distribution of triangular PFNs

The $\mu$ and $\nu$-inverse credibility distribution functions for a triangular PFN $\tilde{N}=\langle [n_1,n_2,n_3];\xi _{\tilde{N}},\eta _{\tilde{N}}\rangle$ are defined below. The graphical representation is provided in Fig. 7.

$$\begin{aligned} Cr_{\mu }^{-1}(\alpha )= & {} {\left\{ \begin{array}{ll} n_1 + \frac{2}{\xi _{\tilde{N}}}(n_2 - n_1)\alpha , &{} \alpha< 0.5,~\xi _{\tilde{N}}=1 \\ 2n_2 - n_3 + \frac{2}{\xi _{\tilde{N}}}(n_3 - n_2)\alpha , &{} \alpha \ge 0.5,~\xi _{\tilde{N}}=1 \end{array}\right. },\\ Cr_{\nu }^{-1}(\alpha )= & {} {\left\{ \begin{array}{ll} \dfrac{2n_2(\alpha - \eta _{\tilde{N}}) + n_3 (1-2\alpha + \eta _{\tilde{N}})}{1 - \eta _{\tilde{N}}}, &{} \alpha < 0.5,~\eta _{\tilde{N}}=0 \\ \dfrac{n_1(2\alpha - \eta _{\tilde{N}} - 1) + 2n_2 (1-\alpha )}{1 - \eta _{\tilde{N}}}, &{} \alpha \ge 0.5,~\eta _{\tilde{N}}=0 \end{array}\right. }. \end{aligned}$$

Fig. 7

Inverse credibility distribution of triangular PFN $\tilde{N}=\langle [0,15,50];1,0\rangle$

4.2.2 Inverse credibility distribution of Cauchy PFNs

The $\mu$ and $\nu$-inverse credibility distribution functions for Cauchy PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ are defined below. The graphical representation is provided in Fig. 8.

$$\begin{aligned} Cr_{\mu }^{-1}(\alpha )= & {} {\left\{ \begin{array}{ll} p- {q_1}^L\sqrt{\frac{1-2\alpha }{2\alpha }}, &{} \alpha< 0.5 \\ p+ {q_1}^R\sqrt{\frac{1-2(1-\alpha ) }{2(1-\alpha )}}, &{} \alpha \ge 0.5 \end{array}\right. },\\ Cr_{\nu }^{-1}(\alpha )= & {} {\left\{ \begin{array}{ll} p+ {q_2}^R\sqrt{\frac{ 1- \sqrt{2\alpha }}{ \sqrt{2\alpha }}}, &{} \alpha < 0.5 \\ p- {q_2}^L\sqrt{\frac{ 1- \sqrt{2(1-\alpha )}}{\sqrt{2(1-\alpha )}}}, &{} \alpha \ge 0.5 \end{array}\right. }. \end{aligned}$$

For simplicity, we may consider ${q_1}^L={q_1}^R$ and ${q_2}^L={q_2}^R.$

Fig. 8

Inverse credibility distribution of Cauchy PFN $\tilde{N}=(11;~5,6;~7,9)$

4.3 Ranking method for Pythagorean fuzzy numbers

For different PFNs, we now suggest a ranking technique based on the computation of expected values.

4.3.1 Expected value based on credibility distribution

Liu and Liu Liu and Liu (2002) proposed the formula to compute Expected Value (EV) of a fuzzy variable in terms of credibility distribution. Following this definition, we provide the formula for EV of PF variables in the following manner.

Let $\tilde{N}$ be a PFN. The EV of $\tilde{N}$ for MF and non-MF are determined, respectively, in Eqs. 21 and 22.

$$\begin{aligned} E_{\mu }(\tilde{N})= & {} \int _0^{+\infty } Cr_{\mu } \{\tilde{N} \ge t\} dr - \int _{-\infty }^0 Cr_{\mu } \{\tilde{N} \le t\} dr, \end{aligned}$$

(21)

$$\begin{aligned} E_{\nu }(\tilde{N})= & {} \int _0^{+\infty } Cr_{\nu } \{\tilde{N} \ge t\} dr - \int _{-\infty }^0 Cr_{\nu } \{\tilde{N} \le t\} dr. \end{aligned}$$

(22)

Definition 12

Let $\tilde{N}$ be a PFN. Then, EV of $\tilde{N}$ is defined in Eq. 23.

$$\begin{aligned} E(\tilde{N}) = \frac{E_{\mu }(\tilde{N})+E_{\nu }(\tilde{N})}{2} \end{aligned}$$

(23)

4.3.2 Expected value based on inverse credibility distribution

For regular FNs, Zhou et al. Zhou et al. (2016) defined an equivalent form of EV. Utilizing their concept, in this section, inverse credibility distribution is used to provide an identical form of EV for regular PFNs.

Definition 13

Let $\tilde{N}$ be a regular PFN. If the EV of $\tilde{N}$ exists, then we have

$$\begin{aligned} E_{\mu }(\tilde{N})= & {} \int _0^1 Cr_{\mu }^{-1} (\alpha ) d\alpha , \end{aligned}$$

(24)

$$\begin{aligned} E_{\nu }(\tilde{N})= & {} \int _0^1 Cr_{\nu }^{-1} (\alpha ) d\alpha , \end{aligned}$$

(25)

where, $Cr_{\mu }^{-1}$ and $Cr_{\nu }^{-1}$ are the $\mu$ and $\nu$-inverse credibility distribution functions of $\tilde{N}.$

Theorem 1

For a regular PFN $\tilde{N},$ if the EV of $\tilde{N}$ exists, then

$$\begin{aligned} E(\tilde{N}) = \frac{1}{2}\bigg [\int _0^1 Cr_{\mu }^{-1} (\alpha ) d\alpha + \int _0^1 Cr_{\nu }^{-1} (\alpha ) d\alpha \bigg ], \end{aligned}$$

where, $Cr_{\mu }^{-1}$ and $Cr_{\nu }^{-1}$ are the $\mu$ and $\nu$-inverse credibility distribution functions of $\tilde{N}.$

Proof

Let $\tilde{N}$ be a regular PFN. Suppose that the EV of $\tilde{N}$ exists. Then, by definition of EV of PFN based on credibility distribution, we obtain the following expression:

$$\begin{aligned} E(\tilde{N})= & {} \frac{1}{2} [E_{\mu }(\tilde{N})+E_{\nu }(\tilde{N})], \\= & {} \frac{1}{2} \bigg [\int _0^{+\infty } Cr_{\mu } \{\tilde{N} \ge t\} dr - \int _{-\infty }^0 Cr_{\mu } \{\tilde{N} \le t\} dr \\{} & {} +\int _0^{+\infty } Cr_{\nu } \{\tilde{N} \ge t\} dr - \int _{-\infty }^0 Cr_{\nu } \{\tilde{N} \le t\} dr\bigg ],\\= & {} \frac{1}{2} \bigg [\int _{Cr_{\mu }(0)}^{1} Cr_{\mu }^{-1} (\alpha ) d\alpha + \int _{0}^{Cr_{\mu }(0)} Cr_{\mu }^{-1} (\alpha ) d\alpha \\{} & {} +\int _{Cr_{\nu }(0)}^{1} Cr_{\nu }^{-1} (\alpha ) d\alpha + \int _{0}^{Cr_{\nu }(0)} Cr_{\nu }^{-1} (\alpha ) d\alpha \bigg ],\\= & {} \frac{1}{2} \bigg [ \int _{0}^{Cr_{\mu }(0)} Cr_{\mu }^{-1} (\alpha ) d\alpha + \int _{Cr_{\mu }(0)}^{1} Cr_{\mu }^{-1} (\alpha ) d\alpha \\{} & {} + \int _{0}^{Cr_{\nu }(0)} Cr_{\nu }^{-1} (\alpha ) d\alpha + \int _{Cr_{\nu }(0)}^{1} Cr_{\nu }^{-1} (\alpha ) d\alpha \bigg ],\\= & {} \frac{1}{2}\bigg [\int _0^1 Cr_{\mu }^{-1} (\alpha ) d\alpha + \int _0^1 Cr_{\nu }^{-1} (\alpha ) d\alpha \bigg ]. \end{aligned}$$

$\square$

Theorem 1 indicates that the EV of a regular PFN is just the area surrounded by two axes, i.e., $\alpha =0~(or~\alpha =1)$ and the curves of $\mu$ and $\nu$-inverse credibility distribution functions $Cr_{\mu }^{-1}$ and $Cr_{\nu }^{-1},$ respectively. The graphical illustration of EV of a regular LR-type PFN is displayed in Fig. 9.

Fig. 9

The EV of a regular LR-type PFN

Theorem 2

The EV $E(\tilde{N})$ of a triangular PFN $\tilde{N}=\langle [n_1,n_2,n_3]: 1, 0 \rangle$ is $\dfrac{n_1+2n_2+n_3}{4}.$

Proof

Let $\tilde{N}=\langle [n_1,n_2,n_3]: 1, 0 \rangle$ be a triangular PFN. According to Definition 13, we obtain the following expression:

$$\begin{aligned} E_{\mu }(\tilde{N})= & {} \int _0^{0.5} {n_1+2(n_2-n_1)\alpha } ~ d\alpha + \int _{0.5}^1 {2n_2-n_3+2(n_3-n_2)\alpha } ~ d\alpha ,\\= & {} \frac{1}{2}n_1+\frac{1}{4}(n_2-n_1)+ \frac{1}{2} (2n_2-n_3) +\ \frac{3}{4} (n_3-n_2),\\= & {} \frac{1}{4} (n_1+2n_2+n_3).\\ E_{\nu }(\tilde{N})= & {} \int _0^{0.5} {2n_2\alpha +n_3(1-2\alpha )} ~ d\alpha + \int _{0.5}^1 {n_1(2\alpha -1)+2n_2(1-\alpha )} ~ d\alpha ,\\= & {} \frac{1}{4}n_2+\frac{1}{4}n_3+ n_1\bigg (\frac{-1}{4} +\frac{1}{2}\bigg ) + 2n_2 \bigg (\frac{1}{8}\bigg ), \\= & {} \frac{1}{4} (n_1+2n_2+n_3). \end{aligned}$$

Using Definition 12, we get the result as follows.

$$\begin{aligned} E(\tilde{N})= & {} \frac{1}{2} (E_{\mu }(\tilde{N})+E_{\nu }(\tilde{N}))=\frac{1}{8} (2n_1+4n_2+2n_3) \\= & {} \frac{1}{4} (n_1+2n_2+n_3). \end{aligned}$$

$\square$

Theorem 3

The EV $E(\tilde{N})$ of a Cauchy PFN $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ is p,  where ${q_1}^L={q_1}^R$ and ${q_2}^L={q_2}^R.$

Proof

Let $\tilde{N}=(p;~{q_1}^L,{q_1}^R;~{q_2}^L,{q_2}^R)$ be a Cauchy PFN such that ${q_1}^L={q_1}^R$ and ${q_2}^L={q_2}^R.$ According to Definition 13, we obtain

$$\begin{aligned} E_{\mu }(\tilde{N}) = & \int _0^{0.5} {p- {q_1}^L\sqrt{\frac{1-2\alpha }{2\alpha }}} ~ d\alpha \\ & + \int _{0.5}^1 {p+ {q_1}^R\sqrt{\frac{1-2(1-\alpha ) }{2(1-\alpha )}}} ~ d\alpha ,\\= & 0.5p - {q_1}^L \int _0^{0.5} { \sqrt{\frac{1-2\alpha }{2\alpha }}} ~ d\alpha + 0.5p \\& + {q_1}^R \int _{0.5}^1 {\sqrt{\frac{1-2(1-\alpha ) }{2(1-\alpha )}}} ~ d\alpha ,\\= & p + \frac{1}{2}{q_2}^R \int _1^{0} { \sqrt{\frac{t}{1-t}}} ~ dt\\ & + \frac{1}{2} {q_2}^L \int _{0}^1 { \sqrt{\frac{t}{1-t}}} ~ dt,\\= & p.\\ E_{\nu }(\tilde{N})= & \int _0^{0.5} {p+ {q_2}^R\sqrt{\frac{ 1- \sqrt{2\alpha }}{ \sqrt{2\alpha }}}} ~ d\alpha \\ & + \int _{0.5}^1 {p- {q_2}^L\sqrt{\frac{ 1- \sqrt{2(1-\alpha )}}{\sqrt{2(1-\alpha )}}}} ~ d\alpha ,\\= & 0.5p + {q_2}^R \int _0^{0.5} {\sqrt{\frac{ 1- \sqrt{2\alpha }}{ \sqrt{2\alpha }}}} ~ d\alpha + 0.5p \\ & - {q_2}^L \int _{0.5}^1 {\sqrt{\frac{ 1- \sqrt{2(1-\alpha )}}{\sqrt{2(1-\alpha )}}}} ~ d\alpha ,\\= & p - {q_2}^R \int _1^{0} { \sqrt{t(1-t)}} ~ dt - {q_2}^L \int _{0}^1 { \sqrt{t(1-t)}} ~ dt,\\= & p. \end{aligned}$$

Using Definition 12, we get the result as follows.

$$\begin{aligned} E(\tilde{N}) = \frac{1}{2} (E_{\mu }(\tilde{N})+E_{\nu }(\tilde{N}))=\frac{1}{2} (p+p)=p. \end{aligned}$$

$\square$

In literature, the methods for unique linear ordering of PFNs do not exist. Thus, one of the core issues with PF theory is the ranking of PFNs. We suggest the following ranking method which relates the credibility theory to the theory of PFSs and is based on EVs.

Definition 14

Let $\tilde{N}_{1}$ and $\tilde{N}_{2}$ be two PFNs and $E(\tilde{N}_{1})$ and $E(\tilde{N}_{1})$ be their EVs, respectively. Then the ranking order between PFNs is as follows:

• (1) If $E(\tilde{N}_1)>E(\tilde{N}_2),$ then $\tilde{N}_1>\tilde{N}_2,$

• (2) If $E(\tilde{N}_1)<E(\tilde{N}_2),$ then $\tilde{N}_1<\tilde{N}_2,$

• (3) If $E(\tilde{N}_1)=E(\tilde{N}_2),$ then $\tilde{N}_1 \approx \tilde{N}_2.$

Seven axioms for ordering fuzzy quantities were developed by Wang and Kerre Wang and Kerre (2001). Since by definition, PFNs are a combination of two FNs, the suggested ranking technique can easily satisfy all seven axioms.

5 Project management: program evaluation and review technique

The project schedule problem is a dynamic process that requires constant monitoring and adjustment throughout the project lifecycle. Project managers need to use effective project scheduling tools, techniques and methodologies to create a well-structured and realistic schedule that can be followed and adapted as the project progresses. A well-planned and managed schedule is essential for meeting project deadlines, optimizing resource utilization, and delivering the project’s intended outcomes successfully.

5.1 Phases of project management

Project management involves a series of phases that help ensure a project is successfully executed from start to finish. The phases you mentioned, Planning, Scheduling, and Control, are indeed essential components of project management, but it is important to note that project management typically involves several other phases and processes as well. Here is an overview of these three phases and how they fit into the broader project management framework:

• 1. Planning Phase:

  Objective: Define the project’s goals, scope, and deliverables.

  Key Activities: Identify stakeholders, create a project charter, outline tasks, allocate resources, estimate costs, and assess risks.

  Outcome: A comprehensive project plan that sets the direction and foundation for the project.

• 2. Scheduling Phase:

  Objective: Establish a timeline for project activities.

  Key Activities: Sequence tasks, assign resources, estimate task durations, and create a project schedule.

  Outcome: A visual representation of when and how project tasks will be executed, often in the form of Gantt charts or network diagrams.

• 3. Control Phase:

  Objective: Monitor project progress, manage changes, and ensure project stays on track.

  Key Activities: Compare actual progress to the plan, address issues, manage risks, maintain quality, and communicate with stakeholders.

  Outcome: A well-controlled project that adheres to the plan and can make informed adjustments as needed.

These phases are essential for effective project management, ensuring that projects are well-prepared, efficiently executed, and closely monitored for successful outcomes.

5.2 Risk assessment

The assessment of risks in the planning phase of a project involves identifying, analyzing, and understanding potential threats and opportunities that could impact the project’s objectives, scope, schedule, budget, and overall success. This process is crucial because it allows project managers and stakeholders to proactively address risks and develop strategies to mitigate or exploit them. Here are the key steps involved in assessing risks during the planning phase:

Risk Identification Identify all possible risks that could affect the project. Risks can be internal (related to the project itself) or external (related to external factors like market conditions or regulatory changes). Encourage input from team members and stakeholders to ensure a comprehensive list.

Risk Analysis Once identified, assess the impact and likelihood of each risk. This involves evaluating the potential consequences of a risk event (such as delays, cost overruns, or quality issues) and the probability of it occurring. This assessment helps prioritize risks based on their significance.

Risk Prioritization Rank risks based on their severity and likelihood. Some risks may have a higher priority due to their potential impact on the project’s success. This prioritization helps allocate resources and attention to the most critical risks.

Risk Response Planning Develop strategies to address identified risks. There are four primary approaches to handling risks:

• 1. Risk Avoidance: Eliminate the risk by changing project plans or avoiding certain activities.

• 2. Risk Mitigation: Take actions to reduce the probability or impact of the risk.

• 3. Risk Transfer: Shift the risk to another party through contracts or insurance.

• 4. Risk Acceptance: Accept the risk as is and have a plan for how to respond if it occurs.

Contingency Planning Develop contingency plans for high-priority risks. These plans outline specific actions to take if a risk event occurs. They ensure that the project team is prepared to respond effectively and minimize the negative impact.

Risk Documentation Document all identified risks, their assessments, prioritization, and planned responses in a risk register or risk management plan. This document serves as a reference throughout the project.

Monitoring and Review Regularly review and update the risk assessment and response plans as the project progresses. New risks may emerge, and the impact of existing risks may change. Continuously monitor the project environment for potential risks.

5.3 Pythagorean fuzzy program evaluation and review technique

Pythagorean fuzzy program evaluation and review technique (PFPERT) is a network-based model which is aimed to associate in the planning, scheduling and control of projects. A project is described as a group of connected tasks, each of which requires time and resources. The main goal of PFPERT is to offer analytical tools for activity scheduling while taking into account the uncertainties and ambiguities of real network models. The project’s activities, their order of precedence, and their time requirements are first defined. A network is then used to illustrate the relationships between the activities in order of precedence. The third step entails precise calculations to create the project’s time schedule. In contrast to PFCPM, the PFPERT relies on activity duration with three assumptions:

• 1. Optimistic duration: while execution occurs exceptionally well.

• 2. Most Likely duration: while execution is performed under typical conditions.

• 3. Pessimistic duration: while execution occurs poorly.

5.4 PFPERT network components and precedence relationships

PFPERT network consists of two major components, namely events and activities. Events in the network diagram represent project milestones, such as the start or the completion of an activity/task and occur at a particular instant of time at which some specific part of the project is to be achieved. While activities in the network diagram represent project operations/tasks to be conducted. An activity is a distinct task that needs to be performed as a part of project. Network models use the following two types of precedence network to show precedence requirements of the activities in the project.

• 1. Activity-on-Node (AON): In AON diagrams, project activities are represented as nodes and the logical relationships between activities are shown using arrows that connect the nodes. In AON diagrams, the critical path is the longest path from the project’s start node to the finish node. Activities on the critical path have zero float, meaning any delay in these activities will delay the project’s overall completion.

• 2. Activity-on-Arc (AOA): In AOA diagrams, activities are represented by arrows, and events represent specific points in time when activities start or finish. Arrows connect events to illustrate task dependencies. In AOA diagrams, the critical path is the longest path from the project’s start event to the finish event. Activities on the critical path have zero float.

Both AON and AOA serve the fundamental purpose of helping project managers plan and schedule tasks, identify critical paths, and ensure project success by managing dependencies and resources effectively. In this paper, only AOA network diagrams will be used.

5.4.1 Rules for activity-on-Arc network construction

An arc indicating the direction of project status is used to depict each project activity. The network’s nodes define the precedence relationships between the various activities. It is convenient to number the nodes in ascending order in the direction of progress in the project. Following three rules are required to construct the network.

Rule 1: One and only one arc is used to indicate every activity.

Rule 2: There must be two unique end nodes for every activity.

Rule 3: Some initial objectives must be addressed in order to preserve the proper precedence relationships in the network:

• (i) Which activity immediately precede the latest activity?

• (ii) Which one follow the latest activity?

• (ii) Which one occur concurrently with the latest activity?

The flowchart in Fig. 10 helps to determine the construction steps of the network with PFNs describing the precedence relationship among different activities.

Fig. 10

Flowchart for construction of a project network

Thus to provide unique end nodes between two concurrent activities and to ensure the correct precedences among the activities of a project, the use of some additional activities is required. An activity which is used to represent two concurrent activities is called dummy activity. A dummy activity consumes no time or resources according to definition. The use of dummy activity rectifies the situation mentioned in Rule 3 of network construction. Dummy activities can be inserted in more than one way to keep the concurrence of two nodes and to offer unique end nodes for two activities. Figure 11 displays the inserting method of a dummy activity to ensure the unique characterization of concurrent activities.

Fig. 11

Method of inserting dummy activity

5.5 Algorithm’s overview

The project network needs to be thoroughly investigated before the risk criteria are examined (that will be utilized to determine the actual critical route). The duration of every project task is described according to this scope using triangular PFNs. A triangular PFN will be indicated as $\tilde{N}=\langle [n_1,n_2,n_3]: \xi _{\tilde{N}}, \eta _{\tilde{N}} \rangle$ in the text that follows, where $n_2$ defines the peak’s location, ${n_1}$ and $n_2$ stands, respectively, for the left and right-hand width of both $\mu _{\tilde{N}}$ and $\nu _{\tilde{N}}.$ Triangular PFNs seem to be an excellent choice, because they provide a reasonable settlement between precision and computation time. In fact, they can depict a clear and concise representation of the expert opinions.

5.5.1 Description of probabilistic time duration

The three-time estimations used in PERT can be defined in a similar way to the parameters used in probability distributions to represent uncertainty. In PFPERT, each activity is assigned by a PFN. The three time estimates can be defined using $(\alpha ,\beta )$-cut approach. Experts (i.e., the individuals responsible for the performance of each activity) are sought to provide this three time estimations in the following manner:

• 1. Most likely duration $n_2$ at $(\alpha ,\beta )$-cut with $(\alpha ,\beta ) = (\xi _{\tilde{N}}, \eta _{\tilde{N}}),$

• 2. Pessimistic durations $n_1^{'}$ at $(\alpha ,\beta )$-cut with $(\alpha ,\beta ) = (0+ \epsilon , 1-\epsilon ),$

• 3. Optimistic durations $n_3^{'}$ at $(\alpha ,\beta )$-cut with $(\alpha ,\beta ) = (0+ \epsilon , 1- \epsilon ),$

where $\epsilon > 0.$ In a nutshell, $n_1^{'}$ and $n_3^{'}$ describe an interval as belonging to the collection of potential durations if and only if its points possess a $\mu$-possibility more than $0+ \epsilon$ and $\nu$-possibility less than $1-\epsilon$, whereas $n_2$ is indisputably a member of the set. Figure 12 depicts this assumption graphically, which shows that the MF decreases gradually from $\xi _{\tilde{N}}$ to 0 and non-MF increases gradually from $\eta _{\tilde{N}}$ to 1,  as x moves from $n_2$ to $n_3.$ Due to this fact, the optimistic duration is considered at $n_3^{'}$ Thus, the execution goes extremely well at $n_3^{'}.$ Similarly, the execution goes extremely poor at $n_1^{'}.$ Therefore, the pessimistic duration is considered at $n_1^{'},$ which is obtained at $(0+ \epsilon , 1- \epsilon )$-level cut. Moreover, the most likely duration is considered at $n_2,$ which can be obtained at $(\xi _{\tilde{N}}, \eta _{\tilde{N}})$-level cut. Thus the most likely duration $n_2$ falls in the range from $n_1^{'}$ to $n_3^{'}.$ In this way, these estimates provide a way to handle imprecise information and model the variability associated with project activities.

Fig. 12

Duration estimates for activities in terms of triangular PFNs

As a special case, we consider a triangular PFN with maximum degree of satisfaction and minimum degree of dissatisfaction, i.e., $\tilde{N}=\langle [n_1,~{n_2},~{n_3}];~1,0 \rangle .$ For this case, the most likely duration $n_2$ is considered at $(\alpha ,\beta )$-cut with $(\alpha ,\beta ) = (\xi _{\tilde{N}}, \eta _{\tilde{N}}),$ the pessimistic and optimistic durations $n_1^{'}$ and $n_3^{'}$ at $(\alpha ,\beta ) = (0.1,0.9)$-level cut.

The optimistic duration denotes the amount of time required if no issues arise and if the resources work diligently to achieve the desired duration. The predicted duration, in a similar vein, denotes the amount of period under analysis that an activity would usually require under ordinary circumstances. The pessimistic time frame also accounts for the safety to manage uncertainty of the activity (i.e., the issues that may arise after an activity has been initiated) and the effects of diversion or interruption that resources generally experience in their organizational context. Although these key occurrences will later be taken into consideration as additional decision criteria for the identification of the actual critical route, they should not be included in the pessimistic duration as they will be kept in mind as decision criteria in the future.

5.6 Methodology

The primal PF network analysis can be carried out after the durations have been computed by swapping out algebraic operations for their PF generalization. Additionally, the project completion time and the length of the routes will be the only metrics computed by the PERT’s forward phase that are part of the risk criteria used to establish the actual critical route. However, the float of sub-critical activities will only be utilized as a scale factor and not as a specific risk criterion, therefore, the backward step is actually conducted to calculate it. This fact, along with the fact that the forward step is perfectly accurate in the simple version of the PFPERT, clearly gives additional support for replacing the crisp operations with their PF equivalents.

We define a Pythagorean fuzzy event (PFE) as a moment in time at which some activities end and others begin in order to do the required computations. Such a PFE is analogous to a node in the network with Pythagorean fuzzy parameters. Let e be a PFE. We define some occurrences of e relative to the beginning and ending dates of the whole project in Table 2.

Table 2 Passes of PF critical route computation

5.6.1 Pythagorean fuzzy forward pass (PFFP)

The calculations proceed recursively from node 1 to end node n.

First Step: Set $F_e = \langle [0,0,0];~1,0\rangle ,$ showing that the project begins at time 0.

jth Step: Given a network with nodes $e_1,e_2,\ldots ,e_n.$ Let $I_i$ be the set of nodes that are joined directly with node j through incoming activities $(e_i,e_j).$ The earliest recorded occurrence of events $e_i$ (represented by nodes) in the set $I_i$ have already been calculated. Thus, the earliest recorded occurrence of event $e_j$ can be calculated according to Eq. 26.

$$\begin{aligned} F_{e_j}&= \max \limits _{i\in I_i}~\{F_{e_i}+D_{ij}\}. \end{aligned}$$

(26)

The PFFP is completed when $F_{e_n}$ has been calculated at node n. By definition, $F_{e_j}$ shows the lengthiest route (duration) to node $e_j.$

5.6.2 Pythagorean fuzzy backward pass (PFBP)

Upon the termination of the PFFP, the PFBP calculations recede recursively from node n to end node 1.

First Step: Set $B_{e_n}=F_{e_n},$ showing that at the end node, the earliest and latest recorded occurrences are equal.

jth Step: Given a network with nodes $e_1,e_2,\ldots ,e_n.$ Let $O_i$ be the set of nodes that are joined directly with node j through outgoing activities $(e_j,e_i).$ The latest recorded occurrence of events $e_i$ (represented by nodes) in the set $O_i$ have already been calculated. Thus, the latest recorded occurrence of event $e_j$ can be calculated according to Eq. 27.

$$\begin{aligned} B_{e_j}&= \min \limits _{i\in O_i} ~\{B_{e_i}-D_{ji}\}. \end{aligned}$$

(27)

The PFBP is complete when $B_{e_1}$ has been calculated at node 1. At this stage, $F_{e_1}=B_{e_1}=0.$

According to calculations made earlier, an activity is found to be critical if it meets the following three criteria: $F_{e_i}=B_{e_i},$ $F_{e_j}=B_{e_j}$ and $F_{e_j}-F_{e_i}=B_{e_j}-B_{e_i}=D_{ij}.$ These three requirements shows that the duration must closely fit inside the given time frame, and the earliest and latest recorded occurrences of end nodes must be equal. Therefore, a non-critical activity is one that does not fulfil any of these three requirements. By definition, a network’s critical activities must create an uninterrupted route that covers the entire network from beginning to end.

The following relationships are employed throughout the work in order to ensure the triangular behavior of the arithmetic operations as well as the maximum and minimum of the set of triangular PFNs.

Definition 15

Let $\tilde{N}_1=\langle [a_1,b_1,c_1];\zeta _{\tilde{N}_1},\eta _{\tilde{N}_1}\rangle$ and $\tilde{N}_2=\langle [a_2,b_2,c_2];\zeta _{\tilde{N}_2},\eta _{\tilde{N}_2}\rangle$ be two triangular PFNs and $\kappa$ be any real number. Then

• 1. $\tilde{N}_1 \oplus \tilde{N}_2=\langle [a_1+a_2,b_1+b_2,c_1+c_2];~\sqrt{\zeta _{\tilde{N}_1}^2 +\zeta _{\tilde{N}_2}^2-\zeta _{\tilde{N}_1}^2 \zeta _{\tilde{N}_2}^2},~\eta _{\tilde{N}_1} \eta _{\tilde{N}_2}\rangle .$

• 2. $\tilde{N}_1 \ominus \tilde{N}_2=\langle [A,B,C];~\sqrt{\zeta _{\tilde{N}_1}^2 +\zeta _{\tilde{N}_2}^2-\zeta _{\tilde{N}_1}^2 \zeta _{\tilde{N}_2}^2},~\eta _{\tilde{N}_1} \eta _{\tilde{N}_2}\rangle ,$ where

  $$\begin{aligned} A= & {} \min \{a_1-a_2,b_1-b_2,c_1-c_2\}, \\ B= & {} \min \{\max \{a_1-a_2,b_1-b_2\},\max \{b_1-b_2,c_1-c_2\}\},\\ C= & {} \max \{a_1-a_2,b_1-b_2,c_1-c_2\}. \end{aligned}$$

• 3. $\tilde{N}_1 \otimes \tilde{N}_2=\langle [a_1 a_2,b_1 b_2,c_1 c_2];~\zeta _{\tilde{N}_1} \zeta _{\tilde{N}_2},~\sqrt{\eta _{\tilde{N}_1}^2 + \eta _{\tilde{N}_2}^2-\eta _{\tilde{N}_1}^2 \eta _{\tilde{N}_2}^2}\rangle .$

• 4. $\tilde{N}_1 \oslash \tilde{N}_2=\langle [A,B,C];~\zeta _{\tilde{N}_1} \zeta _{\tilde{N}_2},~\sqrt{\eta _{\tilde{N}_1}^2 + \eta _{\tilde{N}_2}^2-\eta _{\tilde{N}_1}^2 \eta _{\tilde{N}_2}^2}\rangle ,$ where

  $$\begin{aligned} A= & {} \min \left\{ \frac{a_1}{a_2},\frac{b_1}{b_2},\frac{c_1}{c_2}\right\} , \\ B= & {} \min \left\{ \max \left\{ \frac{a_1}{a_2},\frac{b_1}{b_2}\right\} ,\max \left\{ \frac{b_1}{b_2},\frac{c_1}{c_2}\right\} \right\} ,\\ C= & {} \max \left\{ \frac{a_1}{a_2},\frac{b_1}{b_2},\frac{c_1}{c_2}\right\} , \end{aligned}$$

  provided $0 \not \in [a_2,b_2,c_2].$

• 5. $\tilde{N}_1 \vee \tilde{N}_2 = \langle [\max \{a_1,a_2\},\max \{b_1,b_2\},\max \{c_1,c_2\}];~\min \{\zeta _{\tilde{N}_1},\zeta _{\tilde{N}_2}\},~\max \{\eta _{\tilde{N}_1},\eta _{\tilde{N}_2}\}\rangle .$

• 6. $\tilde{N}_1 \wedge \tilde{N}_2 = \langle [\min \{a_1,a_2\},\min \{b_1,b_2\},\min \{c_1,c_2\}];~\min \{\zeta _{\tilde{N}_1},\zeta _{\tilde{N}_2}\},~\max \{\eta _{\tilde{N}_1},\eta _{\tilde{N}_2}\}\rangle .$

5.7 Decision criteria to measure criticality

Measuring criticality involves assessing the importance or significance of a decision in a given context. The criteria used to determine criticality may vary depending on the specific domain or industry. Integrating risk analysis into the decision-making process using MCDM helps project managers make informed choices that consider both the uncertainties associated with the project and the diverse criteria that impact project success. This integration enhances project planning, risk mitigation and overall project outcomes. Following facts describe that how these concepts intersect within the realm of project management:

• Risk analysis and the MCDM approach can be integrated by considering risk factors as one of the criteria in the decision-making process. For instance, project managers can assign weights to risk-related criteria based on their potential impact on project success.

• When evaluating project alternatives using MCDM, the impact of risks, as quantified through risk analysis, can be factored into the decision model. This ensures that risk management is an integral part of project decision-making.

• Sensitivity analysis within MCDM can also help to assess how variations in risk scenarios affect the selection of the best project alternative, providing insights into the robustness of project plans.

It is required to determine all feasible alternatives and the decision criteria to differentiate them in order to utilize MCDM. Here, the alternatives align with the project’s routes, and the potential risk criteria include duration of route, criticality of route, cost of predicted route, criticality of common resources and external risk factors. These decision criteria are introduced in the manner that follows.

5.7.1 Duration of route

A critical route is often identified using the duration and variability of the route. The duration of a route in a project network is a fundamental decision criterion used in project management. It refers to the time required to complete a particular sequence of interconnected tasks from the project’s start to its end, without considering task dependencies. Because Cauchy PFNs can easily represent a dual information about both expects, their evaluation is simple and can be obtained by simply summing up (in PF sense) the durations of the tasks that correspond to a route. Thus the length of route can be calculated according to Eq. 28.

$$\begin{aligned} \mathcal {D}|_{r}=\sum _{{ij}\in r} \mathcal {D}_{ij} = \bigg \langle \bigg [\sum _{{ij}\in r} {n_1}_{(ij)} , \sum _{{ij}\in r} {n_2}_{(ij)} , \sum _{{ij}\in r} {n_3}_{(ij)}\bigg ];~1,0 \bigg \rangle , \end{aligned}$$

(28)

where $\mathcal {D}_{ij}$ is the time taken to complete an activity on the $r^{th}$ route as a triangular PFN.

5.7.2 Criticality of route

In project schedule analysis, considering resources is a critical aspect of ensuring that the project plan is realistic, feasible, and executable. Resources refer to the people, equipment, materials, and other assets required to perform project activities. Resource management involves evaluating the availability, allocation, and utilization of resources to meet project objectives efficiently.

The criticality of a route in project networks is a crucial decision criterion in project management. It focuses on task dependencies and sequencing within a specific route, emphasizing the impact of delays on the overall project schedule. In other words, a critical route is the longest sequence of dependent activities that must be completed in the shortest possible time to ensure the project’s timely completion. Given that the majority of the paths have the potential to be critical, another parameter is required to assess how much each path contributes to the project finishing time. Let $Len|_{r}=( {n_1}_{(r)}; {n_2}_{(r)}; {n_3}_{(r)})$ be the $r^{th}$-route length and $P_{t_F}=({n_1}_{t_F}; {n_2}_{(t_F)}; {n_3}_{(t_F)})$ be the project’s finishing time in terms of triangular PFN. The Criticality of $r^{th}$-route is typically defined in Eqs. 29 and 30.

$$\begin{aligned} {\mu }-\mathcal {C}r_{r}= & {} Pos_{\mu }\{\mathcal {D}|_{r} ~is~ P_{t_F} \}= \sup \{\mu _{Len|_{r}}(w) \wedge \mu _{P_{t_F}}(w) ~|~ w \in R \}, \end{aligned}$$

(29)

$$\begin{aligned} {\nu }-\mathcal {C}r_{r}= & {} Pos_{\nu }\{\mathcal {D}|_{r}~ is~ P_{t_F} \}= \sup \{\nu _{Len|_{r}}(w) \wedge \nu _{P_{t_F}}(w) ~|~ w \in R \}. \end{aligned}$$

(30)

However, it appears preferable to specify the route criticality $(\mathcal{R}\mathcal{C})$ as a PFN as well, since the actual critical route would be defined using MCDM on PFN. Equation 31 can be used to accomplish this.

$$\begin{aligned} \mathcal{R}\mathcal{C}_r = \mathcal {D}|_{r} ~\oslash ~P_{t_F}, \end{aligned}$$

(31)

where the division operation $\oslash$ can be calculated according to Definition 15.

5.7.3 Cost of predicted route

Another crucial element to take into account is the cost of the predicted route. Predicting the cost associated with this critical path provides valuable insights for decision-making in project networks. It is possible to adequately describe the total expense of each task $e_{ij}$ using triangular PFNs. The project’s execution team is therefore asked for the values at levels $\alpha _1$ and $\alpha _2$ in terms of triangular PFNs $({n_1}^{'}_{(ij)};{n_2}_{(ij)};{n_3}^{'}_{(ij)})$ for each activity in order to calculate the corresponding PF costs $\mathcal {C}_{ij}=({n_1}_{(ij)};{n_2}_{(ij)};{n_3}_{(ij)}).$ Thus to evaluate the cost of $r^{th}$-route, Eq. 32 can be used.

$$\begin{aligned} \mathcal{R}\mathcal{C}=\sum _{{ij}\in r} \mathcal {C}_{ij} = \bigg \langle \bigg (\sum _{{ij}\in r} {n_1}_{(ij)} , \sum _{{ij}\in r} {n_2}_{(ij)} , \sum _{{ij}\in r} {n_3}_{(ij)}\bigg );~1,0 \bigg \rangle . \end{aligned}$$

(32)

5.7.4 Criticality of common resources

Criticality of common resources concentrates on resource allocation and constraints that may affect multiple tasks or routes in the project. Prior to an effective schedule being created for a project that is resource-constrained, resources must be leveled. The effect of resource sharing across many project contexts is our current concern, rather than resource sharing within tasks of the same project. There are persistent pressures on almost any firm to meet major new opportunities, and new projects may begin at any time. As a result, it happens frequently that a project activity is not finished before new projects need reconfiguring priorities. Under these circumstances, common resources try to handle multiple projects at once, which has the impact of making them lose focus, cause delays, and produce organizational issues. In fact, the impacts of common resources on project completion time are too complicated to be adequately captured by a standard quantitative expression. Nonetheless, it appears to be able to identify the resources that are very likely to become essential if new initiatives are launched or certain priorities are altered.

Once the resources have been identified, the project manager can assess their criticality subjectively (using his domain of expertise). If more experts are consulted, the common resource criticality (Res) of the generic r-th resource can then be easily determined by mean of the fuzzy average of all their evaluations. Judgments can then be transformed into triangular PFNs using a set of linguistic variables. Equation 33 provides the formula to calculate resource criticality.

$$\begin{aligned} \mathcal {R} es \mathcal {C}_{r}=\frac{1}{m} \sum _{m} {PFLV}_{K} = \frac{1}{m} \times \bigg \langle \bigg (\sum _{m} {n_1} , \sum _{m} {n_2} , \sum _{m} {n_3}\bigg );~1,0 \bigg \rangle . \end{aligned}$$

(33)

where m is the number of experts and the k-th PFLV is a triangular PFN ${PFLV}_k=\langle ({n_1}_k,{n_2}_k,{n_3}_k);~1,0\rangle .$

By considering the criticality of common resources, project managers can make well-informed decisions to optimize resource utilization, mitigate risks, and ensure timely project completion. It allows for better resource planning, allocation, and coordination, which are vital aspects of successful project management.

5.7.5 External risk factors

External risk factors are factors that lie outside the direct control of the project team but can significantly impact the project’s success. These risk factors are often associated with the external environment in which the project operates. Evaluating external risk factors as decision criteria for project networks is crucial because it helps project managers understand potential threats and uncertainties that can affect the project. A number of factors, such as logistical or transportation issues, equipment breakdowns, unreliable suppliers, and unfavorable environmental conditions, might affect the length of a project in a normal setting. However, the project manager is unable to fully affect it (i.e., external risks factors).

It can be challenging to fully identify and define external risks. Consequently, a method based on PFLVs can be utilized to quantify their potential consequences. In this scenario, the experts are requested to provide a subjective assessment of the risk due to external factors (REF) for each task of the project. To acquire the final evaluation of the external risk of each k-th path, these evaluations must be transformed into PFLVs and then aggregated according to Eq. 34.

$$\begin{aligned} {Ris}_{k}= \sum _{{ij}\in r} {REF}_{ij} \end{aligned}$$

(34)

For the case when more experts are consulted, the external risk factor of k-th route can be obtained by taking fuzzy average of all the assessments provided.

Quantitative risk analysis techniques are required for a more comprehensive risk assessment. Risks related to the project’s scope and quality, resource constraints or resource-driven risks, external risks, such as changes in regulations, market conditions, or natural disasters, and critical path risks that can have significant implications for the project’s success, are all the types of risks that can be analyzed.

6 Critical route detection using VIKOR method

The Program Evaluation and Review Technique (PERT) is a project management tool used to schedule, organize and coordinate tasks within a project. In this section, PERT is designed for Pythagorean fuzzy case to help project managers to identify the PF critical route, or the sequence of tasks that must be completed on time in order for the project to be completed on schedule, where the time duration are in terms of PFNs. This technique involves creating a network diagram that visually represents the relationships/dependencies between tasks in the project. Each task is assigned a duration as well as cost in terms of PFNs, which is used to calculate the most critical route. It also uses three time estimates for each task: the optimistic time, the most likely time, and the pessimistic time, which have been defined/considered involving $\alpha$-cuts at specific levels. These estimates are used to calculate the expected duration of each task and the overall project duration. Using an MCDM approach, the predefined indexes can be aggregated to determine the criticality ranking of routes. The VIKOR method is based on compromise programming, which is a mathematical optimization technique that seeks to find the best solution that balances conflicting objectives. The VIKOR method considers both the maximum group utility and the minimum individual regret to rank alternatives. There is a lot of literature on PF VIKOR, and some interesting applications can be seen in Mishra et al. (2022), Zahid and Akram (2023).

The PF VIKOR method allows decision-makers to express their preferences using linguistic terms, which makes it easier to handle imprecise and uncertain information and to provide a more accurate and realistic ranking of alternatives. In the context of critical path detection, the alternatives represent different paths or sequences of tasks in a project, and the criteria represent various project constraints, such as time, cost, resource availability and risk factors.

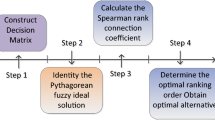
The proposed method uses the following steps to aggregate the decision criteria for each alternative and to obtain the compromise ranking of routes in the project network.

Step 1 Define the decision matrix and normalize it. The weight coefficients which reflect the importance of each criterion in the decision-making process can be normalized by dividing each criteria weight with the sum of all criteria weights.

Step 2 Determine the best $f_{j}^*$ and worst $f_{j}^-$ values for each decision criteria according to the formulas given in Eqs. 35 and 36.

$$\begin{aligned} f_{j}^*= & {} \max _{k} f_{kj}, \end{aligned}$$

(35)

$$\begin{aligned} f_{j}^-= & {} \min _{k} f_{kj}, \end{aligned}$$

(36)

where $f_{kj}$ denotes the values of corresponding criteria $C_j$ for all k.

Step 3 Compute the utility value $(\mathcal {S}_k)$ and regret value $(\mathcal {R}_k).$ The utility value represents the overall performance of an alternative in comparison to the other alternatives. The regret value represents the difference between the best and worst performance for each criterion. The $\mathcal {S}_k$ and $\mathcal {R}_k$ values are calculated using the relations provided in Eqs. 37 and 38.

$$\begin{aligned} \mathcal {S}_k= & {} \sum _{j=1}^{m} {w_j}{\frac{|f_{j}^*-f_{kj}|}{|f_{j}^*-f_{j}^-|}}, \end{aligned}$$

(37)

$$\begin{aligned} \mathcal {R}_k= & {} \max _j {w_j}{\frac{|f_{j}^*-f_{kj}|}{|f_{j}^*-f_{j}^-|}}, \end{aligned}$$

(38)

where $w_j$ are the weight of criteria indicating their relative importance.

Step 4 Compute the VIKOR score $(\mathcal {Q}_k)$ for each alternative by the formula given in Eq. 39.

$$\begin{aligned} \mathcal {Q}_k= {v}{\frac{\mathcal {S}_{k}-\mathcal {S}^*}{\mathcal {S}^- -\mathcal {S}^*}}+(1-v){\frac{\mathcal {R}_{k}-\mathcal {R}^*}{\mathcal {R}^- -\mathcal {R}^*}}, \end{aligned}$$

(39)

where $\mathcal {S}^*=\min _k \mathcal {S}_k,~\mathcal {S}^-=\max _k \mathcal {S}_k,~\mathcal {R}^*=\min _j \mathcal {R}_j$ and $~\mathcal {R}^-=\max _j \mathcal {R}_j.$ $v \in {0,1}$ stands for how heavily the majority of criteria were considered in the overall strategy.

Step 5 The alternatives ${(\alpha _i;~i=1,\ldots ,n)}$ are arranged in ascending order by ordering the values of $\mathcal {S}_k,~\mathcal {R}_k$ and $\mathcal {Q}_k.$ As a result, we get three ranking lists based on the values $\mathcal {S}_k,~\mathcal {R}_k$ and $\mathcal {Q}_k,$ which are then used to suggest the compromise solution of alternatives.

Step 6 The alternative $\alpha _1$ has a compromise solution that, if it meets both of the following two criteria, is ranked highest by the measure $\mathcal {Q}_k$ (minimum score).

• A. $\mathcal {Q}(\alpha _2)-\mathcal {Q}(\alpha _1)\ge D \mathcal {Q},$ where $\alpha _2$ is the second-placed alternative in ordering list $\mathcal {Q}$ and $D \mathcal {Q}=\frac{1}{n-1},$ where n is the total number of alternatives.

• B. The alternative $\alpha _1$ must also be the best-ranked alternative by $\mathcal {S}$ and $\mathcal {R}.$

A set of compromise solutions is derived if any one of the aforementioned conditions is not met.

• The options $\alpha _1$ and $\alpha _2$ make up the set of compromise solutions if only criterion B is not met.

• The alternatives $\alpha _1,~\alpha _2,\ldots \alpha _n$ are included in the compromise solution set if only the condition A is not met; $\alpha _n$ is produced by the relation $\mathcal {Q}(\alpha _n)- \mathcal {Q}(\alpha _1) <D\mathcal {Q}$ for maximum value of n.

For some decision criteria, the project completion time are too complicated to be adequately captured by some standard quantitative expressions. These are reported in linguistic terms. We define triangular PFNs, described in Fig. 13, that correspond to the linguistic values from the term set “Extremely Poor (EP), Poor (P), Slightly Poor (SP), Average (A), Slightly Good (SG), Good (G), Extremely Good(EG)”.

Fig. 13

Pythagorean fuzzy linguistic terms for decision criteria

7 An automated greenhouse construction project

The application of project scheduling for the analysis of the development of an automated greenhouse is shown in order to better explain the suggested methodology. This study, which is adapted from Monjezi et al. (2012), was carried out in Iran. The data were collected from variety of sources, such as reports and statistics of agricultural organization, by Monjezi et al. Monjezi et al. (2012).

A greenhouse is a great way to extend the growing season and protect the plants from harsh weather conditions. A greenhouse construction project includes some main activities like, planing ahead, consideration of climate, selection of right materials, utilization of proper ventilation, incorporation of automation and taking safety precautions. Minor construction activities are also needed to provide the infrastructure for greenhouse development and to stabilize the ground. A list of particular tasks which are helpful in planing and executing the greenhouse construction project is provided in Table 3. The input data is converted into triangular PFNs in Table 3 based on the research conducted by Monjezi et al. Monjezi et al. (2012). All the information needed for the analysis is included in the table (dependencies, durations and costs). Fig. 14 depicts the resulting activity on arcs of the project network.

Table 3 Input details to measure criticality in automated greenhouse construction project

7.1 Results and discussion

The critical path represents the longest sequence of dependent activities that determines the minimum duration to complete the entire project. Activities that are not on the critical path have some scheduling flexibility and can be delayed without affecting the overall project completion time. To schedule the project plan tasks, we use PFPERT to provide visual representation of the above data. PFPERT visualizes PF critical paths on three estimates of time and to map out the progress of a project. The duration and costs of activities, which are provided in terms of triangular PFNs, are given in Table 3. The network diagram of greenhouse construction project defines a clear and appropriate order of project activities. Figure 14 emphasizes the connections and pathways between tasks to guarantee the proper execution of the project.

7.1.1 Detailed steps of proposed method

In this section, in order to fully comprehend the proposed strategy, the steps of the proposed method are thoroughly covered in this section.

Step 1: Construction of Network The network outlining the precedence relationships between the various activities is shown in Fig. 14. According to proposed method, the nodes of the network are corresponding to the PFEs $(e_i).$ Thus, there are 45 PFEs $(e_i,~i=1,2,\ldots ,45).$

Fig. 14

Automated greenhouse construction project network

Observe that in Fig. 14, the red colored arrows show the critical activities and determine the critical route in the greenhouse construction project. These activities are considered critical because they have a significant impact on the project’s timeline, budget or quality, and help project managers to determine the optimal sequence of activities. To provide unique end nodes between two concurrent activities and to ensure the correct precedences among the activities of the case study, the use of some additional activities is required. Thus, the dummy activities (dotted lines) are created to guarantee proper precedences among the activities of greenhouse construction project. The duration of the dummy activity is usually zero PFN, i.e., $\langle [0,0,0],~1,0 \rangle ,$ as it does not represent any real work or time. The nodes are numbered in ascending order in the direction of progress in the greenhouse construction project.

Step 2: Computations of PF Forward and Backward Passes: In this step, we perform particular computations to conveniently apply the proposed method to greenhouse construction project. It is easy to observe that the earliest recorded occurrence of PFE $e_i,$ calculated using Eq. 26, is responsible for the computation of PFFP. Similarly, the latest recorded occurrence of PFEs, calculated using Eq. 27, are responsible for the computation of PFBP.

In forward pass calculations, we start by taking $F_{e_1}=0$ and proceed recursively to PFE $e_{45}.$ While in backward pass calculations, we start by taking $B_{e_{45}}=F_{e_{45}}$ and recede recursively to PFE $e_{1}.$ Table 4 provides the computational details of forward and backward passes in PF critical path evaluations.

Table 4 Passes of PF critical path computations

Step 3: Calculations of Decision Criteria for each Route Project management with multi criteria involves using a set of criteria to evaluate the project’s performance against multiple objectives. The present study discusses the following five criteria: route length, route criticality, route cost, resource criticality and risk factors. The calculation details of these criteria for the Route A is provided below:

Consider the Route $A:~1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 6 \rightarrow 7 \rightarrow 8 \rightarrow 10 \rightarrow 23 \rightarrow 44 \rightarrow 45.$

Route Duration The length of the Route A can be calculated according to Eq. 28, where 1, 2, 3, 5, 6, 7, 8, 10, 23, 44, 45 represents the events in the project network which involve the activities 1, 2, 4, 5, 6, 8, 21 and 34. Thus the durations of all these activities have been added to obtain the required result.

$$\begin{aligned} \mathcal {D}|_{A}= & {} \langle [11,14,17];~1,0\rangle + \langle [6,7,8];~1,0\rangle + \langle [0,0,0];~1,0\rangle \\{} & {} +\langle [10,40,70];~1,0\rangle + \langle [1,7,12];~1,0\rangle \\{} & {} +\langle [3,7,11];~1,0\rangle + \langle [40,45,50];~1,0\rangle +\langle [6,7,8];~1,0\rangle \\{} & {} + \langle [0,0,0];~1,0\rangle + \langle [5,5,6];~1,0\rangle ,\\= & {} \langle [114,180,145];~1,0\rangle . \end{aligned}$$

Route Criticality From the calculations of forward and backward passes, we have obtained the project’s finishing time $\langle [122,201,279];~1,0\rangle .$ The results of Criteria 1 yield the $A^{th}$-route length $\langle [114,180,145];~1,0\rangle .$ The criticality of $A^{th}$-route $(\mathcal{R}\mathcal{C}r_A)$ as a PFN can be calculated using Eq. 31 by utilizing the division operation of triangular PFNs.

$$\begin{aligned} \mathcal{R}\mathcal{C}r_A= & {} \mathcal {D}|_{A} ~\oslash ~P_{t_F}, \\= & {} \langle [114,180,145];~1,0\rangle ~\oslash ~\langle [122,201,279];~1,0\rangle , \\= & {} \langle [0.88,0.89,0.93];~1,0\rangle . \end{aligned}$$

Cost of Predicted Route To evaluate the cost of $A^{th}$-route, we use Eq. 32. Thus, the costs of all the activities 1, 2, 4, 5, 6, 8, 21 and 34,  involved in Route A,  have been added to obtain the required result.

$$\begin{aligned} \mathcal{R}\mathcal{C}_A= & {} \langle [4.5,4.73,4.8];~1,0\rangle + \langle [0,0.024,0.3];~1,0\rangle + \langle [0,0,0];~1,0\rangle + \langle [0.02,0.024,0.035];~1,0\rangle \\{} & {} +\langle [0.02,0.024,0.035];~1,0\rangle + \langle [1.2,1.28,1.3];~1,0\rangle \\{} & {} + \langle [33,33.54,34];~1,0\rangle + \langle [2.2,2.48,2.7];~1,0\rangle \\{} & {} +\langle [0,0,0];~1,0\rangle + \langle [0.2,0.26,0.3];~1,0\rangle ,\\= & {} \langle [41.26,42.46,43.32];~1,0\rangle . \end{aligned}$$

Criticality of Common Resources Since this factor is too complicated to be adequately captured by a standard quantitative expression, the expert provides their evaluation as a PF linguistic term i.e., Slightly Poor (SP) $=\langle [6,8,10];~1,0\rangle .$ For the case when more experts are consulted, the criticality of common resources of the A-th route can be obtained by using Eq. 33, i.e., taking fuzzy average of all the assessments provided.

External Risk Factors Since identification of external risks is challenging, therefore, PF linguistic terms can be utilized to quantify their potential consequences. Thus, the expert provides a subjective assessment of the risk due to external factors for A-th route of the project i.e., Average (A) $=\langle [9,11,13];~1,0\rangle .$ For the case when more experts are consulted, the external risk factor of A-th route can be obtained by taking fuzzy average of all the assessments provided.

Calculations for all other routes can be carried out in similar manner. Table 5 provides the resultant values of all five criteria corresponding to each path of the network.

Table 5 Assessment of Decision Criteria

Step 4: Ranking of Routes using VIKOR Technique To ensure that the green house construction project meets all of its objectives and delivers the desired benefits within specified time period, we use VIKOR method to identify the worst path. For this, first we assign weights to each criterion in terms of PFNs based on their relative importance (see Table 15). A scale of 0 to 1 is used. We define PFNs, described in Fig. 15, that correspond to the linguistic values from the term set “Extremely Low (EL), Low (L), Slightly Low (SL), Average (A), Slightly High (SH), High (H), Extremely High (EH)”.

Fig. 15

Pythagorean fuzzy linguistic terms for relative importance

To discuss the criticality ranking of routes of the project network, all the decision criteria are aggregated using VIKOR method. The framework for determining the greenhouse construction project strategy is sketched in Fig. 16.

Fig. 16

Framework for determining the most critical route in greenhouse construction project network

VIKOR evaluates each route of the network based on five decision criteria and calculates a score for each route. The route with the least score (worst path) is then selected as the real critical path. The calculation details of VIKOR method are provided below.

The decision problem, the alternatives and the criteria are clearly defined above. We have assigned the weights to each criterion in Table 5 based on their relative importance according to Fig. 15. The criteria weights are normalized to ensure that each criterion is on the same scale. This is done by dividing each criterion value by the sum of all criteria value of that criterion. Normalized criteria weights are defuzzified and given in Table 6.

Table 6 Normalized criteria weights

${\mathcal {S}}$ (best) and ${\mathcal {R}}$ (worst) values for each route and each criterion are calculated according to Eqs. 37 and 38. This is done by finding the maximum and minimum values for each criterion across all alternatives by Eqs. 35 and 36. The results are given in Table 7). Results are shown in Table 8.

Table 7 $f_{j}^*$ and $f_{j}^-$ values of criteria functions

Next, the VIKOR score $({\mathcal {Q}})$ is calculated for each route of the network according to Eq. 39 using weight of strategy $v=0.5.$ The results are given in Table 8). For calculations of ${\mathcal {Q}},$ we obtain ${\mathcal {S}^*}=0.02,~ {\mathcal {S}^-}=0.8333$ and ${\mathcal {R}^*}=0.02,~ {\mathcal {R}^-}=0.28.$

Table 8 ${\mathcal {S},~ \mathcal {R}}$ and ${\mathcal {Q}}$ values for each route

Ranking the routes, sorting by the values ${\mathcal {S},~ \mathcal {R}}$ and ${\mathcal {Q},}$ are done. The results are three ranking lists shown in Table 9.

Table 9 Ranking of routes by ${\mathcal {S},~\mathcal {R}}$ and ${\mathcal {Q}}$

Final ranking of the routes of the greenhouse construction project network are based on their VIKOR scores $( {\mathcal {Q}}).$ These scores are calculated using a weighted compromise solution approach that takes into account both the best and worst performances of each route on each criterion. The route with the least score is selected as the best critical route. Hence, Route E, i.e., $1 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 6 \rightarrow 7 \rightarrow 8 \rightarrow 10 \rightarrow 35 \rightarrow 36 \rightarrow 41 \rightarrow 43 \rightarrow 44 \rightarrow 45$ is the actual critical route which is highlighted in red color in greenhouse construction project network.

8 Comparative analysis

In this section, we conduct a comparative assessment between our proposed approach and the fuzzy PERT method introduced by Zammori et al. Zammori et al. (2009). Our methodology is employed in the context of a project network designed for establishing a road connection between two urban centers, as depicted in Zammori et al. (2009). To authenticate the efficacy of our implementation, we compare the outcomes obtained.

Consider a project network, illustrated in Fig. 17, comprising 22 activities. We assume that the durations and costs associated with the network’s activities are represented as fuzzy numbers (FNs), as delineated in Table 10. Utilizing our approach, we identify the critical path commencing with Activity 1 and concluding with Activity 22. The determination of respective durations necessitates the process of defuzzifying the FNs assigned to the project’s activities.

Table 10 Input details to determine real critical path

Fig. 17

Realization of road connection project network (adapted from Zammori et al. (2009))

The comparative analysis reveals identical critical paths, as detailed in Table 11. This case study confirms that the decision outcomes established by Zammori et al. Zammori et al. (2009) align with our proposed approach, endorses the authenticity of our method.

Table 11 List of Paths

To ascertain the criticality ranking of paths in the road connection project network, the fuzzy TOPSIS procedure is utilized for aggregating risk criteria. This process involves the creation of a weighted decision matrix by evaluating seven risk criteria for each of the ten paths. The positive ideal and negative ideal solutions are then derived from the matrix values. By computing the Euclidean distance for each alternative or path from both the positive ideal and negative ideal solutions, a vector is produced to indicate the relative closeness rating. The path with the lowest score is identified as the optimal critical route, with Path 5 represented as $1 \rightarrow 2 \rightarrow 5 \rightarrow 6 \rightarrow 8 \rightarrow 9 \rightarrow 10 \rightarrow 22 \rightarrow 23.$ The comparison of decision outcomes between the proposed method and that of Zammori et al. Zammori et al. (2009) is elaborated upon in Table  12.

Table 12 Comparison of optimal results

The innovation of the presented work resides in its capacity to deliver enhanced accuracy and dependability in project scheduling, especially in the presence of multiple criteria with uncertain conditions. This empowers project managers to effectively pinpoint critical activities and allocate resources with greater precision, ultimately minimizing the risk of delays. Moreover, it provides a transparent approach to decision-making that is based on objective criteria. This helps to increase transparency and accountability, ensuring that decisions are made based on a consistent set of criteria. Moreover, it helps to identify and evaluate the risks associated with various decision alternatives. This allows managers to mitigate risks and reduce the likelihood of unexpected outcomes.

9 Conclusions and future scope

Project management involves supervising a team’s activities to achieve all project objectives within specified constraints. PERT has been extensively utilized in the management of challenging projects by incorporating three estimates for time parameters. The presented approach is an extremely useful tool for incorporating PF parameters into mathematical models to address uncertainties. We have largely focused on the credibility theory for PFSs. Finding the best solutions, when dealing with ambiguous facts, necessitates thorough consideration of the ideas of possibility, necessity, and credibility measures. Moreover, the idea of Cauchy PFNs is presented, and it can be used to realistically simulate a wide range of real-world scenarios. The current research has shown that a more realistic extension can be achieved by incorporating PFNs as scales for both time and cost in the assessment of activities. Thus, a novel PFPERT approach is proposed to measure criticality with multi-criteria in project management problems. PFPERT can be used, for instance, to assess and balance the various requirements for a project that has numerous goals, such as finishing it on schedule, within budgetary constraints, and to a specific quality level. The proposed methodology has been implemented in a greenhouse construction project plan, demonstrating its practicality and user-friendliness. Notably, it does not necessitate explicit knowledge of membership functions for PF activity periods. Therefore, this novel concept proves to be an effective and robust tool for efficiently managing complex projects within uncertain environments. Using this technique, project managers are able to spot any delays in the project timeline and make necessary adjustments.

Following points outline the potential contributions and implications of the study for future research and practical applications.

• 1. The suggested method can be applied to fields like engineering, developing software, and construction where complicated projects may entail several tasks, dependencies, and requirements.

• 2. It is an effective tool that supports project managers in streamlining projects in uncertain situations and making the best use of their resources.

• 3. Critical activities in a project may include the design and testing of a product, the development of a software application, or the construction of a building.

• 4. In business processes, critical activities might entail finding and training staff, finishing financial reports, or completing customer orders.

• 5. In project analysis, multi-criteria analysis is frequently used to evaluate the viability and potential impact of various project solutions. Project managers can make sure that their conclusions are supported by a thorough analysis of every relevant factor by employing this decision-making process, which can result in more effective and fruitful projects.