Pythagorean fuzzy multi-criteria decision-making approach based on Spearman rank correlation coefficient

Abstract

Due to the complexity of objective world, as well as the ambiguity of human thinking, the practical decision-making issues become more and more difficult. Pythagorean fuzzy set is an effective tool for depicting uncertainty of the multi-criteria decision-making problems. This study aims to develop a Pythagorean fuzzy multi-criteria decision-making approach to deal with decision-making problem under uncertainty circumstance. Firstly, the concept, representation and related properties of Spearman rank correlation coefficient (SRCC) originated from statistical theory between two PFSs are introduced, which is used to measure the closeness degree between ideal alternative and each alternative. Then, a multi-criteria decision-making approach with Pythagorean fuzzy environment is developed based on the proposed SRCC. Finally, to illustrate the applicability and effectiveness of the proposed method, a real-world infrastructure project decision-making was demonstrated. The result shows that the main advantage of the proposed decision rule would reduce the complexity of the decision-making problem both in theory and practice.

1 Introduction

Multi-criteria decision-making (MCDM) is the process of determining an ideal alternative among all alternatives (Chen et al. 2019; Quek et al. 2019; Su et al. 2019; Li et al. 2019). However, due to the complexity of objective world, as well as the ambiguity of human thinking, the decision-making problem is becoming increasingly difficult to deal with. So far, many MCDM issues are dealt with using fuzzy theory. And a critical restriction is that fuzzy set theory is valid when the sum of membership degree and non-membership degree is less than or equal to 1. However, in reality life, it is not always possible for a decision maker or an expert to give their preferences under this restriction. For instance, when a decision maker gives his decision support for membership of an option is 0.8 and non-membership is 0.6, and the sum of his support membership degree and non-membership degree is larger than 1. Obviously, it does not satisfy the condition in fuzzy set theories. Under such circumstances, Yager and Abbasov introduced Pythagorean fuzzy set (PFS) theory, which only satisfies the case that the square sum of membership degree and non-membership degree is less than or equal to 1 (Yager and Abbasov 2013).

Recently, many scholars have focused on the investigation into the properties and operations of PFS. Yager and Abbasov showed that the Pythagorean degrees are the subclasses of the complex numbers (Yager and Abbasov 2013). Yager developed various aggregation operators, namely Pythagorean fuzzy weighted average (PFWA) operator, Pythagorean fuzzy weighted geometric average (PFWGA) operator, Pythagorean fuzzy weighted power average (PFWPA) operator and Pythagorean fuzzy weighted power geometric average (PFWPGA) operator, to aggregate different Pythagorean fuzzy numbers (Yager 2014). Under PFS information, Peng and Yang defined two arithmetical operations: division and subtraction, and then investigated their corresponding properties, such as boundness, idempotency and monotonicity (Peng and Yang 2015). Garg defined the concepts of correlation and correlation coefficients of PFSs (Garg 2016a). Garg further presented a generalized averaging aggregation operator under the Pythagorean fuzzy set environment by utilizing the Einstein norm operations (Garg 2016c; Garg 2017).

The most popular application field of PFS is to deal with decision-making issue (Liu et al. 2017; Liang et al. 2018a; Garg 2018; Wan et al. 2018; Wei et al. 2018). Also, Garg presented a novel accuracy function under the interval-valued Pythagorean fuzzy set (IVPFS) for solving the decision-making problems (Garg 2016b). Zhang and Xu proposed a score function based comparison method to identify the Pythagorean fuzzy positive ideal solution and the Pythagorean fuzzy negative ideal solution (Zhang and Xu 2014). Then, they developed an extended technique for order preference by similarity to determinate ideal solution method. Based on the prospect theory, Ren et al. extended the TODIM approach to solve the MCDM problems with Pythagorean fuzzy information (Ren et al. 2016). Wei and Lu investigated the multiple attribute decision-making (MADM) problem based on the Hamacher aggregation operators with dual Pythagorean hesitant fuzzy information (Wei and Lu 2017). Liang et al. constructed a new model of Pythagorean fuzzy decision-theoretic rough sets (PFDTRSs) based on the Bayesian decision procedure and constructed a three-way decision-making procedure based on ideal solutions in the Pythagorean fuzzy information system (Liang et al. 2018b). Rahman and Abdullah presented a multiple-attribute group decision-making method, where the attribute values were measured by the interval-valued Pythagorean fuzzy numbers, based on some generalized interval-valued Pythagorean fuzzy aggregation operators, i.e., generalized interval-valued Pythagorean fuzzy weighted geometric (GIVPFWG) aggregation operator, generalized interval-valued Pythagorean fuzzy ordered weighted geometric (GIVPFOWG) aggregation operator and generalized interval-valued Pythagorean fuzzy hybrid geometric (GIVPFHG) aggregation operator (Rahman and Abdullah 2018).

These existing researches have provided abundant theories and practical improvements to study MCDM problem. One of the key steps is to measure the “closeness” degree between each alternative among all alternatives and ideal alternative. The correlation coefficient is an important tool to judge the relation between two objects. The correlation coefficients have been widely employed to data analysis, classification, decision-making and pattern recognition (Park et al. 2009; Szmidt and Kacprzyk 2010; Wei et al. 2011; Kriegel et al. 2008; Ye 2010a; Bonizzoni et al. 2008). Many researchers have paid attention to correlation coefficients under fuzzy environments (Hanafy et al. 2012, 2013; Broumi and Smarandache 2013). Hong proposed fuzzy measures for a correlation coefficient of fuzzy numbers under the weakest t-norm-based fuzzy arithmetic operations (Hong 2006). As an extension of fuzzy correlations, Wang and Li introduced the correlation and information energy of interval-valued fuzzy numbers (Wang and Li 1999). Gerstenkorn and Manko developed the correlation coefficients of intuitionistic fuzzy sets (IFSs) (Gerstenkorn and Manko 1991). Hung and Wu also proposed a method to calculate the correlation coefficients of IFSs by centroid method (Hung and Wu 2009). Ye studied the fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment (Ye 2010b). Bustince and Burillo (Bustince and Burillo 1995) and Hong (Hong 1998) further developed the correlation coefficients for interval-valued intuitionistic fuzzy sets (IVIFSs). Ye presented the correlation coefficient of Single-Valued Neutrosophic Sets (SVNSs) based on the extension of the correlation coefficient of IFSs and proved that the cosine similarity measure of SVNSs was a special case of the correlation coefficient of SVNSs (Ye 2013). Pramanik et al. developed a correlation coefficient measure between any two rough neutrosophic sets and introduced a new multiple attribute group decision-making method based on it (Pramanik et al. 2017). A correlation coefficient and a weighted correlation coefficient between Dynamic Single Valued Neutrosophic Multiset (DSVNMs) were presented to measure the correlation degrees between DSVNMs (Ye 2017).

For a practical decision-making problem, according to the evaluation values for all types of MCDM with respect to criteria, a suitable alternative for a given MCDM issue is selected using different MCDM methods. When using fuzzy set theory, it usually requires that the sum of membership degree and non-membership degree is smaller than 1. That is to say, a decision maker or an expert always faces a constraint that the sum of membership and non-membership degrees cannot larger than 1. However, in practical, it is an inevitable reality that the sum of membership and non-membership degrees is larger than 1 given by decision makers or experts. Therefore, it is the limitation that fuzzy theory is employed for MCDM. PFS theory is an extension of IFS, and it only needs to satisfy that the square sum of membership degree and non-membership degree smaller than 1. Further, the weight of each evaluation criteria plays an important role in decision-making process. There are several methods to calculate the weights, such as Delphi method, AHP and information entropy. It is difficult to choose an appropriate method to determinate the weights. To fill the gap on calculation of weight, this study introduces Spearman rank correlation coefficient (SRCC) originated from statistic to PFS circumstance, which is considered as the best known nonparametric measure of relationship (Dikbas 2018). The contributions of this paper are as follows: (1) the concept, representation and related properties of Spearman rank correlation coefficient (SRCC) originated from statistical theory between two PFSs are introduced, which is used to measure the closeness degree between ideal alternative and each alternative. (2) A multi-criteria decision-making approach with Pythagorean fuzzy environment is developed based on the proposed SRCC. (3) A novelty decision rule is provided from a new perfective using SRCC, which can reduce the complexity of the practical problem in the process of decision-making both in theory and practice.

The remainder of this paper is organized as follows. In Sect. 2, some basic concepts and calculation principles about PFSs are provided, and the concept, representation and related properties of SRCC between two PFSs are introduced. Section 3 develops a Pythagorean fuzzy MCDM method. A case study is demonstrated to illustrate the feasibility and effectiveness of the proposed method in Sect. 4: this section consists of three parts: data collection, decision-making procedure and comparative analysis. The conclusions are appeared in Sect. 5.

2 Spearman rank correlation coefficient between PFSs

The section provides the concept of SRCC, and investigates its properties. For this purpose, two subsections are designed including preliminaries for PFSs and the concept of SRCC between PFSs.

2.1 Preliminaries for PFSs

Definition 1

(Yager 2013; Yager 2014) Let $X$ be a universe of discourse. A PFS $P$ in $X$ denoted by.

$$P = \left\{ {\left\langle {x,u_{P} \left( x \right),v_{P} \left( x \right)} \right\rangle \left| {x \in X} \right.} \right\}$$

(1)

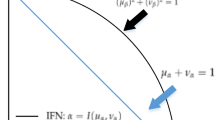
where $u_{P} \left( x \right):X \to [0,1]$ denotes the degree of membership and $v_{P} \left( x \right):X \to [0,1]$ denotes the degree of non-membership of the element $x \in X$ to $P$ , respectively, with the condition that $0 \le u_{P}^{2} \left( x \right) + v_{P}^{2} \left( x \right) \le 1$. The degree of indeterminacy is $\pi_{P} \left( x \right) = \sqrt {1 - u_{P}^{2} \left( x \right) - v_{P}^{2} \left( x \right)}$.

For convenience, $\left( {u_{P} \left( x \right),v_{P} \left( x \right)} \right)$ is called a PFN and denoted as $\overline{P} = \left( {u_{{\overline{P}}} ,v_{{\overline{P}}} } \right)$.

From the definitions of IFS and PFS, we can easily see that the main difference between PFN and IFN is their corresponding constraint condition. Obviously, an IFN must be a PFN, but the converse is not true in generally. For instance, $\overline{P} = \left( {0.5,0.8} \right)$ is a PFN but not an IFN because $0.5 + 0.8 > 1$. Therefore, some concepts of an IFN must be generalized to the case of a PFN under certain circumstance.

To make a reasonable comparison between two PFSs, Peng and Yang (Peng and Yang 2015) presented accuracy function to modify the comparison rules presented by Zhang and Xu (Zhang and Xu 2014).

Definition 2

(Zhang and Xu 2014) Let $p = \left( {u_{p} ,v_{p} } \right)$ be a PFN, then the score function of $p$ can be defined as follows:

$${\rm{S}}\left( p \right) = \left( {u_{p} } \right)^{2} - \left( {v_{p} } \right)^{2}$$

where ${\rm{S}}\left( p \right) \in \left[ { - 1,1} \right]$.

Definition 3

(Zhang and Xu 2014) Let $p = \left( {u_{p} ,v_{p} } \right)$ be a PFN, then the accuracy function of $p$ can be defined as follows:

$${\rm{K}}\left( p \right) = \left( {u_{p} } \right)^{2} + \left( {v_{p} } \right)^{2}$$

where ${\rm{K}}\left( p \right) \in \left[ {0,1} \right]$.

The modified comparison rules are shown as follows (Zhang and Xu 2014):

For any two PFNs $p_{1}$ and $p_{2}$,

(C1) if ${\rm{S}}\left( {p_{1} } \right) < {\rm{S}}\left( {p_{2} } \right)$, then $p_{1} \prec p_{2}$;

(C2) if ${\rm{S}}\left( {p_{1} } \right){\rm{ = S}}\left( {p_{2} } \right)$, then,

(a) if ${\rm{K}}\left( {p_{1} } \right) < {\rm{K}}\left( {p_{2} } \right)$, then $p_{1} \prec p_{2}$;

(b) if ${\rm{K}}\left( {p_{1} } \right){\rm{ = K}}\left( {p_{2} } \right)$, then $p_{1} \sim p_{2}$.

Definition 4

(Yager 2014) Let $p_{i} { = }\left( {u_{i} ,v_{i} } \right)$ $\left( {i = 1,2, \ldots ,n} \right)$ be a collection of PFNs and $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}$ be the weight vector of $p_{i}$$\left( {i = 1,2, \ldots ,n} \right)$, with $\sum\limits_{i = 1}^{n} {w_{i} = 1}$, then a ${\rm{PFWA}}$ operator is a mapping ${\rm{PFWA}}$: $P^{n} \to P$, where

${\rm{PFWA}}\left( {p_{1} ,p_{2} , \ldots ,p_{n} } \right) = \left( {\sum\limits_{i = 1}^{n} {w_{i} u{}_{i}} ,\sum\limits_{i = 1}^{n} {w_{i} v{}_{i}} } \right)$.

2.2 SRCC between PFSs

To introduce the concept of SRCC between two PFNs, we firstly give some preliminaries in statistics.

Definition 5

(Mafakheri et al. 2007; Aczel 1999) Let $\left( {X_{1} , \ldots ,X_{n} } \right)$ be a sample from a population, the corresponding sample observations $\left( {x_{1} , \ldots ,x_{n} } \right)$ are sorted in an ascending order, that is, $x_{\left( 1 \right)} < \cdots < x_{\left( n \right)}$. If $x_{i} = x_{\left( k \right)}$, then $k$ is called rank of the sample $X_{i}$, i.e., $R_{i} = k$, $i = 1,2, \ldots ,n$.

In each repeatedly sampling, $R_{i}$ is a random variable. If a case occurs that some $x$ is the same, for instance, there exists $x_{i} = x_{j}$ for $i \ne j$, then their ranks can be calculated by taking the average of those ranks. For example, if the sequence of a sample is: $1\begin{array}{*{20}c} {} & {} \\ \end{array} 1\begin{array}{*{20}c} {} & {} \\ \end{array} 2\begin{array}{*{20}c} {} & {} \\ \end{array} 2\begin{array}{*{20}c} {} & {} \\ \end{array} 2\begin{array}{*{20}c} {} & {} \\ \end{array} 3$, then the ranks of the two 1 are all $\frac{{1{ + }2}}{2}{ = }1.5$ and the ranks of three 2 are all $\frac{{3{ + }4{ + }5}}{3}{ = }4$.

In statistics, the Spearman rank correlation coefficient is the Pearson correlation coefficient applied to the ranks $R$. When there are not two values of $X$ or two values of $Y$ with the same rank (so called ties), there is an easier way to compute the Spearman correlation coefficient (Mafakheri et al. 2007; Aczel 1999):

$$r_{{\rm{s}}} = 1 - \frac{{6\sum\limits_{i = 1}^{n} {d_{i}^{2} } }}{{n\left( {n^{2} - 1} \right)}}$$

(2)

where $d_{i}$, $i = 1,2, \ldots ,n$ are the differences in the ranks of $x_{i}$ and $y_{i}$: $d_{i} = R\left( {x_{i} } \right) - R\left( {y_{i} } \right)$. If there are ties (two values of $X$ or two values of $Y$ with the same rank), the number of ties is smaller compared with $n$. And Eq. 2 still holds.

The Spearman correlation coefficient fulfills the requirements of the correlation measures. Because Eq. 2 is obtained from the Pearson coefficient for ranks, it fulfills the same properties as the Pearson coefficient (Myers and Well 2003), namely:

$$(P1)\,\,\,\,\,r_{s} \left( {A,B} \right) = r_{s} \left( {B,A} \right)$$

$$(P2)\,\,\,If\,\,\,A = B,\,\,\,then\,\,r_{s} \left( {A,B} \right) = 1,$$

$$(P3)\,\,\,\left| {r_{s} \left( {A,B} \right)} \right| \le 1.$$

When the variables $X$ and $Y$ are perfectly positively related, i.e., when $X$ increases whenever $Y$ increases, $r_{s}$ is equal to 1. When $X$ and $Y$ are perfectly negatively related, i.e., when $X$ increases whenever $Y$ decreases, $r_{s}$ is equal to -1. $r_{s}$ is equal to zero when there is no relation between $X$ and $Y$. Values between -1 and 1 give a relative indication of the degree of relationship between $X$ and $Y$. In other words, $- 1 \le r_{s} \le 1$.

Based on the correlation coefficient between two Atanassov’s intuitionistic fuzzy sets proposed by Szmidt and Kacprzyk (Szmidt and Kacprzyk 2010), the Spearman rank correlation coefficient between two PFSs is provided below.

Definition 6

The Spearman rank correlation coefficient between two PFSs $A$ and $B$ is defined as:

$$r_{{s - {\rm{PFS}}}} = \frac{1}{3}\left( {r_{{\rm{su - PFS}}} + r_{{\rm{sv - PFS}}} + r_{{{\rm{s}}\pi - {\rm{PFS}}}} } \right)$$

(3)

where $r_{su - PFS}$,$r_{sv - PFS}$ and $r_{s\pi - PFS}$ are the Spearman rank correlation coefficients between $A$ and $B$ with respect to their membership function, non-membership function, and indeterminacy function, respectively. $r_{su - PFS}$ is given as

$$r_{{\rm{su - PFS}}} = 1 - \frac{{6\sum\limits_{i = 1}^{n} {d_{ui}^{2} } }}{{n\left( {n^{2} - 1} \right)}}$$

(4)

where $d_{ui}$, $i = 1, \ldots ,n$ are the differences in the ranks with respect to the membership functions: $d_{ui} = R\left( {u_{A} \left( {x_{i} } \right)} \right) - R\left( {u_{B} \left( {x_{i} } \right)} \right)$. $r_{sv - PFS}$ is given as

$$r_{{\rm{sv - PFS}}} = 1 - \frac{{6\sum\limits_{i = 1}^{n} {d_{vi}^{2} } }}{{n\left( {n^{2} - 1} \right)}}$$

(5)

where $d_{vi}$, $i = 1, \ldots ,n$ are the differences in the ranks with respect to the non-membership functions: $d_{vi} = R\left( {v_{A} \left( {x_{i} } \right)} \right) - R\left( {v_{B} \left( {x_{i} } \right)} \right)$. $r_{s\pi - PFS}$ is given as

$$r_{{{\rm{s}}\pi - {\rm{PFS}}}} = 1 - \frac{{6\sum\limits_{i = 1}^{n} {d_{\pi i}^{2} } }}{{n\left( {n^{2} - 1} \right)}}$$

(6)

where $d_{\pi i}$, $i = 1, \ldots ,n$ are the differences in the ranks with respect to the indeterminacy functions: $d_{\pi i} = R\left( {\pi_{A} \left( {x_{i} } \right)} \right) - R\left( {\pi_{B} \left( {x_{i} } \right)} \right)$.

Obviously, for the SRCC in Eq. 3, the same properties as for the Pearson correlations coefficient are valid, namely:

• 1. $r_{{\rm{s - PFS}}} \left( {A,B} \right) = r_{{\rm{s - PFS}}} \left( {B,A} \right)$

• 2. If $A = B$, then $r_{{{\rm{s}} - {\rm{PFS}}}} \left( {A,B} \right) = 1$,

• 3. $\left| {r_{{{\rm{s}} - {\rm{PFS}}}} \left( {A,B} \right)} \right| \le 1$.

The separate components of the SRCC in Eq. 3 i.e., Eqs. 4–6 fulfill the above properties, too. Obviously, in the case of crisp sets, $r_{{\rm{s - PFS}}}$ in Eq. 3 reduces to $r_{s}$ in Eq. 2.

Example 1

There are two PFSs $A$ and $B$ described below:

$$\begin{gathered} A = \left\{ {\left( {x_{1} ,0.9,0.4} \right),\left( {x_{2} ,0.7,0.6} \right),} \right. \hfill \\ \left. {^{{}} \begin{array}{*{20}c} {} & {\left( {x_{3} ,0.5,0.8} \right),\left( {x_{4} ,0.6,0.3} \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered}$$

and

$$B = \left\{ {\left( {x_{1} ,0.4,0.7} \right),\,\,\left( {x_{2} ,0.9,0.2} \right),\,\,\left. {\left( {x_{3} ,0.8,0.15} \right),\,\,\left( {x_{4} ,0.5,0.3} \right)} \right\}} \right.$$

From Eqs. 4–6, we calculate the membership degree, non-membership degree and indeterminacy degree, respectively. Corresponding results are shown in Tables 1,2 and 3. And the SRCC between PFSs $A$ and $B$ is obtained $r_{{\rm{s - PFS}}} \left( {A,B} \right) = - \frac{1}{3}$ by Eq. 3.

Table 1 Example 1-calculations of membership function using Eq. 4

Table 2 Example 1-calculations of non-membership function using Eq. 5

Table 3 Example 1-calculations of indeterminacy function using Eq. 6

3 Pythagorean fuzzy multi-criteria decision-making approach based on Spearman rank connection coefficient

Let $A = \left\{ {A_{1} , \ldots ,A_{m} } \right\}$ be a set of alternatives for a given decision-making problem and $C = \left\{ {C_{1} , \ldots ,C_{n} } \right\}$ be the set of criteria with unknown weight measured by PFNs $U_{ij} { = }\left( {u_{ij} ,v_{ij} } \right)$$\left( {i = 1,2, \ldots ,m} \right.$,$\left. {j = 1,2, \ldots ,n} \right)$. Assume that $E = \left\{ {E_{1} ,E_{2} , \ldots ,E_{k} } \right\}$ is the set of experts giving the evaluating values to $C_{j}$ with respect to alternative $A_{i}$, and $U_{m \times n}^{\left( l \right)} = \left( {U_{ij}^{\left( l \right)} } \right)_{m \times n} { = }\left( {u_{ij}^{\left( l \right)} ,v_{ij}^{\left( l \right)} } \right)_{m \times n}$ denotes a PFN evaluation matrix from the $l{\rm{th}}$ expert.

On the basis of the SRCC between two PFSs, we develop a new Pythagorean fuzzy multi-criteria decision-making approach, which starts with the determination of the Pythagorean fuzzy ideal solution. Here, we utilize the score function and the accuracy function to identify the Pythagorean fuzzy ideal solution. Generally speaking, there is no Pythagorean fuzzy ideal solution in the real selection process (Wang and Li 1999). In other words, the Pythagorean fuzzy ideal solution vector $A^{*}$ is usual not be the feasible alternative, namely, $A^{*} \notin A$. Otherwise, the Pythagorean fuzzy ideal solution vector $A^{*}$ is the optimal alternative vector of the selection problem.

From the above analysis, a multi-criteria decision-making algorithm is proposed, which measure the closeness degree between ideal alternative and each alternative based on the SRCC, The algorithm can be described by the following steps and the selection processes are shown in Fig. 1.

Fig. 1

The process of decision-making based on Spearman rank connection coefficient

Step 1: For a MCDM problem with PFNs, using Definition 4, the decision matrix $U_{m \times n} = \left( {U_{ij} } \right)_{m \times n}$ is constructed, where

$$U_{ij} = PFWA\left( {U_{ij}^{\left( 1 \right)} ,U_{ij}^{\left( 1 \right)} , \ldots ,U_{ij}^{\left( k \right)} } \right){\rm{ = p}}_{ij} \left( {\sum\limits_{l = 1}^{k} {W_{l} u_{ij}^{\left( l \right)} } ,\sum\limits_{l = 1}^{k} {W_{l} v_{ij}^{\left( l \right)} } } \right)$$

(7)

and $U_{ij}^{\left( l \right)}$ $\left( {i = 1,2, \ldots ,m;j = 1,2, \ldots ,n;l = 1,2, \ldots ,k} \right)$ is the evaluation value of the alternative $A_{i} \in A$ with respect to the criterion $C_{j} \in C$ from the $l{\rm{th}}$ expert, and $W_{l}$ is the $l{\rm{th}}$ expert’ weight.

Step 2: Identify the Pythagorean fuzzy ideal solution $A^{*}$ by the following equation:

for benefit criteria:

$$A^{*} = \left\{ {A_{1}^{*} ,A_{2}^{*} , \ldots ,A_{m}^{*} } \right\}\,\,{\rm{where}}\,\,A_{j}^{*} = \left\{ {C_{j} ,\mathop {\max }\limits_{i} \left\{ {U_{{ij}} } \right\}\left| {j = 1,2, \ldots ,n} \right.} \right\};$$

and for cost criteria:

where

$$A^{*} = \left\{ {A_{1}^{*} ,A_{2}^{*} , \ldots ,A_{m}^{*} } \right\}\,\,\,{\rm{where}}\,\,A_{j}^{*} = \left\{ {C_{j} ,\mathop {{\rm{min}}}\limits_{i} \left\{ {U_{{ij}} } \right\}\left| {j = 1,2, \ldots ,n} \right.} \right\}.$$

Step 3: Calculate the Spearman rank connection coefficient between ideal alternative and each alternative by using Eqs. 3–6.

Step 4: From Spearman rank connection coefficients obtained from Step 3, the larger the SRCC is, the better the corresponding alternative is. Therefore, the optimal ranking order of the alternatives and the optimal alternative are determined.

4 Case study

In this section, the proposed model is applied to a real-world infrastructure project. There are four project delivery systems (PDSs) including design build (DB), engineering procurement construction (EPC), construction management at risk method (CM at-Risk) and design bid build (DBB); the owner intends to select a most suitable PDS among them using the proposed method. The criteria for selecting PDS are shown in Table 4.

Table 4 Criteria for selecting PDS

To ensure the reliability and availability of data, five experts including academics, owners and engineers were invited to set up a selection committee. Firstly, they were invited to investigate the construction site and discussed together. Secondly, we provided the preliminary design document of the project, and the organizational structure and construction experience documents of the owner to the experts. Thirdly, the questionnaires documents about the criteria for selection of PDS were presented to the experts individually, and ask them to choose the proper opinion. Finally, we collected the questionnaires and processed the data. The procedure of decision-making is as follows.

4.1 Data collection

Let $A = \left\{ {A_{1} , \ldots ,A_{4} } \right\}$ be the set of PDS options for a given infrastructure project, $C = \left\{ {C_{1} , \ldots ,C_{10} } \right\}$ be the set of criteria about each PDS, and $E = \left\{ {E_{1} ,E_{2} , \ldots ,E_{5} } \right\}$ be the set of experts. We assume that $\left( {u_{ij}^{\left( l \right)} ,v_{ij}^{\left( l \right)} } \right)$$\left( {i = 1,2,3,4} \right.$, $\left. {j = 1,2, \ldots ,10l = 1, \ldots ,5} \right)$ is the evaluation value from the $l{\rm{th}}$ expert to $C_{j}$ with respect to delivery option $A_{i}$, and $U_{4 \times 10}^{\left( l \right)} = \left( {U_{ij}^{\left( l \right)} } \right)_{4 \times 10} { = }\left( {u_{ij}^{\left( l \right)} ,v_{ij}^{\left( l \right)} } \right)_{4 \times 10}$ denotes a PFN evaluation matrix from the $l{\rm{th}}$ expert. Every expert should give the evaluation value $\left( {u_{ij}^{\left( l \right)} ,v_{ij}^{\left( l \right)} } \right)$$\left( {i = 1,2,3,4,j = 1, \ldots ,10} \right)$, and the weight of each expert is $W_{1} = \cdots = W_{5} = 0.2$.

We obtain Pythagorean fuzzy evaluation values for four PDSs from five experts, shown in Tables 5, 6, 7, 8 and 9, respectively, where $E_{l}$ $\left( {l = 1, \ldots ,5} \right)$ denotes the $l{\rm{th}}$ expert.

Table 5 Pythagorean Fuzzy Evaluation Values from expert $E_{1}$

Table 6 Pythagorean Fuzzy Evaluation Values from expert $E_{2}$

Table 7 Pythagorean Fuzzy Evaluation Values from expert $E_{3}$

Table 8 Pythagorean Fuzzy Evaluation Values from expert $E_{4}$

Table 9 Pythagorean Fuzzy Evaluation Values from expert $E_{5}$

4.2 Decision-making procedure

Step 1: From the evaluation values in Tables 5, 6, 7, 8 and 9 and Eq. 7, the evaluation decision matrix aggregated evaluation matrices of five experts is determined:

$$\begin{aligned} U_{{4 \times 10}} & = \left( {{\rm{p}}_{{ij}} \left( {\sum\limits_{{l = 1}}^{5} {W_{l} u_{{ij}}^{{\left( l \right)}} } ,\sum\limits_{{l = 1}}^{5} {W_{l} v_{{ij}}^{{\left( l \right)}} } } \right)} \right)_{{4 \times 10}} \\ & = \left( {\begin{array}{*{20}c} {{\rm{p}}(0.60,0.54){\rm{p}}(0.56,0.58){\rm{p}}(0.60,0.44)} \\ {{\rm{p}}(0.74,0.40){\rm{p}}(0.76,0.38){\rm{p}}(0.68,0.50)} \\ {{\rm{p}}(0.56,0.58){\rm{p}}(0.46,0.50){\rm{p}}(0.66,0.44)} \\ {{\rm{p}}(0.44,0.36){\rm{p}}(0.60,048){\rm{p}}(0.62,0.38)} \\ \end{array} } \right.\begin{array}{*{20}c} {} \\ {} \\ {} \\ {} \\ \end{array} \begin{array}{*{20}c} {{\rm{p}}(0.58,0.46){\rm{p}}(0.64,0.46){\rm{p}}(0.58,0.38)} \\ {{\rm{p}}(0.62,0.48){\rm{p}}(0.58,0.46){\rm{p}}(0.68,0.38)} \\ {{\rm{p}}(0.56,0.42){\rm{p}}(0.42,0.48){\rm{p}}(0.62,0.52)} \\ {{\rm{p}}(0.66,0.42){\rm{p}}(0.56,044){\rm{p}}(0.60,0.42)} \\ \end{array} . \\ & \begin{array}{*{20}c} {{\rm{p}}(0.58,0.46){\rm{p}}(0.64,0.46){\rm{p}}(0.58,0.38)} \\ {{\rm{p}}(0.62,0.48){\rm{p}}(0.58,0.46){\rm{p}}(0.68,0.38)} \\ {{\rm{p}}(0.56,0.42){\rm{p}}(0.42,0.48){\rm{p}}(0.62,0.52)} \\ {{\rm{p}}(0.66,0.42){\rm{p}}(0.56,044){\rm{p}}(0.60,0.42)} \\ \end{array} \begin{array}{*{20}c} {} \\ {} \\ {} \\ {} \\ \end{array} \left. \begin{array}{*{20}c} {{\rm{p}}\left( {0.62,0.50} \right){\rm{p}}\left( {0.60,0.54} \right){\rm{p}}\left( {0.58,0.44} \right){\rm{p}}\left( {0.52,0.52} \right)} \\ {{\rm{p}}\left( {0.56,0.42} \right){\rm{p}}\left( {0.64,0.44} \right){\rm{p}}\left( {0.60,0.48} \right){\rm{p}}\left( {0.70,0.40} \right)} \\ {{\rm{p}}\left( {0.56,0.46} \right){\rm{p}}\left( {0.66,0.48} \right){\rm{p}}\left( {0.58,0.40} \right){\rm{p}}\left( {0.42,0.58} \right)} \\ {{\rm{p}}\left( {0.66,0.46} \right){\rm{p}}\left( {0.60,0.46} \right){\rm{p}}\left( {0.62,0.44} \right){\rm{p}}\left( {0.60,0.38} \right)}\end{array} \right) \\ \end{aligned}$$

Step 2: Using comparison rule C1 and C2, we can obtain the ideal solution vector:

$$A^{*} = \left\{ {{\rm{p}}\left( {0.56,0.58} \right), \,\,{\rm{p}}\left( {0.76,0.38} \right), \,\,{\rm{p}}\left( {0.60,0.44} \right),} \right.\,\,{\rm{p}}\left( {0.58,0.46} \right){\rm{,}}\,\,{\rm{p}}\left( {0.64,0.46} \right),\,\,{\rm{p}}\left( {0.68,0.38} \right),{\rm{ }}\left. {{\rm{p}}\left( {0.66,0.46} \right) {\rm{,}}\,\,{\rm{p}}\left( {0.66,0.48} \right) {\rm{,}}\,\,{\rm{p}}\left( {0.58,0.44} \right) {\rm{,}}\,\,{\rm{p}}\left( {0.70,0.40} \right)} \right\}{\rm{ }}$$

Step 3: Calculate the Spearman rank connection coefficient between ideal alternative and each alternative.

The results in Table 10, 11 and 12 represent the differences in the ranks with the membership degree, non-membership degree and indeterminacy degree for DB. From Eqs. 4–6, we can obtain that.

$$r_{{{\rm{uEPC}}}} = 1 - \frac{{6 \times 117.5}}{{990}} \approx 0.2879,\,\,\,r_{{{\rm{vEPC}}}} = 1 - \frac{{6 \times 104}}{{990}} \approx 0.3697,\,\,\,r_{{\pi {\rm{EPC}}}} = 1 - \frac{{6 \times 116.5}}{{990}} \approx 0.2939;$$

Table 10 Calculations of differences in the ranks with respect to membership about DB

Table 11 Calculations of differences in the ranks with respect to non-membership about DB

Table 12 Calculations of differences in the ranks with respect to indeterminacy about DB

$$r_{{{\rm{uDB}}}} = 1 - \frac{6 \times 225}{{990}} \approx - 0.3636, \,\,r_{{{\rm{vDB}}}} = 1 - \frac{6 \times 112.5}{{990}} \approx 0.3182,\,\,r_{{\pi {\rm{DB}}}} = 1 - \frac{6 \times 32.5}{{990}} \approx 0.8030:$$

thus, by Eq. 3, $r_{{{\rm{DB}}}} \approx 0.2525.$

In the same way, from Eqs. 4–6, we can obtain that.

$$r_{{{\rm{uEPC}}}} = 1 - \frac{6 \times 117.5}{{990}} \approx 0.2879,\,\,r_{{{\rm{vEPC}}}} = 1 - \frac{6 \times 104}{{990}} \approx 0.3697,\,\,r_{{\pi {\rm{EPC}}}} = 1 - \frac{6 \times 116.5}{{990}} \approx 0.2939;$$

$$r_{{{\rm{uCM}}}} = 1 - \frac{6 \times 201.5}{{990}} \approx - 0.2212, \,\,r_{{{\rm{vCM}}}} = 1 - \frac{6 \times 186}{{990}} \approx - 0.1273, \,\,r_{{\pi {\rm{CM}}}} = 1 - \frac{6 \times 138.5}{{990}} \approx 0.1606;$$

$$r_{{u{\rm{DBB}}}} = 1 - \frac{6 \times 171}{{990}} \approx - 0.0364, \,\,r_{{v{\rm{DBB}}}} = 1 - \frac{6 \times 181.5}{{990}} \approx - 0.1,\,\,r_{{\pi {\rm{DBB}}}} = 1 - \frac{6 \times 192.5}{{990}} \approx - 0.1667:$$

thus, by Eq. 3, $r_{{{\rm{EPC}}}} \approx 0.3172, \,\,r_{{{\rm{CM}}}} \approx - 0.0626, \,\,r_{{{\rm{DBB}}}} \approx - 0.1010.$

Step 4: From the results in Step 3 $\left| {r_{{{\rm{EPC}}}} } \right| > \left| {r_{{{\rm{DB}}}} } \right| > \left| {r_{{{\rm{DBB}}}} } \right| > \left| {r_{{{\rm{CM}}}} } \right|,$ we can rank the four PDSs as follows: EPC, DB, DBB and CM. That is, EPC is the most suitable PDS for this project followed by DB. CM is the least suitable PDS. From the results, we can see that the ranking order is acceptable for the practical application.

4.3 Comparative analysis

The purpose of this subsection is to state the advantage of the proposed model through comparing with two existing methods.

The first comparative method is extended TOPSIS proposed by Zhang and Xu (Zhang and Xu 2014), in which the criteria are characterized by PFS. According to the proposal decision method, the ranking result of the four PDSs is ${\rm{DB}} \succ {\rm{EPC}} \succ {\rm{DBB}} \succ {\rm{CM}}$. That is, DB and CM are the best and the worst PDSs, respectively. The second method is fuzzy VIKOR, according to the steps of the decision-making process in (Chen 2018): the order of four PDSs is ${\rm{EPC}} \succ {\rm{DB}} \succ {\rm{DBB}} \succ {\rm{CM}}$. It is shown that EPC is the best option for this project followed by DB. From the result in this study, the order of the four PDSs using the proposed method is: ${\rm{EPC}} \succ {\rm{DB}} \succ {\rm{DBB}} \succ {\rm{CM}}$. It is given the same result as fuzzy VIKOR method. It should be noted that the procedure of the proposed method is more concise than fuzzy VIKOR method. Specifically, the best suitable alternative can be chosen according to the Spearman rank connection coefficient in the proposed method, which avoids the calculation of weights in the practical decision-making problem and then simplifies solution procedures. The ranking results of the three methods are shown in Table 13, and the ranking trends are also given in Fig. 2.

Table 13 The ranking results of three methods

Fig. 2

The ranking comparison of three methods

The above ordering results appear a slight difference in ranking orders. In practice, the construction project was implemented under high level of complexity and uncertainty. The owner just has few staff and rarely experience to management the proposed project. Therefore, the coordination work between design and construction is a tough task for the owner. So the owner needs a single responsibility delivery method for the design and construction. Both EPC and DB are suitable for this project. And the final choice depends on the preference of owner.

5 Conclusions

Multi-criteria decision-making issue is a difficult task due to the complexity of objective world. And Pythagorean fuzzy set (PFS) is an effective tool for depicting uncertainty of the MCDM problems. This study aims to develop a Pythagorean fuzzy multi-criteria decision-making approach to deal with decision-making problem under uncertainty circumstance. For our purposes, firstly, the concept of SRCC between two PFSs is introduced, which originate from statistical theory, and it is used to measure the degree of closeness between ideal alternative and each alternative. Then, using the proposed SRCC, a Pythagorean fuzzy multi-criteria decision-making approach is constructed. Finally, a real-world infrastructure project is demonstrated to state the feasibility and effectiveness of the proposed method.

This study aims to develop a Pythagorean fuzzy multi-criteria decision-making approach to deal with decision-making problem under uncertainty circumstance. The contributions of this paper are as follows: (1) the concept, representation and related properties of SRCC originated from statistical theory between two PFSs are introduced, which is used to measure the closeness degree between ideal alternative and each alternative. (2) A multi-criteria decision-making approach with Pythagorean fuzzy environment is developed based on the proposed SRCC. (3) A novelty decision rule is provided from a new perfective using SRCC, which can reduce the complexity of the practical problem in the process of decision-making both in theory and practice. Finally, to illustrate the applicability and effectiveness of the proposed method, a real-world infrastructure project was demonstrated.

On the one hand, this research is discussed under Pythagorean fuzzy information. Due to the complexity of decision making and the fuzziness of human perceive, the evaluation information of experts for evaluation factors affecting decision-making problem is usually characterized by fuzzy theories, i.e., fuzzy set, intuitionistic fuzzy set (IFS), etc. However, fuzzy theory, taking IFS, for example, is characterized by a membership degree and a non-membership degree, and therefore can depict the fuzzy character of data in a comprehensive way. The prominent characteristic of IFS is that it assigns to each element a membership degree and a non-membership degree with their sum equal to or less than 1. However, in some practical decision-making process, the sum of the membership degree and the non-membership degree may be bigger than 1, which satisfies the case in this study of the sum of bigger than 1. In other words, existing results using fuzzy theory are limited, and Pythagorean fuzzy theory is an extension of IFS.

On the other hand, weighting the importance of each evaluation criteria plays an important role in decision-making process. There are several methods to calculate the weight, such as Delphi method, AHP, and information entropy. Different kinds of weights have different mechanisms, and different weighting methods meet different decision making environment. Therefore, it is difficult to choose an appropriate method to determinate the weights. This study introduces the concept of Spearman rank connection coefficient, and the best suitable alternative can be chosen according to the Spearman rank connection coefficient. In the practical decision-making problem, the calculation of weights is avoided, which simplifies solution procedures and promotes computational efficiency.

In summary, the statistics of SRCC was introduced to establish MCDM method. It can avoid the calculation of the criteria weights. In a sense, the difficulty in determining the weight of criteria in the selection process is solved. And the proposed model based on SRCC makes the problem with the PFN form more simplification, intuitive thinking, operating simply, and avoiding the complexity of PFN in calculation and application.