1 Introduction

Zadeh (1965) developed the concept of fuzzy set (FS) to deal with unclear information. Many investigations on the generalizations of the FS idea were subsequently conducted. It is believed to have numerous theoretical and practical applications in a variety of disciplines, including engineering, humanities, life sciences, physical sciences, health sciences, and computer science. A lot of work in the field of FS theory has been done in Chen and Niou (2011), Chen and Phuong (2017), Chen and Wang (2009). Further applications of FSs can be explored in Chen and Chen (2001), Chen and Wang (2010), Chen et al. (2009), Chen and Jian (2017), Shen et al. (2013), Chen and Lin (2005), Chen and Fang (2005). The intuitionistic fuzzy sets (IFSs) are one of the intriguing and extensively applicable generalizations of FSs, according to Atanassov’s definition (Atanassov 1986). “However, there are several situations when the decision-maker may specify the membership function (MF) and non-membership function (NMF) of a certain characteristic in a way that makes their sum greater than 1. Yager (2014) proposed the concept of Pythagorean fuzzy set (PFS) as a generalization of IFS to deal with uncertain situations more skillfully. The PFS designs can be used to explain ambiguous data more precisely and effectively than IFS designs. Ibrahim et al. (2021) described a different type of generalized PFS known as (3, 2)-FS. In addition to conduct research on FFS, Senapati and Yager (2020) also incorporated fundamental operations to the FFS. Compared to the (3, 2)-FS, the (3,4)-FS, which (Murad and Ibrahim 2022) introduced, applied with more ambiguous cases. Yang and Yao (2021) examined the development of shadowing sets from Atanassov IFS in the context of the three-way choice. A q-ROFS (Yager 2017) is one of the most helpful generalization of the FS for dealing with informational uncertainty. Ibrahim and Alshammari (2022) presented a brand-new FS extension type called \((p, q)-\)ROFS.

A method known as multiple-attribute decision-making (MADM) places a lot of emphasis on the greatest possible solutions. To manage the complexity and challenges of MADM situations, many helpful mathematical tools, such as SS and FSS, were improved. According to Xu (2007), many AOs under IF data have been proposed. Different geometric hybrid weighted operators were introduced in an IFS context by Xu and Yager (2006). Yager and Abbasov (2013); Yager (2014) first discussed the notions of “weighted averaging and ordered weighted averaging” operators over PFS. Senapati and Yager (2019) defined the FFWPA operator over FFS and then went into great detail into its characteristics. Using a brand-new MAGDM method, Shahzadi and Akram (2021) presented a technique for choosing an antivirus mask in an FF soft environment. Shahzadi et al. (2022) selected an IMS using the MOORA approach and FF data. A brand-new “MULTIMOORA” technique was presented as a solution to MADM problems in Rani and Mishra’s (2021) investigation of Einstein operators under FF environmental. Garg et al. (2020) combined the advantageous traits of the FFSs with the Yager operators to produce a number of AOs. Additionally, Akram et al. (2022a, 2022b, 2023d) presented new classes of “linguistic FF Hamy mean operators” and implementations of the COPRAS method under FFSs. Some PF Hamacher power AOs were created by Wei (2019).

Hadi et al. (2021) established novel FFS procedures and outlined their core operations using “Hamacher t-con-orm and t-norm”. The authors put forth FF Hamacher AOs, which were brought about through FFS and Hamacher operations. A variety of AOs, including FF Hamacher interactive averaging and geometric operators, were provided by Shahzadi et al. (2021a, 2021b) and employed in the MADM issues to evaluate the options that were given. Three authors have made significant contributions to the field of Hamacher AOs: Donyatalab et al. (2020), Akram et al. (2022a, 2022b, 2023d), and Jan et al. (2021). Verma (2021) introduced four more order-divergence measures between two IFSs to address MAGDM difficulties where the attribute weights are either fully unknown or only partially known. To assess and prioritize the hazards associated with self-driving automobiles, Bakioglu and Atahan (2021) applied three different MADM techniques in a PF environment: PF-TOPSIS, PF-VIKOR, and IVPF-AHP” for weight determination. Deng and Wang (2021) defined two novel distance measuring techniques for FSs. Garg (2020) elaborated the ST operators as a result of q-ROFS. The ST Fermatean fuzzy AOs were first presented by Akram et al. (2023a, 2023b, 2023c). “ITARA-VIKOR” approach is used by Khan et al. (2023) to elaborate the DM for 2-tuple linguistic q-RPFSs. In the context of 2-tuple linguistic FFSs, distinct MAGDM were described by Akram et al. (2023a, 2023b, 2023c). Two novel logarithmic and exponentially based order-\(\alpha\) divergence metrics between \(q-\)ROFSs were created by Verma (2020). (Liu et al. 2022; Akram et al. 2021; Rani et al. 2022) explore numerous additional DM strategies. The idea of bidirectional approximate reasoning and pattern analysis under the FF similarity metric is elaborated by Al-Qudah and Ganie (2023). Akram et al. (2023a, 2023b, 2023c) proposed an FF multi-objective transportation model utilizing an DEA framework. Moreover, Sarwar et al. (2023) discussed the properties and effects of \(\delta -\)approximations of complex fuzzy sets under rough information. They also illustrated the feasibility of a developed model through a pragmatic application. For further study, readers can see the articles given by Luqman and Shahzadi (2023a, 2023b) and Peng (2023).

The SIR approach is an abstraction of the famed PROMETHEE technique. The supremacy components and submission of numerous choices, from which SIR drifts are produced, are evaluated using this method’s use of superiority and inferiority information, which also serves to reflect the behavior of decision-makers toward each criterion. The subject was initially raised by Xu (2001). “Chai and Liu (2010) submitted the IF-SIR approach to address MCGDM issues. The SIR approach was first used using PF data by Peng and Yang (2015). Zhu et al. (2021) suggested the SIR approach for q-ROFS. Selvaraj and Jeonghwan (2022) made the initial discovery of the SIR approach for interval type 2-hesitant fuzzy set.

The main characteristics of \((p,q)-\)ROFS serve as our inspiration for providing specific AOs and SIR technique for \((p,q)-\)ROFS. These motives are described as follows:

  • Sine trigonometric functions and their outcomes are more efficient and flexible when compared to basic operators and their outcomes. To handle the \((p,q)-\)

    ROF data, however, there is no literature on the Sine trigonometric operators under \((p,q)-\)ROFS.

  • There are a number of noteworthy sine trigonometric AOs for \((p,q)-\)ROFS characteristics, but no studies have been done to look into them in the corpus of literature now in existence.

  • The bulk of AOs for handling \((p,q)-\)ROF data indicate constraints and limitations; nevertheless, the traditional DM techniques based on AOs are generalized using various confusing and unclear bits of information.

  • The SIR approach for MAGDM is essential for resolving issues with decision-making. Out of a variety of options, it presents the one that is most enticing and wanted.

Since uncertainty is a significant issue in various disciplines and its complexity increases day by day, it becomes necessary for some improvements for \(q-\)ROFSs to keep up with these developments. Recently, some authors have suggested coping with the input data using different significances for membership and non-membership degrees. This approach will be useful to describe some real-life issues and enlarge the spaces of data under study. To address the aforementioned motivations, the key contributions of this work are listed in the following list:

  • The set of ST operations for \((p,q)-\)ROFS has been introduced, and the salient features of them have been discussed.

  • A number of AOs are introduced to aggregate the

    • \((p,q)-\)ROFS, including \((p,q)-\)ROFYWA,

    • \((p,q)-\)ROFYOWA, \((p,q)-\)ROFYHWA,

    • \((p,q)-\)ROFYWG, \((p,q)-\)ROFYOWG,

    • \((p,q)-\)ROFYHWG, etc.

  • We swiftly go over a few of the suggested operators’ advantageous and productive qualities.

  • A technique termed \((p,q)-\)ROF-SIR has been created to quantify the relative performance of each option in a clear mathematical way.

Moreover, the aims of writing this research are, first, to join a new class of \(q-\)ROFSs called (p, q)-ROFSs with SIR technique, which helps to expand the degrees of membership and non-membership more than all types of \(q-\)RO FSs classes. Second, the proposed method enables us to evaluate the input data with different significance for grades of membership and non-membership, which is appropriate for some real-life issues. This matter is not applicable to the other generalizations of \(q-\)ROFSs, because they give an equal significance to grades of membership and non-membership: 2 in PFSs, 3 in FFSs, and q in \(q-\) ROFSs. Third, to establish new kinds of weighted aggregation operators, STOLs scrutinize their characterizations. Finally, we exhibit an multi-criteria decision-making (MCDM) method based on the SIR technique. Fuzzy based MCDM methods have been successfully integrated into various problems (Bouraima et al. 2024; Xu et al. 2024; Yüksel et al. 2024; Lo et al. 2024).

The SIR method is ranking the alternatives based on the two ranking lists. In this method, alternatives are ranked by superiority ranking list and inferiority ranking list. The main advantage to utilize the SIR method is that it combines the properties of other MCDM methods, namely, TOPSIS, SAW, and PROMETHEE. In this paper, we first generalize the notions of superiority and inferiority scores taking the differences between criteria values and different types of generalized criterion into account as what was done in the first step of the PROMETHEE methods. For this purpose, in step 1 of our method, the generalized criteria are carefully chosen by the decision-maker and the analyst. Then, the superiority matrix, made up of the superiority indexes, and the inferiority matrix, made up of the inferiority indexes, are built from the original decision matrix. In step 2, we employ some aggregation procedure to derive two types of flows, the superiority flow and the inferiority flow. Since different aggregation procedures produce different kinds of flows, the superiority and inferiority ranking (SIR) method is, in fact, not a single method. It represents a family of methods. When using simple additive weighting (SAW) as the aggregation procedure in this step, our method coincides with the second step of PROMETHEE methods, i.e., the derived superiority flow and the inferiority flow are exactly the leaving flow and the entering flow, respectively. However, we have more choices here. Some other aggregation procedures can be used in this step. It is in this sense that our method can be thought of as a further extension of the PROMETHEE methods. In step 3, the superiority and inferiority flows and are used to derive two complete rankings, and of the alternatives and the two complete rankings are then combined into a final partial ranking as the intersection of the two: in step 4. Like the PROMETHEE methods, the SIR method also gives a complete ranking of alternatives. When a complete ranking is requested by the decision-maker, some synthesizing flows, like the net flow in PROMETHEE and relative distance in TOPSIS, can be used to derive a complete ranking. The derived ranking (partial or complete) is then proposed to the decision-maker for further exploitation before a final decision is made.

We go over certain ideas from Sect. 2 that are critical for future study. We analyze the STOLs for \((p, q)-\) ROF data in Sect. 3. The concepts of ST-\((p, q)-\)ROFWA, ST-\((p, q)-\)ROFOWA, ST-\((p, q)-\)ROFHWA, ST-\((p, q)-\)ROFWG, ST-\((p, q)-\)ROFOWG, and ST-\((p, q)-\)ROFYHWG are investigated in Sect. 4. In Sect. 5, some fundamental characteristics relating to the operators are covered. In Sect. 6, the suggested approach for SIR under \((p, q)-\)ROF data is laid out. We carefully compare the suggested method with a number of currently used approaches in Sect. 7. Section 8 discusses conclusions, flaws in the proposed work, and possible future study direction. The abbreviations and acronyms used in this work are mentioned in Table 1.

Table 1 Abbreviations and acronyms
Full size table

2 Preliminaries

Definition 1

(Senapati and Yager 2020) Let \(\mathcal {Q}\) represents a general set. According to the FFS \(\mathcal {F}\) on \(\mathcal {Q}\)

$$\begin{aligned} \mathcal {F}=\left\{ \left\langle x, \mathcal {T}_\mathcal {F}(x), \mathcal {R}_\mathcal {F}(x)\right\rangle \right\} , \end{aligned}$$

wherever \(\mathcal {T}_\mathcal {F}, \mathcal {R}_\mathcal {F}: \mathcal {Q}\rightarrow [0,1]\) and \(\pi _\mathcal {F}(x)=\root 3 \of {1-(\mathcal {T}_\mathcal {F}(x))^3-(\mathcal {R}_\mathcal {F}(x))^3}\) show MF, NMF and InF, respectively.

Definition 2

(Yager 2017) A q-ROFS Q on domain \(\mathcal {Q}\) is elaborated by

$$\begin{aligned} Q=\left\{ \left\langle x, \mathcal {T}_Q(x), \mathcal {R}_Q(x)\right\rangle \right\} , \end{aligned}$$

wherever \(\mathcal {T}_Q, \mathcal {R}_Q: \mathcal {Q}\rightarrow [0,1]\) and \(\pi _Q(x)=\root q \of {1-(\mathcal {T}_Q(x))^q-(\mathcal {R}_Q(x))^q}\) show MF, NMF, and InF, respectively.

Definition 3

(Ibrahim et al. 2021) Assume \(\mathcal {Q}\) is a universal set and N is a set of all natural numbers. Then, the definition of the \((p, q)-\)ROFS \(\varPsi\), a collection of ordered pairs over \(\mathcal {Q}\), is as follows:

$$\begin{aligned} \varPsi =\left\{ \left\langle x, \mathcal {T}_\varPsi (x), \mathcal {R}_\varPsi (x)\right\rangle \right\} , \end{aligned}$$

wherever \(\mathcal {T}_{\varPsi }, \mathcal {R}_{\varPsi }: \mathcal {Q}\rightarrow [0,1]\) and \(\pi _{\varPsi }(x)=\root p+q \of {1-(\mathcal {T}_{\varPsi }(x))^p-(\mathcal {R}_{\varPsi }(x))^q}, p\ne q\) show MF, NMF, and InF, respectively with condition:

$$\begin{aligned} 0\le \left( \mathcal {T}_\varPsi (x)\right) ^p+ \left( \mathcal {R}_\varPsi (x)\right) ^q\le 1. \end{aligned}$$

Definition 4

(Ibrahim et al. 2021) The score and accuracy functions for \((p, q)-\)ROFS are defined as

$$\begin{aligned} S(\varPsi )= & {} \mathcal {T}_{\varPsi }^p-\mathcal {R}_{\varPsi }^q,~S(\varPsi )\in [-1,1], \\ A(\varPsi )= & {} \mathcal {T}_{\varPsi }^p+\mathcal {R}_{\varPsi }^q,~A(\varPsi )\in [0,1]. \end{aligned}$$

Remark 1

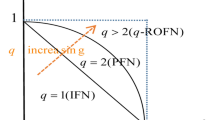
In Fig. 1 the set of \((p, q)-\)ROF MGs for \(p = 1\), \(q\in \{2,3,4, \ldots \}\) is greater than the set of intuitionistic MGs.

Fig. 1
figure 1

MGs of \((1, q)-\)ROFS with q vary

Full size image

Remark 2

In Fig. 2, the set of \((p, q)-\) ROF MGs for \(p = 2, q= \{3,4,5, \ldots \}\) is greater than the set of Pythagorean MGs.

Fig. 2
figure 2

MGs of \((2, q)-\)ROFS with q vary

Full size image

Remark 3

In Fig. 3, the set of \((p, q)-\)ROF MGs for \(p = 3, q \in \{4,5,6, \ldots \}\) is greater than the set of Fermatean MGs.

Fig. 3
figure 3

MGs of \((3, q)-\)ROFS with q vary

Full size image

Remark 4

In Fig. 4, the set of \((p, q)-\)ROF MGs for \(p \in \{4,5,6, \cdots \}, q\in \{3,4,5, \ldots \}\) is greater than the sets of Intuitionistic, Pythagorean, and Fermatean MGs.

Fig. 4
figure 4

MGs of \((p, q)-\)ROFS with (p, q) vary

Full size image

Example 1

Suppose that \(\mathcal {T}_{\varPsi }(x)=0.9\) and \(\mathcal {R}_{\varPsi }(x)=0.7\). Hence, \(0.9+0.7=1.6 > 1\), \((0.9)^2+ (0.7)^2=1.3 > 1\) and \((0.9)^3+(0.7)^3=1.072 > 1\), but \((0.9)^4+(0.7)^3=0.9991<1\) and \((0.9)^3+(0.7)^4 =0.9691< 1\). Thus, (0.9, 0.7) is both \(3,4-\)ROFS and \(4,3-\)ROFS, but is neither IFS nor PFS nor FFS.

3 \((p, q)-\)ROFNs under STOLs

Definition 5

Let \(\varPsi =\{\langle x, \mathcal {T}_{\varPsi }(x), \mathcal {R}_{\varPsi }(x) \rangle ~|~x\in \mathcal {Q}\}\) be an \((p, q)-\)ROFN on universal set \(\mathcal {Q}\), then a STOL of \((p, q)-\)ROFN \(\varPsi\) is

$$\begin{aligned} \sin \varPsi= & {} \left\{ \left\langle x, \sin \left( \frac{\pi }{2}\mathcal {T}_{\varPsi }\right) , \root p \of {1-\sin ^p\Big (\frac{\pi }{2}\root p \of {1-(\mathcal {R}_{\varPsi })^q}}\right\rangle ~|~\right. \nonumber \\{} & {} \left. x\in \mathcal {Q}\right\} . \end{aligned}$$
(1)

By \((p, q)-\)ROFN, \(\mathcal {T}_{\varPsi }:\mathcal {Q}\rightarrow [0,1]\), \(\mathcal {R}_{\varPsi }:\mathcal {Q}\rightarrow [0,1]\) and \(0\le (\mathcal {T})^p+(\mathcal {R})^q\le 1\). Furthermore

$$\begin{aligned}{} & {} \sin \left( \frac{\pi }{2}\mathcal {T}_{\varPsi }\right) :\mathcal {Q}\rightarrow [0,1], \\{} & {} \root p \of {1-\sin ^p\Big (\frac{\pi }{2}\root p \of {1-(\mathcal {R}_{\varPsi })^q}}\Big ):\mathcal {Q}\rightarrow [0,1]. \end{aligned}$$

Therefore, \(\sin \varPsi =\{\langle x, \sin (\frac{\pi }{2}\mathcal {T}_{\varPsi }), \root q \of {1-\sin ^q(\frac{\pi }{2}\root q \of {1-(\mathcal {R}_{\varPsi })^q}}\rangle \}\) is a \((p, q)-\)ROFN.

Definition 6

Suppose \(\varPsi =\langle \mathcal {T}, \mathcal {R}\rangle\) is an \((p, q)-\)ROFN. If

$$\begin{aligned} \sin \varPsi =\left\langle \sin \left( \frac{\pi }{2}\mathcal {T}_{\varPsi }\right) , \root p \of {1-\sin ^p\Big (\frac{\pi }{2}\root p \of {1-(\mathcal {R}_{\varPsi })^q}}\right\rangle , \end{aligned}$$
(2)

the function \(\sin \varPsi\) is known as ST operator and the value \(\sin \varPsi\) is known as sine trigonometric \((p, q)-\)ROFN (ST-\((p, q)-\)ROFN).

Theorem 1

For \((p, q)-\)ROFN \(\varPsi\), the value of operator \(\sin \varPsi\) is an \((p, q)-\)ROFN.

Proof

To proof that \(\sin \varPsi\) is an \((p, q)-\)ROFN, we will show that:

  1. 1.

    \(\sin (\frac{\pi }{2}\mathcal {T}),\root p \of {1-\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R})^q}})\in [0,1].\)

  2. 2.

    \(\sin ^p(\frac{\pi }{2}\mathcal {T})+1-\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R})^q})\le 1.\)

As \(0\le \mathcal {T}\le 1,\) so \(0\le \frac{\pi }{2}\mathcal {T}\le \frac{\pi }{2}\). Since “sin” is an increasing function (InF) in 1st quadrant, that is why, \(0\le \sin (\frac{\pi }{2}\mathcal {T})\le 1.\) In the same way, as \(0\le \mathcal {R}\le 1,\) so \(0\le \frac{\pi }{2}(\root p \of {1-(\mathcal {R})^q})\le \frac{\pi }{2}\). This implies \(0\le \root p \of {1-\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R})^q}})\le 1\). As \(\sin ^px, x\in [0,1]\) is an InF, for \(\frac{\pi }{2}\mathcal {T}, \frac{\pi }{2}\root p \of {1-(\mathcal {R})^q}\in [0,1]\) s.t \(\frac{\pi }{2}\mathcal {T}\le \frac{\pi }{2}\root p \of {1-(\mathcal {R})^q}\) and by \(\sin ^px\) is an InF, we have \(\sin ^p(\frac{\pi }{2})\mathcal {T}\le \sin ^p(\frac{\pi }{2}\root p \of {1-\mathcal {R}^q})\). This shows that

$$\begin{aligned} \sin ^p\left( \frac{\pi }{2}\mathcal {T}\right) +1-\sin ^p\left( \frac{\pi }{2}\root p \of {1-(\mathcal {R})^q}\right) \le 1. \end{aligned}$$

Hence, \(\sin \varPsi\) is an \((p, q)-\)ROFN.” \(\square\)

Theorem 2

Suppose \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle , (\hbar =1, 2)\) are \((p, q)-\) ROFNs and \(k, k_1, k_2 >0\).

  1. 1.

    \(k(\sin \varPsi _1\oplus \sin \varPsi _2)=k\sin \varPsi _1\oplus k\sin \varPsi _2.\)

  2. 2.

    \((\sin \varPsi _1\otimes \sin \varPsi _2)^k=(\sin \varPsi _1)^k\otimes (\sin \varPsi _2)^k.\)

  3. 3.

    \(k_1\sin \varPsi _1\oplus k_2\sin \varPsi _1=(k_1+k_2)\sin \varPsi _1.\)

  4. 4.

    \(((\sin \varPsi _1)^{k_1})^{k_2}=(\sin \varPsi _1)^{k_1k_2}.\)

Proof

1. “For \((p, q)-\)ROFNs \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle\) and \(k>0\). Let \(\Im _\hbar =\sin ^p(\frac{\pi }{2}\mathcal {T}_\hbar )\), \(\mathfrak {z}_\hbar =\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R}_\hbar )^q})\). From Definition 6, \(\sin \varPsi _\hbar =\left\langle \root p \of {\Im _\hbar }, \root p \of {1-\mathfrak {z}_\hbar }\right\rangle\) for \(\hbar =1,2\) and

$$\begin{aligned} \sin \varPsi _1\oplus \sin \varPsi _2= & {} \left\langle \root p \of {1-(1-\Im _1)(1-\Im _2)},\right. \\{} & {} \left. \root p \of {1-\mathfrak {z}_1}.\root p \of {1-\mathfrak {z}_2}\right\rangle \\ k\left( \sin \varPsi _1\oplus \sin \varPsi _2\right)= & {} \left\langle \root p \of {1-(1-\Im _1)^k(1-\Im _2)^k},\right. \\{} & {} \left. \root p \of {(1-\mathfrak {z}_1)^k}.\root p \of {(1-\mathfrak {z}_2)^k}\right\rangle \\= & {} \left\langle [\root p \of {1-(1-\Im _1)^k}, \root p \of {(1-\mathfrak {z}_1)^k}\right\rangle \\{} & {} \oplus \left\langle \root p \of {1-(1-\Im _2)^k}, \root p \of {(1-\mathfrak {z}_2)^k}\right\rangle \\= & {} k\sin \varPsi _1\oplus k\sin \varPsi _2. \end{aligned}$$

3. As \(k_1\sin \varPsi _1\oplus k_2\sin \varPsi _1\)

$$\begin{aligned}= & {} \left\langle \root p \of {1-(1-\Im _1)^{k_1}}, \root p \of {(1-\mathfrak {z}_1)^{k_1}}\right\rangle \\{} & {} \oplus \left\langle \root p \of {1-(1-\Im _1)^{k_2}}, \root p \of {(1-\mathfrak {z}_1)^{k^2}}\right\rangle \\= & {} \left\langle \root p \of {1-(1-\Im _1)^{k_1+k_2}}, \root p \of {(1-{\mathfrak {z}_1})^{k_1+k_2}}\right\rangle \\= & {} (k_1+k_2)\sin \varPsi _1. \end{aligned}$$

\(\square\)

Theorem 3

Let \(\varPsi =\langle \mathcal {T}_\varPsi , \mathcal {R}_\varPsi \rangle\) and \(L=\langle \mathcal {T}_L, \mathcal {R}_L\rangle\) be \((p, q)-\)ROFNs s.t \(\mathcal {T}_\varPsi \ge \mathcal {T}_L\) and \(\mathcal {R}_\varPsi \le \mathcal {R}_L\), then \(\sin \varPsi \ge \sin L\).

Proof

For \((p, q)-\)ROFNs \(\varPsi =\langle \mathcal {T}_\varPsi , \mathcal {R}_\varPsi \rangle\) and \(L=\langle \mathcal {T}_L, \mathcal {R}_L^{lb}\rangle\) s.t \(\mathcal {T}_\varPsi \ge \mathcal {T}_L\). As \(``\sin\)” is an InF for \([0, \frac{\pi }{2}]\), so \(\sin (\frac{\pi }{2}\mathcal {T}_\varPsi )\ge \sin (\frac{\pi }{2}\mathcal {T}_L)\). Similarly, for \(\mathcal {R}_\varPsi \le \mathcal {R}_L\),

$$\begin{aligned} \sin \left( \frac{\pi }{2}\root p \of {1-(\mathcal {R}_\varPsi )^q}\right)\ge & {} \sin \left( \frac{\pi }{2}\root p \of {1-(\mathcal {R}_L)^q}\right) \end{aligned}$$

\(\Rightarrow\)

$$\begin{aligned} \root p \of {1-\sin ^p\left( \frac{\pi }{2}\root p \of {1-(\mathcal {R}_\varPsi )^q}\right) }\le & {} \root p \of {1-\sin ^p\left( \frac{\pi }{2}\root p \of {1-(\mathcal {R}_L)^p}\right) }. \end{aligned}$$

This concludes \(\sin \varPsi \ge \sin L\). \(\square\)

Theorem 4

For \((p, q)-\)ROFNs, \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle\) and \(\varPsi =\langle \mathcal {T}, \mathcal {R}\rangle\), \(\sin \varPsi _\hbar \oplus \sin \varPsi \ge \sin \varPsi _\hbar \otimes \sin \varPsi\).

Proof

For \((p, q)-\)ROFNs \(\varPsi _\hbar\) and \(\varPsi\), let \(\Im =\sin ^p(\frac{\pi }{2}\mathcal {T})\), \(\Im _\hbar =\sin ^p(\frac{\pi }{2}\mathcal {T}_\hbar )\), \(\mathfrak {z}=\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R})^q})\) and \(\mathfrak {z}_\hbar =\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R}_\hbar )^q})\), then

$$\begin{aligned} \sin \varPsi _\hbar \oplus \sin \varPsi= & {} \left\langle \root p \of {1-(1-\Im _\hbar )(1-\Im )},\right. \nonumber \\{} & {} \left. \root p \of {1-\mathfrak {z}_\hbar }.\root p \of {1-\mathfrak {z}}\right\rangle \end{aligned}$$
(3)

and

$$\begin{aligned} \sin \varPsi _\hbar \otimes \sin \varPsi= & {} \langle \root p \of {\Im _\hbar \Im }, \root p \of {1-\mathfrak {z}_\hbar \mathfrak {z}}\rangle . \end{aligned}$$
(4)

As \(\Im , \Im _\hbar , \mathfrak {z}, \mathfrak {z}_\hbar \in [0,1]\) and \(\frac{\Im +\Im _\hbar }{2}\ge \Im \Im _\hbar\), this implies \(1-(1-\Im _\hbar )(1-\Im )\ge \Im \Im _\hbar\)

$$\begin{aligned} \root p \of {1-(1-\Im _\hbar )(1-\Im )}\ge & {} \root p \of {\Im \Im _\hbar }. \end{aligned}$$

Similarly

$$\begin{aligned} \root p \of {1-\mathfrak {z}_\hbar \mathfrak {z}}\ge & {} \root p \of {1-\mathfrak {z}_\hbar }.\root p \of {1-\mathfrak {z}}. \end{aligned}$$

Therefore, using Eqs. 3 and 4

$$\begin{aligned} \sin \varPsi _\hbar \oplus \sin \varPsi\ge & {} \sin \varPsi _\hbar \otimes \sin \varPsi . \end{aligned}$$

\(\square\)

Theorem 5

For \((p, q)-\)ROFN \(\varPsi\) and \(j>0\), \(j\sin \varPsi \ge (\sin \varPsi )^j\) iff \(j\ge 1\) and \(j\sin \varPsi \le (\sin \varPsi )^j\) if and only if \(j\in (0,1]\).

Proof

It is easily demonstrated using the same justifications as in Theorem 4 which are applied. \(\square\)

4 AOs for \((p, q)-\)ROFNs under ST function

Definition 7

Let \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle (\hbar =1,2,\ldots ,n)\) be a series of \((p, q)-\)ROFNs and \(ST-(p, q)-ROFWA:\theta ^n\rightarrow \theta\), if \(ST-(p, q)-ROFWA\)

$$\begin{aligned}= & {} \varDelta _1\sin \varPsi _1\oplus \varDelta _2\sin \varPsi _2\oplus \cdots \oplus \varDelta _n\sin \varPsi _n, \end{aligned}$$
(5)

where \(\varDelta _\hbar =(\varDelta _1, \varDelta _2, \ldots , \varDelta _n)^T\) is the weight vector (WV) of \(\sin \varPsi _\hbar\) with condition \(\varDelta _\hbar >0\), \(\sum \nolimits _{\hbar =1}^n\varDelta _\hbar =1\).

Theorem 6

Let \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle\) be a series of \((p, q)-\)ROFNs. The compiled value by applying the \(ST-(p, q)-ROFWA\) operator is given by

$$\begin{aligned}{} & {} ST-(p, q)-ROFWA\left( \varPsi _1, \varPsi _2, \ldots , \varPsi _n\right) \nonumber \\{} & {} \quad = \left\langle \root p \of {1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }},\right. \nonumber \\{} & {} \left. \qquad \root p \of {\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{\varDelta _\hbar }}\Big ]\right\rangle . \end{aligned}$$
(6)

Proof

Utilizing the idea of operational law for \((p, q)-\)ROFNs and concepts of \(\sin \varPsi\), one may demonstrate the validity of Eq. 6. \(\square\)

Property 1

If all \((p, q)-\)ROFNs \(\varPsi _\hbar =\varPsi\), then

$$\begin{aligned} ST-(p, q)-ROFWA\left( \varPsi _1, \varPsi _2, \ldots , \varPsi _n\right)= & {} \sin \varPsi . \end{aligned}$$

Proof

As \(\varPsi _\hbar =\varPsi , \forall \hbar\), then \(\varDelta _\hbar \varPsi _\hbar =\varDelta _\hbar \varPsi\). Therefore, using the idea \(\sum \nolimits _{\hbar =1}^n\varDelta _\hbar =1\) and Eq. 6

$$\begin{aligned}{} & {} ST-(p, q)-ROFWA\left( \varPsi _1, \varPsi _2, \ldots , \varPsi _n\right) \\{} & {} \quad =\sum \limits _{\hbar =1}^n\varDelta _\hbar \sin \varPsi =\sin \varPsi . \end{aligned}$$

\(\square\)

Property 2

If \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle , \varPsi ^-=\langle \min _\hbar \{\mathcal {T}_\hbar \}, \max _\hbar \{\mathcal {R}_\hbar \}\rangle\) and \(\varPsi ^+=\langle \max _\hbar \{\mathcal {T}_\hbar \}, \min _\hbar \{\mathcal {R}_\hbar \}\rangle\) be \((p, q)-\)ROFNs, then

$$\begin{aligned} \sin \varPsi ^-\le ST-(p, q)-ROFWA\left( \varPsi _1, \varPsi _2, \ldots , \varPsi _n\right) \le \sin \varPsi ^+. \end{aligned}$$

Proof

As \(\min _\hbar \{\mathcal {T}_\hbar \}\le \mathcal {T}_\hbar \le \max _\hbar \{\mathcal {T}_\hbar \}\), \(\forall \hbar\) and \(\min _\hbar \{\mathcal {R}_\hbar \}\le \mathcal {R}_\hbar \le \max _\hbar \{\mathcal {R}_\hbar \}\). It means that \(\varPsi ^-\le \varPsi _\hbar \le \varPsi ^+.\) It can be assumed that \(ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)=\sin \varPsi =\langle \mathcal {T}_\varPsi , \mathcal {R}_\varPsi \rangle , \sin \varPsi ^-=\langle \mathcal {T}_{\varPsi ^-}^{lb}, \mathcal {R}_{\varPsi ^-}\rangle , \sin \varPsi ^+=\langle \mathcal {T}_{\varPsi ^+}, \mathcal {R}_{\varPsi ^+}\rangle .\) By the outcomes of ST function, \(\Im _{\varPsi _\hbar ^-}= \sin (\frac{\pi }{2}\min _\hbar \{\mathcal {T}_\hbar \})\le \sin (\frac{\pi }{2}\mathcal {T}_\hbar )=\Im _{\varPsi _\hbar }\) and \(\Im _{\varPsi _\hbar ^+}= \sin (\frac{\pi }{2}\max _\hbar \{\mathcal {T}_\hbar \})\ge \sin (\frac{\pi }{2}\mathcal {T}_\hbar )=\Im _{\varPsi _\hbar }.\) Thus

$$\begin{aligned} \mathcal {T}_\varPsi= & {} \root p \of {1-\prod \limits _{\hbar =1}^n\left( 1-\Im _{\varPsi _\hbar }\right) ^{\varDelta _\hbar }} \\\ge & {} \root p \of {1-\prod \limits _{\hbar =1}^n\left( 1-\Im _{\varPsi _\hbar ^-}\right) ^{\varDelta _\hbar }} \\= & {} \mathcal {T}_{\varPsi ^-} \end{aligned}$$

and

$$\begin{aligned} \mathcal {T}_\varPsi= & {} \root p \of {1-\prod \limits _{\hbar =1}^n\left( 1-\Im _{\varPsi _\hbar }\right) ^{\varDelta _\hbar }} \\\le & {} \root p \of {1-\prod \limits _{\hbar =1}^n\left( 1-\Im _{\varPsi _\hbar ^+}\right) ^{\varDelta _\hbar }} \\= & {} \mathcal {T}_{\varPsi ^+}. \end{aligned}$$

Similarly

$$\begin{aligned} \mathcal {T}_\varPsi\le & {} \mathcal {T}_{\varPsi ^+}. \end{aligned}$$

In this way, \(\mathcal {T}_{\varPsi ^-}\le \mathcal {T}_{\varPsi }\le \mathcal {T}_{\varPsi ^+}.\) Likewise, we can obtain \(\mathcal {R}_{\varPsi ^-}\le \mathcal {R}_{\varPsi }\le \mathcal {R}_{\varPsi ^+}\). Therefore, given result is completed. \(\square\)

Property 3

Assume \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle\) and \(\varPsi _\hbar ^*=\langle {\mathcal {T}_\hbar ^*}, {\mathcal {R}_\hbar ^*}\rangle\) are two collection of \((p, q)-\)ROFNs. If \(\mathcal {T}_\hbar \le {\mathcal {T}_\hbar ^*}, \mathcal {R}_\hbar \ge {\mathcal {R}_\hbar ^*}\), then

$$\begin{aligned}{} & {} ST-(p, q)-ROFWA\left( \varPsi _1, \varPsi _2, \ldots , \varPsi _n\right) \\{} & {} \quad \le ST-(p, q)-ROFWA\left( \varPsi _1^*, \varPsi _2^*, \ldots , \varPsi _n^*\right) . \end{aligned}$$

Proof

In the approach outlined above, we can show it. \(\square\)

Definition 8

Suppose \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle (\hbar =1,2,\ldots ,n)\) is a series of \((p, q)-\)ROFNs and suppose \(ST-(p, q)-ROFWG:\theta ^n\rightarrow \theta\), if \(ST-(p, q)-ROFWG\)

$$\begin{aligned}= & {} \left( \sin \varPsi _1\right) ^{\varDelta _1}\otimes \left( \sin \varPsi _2\right) ^{\varDelta _2}\otimes \cdots \otimes (\sin \varPsi _n)^{\varDelta _n}\nonumber \\= & {} \left\langle \root p \of {\prod \limits _{\hbar =1}^n(\Im _\hbar )^{\varDelta _\hbar }}, \root p \of {1-\prod \limits _{\hbar =1}^n(\mathfrak {z}_\hbar )^{\varDelta _\hbar }}\right\rangle ; \end{aligned}$$
(7)

here, \(ST-(p, q)-ROFWG\)) is used.

Definition 9

Let \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle\) be a series of \((p, q)-\)ROFNs and suppose \(ST-(p, q)-ROFOWA:\theta ^n\rightarrow \theta\), if \(ST-(p, q)-ROFOWA\)

$$\begin{aligned}= & {} \varDelta _1\sin \varPsi _{\sigma (1)}\oplus \varDelta _2\sin \varPsi _{\sigma (2)}\oplus \cdots \oplus \varDelta _n\sin \varPsi _{\sigma (n)}\\= & {} \left\langle \root p \of {1-\prod \limits _{\hbar =1}^n(1-\Im _{\sigma (\hbar )})^{\varDelta _\hbar }}, \root p \of {\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_{\sigma (\hbar )})^{\varDelta _\hbar }}\right\rangle , \end{aligned}$$

where \(\Im _{\sigma (\hbar )}=\sin ^p(\frac{\pi }{2}\mathcal {T}_{\sigma (\hbar )})\), \(\mathfrak {z}_{\sigma (\hbar )}=\sin ^p(\frac{\pi }{2}\root p \of {1-(\mathcal {R}_{\sigma (\hbar )})^q})\) and \(\sigma\) is the permutation of \((1,2,\ldots ,n)\) s.t \(\varPsi _{\sigma (\hbar -1)}\ge \varPsi _{\sigma (\hbar )}\).

Definition 10

Let \(\varPsi _\hbar =\langle \mathcal {T}_\hbar , \mathcal {R}_\hbar \rangle\) be a series of \((p, q)-\)ROFNs and suppose \(ST-(p, q)-ROFOWG:\theta ^n\rightarrow \theta\), if \(ST-(p, q)-ROFOWG\)

$$\begin{aligned}= & {} \left( \sin \varPsi _{\sigma (1)}\right) ^{\varDelta _1}\otimes \left( \sin \varPsi _{\sigma (2)}\right) ^{\varDelta _2}\otimes \cdots \otimes \left( \sin \varPsi _{\sigma (n)}\right) ^{\varDelta _n}\nonumber \\= & {} \left\langle \root p \of {\prod \limits _{\hbar =1}^n(\Im _{\sigma (\hbar )})^{\varDelta _\hbar }}, \root p \of {1-\prod \limits _{\hbar =1}^n(\mathfrak {z}_{\sigma (\hbar )})^{\varDelta _\hbar }}\right\rangle ; \end{aligned}$$
(8)

here, \(ST-(p, q)-ROFOWG\)) is used.

Definition 11

The operator \(ST-(p, q)-ROFHWA\) is a mapping \(ST-(p, q)-ROFHWA:\theta ^n\rightarrow \theta\) with \(\varXi =(\varXi _1, \varXi _2, \ldots , \varXi _n)^T\), \(\varXi _\hbar >0\) and \(\sum \nolimits _{\hbar =1}^n\varXi _\hbar =1\), given by \(ST-(p, q)-ROFHWA\)

$$\begin{aligned}= & {} \varXi _1\sin \dot{\varPsi }_{\sigma (1)}\oplus \varXi _2\sin \dot{\varPsi }_{\sigma (2)}\oplus \cdots \oplus \varXi _n\sin \dot{\varPsi }_{\sigma (n)}\\= & {} \left\langle \root p \of {1-\prod \limits _{\hbar =1}^n(1-\dot{\Im }_{\sigma (\hbar )})^{\varXi _\hbar }}, \root p \of {\prod \limits _{\hbar =1}^n(1-\dot{\mathfrak {z}}_{\sigma (\hbar )})^{\varXi _\hbar }}\right\rangle , \end{aligned}$$

where \(\dot{\varPsi }=n\varDelta _\hbar \varPsi _\hbar\) and \(\dot{\Im }_{\sigma (\hbar )}=\sin ^p(\frac{\pi }{2}\dot{\mathcal {T}}_{\sigma (\hbar )}),\) \(\dot{\mathfrak {z}}_{\sigma (\hbar )}=\sin ^p(\frac{\pi }{2}\root p \of {1-(\dot{\mathcal {R}}_{\sigma (\hbar )})^q}).\)

Definition 12

The operator \(ST-(p, q)-ROFHWG\) is a mapping \(ST-(p, q)-ROFHWG:\theta ^n\rightarrow \theta\) with \(\varXi =(\varXi _1, \varXi _2, \ldots , \varXi _n)^T\), \(\varXi _\hbar >0\) and \(\sum \nolimits _{\hbar =1}^n\varXi _\hbar =1\), given by \(ST-(p, q)-ROFHWG\)

$$\begin{aligned}= & {} (\sin \dot{\varPsi }_{\sigma (1)})^{\varXi _1}\otimes (\sin \dot{\varPsi }_{\sigma (2)})^{\varXi _2}\otimes \cdots \otimes (\sin \dot{\varPsi }_{\sigma (n)})^{\varXi _n}\nonumber \\= & {} \left\langle \root p \of {\prod \limits _{\hbar =1}^n(\dot{\Im }_{\sigma (\hbar )})^{\varXi _\hbar }}, \root p \of {1-\prod \limits _{\hbar =1}^n(\dot{\mathfrak {z}}_{\sigma (\hbar )})^{\varXi _\hbar }}\right\rangle , \end{aligned}$$
(9)

where \(\dot{\varPsi }=\varPsi _\hbar ^{n\varDelta _\hbar }\).

Remark 5

The ST-(p, q)-ROFWG, ST-(p, q)-ROFOWA, and ST-(p, q)-ROFOWG operators satisfy qualities 1, 2 and 3 but only boundedness and monotonicity are satisfied by ST-(p, q)-ROFHWA, ST-(p, q)-ROFHWG operators.

5 Basic characteristics of sine trigonometric \((p, q)-\)rung orthopair fuzzy AOs

Here, we discusses the numerous links between the suggested operators.

Lemma 1

For \(j_\hbar \ge 0\) and \(o_\hbar \ge 0\) with \(\sum \nolimits _{\hbar =1}^no_\hbar =1\)

$$\begin{aligned} \prod \limits _{\hbar =1}^nj_\hbar ^{o_\hbar }\le \sum \limits _{\hbar =1}^no_\hbar j_i. \end{aligned}$$

Equality holds iff \(j_1=j_2=\cdots =j_n\).

Lemma 2

Suppose \(j, o \in [0,1]\) and \(f\ge 1\) be an integer, then \(\root f \of {1-(1-j^f)(1-o^f)}\ge jo.\)

Theorem 7

For \((p, q)-\)ROFNs \(\varPsi _\hbar\), the following inequality holds between operators ST-(p, q)-ROFWA and ST-(p, q)-ROFWG:

$$\begin{aligned}{} & {} ST-(p, q)-ROFWA\left( \varPsi _1,\varPsi _2,\ldots ,\varPsi _n\right) \ge \\{} & {} ST-(p, q)-ROFWG\left( \varPsi _1,\varPsi _2,\ldots ,\varPsi _n\right) , \end{aligned}$$

and equality takes iff \(\varPsi _1=\varPsi _2=\cdots =\varPsi _n\).

Proof

As \(ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\)

$$\begin{aligned}= & {} \left\langle \root p \of {1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }}, \root p \of {\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{\varDelta _\hbar }}\right\rangle \end{aligned}$$

and \(ST-(p, q)-ROFWG\left( \varPsi _1, \varPsi _2, \ldots , \varPsi _n\right)\)

$$\begin{aligned}= & {} \left\langle \root p \of {\prod \limits _{\hbar =1}^n(\Im _\hbar )^{\varDelta _\hbar }}, \root p \of {1-\prod \limits _{\hbar =1}^n(\mathfrak {z}_\hbar )^{\varDelta _\hbar }}\right\rangle \end{aligned}$$

Utilizing Lemma 1

$$\begin{aligned} 1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\ge & {} 1- \sum \limits _{\hbar =1}^n\varDelta _\hbar (1-\Im _\hbar )\\= & {} \sum \limits _{\hbar =1}^n\varDelta _\hbar \Im _\hbar \\\ge & {} \prod \limits _{\hbar =1}^n(\Im _\hbar )^{\varDelta _\hbar }, \end{aligned}$$

which means

$$\begin{aligned} \root p \of {1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }}\ge \root p \of {\prod \limits _{\hbar =1}^n(\Im _\hbar )^{\varDelta _\hbar }}. \end{aligned}$$
(10)

By Lemma 1 and for \(\varDelta _\hbar ,\mathfrak {z}_\hbar \in [0,1]\)

$$\begin{aligned} \root p \of {\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{\varDelta _\hbar }}\ge \root p \of {1-\prod \limits _{\hbar =1}^n(\mathfrak {z}_\hbar )^{\varDelta _\hbar }}. \end{aligned}$$
(11)

Equations 10 and 11 are used to verify the necessary result. \(\square\)

Theorem 8

Suppose \(\varPsi _\hbar , \varPsi\) are \((p, q)-\)ROFNs, then

  1. 1.

    \(ST-(p, q)-ROFWA(\varPsi _1\oplus \varPsi , \varPsi _2\oplus \varPsi , \ldots , \varPsi _n\oplus \varPsi )\ge ST-(p, q)-ROFWA(\varPsi _1\otimes \varPsi , \varPsi _2\otimes \varPsi , \ldots , \varPsi _n\otimes \varPsi );\)

  2. 2.

    \(ST-(p, q)-ROFWG(\varPsi _1\oplus \varPsi , \varPsi _2\oplus \varPsi , \ldots , \varPsi _n\oplus \varPsi )\ge ST-(p, q)-ROFWG(\varPsi _1\otimes \varPsi , \varPsi _2\otimes \varPsi , \ldots , \varPsi _n\otimes \varPsi ).\)

Proof

We obtain \(\varPsi _\hbar \oplus \varPsi \ge \varPsi _\hbar \otimes \varPsi\) using the operational laws for \((p, q)-\)ROFNs \(\varPsi _\hbar , \varPsi\). As a result, according to the ST-(p, q)-ROFWA operator’s monotonicity property, we have \(ST-(p, q)-ROFWA(\varPsi _1\oplus \varPsi , \varPsi _2\oplus \varPsi , \ldots , \varPsi _n\oplus \varPsi )\ge ST-(p, q)-ROFWA(\varPsi _1\otimes \varPsi , \varPsi _2\otimes \varPsi , \ldots , \varPsi _n\otimes \varPsi ).\) \(\square\)

Theorem 9

For \((p, q)-\)ROFNs \(\varPsi _\hbar , \varPsi\)

  1. 1.

    \(ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\oplus \sin \varPsi \ge ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\otimes \varPsi ;\)

  2. 2.

    \(ST-(p, q)-ROFWG(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\oplus \sin \varPsi \ge ST-(p, q)-ROFWG(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\otimes \varPsi .\)

Proof

Since \((p, q)-\)ROFNs are the values for the operators \(ST-(p, q)-ROFWA, ST-(p, q)-ROFWG,\) and \(\sin \varPsi\). As a result, by Theorem 4, we reach the intended result. \(\square\)

Theorem 10

For \((p, q)-\)ROFNs \(\varPsi _\hbar , \varPsi\) and \(\lambda \in [0,1]\)

  1. 1.

    \(\lambda ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\oplus \sin \varPsi \ge (ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n))^\lambda \otimes \varPsi .\)

  2. 2.

    \(\lambda ST-(p, q)-ROFWG(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\oplus \sin \varPsi \ge (ST-(p, q)-ROFWG(\varPsi _1, \varPsi _2, \ldots , \varPsi _n))^\lambda \otimes \varPsi .\)

  3. 3.

    \((ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n))^\lambda \oplus \sin \varPsi \ge \lambda ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\otimes \varPsi .\)

  4. 4.

    \((ST-(p, q)-ROFWG(\varPsi _1, \varPsi _2, \ldots , \varPsi _n))^\lambda \oplus \sin \varPsi \ge \lambda ST-(p, q)-ROFWG(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\otimes \varPsi .\)

Proof

For \(\lambda \in [0,1]\) and \((p, q)-\)ROFNs \(\varPsi _\hbar , \varPsi\), \(\lambda ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\)

$$\begin{aligned}= & {} \left\langle \root p \of {1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\lambda {\varDelta _\hbar }}}, \root p \of {\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{\lambda {\varDelta _\hbar }}}\right\rangle \end{aligned}$$

and \((ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n))^\lambda\)

$$\begin{aligned}= & {} \left\langle \root p \of {\Big (1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{{\varDelta _\hbar }}}\Big )^\lambda , \root p \of {1-\big (1-\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{{\varDelta _\hbar }}}\big )^\lambda \right\rangle . \end{aligned}$$

Hence, \(\lambda ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n)\oplus \sin \varPsi\)

$$\begin{aligned}= & {} \left\langle \root p \of {1-(1-\Im )\Big (\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{{\varDelta _\hbar }}}\Big )^\lambda ,\right. \nonumber \\{} & {} \left. \quad \root p \of {(1-\mathfrak {z})\big (\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{{\varDelta _\hbar }}}\big )^\lambda \right\rangle \end{aligned}$$
(12)

and \((ST-(p, q)-ROFWA(\varPsi _1, \varPsi _2, \ldots , \varPsi _n))^\lambda \otimes \varPsi\)

$$\begin{aligned}= & {} \left\langle \root p \of {\Im \Big (1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{{\varDelta _\hbar }}}\Big )^\lambda ,\right. \nonumber \\{} & {} \left. \quad \root p \of {1-\big (1-\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{{\varDelta _\hbar }}\big )^\lambda .\mathfrak {z}^{lb}} \right\rangle . \end{aligned}$$
(13)

As \((\prod \nolimits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar })^\lambda \in [0,1]\). Therefore, applying Lemma 2

$$\begin{aligned} \Im \left( 1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\right) ^\lambda +(1-\Im )\left( \prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\right) ^\lambda\le & {} 1. \end{aligned}$$

This implies that

$$\begin{aligned} \Im \left( 1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\right) ^\lambda\le & {} 1- (1-\Im )\left( \prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\right) ^\lambda \\ \root p \of { \Im \left( 1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\right) ^\lambda }\le & {} \root p \of {1-(1-\Im )\Big (\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar }\Big )^\lambda }. \end{aligned}$$

In the same way, for \(\mathfrak {z},\) \((\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{\varDelta _\hbar })^\lambda\), \((1-\prod \limits _{\hbar =1}^n(1-\Im _\hbar )^{\varDelta _\hbar })^\lambda \in [0,1]\). Then, by Lemma 2

$$\begin{aligned} \root p \of {(1-\mathfrak {z})\big (\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{{\varDelta _\hbar }}}\big )^\lambda\le & {} \root p \of {1-\left( 1-\prod \limits _{\hbar =1}^n(1-\mathfrak {z}_\hbar )^{{\varDelta _\hbar }}\right) ^\lambda .\mathfrak {z}}. \end{aligned}$$

Therefore, result (i) holds for \(\lambda \in [0,1]\) according to Eqs. 12 and 13. \(\square\)

6 \((p, q)-\) rung orthopair fuzzy SIR technique

A group of decision-makers, a list of requirements, and a finite number of possibilities make up an MAGDM problem. The finest option among those provided must be picked to address a MAGDM issue. Let \(C=\{c_1, c_2, \ldots , c_n\}\) and \(u =\{ u_1, u_2,\ldots , u_m\}\) be the collection of criteria and options, respectively. Assume that the group of decision-makers has the composition \(E=\{e_1, e_2,\ldots , e_l\}\) and that their weight vector has the composition \(\varXi =\{\varXi _1, \varXi _2,\ldots , \varXi _l\}\), where all of the weights are \((p, q)-\)ROFNs. Create the individual decision matrices \(H_k=(h_{\hbar j}^k)_{m\times n}\), where \(h_{\hbar j}^k\) represents the evaluation data of the alternative \(u_\hbar\), \(\hbar =1,2,3,\ldots ,m\), with respect to the criterion \(c_j\), \(j=1,2,3,\ldots ,n\), supplied by the decision-maker \(e_k\), \(k=1,2,3,\ldots ,l\), in the form of \((p, q)-\)ROFNs. Assume that the criterion weight matrix \(\varphi =(\varphi _j^k)_{l \times n}\), \((j=1,2,3,\ldots ,n, k=1,2,3,\ldots ,l)\) is the matrix in which the weight of the criteria \(c_j\), \(j=1,2,3,\ldots ,n\), assigned by the decision-maker \(e_k\), \(k=1,2,3,\ldots ,l\), in the form of \((p, q)-\)ROFNs is represented by \(\varphi _j^k\), \((j=1,2,3,\ldots ,n, k=1,2,3,\ldots ,l)\). To solve the MAGDM problem, the \((p, q)-\)ROF-SIR approach is described in this section. Following are the steps for applying this technique:

Step 1.:

Calculate relative propinquity coefficient for each \(\varXi _k, k =1, 2,\ldots , l,\) using the equation

$$\begin{aligned} \eta _k=\frac{d(\varXi _k, \underline{\varXi })}{d(\varXi _k, \underline{\varXi })+d(\varXi _k, \overline{\varXi })} \end{aligned}$$
(14)

wherever \(\underline{\varXi }=\langle \min \limits _{k}(\mathcal {T}_{\varXi _k}), \max \limits _{k}(\mathcal {R}_{\varXi _k})\rangle .\) \(\overline{\varXi }=\langle \max \limits _{k}(\mathcal {T}_{\varXi _k}), \min \limits _{k}(\mathcal {R}_{\varXi _k})\rangle .\) These relative coefficients measure interrelationships among behaviors as a direct function of their intrinsic organization within a sequence. The coefficient does not depend on a user-defined “window" of analysis and provides an efficient use of data that facilitates comparisons across decision-makers.

Step 2.:

Then, these relative closeness coefficients \(\eta _k, k=1, 2, \ldots , l\) are normalized using Eq. 15

$$\begin{aligned} \zeta _k=\frac{ \eta _k}{ \sum _{k=1}^l\eta _k}. \end{aligned}$$
(15)

Thus, a normalized vector of relative propinquity coefficients of the form \(\zeta =\{\zeta _1, \zeta _2, \ldots , \zeta _l\}\) is obtained.

Step 3.:

Using the \(ST-(p, q)-ROFWA\) operator, the accumulated \((p, q)-\) rung orthopair fuzzy decision matrix is obtained as follows: the criterion weight vector as follows:

$$\begin{aligned} \widetilde{ h_{\hbar j}}= & {} ST-(p, q)-ROFWA(h_{\hbar j}^1, h_{\hbar j}^2, \ldots , h_{\hbar j}^l)\nonumber \\= & {} \big \langle \root p \of {1-\prod \limits _{k=1}^l\left( 1-\sin ^p(\frac{\pi }{2}{\mathcal {T}_{\hbar j}^k}\right) ^{\zeta _k}},\nonumber \\{} & {} \root p \of {\prod \limits _{k=1}^l\left( 1-\sin ^p(\frac{\pi }{2}\root q \of {{1-(\mathcal {R}_{\hbar j}^k})^q}\right) ^{\zeta _k}}\big \rangle . \end{aligned}$$
(16)

Similarly, the criterion weight vector is computed as follows:

$$\begin{aligned} \widetilde{ \varphi _{j}}= & {} ST-(p, q)-ROFWA\left( \varphi _{j}^1, \varphi _{j}^2, \ldots , \varphi _{j}^l\right) \nonumber \\= & {} \left\langle [\root p \of {1-\prod \limits _{k=1}^l(1-\sin ^p(\frac{\pi }{2}{\mathcal {T}_{\varphi _{j}^k}})^{\zeta _k}},\right. \nonumber \\{} & {} \left. \root p \of {\prod \limits _{k=1}^l(1-\sin ^p(\frac{\pi }{2}\root p \of {{1-(\mathcal {R}_{\varphi _{j}^k})^q}})^{\zeta _k}}\right\rangle . \end{aligned}$$
(17)

Note that, \(j=1,2,3,\ldots ,n\), \(k=1,2,3,\ldots ,l\), \(\hbar =1,2,3,\ldots ,m\), p and q are parametric values ranging from \(p, q=1,2,3,\ldots .\)

Step 4.:

The following steps can be taken to obtain the relative efficiency function \(f_{ij}\):

$$\begin{aligned} f_{\hbar j}=\frac{d(\widetilde{ h_{\hbar j}}, \underline{\widetilde{h}})}{d(\widetilde{ h_{\hbar j}}, \underline{\widetilde{h}})+d(\widetilde{ h_{\hbar j}}, \overline{\widetilde{h}})} \end{aligned}$$
(18)

wherever \(\underline{\widetilde{h}}=\langle \min \limits _{\hbar }(\mathcal {T}_{\widetilde{ h}_{\hbar j}}), \max \limits _{i}(\mathcal {R}_{\widetilde{ h}_{\hbar j}})\rangle\), \(\overline{\widetilde{h}}=\langle \max \limits _{\hbar }(\mathcal {T}_{\widetilde{ h}_{\hbar j}}), \min \limits _{\hbar }(\mathcal {R}_{\widetilde{ h}_{\hbar j}})\rangle .\) The relative efficiency function \(f_{ij}\) estimates the relative efficiency value of alternatives with respect to the criteria.

Step 5.:

Calculate the preference intensity \(PI_j(u_\hbar , u_t)(\hbar , t = 1, 2, \ldots , m, \hbar \ne t)\), which indicates the extent to which alternative \(u_\hbar\) is preferred over alternative \(u_t\) with respect to criteria \(c_j\). It is defined as follows:

$$\begin{aligned} PI_j(u_\hbar , u_t)=\kappa _j\left( f_{\hbar j}-f_{tj}\right) , \end{aligned}$$
(19)

\(j=1,2,3,\ldots ,n\), \(\hbar =1,2,3,\ldots ,m\). The \(\kappa _j\) threshold function is given by \(\kappa _j(x)=\left\{ \begin{array}{ll} 0.01, &{} {x>0;} \\ 0, &{} {x\le 0.} \end{array} \right.\)

Step 6.:

The superiority matrix \(S =(S_{\hbar j})_{m\times n}\) and the inferiority matrix \(I=(I_{\hbar j})_{m\times n}\) are calculated using the following equations:

$$\begin{aligned} S_{\hbar j}=\sum \limits _{t}\limits ^{m}\kappa _j\left( f_{\hbar j}-f_{tj}\right) \end{aligned}$$
(20)
$$\begin{aligned} I_{\hbar j}=\sum \limits _{t}\limits ^{m}\kappa _j\left( f_{tj}-f_{\hbar j}\right) . \end{aligned}$$
(21)

Note that the superiority matrix obtained from the superiority indices and inferiority matrix computed from the inferiority indices are obtained from the original decision matrix.

Step 7.:

The superiority flow (S-flow) and inferiority flow (I-flow) can be found by the following:

$$\begin{aligned} \kappa ^{\curlywedge }(u_\hbar )= & {} ST-(p, q)-ROFWA\left( \widetilde{\varphi _{j}^1}, \widetilde{\varphi _{j}^2}, \ldots , \widetilde{\varphi _{j}^l}\right) \nonumber \\ {}= & {} \left\langle [\root p \of {1-\prod \limits _{j=1}^n(1-\sin ^p(\frac{\pi }{2}{\mathcal {T}_{\widetilde{\varphi _{j}}}})^{S_{\hbar j}}},\right. \nonumber \\{} & {} \left. \root p \of {\prod \limits _{j=1}^n(1-\sin ^p(\frac{\pi }{2}\root p \of {{1-\mathcal {R}_{\widetilde{\varphi _{j}}}^q}})^{S_{\hbar j}}}\right\rangle . \end{aligned}$$
(22)
$$\begin{aligned} \kappa ^{\curlyvee }(u_\hbar )= & {} ST-(p, q)-ROFWA\left( \widetilde{\varphi _{j}^1}, \widetilde{\varphi _{j}^2}, \ldots , \widetilde{\varphi _{j}^l}\right) \nonumber \\ {}= & {} \left\langle [\root p \of {1-\prod \limits _{j=1}^n(1-\sin ^p(\frac{\pi }{2}{\mathcal {T}_{\widetilde{\varphi _{j}}}})^{I_{\hbar j}}},\right. \nonumber \\{} & {} \left. \root p \of {\prod \limits _{j=1}^n(1-\sin ^p(\frac{\pi }{2}\root p \of {{1-\mathcal {R}_{\widetilde{\varphi _{j}}}}^q})^{I_{\hbar j}}}\right\rangle . \end{aligned}$$
(23)

These flows can be calculated through different kinds of aggregation operators. Thus, the distinct techniques can produce different types of flows.

Step 8.:

Calculate the scoring formulas of \(\kappa ^{\curlywedge }(u_\hbar )\) and \(\kappa ^{\curlyvee }(u_\hbar )\), \(\hbar =1, 2, \ldots , m,\) by using Definition 4.

Step 9.:

Use the SR-laws (superiority ranking laws) and IR-laws (inferiority ranking laws) in the manner described below: SR Law: If \(\kappa ^{\curlywedge }(u_\hbar )\succ \kappa ^{\curlywedge }(u_t)\) and \(\kappa ^{\curlyvee }(u_\hbar )\prec \kappa ^{\curlyvee }(u_t)\), then \(u_\hbar \succ u_t\).

If \(\kappa ^{\curlywedge }(u_\hbar )\succ \kappa ^{\curlywedge }(u_t)\) and \(\kappa ^{\curlyvee }(u_\hbar )=\kappa ^{\curlyvee }(u_t)\), then \(u_\hbar \succ u_t\).

If \(\kappa ^{\curlywedge }(u_\hbar )=\kappa ^{\curlywedge }(u_t)\) and \(\kappa ^{\curlyvee }(u_\hbar )\prec \kappa ^{\curlyvee }(u_t)\), then \(u_\hbar \succ u_t\).

IR Law: If \(\kappa ^{\curlywedge }(u_\hbar )\prec \kappa ^{\curlywedge }(u_t)\) and \(\kappa ^{\curlyvee }(u_\hbar )\succ \kappa ^{\curlyvee }(u_t)\), then \(u_\hbar \prec u_t\).

If \(\kappa ^{\curlywedge }(u_\hbar )\prec \kappa ^{\curlywedge }(u_t)\) and \(\kappa ^{\curlyvee }(u_\hbar )=\kappa ^{\curlyvee }(u_t)\), then \(u_\hbar \prec u_t\).

If \(\kappa ^{\curlywedge }(u_\hbar )=\kappa ^{\curlywedge }(u_t)\) and \(\kappa ^{\curlyvee }(u_\hbar )\succ \kappa ^{\curlyvee }(u_t)\), then \(u_\hbar \prec u_t\).

Step 10.:

Hence, the superiority flow and inferiority flow are utilized to derive two complete rankings. These two complete rankings are then combined to obtain a new final ranking. The obtained ranking is then proposed to decision-makers for further exploitation before giving a final decision.

6.1 Illustrative example

For researchers and academics, looking to publish their work and make a contribution to the scholarly community, choosing the top journals is an essential task. When choosing the best publication for a specific research paper, a number of important aspects are taken into consideration. To guarantee that their work gets seen by the right people and is given the credit it merits, researchers must first locate journals that are respected in their particular field of study. Second, the subject and goals of the research must coincide with the journal’s breadth and concentration. Submissions to journals that focus on the particular topic have a higher chance of being accepted and generate more interest from readers who are really interested in the research field.

It can also be helpful to take the journal’s impact factor and citation data into account. An academic journal’s influence and reach are often indicated by the frequency with which its articles are cited, or impact factor. To choose the finest journal, it is important to carefully analyze a number of variables, such as reputation, relevance, influence, accessibility, and practical considerations. Researchers can greatly advance the body of knowledge in their subject and maximize the impact of their work by making an informed choice.

We present a numerical example for choosing the best journal for submitting the research article using \((p, q)-\)R OFNs to explain the strategy we suggested. Four potential journals are listed on a panel for selection: \(u_\hbar (\hbar = 1, 2, 3, 4)\). Three criteria are chosen by the experts to compare the four potential journals:

  • \(C_1\) stands for indexing,

  • \(C_2\) stands for journal rank,

  • \(C_3\) stands for impact factor.

The \((p, q)-\)ROF weights of decision-makers are given in Table 2. These weights represent the relative preference of each decision-maker corresponding to their capabilities.

Table 2 \((p, q)-\)ROF weights of decision-makers
Full size table

The relative importance of each criterion is represented in Table 3 provided by the decision-makers \(e_k\) in terms of \((p, q)-\)ROFNs. The decision-makers provide their evaluation via \((p, q)-\)ROFNs after evaluating each alternative \(u_\hbar\) in relation to each criterion \(C_j\).

Table 3 \((p, q)-\)ROF weights of criteria
Full size table

In Tables 4, 5, 6 three decision matrices are provided corresponding to three decision-makers \(e_1\), \(e_2\), and \(e_3\), respectively.

Table 4 \((p, q)-\)ROF decision matrix \(H_1\)
Full size table
Table 5 \((p, q)-\)ROF decision matrix \(H_2\)
Full size table
Table 6 \((p, q)-\)ROF decision matrix \(H_3\)
Full size table
Step 1.:

Using Eq. 14, the following relative propinquity coefficients are calculated:

$$\begin{aligned} \eta =\{1, 0.269, 0\}. \end{aligned}$$
(24)
Step 2.:

Using Eq. 15, the normalized vector is created as follows:

$$\begin{aligned} \zeta =\{0.79, 0.21, 0\}. \end{aligned}$$
(25)
Step 3.:

Using Eq. 16, which is shown in Table 7, the collected \((p, q)-\)ROF decision matrix is acquired. The collected weights of the criterion are calculated using Eq. 17, and they are as follows.

$$\begin{aligned} \widetilde{\varphi _1}= & {} \langle 0.66, 0.35\rangle \nonumber \\ \widetilde{\varphi _2}= & {} \langle 0.98, 2.6\times 10^{-8}\rangle \nonumber \\ \widetilde{\varphi _3}= & {} \langle 0.86, 0.04\rangle . \end{aligned}$$
(26)
Table 7 Accumulated \((p, q)-\)ROF decision matrix
Full size table
Step 4.:

Using Eq. 18, we can calculate the relative efficiency function as follows:

$$\begin{aligned} f_{\hbar j}=\left( \begin{array}{ccc} 0.279 &{} 1 &{} 0.99 \\ 0.471 &{} 0 &{} 0.418 \\ 0.193 &{} 0.080 &{} 0.655 \\ 1 &{} 0.844 &{} 0.584 \\ \end{array} \right) . \end{aligned}$$
(27)

Step 5.

  • The preference intensity (superiority) for alternative \(u_1\) over the other alternatives \(u_t, t=2,3,4\) is 0, 0.01, 0, respectively, corresponding to parameter \(C_1\).

  • The preference intensity (superiority) for alternative \(u_1\) over the other alternatives \(u_t, t=2,3,4\) is 0.01, 0.01, 0.01, respectively, corresponding to parameter \(C_2\).

  • The preference intensity (superiority) for alternative \(u_1\) over the other alternatives \(u_t, t=2,3,4\) is 0.01, 0.01, 0.01, respectively, corresponding to parameter \(C_3\).

  • The preference intensity (inferiority) for alternative \(u_1\) over the other alternatives \(u_t, t=2,3,4\) is 0.01, 0, 0.01, respectively, corresponding to parameter \(C_1\).

  • The preference intensity (inferiority) for alternative \(u_1\) over the other alternatives \(u_t, t=2,3,4\) is 0, 0, 0, respectively, corresponding to parameter \(C_2\).

  • The preference intensity (inferiority) for alternative \(u_1\) over the other alternatives \(u_t, t=2,3,4\) is 0, 0, 0, respectively, corresponding to parameter \(C_3\).

Similarly, we can calculate for other alternatives.

Step 6.:

The following is how the superiority and inferiority matrices are created using Eq. 20 and Eq. 21:

$$\begin{aligned} S=\left( \begin{array}{ccc} 0.01 &{} 0.03 &{} 0.03 \\ 0.02 &{} 0 &{} 0 \\ 0 &{} 0.01 &{} 0.02 \\ 0.03 &{} 0.02 &{} 0.01 \\ \end{array} \right) \end{aligned}$$
(28)
$$\begin{aligned} I=\left( \begin{array}{ccc} 0.02 &{} 0 &{} 0 \\ 0.01 &{} 0.03 &{} 0.03 \\ 0.03 &{} 0.02 &{} 0.01 \\ 0 &{} 0.01 &{} 0.02 \\ \end{array} \right) . \end{aligned}$$
(29)
Step 7:

To find the S-flow and I-flow for each alternative \(\hbar =1,2,3,4\), utilize Eqs. 22 and  23. Table 8 represents the result of S-flow and I-flow for each alternative.

Table 8 The (p, q)-ROF-SIR flows
Full size table
Step 8:

To find out the score value for each \(\lambda ^{\curlywedge }(u_\hbar )\) and \(\lambda ^{\curlyvee }(u_\hbar )\) \(\hbar =1,2,3,4\), apply the Definition 4. Table 9 represents the result of score values for them.

Table 9 Score values of \(\lambda ^{\curlywedge }(u_\hbar )\) and \(\lambda ^{\curlyvee }(u_\hbar )\)
Full size table
Step 9.:

Table 8’s ranking is as follows after applying SR-laws to it:

$$\begin{aligned} u_1\succ u_4 \succ u_3 \succ u_2. \end{aligned}$$

The following ranking order is obtained by applying IR-laws to Table 8:

$$\begin{aligned} u_1\succ u_4 \succ u_3 \succ u_2. \end{aligned}$$
Step 10.:

The best option is based on both SR and IR rules, and it is \(u_1\), as shown in Fig. 5”.

Fig. 5
figure 5

Ranking orders of alternatives

Full size image

7 Comparison analysis

It has demonstrated that the \((p, q)-\)ROF-SIR techniques are applicable in actual circumstances by overcoming the best journal selection problem. “In addition, to demonstrate the compatibility of our conclusions, we apply the various MADM methodologies to the same situation.

7.1 q-ROF-SIR technique

The optimal journal selection problem is demonstrated in this subsection using the q-ROF-SIR approach (Zhu et al. 2021). Four possibilities are taken into account as journal options, and three criteria are taken into account, to illustrate the aforementioned technique. The rest of the data and values are taken to be identical to those in Sect. 6. The ranking order of alternatives is given as \(u_1\succ u_4 \succ u_3 \succ u_2\), shown in Fig. 6.

Fig. 6
figure 6

Final ranking order of alternatives through \(q-\)ROF−SIR

Full size image

7.2 \(q-\)ROF TOPSIS technique

Pinar et al. (2021) created and suggested the q-ROF TOPSIS approach. This method obtains the preference weights of DMs and modifies linguistic evaluations to q-ROFNs. The value of the q parameter is assumed to be three throughout the calculations. After that, the linguistic weights are converted to q-ROFNs, and the q-ROFWA operator is used to aggregate the data. Finally, the ranking order of alternatives is given as \(u_1\succ u_4 \succ u_3 \succ u_2\), as shown in Fig. 7.

Fig. 7
figure 7

Final ranking order of alternatives through \(q-\)ROF TOPSIS

Full size image

7.3 Comparison with several other techniques

Table 10 Comparison analysis
Full size table

We continue to employ more techniques based on the FFYWA (Garg et al. 2020), FFYWG (Liu et al. 2022), FF TOPSIS (Senapati and Yager 2020), IF-SIR (Chai and Liu 2010), and PF-SIR (Ul Haq et al. 2022). Table 10 presents the findings. Table 10 demonstrates that all outcomes solved by the all techniques have the same ranking order of alternatives except IF-SIR (Chai and Liu 2010). Additionally, \(u_2\) is the solution provided by all approaches to be the best alternative. Through comparison with other existing methodologies, the \((p, q)-\)ROF-SIR technique’s practical usefulness and consistency have been confirmed. The data shown in Figs. 6, 7 show how each alternative was ranked using various methodologies, and it is seen that \(u_1\) is always the best choice. “The numerous criteria involved in the aforementioned methodologies account for the variation in the ranking order of other alternatives. The AOs were completely applied to the aforementioned approaches. Most present theories can be handled only if the qualities are independent of one another. On the other hand, the methodology used in this work typically relies on outranking techniques that ignore the independence or dependence between the qualities. As a result, the \((p, q)-\)ROF-SIR technique produces a more logical evaluation of options than other theories.

7.4 Results and discussion

From the above, it can be noted that the selection of the optimal journal is based on two factors, first one is the type of \((p, q)-\)ROFSs, which are estimated by the system experts. The second one is the aggregation operator combined with SIR technique applied to evaluate the journals. According to the given illustrative example, one can note the following: It cannot handle the ordered pairs of data given in the illustrative example using IFSs, because the sum of the degrees of non-membership and membership is greater than one. The decision-makers proposed different importance for the degrees of membership and non-membership, which cannot be treated using the extensions of IFSs known in the published manuscripts. Herein, we have discussed a new type of orthopair fuzzy sets called \((p, q)-\)ROFSs and revealed its connections with other kinds of orthopair fuzzy sets. Two of the merits of \((p, q)-\)ROFSs are to, first, expand the grades of membership and non-membership more than \(q-\)ROFSs in a way that enables us to cover more situations than IFSs, PFSs, and \(q-\)ROFSs. That is, make us in a position to cope with the information data in which the sum of their grades of membership and non-membership grades is greater than one. Second, to create appropriate environments to address numerous kinds of real-life problems that cannot be evaluated under the same ranks of importance for the membership and non-membership grades. On the other hand, the different importance given for the grades of membership and non-membership is a new task for the evaluation process induced from the proposed approach which does not exist in the foregoing generalizations of IFSs, PFSs, and \(q-\)ROFSs. In fact, it needs a comprehensive realization of the situation under study by the experts authorized to evaluate the system inputs.

Through this paper, we have familiarized some properties and AOs for \((p, q)-\)ROFSs and characterized them. Then, the SIR method, as a widely used and popular method in soft computing, has been extended to be used with \((p, q)-\)ROFSs. In the end, these aggregation operators and SIR technique have been employed to diagnose and analyze decision-making issues. An interpretative example has been provided to illustrate how the proposed approach assisted us with being effective in decision problems than cannot be coped with by the previous classes of IFSs, PFSs, and \(q-\)ROFSs.”

7.5 Benefits of the proposed strategy

By comparing the strategy based exclusively on \((p,q)-\) ROFNs to existing methodologies and assessing the adaptability and effectiveness of the suggested operators, we discover that the proposed scheme has the following benefits:

  • The membership grades \((p,q)-\)ROF integrate the IF, PF, FF, and q-ROF while producing the proper area of unclear facts and figures.

  • When the parameter p, q is increased, \((p,q)-\)ROFSs have a greater capacity to deal with unclear and imprecise information than other extensions.

  • The methodologies mentioned in Garg et al. (2020) are entirely dependent on the aggregation operators. Typically, these strategies necessitate attribute independence. While the proposed \((p,q)-\)ROF-SIR approaches fall under the category of outranking methods, which are unconcerned about whether the qualities are independent or dependent on one another. We can see from the above numerical example that it is unable to ensure the independence of the various attributes \(C_j (j = 1, 2, 3)\). As a result, the \((p,q)-\)ROF-SIR approaches produce a more rational ranking of possibilities than the other methods.

  • The strategies presented in Chai and Liu (2010) fail to deal with the given data, since their area is limited as compared to proposed theory.

8 Conclusions

In this study, we used SIR approach to work on an aggregation operator called the \((p, q)-\) ROF sine trigonometric operator for the \((p, q)-\) ROFNS. We analyze certain features, including idempotency, boundedness, and monotonicity, depending on the \((p, q)-\)ROF aggregating operator. This ST AO structure is more generalized and successfully integrates the complex problems, since it is built on t-norm and t-conorm with SIR approaches. “For the MADM problems with \((p, q)-\)ROFSs, the \((p, q)-\)ROF-SIR method is given. First, the entropy of \((p, q)-\)ROFSs was introduced to describe the uncertainty of \((p, q)-\)ROFSs. Then, we developed the PD of \((p, q)-\)ROFNs to reasonably measure the possibility degree of one \((p, q)-\)ROFN no less than another. Next, we introduced the PI of \((p, q)-\) ROFNs to improve the preference intensity. Subsequently, considering the weight vector of attributes, S-flow and I-flow were obtained to rank alternatives. If the attribute weights were not given, the \((p, q)-\)ROF-EW method was applied to determine the weights of the attribute. After that, the scores of S-flow and I-flow were employed to determine the partial ranking order of alternatives in the \((p, q)-\)ROF-SIR I method.

Moreover, we analyzed the sensitivity of parameters (p, q) in the proposed work. Further, we compared the proposed method with other aggregation methods as well as the PF-SIR method. The final results show that the \((p, q)-\)ROF-SIR method has two main characteristics. First, it is reasonable to use the PD of \((p, q)-\)ROFNs to compare two \((p, q)-\)ROFNs. Second, the proposed method is more reliable and powerful than the other mentioned methods.

We will expand our research into various aggregation operators using SIR approaches, including power mean AOs, Bonferroni mean AOs, Hamacher AOs, Hamy mean AOs, and Dombi AOs. Machine learning, information retrieval, data mining, artificial intelligence, social network analysis”, and many more fields have a lot of potential in the future. These are all great subjects to research in the future.