1 Introduction

In real life, people often need to rank alternatives or choose the best one among many different alternatives. In order to do it, the decision maker needs to supply the evaluation value of each alternative under different attributes. Sometimes, due to the complexity and uncertainty of the problems studied, it is too difficult for decision makers to give crisp evaluation values. To handle such fuzzy or uncertain phenomenon in MADM problems, Bellman and Zadeh [1] utilized membership degree rather than crisp value to describe uncertainty. The membership function is the key point of the famous fuzzy set (FS) theory. Atanassov [2] extended FSs into IFSs. Specially, the characteristic of IFSs is that the sum of the membership degree (MD) and non-membership degree (NMD) must be no more than 1. In 2014, Yager [3] further extended IFSs into PFSs, which are characterized that the square sum of MD and NMD is no more than 1. Obviously, there are more ordered pairs into PFSs than IFSs. Therefore, PFSs can express much wider application in fuzzy information. For example, someone is invited to assess the comfort of a house. She may use the Pythagorean fuzzy number (PFN) \(<0.8,0.6>\) to express her opinion rather than the intuitionistic fuzzy number (IFN). The reason is that \(0.8+0.6=1.4>1\) while \(0.8^2+0.6^2\le 1\).

More recently, Yager [4] further extended PFSs to q-ROFSs. The distinguishing feature of q-ROFSs is that the sum of the qth power of MD and NMD is no more than 1. It shows that the q-ROFS is more widely used than the IFS and the PFS, because in q-ROFSs, \(q=1\) and \(q=2\) denotes IFSs and PFSs, respectively. Take \(<0.8,0.7>\) which is the attribute evaluation value for example, it can use the q-ROFN (\(q\ge 3\)) to express the data rather than the IFN and the PFN. Because \(0.8^3+0.7^3=0.855\le 1\) while \(0.8^2+0.7^2=1.13>1\). In other words, q-ROFSs have more ordered pairs than PFSs and IFSs. Up to now, some scholars investigated the theory and application of q-ROFSs [4,5,6,7,8,9,10].

The superiority and inferiority ranking (SIR) method, proposed by Xu [11], is an import outranking method. In [11], Xu has proved that the SIR method is an extension of the classical PROMETHEE method [12, 13]. Since then, some researchers have extended the SIR methods to deal with various fuzzy information [14,15,16,17,18]. At the same time, the PROMETHEE methods have been extended to deal with different MADM problems [12, 13, 19,20,21,22,23,24,25,26,27,28,29]. However, the existing extended SIR methods or PROMETHEE methods can only deal with FSs [25], IFSs [26], hesitate fuzzy sets (HFSs) [16], PFSs [17], linguistic term sets (LTSs) [27] or 2-dimension linguistic term sets (2DLTSs) [29, 30]. In other words, PROMETHEE methods or the extended SIR methods can’t be directly applied to the MADM problems evaluated by q-ROFNs. Moreover, there are little investigation about the SIR methods or PROMETHEE methods with q-ROFSs.

The aim of this paper is to give a novel SIR method, named q-ROF-SIR method, to solve the MADM problems assessed by q-ROFNs. It is known that how to design the preference intensity is the key step of the SIR methods. In order to reasonably measure the difference of q-ROFNs, we propose the notion of PD of q-ROFNs to improve the preference intensity. At the same time, suppose the attribute weights are unknown, this paper develops the q-ROF-EW method to calculate the weights of attributes. Therefore, two new concepts, the entropy of q-ROFSs and the PD of q-ROFNs, are proposed to build foundations for the q-ROF-EW method and the q-ROF-SIR method.

Although there are many academic achievements of q-ROFSs, it finds that few researches are about the entropy of q-ROFSs. Fuzzy entropy is a very useful tool to measure the uncertainty of any FSs. Many scholars have proposed the various entropy of FSs [31,32,33,34,35], IFSs [36,37,38,39,40,41], Hesitate FSs [42] and PFSs [43, 44]. Guo [41] defined a new intuitionistic fuzzy entropy, which includes the distance part between IFS and its complement and the hesitancy part. Further, in 2018, Xue et al. [44] developed the Pythagorean fuzzy entropy, which is based on the similarity part between a PFS and its complement and the hesitancy part. Inspired by the entropy of IFSs [41] and PFSs [44], this paper will introduce the entropy of q-ROFSs to measure the uncertainty and fuzziness of q-ROFSs. Next, the q-ROF-EW method is developed to compute the attribute weights.

On the other hand, PD is an important mathematical tool to measure two objects, which reflects the probability of one object relative to another object. There are many literatures about PD of different fuzzy numbers. Such as, Xu and Da [45] introduced PD of the interval numbers to rank objects. Wei and Tang [46] presented PD of the IFNs. Wan and Dong [47] proposed PD of interval-valued IFNs from the probability viewpoint. Chen [24] proposed PD of interval type-2 fuzzy numbers. Gao [48] and Dammak et al. [49], respectively, gave an overview of PD of interval-valued IFSs. Zhao et al. [29] introduced PD of 2-dimension linguistic elements (2DLEs). However, there are little research about PD of q-ROFNs. Hence it is necessary to build the concept of PD for q-ROFNs to compare different q-ROFNs.

The main contributions of this paper are divided into four parts. (1) The entropy for q-ROFNs is introduced to measure the uncertainty of q-ROFSs. (2) The notion of PD for q-ROFNs is proposed to measure the possibility of one q-ROFN no less than another. (3) The q-ROF-EW method is presented. (4) The q-ROF-SIR methods are developed. The rest of this paper is arranged as follows. Section 2 introduces the preliminaries of q-ROFSs. Section 3 gives a new entropy formula of q-ROFSs. Section 4 defines two notions of PD and PI for q-ROFNs. Section 5 proposes the q-ROF-EW method and the q-ROF-SIR I and II methods. Section 6 gives a practical example. Section 7 concludes.

2 q-ROFSs

In this section, some notions of q-ROFSs [4] are introduced to provide a basis of this paper.

Definition 2.1

[4, 5] Let Y be a finite universe, the function \(u_{QF}: Y\rightarrow [0,1]\) be the degree of membership and \(v_{QF}: Y\rightarrow [0,1]\) be the degree of nonmembership. If for every \(y\in Y\), \(u_{QF}^q(y)+v_{QF}^q(y)\le 1,\) where \(q\in N, q\ge 1\), then a set QF, which has the form

$$\begin{aligned} QF=\{<y, u_{QF}(y),v_{QF}(y)>|y\in Y\}, \end{aligned}$$

is called a q-ROFS. \(<u_{QF}(y),v_{QF}(y)>\) is called a q-rung orthopair fuzzy number (q-ROFN), denoted by \(<u_{QF},v_{QF}>\). \(\pi _{QF}(y)=\root q \of {1-u_{QF}^q(y)-v_{QF}^q(y)}\) denotes the indeterminacy degree of of QF.

Yager [4] have proved that a q-ROFS with \(q=1\) is an IFS and a q-ROFS with \(q=2\) is a PFS. To help readers understand the q-ROFN intuitively, a geometric explanation of the q-ROFS membership is shown in Fig. 1 [4, 6].

Fig. 1
figure 1

Geometric space range of q-ROFS membership

Full size image

Given three q-ROFNs, \(Q_i=<u_i,v_i> ( i=1, 2, 3)\), then the operations are defined:

$$\begin{aligned}&(1)\ \ \overline{Q_1}=<v_1,u_1>,\\&(2)\ \ Q_1\oplus Q_2=<\root q \of {u_1^q+u_2^q-u_1^qu_2^q},v_1v_2>,\\&(3)\ \ Q_1\otimes Q_2=<u_1u_2,\root q \of {v_1^q+v_2^q-v_1^qv_2^q}>,\\&(4)\ \ \lambda Q_1=<\root q \of {1-(1-u_1^q)^{\lambda }},v_1^{\lambda }>,\\&(5)\ \ Q_1^{\lambda }=<u_1^{\lambda },\root q \of {1-(1-v_1^q)^{\lambda }}>.\\ \end{aligned}$$

Let \(Q=<u,v>\) be a q-ROFN, then \(S(Q)=u^q-v^q\) and \(H(Q)=u^q+v^q\) are called the score function and accuracy function of Q, respectively [5]. According to the score and accuracy functions of any two q-ROFNs, we can compare two q-ROFNs.

Definition 2.2

[5] Let \(Q_i=<u_i,v_i> (i=1,2)\) be any two q-ROFNs.

  1. (1)

    If \(S(Q_1) > S(Q_2)\), then \(Q_1\) is better than \(Q_2\), denoted by \(Q_1 > Q_2\);

  2. (2)

    If \(S(Q_1) = S(Q_2)\) and \(H(Q_1) > H(Q_2)\), then \(Q_1\) is better than \(Q_2\), denoted by \(Q_1>Q_2\);

  3. (3)

    If \(S(Q_1) = S(Q_2)\) and \(H(Q_1) = H(Q_2)\), then \(Q_1\) is equivalent to \(Q_2\), denoted by \(Q_1=Q_2\).

In [6], Liu et al. proposed the normalized Hamming distance between two q-ROFNs. Obviously, if \(q=2\), it is the distance between two PFNs proposed by Zhang et al. [50].

Definition 2.3

[6] Let \(Q_i=<u_i,v_i> (i=1,2)\) be two q-ROFNs, \(\pi _i=\root q \of {1-u_i^q-v_i^q}\), \((i=1,2)\). The function

$$\begin{aligned} d(Q_1,Q_2)=\dfrac{1}{2}\left( |u_1^q-u_2^q|+|v_1^q-v_2^q|+|\pi _1^q-\pi _2^q|\right) , \end{aligned}$$

is called the normalized Hamming distance between \(Q_1\) and \(Q_2\), where \(q\ge 1\).

3 New entropy for q-ROFSs

The entropy of FSs which can measure the fuzziness of information was firstly introduced by Zadeh [51]. After that, Luca et al. [31] gave the axioms of fuzzy entropy. Further, Szmidt et al. [37] extended the axioms of fuzzy entropy to IF environment. Inspired by the axioms of entropy for FSs and IFSs, we give the axioms of entropy for q-ROFSs.

Definition 3.1

Let qROFS(X) be a set of all q-ROFSs. A function \(E_q: qROFS(X)\rightarrow [0,1]\) is called an entropy on q-ROFSs if it satisfies that:

\((E_1)\):

\(E_q (QF)=0\) if and only if QF is a crisp set;

\((E_2)\):

\(E_q(QF)=1\) if and only if \(u_{QF}(y)=v_{QF}(y)\);

\((E_3)\):

If \(u_{QF_1}(y)\le u_{QF_2}(y) \le v_{QF_2}(y)\le v_{QF_1}(y)\) or \(u_{QF_1}(y)\ge u_{QF_2}(y) \ge v_{QF_2}(y)\ge v_{QF_1}(y)\), then \(E_q(QF_1) \le\)

\(E_q(QF_2)\).

\((E_4)\):

\(E_q(QF)=E_q({\overline{QF}})\), where \({\overline{QF}}=\{<y, v_{QF}(y),u_{QF}(y)>|y\in Y\}\).

Similar to the entropy for PFSs [44], we define a new entropy for q-ROFSs, which includes the similarity part and the indeterminacy part. Let QF be a q-ROFN, the similarity part is equal to \(1-d(QF,{\overline{QF}})\). The larger the similarity part, the bigger the entropy for q-ROFNs. On the other hand, the indeterminacy part is based on the indeterminacy degree \(\pi _{QF}\). Let a q-ROFN \(QF=<u_{QF},v_{QF}>\), if \(u_{QF}=v_{QF}\), then \(\pi _{QF}=1\). In such situation, we can learn less valuable information, therefore we suppose \(E(QF)=1\) if and only if \(\pi _{QF}=1\). Similarly, the larger the indeterminacy degree \(\pi _{QF}\), the bigger the entropy for q-ROFNs.

According to the above analysis, we define an entropy for q-ROFNs as \(E_q(QF)=1-d(QF,{\overline{QF}})+\pi _{QF}^qd(QF,{\overline{QF}}),\) where the distance function d is the normalized Hamming distance described in Definition 2.3.

Since \(d(QF,{\overline{QF}})=|u_{QF}^q-v_{QF}^q|,\) where \(QF=<u_{QF},v_{QF}>\), according to Definition 2.3, an entropy for q-ROFN QF can be represented as follows:

$$\begin{aligned} E_q(QF)=1-|u_{QF}^q-v_{QF}^q|+\pi _{QF}^q |u_{QF}^q-v_{QF}^q|=1-|u_{QF}^{2q}-v_{QF}^{2q}|, \end{aligned}$$
(1)

where \(\pi _{QF} =\root q \of {1-u_{QF}^q-v_{QF}^q}\).

Let QF be a q-ROFS, then the entropy for QF can be defined as:

$$\begin{aligned} E_q(QF)=\dfrac{1}{n}\displaystyle {\sum _{i=1}^{n}}E_q(QF_i)=1-\dfrac{1}{n}\displaystyle {\sum _{i=1}^{n}}|u_{QF_i}^{2q}-v_{QF_i}^{2q}|, \end{aligned}$$
(2)

where \(QF_i=<u_{QF_i},v_{QF_i}>\) be q-ROFNs.

Theorem 3.1

\(E_q(QF)\) is an entropy measure for q-ROFSs which satisfies Definition 3.1.

Proof

\((E_1)\) :

Since \(0\le u_{QF_i}\le 1\) and \(0\le v_{QF_i}\le 1\), then we have

\(E_q(QF)=0\) \(\Longleftrightarrow\) \(\dfrac{1}{n} {\sum _{i=1}^{n}}|u_{QF_i}^{2q}-v_{QF_i}^{2q}|=1\) \(\Longleftrightarrow\) \(<u_{QF_i},v_{QF_i}>=<1,0>\) or \(<u_{QF_i},v_{QF_i}>=<0,1>.\)

\((E_2)\) :

\(E_q(QF)=1\) \(\Longleftrightarrow\) \(\dfrac{1}{n} {\sum _{i=1}^{n}}|u_{QF_i}^{2q}-v_{QF_i}^{2q}|=0\) \(\Longleftrightarrow\) \(u_{QF_i}=v_{QF_i}.\)

\((E_3)\) :

If \(u_{QF_1}(y)\le u_{QF_2}(y) \le v_{QF_2}(y)\le v_{QF_1}(y)\), then \(|u_{QF_1}^{2q}-v_{QF_1}^{2q}|\ge |u_{QF_2}^{2q}-v_{QF_2}^{2q}|\). It follows that

$$\begin{aligned} 1-|u_{QF_1}^{2q}-v_{QF_1}^{2q}|\le 1-|u_{QF_2}^{2q}-v_{QF_2}^{2q}|, \end{aligned}$$

that is \(E_q(QF_1)\le E_q(QF_2)\).

Similarly, if \(u_{QF_1}(y)\ge u_{QF_2}(y) \ge v_{QF_2}(y)\ge v_{QF_1}(y)\), then \(|u_{QF_1}^{2q}-v_{QF_1}^{2q}|\ge |u_{QF_2}^{2q}-v_{QF_2}^{2q}|\). Therefore we have \(E_q(QF_1)\le E_q(QF_2)\).

\((E_4)\) :

Since \(|u_{QF}^{2q}-v_{QF}^{2q}|=|v_{QF}^{2q}-u_{QF}^{2q}|\), then we have \(E(QF)=E({\overline{QF}})\).

\(\square\)

4 Possibility degree measures for q-ROFNs

To reasonably measure the difference between two q-ROFNs, we propose the PD for q-ROFNs in this section. The comparison method between two q-ROFNs can be improved through comparing two q-ROFNs in pairs. Subsequently, suppose there is a set of q-ROFNs, the possibility degree outranking index (PI) for q-ROFNs is given to measure the prior degree of one q-ROFN against the other q-ROFNs.

4.1 PD of q-ROFNs

Firstly, the concept of PD for q-ROFNs is proposed, which can compare any two q-ROFNs in probability senses. Then we investigate some properties of the PD for q-ROFNs.

Definition 4.1

Let \(Q_i=<u_i,v_i> (i=1,2)\) be two q-ROFNs, \(\pi _i=\root q \of {1-u_i^q-v_i^q}(i=1,2)\). If either \(\pi _1\ne 0\) or \(\pi _2\ne 0\), then the possibility degree of q-ROFNs \(Q_1\) and \(Q_2\), is proposed as

$$\begin{aligned} P(Q_1\ge Q_2)=\min \left\{ \max \left( \dfrac{u_1^q+\pi _1^q-u_2^q}{\pi _1^q+\pi _2^q},0\right) ,1\right\} . \end{aligned}$$
(3)

On the other hand, if \(\pi _1=0\) and \(\pi _2=0\), then define

$$\begin{aligned}P(Q_1\ge Q_2)= {\left\{ \begin{array}{ll} 0, &{} u_1< u_2,\\ \\ 0.5, &{} u_1=u_2,\\ \\ 1, &{} u_1> u_2.\\ \end{array}\right. } \end{aligned}$$

Example 4.1

Let \(Q_1=<0.6,0.1>\), \(Q_2=<0.7,0.2>\) be two q-ROFNs, where \(q=2\).

We can compute that \(P(Q_1\ge Q_2)=0.4545\) and \(P(Q_2\ge Q_1)=0.5455\) by Definition 4.1. It obtains that \(Q_1\) is not better than \(Q_2\) in probability sense, which conforms to human’s intuition. In other words, it is suitable to use Definition 4.1 for comparing two q-ROFNs.

Some properties of PD for q-ROFNs are given.

Proposition 4.1

Let \(Q_i=<u_i,v_i> (i=1,2)\) be two q-ROFNs, then

  1. (1)

    \(0\le P(Q_1\ge Q_2) \le 1\);

  2. (2)

    If \(Q_1=Q_2\), then \(P(Q_1\ge Q_2)=0.5\);

  3. (3)

    \(P(Q_1\ge Q_2 ) +P(Q_2\ge Q_1)=1\).

Proof

  1. (1)

    According to Definition 4.1, \(0\le P(Q_1\ge Q_2)\) holds obviously. We only need to prove \(P(Q_1\ge Q_2)\le 1\).

    Let \(\xi =\dfrac{u_1^q+\pi _1^q-u_2^q}{\pi _1^q+\pi _2^q}\), then three cases are considered as follows:

    1. (a)

      if \(\xi \ge 1\), then \(P(Q_1\ge Q_2)=\min \{\max (\xi ,0),1\}=1;\)

    2. (b)

      if \(\xi \le 0\), then \(P(Q_1\ge Q_2)=\min \{\max (\xi ,0),1\}=0;\)

    3. (c)

      if \(0<\xi < 1\), then \(P(Q_1\ge Q_2)=\min \{\max (\xi ,0),1\}=\xi.\)

      Therefore, we have \(P(Q_1\ge Q_2)\le 1.\)

  2. (2)

    If \(Q_1=Q_2\), then we have \(u_1=u_2\) and \(\pi _1=\pi _2\). Let \(\xi =\dfrac{u_1^q+\pi _1^q-u_2^q}{\pi _1^q+\pi _2^q}\), then \(\xi =\dfrac{\pi _1^q}{2\pi _1^q}=0.5\).

    Therefore we have \(P(Q_1\ge Q_2)=\min \{\max (0.5,0),1\}=0.5\).

  3. (3)

    Let \(\xi _1=\dfrac{u_1^q+\pi _1^q-u_2^q}{\pi _1^q+\pi _2^q}\) and \(\xi _2=\dfrac{u_2^q+\pi _2^q-u_1^q}{\pi _1^q+\pi _2^q}\), then we have

    $$\begin{aligned} \xi _1+\xi _2=\dfrac{\pi _1^q+\pi _2^q}{\pi _1^q+\pi _2^q}=1. \end{aligned}$$

There are three cases need considering:

  1. (a)

    if \(\xi _1 \le 0\) and \(\xi _2\ge 1\), then

    \(P(Q_1\ge Q_2)+P(Q_2\ge Q_1)=0+1=1\);

  2. (b)

    if \(\xi _1 \ge 1\) and \(\xi _2\le 0\), then

    \(P(Q_1\ge Q_2)+P(Q_2\ge Q_1)=1+0=1\);

  3. (c)

    if \(0<\xi _1 <1\) and \(0<\xi _2<1\), then

    \(P(Q_1\ge Q_2)+P(Q_2\ge Q_1)=\xi _1+\xi _2=1\).

    That is, in all cases, \(P(Q_1\ge Q_2 ) +P(Q_2\ge Q_1)=1\) holds.

\(\square\)

4.2 PI of q-ROFNs

This subsection proposes the notion of PI for q-ROFNs. Given a set of q-ROFNs, the PI of q-ROFNs can measure the prior degree of one q-ROFN against others. Then some propositions of PI for q-ROFNs are investigated.

Definition 4.2

Let \(A=\{Q_1,\ldots ,Q_M\}\), in which \(Q_{i}=<u_{i},v_{i}>\) is a q-ROFN, \(i=\{1,2,\ldots ,M\}\), \(P(Q_{i}\ge Q_{k})\) be the PD between two q-ROFNs \(Q_{i}\) and \(Q_{k}\). Then the possibility degree outranking index (PI) of the q-ROFN \(Q_{i}\), is defined as

$$\begin{aligned} PI(Q_{i})=\dfrac{1}{M(M-1)}\left( \displaystyle {\sum _{k=1}^{M}} P(Q_{i}\ge Q_{k})+\frac{M}{2}-1\right) . \end{aligned}$$
(4)

Example 4.2

Assume there is a set of q-ROFNs \(\{Q_1, Q_2,Q_3,Q_4,Q_5\}\), where \(Q_1=<0.5,0.2>, Q_2=<0.6,0.3>,Q_3=<0.3,0.4>\), \(Q_4=<0.7,0.4>,Q_5=<0.7,0.6>\) and \(q=3\).

According to Definition 4.1, it can compute that \(P(Q_1\ge Q_2)=0.4778,P(Q_1\ge Q_3)=0.5434, P(Q_1\ge Q_4)=0.4445,P(Q_1\ge Q_5)=0.4962\), \(P(Q_2\ge Q_3)=0.5678,P(Q_2\ge Q_4)=0.4667,P(Q_2\ge Q_5)=0.5259,P(Q_3\ge Q_4)=0.3948,P(Q_3\ge Q_5)=0.4393,P(Q_4\ge Q_5)=0.5735\).

Then by Definition 4.2, we can compute that

\(PI(Q_1)=0.1981\), \(PI(Q_2)=0.2041\), \(PI(Q_3)=0.1861\), \(PI(Q_4)=0.2134\), \(PI(Q_5)=0.1983\).

According to the outcomes of PI for q-ROFNs, we can compare these q-ROFNs. That is, the bigger the value of PI for q-ROFN, the better the q-ROFN. Because \(PI(Q_4)>PI(Q_2)>PI(Q_5)>PI(Q_1)>PI(Q_3)\) in Definition 4.2, it can get that the prior order of \(Q_i\) \((i=1,2,3,4,5)\) is \(Q_4>Q_2>Q_5>Q_1>Q_3\).

Finally, we give the proposition of PI for q-ROFNs as follows.

Proposition 4.2

Let \(A=\{Q_1,\ldots ,Q_M\}\) be a set of q-ROFNs, in which \(Q_{i}=<u_{i},v_{i}>\) is a q-ROFN, \(\{i=1,2,\ldots ,M\}, (M \ge 2)\). Then

  1. (1)

    \(0\le PI(Q_{i}) \le 1\);

  2. (2)

    \(PI(Q_{1})+PI(Q_{2})+\cdots +PI(Q_{M})=1\).

Proof

  1. (1)

    According to Proposition 4.1, we have \(0\le P(Q_{i}\ge Q_{k} ) \le 1\).

    Let \(\xi ={\sum _{k=1}^{M}} P(Q_{i}\ge Q_{k})+\frac{M}{2}-1\), then we have \(0\le \dfrac{M}{2}-1\le \xi \le (M-1)+\dfrac{M}{2}\).

    According to Definition 4.2, we have \(PI(Q_{i})=\dfrac{\xi }{M(M-1)}\), that is \(0\le \dfrac{\xi }{M(M-1)}\le \dfrac{1}{M}+\dfrac{1}{2(M-1)}\le 1\).

    Therefore the conclusion holds.

  2. (2)

    According to Proposition 4.1, we have \(P(Q_{i}\ge Q_{i})=0.5\) and \(P(Q_{i}\ge Q_{k} ) +P(Q_{k}\ge Q_{i})=1\).

Let \(\eta ={\sum _{i=1}^{M}}{\sum _{k=1}^{M}} P(Q_{i}\ge Q_{k})\), then we have \(\eta =\dfrac{M(M-1)}{2}+\dfrac{M}{2}\).

Since

$$\begin{aligned} {\sum _{i=1}^{M}}PI(Q_{i})= & {} \dfrac{1}{M(M-1)}\displaystyle {\sum _{i=1}^{M}}\left( \displaystyle {\sum _{k=1}^{M}} P(Q_{i}\ge Q_{k})+\frac{M}{2}-1\right) \\= & {} \dfrac{1}{M(M-1)}\left( \displaystyle {\sum _{i=1}^{M}}\displaystyle {\sum _{k=1}^{M}} P(Q_{i}\ge Q_{k})+M(\frac{M}{2}-1)\right) \\= & {} \dfrac{1}{M(M-1)} \left( \eta +M(\dfrac{M}{2}-1)\right) , \end{aligned}$$

and \(\eta +M(\dfrac{M}{2}-1)=\dfrac{M(M-1)}{2}+\dfrac{M}{2}+M(\dfrac{M}{2}-1)=M(M-1)\), we have \({\sum _{i=1}^{M}}PI(Q_{i})=1\). \(\square\)

5 q-ROF-SIR methods to MADM with q-ROF information

In order to address MADM problems evaluated by q-ROFNs, this section presents the q-ROF-SIR methods. Firstly, based on the PI of q-ROFNs, we improve the preference intensity in the classical SIR methods [11] to obtain the superiority matrix (S-matrix) and inferiority matrix (I-matrix). Subsequently, when considering the weight vector of the attributes, superiority flow (S-flow) and inferiority flow (I-flow) are developed to establish the q-ROF-SIR methods. If the attribute weights are unknown, we give the q-ROF-EW method which is based on the entropy of q-ROFSs to obtain the attribute weights. Finally, we compare the scores of S-flow and I-flow to determine q-ROF-SIR partial ranking order or q-ROF-SIR total ranking order of alternatives.

5.1 q-ROF-SIR methods

Given a MADM problem, \(A=\{A_1,\ldots ,A_n\}\) represents a set of alternatives, where \(A_i\) denotes the ith alternative and \(C=\{C_1,\ldots ,C_m\}\) represents a set of attributes, where \(C_j\) denotes the jth attribute. In some uncertain environment, an expert prefers to assess the alternative \(A_i\) on the attribute \(C_j\) by using of q-ROFNs \(Q_{ij}=<u_{ij},v_{ij}>\). Then a q-ROFN decision making matrix \(QR=(Q_{ij})_{n\times m}\) can be established according to the assessments of the expert.

It is known that the higher the benefit attribute, the better the alternative, while the lower the cost attribute, the better the attribute. Assume the original assessment of alternative \(A_i\) on attribute \(C_j\) is represented by q-ROFN \(Q_{ij}=<u_{ij},v_{ij}>\), then \(Q_{ij}=<u_{ij},v_{ij}>\) needs to be normalized as follows:

$$\begin{aligned}Q_{ij}= {\left\{ \begin{array}{ll}<u_{ij},v_{ij}>, &{} C_j \ \text { belongs to the benefit attribute set;} \\ <v_{ij},u_{ij}>, &{} C_j \ \text { belongs to the cost attribute set.} \end{array}\right. } \end{aligned}$$

In other words, if the attribute \(C_j\) is a benefit attribute, the evaluation value \(Q_{ij}=<u_{ij},v_{ij}>\) does not change. While if the attribute \(C_j\) is a cost attribute, we must replace \(Q_{ij}\) with its complement \(\overline{Q_{ij}}=<v_{ij},u_{ij}>\).

5.1.1 Improved preference intensity

Motivated by the preference intensity proposed in [11, 12], we define the improved preference intensity as follows:

$$\begin{aligned} F_j(Q_{ij},Q_{kj})= & {} \psi _j(PI(Q_{ij})-PI(Q_{kj}))=\psi _j(t). \end{aligned}$$
(5)

where \(t=PI(Q_{ij})-PI(Q_{kj})\) measures the PI difference of between alternatives \(A_i\) and alternatives \(A_k\) under the attribute \(C_j\). Usually, the decision maker can select \(\psi _j\) from the six various kinds of preference functions introduced by Brans and Mareschal [21] or define \(\psi _j (t)\) by themselves.

5.1.2 Superiority matrix and inferiority matrix

According to the improved preference intensity, S-matrix \(S=(S_{ij})_{n\times m}\) and I-matrix \(I=(I_{ij})_{n\times m}\) can be obtained, where

$$\begin{aligned} S_{ij}= & {} \displaystyle {\sum _{t=1}^{n}} F_j(Q_{ij},Q_{tj}), \end{aligned}$$
(6)
$$\begin{aligned} I_{ij}= & {} \displaystyle {\sum _{t=1}^{n}} F_j(Q_{tj},Q_{ij}). \end{aligned}$$
(7)

5.1.3 The q-ROF-EW method

Assume \(w_j\) be the weight of attribute \(C_j\) such that \(0\le w_j\le 1\) and \({\sum _{j=1}^{m}}w_j=1\). Let \((E_q)_j=\dfrac{1}{n}{\sum _{i=1}^{n}} E_q(Q_{ij})\), then a q-ROF entropy weight model based on the entropy of q-ROFSs can be defined as follows:

$$\begin{aligned} w_j=\dfrac{1-(E_q)_j}{{\sum _{j=1}^{m}}\left[ 1-(E_q)_j\right] }. \end{aligned}$$
(8)

Such model to obtain the attribute weights is called the q-ROF-EW method.

5.1.4 S-flow and I-flow

According to the attribute weight \(w_j\), S-flow \(\Delta ^+(A_i)\) and I-flow \(\Delta ^-(A_i)\) can be defined as:

$$\begin{aligned} \Delta ^+(A_i)= & {} \displaystyle {\sum _{j=1}^{m}}w_jS_{ij}, \end{aligned}$$
(9)
$$\begin{aligned} \Delta ^-(A_i)= & {} \displaystyle {\sum _{j=1}^{m}}w_jI_{ij}. \end{aligned}$$
(10)

Now, S-flow and I-flow are respectively the exiting flows and the entering flows of PROMETHEE. As discussed in [11], if we select simple additive weighting (SAW) as the aggregation function to compute S-flow and I-flow, then the SIR method is the PROMETHEE method. Similarly, the decision maker can select other aggregation functions to obtain S-flow and I-flow according to the real situation or their experiences.

5.1.5 Superiority ranking rule and inferiority ranking rule

Superiority ranking (SR) rule can be defined as \(A_i R^+ A_k\) if and only if \(\Delta ^+(A_i) \ge \Delta ^+(A_k)\), while inferiority ranking (IR) rule \(R^-\) is defined as \(A_i R^- A_k\) if and only if \(\Delta ^-(A_i) \le \Delta ^-(A_k)\).

Obviously, \(R^+\) and \(R^-\) are two complete ranking orders. The higher \(\Delta ^+(A_i)\) the better alternative \(A_i\), and the smaller \(\Delta ^-(A_i)\) the better alternative \(A_i\).

5.1.6 q-ROF-SIR partial ranking order

Finally, we establish the q-ROF-SIR partial ranking order \(R=R^+\cap R^-=(\ge _I,\sim _I,||_I)\) as follows:

  1. (1)

    \(A_i\) outranks \(A_k\), denoted by \(A_i\ge _I A_k\), if and only if \(A_i R^+ A_k\) and \(A_i R^- A_k\);

  2. (2)

    \(A_i\) is incomparable to \(A_k\), denoted by \(A_i||_I A_k\), if and only if \(A_i R^+ A_k\) and \(A_k R^- A_i\) or \(A_k R^+ A_i\) and \(A_i R^- A_k\) .

  3. (3)

    \(A_i\) is indifferent to \(A_k\), denoted by \(A_i\sim _I A_k\), if and only if \(\Delta ^+(A_i) = \Delta ^+(A_k)\) and \(\Delta ^-(A_i) = \Delta ^-(A_k)\).

5.1.7 q-ROF-SIR total ranking order

Sometimes, we want to obtain the total relationships among alternatives in MADM problems. Firstly, we should compute the net flow (N-flow) which is the difference between S-flow and I-flow, denoted by \(\Delta ^N(A_i)\),

$$\begin{aligned} \Delta ^N(A_i)=\Delta ^+(A_i)-\Delta ^-(A_i). \end{aligned}$$
(11)

Because the bigger the \(\Delta ^N(A_i)\), the better the alternative \(A_i\), we can define the complete ranking order \((>_{II},\sim _{II})\) to receive the total relationships of alternatives as follows:

  1. (1)

    \(A_i\) outranks \(A_k\), denoted by \(A_i >_{II} A_k\), if and only if \(\Delta ^N(A_i) > \Delta ^N(A_k)\);

  2. (2)

    \(A_i\) is indifferent to \(A_k\), denoted by \(A_i \sim _{II} A_k\), if and only if \(\Delta ^N(A_i) = \Delta ^N(A_k)\).

In the end, we construct the q-ROF-SIR I method by the q-ROF-SIR partial ranking order, then the q-ROF-SIR II method by the q-ROF-SIR total ranking order to handle the MADM problems evaluated by q-ROFNs.

5.2 The procedures of the q-ROF-SIR methods

Fig. 2
figure 2

The flow chart of q-ROF-SIR methods

Full size image

For the convenience of application, we summarize the procedures of the q-ROF-SIR methods in this subsection.

Algorithm I ( for the q-ROF-SIR method I )

   Step 1 According to real problem, select the appropriate q and the improved preference intensity .

   Step 2 Calculate the \(P(Q_{ij}\ge Q_{kj})\) for each pair \((Q_{ij},Q_{kj})\) according to Definition 4.1.

   Step 3 Compute the \(PI(Q_{ij})\) by Definition 4.2.

   Step 4 Calculate the values of \(F_j(Q_{ij}, Q_{kj})\) according to formula (5).

   Step 5 Compute \(S=(S_{ij})_{n\times m}\) and \(I=(I_{ij})_{n\times m}\) according to formulas (6) and (7).

   Step 6 If \(w_j (j=1,2,\cdots , m)\) is unknown, compute \(w_j\) in the light of the q-ROF-EW method ( formula (8) ).

   Step 7 Calculate S-flow \(\Delta ^+(A_i)\) and I-flow \(\Delta ^-(A_i)\), according to formulas (9) and (10).

   Step 8 Determine SR order \(R^+\) and IR order \(R^-\).

\(A_i R^+ A_k \Leftrightarrow \Delta ^+(A_i) \ge \Delta ^+(A_k)\) and \(A_i R^- A_k\Leftrightarrow \Delta ^-(A_i) \le \Delta ^-(A_k)\).

   Step 9 Rank \(A_i\) in the light of the \((>_I, \sim _I, \mid \mid _I)\), which is the defined partial ranking order in Sect. 5.1.6.

Algorithm II ( for the q-ROF-SIR method II)

   Steps 1’–7’ is similar to Steps 1–7 of Algorithm I.

   Step 8’ Compute the N-flow \(\Delta ^N(A_i)\) according to formula (11).

   Step 9’ Rank \(A_i\) in the light of the \((>_{II}, \sim _{II})\), which is the defined total ranking order in Sect. 5.1.7.

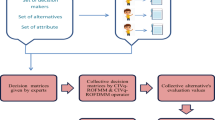
We further give the flow chart of q-ROF-SIR methods, shown in Fig. 2.

6 Illustrative example

This section utilizes the proposed q-ROF-SIR methods to solve the investment company selection problem [5]. After that, the sensitivity of the parameters q is discussed. Further, we compare the proposed methods with other aggregation methods [5,6,7, 10] and PF-SIR methods [17].

Example 6.1

[5] An investor plans to select one company from five potential companies (\(A_1,A_2,A_3,A_4,A_5\)) to invest it. The investor assesses the five companies regarding six attributes (\(C_1,C_2,C_3,C_4,C_5,C_6\)), where the technical ability is denoted by \(C_1\), the expected benefit \(C_2\), the competitive power on the market \(C_3\), the ability to bear risk \(C_4\), the management capability \(C_5\) and the innovative ability \(C_6\). The investor prefers to evaluate each alternative \(A_i\) with respect to every attribute \(C_j\) by the q-ROFNs \(Q_{ij}=<u_{ij},v_{ij}>\). The corresponding q-ROFN decision making matrix \(QR=(Q_{ij})_{5\times 6}\) is listed as follows:

$$\begin{aligned} QR= \left( \begin{matrix}<0.5,0.2> &{}<0.8,0.3> &{}<0.8,0.3> &{}<0.7,0.3> &{}<0.4,0.2> &{}<0.4,0.8> \\<0.6,0.3> &{}<0.5,0.8> &{}<0.6,0.5> &{}<0.6,0.5> &{}<0.7,0.4> &{}<0.5,0.6> \\<0.3,0.4> &{}<0.8,0.5> &{}<0.7,0.6> &{}<0.6,0.4> &{}<0.6,0.2> &{}<0.4,0.7> \\<0.7,0.4> &{}<0.5,0.6> &{}<0.7,0.4> &{}<0.5,0.5> &{}<0.7,0.6> &{}<0.6,0.5> \\<0.7,0.6> &{}<0.6,0.4> &{}<0.4,0.7> &{}<0.4,0.3> &{}<0.7,0.7> &{}<0.5,0.4> . \end{matrix}\right) \end{aligned}$$

6.1 Illustration of the q-ROF-SIR methods

The proposed q-ROF-SIR methods are applied to rank the candidate companies, which are cited from literature [5]. In this example, all attributes are the benefit attributes.

In step 1, choose the parameter q=3 for q-ROF-SIR methods, and the improved preference intensity \(\psi _j(t)\) for each attribute \(C_j\), where

$$\begin{aligned}\psi _j(t)= {\left\{ \begin{array}{ll} 0, &{}\text {if}\ \ t \le 0, \\ \dfrac{t}{0.5}, &{}\text {if}\ \ 0< t \le 0.5, \\ 1, &{}\text {if}\ \ t > 0.5. \end{array}\right. } \end{aligned}$$

In Step 2, according to Definition 4.1, compute the \(P(Q_{ij}\ge Q_{kj})\), which are presented in Table 1.

Table 1 Possibility degree under each attribute \(C_j\)
Full size table
Table 2 Results of PI under each attribute \(C_j\)
Full size table

In Step 3, according to Definition 4.2, we calculate the \(PI(Q_{ij})\), which are indicated in Table 2.

For example, in Table 2, one can compute \(PI(Q_{11})=\dfrac{1}{5\times (5-1)}[(0.5+0.4778+ 0.5434+ 0.4445+ 0.4962)\) \(+\frac{5}{2}-1]=0.198095\approx 0.198\).

In Step 4, calculate the values of \(F_j(Q_{ij}, Q_{kj})=\psi _j(t)\) according to formula (5). The results are shown as Table 3.

Table 3 Results of \(F_j(Q_{ij},Q_{kj})\) under each attribute \(C_j\)
Full size table
Table 4 Results of the attribute weights
Full size table
Table 5 Results of S-flow, I-flow and N-flow
Full size table

In Step 5, compute S-matrix and I-matrix according to formulas (6) and (7). The results are shown as follows:

$$\begin{aligned} S= & {} \left( \begin{matrix} 0.024 &{} 0.479&{}0.417&{}0.177&{}0.023&{}0 \\ 0.060 &{} 0&{}0.082&{}0.022&{}0.163&{}0.120 \\ 0 &{} 0.409&{}0.094&{}0.055&{}0.092&{}0.044 \\ 0.134 &{} 0.096&{}0.198&{}0&{}0.048&{}0.238 \\ 0.025 &{} 0.200&{}0&{}0.008&{}0&{}0.195 \end{matrix}\right) \\ I= & {} \left( \begin{matrix} 0.043 &{} 0&{}0&{}0.177&{}0.084&{}0.351 \\ 0.018 &{} 0.697&{}0.142&{}0.022&{}0&{}0.061 \\ 0.139 &{} 0.017&{}0.124&{}0.055&{}0.018&{}0.175 \\ 0 &{} 0.313&{}0.055&{}0&{}0.047&{}0 \\ 0.042 &{} 0.157&{}0.471&{}0.008&{}0.178&{}0.011 \end{matrix}\right) \end{aligned}$$

In Step 6, because the attribute weights are unknown, we use formula (8) to calculate the attribute weights. The results are indicated in Table 4.

In Step 7, calculate S-flow and I-flow according to formulas (9) and (10). The results are indicated in the second block of Table 5.

In Step 8, combine Table 5 with SR rule and IR rule, determine \(R^+\) and \(R^-\) as follows:

\(A_1\ \ R^+\ \ A_3\ \ R^+\ \ A_4\ \ R^+\ \ A_5\ \ R^+\ \ A_2\) and \(A_1\ \ R^-\ \ A_3\ \ R^-\ \ A_4\ \ R^-\ \ A_5\ \ R^-\ \ A_2\).

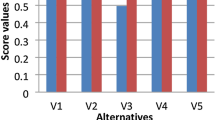
In Step 9, according to the defined partial ranking order in Sect. 5.1.6, we obtain the final results as \(A_1>_I A_3>_IA_4>_I A_5>_IA_2\), shown in Fig.3.

Fig. 3
figure 3

Partial ranking by q-ROF-SIR I

Full size image
Fig. 4
figure 4

Total ranking by q-ROF-SIR II

Full size image

Subsequently, we use the q-ROF-SIR II method to solve this problem.

Steps 1’–6’ are similar to Steps 1–6.

In Step 7’, we can compute N-flow \(\Delta ^N(A_i)\) by formula (11), which are presented in the third block of Table 5.

In Step 8’, rank the alternatives \(A_i\) in the light of \((>_{II}, \sim _{II})\), which is the defined total ranking order in Sect. 5.1.7. The final ranking order of alternatives is \(A_1>_{II}A_3>_{II}A_4>_{II} A_5 >_{II} A_2\), which is illustrated in Fig. 4.

6.2 The influence of parameter q on the final ranking order

Table 6 Ranking values of different parameter q by the q-ROF-SIR methods
Full size table
Fig. 5
figure 5

Ranking values of different parameter q by the q-ROF-SIR method II

Full size image

Furthermore, the influence of different parameter q on the final results are discussed by using the q-ROF-SIR methods. The results with different parameter q are shown in Table 6 and Fig. 5.

From Table 6, we find that when parameter \(q=2,3,4,5\), the ranking order are all the same if we use the q-ROF-SIR II method. It can find that when \(q=2\), alternative \(A_3\) is incomparable to alternative \(A_4\) in accordance with the q-ROF-SIR I method, while when \(q=4\) and \(q=5\), alternative \(A_3\) is incomparable to alternative \(A_1\) in accordance with the q-ROF-SIR I method.

Fig. 5 only shows that the ranking results of alternatives are solved by the proposed q-ROF-SIR II method with different value q. From Fig. 5, we find that when parameter q takes different value, the ranking results of alternatives are the same. However, the bigger the parameter q, the smaller the difference of the net flows of alternatives. In general, the decision makers can select the suitable parameter q according to their preferences or experiences.

6.3 Comparative analysis

Table 7 Ranking results by different methods
Full size table

It has validated the practical applicability of the q-ROF-SIR methods through solving the investment company selection problem. We still use other seven methods based on the q-ROFWA [5], the q-ROFWG [5], the q-ROFPWA [6], the q-ROFWBM [7], q-ROFWGBM [7], q-ROFWGHM [10], q-ROFGWHM [10] and PF-SIR [17] to solve the same problem. The results are provided in Table 7. From Table 7, it shows that the ranking order of alternatives are all the same except the results solved by the q-ROFWG [5] and the q-ROFWGBM [7]. Furthermore, \(A_1\) is the best alternative solved by all the methods.

The mentioned seven methods [5,6,7, 10] are completely dependent on the aggregation operators. These methods usually require the independence between attributes. While the proposed q-ROF-SIR methods belong to the outranking methods, which don’t care about the dependence or independence between the attributes. In Example 6.1, we find that it can not assure that the different attributes \(C_j\) \((j=1,\ldots ,6)\) are independent from each other. Therefore, it produces more reasonable ranking result of alternatives by the q-ROF-SIR methods than the other methods.

On the other hand, from Table 7, it finds that the same ranking order of alternatives is solved by the PF-SIR method and the q-ROF-SIR method. However, the preference intensity of the PF-SIR methods [17] is based on the distance of PFNs, and the preference intensity of the proposed methods is based on the PD of q-ROFNs. When compare two q-ROFNs, it is more suitable to use the possibility degree than the distance of q-ROFNs. Besides, the PF-SIR methods can only deal with PFNs while the proposed methods can handle q-ROFNs including PFNs. Therefore, from above comparison analysis, it can be seen that the proposed q-ROF-SIR methods are reasonable and flexible to solve MADM problems evaluated by q-ROFNs.

7 Conclusions

With the parameter q increasing, q-ROFSs have greater capability to express uncertain information than IFSs and PFSs. For the MADM problems with q-ROFSs, the q-ROF-SIR methods are given. Firstly, the entropy of q-ROFSs was introduced to describe the uncertainty of q-ROFSs. Then we developed the PD of q-ROFNs to reasonably measure the possibility degree of one q-ROFN no less than another. Next we introduced the PI of q-ROFNs to improve the preference intensity. Subsequently, considering the weight vector of attributes, S-flow and I-flow were obtained to rank alternatives. If the attribute weights were not given, the q-ROF-EW method was applied to determine the weights of attribute. After that, the scores of S-flow and I-flow were employed to determine the partial ranking order of alternatives in the q-ROF-SIR I method. Further, the scores of N-flow are computed to acquire the total ranking order of alternatives in the q-ROF-SIR II method. Finally, a MADM example was considered to validate the practical applications of the proposed q-ROF-SIR methods.

Moreover, we analysed the sensitivity of parameter q in the proposed q-ROF-SIR methods. Further, we compared the proposed methods with other aggregation methods as well as PF-SIR methods. The final results show that the q-ROF-SIR methods have two main characteristics. Firstly, it is reasonable to use the PD of q-ROFNs to compare two q-ROFNs. Secondly, the proposed methods are more reliable and powerful than the other mentioned methods.

In the future, besides SAW, we will develop other aggregation functions to compute S-flow and I-flow in the q-ROF-SIR methods. Furthermore, we will apply the q-ROF-SIR methods to handle the MADM problems in many other fields under uncertain environment, such as risk analysis, financial market, contingency management, et al.