1 Introduction

Grey relational analysis (GRA) is an important part of grey system theory, which is used to conduct relational analysis of uncertainty of the system. There are many applications of this method in different multi-attribute decision making (MADM) problems (Zhang et al. 2005; Wei 2011; Wei et al. 2011). However, in practice, decision makers face difficulties to collect accurate information of preference values of alternatives in MADM due to imprecise and incomplete data (Xu 2015).

During the past several years, fuzzy sets (Zadeh 1965), intuitionistic fuzzy sets (Atanasso 1986), and neutrosophic sets (Smarandache 1999) have gained much attention from the researchers to deal with uncertain information in decision making problems. Fuzzy sets is used in various optimization techniques (Chen and Wang 1995; Chen and Tanuwijaya 2011; Chen and Chang 2011; Cheng et al. 2016; Lee and Chen 2008; Chen and Huang 2003. Intuitionistic fuzzy set is useful to handle various MCDM problems (Chen and Chang 2015; Chen et al. 2016a, b, Liu and Chen 2018a; Liu et al. 2017). Recently, MADM method is being developed under hesitant fuzzy sets and type-2 fuzzy sets (Mishra et al. 2018; Qin 2017). GRA method is one of the accepted MADM methods among TOPSIS (Hwang and Yoon 1981), VIKOR (Opricovic and Tzeng 2004), PROMETHEE (Brans et al. 1986), AHP (Wind and Saaty 1980), etc. Researchers have extended the GRA method for MADM problem in different environments. Wei (2010) introduced GRA method for intuitionistic fuzzy MADM problem with incomplete weight information. Zhang and Liu (2011) proposed GRA method based on intuitionistic fuzzy multi-criteria group decision making problem (MCGDM). Pramanik and Mukhopadhyaya (2011) employed GRA method for intuitionistic fuzzy MCGDM in teacher selection problem. Dey et al. (2015) applied GRA method for intuitionistic fuzzy MCGDM for weaver selection in Khadi institution.

Neutrosophic set, pioneered by Smarandache (1999), is an extension of fuzzy set and intuitionistic fuzzy set. Neutrosophic set can be used in various branches of Mathematics (Singh 2019; Dey et al. 2019). It is useful for solving multi-criteria decision making problems as indeterminant and incomplete information can be treated well by this set. Single-valued neutrosophic set (Haibin et al. 2010), a simplified version of neutrosophic set, has been successfully applied in MADM or multi-attribute group decision making problems (Sahin and Liu 2016; Ye 2013; Kahraman and Otay 2019).

Biswas et al. (2014) proposed GRA method for MADM under single-valued neutrosophic environment using entropy method. Mondal and Pramanik (2015a) developed a neutrosophic MADM model for clay-brick selection in construction field and solved the problem with GRA method. Pramanik and Mondal (2015) extended GRA method for MADM under interval neutrosophic environment. Biswas et al. (2016a, b) applied GRA method for MADM with single-valued neutrosophic hesitant fuzzy set. Mondal and Pramanik (2015b) proposed a GRA method for rough neutrosophic MADM.

Single-valued trapezoidal neutrosophic number (SVTrNN) (Subas 2015; Ye 2017) is an extension of trapezoidal fuzzy number. It is presented by a trapezoidal number which has three independent membership functions—the truth membership function, the indeterminate membership function, and the falsity membership function. This number can present incomplete or indeterminate information effectively with its three membership degrees. Therefore, it has an advantage over the trapezoidal fuzzy number and the trapezoidal intuitionistic fuzzy number. Deli and Subas (2017) developed a ranking method for single-valued neutrosophic number and employed the method for solving MADM problem. Biswas et al. (2016a, b) proposed GRA method for SVTrNN based MADM with value and ambiguity-based ranking strategy. Biswas et al. (2018) developed TOPSIS strategy for SVTrNN based MADM with unknown weight information. However, the GRA method has not been studied yet to deal with MADM problems with partially known or completely unknown weight information in the framework of SVTrNN, which can although play an effective role to deal with uncertain and indeterminate information in MADM problem. In view of the above facts, the primary objectives of this study are as follows:

  • To study MADM problem, where the rating values of the attributes are SVTrNNs and weight information is partially known or completely unknown.

  • To define a new distance measure of SVTrNN and study some of its properties.

  • To develop optimization models to determine the weights of attributes.

  • To extend GRA method for solving SVTrNN based MADM problem using a new distance measure.

  • To validate the proposed approach with a numerical example.

  • To compare the proposed approach with some existing methods including TOPSIS.

The structure of the paper is as follows: In Sect. 2, we present some preliminaries of neutrosophic set, trapezoidal fuzzy number, and single-valued trapezoidal neutrosophic number. In this section, we also define a new distance measure. In Sect. 3, we propose GRA method for SVTrNN based MADM, where the weight information of attributes is partially known or completely unknown. Section 4 deals with a numerical example to demonstrate the developed model. Finally, in Sect. 5, we conclude the paper with some remarks.

2 Preliminaries

Smarandache (1999) introduced the concept of neutrosophic set. A neutrosophic set A is a set in a universal set X whose characteristic function is expressed by truth-membership function \(T_A(x)\), indeterminacy function \(I_A(x)\), and falsity membership function \(F_A(x)\). These functions are subsets of \(]^- 0,1^+[\), i.e., \(T_A(x):X\rightarrow ]^- 0,1^+[\), \(I_A(x):X\rightarrow ]^-0,1^+[\), and \(F_A(x):X\rightarrow ]^-0,1^+[\)   so that \(^-0\le \sup ~T_A(x)+\sup ~I_A(x)+\sup ~F_A(X)\le 3^+\).

Definition 1

(Dubois and Prade 1983; Heilpern 1992) A generalized trapezoidal fuzzy number is an extension of trapezoidal fuzzy number which is denoted by \(A=(a,b,c,d;w)\) and subset real number \({\mathbb {R}}\) with membership function \(\mu _A\) given by

$$\begin{aligned} \mu _A(x)= \left\{ \begin{array}{lcl} \dfrac{(x-a)w}{b-a} , &{}\quad a \le x< b\\ w, &{}\quad b \le x \le c\\ \dfrac{(d-x)w}{d-c}, &{}\quad c < x \le d\\ 0, &{}\quad \mathrm{otherwise}, \end{array} \right. \end{aligned}$$

where \(a,b,c,d \in {\mathbb {R}}\) and w is called membership degree.

Definition 2

(Subas 2015; Ye 2017) A single-valued trapezoidal neutrosophic number \(\alpha\) is a generalization of trapezoidal fuzzy number and its membership functions are given by

$$\begin{aligned} T_\alpha (x)= & {} \left\{ \begin{array}{lcl} \dfrac{(x-a)t_\alpha }{b-a} , &{}\quad a \le x< b\\ t_\alpha , &{}\quad b \le x \le c\\ \dfrac{(d-x)t_\alpha }{d-c}, &{}\quad c< x \le d\\ 0, &{}\quad \mathrm{otherwise}. \end{array} \right. \\ I_\alpha (x)= & {} \left\{ \begin{array}{lcl} \dfrac{b-x+(x-a)i_\alpha }{b-a} , &{}\quad a \le x< b\\ i_\alpha , &{}\quad b \le x \le c\\ \dfrac{x-c+(d-x)i_\alpha }{d-c}, &{}\quad c< x \le d\\ 0, &{}\quad \mathrm{otherwise}. \end{array} \right. \\ F_\alpha (x)= & {} \left\{ \begin{array}{lcl} \dfrac{b-x+(x-a)f_\alpha }{b-a} , &{}\quad a \le x< b\\ f_\alpha , &{}\quad b \le x \le c\\ \dfrac{x-c+(d-x)f_\alpha }{d-c}, &{}\quad c < x \le d\\ 0, &{}\quad \mathrm{otherwise}, \end{array} \right. \end{aligned}$$

where \(T_\alpha\), \(I_\alpha\), and \(F_\alpha\) are truth membership function, indeterminacy membership function, and falsity membership function, respectively, and they lie between 0 and 1 and their sum lies between 0 and 3 where a, b, c and d are real numbers. Therefore, \(\alpha = ([a,b,c,d];t_\alpha ,i_\alpha ,f_\alpha )\) is called a single-valued trapezoidal neutrosophic number (SVTrNN).

Definition 3

Let \({{\tilde{\alpha }}} = ([p_1, q_1, r_1, s_1]; t_1,i_1,f_1)\) and \({{\tilde{\beta }}} =([p_2, q_2, r_2, s_2];t_2,i_2,f_2)\) be two SVTrNNs. Then we define the distance measure between these two numbers as

$$\begin{aligned} d({{\tilde{\alpha }}}, {{\tilde{\beta }}})&=\dfrac{1}{3} \left( \Big |\Big (1-\frac{p_1+q_1+r_1+d_1}{4}\Big )t_1 \quad-\Big (1-\frac{p_2+q_2+r_2+s_2}{4}\Big )t_2\Big | \right. \nonumber \\&\quad +\Big |\Big (1-\frac{p_2+q_2+r_2+s_2}{4}\Big )i_2 \quad-\Big (1-\frac{p_1+q_1+r_1+s_1}{4}\Big )i_1\Big |\nonumber \\&\quad \left. +\Big |\Big (1-\frac{p_2+q_2+r_2+s_2}{4}\Big )f_2 \quad-\Big (1-\frac{p_1+q_1+r_1+s_1}{4}\Big )f_1\Big | \right) \end{aligned}$$
(1)

A real-valued function \(d:X\times X\longrightarrow [0,1]\) is said to be distance function if it satisfies the following properties:

  1. 1.

    \(d({{\tilde{\alpha }}},{{\tilde{\beta }}}) \ge 0\)

  2. 2.

    \(d({{\tilde{\alpha }}},{{\tilde{\beta }}})=d({{\tilde{\beta }}},{{\tilde{\alpha }}})\)

  3. 3.

    \(d({{\tilde{\alpha }}},{{\tilde{\gamma }}})\le d({{\tilde{\alpha }}},{{\tilde{\beta }}})+d({{\tilde{\beta }}},{{\tilde{\gamma }}})\)   \(\forall ~{{\tilde{\alpha }}},{{\tilde{\beta }}},{{\tilde{\gamma }}}\ \in X\)

Proof

  1. 1.

    The distance measure \(d({{\tilde{\alpha }}},{{\tilde{\beta }}})\) is non-negative and \(d({{\tilde{\alpha }}},{{\tilde{\beta }}})=0\) when \({{\tilde{\alpha }}}={{\tilde{\beta }}}\), i.e., \(p_1 = p_2, q_1 = q_2, r_1 = r_2, s_1 = s_2, t_1 = t_2, i_1 = i_2\)   and   \(f_1 = f_2\). Therefore, \(d({{\tilde{\alpha }}},{{\tilde{\beta }}})\ge 0.\)

  2. 2.

    It is obvious that \(d({{\tilde{\alpha }}},{{\tilde{\beta }}})=d({{\tilde{\beta }}},{{\tilde{\alpha }}})\).

  3. 3.
    $$\begin{aligned}&d({{\tilde{\alpha }}},{{\tilde{\gamma }}})\\&\quad =\dfrac{1}{3} \left( \Big |\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )t_1 -\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )t_3\Big |\right. \\&\qquad ~~ +\Big |\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )i_3 -\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )i_1\Big |\\&\qquad \left. ~~+\Big |\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )f_3 -\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )f_1\Big | \right) \\&\quad = \dfrac{1}{3} \left( \Big |\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )t_1-\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )t_2\right. \\&\qquad ~~+\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )t_2-\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )t_3\big |\\&\qquad ~~+\Big |\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )i_3-\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )i_2\\&\qquad ~~+\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )i_2 -\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )i_1\Big |\\&\qquad ~~+\Big |\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )f_3-\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )f_2\\&\qquad \left. ~~+\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )f_2 -\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )f_1\Big | \right) \\&\le \dfrac{1}{3} \left( \Big |\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )t_1 -\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )t_2\Big |\right. \\&\qquad ~~+\Big |\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )i_2 -\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )i_1\Big |\\&\qquad \left. ~~+\Big |\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )f_2 -\big (1-\frac{p_1+q_1+r_1+s_1}{4}\big )f_1\Big | \right) \\&\qquad ~~+\dfrac{1}{3} \left( \Big |\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )t_2 -\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )t_3\Big |\right. \\&\qquad ~~+\Big |\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )i_3 -\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )i_2\Big |\\&\qquad \left. ~~+\Big |\big (1-\frac{p_3+q_3+r_3+s_3}{4}\big )f_3 -\big (1-\frac{p_2+q_2+r_2+s_2}{4}\big )f_2\Big | \right) \\&\quad = d({{\tilde{\alpha }}},{{\tilde{\beta }}})+d({{\tilde{\beta }}},{{\tilde{\gamma }}}) \end{aligned}$$

    Therefore, \(d({{\tilde{\alpha }}},{{\tilde{\gamma }}})\le d({{\tilde{\alpha }}},{{\tilde{\beta }}})+d({{\tilde{\beta }}},{{\tilde{\gamma }}})\)   \(\forall ~{{\tilde{\alpha }}},{{\tilde{\beta }}},{{\tilde{\gamma }}}\ \in X.\)

\(\square\)

Fig. 1
figure 1

A schematic diagram of the GRA Method

Full size image

3 GRA method

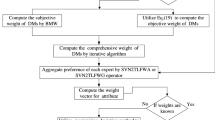
Grey relational analysis (GRA) is an important section of grey system theory which was proposed by Deng (1989). GRA is mainly used to conduct relational analysis of uncertainty of a system having incomplete information. This method is applicable to discrete sequence for co-relational analysis of such sequence with processing uncertainty, multi-variate input, and discrete data. GRA method has been successfully applied for multi-criteria decision making problems. The method can be described as given below (see also Fig. 1):

  • Grey relational generating

    Translate all the alternatives to comparability sequence. This process is called grey relational generating.

  • Defined ideal target sequence

    Define the ideal target of the sequence of each alternative.

  • Calculate Grey relational coefficient

    Calculate the grey relational coefficient between ideal target sequence and comparability sequence.

  • Determine Grey relational degree

    If an alternative achieves the maximum grey relational degree between the ideal target sequence and itself, then that alternative is the optimal choice of alternative.

3.1 GRA method for multi-attribute decision making based on SVTrNN with incomplete weight information

Let \(A=\{A_1,A_2, \ldots A_m\}\) be a finite set of alternatives, \(C=\{C_1,C_2, \ldots ,C_n\}\) be the set of attributes, and the rating values of attributes be represented by SVTrNNs. Let \(x_{ij}=([a_{ij},b_{ij},c_{ij},d_{ij}];t_{ij},i_{ij},f_{ij})\) be the rating values of \(A_i\), the i-th alternative over the attribute \(C_j\). Then the decision matrix is given by

(2)

Let \(W=\{w_1,w_2,\ldots ,w_n\}\) be the weight vector for the attributes and \(\Delta\) be the set of known weight information which can be constructed in the form as given by Park et al. (1997, 2011) and Park (2004):

  1. 1.

    When weak ranking: \(\{w_i\ge w_j\}\), \(i\ne j\);

  2. 2.

    When strict ranking: \(\{w_i- w_j\ge \epsilon _i~(>0)\}\), \(i\ne j\);

  3. 3.

    The ranking of difference: \(\{w_i- w_j\ge w_k- w_p\}\), \(i\ne j\ne k\ne p\);

  4. 4.

    The ranking with multiples: \(\{w_i\ge \alpha _i w_j\}\), \(0\le \alpha _i\le 1, i\ne j\);

  5. 5.

    An interval form: \(\{\beta _i\le w_i\le \beta _i+\epsilon _i(>0)\}\), \(0\le \beta _i\le \beta _i+\epsilon _i\le 1\).

We now propose the GRA method for MADM based on SVTrNN with partially known and completely unknown weight information. The steps are as follows:

Step 1: Normalize the decision matrix

This step transforms dimensional attributes into non-dimensional attributes which permit comparison among criteria because different criteria are usually measured in different units. In general, there are two types of attribute. One is benefit type attribute and another one is cost type attribute. Let \(X=(x_{ij})_{m\times n} ~\) be a decision matrix, where SVTrNN \(x_{ij}=\left( \left[ a_{ij},b_{ij},c_{ij},d_{ij}\right] ;t_{ij},i_{ij},f_{ij}\right)\) is the rating value of the alternative \(A_i\) with respect to the attribute \(C_j\).

In order to eliminate the influence of attribute type, we consider the following technique and obtain the standardize matrix \(R =(r_{ij})_{m\times n}\), where \(r_{ij}=\left( \left[ r^1_{ij},r^2_{ij},r^3_{ij},r^4_{ij}\right] ;t_{ij},i_{ij},f_{ij} \right)\) is SVTrNN. Then we have

$$\begin{aligned} r_{ij}&= \left( \left[ \dfrac{a_{ij}}{u^+_j},\dfrac{b_{ij}}{u^+_j},\dfrac{c_{ij}}{u^+_j},\dfrac{d_{ij}}{u^+_j} \right] ;t_{ij},i_{ij},f_{ij} \right) , \quad \text {for \, benefit \; type \; attribute}. \end{aligned}$$
(3)
$$\begin{aligned} r_{ij}&= \left( \left[ \dfrac{u^-_j}{d_{ij}},\dfrac{u^-_j}{c_{ij}},\dfrac{u^-_j}{b_{ij}},\dfrac{u^-_j}{a_{ij}}\right] ; t_{ij},i_{ij},f_{ij} \right) , \quad \text {for \; cost \; type \; attribute}. \end{aligned}$$
(4)

where \(u^+_j= \max \{d_{ij}, ~\text {for}\; i=1,2,\ldots ,m \}\) and \(u^-_j= \min \{a_{ij} ,~\text {for}\; i=1,2,\ldots ,m \}\) for \(j=1,2,...,n\).

Step 2: Calculate positive and negative ideal solutions

The positive ideal solution and the negative ideal solution of SVTrNN are \(P^+\) and \(N^-\), respectively, for the matrix \(R=(r_{ij})_{m\times n}\), and those are given below:

  • For benefit type attribute,

    \(P^+=\left\{ P^+_1,P^+_2, \ldots ,P^+_n\right\}\)

    where \(P^+_j=\left( \left[ \underset{i}{\max }\left( r^1_{ij}\right) ,\underset{i}{\max }\left( r^2_{ij}\right) ,\underset{i}{\max }\left( r^3_{ij}\right) , \underset{i}{\max }\left( r^4_{ij}\right) \right] ; \underset{i}{\max }(t_{ij}),\underset{i}{\min }(i_{ij}), \underset{i}{\min }(f_{ij})\right)\)

    and \(N^-=\left\{ N^-_1,N^-_2, \ldots ,N^-_n\right\}\)

    where \(N^-_j=\left( \left[ \underset{i}{\min }\left( r^1_{ij}\right) ,\underset{i}{\min }\left( r^2_{ij}\right) ,\underset{i}{\min }\left( r^3_{ij}\right) , \underset{i}{\min }\left( r^4_{ij}\right) \right] ; \underset{i}{\min }(t_{ij}),\underset{i}{\max }(i_{ij}), \underset{i}{\max }(f_{ij})\right)\)

  • For cost type attribute,

    \(P^+=\left\{ P^+_1,P^+_2, \ldots ,P^+_n\right\}\)

    where \(P^+_j=\left( \left[ \underset{i}{\min }\left( r^1_{ij}\right) ,\underset{i}{\min }\left( r^2_{ij}\right) ,\underset{i}{\min }\left( r^3_{ij}\right) , \underset{i}{\min }\left( r^4_{ij}\right) \right] ; \underset{i}{\min }(t_{ij}),\underset{i}{\max }(i_{ij}), \underset{i}{\max }(f_{ij})\right)\)

    and \(N^-=\left\{ N^-_1,N^-_2, \ldots ,N^-_n\right\}\)

    where \(N^-_j=\left( \left[ \underset{i}{\max }\left( r^2_{ij}\right) ,\underset{i}{\max }\left( r^2_{ij}\right) ,\underset{i}{\max }\left( r^3_{ij}\right) , \underset{i}{\max }\left( r^4_{ij}\right) \right] ; \underset{i}{\max }(t_{ij}),\underset{i}{\min }(i_{ij}), \underset{i}{\min }(f_{ij})\right)\)

Step 3: Calculate the grey relational coefficient

In this step, we determine the grey relational coefficient of each alternative from positive ideal solution \(P^+\) and negative ideal solution \(N^-\), which can be obtained from the following:

$$\begin{aligned} \xi ^+_{ij}&=\dfrac{\underset{1\le i\le m}{\min }~\underset{1\le j\le n}{\min }d\left( r_{ij},P^+_j\right) +\rho \underset{1\le i\le m}{\max }~\underset{1\le j\le n}{\max }d\left( r_{ij},P^+_j\right) }{d\left( r_{ij},P^+_j\right) +\rho \underset{1\le i\le m}{\max }~\underset{1\le j\le n}{\max }d\left( r_{ij},P^+_j\right) } \end{aligned}$$
(5)
$$\begin{aligned} \xi ^-_{ij}&=\dfrac{\underset{1\le i\le m}{\min }~\underset{1\le j\le n}{\min }d\left( r_{ij},N^-_j\right) +\rho \underset{1\le i\le m}{\max }~\underset{1\le j\le n}{\max }d\left( r_{ij},N^-_j\right) }{d\left( r_{ij},N^-_j\right) +\rho \underset{1\le i\le m}{\max }~\underset{1\le j\le n}{\max }d\left( r_{ij},N^-_j\right) } \end{aligned}$$
(6)

\(\rho\) is the identification coefficient and we consider \(\rho = 0.5\) in this study.

Step 4: Calculate the attribute weight

When the attribute weights are known, calculate the largest degree of grey relation from positive ideal solution and the smallest degree from negative ideal solution and determine the best alternative in GRA method. We develop the following models when the weight information is partially known or completely unknown:

1. Weight information is partially known

If the weight information is partially known then we develop the following optimization model:

$${\text{Model-1}}\left\{ {\begin{array}{*{20}l} {\min \quad \xi _{i}^{ - } = \sum\limits_{{j = 1}}^{n} {w_{j} } \xi _{{ij}}^{ - } } \hfill \\ {\max \quad \xi _{i}^{ + } = \sum\limits_{{j = 1}}^{n} {w_{j} } \xi _{{ij}}^{ + } } \hfill \\ {{\text{subject}}\;{\text{to}}\;w \in \Delta ,\quad \sum\limits_{{i = 1}}^{n} {w_{j} } = 1,w_{j} \ge 0,} \hfill \\ {{\text{ for}}{\text{ }}\quad j = 1,2, \ldots ,n.} \hfill \\ \end{array} } \right.$$

Since every alternative is important, no preference should be given to any alternative. We can aggregate the above multi-objective optimization model into the following single-objective model with equal weights:

$${\text{Model-2}}\left\{ {\begin{array}{*{20}l} {\min \quad \xi = \sum\limits_{{j = 1}}^{n} {\sum\limits_{{i = 1}}^{m} ( } \xi _{{ij}}^{ - } - \xi _{{ij}}^{ + } )w_{j} } \hfill \\ {{\text{subject}}\;{\text{to}}\;w \in \Delta ,\quad \sum\limits_{{j = 1}}^{n} {w_{j} } = 1,w_{j} \ge 0,} \hfill \\ {{\text{ for }}\quad j = 1,2, \ldots ,n.} \hfill \\ \end{array} } \right.$$

We find the optimal solution of Model-2 and use it as weight vector.

2. Weight information is completely unknown

In this case, we have the following single-objective model:

$${\text{Model-3}}\left\{ {\begin{array}{*{20}l} {\min \quad \xi = \sum\limits_{{j = 1}}^{n} {\sum\limits_{{i = 1}}^{m} ( } \xi _{{ij}}^{ - } - \xi _{{ij}}^{ + } )w_{j} } \hfill \\ {{\text{subject}}\;{\text{to}}\quad w \in \Delta ,~~\sum\limits_{{j = 1}}^{n} {w_{j}^{2} } = 1,w_{j} \ge 0,} \hfill \\ {{\text{ for}}\quad j = 1,2, \ldots ,n.} \hfill \\ \end{array} } \right.$$

To solve this model, we construct the Lagrangian function

$$\begin{aligned} L(w,\theta )=\sum \limits _{i=1}^{m} \sum \limits _{j=1}^{n} \left( \xi ^-_{ij}-\xi ^+_{ij}\right) +\frac{\theta }{2}\left( \sum \limits _{j=1}^{n}w^2_j-1\right) , \end{aligned}$$
(7)

where \(~\theta \in {\mathbb {R}} ~\) is the Lagrange multiplier. The first-order conditions for optimality of L give

$$\begin{aligned} \dfrac{\partial L}{\partial w_i}=\sum \limits _{i=1}^{m} \left( \xi ^-_{ij}-\xi ^+_{ij}\right) +\theta w_j=0 \end{aligned}$$
(8)
$$\begin{aligned} \dfrac{\partial L}{\partial \theta }= \sum \limits _{j=1}^{n}w^2_j-1=0 \end{aligned}$$
(9)

From Eq. (8), we get the weight vector of the form

$$\begin{aligned} w_j=\dfrac{-\sum \nolimits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})}{\theta },\quad j=1,2, \ldots n. \end{aligned}$$
(10)

Putting this value in Eq. (9), we get

$$\begin{aligned} \theta ^2= & {} \sum \limits _{j=1}^{m}\sum \limits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})^2 \end{aligned}$$
(11)
$$\begin{aligned} \mathrm{i.e.},\quad \theta= & {} -\sqrt{\sum \limits _{j=1}^{n}\sum \limits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})^2}\quad \text {for}\; \theta < 0 \end{aligned}$$
(12)
$$\begin{aligned} \theta= & {} \sqrt{\sum \limits _{j=1}^{n}\sum \limits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})^2}\quad \text {for}\; \theta > 0 \end{aligned}$$
(13)

From Eqs. (10), (12) and (13), we get the weight vector of the form

$$\begin{aligned} w_j= & {} \dfrac{\sum \nolimits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})}{\sqrt{\sum \nolimits _{j=1}^{n}\sum \nolimits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})^2}}\quad {\text {for}}\; w_j > 0 \end{aligned}$$
(14)
$$\begin{aligned} w_j= & {} -\dfrac{\sum \nolimits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})}{\sqrt{\sum \nolimits _{j=1}^{n}\sum \nolimits _{i=1}^{m} (\xi ^-_{ij}-\xi ^+_{ij})^2}}\quad {\text {for}}\; w_j < 0 \end{aligned}$$
(15)

Therefore, the normalized weight vector is given by

$$\begin{aligned} {{\bar{w}}}_j=\dfrac{w_j}{\sum \nolimits _{j=1}^n w_j} \end{aligned}$$
(16)

Step 5: Determine the degree of grey relational coefficient

The degree of grey relational coefficient of each alternative \(A_i\) from the positive ideal solution and that from the negative ideal solution with respect to attribute weight can be obtained, respectively, from the following:

$$\begin{aligned} \xi ^+_i= & {} \sum \limits _{j=1}^n w_j\xi ^+_{ij},\quad i=1,2, \ldots m. \end{aligned}$$
(17)
$$\begin{aligned} \xi ^-_i= & {} \sum \limits _{j=1}^n w_j\xi ^-_{ij},\quad i=1,2, \ldots m. \end{aligned}$$
(18)

Step 6: Compute the relative closeness co-efficient

In this step, we determine the relative closeness co-efficient \(\xi _i\) of each alternative \(A_i\) with respect to the ideal alternative \(A^+\) as

$$\begin{aligned} \xi _i=\dfrac{\xi ^+_i}{\xi ^+_i + \xi ^-_i} ,\quad \hbox {for}~~i=1,2,\ldots ,m. \end{aligned}$$
(19)

Step 7: Rank the alternatives

Rank each alternative \(A_i\) with respect to \(\xi _i\). The greatest value of \(\xi _i (i=1,2,\ldots m)\) of alternative \(A_i (i=1,2,\ldots m)\) is the best alternative.

4 Numerical example

To demonstrate the proposed GRA method, we consider the following problem:

In supply chain management, supplier selection is a major issue. Supplier evaluation is the process to access new or existing suppliers based on their price, production, delivery, quality of service, etc. Evaluation criteria of supplier are uncertain. Purchasing department of an overseas multi-national company intends to pick a suitable supplier to get better development.

To formulate the problem, suppose that there are four suppliers \(\{A _1,A_2,A_3,A_4\}\) and each supplier has four attributes such as price, quality, delivery, and e-commerce capability. We consider \(C_1,C_2,C_3,C_4\) for price, quality, delivery, and e-commerce capability, respectively. The rating values of the attributes are SVTrNN numbers. Then we get the following decision matrix:

figure a

We now determine the best alternative with the help of the proposed GRA method. For this, we adopt the following steps:

Step 1: Normalize the decision matrix.

In the decision matrix, the first column \(C_{1}\) represents the cost attribute, and second (\(C_{2}\)), third (\(C_{3}\)) and fourth (\(C_{4}\)) columns represent benefit type of attribute. Then, from Eqs. (3) and (4), we get the standardized decision matrix as given below.

figure b

Step 2: Calculate the positive and negative ideal solutions.

In the decision matrix, the first column \(C_{1}\) represents the cost attribute, and other columns represent benefit attribute. Therefore, the positive ideal solution \(P^+=\{P^+_1,P^+_2,P^+_3,P^+_4\}\) is given by

$$\begin{aligned} \left( \begin{array}{c} \Big ([0.30,0.33,0.37,0.42];0.3,0.7,0.8\Big ) \\ \Big ([0.66,0.77,0.88,1.00];0.4,0.4,0.5\Big ) \\ \Big ([0.66,0.77,0.88,1.00];0.4,0.2,0.3\Big ) \\ \Big ([0.70,0.80,0.90,1.00];0.4,0.4,0.5\Big ) \\ \end{array} \right) \end{aligned}$$

and the negative ideal solution \(N^-=\{N^-_1,N^-_2,N^-_3,N^-_4\}\) is given by

$$\begin{aligned} \left( \begin{array}{c} \Big ([0.50,0.60,0.75,1.00];0.6,0.4,0.0.5\Big ) \\ \Big ([0.11,0.22,0.33,0.44];0.3,0.5,0.6\Big ) \\ \Big ([0.33,0.44,0.55,0.66];0.2,0.6,0.7\Big ) \\ \Big ([0.40,0.50,0.60,0.70];0.3,0.5,0.6\Big ) \\ \end{array} \right) \end{aligned}$$

Step 3: Calculate the grey relational coefficient.

Grey relational coefficients of alternatives from ideal solutions (positive, negative) are given by

$$\begin{aligned} \xi ^+= & {} (\xi ^+_{ij})_{4\times 4}=\left( \begin{array}{cccc} 0.562 &{} \quad 1.00 &{} \quad 0.80 &{} \quad 0.593 \\ 0.479 &{} \quad 0.567 &{} \quad 0.899 &{} \quad 1.00 \\ 0.428 &{} \quad 0.355 &{} \quad 0.629 &{} \quad 0.753 \\ 0.629 &{} \quad 0.478 &{} \quad 0.389 &{} \quad 0.701 \\ \end{array} \right) \\ \xi ^-= & {} (\xi ^-_{ij})_{4\times 4}=\left( \begin{array}{cccc} 0.625 &{} \quad 0.396 &{} \quad 0.501 &{} \quad 0.961 \\ 0.742 &{} \quad 0.572 &{} \quad 0.513 &{} \quad 0.574 \\ 0.862 &{} \quad 1.00 &{} \quad 0.576 &{} \quad 0.711 \\ 0.427 &{} \quad 0.708 &{} \quad 0.849 &{} \quad 0.761 \\ \end{array} \right) \end{aligned}$$

Step 4: Calculate the attribute weight.

Here we consider two cases for the attribute weights: (1) when information of the attribute weights is partially known and (2) when information of the attribute weights is completely unknown.

Case 1: When the information of the attribute weights is partially known. Suppose that we have the following weight information:

$$\begin{aligned} \Delta =\left\{ \begin{array}{l} 0.15\le w_1 \le 0.20 \\ 0.20\le w_2 \le 0.40\\ 0.30\le w_3 \le 0.45 \\ 0.05\le w_4 \le 0.15 \\ \text{ and }~ w_1+w_2+w_3+w_4=1 \end{array} \right. \end{aligned}$$

Using Model-2, we construct the single objective programming problem as

$$\begin{aligned} \left\{ \begin{array}{l} \min \quad \xi (w)=0.558w_1+0.249w_2-0.278w_3-0.036w_4 \\ \text{ subject } \text{ to } \quad w\in \Delta ~\text{ and } ~ \sum _{j=1}^{4}w_j=1, ~w_j >0,\\ {\text { for}} \quad j=1,2,3,4. \end{array} \right. \end{aligned}$$

Solving this problem with the optimization software LINGO 11, we get the optimal weight vector as

$$\begin{aligned} {{\bar{w}}}=(0.15,0.38,0.45,0.02). \end{aligned}$$

Case 2 : In this case, the attribute weights are completely unknown. Using Model–3 and Eqs. (14), (15), and (16), we get the following weight vector:

$$\begin{aligned} {{\bar{w}}}=(0.498,0.222,0.248,0.032). \end{aligned}$$

Step 5: Compute the degree of grey relational coefficient.

Using Eq. (17), the degree of grey relational coefficient from positive ideal solution is obtained as

\(\xi ^+_i=\{\xi ^+_1,\xi ^+_2,\xi ^+_3,\xi ^+_4 \}\) which is given in Table 1.

Table 1 Relative closeness co-efficient
Full size table

Similarly, using Eq. (18), the degree of grey relational coefficient from negative ideal solution is obtained as \(\xi ^-_i=\{\xi ^-_1,\xi ^-_2,\xi ^-_3,\xi ^-_4 \}\) which is given in Table 2.

Table 2 Relative closeness co-efficient
Full size table

Step 6: Calculate the relative relational degree.

Using Eq. (19), the relative closeness co-efficient of each alternative can be obtained as given in Table 3.

From Table 3, we see that, in Case 1, the relational degrees are in the order \(\xi _2> \xi _1> \xi _4 > \xi _3\), whereas in Case 2, the relational degrees are in the order \(\xi _2> \xi _1> \xi _4 > \xi _3\).

Table 3 Relative relational degree
Full size table

Step 7: Rank the alternatives

Considering the relative relational degrees, we determine the ranking of the alternatives as follows:

Case 1: \(A_2 \succ A_1 \succ A_4 \succ A_3\)

Case 2: \(A_2 \succ A_1 \succ A_4 \succ A_3\)

The above shows that the ranking is same in two cases. However, in both the cases, \(A_2\) emerges as the best alternative.

In the following, we compare our proposed approach with the method suggested by Biswas et al. (2018), because only Biswas et al.’s method  (2018) is suitable for the considered MADM problem where the preference values of alternatives take the form of SVTrNN and attribute weights are partially known or incompletely unknown. We solve the numerical example using Biswas et al.’s (2018) method and obtain the similar ranking result which demonstrates the validity of our proposed approach. A comparison of the results is shown in Table 4.

Table 4 A comparison of the results
Full size table

The proposed GRA method is flexible to deal with MADM problems with SVTrNNs because the decision maker can analyze solution results by choosing different referential sequences and distinguishing coefficients. On the other hand, Biswas et al.’s (2018) method is limited because it depends only on distance measure. Therefore, the proposed approach is better than Biswas et al.’s method to deal with MADM problems. Currently some other methods (Subas 2015; Ye 2017; Deli and Subas 2017) are available for MADM problem with SVTrNNs, where the weight information of attributes is assumed to be completely known. These methods cannot deal with SVTrNN based MADM problem with partially known or completely unknown weight information. On the other hand, our proposed method can handle SVTrNN based MADM problem with known weight information, partially known weight, and completely unknown weight information. Therefore, our method is better than the existing methods.

The proposed method has the following features:

  • The method considers the preference values of the alternatives in terms of SVTrNNs that effectively deal with neutrosophic information in MADM problem.

  • The method offers flexible choices for choosing the importance of attribute weights.

  • The method only considers relative closeness coefficient obtained from GRA to rank the alternatives. Therefore, the method is simple and understandable.

  • The proposed strategy is free from information loss due to use of any complex aggregation operator or transformation of SVTrNN based attribute values into crisp values.

  • The method considers a new distance measure for solving MADM problems.

5 Conclusion

Single-valued trapezoidal neutrosophic number is a well-built tool for dealing with indeterminate and incomplete information that exists in real MADM problems. In this paper, we have extended GRA method for MADM problem based on SVTrNN, where the weight information is partially known and completely unknown. We have calculated grey relational degrees between every alternative and positive ideal solution, and between every alternative and negative ideal solution, and then defined relative relational degrees to determine the ranking of the alternatives. In order to determine the attribute weights, we have developed two optimization models under the condition that the attribute weights are partially known or completely unknown. We have provided a numerical example to demonstrate the developed method. The proposed model can be utilized in many practical problems like personnel selection, medical diagnosis, center location selection (Pramanik et al. 2016), weaver selection (Dey et al. 2016), etc. under SVTrNN environment.