1 Introduction

New developments in MEMS (microelectromechanical systems) technology have completely changed how small devices like sensors, actuators, and resonators are made. These devices have sizes between microns and sub-microns (Judy 2001). These gadgets have become widely used because of their compact size, exceptional sensitivity, and low power consumption. Comprehending and defining the mechanical features of microscale structures is essential for guaranteeing the effectiveness and dependability of MEMS devices. Scientists are currently conducting a thorough study to examine these characteristics using a combination of experimental testing, model creation, and numerical simulation (Lobontiu and Garcia 2004). Scientists create mathematical models and theoretical frameworks that combine ideas from solid mechanics to precisely explain the mechanical behavior of objects at the microscale. These models incorporate a range of mechanical phenomena, such as elasticity, viscoelasticity, and structural dynamics. They provide the forecasting and examination of crucial mechanical attributes of microscale structures, including deflection, stress distribution, and vibration characteristics (Lee 2011). The mechanical operation of micro-scale structures is governed by equations, which are solved using analytical and numerical approaches. These methodologies offer vital insights into the efficiency and behavior of such systems. Nevertheless, performing experimental testing on micro-scale structures presents numerous obstacles. The intricate nature of these structures, together with their unique characteristics and small scale, presents challenges in their manufacture and handling (Chircov and Grumezescu 2022). Manufacturing processes must possess the ability to produce structures with great precision and uniformity. Furthermore, the task of overseeing and altering these fragile formations without causing harm or contamination can present difficulties. Smaller structures, known as microscale structures, are more susceptible to environmental interactions as compared to bigger ones (Lyshevski 2018). The mechanical behavior of structures can be greatly influenced by factors, such as temperature, humidity, and surface forces, which can greatly influence the mechanical behavior of objects. It is therefore necessary to control and minimize these environmental variables during testing in order to achieve accurate and reliable results (Vlase et al. 2017).

The Kirchhoff plate theory is a prevalent mathematical framework employed to analyze the mechanical characteristics of plates at the microscale. This is a simplified version of the three-dimensional elasticity theory that focuses on thin plates with small thickness in relation to their lateral dimensions. The Kirchhoff plate theory assumes that the plate is both thin and malleable, exhibiting small transverse displacements and rotations (Mittelstedt 2023). The hypothesis disregards the influence of transverse shear deformation and assumes that the plate undergoes just in-plane loads. This simplification allows for the examination of plate deflections and stresses using two-dimensional equations. The control equations of Kirchhoff's plate theory include force balance and plate deformation consistency. These equations relate to the plate's deflection, which refers to the displacement of points on the plate in a direction perpendicular to the plane, as well as the plate's bending moment and shear forces (Zhang et al. 2022). The theory also includes material parameters, such as the Young's modulus and Poisson's ratio, to describe the mechanical behavior of the plate. The Kirchhoff plate theory allows for the examination of many mechanical phenomena in microscale plates, such as bending, buckling, vibration, and dynamic response. It enables the calculation of quantities such as deflection profiles, stress distributions, and the plate's natural frequencies (Zhao et al. 2022). Nevertheless, it is crucial to acknowledge that the Kirchhoff plate theory is not without its constraints. It is unsuitable for assessing plates that experience significant transverse shear deformation or plates with thicknesses that are similar to their lateral dimensions. For such situations, it may be preferable to employ more sophisticated plate theories, such as the Reissner–Mindlin theory or higher-order theories (Zhou and Huang 2023).

Circular plates and their composite structures are widely used in numerous engineering disciplines, particularly in electromechanical systems. These structures have been employed in electromagnetic applications to tackle special difficulties and exploit their distinctive characteristics (Zhang et al. 2015). One research topic focuses on the nonlinear mixed-resonance problem of magnetic circular plates subjected to transverse alternating magnetic fields. The interplay between the magnetic field and the ferromagnetic material results in nonlinear behavior. Investigating resonance phenomena in these systems is critical for understanding their responses and improving their design (Reddy 2022). Another area of research is the study of how conductive circular plates behave under time-dependent magnetic fields, taking into account their electromagneto-thermo-mechanical properties. The objective of these investigations is to examine the interconnected impacts of electromagnetic, thermal, and mechanical phenomena on conductive circular plates. Understanding these interactions is crucial for the functioning of equipment like sensors, actuators, and energy-harvesting devices (Shen et al. 2021). Furthermore, the utilization of circular plates in rotating machines, transformers, and magnetic bearings has been investigated. Ferromagnetic materials possess distinctive characteristics, including their capacity to concentrate magnetic flux and amplify magnetic fields, rendering them well-suited for a range of electromechanical devices. These systems can utilize circular plates as components to attain certain capabilities and enhance their performance (Kaur and Singh 2021).

Because of their distinctive mechanical properties, viscoelastic materials are frequently used in the production of small-scale plates. These materials demonstrate both viscous (depending on time) and elastic (independent of time) properties, which can be beneficial for specific uses in micro-scale electronics (Cappelli et al. 2019). Microscale plates composed of viscoelastic materials provide numerous advantages. The materials possess viscoelastic properties that enable them to dissipate energy and relax stress, thereby reducing the impact of dynamic loads, vibrations, and collisions. This tendency can improve the longevity and dependability of microscale plates, particularly in situations where there is frequent loading or vibrations at high frequencies (Ghayesh et al. 2020). Viscoelastic microscale plates display both time-dependent deflection and creep. Creep is the slow and continuous deformation that happens when an object is subjected to a steady load over time. This phenomenon is particularly significant in situations where long-term stability and performance are crucial. Models that integrate both elastic and viscous components can be used to describe the mechanical behavior of viscoelastic micro-scale plates (Chinnaboon et al. 2023). The Kelvin-Voigt model is an example of a viscoelastic behavior representation that combines a linear spring, which represents the elastic response, with a dashpot, which represents the viscous response. These models can be used to predict the distortion, stress distribution, and dynamic reaction of microscale plates made of viscoelastic materials (Qu et al. 2024). Gaining insight into the mechanical behavior of viscoelastic micro-scale plates is essential for the purpose of designing and enhancing microscale devices, including sensors, actuators, and resonators. Engineers can enhance device performance and reliability by incorporating the time-dependent properties of viscoelastic materials into their models and simulations (Xie et al. 2023). The characterization and modeling of viscoelastic behavior in micro-scale plates can be hard because of the small length scales involved, which is important to acknowledge. Employed methods for studying the viscoelastic properties of microscale plates and validating models include experimental approaches such as nanoindentation and dynamic mechanical analysis, as well as numerical simulations.

A microscale structure is supported by an elastic foundation that follows the Winkler model. The foundation serves as an elastic basis of the Winkler type to maintain small-scale structures. The Winkler model simplifies an elastic foundation by assuming a linear correlation between the applied load and the resulting deflection. In this layout, the elastic base is positioned atop the microscale structures, such as beams, plates, or foundations (Singh et al. 2018). The elastic foundation mimics the support provided by the substrate or neighboring material, which can be made of various materials, such as metals, polymers, or composites. When the elastic foundation consists of a set of individual linear springs that are evenly distributed over the contact region between the structure and the base, the Winkler model is used. Every spring symbolizes the foundation's firmness and provides resistance to distortion. The microscale structure's deflection is determined by the cumulative effect of the deflections caused by each individual spring (Gholami and Alizadeh 2022). The Winkler model simplifies the study of microscale structures on elastic grounds by transforming the scattered support into an equivalent discrete support. This approach enables the calculation of deflections, stresses, and other mechanical parameters of structures subjected to applied loads. The Winkler model is commonly used to analyze a variety of small-scale structures, such as foundations, plates, and beams. It enables the creation of realistic estimates for a variety of practical applications and simplifies complex continuum models (Ye et al. 2020). It is crucial to recognize that the Winkler model has limitations. It relies on linear behavior and does not take into account the impact of local material qualities and gradients. In such cases, it might be necessary to use more complex models, such as the Pasternak model or the finite element method, to accurately represent the interactions of small structures with elastic foundations (Boral et al. 2023).

Thermoelasticity is a scientific discipline that examines the impact of temperature variations on the mechanical properties of materials. It integrates concepts from thermodynamics and elasticity to comprehend the thermal deformation and stress encountered by substances when subjected to different temperature settings (Nowinski 1978). Classical thermoelasticity is a foundational theory that assumes immediate heat transfer and predicts an unlimited velocity of thermal wave propagation. It offers a streamlined framework for examining how materials react to fluctuations in temperature. This theory has a broad range of practical applications and offers useful insights into the thermal behavior of materials. Nevertheless, it possesses constraints in precisely predicting certain phenomena, such as high heat flow or transitory behavior. Generalized thermoelastic models have been created to address classical thermoelastic constraints. These models include extra elements or introduce new variables to account for the finite speeds at which thermal waves propagate, as well as other related phenomena (Ignaczak and Ostoja-Starzewski 2009). These models offer a more accurate depiction of the thermal behavior of materials by taking into account the finite speed at which thermal waves propagate.

The Lord and Shulman model (Lord and Shulman 1967) and the dual-phase-lag thermoelasticity models (Tzou 1995a, b, 1997) are both examples of generalized thermoelasticity models that are superior to classical thermoelasticity because they provide more accurate depictions of how materials behave when they are heated. These models provide useful insights into how temperature changes affect the mechanical properties of solids. They are used in numerous fields, such as thermal barrier coatings, heat exchangers, and materials science. The Lord and Shulman model (Lord and Shulman 1967) incorporates a relaxation time element into Fourier's law of heat conduction. By incorporating this relaxation time, the model takes into consideration the limited velocity at which heat is transmitted in materials. Dual-phase-lag thermoelasticity models (Tzou 1995a, b, 1997) take into account the limited velocity of heat propagation and the time lag between temperature gradients and heat fluxes. These theories assume that temperature gradients and heat fluxes are regulated by distinct time lags or phases. The delay is accounted for by incorporating dual-phase delays into the thermal calculation. By including these delays, these models provide a more accurate depiction of the heat transfer process, especially in scenarios with fast heat transfer or thermal waves of high frequency. Also, the GN-I, GN-II, and GN-III theories proposed by Green and Naghdi (Green and Naghdi 1991, 1992, 1993) are distinct formulations of generalized thermoelasticity. These theories take into account temperature, temperature gradient, and thermal displacement as individual variables.

This study was primarily motivated to develop a model for analyzing the behavior of thin, thermoplastic Kirchhoff–Love sheets. The sheets were supported in a straightforward manner and placed on a flexible Winkler foundation. The time-varying external load acting on the plate was considered, and the Kelvin-Voigt model was used to simulate the plate's viscoelastic behavior. A modified dual-phase-lag (DPL) thermoelasticity model was used to accurately model the elastic plate and how thermal and mechanical events interact with each other. The DPL model takes advantage of the limited rate at which heat spreads and introduces a dual-phase delay in the thermal equation. By measuring and incorporating these phase delays, the model offers a more accurate depiction of the panel's heat conduction process.

The results of the present study can provide valuable insights into the interrelationship between the thermal and mechanical properties of flexible panels. Additionally, these materials could be utilized in engineering applications for thin structures that experience to variations in temperature and mechanical stress. The effects of the viscoelastic coefficient, Winkler's basis, and angular frequency of the distributed load on the behavior of physical fields in circular plate structures were considered. These factors were examined to understand how they influence the characteristics of the circular plate structures. The results derived from the suggested model were also compared to previously published research to validate the model's accuracy and dependability, assess the effectiveness of the proposed methodology, and confirm the validity of the findings.

2 Governing Equations

The constitutive equations, strain–displacement relationships and the equation of motion for an anisotropic thermoelastic medium can be expressed as follows (Marin et al. 2020; Zhou et al. 2022):

$$\sigma_{ij} = 2\mu \varepsilon_{ij} + \left[ {\lambda \varepsilon_{kk} - \gamma \theta } \right]\delta_{ij} ,$$
(1)
$$\varepsilon_{ij} = \frac{1}{2}\left( {\frac{\partial u_i }{{\partial x_j }} + \frac{\partial u_j }{{\partial x_i }}} \right).$$
(2)
$$\sigma_{ji,j} + \rho F_i = \rho \frac{\partial^2 u_i }{{\partial t^2 }},\,$$
(3)

In this equation, the stress tensor components are denoted by \(\sigma_{ij}\), the increment in temperature is represented by \(\theta = T - T_0\), the uniform reference temperature is denoted by \(T_0\), and the Lamé constants are represented by \(\lambda\) and \(\mu\), \(\gamma = \frac{E\alpha_t }{{1 - 2\nu }} = \alpha_T E\), in which \(E\) and \(\nu\) represent the Young's modulus and Poisson's ratio of the plate material, respectively, the thermal expansion coefficient is represented by \(\alpha_t\), and the function of Kronecker's delta is denoted by \(\delta_{ij}\). Also, the components of the strain tensor are denoted by the symbols \(\varepsilon_{ij}\), \(F_i\), which represent the external body forces, \(u_i\), which stand for the components of the displacement vector, \(\varepsilon_{kk} = u_{i,i}\), and \(\rho\), which stand for the density of the material.

It is important to note that Lamé's constants, \(\lambda\) and \(\mu\), can be expressed in terms of the Young's modulus (\(E\)) and Poisson's ratio (\(\nu\)), using the relations \(\lambda = \frac{E\nu }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}},{ }\mu = \frac{E}{{2\left( {1 + \nu } \right)}}\).

The entropy-strain-temperature relation and the energy equation are respectively expressed as (Ignaczak and Ostoja-Starzewski 2009):

$$\rho \eta = \gamma \varepsilon_{kk} + \frac{\rho C_E }{{\theta_0 }}\theta ,$$
(4)
$$\rho \theta_0 \dot{\eta }_i = - q_{i,i} + Q,$$
(5)

where \(\eta\) represents the entropy per unit volume, \(Q\) represents the heat supply per unit volume, \(C_E\) represents the specific heat, and \(q_i\) encompasses the components of the heat flux.

Tzou (Tzou 1995a, 1995b) provided a generalization of the Fourier using Taylor series expansions, which can be expressed as follows:

$$- K\left( {1 + \tau_T \frac{\partial }{\partial t}} \right)\theta_{,i} = \left( {1 + \tau_f \frac{\partial }{\partial t} + \frac{1}{2}\tau_f^2 \frac{\partial^2 }{{\partial t^2 }}} \right)q_i$$
(6)

In this context, the phase lag of the heat flow is denoted by \(\tau_f\), whereas the phase lag of the temperature gradient is denoted by \(\tau_T\). The Eqs. (4)–(6) provide the formulation of the generalized theory of thermoelasticity with phase delays, as follows (Tzou 1995a, b, 1997):

$$\left( {1 + \tau_T \frac{\partial }{\partial t}} \right)\nabla \cdot \left( {K\,\nabla \theta } \right) = \left( {1 + \tau_f \frac{\partial }{\partial t} + \frac{1}{2}\tau_f^2 \frac{\partial^2 }{{\partial t^2 }}} \right)\left( {\rho C_E \frac{\partial \theta }{{\partial t}} + \gamma \,T_0 \frac{{\partial \varepsilon_{kk} }}{\partial t}} \right)$$
(7)

In the Kelvin-Voigt viscoelastic model, the constitutive relationship involves aspects of thermoelasticity and viscoelasticity. To accommodate the material's viscoelastic properties, the Young's modulus (\(E\)) form has been reformulated. The Kelvin-Voigt model defines the modified Young's modulus as follows (Serra-Aguila et al. 2019; Bulıcek et al. 2012):

$$E \to E_0 \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right),$$
(8)

The symbol \({\uptau }_{\text{v}}\) indicates the viscosity coefficient, which denotes the internal damping coefficient of the material and \(E_0\) denotes the elastic Young's modulus. Integrating the revised Young's modulus into the constitutive equation of the Kelvin-Voigt viscoelastic model allows for the consideration of the material's viscoelastic characteristics and examination of how it reacts to external forces and its time-dependent features. By setting \({\uptau }_{\text{v}} = 0\) in the modified Young's modulus Eq. (8), we effectively remove the effect of internal viscosity, and only the thermoelastic behavior of the elastic material is taken into account.

3 Thermal Modeling of Circular Microplates

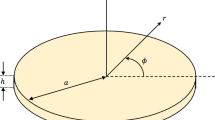
Figure 1 represents a Winkler-based Kelvin–Voigt thermoviscoelastic circular plate resonator. It was assumed that the plate is isotropic, homogeneous, and thermally conductive, with a radius \(R\) and a uniform thickness \(h\). Cylindrical coordinates \(\left( {r,{\Theta }, z} \right)\) were used, with the origin of the coordinate system located in the middle of the plate. At a reference temperature of \(T_0\), it was assumed that the plate was in equilibrium and free of any external forces or deformations. It was also taken into account that the upper layer of the plate is exposed to a varying external load that depends on time.

Fig. 1
figure 1

Diagram of a circular plate supported by a Winkler foundation

Full size image

According to Kirchhoff-plate-theory, it was presumed that the plate is relatively thin in relation to its radius and that the displacements and rotations between the plates are relatively minor. To describe the axisymmetric deformation of a Kirchhoff circular plate, it will be taken into account that the field variables do not depend on the angular coordinate (\({\Theta }\)) and depend only on the radial coordinates (\(r\)) and vertical coordinates (\(z\)), in addition to the time variable \(t\). As a result, the displacement components of a circular Kirchhoff plate can be expressed as follows (Shen et al. 2021; Kaur and Singh 2021):

$$u_r \left( {r, z,t} \right) = - z\frac{{\partial w\left( {r, t} \right)}}{\partial r},u_{\Theta } \left( {r, z,t} \right) = 0,u_z = w\left( {r, t} \right).$$
(9)

In this instance, the deflection of the plate is represented by the function \(w\left( {r, t} \right)\). As a result, the strain components, denoted by \(\varepsilon_{rr}\), \(\varepsilon_{{{\Theta \Theta }}}\), and \(\varepsilon_{r{\Theta }}\), and the cubical dilatation \(e\) are expressed by Chugh and Partap (2021); Gaikwad 2019):

$$\varepsilon_{rr} = - z\frac{\partial^2 w}{{\partial r^2 }}, \;\;\varepsilon_{\Theta \Theta } = - \frac{z}{r}\frac{\partial w}{{\partial r}},\;\; \varepsilon_{r\Theta } = 0,$$
(10)
$$e = \varepsilon_{rr} + \varepsilon_{{{\Theta \Theta }}} = - z\left( {\frac{\partial^2 w}{{\partial r^2 }} + \frac{1}{r}\frac{\partial w}{{\partial r}}} \right) = - z\nabla^2 w.$$
(11)

When it comes to thermal stress tensor, the nan-vanishing components \(\sigma_{rr}\) and \(\sigma_{{{\Theta \Theta }}}\), are given by Chugh and Partap (2021); Gaikwad 2019)

$$\begin{aligned} \sigma_{rr} & = \frac{E}{(1 - v^2 )}\left[ {\varepsilon_r + v\varepsilon_\theta - \left( {1 + v} \right)\alpha_t \theta } \right] \\ & = - \frac{E}{{\left( {1 - v^2 } \right)}}\left[ {z\frac{\partial^2 w}{{\partial r^2 }} + \frac{vz}{r}\frac{\partial w}{{\partial r}} + \left( {1 + v} \right)\alpha_t \theta } \right], \\ \end{aligned}$$
(12)
$$\begin{aligned} \sigma_{{{\Theta \Theta }}} & = \frac{E}{(1 - v^2 )}\left[ {\varepsilon_\theta + v\varepsilon_r - \left( {1 + v} \right)\alpha_T \theta } \right] \\ & = - \frac{E^* }{{\left( {1 - v^2 } \right)}}\left[ {\frac{z}{r}\frac{\partial w}{{\partial r}} + vz\frac{\partial^2 w}{{\partial r^2 }} + \left( {1 + v} \right)\alpha_t \theta } \right]. \\ \end{aligned}$$
(13)

By utilizing relationships (12) and (13), we can derive the constituent components of the bending moments \(M_{rr}\) and \(M_{\theta \theta }\) in the following manner (Rao 2019):

$$M_{rr} = \mathop \int \limits_{ - \frac{h}{2}}^\frac{h}{2} \sigma_{rr} zdz = - D\left[ {\frac{\partial^2 w}{{\partial r^2 }} + \frac{v}{r}\frac{\partial w}{{\partial r}} + \left( {1 + v} \right)\alpha_t M_T } \right],$$
(14)
$$M_{{{\Theta \Theta }}} = \mathop \int \limits_{ - \frac{h}{2}}^\frac{h}{2} \sigma_{{{\Theta \Theta }}} zdz = - D\left[ {v\frac{\partial^2 w}{{\partial r^2 }} + \frac{1}{r}\frac{\partial w}{{\partial r}} + \left( {1 + v} \right)\alpha_t M_T } \right].$$
(15)

where \(D = D_0 \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\) in which \(D_0 = \frac{h^3 E_0 }{{12(1 - v^2 )}}\) denotes the flexural rigidity of the plate.

Also, the thermal moment, referred to by the symbol \(M_T\) in Eqs. (14) and (15), can be determined from the relationship

$$M_T = \frac{12}{{h^3 }}\mathop \int \limits_{ - \frac{h}{2}}^\frac{h}{2} z{ }\theta \left( {r, z,t} \right)dz.$$
(16)

The transverse motion equation governing the behavior of a circular plate supported by Winkler's basis under the action of external forces \(q\left( {r,{ }z,t} \right)\) can be expressed as follows (Zhou et al. 2014):

$$\frac{\partial^2 M_r }{{\partial r^2 }} + \frac{2}{r}\frac{{\partial^2 M_{r{\Theta }} }}{{\partial r\partial {\Theta }}} + \frac{2}{r}\frac{\partial M_r }{{\partial r}} - \frac{1}{r}\frac{{\partial M_{\Theta } }}{\partial r} + \frac{2}{r^2 }\frac{{\partial M_{r{\Theta }} }}{{\partial {\Theta }}} + \frac{1}{r^2 }\frac{{\partial^2 M_{\Theta } }}{{\partial {\Theta }^2 }} + {\text{K}}_{\text{s}} w + q = \rho A\frac{\partial^2 w}{{\partial t^2 }},$$
(17)

The parameter \({\text{K}}_{\text{s}}\) denotes the Winkler foundation, which represents the resistance offered by the foundation to the plate's deformation.

By substituting Eqs. (14) and (15) in Eq. (17), the differential equation can be extracted from the transverse vibration of the slight circular plate as follows:

$$D\nabla^2 \nabla^2 w + D\left( {1 + v} \right)\alpha_t \nabla^2 M_T + \rho A\frac{\partial^2 w}{{\partial t^2 }} = K_s w + q.$$
(18)

It has been assumed that the circular plate is supported by its edges, is subject to a uniformly distributed load \(q\), and varies in harmony over time. The distributed external load equation can be expressed uniformly as follows (Wawrzynski 2021; Xu et al. 2021):

$$q\left( {r,{ }z,t} \right) = q\left( t \right) = q_0 \cos \left( {\omega t} \right),$$
(19)

where \(q_0\) represents the loading capacity (load magnitude) and \(\omega\) represents the angular frequency of the distributed load. It is worth noting here that in the case of \(\omega = 0\), the external loading will be a fixed and distributed amount in a uniform.

Without the heat source (\(Q = 0\)), the generalized DPL heat transfer Eq. (7) developed by Tzou (Green and Naghdi 1993; Marin et al. 2020) can be expressed in the following form:

$$K\left( {1 + \tau_T \frac{\partial }{\partial t}} \right)\nabla^2 \theta = \left( {1 + \tau_f \frac{\partial }{\partial t} + \frac{1}{2}\tau_f^2 \frac{\partial^2 }{{\partial t^2 }}} \right)\left( {\rho C_E \frac{\partial \theta }{{\partial t}} - \gamma \,T_0 z\frac{\partial }{\partial t}\nabla^2 w} \right)$$
(20)

4 Analytic Solution of Governing Equations

Assuming no heat flow transfer occurs across the surfaces of the circular plate (i.e., \(\partial \theta /\partial z = 0\) when \(z = \pm h/2\)) and the temperature change follows a sinusoidal pattern in the z-direction. In this case, the temperature distribution within the thin plate can be mathematically represented by equation:

$$\theta \left( {r, z, t} \right) = \phi \left( {r, t} \right)\sin \left( {z\pi /h} \right).$$
(21)

By employing Eq. (21) and substituting it into Eqs. (18) and (20), and subsequently simplifying, we obtain the following the equations:

$$D\left( {\nabla^2 \nabla^2 w + \frac{{24\left( {1 + v} \right)\alpha_t }}{\pi^2 h^2 }\nabla^2 \phi } \right) + \rho A\frac{\partial^2 w}{{\partial t^2 }} - {\text{K}}_{\text{s}} w - q = 0,$$
(22)
$$\left( {1 + \tau_T \frac{\partial }{\partial t}} \right)\left( {\nabla^2 - \frac{\pi^2 }{{h^2 }}} \right)\phi = \left( {1 + \tau_f \frac{\partial }{\partial t} + \frac{1}{2}\tau_f^2 \frac{\partial^2 }{{\partial t^2 }}} \right)\left( {\frac{\rho C_E }{K}\frac{\partial \phi }{{\partial t}} - \frac{T_0 \pi^2 \gamma h}{{24K}}\frac{\partial }{\partial t}\nabla^2 w} \right).$$
(23)

In addition, the bending moments, expressed in Eqs. (14) and (15), can be written as

$$M_{rr} = - D\left[ {\frac{\partial^2 w}{{\partial r^2 }} + \frac{v}{r}\frac{\partial w}{{\partial r}} + \frac{{24\left( {1 + v} \right)\alpha_t }}{\pi^2 h}\phi } \right],$$
(24)
$$M_{\theta \theta } = - D\left[ {v\frac{\partial^2 w}{{\partial r^2 }} + \frac{1}{r}\frac{\partial w}{{\partial r}} + \frac{{24\left( {1 + v} \right)\alpha_t }}{\pi^2 h}\phi } \right],$$
(25)

In order to provide a more convenient solution, dimensionless parameters will be used to simplify the governing equations. It is possible to use the following dimensionless parameters for the problems of flexibility and thermoelasticity:

$$\begin{aligned} \left\{ {r^{\prime} ,z^{\prime} ,w^{\prime} ,a^{\prime} ,h^{\prime} } \right\} & = c_0 \eta \left\{ {r,z,w,a,h} \right\},\left\{ {t^{\prime} ,\tau_f^{\prime} ,\tau_T^{\prime} ,{\uptau }_{\text{v}}^{\prime} } \right\} = c_0^2 \eta \left\{ {t,\tau_f ,\tau_T ,{\uptau }_{\text{v}} } \right\}, \\ M_{ij}^{\prime} & = - \frac{1}{\eta^2 c_0^2 D_0 }M_{ij} ,\sigma_{ij}^{\prime} = \frac{{\left( {1 - v^2 } \right)}}{E_0 }\sigma_{ij} ,\theta^{\prime} = \frac{1}{T_0 }\theta ,\phi^{\prime} = \frac{\phi }{T_0 },q^{\prime} = \frac{q}{Kc_0 }, \\ \end{aligned}$$
(26)

where \(c_{0 }^2 = \frac{E_0 }{\rho }\) and \(\eta = \frac{\rho C_E }{K}\).

By introducing these dimensionless parameters, the governing equations can be rewritten in a more convenient form (primes are dropped for convenience):

$$\left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\nabla^2 \nabla^2 w + \alpha_1 \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\nabla^2 \phi + \alpha_2 \frac{\partial^2 w}{{\partial t^2 }} - {\overline{\text{K}}}_{\text{s}} w - q = 0,$$
(27)
$$\left( {1 + \tau_T \frac{\partial }{\partial t}} \right)\left( {\nabla^2 - \frac{\pi^2 }{{h^2 }}} \right)\phi = \left( {1 + \tau_f \frac{\partial }{\partial t} + \frac{1}{2}\tau_f^2 \frac{\partial^2 }{{\partial t^2 }}} \right)\left[ {\frac{\partial \phi }{{\partial t}} - \alpha_4 \frac{\partial }{\partial t}\left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\nabla^2 w} \right],$$
(28)
$$M_{rr} = \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\left[ {\frac{\partial^2 w}{{\partial r^2 }} + \frac{v}{r}\frac{\partial w}{{\partial r}} + \alpha_5 \phi } \right],$$
(29)
$$M_{\theta \theta } = \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\left[ {v\frac{\partial^2 w}{{\partial r^2 }} + \frac{1}{r}\frac{\partial w}{{\partial r}} + \alpha_5 \phi } \right],$$
(30)
$$\sigma_{rr} = \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\left[ {z\frac{\partial^2 w}{{\partial r^2 }} + \frac{vz}{r}\frac{\partial w}{{\partial r}} + \alpha_6 {\Theta }} \right],$$
(31)
$$\sigma_{\theta \theta } = \left( {1 + {\uptau }_{\text{v}} \frac{\partial }{\partial t}} \right)\left[ {z\frac{{\text{z}}}{r}\frac{\partial w}{{\partial r}} + vz\frac{\partial^2 w}{{\partial r^2 }} + \alpha_6 {\Theta }} \right],$$
(32)

where

$$\begin{aligned} \alpha_1 & = \frac{{24\left( {1 + v} \right)\alpha_t T_0 }}{\pi^2 h},\alpha_2 = \frac{\rho \pi a^2 }{{\eta^4 c_0^2 D_0 }}, {\overline{\text{K}}}_{\text{s}} = \frac{{{\text{K}}_{\text{s}} }}{\eta^4 c_0^2 D_0 }, \alpha_4 = \frac{\alpha_t E_0 \pi^2 h}{{24K\eta^2 c_0^2 (1 - 2v)}}, \\ \alpha_5 & = \frac{{24\left( {1 + v} \right)\alpha_t }}{c_0 \eta \pi^2 h},\alpha_6 = T_0 \alpha_t \left( {1 + v} \right). \\ \end{aligned}$$
(33)

In order to solve the governing equations of the problem, it is necessary to take into account both the starting conditions and the boundary conditions. The problem assumes that the starting conditions are homogeneous. Therefore, the initial conditions at \(t = 0\) are assumed as follows:

$$\phi \left( {r, 0} \right) = 0, \left. {\left. {\frac{{\partial \phi \left( {r,t } \right)}}{\partial t}} \right|_{t = 0} = 0,w\left( {r,0} \right) = 0, { }\frac{{\partial w\left( {r, t} \right)}}{\partial t}} \right|_{t = 0} = 0.$$
(34)

When a circular plate is clamped at the edges, it is mechanically restricted from moving in a perpendicular direction to its surface, preventing any transverse displacement. This scenario is frequently encountered in applications where the circular plate must provide a level and steady surface to support or enclose other components. The clamping mechanism used to secure the panel's edges can vary depending on the structure's design and specific needs. To describe the mechanical boundary conditions on the edges of a clamped circular plate, we may use the following conditions:

$$w\left( {r,t} \right) = 0,\;\;\;\; \frac{{\partial w\left( {r, t} \right)}}{\partial r} = 0\;\;\;\; {\text{at}}\;\;\; r = R.$$
(35)

When examining the behavior of an elastic circular plate exposed to thermal shock, it is crucial to take into account the impacts of swift and substantial temperature changes in close proximity to the plate's edges. Thermal shock can cause significant deviations in pressure and heat within the plate, potentially impacting its structural integrity and performance. The thermal shock condition at the ends of the circular plate can be expressed by the following equation:

$$\phi \left( {r,t } \right) = \phi_0 H\left( t \right) {\text{at}} r = R.$$
(36)

5 Solution of the Problem

The Laplace transform is an exceptionally effective technique for solving differential equations, particularly those that emerge in engineering, physics, and mathematics. The following integral defines the Laplace transform:

$$\overline{f}\left( {r,s} \right) = \mathop \int \limits_0^\infty f\left( {r,t} \right)e^{ - st} dt, s > 0.$$
(37)

In this equation, \(\overline{f}\left( {r,s} \right)\) represents the Laplace transform of the function \(f\left( {r,t} \right)\), and the parameter \(s\) is a complex number with a positive real part. The following sets of equations are obtained by applying the Laplace transform to Eqs. (27)–(32):

$$\left( {1 + {\uptau }_{\text{v}} s} \right)\nabla^2 \nabla^2 \overline{w} + \alpha_1 \left( {1 + {\uptau }_{\text{v}} s} \right)\nabla^2 \overline{\phi } + \left( {\alpha_2 s^2 - {\overline{\text{K}}}_{\text{s}} } \right)\overline{w} = \overline{q}\left( s \right),$$
(38)
$$\left( {1 + \tau_T s} \right)\left( {\nabla^2 - \frac{\pi^2 }{{h^2 }}} \right)\overline{\phi } = s\left( {1 + \tau_f {\text{s}} + \frac{1}{2}\tau_f^2 s^2 } \right)\left( {\overline{\phi } - \alpha_4 \left( {1 + {\uptau }_{\text{v}} s} \right)\nabla^2 \overline{w}} \right),$$
(39)
$$\overline{M}_{rr} = \left( {1 + {\uptau }_{\text{v}} s} \right)\left[ {\frac{{d^2 \overline{w}}}{dr^2 } + \frac{v}{r}\frac{{d\overline{w}}}{dr} + \alpha_5 \overline{\phi }} \right],$$
(40)
$$\overline{M}_{\theta \theta } = \left( {1 + {\uptau }_{\text{v}} s} \right)\left[ {v\frac{{d^2 \overline{w}}}{dr^2 } + \frac{1}{r}\frac{{d\overline{w}}}{dr} + \alpha_5 \overline{\phi }} \right],$$
(41)
$$\overline{\sigma }_{rr} = \left( {1 + {\uptau }_{\text{v}} s} \right)\left[ {z\frac{{d^2 \overline{w}}}{dr^2 } + \frac{vz}{r}\frac{{d\overline{w}}}{\partial r} + \alpha_6 \overline{\theta }} \right],$$
(42)
$$\overline{\sigma }_{\theta \theta } = \left( {1 + {\uptau }_{\text{v}} s} \right)\left[ {\frac{z}{r}\frac{{d\overline{w}}}{dr} + vz\frac{{d^2 \overline{w}}}{dr^2 } + \alpha_6 \overline{\theta }} \right].$$
(43)

Equations (38) and (39) can be reformulated as follows:

$$\left( {\nabla^4 + \alpha_7 } \right)\overline{w} = - \alpha_1 \nabla^2 \overline{\phi } + \alpha_{10} ,$$
(44)
$$- \alpha_9 \nabla^2 \overline{w} = \left( {\nabla^2 - \alpha_8 } \right)\overline{\phi },$$
(45)

where

$$\begin{aligned} \alpha_7 & = \frac{{\alpha_2 s^2 - {\overline{\text{K}}}_{\text{s}} }}{{1 + {\uptau }_{\text{v}} s}},\;\;\alpha_8 = \alpha_0 + \frac{\pi^2 }{{h^2 }},\;\;\alpha_9 = \alpha_4 \alpha_0 \left( {1 + {\text{E}}_{\text{v}} s} \right), \\ \alpha_0 & = \frac{{s\left( {1 + \tau_f {\text{s}} + \frac{1}{2}\tau_f^2 s^2 } \right)}}{{\left( {1 + \tau_T s} \right)}}, \;\;\alpha_{10} = \frac{{\overline{q}\left( s \right)}}{{1 + {\uptau }_{\text{v}} s}},\;\;\overline{q}\left( s \right) = \frac{sq_0 }{{s^2 + \omega^2 }}. \\ \end{aligned}$$
(46)

Eliminating the variable \(\overline{w}\) or \(\overline{\phi }\) yields the following results from Eqs. (44) and (45):

$$\left( {\nabla^6 - \left( {\alpha_8 + \alpha_1 \alpha_9 } \right)\nabla^4 + \alpha_7 \nabla^2 - \alpha_7 \alpha_8 } \right)\overline{w} = - \alpha_{10} \alpha_8 .$$
(47)
$$\left( {\nabla^6 - \left( {\alpha_8 + \alpha_1 \alpha_9 } \right)\nabla^4 + \alpha_7 \nabla^2 - \alpha_7 \alpha_8 } \right)\overline{\phi } = 0.$$
(48)

The solutions to Eqs. (47) and (48) can be expressed as

$$\overline{w}\left( {r,s} \right) = \mathop \sum \limits_{i = 1}^3 A_i I_0 { }\left( {k_i r} \right) - \alpha_{10} /\alpha_7 ,$$
(49)
$$\overline{\phi }\left( {r,s} \right) = - \alpha_9 \mathop \sum \limits_{i = 1}^3 \left( {\frac{k_i^2 }{{k_i^2 - \alpha_8 }}} \right)A_i I_0 { }\left( {k_i r} \right).$$
(50)

The second kind of order zero modified Bessel function in these equations is denoted by \(I_0 \left( {k_i r} \right)\). Furthermore, the parameter \(k_i\), \(i = 1\), 2, and 3, is given by the roots of the equation:

$$k^6 - \left( {\alpha_8 + \alpha_1 \alpha_9 } \right)k^4 + \alpha_7 k^2 - \alpha_7 \alpha_8 = 0.$$
(51)

After applying the Laplace transform to Eq. (9) and making use of Eq. (49), the transformed displacement \(\overline{u}\) can be expressed as:

$$\overline{u}\left( {r,s} \right) = - z\frac{{\partial \overline{w}}}{\partial r} = - z\mathop \sum \limits_{i = 1}^3 k_i A_i I_1 { }\left( {k_i r} \right),$$
(52)

Using the solutions of the functions \(\overline{w}\) and \(\overline{\phi }\) and substituting them into Eqs. (40)-(43), the solutions for the bending moments and thermal stresses can be derived as follows:

$$\frac{{\overline{M}_{rr} }}{{\left( {1 + {\uptau }_{\text{v}} s} \right)}} = \frac{v}{r}\mathop \sum \limits_{i = 1}^3 k_i A_i I_1 { }\left( {k_i r} \right) + \mathop \sum \limits_{i = 1}^3 \left( {k_i^2 - \frac{\alpha_5 \alpha_9 k_i^2 }{{k_i^2 - \alpha_8 }}} \right)A_i I_0 { }\left( {k_i r} \right),$$
(53)
$$\frac{{\overline{M}_{\theta \theta } }}{{\left( {1 + {\uptau }_{\text{v}} s} \right)}} = \frac{1}{r}\mathop \sum \limits_{i = 1}^3 k_i A_i I_1 { }\left( {k_i r} \right) + \mathop \sum \limits_{i = 1}^3 \left( {vk_i^2 - \frac{\alpha_5 \alpha_9 k_i^2 }{{k_i^2 - \alpha_8 }}} \right)A_i I_0 { }\left( {k_i r} \right),$$
(54)
$$\frac{{\overline{\sigma }_{rr} }}{{\left( {1 + {\uptau }_{\text{v}} s} \right)}} = \frac{v}{r}z\mathop \sum \limits_{i = 1}^3 k_i A_i I_1 { }\left( {k_i r} \right) + \mathop \sum \limits_{i = 1}^3 \left( {zk_i^2 - \frac{\alpha_5 \alpha_9 k_i^2 }{{k_i^2 - \alpha_8 }}\sin \left( {z\pi /h} \right)} \right)A_i I_0 { }\left( {k_i r} \right),$$
(55)
$$\frac{{\overline{\sigma }_{\theta \theta } }}{{\left( {1 + {\uptau }_{\text{v}} s} \right)}} = \frac{1}{r}z\mathop \sum \limits_{i = 1}^3 k_i A_i I_1 { }\left( {k_i r} \right) + \mathop \sum \limits_{i = 1}^3 \left( {vzk_i^2 - \frac{\alpha_5 \alpha_9 k_i^2 }{{k_i^2 - \alpha_8 }}\sin \left( {z\pi /h} \right)} \right)A_i I_0 { }\left( {k_i r} \right).$$
(56)

Through the process of applying the Laplace transform to the boundary conditions represented by Eqs. (35) and (36), the following formulas are obtained:

$$\overline{w}\left( {r,s} \right) = 0,\;\;\;\; \frac{{d\overline{w}\left( {r,s} \right)}}{dr} = 0\;\;\;\; {\text{at}}\;\;\;r = R,$$
(57)
$$\overline{\phi }\left( {r,s } \right) = \frac{\phi_0 }{s}, \;\;\;\; {\text{at}}\;\;\;r = R.$$
(58)

By introducing the functions \(\overline{w}\) and \(\overline{\phi }\) into the boundary conditions (57) and (58), the linear equations can be derived for the unknown constants as follows:

$$\mathop \sum \limits_{i = 1}^3 A_i I_0 { }\left( {k_i R} \right) = \alpha_{10} /\alpha_7 ,$$
(59)
$$\mathop \sum \limits_{i = 1}^3 k_i A_i I_1 { }\left( {k_i R} \right) = 0,$$
(60)
$$\mathop \sum \limits_{i = 1}^3 \left( {\frac{k_i^2 }{{k_i^2 - \alpha_8 }}} \right)A_i I_0 { }\left( {k_i R} \right) = - \frac{\phi_0 }{{s\alpha_9 }}.$$
(61)

By solving this system of linear equations, the unknown parameters \(A_1\), \(A_2\), and \(A_3\) can be determined, which are necessary to calculate the Laplace physical fields being investigated, such as displacements, pressures, or temperatures. Next, these studied domains must be converted back to the time domain.

6 Inversion of the Laplace Transforms

There are several instances in which it is not possible to get inverse Laplace transforms of complex functions by analytical means. As a result, numerical approaches are required to approximate solutions in the time domain. The Fast Fourier Transform (FFT) is a commonly employed method for estimating the time-domain solution from the frequency domain in the context of the inverse Laplace transform. The FFT-based method is a common and widely used numerical approach for estimating the inverse Laplace transform and getting time-domain solutions in many fields, including physics, engineering, and signal processing.

Based on this methodology, the inverse Laplace transform of , represented by , can be estimated as follows (Davies and Martin 1979):

(65)

The equation involves the parameter \(\mathcalligra{m}\), associated with the Laplace domain, while \(\mathcalligra{n}\) represents the total number of terms in the summation. It is important to note that the exact values of \(t\) and \(\mathcalligra{m}\), as well as the choice of \(\mathcalligra{n}\), depend on the problem and the properties of the transformed Laplace function. These values can be determined via numerical experiments or relevant literature in the specific problem domain.

7 Validation of Results and Discussion

This section of the essay presents three distinct case studies to examine, analyze, and validate the importance of the problem under investigation and the efficacy of the theoretical framework employed. Each case study focuses on a specific aspect and examines how it affects the behavior of physical fields within a thin circular elastic plate.

Case Study 1: The Impact of Viscosity (Please remove the sub-section numbering

The objective of this case is to investigate the impact of viscosity on the dynamics of physical fields in a thin circular elastic plate. The study aims to understand how viscosity affects different things in the plate, like displacements, stresses, and other physical properties, by looking at the theoretical model and combining parameters that have to do with viscosity.

Case Study 2: The Winkler Base Effect

This scenario includes analyzing the effect of the Winkler basis parameter on the distribution of variables within the panel, which depicts the interaction between the elastic structure and the elastic base. By manipulating the Winkler foundation modulus, the study seeks to investigate how varying levels of foundation or support stiffness affect the distribution of physical quantities in the elastic plate.

Case Study 3: The Impact of the External Mechanical Load

The third case study investigates the presence and absence of an external mechanical load applied to the flexible plate. By looking at different loading conditions, the study seeks to understand the panel's behavior under multiple loading scenarios, including constant loads, time-dependent loads, or a combination of both. This case study aims to evaluThe study specifically examines the thermoelastic coupling phenomena in a circular plate made of magnesium, which exhibits thermo-viscoelastic behavior. To investigate this phenomenon, several magnesium material properties are given as follows (Tang et al. 2022; Abouelregal 2022):

$$\begin{aligned} T_0 & = 298\,{\text{K}},\;\;\lambda = 2.696 \times 10^{10} \left( {{\text{kg}}/{\text{ms}}} \right),\;\;\mu = 1.639 \times 10^{10} \left( {{\text{kg}}/{\text{ms}}} \right), \\ \alpha_T & = 1.78 \times 10^{ - 5} \,{\text{K}}^{ - 1} ,\;\;\nu = 0.37,\;\;K = 170\,{\text{W/}}\left( {{\text{mK}}} \right),\;\;\tau_f = 0.04\,{\text{s}}, \\ C_E & = 1.04 \times 10^3 \left( {{\text{J}}/{\text{kgK}}} \right),\;\;E = 40\,{\text{GPa}},\;\;\rho = 1740\,{\text{kg/m}}^3 ,\;\;\tau_T = 0.025\,{\text{s}} \\ \end{aligned}$$

ate the effect of an applied mechanical load on the physical properties of the plate, including deformations, temperature change, stresses, and deflection.

7.1 The Effect of Viscosity on Different Fields

The impact of viscosity on the reactions of thermoelastic macroscale beams and plates pertains to the influence of viscous damping on the thermal and mechanical characteristics of these structures. Viscous damping occurs when energy is dissipated by internal friction inside a substance or between the structure and its surrounding environment. Within the framework of thermoelasticity, viscous damping encompasses the process of dissipating heat energy and mechanical vibrations.

The objective of this case study is to investigate the impact of viscosity, as indicated by the viscosity coefficient \({\uptau }_{\text{v}}\), on the behavior and mechanical characteristics of flexible plates and beams. The evaluation will be conducted using the modified DPL thermo-viscoelastic model (DPL-VTE). The DPL-VTE model incorporates the fundamental thermoelasticity equations as well as the Kleven-Voigt model, which accounts for the influence of viscosity and damping. When analyzing the impact of viscosity on the thermoelastic reactions of a tiny magnesium plate resonator, the viscosity coefficient \({\uptau }_{\text{v}}\) will be assigned the values of 0.03 and 0.05. In the absence of viscosity effects (pure thermoelasticity), \({\uptau }_{\text{v}}\) is set to 0. We will analyze the gathered data and present the results in Figs. 2, 3, 4, 5, 6. The dynamic response of thermoelastic microplates is greatly influenced by the viscous thermal damping parameter \({\uptau }_{\text{v}}\). These results demonstrate the impact of viscosity on various distributions, such as bending moment, deviation, and stress range values. This consistency aligns with the conclusions reached in Abouelregal (2022); Zhao et al. 2024), indicating that viscosity plays a crucial role in influencing the mechanical behavior and responses of nanostructures.

Fig. 2
figure 2

The transverse deflection \(w\) via viscous thermal damping parameter \({\uptau }_{\text{v}}\)

Full size image
Fig. 3
figure 3

The temperature change \(\theta\) via viscous thermal damping parameter \({\uptau }_{\text{v}}\)

Full size image
Fig. 4
figure 4

The radial displacement \(u\) via viscous thermal damping parameter \({\uptau }_{\text{v}}\)

Full size image
Fig. 5
figure 5

The flexure moment \(M_{rr}\) via viscous thermal damping parameter \({\uptau }_{\text{v}}\)

Full size image
Fig. 6
figure 6

The radial thermal stress \(\sigma_{rr}\) via viscous thermal damping parameter \({\uptau }_{\text{v}}\)

Full size image

Figure 2 illustrates the dynamic deflection \(w\), which quantifies the plate's dynamic deformation over time under the influence of viscosity and in its absence. The figure illustrates that an increase in \({\uptau }_{\text{v}}\) results in a decrease in the deflection capacity. This indicates that stronger damping leads to faster stabilization and a reduction in the maximum deflection. The amount of deflection change is most pronounced around the plate boundaries and decreases toward the center. Figure 3 depicts the temperature distribution \(\theta\), which examines the temperature changes within the panel under external and thermal stresses. The figure shows that viscous damping indirectly affects the temperature distribution through its effect on mechanical interaction. Also, systems with higher \({\uptau }_{\text{v}}\) show less variation in temperature profiles. In line with what was found, the results in reference (Abouelregal 2021) confirm the well-known and studied effect of viscosity on the dynamic features, damping properties, and stress distribution in very small systems.

Figure 4 shows how the radial displacement component \(u\) changes as the plate radius changes. This is done so that we can figure out how the flexible plate deforms when it is subjected to thermal and mechanical loads. The data indicates an inverse relationship between the viscosity coefficient (\({\uptau }_{\text{v}}\)) and the minimum displacement values near the outer plate surface throughout the range \(1.0 \le {\text{r}} \le 0.9\). In addition, the maximum displacement values at the inner surface decrease as \({\uptau }_{\text{v}}\) increases throughout the range \(0 \le {\text{r}} \le 0.9\). Viscosity dampens the system, allowing it to dissipate energy from external loads. This minimizes oscillations and stabilizes the system, resulting in diminished deformations over time. This is of utmost importance in applications where reduced motion is essential, such as precision instruments.

Figure 5 shows the effect of bending moment (\(M_{rr}\)) due to thermo-mechanical loads. Since the bending moment \(M_{rr}\) is directly related to deflection, with increasing values of the viscosity constant \({\uptau }_{\text{v}}\), the bending moment values are less pronounced due to the decrease in deflection. Figure 6 shows the distribution of stress \(\sigma_{rr}\) in the radial direction and its effect on the change of the viscosity parameter. The picture clearly shows that as the viscosity (\({\uptau }_{\text{v}}\)) goes up, the radial stress (\(\sigma_{rr}\)) distribution goes down, with smaller peaks. This is because higher damping changes the stresses caused by outside forces. These results emphasize the importance of taking viscosity into account when analyzing the dynamic behavior, damping effects, and how stress is distributed in microscopic systems.

The viscous parameter \({\uptau }_{\text{v}}\) is critical in regulating the deflection characteristics of the microplate. By adjusting the viscosity index values (\({\uptau }_{\text{v}}\)), we can fine-tune how a microplate responds to external forces and temperature changes. This allows us to optimize its performance for specific applications, such as enhancing its stability, responsiveness, or sensitivity in various environments. For example, in applications where precise control of vibrational characteristics is crucial, varying \({\uptau }_{\text{v}}\) could help achieve the desired level of damping or resonance. This capability is especially valuable in fields like micro-electromechanical systems (MEMS), where precise mechanical behavior is essential. Also, higher \({\uptau }_{\text{v}}\) values can indeed help in applications requiring minimal deflection and high precision, as they contribute to greater stiffness and stability. Conversely, lower \({\uptau }_{\text{v}}\) values can enhance adaptability and flexibility, which is useful in dynamic or variable conditions.

The revised DPL (dual phase lag) theory of thermoelasticity, with its integration of a thermal conductivity model, is a robust framework for simulating these effects. It offers a more nuanced understanding of how thermal and mechanical interactions affect system dynamics, which is crucial for optimizing performance in various applications. This approach can provide better predictions and control over how materials and devices will behave under different conditions. The analysis and discussion clearly demonstrate that the results obtained in the current study align closely with the findings of previous studies (Xu et al. 2022; Feri et al. 2022). This consistency in the simulation helps to improve the reliability of the results obtained, as well as increase confidence in the accuracy of the numerical results and modeling techniques used in the present work.

7.2 The Effect of Winkler Foundation Parameter

By examining the vibration characteristics of thermoelastic microplates on a Winkler viscoelastic basis, a critical aspect of small-scale engineering can be addressed. The Winkler basis model is indeed a useful representation for understanding how support conditions affect the behavior of circular microplates. Including the effects of temperature and viscosity in this study expands the analysis, as these factors have a significant impact on the material properties and the behavior of microplates (Abouelregal 2021). The present results give a full picture of how changes in temperature and mechanical loads impact the performance of microplates because they use generalized thermoelastic models to include these effects. This approach could lead to valuable insights for applications in nanotechnology and MEMS devices, where precise control of vibration and stability is of paramount importance.

Studying the vibration characteristics of a circular thermoelastic microplate on a Winkler viscoelastic substrate over time is essential for comprehending the influence of foundations on its vibrational response. The rigidity of the foundation is a crucial factor in determining the amount of bending or deformation (Abouelregal et al. 2023). Engineers can modify the stiffness of the microplate's deflection properties to suit specific design needs. It is possible to achieve the desired balance between rigidity and flexibility by adjusting the stiffness of the foundation, thus improving the performance of the microplate for its intended purpose.

In the field of vibration analysis of thermoelastic microplates, there has been a lack of published material focusing on foundations and considering the effects of temperature and viscosity. This subsection addresses this gap by utilizing generalized thermoelastic DPL models to investigate how foundations influence the vibration properties of a circular thermoelastic plate grown on a Winkler viscoelastic substrate. Figures 7, 8, 9, 10, 11 depict the influence of Winkler's foundation parameter \({\text{K}}_{\text{s}}\) on temperature change \(\theta\), thermal deflection \(w\), radial thermal stress \(\sigma_{rr}\), flexure moment \(M_{rr}\), and displacement \(u\) in the case of a clamped microplate. Three specific values for the Winkler's foundation coefficient are provided: \({\text{K}}_{\text{s}} = 0\), \({\text{K}}_{\text{s}} = 10\), and \({\text{K}}_{\text{s}} = 30\). It is important to note that \({\text{K}}_{\text{s}}\) represents the stiffness of the springs in the foundation, with lower values indicating a more flexible foundation and higher values indicating a more solid foundation.

Fig. 7
figure 7

The deflection \(w\) via Winkler’s foundation coefficient \({\text{K}}_{\text{s}}\)

Full size image
Fig. 8
figure 8

The temperature change \(\theta\) via Winkler’s foundation coefficient \({\text{K}}_{\text{s}}\)

Full size image
Fig. 9
figure 9

The radial displacement \(u\) via Winkler’s foundation coefficient \({\text{K}}_{\text{s}}\)

Full size image
Fig. 10
figure 10

The flexure moment \(M_{rr}\) via Winkler’s foundation coefficient \({\text{K}}_{\text{s}}\)

Full size image
Fig. 11
figure 11

The radial thermal stress \(\sigma_{rr}\) via Winkler’s foundation coefficient \({\text{K}}_{\text{s}}\)

Full size image

The Figures show that the stiffness of the foundation, which is shown by the parameter \({\text{K}}_{\text{s}}\) in the Winkler foundation model, impacts many parts of the system, such as the microplate's deflection and thermal stress. Figure 7 shows that a stiffer foundation (higher \({\text{K}}_{\text{s}}\)) increases the resistance of the microplate to deflection \(w\). As a result, the microplate has smaller deflections. A more flexible foundation (lower \({\text{K}}_{\text{s}}\)) also allows smaller deflections, making the microplate more adaptable to external forces. This means that for small deformations or small loads, the microplate experiences less deflection because the stiffer foundation resists bending more effectively.

Figure 8 demonstrates that the stiffness of the foundation (\({\text{K}}_{\text{s}}\)) influences the distribution of temperature changes (\(\theta\)) within the structure. A more rigid foundation (with a higher \({\text{K}}_{\text{s}}\) value) has the tendency to uniformly disperse heat, resulting in a more consistent distribution of temperature \(\theta\). This is because the inflexible foundation has the capacity to effectively transmit and distribute heat energy. Conversely, a more adaptable foundation (with lower \({\text{K}}_{\text{s}}\)) might lead to uneven temperature distributions and localized temperature fluctuations. The restricted capacity of the springs in a flexible foundation to equally transfer thermal loads results in concentrated temperature fluctuations within the foundation (Kardooni et al. 2022). The findings emphasize the importance of the foundation's stiffness in regulating both mechanical and thermal reactions in microplate systems. Engineers can optimize performance in diverse applications by manipulating the value of \({\text{K}}_{\text{s}}\) to construct microplates with precise deflection characteristics and predictable temperature.

Figure 9 demonstrates that a foundation with higher stiffness (\({\text{K}}_{\text{s}}\)) not only offers greater resistance to deformation but also ensures a more uniform distribution of displacement (\(u\)) throughout the structure. This leads to a more consistent and balanced distribution of deformations throughout the microplate, resulting in improved structural integrity and stability. On the other hand, a foundation that is more adaptable (\({\text{K}}_{\text{s}}\)) enables greater localized deformations, resulting in an unequal distribution of displacement \(u\). This can lead to elevated stress concentrations and possible structural vulnerabilities in specific regions. Having a clear understanding of how the stiffness of a foundation affects the displacement \(u\) is essential when it comes to creating microplates with specific mechanical characteristics. Uniform deformation and minimal localized stresses are crucial for reliable operation, especially in precision applications.

The distribution of bending moments \(M_{rr}\) throughout the structure is an important factor affected by the foundation's stiffness, as depicted in Fig. 10. A stiffer foundation distributes applied loads more uniformly, resulting in a more even distribution of bending moments along the shape of the structure. This can reduce the incidence of localized excessive bending moments and potential structural failures. Conversely, a more flexible foundation may lead to an uneven distribution of bending moments, potentially causing localized high moments in certain areas. A higher Winkler's foundation coefficient results in fewer bending moments as the stiffness of the springs aids in foundation support and resistance to bending. Conversely, a lower Winkler's foundation coefficient may lead to more bending moments due to reduced foundation support and bending resistance. These results align with findings reported in previous studies (Abouelregal et al. 2022), reinforcing the reliability of our conclusions. Understanding the distribution of bending moments and their relationship with foundation stiffness is vital for designing microplates that are both strong and resilient, especially in applications where structural integrity is critical. By optimizing the foundation stiffness, engineers can ensure that microplates handle applied loads effectively, minimizing the risk of localized stresses and enhancing the overall performance and longevity of the structure.

The stiffness of the foundation also influences the distribution and magnitude of thermal stresses \(\sigma_{rr}\) in the circular thermoelastic microplate, as shown in Fig. 11. A stiffer foundation with a higher \({\text{K}}_{\text{s}}\) value tends to distribute thermal stresses more evenly throughout the microplate, resulting in a decrease in localized stress concentrations. In contrast, a more flexible foundation with a lower \({\text{K}}_{\text{s}}\) value may lead to localized stress concentrations in specific areas of the microplate. By studying the effect of the foundation stiffness on the thermal stress distribution in thermoelastic materials, one can ensure that the laminates can withstand thermal fluctuations efficiently. This ensures that structural integrity and optimum performance are maintained in situations where thermal stability is important.

7.3 The Effect of External Mechanical Load

The external mechanical load applied to the elastic thermal plate induces mechanical pressures on the fine panels. These mechanical pressures result in deformations, displacements, and internal stresses within the plate (Abouelregal 2021). The magnitude, direction, and distribution of the mechanical load influence the response of the plate, leading to bending, twisting, or stretching deformations. An investigation into the impact that the external mechanical load (\(q\left( t \right) = q_0 \cos \left( {\omega t} \right)\)) has on the elastic thermal plate is going to take place in this part of the examination. How which the mechanical pressures, thermal pressures, and qualities of the materials that make up the fine panels interact with one another will be the determining factor in the effect that the outer load has. Through a thorough examination of these factors, we will gain a comprehensive understanding of how external mechanical loads influence the behavior of the elastic thermal plate. Understanding this information is critical for creating plates that can efficiently handle and adapt to changing loads, ensuring the structure's durability and effectiveness in a variety of scenarios.

Figures 12, 13, 14, 15, and 16 show what happens to the fields when an outside mechanical load (\(q_0\)) is applied while the viscous coefficient \({\uptau }_{\text{v}}\) and Winkler foundation parameter \({\text{K}}_{\text{s}}\) stay fixed. These forms illustrate that the size of the mechanical load (\(q_0\)) greatly affects the distribution of several physical field parameters. Raising the mechanical load results in an increase in thermodynamic temperature, displacement, and lateral fields, which is particularly evident at the highest points of the curves. When \(q_0 = 0\), it indicates that there is no external mechanical impact. Furthermore, when \(\omega = 0\), it indicates that the mechanical load is a constant, non-negotiable regulator. Furthermore, the data suggests that as the intensity of the external stimulus increases, so does the amplitude of lateral oscillation, temperature, displacement, and bending torque. Nevertheless, it is noteworthy that the bending torque diminishes as \(q_0\) increases. This phenomenon can be attributed to the dynamic reaction that decreases the rigidity of the nanoparticle when subjected to bending.

Fig. 12
figure 12

The transverse deflection \(w\) via the external mechanical load \(q_0\)

Full size image
Fig. 13
figure 13

The temperature change \(\theta\) via the external mechanical load \(q_0\)

Full size image
Fig. 14
figure 14

The radial displacement \(u\) via the external mechanical load \(q_0\)

Full size image
Fig. 15
figure 15

The radial thermal stress \(\sigma_{rr}\) via the external mechanical load \(q_0\)

Full size image
Fig. 16
figure 16

The flexure moment \(M_{rr}\) via the external mechanical load \(q_0\)

Full size image

This subsection explains how the external mechanical load changes temperature (\(\theta\)), thermal deflection (\(w\)), radial thermal stress (\(\sigma_{rr}\)), flexure moment (\(M_{rr}\)), and displacement (\(u\)) in a clamped microplate (see Figs. 12, 13, 14, 15, 16). Figure 12 illustrates the effect of external mechanical loads on the thermal deflection (\(w\)) of the clamped microplate. The association indicates that mechanical stress has a significant impact on the microplate deformation and bending caused by heat processes. Elevating the mechanical load causes changes in the microplate's deflection profile. The thermal deflection (\(w\)) is directly proportional to the external mechanical load, implying that larger loads lead to greater deflection (Chen and Wang 2021). The observed deflection (\(w\)) is the result of a combination of thermal expansion and mechanical deformation. This emphasizes the significance of considering both thermal and mechanical aspects when examining the response of microplates to external stressors.

Figure 13 depicts the impact of external mechanical forces on the temperature change (\(\theta\)) in the clamped microplate. Modifying the external mechanical stress might change the way heat is distributed, which may affect the thermal properties of the microplate. Variations in temperature distribution caused by mechanical loading can result in uneven thermal expansion, which can impact the overall structural performance.

Figure 14 shows the relationship between the external mechanical load \(q_0\) and the displacement change (\(u\)) in a circular flexible microplate. It can be seen from the figure that the total displacement (\(u\)) decreases with the magnitude of the external mechanical force at some points near the outer surface while it increases at other points inside the surface. Excessive displacement caused by increased loads can lead to structural failure or functional problems, especially in precision applications where maintaining structural integrity is of paramount importance. These results emphasize the importance of considering both thermal and mechanical effects when studying and constructing a microplate.

Figure 15 shows the effect of an external mechanical force on the radial thermal stress (\(\sigma_{rr}\)) in the clamped microplate. The amount and spread of stress caused by thermal processes are affected by the mechanical load. When the mechanical load changes, so do the size and arrangement of radial thermal stress. Applying an external mechanical load causes a rise in radial thermal stress, especially in areas experiencing higher mechanical loads, leading to intensified radial strains. Monitoring the radial stress (\(\sigma_{rr}\)) is essential to ensure it does not exceed the material's yield strength, as high radial stress may result in structural collapse. Figure 16 shows how an external mechanical load affects the clamped microplate's bending moment (\(M_{rr}\)). Mechanical stress influences the distribution of bending moments produced by thermal processes. The bending moment (\(M_{rr}\)) drops in direct proportion to an increase in external mechanical stress, suggesting that higher mechanical loads result in reduced bending moments within the microplate.

Selecting materials with suitable mechanical and thermal qualities is essential to withstand expected loads and thermal stresses while maintaining deflection and stress levels within acceptable thresholds. By accurately estimating the mechanical load, designers can regulate deflection and ensure that it stays within the specified range for the application (Djabrouhou et al. 2024). Performing a comprehensive examination of stress distribution is crucial to guaranteeing that mechanical loads do not surpass the yield strength of the material. This may entail improving the shape of the microplate, incorporating reinforcements, or modifying mechanical loads to minimize stress concentrations and mitigate the likelihood of structural collapse (Chen and Lin 2024; Marin et al. 2021).

8 Conclusions

The study examines the viscoelastic properties of Kelvin-Voigt-type circular plate resonators, taking into account the effects of thermoelastic coupling. These resonators are assumed to have uniform composition and properties in all directions, in line with Winkler's principle. They are subjected to a harmonic external flow that changes over time. The study uses a modified two-phase thermoelasticity (DPL) model that incorporates limited thermomechanical diffusion and viscous effects. It aims to understand the behavior of various physical fields within the resonators and evaluate how different conditions affect their performance. Specifically, the research examines the effects of viscosity, Winkler foundation, mechanical excitation intensity, and phase delay on the physical fields. The study provides valuable insights into the viscoelastic characteristics of circular plate resonators by analyzing results under specific boundary conditions, highlighting the significance of thermoelastic coupling, viscosity, Winkler foundation, mechanical excitation, and phase delay in determining their performance.

We can summarize the key findings of this study as follows:

  • The viscous thermal damping parameter has a significant impact on the dynamic response of thermoelastic microplates. The numerical simulation findings indicate that an increase in viscous parameter leads to a reduction in deflection.

  • Accurate representation of viscous phenomena is essential for accurately forecasting the performance and durability of resonators in real-world scenarios.

  • The revised DPL theory of thermoelasticity, which integrates a thermal conductivity model, demonstrates efficacy in accurately modelling these effects.

  • Increasing the rigidity of the foundation improves the regulation of heat within the microplate, resulting in an even distribution of temperature and perhaps decreasing the occurrence of concentrated thermal stress.

  • The rigidity of the Winkler foundation has a substantial impact on the dynamic behavior of the microplate. Increased stiffness results in enhanced resistance to deformation and more even distribution of load and temperature.

  • A stiffer foundation minimizes localized bending moments, enhancing the durability and reliability of the structure.

  • The displacement initially decreases with the amount of external mechanical force at some points near the outer surface while it increases at other points inside the surface.

  • When the microplate is subjected to external forces, the energy generated by the mechanical stress can be converted into heat within the microplate material. This temperature increase is due to the dissipation of mechanical energy as heat energy inside the microplate.

  • Increased loading can lead to a decrease in bending resistance, which in turn affects stability. Furthermore, increased mechanical stresses result in a larger total displacement, which has a significant impact on the structural integrity.

  • These findings are crucial for the development and improvement of micro-electromechanical systems (MEMS), which necessitate accurate management of mechanical and thermal reactions.

  • In the future, the model can be expanded to encompass nonlinear systems. Additional inquiry and empirical examination in this domain may also result in progress in the development and improvement of resonator systems.