1 Introduction

In recent years, along with the rapid development of nanotechnology, nanoelectromechanical devices have become one of the basic components of novel mechanical systems. Among unparalleled properties of a NEMS device are miniature size, low cost manufacturing process, remarkable reliability, low consumption of energy, and high precision. NEMS systems are applicable in wide variety of engineering devices such as resonators, capacitive sensors, nanoswitches, nanorelays, nanovalves, bandpass filters, mass and force detection, pressure sensors, biosensors, nano energy harvesters, and atomic force microscopes. Nanobeams and nanoplates are known as the main components of such devices so that their operations are based on the bending vibration or resonant oscillations for the case of resonators. Thus, it is essential to analyze the dynamic characteristics of novel NEMS structures with the aim of improving performance.

A great deal of research has been carried out on the nonlinear dynamic response of NEMS/MEMS resonators under electrostatic actuation. Furthermore, many valuable researches have been performed on the static and dynamic pull-in instabilities of nanoswitches and nanosensors under the effect of DC electrostatic load (Askari and Tahani 2017; Dai and Wang 2017; Fakhrabadi and Yang 2015; Miandoab et al. 2017; Mirkalantari et al. 2017; Rokni et al. 2013; Shaat and Mohamed 2014; SoltanRezaee and Afrashi 2016; SoltanRezaee et al. 2016). Zhao et al. (2003) presented a review article in 2005, in which the mechanics of adhesion in MEMS systems has been investigated. In their study, roughness ratio was introduced as a key parameter to describe the importance of surface roughness for adhesion contact which can be due to Casimir force in NEMS structures, or carbon nanotubes sticking to a substrate, as examples. Hui et al. (Wen-Hui and Ya-Pu 2003) examined the effects of geometrical properties of nanoscale electrostatic actuator on bifurcation of equilibrium points from the case in which there exists no equilibrium point to the case including two equilibrium points. They also considered the same nanoactuator to study the effect of Casimir dispersion force on the nonlinear dynamics of the system (Lin and Zhao 2005b). Guo et al. (Guo and Zhao 2004) proposed a model for stability analysis of electrostatic torsional NEMS devices incorporating both the influences of Van Der Waals (vdW) and Casimir regimes. Their results showed that even for the case of zero voltage load, pull-in can still occur for sufficiently small gaps, that is due to existence of vdW and Casimir torques. Kacem et al. (Kacem et al. 2012) studied the nonlinear dynamics of NEMS-based sensors under superharmonic resonance using the method of multiple scales. Their results revealed that the dynamic pull-in voltage will be retarded by decreasing the AC voltage. Abdel-Rahman and Nayfeh (Abdel-Rahman and Nayfeh 2003) examined the secondary resonances of electrostatically actuated resonant microsensors. They employed the method of the multiple scales to obtain the frequency–response equation. Lin et al. (Lin and Zhao 2005a) presented an analytical solution for the pull-in gap in nanometer switches considering the effect of Casimir force using perturbation theory. Ouakad and Younis (2010) investigated nonlinear dynamics of an electrically actuated carbon nanotube (CNT) resonator. According to the two sources of nonlinearities (midplane stretching and electrostatic force), the appearance of various interesting dynamic behaviors are reported including hardening (Alsaleem et al. 2009; Mehrdad Pourkiaee et al. 2015; Najar et al. 2010a), softening (Najar et al. 2010b), hysteresis (Azizi et al. 2014; Kacem et al. 2009), jump phenomenon and multi-valued response (Younis 2011). Dynamic behavior of bonded double-piezoelectric nanobeam-based devices was examined by Arani et al. (2014). They focused on the piezoelectric control of the proposed system based on wave propagation theory in three different cases, in-plane wave, out-of plane wave, and wave propagation while one nanobeam is considered to be fixed. Arani et al. (Ghorbanpour Arani et al. 2017) performed vibrational analysis of the double of sandwich beams which are connected by viscoelastic medium. In their system, each sandwich beam consists of one magnetorheological core and two carbon nanotubes/fiber/polymer composite face sheets. They reported on the influences of various parameters such as core-to-face sheets thickness ratio, magnetic field intensity, visco-Pasternak coefficients on the natural frequencies and loss factors of coupled system. They stated that the modal loss factor decreases by increasing magnetic field intensity. Pourkiaee et al. (2016) presented an investigation on the subharmonic resonance of an electrically actuated piezoelectric nanobeam resonator incorporating surface effects and dispersion Van Der Waals force. The influence of piezoelectric voltage, surface effects and interatomic forces was studied on the natural frequencies, static equilibrium, pull-in voltages, and principle parametric resonance of the nanoresonator. They also examined the nonlinear modal interactions and bifurcations of the same system with three-to-one internal resonances (Pourkiaee et al. 2017). Their results show that the system exhibits rich dynamic behaviors such as Hopf bifurcations, periodic and quasi-periodic motions. Viscoelasticity effects on resonant response of a shear deformable extensible microbeam were studied by Farokhi and Ghayesh (2017). They found that viscoelastic model is an amplitude-dependent energy mechanism which gives more accurate results compared to a purely elastic model. The stability and the nonlinear oscillations of both single-walled and double-walled CNTs under electrostatic excitation were investigated in depth by Hajnayeb and Khadem (2011). Arani et al. (2015a) investigated nonlinear vibration and instability of smart composite microtube conveying fluid based on modified couple-stress theory. They parametrically studied the combined effects of the Knudsen number, couple-stress parameter, fibers volume percentage, temperature change, elastic medium, and aspect ratio on the nonlinear frequency and critical fluid speed. Their results indicated that, the more the impact of the small-scale parameter, the larger the natural frequency and critical fluid velocity. Xu and Younis (2016) investigated the nonlinear behaviors of a CNT actuated under large electrostatic forces. They expanded the nonlinear displacement-dependent term into enough number of terms of the Taylor series. Wang et al. (2010) proposed a methodology to study the effect of residual surface stress induced in the bulk material on the elastic properties of nanostructures. The surface elasticity notation was introduced in terms of both the Lagrangian and Eulerian coordinates systems, and it was proved that even for the case of infinitesimal deformations, difference must be made between the undeformed and deformed configurations of elastic body. As a case study, they focused on Al nanowires to analyze the size-dependent characteristics of pure bending problem. They reported that the effective Young’s modulus of Al nanowires was remarkably affected by the impact of surface tension. Li et al. (2012) investigated both experimentally and theoretically the nonlinear dynamics of a resonant pressure sensor under electro-thermal excitation; they employed the multiple time scales method together with the Galerkin’s procedure to obtain the frequency–response behavior of the system. There are also numerous papers in the literature which have employed surface elasticity theory to study pull-in instability (Fu and Zhang 2011), buckling (Wang and Feng 2009; Yan and Jiang 2012) and free vibration (Zhang and Wang 2012) of nanostructures.

In this work, the nonlinear characteristics of a double-layered viscoelastic NEMS device under simultaneous electrostatic and piezoelectric actuations are studied. To include the effects of size-dependency and surface energy, the modified couple-stress theory and Gurtin–Murdoch elasticity theory are employed, respectively. In addition, the Casimir force is considered as intermolecular dispersion force between the fixed and movable electrodes. The frequency–response behavior of the system for large-amplitude of AC voltage, which is known as hard excitation is obtained through numerical simulations. The influences of different parameters such as viscoelasticity impact, size-dependency, surface effects, and piezoelectric voltage value on the frequency–response behavior of the system is examined near the superharmonic resonance.

2 Mathematical Model

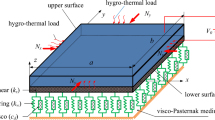
Schematic of a clamped–clamped double-layered viscoelastic NEMS system under the simultaneous piezoelectric and electrostatic actuations is illustrated in Fig. 1. The two viscoelastic piezoelectric nanobeams (VPNBs) are coupled by visco-Pasternak medium which is modeled by spring constant of Winkler-type, \(k_{\text{w}}\), shear constant of Pasternak-type, \(k_{\text{g}}\), and damping coefficient, \(C\). The two VPNBs are of length \(L\), width \(b\) and thickness \(h\), and are surrounded by surface layers. A direct current polarization voltage of \(V_{\text{p}}\) is applied to each of the nanobeams. \(g_{0}\) and \(V_{\text{l}}\) denote the initial gap between the lower nanobeam and the fixed electrode, and the applied electrostatic voltage load, respectively. It is assumed that the voltage load is a combination of a DC bias voltage, \(V_{\text{DC}}\), and an AC voltage with amplitude \(V_{\text{AC}}\) and frequency \(\varOmega\). As depicted in Fig. 1, the \(xyz\) inertial coordinates system passes through the centroidal axis of the undeformed beam and is located at the left clamped end of the nanobeam. The horizontal and vertical displacements of any point located on the neutral axis of the beam in \(x\) and \(z\) directions are represented by \(u\left( {x,t} \right)\) and \(w\left( {x,t} \right)\), respectively.

Fig. 1
figure 1

Schematic of a clamped–clamped double-layered viscoelastic piezoelectric NEMS system

Full size image

The Casimir regime as distributed inner atomic force induces an attractive force between the lower nanobeam and stationary electrode in the form of

$$F_{\text{cas}} = \frac{{\pi^{2} \hbar cb}}{{240\left( {g_{0} - w\left( {x,t} \right)} \right)^{4} }}$$
(1)

where \(\hbar = 1.055 \times 10^{ - 34} \;{\text{J}}\) denotes the Planck’s constant divided by \(2\pi\), and \(c = 2.998 \times 10^{8} \;{\text{m}}/{\text{s}}\) is the light speed (Lamoreaux 2004). The distributed electrostatic force can be given by

$$F_{\text{elec}} = \frac{{\varepsilon_{0} bV_{l}^{2} }}{{2\left( {g_{0} - w\left( {x,t} \right)} \right)^{2} }}\left( {1 + 0.65\frac{{\left( {g_{0} - w\left( {x,t} \right)} \right)}}{b}} \right)$$
(2)

In expressing Eq. (2), this fact has been taken into account that the geometry is far from the infinite plate capacitors, where the fringing field effect is negligible (Gupta 1997; Huang et al. 2001).

2.1 Surface Energy Contribution

According to the surface elasticity theory proposed by Gurtin and Murdoch, the non-zero components of the surface stresses based on the Kelvin–Voigt model are given by (Gurtin and Murdoch 1975)

$$\tau_{xx} = \tau_{0} + \left( {1 + \eta \frac{\partial }{\partial t}} \right)E^{\text{s}} \varepsilon_{xx} = \tau_{{xx\left( {\text{el}} \right)}} + \tau_{{xx\left( {\text{vs}} \right)}} ,\;\tau_{nx} = \tau_{0} n_{z} \frac{\partial w}{\partial x},\,\,\,\,\,\,n = y,z$$
(3)

where \(\tau_{0}\), \(E^{\text{s}}\), and \(\eta\) are the residual surface stress, surface elastic modulus and the structural viscoelastic damping parameter, respectively. The subscripts (el) and (vs) denote the elastic and viscous parts, respectively. \(n_{z}\) represents the \(z\)-component of the unit outward normal vector, \(n\), to the beam surface. It is worth mentioning that, since the out-of-plane surface stress component \(\left( {\tau_{nx} } \right)\) is independent of the surface modulus, the impact of viscoelasticity is not included in this stress component (Oskouie et al. 2017). For the Euler–Bernoulli beam assumption, the displacement field for each arbitrary material point can be expressed as

$$\tilde{u}\left( {x,z,t} \right) = u\left( {x,t} \right) - z\frac{{\partial w\left( {x,t} \right)}}{\partial x},\,\,\,\,\,\,\,\,\tilde{v}\left( {x,z,t} \right) = 0,\,\,\,\,\,\,\,\,\tilde{w}\left( {x,z,t} \right) = w\left( {x,t} \right)$$
(4)

Assuming low slope for the beam after deformation and using the von-Karman nonlinearity for midplane stretching, the only non-zero component of the strain tensor can be expressed as

$$\varepsilon_{xx} = \frac{{\partial \tilde{u}}}{\partial x} + \frac{1}{2}\left( {\frac{{\partial \tilde{w}}}{\partial x}} \right)^{2} = \frac{{\partial u\left( {x,t} \right)}}{\partial x} - z\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{{\partial w\left( {x,t} \right)}}{\partial x}} \right)^{2}$$
(5)

The contribution of the surface energy to the system’s total strain energy is given by (Ru 2010)

$$\delta U_{\text{S}} = \oint_{\partial A} {\left( {\tau_{{xx\left( {\text{el}} \right)}} \delta \varepsilon_{xx} + \tau_{nx} \delta u_{n,x} } \right)} {\text{d}}S,\,\,\,\,u_{n} \left( {x,t} \right) = n_{z} w\left( {x,t} \right)$$
(6)

where \(\partial A\) is the undeformed surface area of the beam. For a differential element of the surface layer, \({\text{d}}S = {\text{d}}\bar{A}\,{\text{d}}x\), \({\text{d}}\bar{A}\) is the differential perimeter element. The surface virtual work of Kelvin–Voigt damping can be written as

$$\delta W_{\text{S}} = - \oint_{\partial A} {\tau_{{xx\left( {\text{vs}} \right)}} \delta \varepsilon_{xx} } \,{\text{d}}S\,$$
(7)

Note that, here, the piezoelectricity effects on the surface layer are ignored due to lack of strong and comprehensive theoretical model in the literature. The variation of the kinetic energy of the surface layer is as follows:

$$\delta T_{\text{S}} = \int_{0}^{L} {\rho^{\text{s}} A^{\text{s}} \left( {\frac{\partial u}{\partial t}\delta \left( {\frac{\partial u}{\partial t}} \right) + \frac{\partial w}{\partial t}\delta \left( {\frac{\partial w}{\partial t}} \right)} \right){\text{d}}x} ,$$
(8)

where \(\rho^{\text{s}}\) is the mass density of the surface layer, and \(A^{\text{s}} = 2\left( {b + h} \right)\) is the perimeter of the cross section.

2.2 Bulk Energy Contribution

In the present work, the modified couple-stress theory is employed to consider the size effect and discrete nature of the nanobeam keeping the continuity assumption. Taking into consideration the MCST for piezoelectric materials, the strain energy density stored in elastic bulk materials with infinitesimal deformation occupying volume \(V\) is given by (Yang et al. 2002)

$$U_{\text{B}} = \frac{1}{2}\int_{V} {\left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} - E_{k} D_{k} } \right)} \,{\text{d}}V$$
(9)

where \(\sigma_{ij}\), \(\varepsilon_{ij}\), \(m_{ij}\), \(\chi_{ij}\), \(D_{k}\), \(E_{k}\), are stress tensor, strain tensor, deviatoric part of couple-stress tensor, symmetric curvature tensor, electric displacement and electric field, respectively. According to the Kelvin–Voigt model, these mechanical and electrical components can be obtained as (Arefi and Zenkour 2017)

$$\begin{aligned} & \sigma_{ij} = \left( {1 + \eta \frac{\partial }{\partial t}} \right)\left( {C_{ijkl} \varepsilon_{kl} - e_{kij} E_{k} } \right) = \sigma_{{ij\left( {\text{el}} \right)}} + \sigma_{{ij\left( {\text{vs}} \right)}} ;\,\,\,\,\,\,D_{i} = \left( {1 + \eta \frac{\partial }{\partial t}} \right)\left( {e_{ikl} \varepsilon_{kl} + \lambda_{ik} E_{k} } \right) = D_{{i\left( {\text{el}} \right)}} + D_{{i\left( {\text{vs}} \right)}} \\ & m_{ij} = 2G_{xy} l^{2} \left( {1 + \eta \frac{\partial }{\partial t}} \right)\chi_{ij} = m_{{ij\left( {\text{el}} \right)}} + m_{{ij\left( {\text{vs}} \right)}} ;\,\,\,\,\,\,\,\chi_{ij} = \frac{1}{2}\left( {\frac{{\partial \theta_{i} }}{{\partial x_{j} }} + \frac{{\partial \theta_{j} }}{{\partial x_{i} }}} \right)\,\,\,\,\,i,j = 1,2,3;\,\,\,\theta_{i} \, = \frac{1}{2}\varepsilon_{ijk} u_{k,j} \\ \end{aligned}$$
(10)

where \(l\) is a materials’ size effect parameter that varies from one material to another or from one scale to another scale, and \(\theta\) is the rotation vector. Additionally, \(C_{ijkl}\), \(e_{kij}\), \(\lambda_{ik}\) denote the elastic constant, piezoelectric voltage’s constant and dielectric constant, respectively. Due to the small thickness of the nanobeams, the one-dimensional electric field is assumed to be constant and it can be written as

$$E_{z} = \frac{{V_{\text{p}} }}{h}$$
(11)

where \(V_{\text{p}}\) is the bias piezoelectric voltage. Hence, based on Eq. (10), \(D_{z}\) is the one-dimensional electric displacement and it can be expressed as

$$D_{z} = \left( {1 + \eta \frac{\partial }{\partial t}} \right)\left( {\bar{e}_{31} \varepsilon_{xx} + \lambda_{33} E_{z} } \right) = D_{{z\left( {\text{el}} \right)}} + D_{{z\left( {\text{vs}} \right)}}$$
(12)

According to the Euler–Bernoulli beam assumption, the only non-zero component of the force stress tensor can be expressed as

$$\sigma_{xx} = \left( {1 + \eta \frac{\partial }{\partial t}} \right)\underbrace {{\left( {C_{11} - \frac{{C_{13}^{2} }}{{C_{33} }}} \right)}}_{{\bar{C}_{11} }}\varepsilon_{xx} - \left( {1 + \eta \frac{\partial }{\partial t}} \right)\underbrace {{\left( {e_{31} - \frac{{C_{13} }}{{C_{33} }}e_{33} } \right)}}_{{\bar{e}_{31} }}E_{z} + \underbrace {{\left( {\frac{{C_{13} }}{{C_{33} }}} \right)}}_{\upsilon }\sigma_{zz} = \sigma_{{xx\left( {\text{el}} \right)}} + \sigma_{{xx\left( {\text{vs}} \right)}}$$
(13)

Here, \(\bar{C}_{11}\) and \(\bar{e}_{11}\), respectively, denote the reduced elastic and piezoelectric voltage constants. The symmetric curvature tensor \(\chi\) has two non-zero components given by

$$\chi_{xy} = - \frac{1}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }}\,\,\,\,\,,\,\,\chi_{yx} = \chi_{xy} \,\,$$
(14)

The corresponding components of m can be obtained as

$$m_{xy} = 2l^{2} C_{66} \left( {1 + \eta \frac{\partial }{\partial t}} \right)\chi_{xy} = m_{{xy\left( {\text{el}} \right)}} + m_{{xy\left( {\text{vs}} \right)}}$$
(15)

It is worth mentioning that, in the above equations, the influence of electrical hysteresis (Arefi and Zenkour 2017) is also considered. According to Lu et al. (2006), \(\sigma_{zz}\) varies linearly through the thickness of the nanobeam as follows:

$$\sigma_{zz} = \frac{2z}{h}\left( {\tau_{0} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} - \rho^{s} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }}} \right)$$
(16)

Based on Eqs. (12)–(16), the variational form of the potential energy of the system, on the basis of MCST, can be formulated as

$$\delta U_{\text{B}} = \int_{V} {\left( {\sigma_{{xx\left( {\text{el}} \right)}} \delta \varepsilon_{xx} + 2m_{{xy\left( {\text{el}} \right)}} \delta \chi_{xy} - E_{z} \delta D_{{z\left( {\text{el}} \right)}} } \right)} \,{\text{d}}V$$
(17)

The nonconservative work done by the viscous parts of the stress and the deviatoric part of the symmetric couple-stress tensors can be written as

$$\delta W_{\text{B}} = - \int_{V} {\left( {\sigma_{{xx\left( {\text{vs}} \right)}} \delta \varepsilon_{xx} + 2m_{{xy\left( {\text{vs}} \right)}} \delta \chi_{xy} - E_{z} \delta D_{{z\left( {\text{vs}} \right)}} } \right)} \,{\text{d}}V$$
(18)

The variation of the kinetic energy of the bulk material can be written as

$$\delta T_{\text{B}} = \int_{0}^{L} {\rho A\left( {\frac{\partial u}{\partial t}\delta \left( {\frac{\partial u}{\partial t}} \right) + \frac{{\partial \tilde{w}}}{\partial t}\delta \left( {\frac{\partial w}{\partial t}} \right)} \right){\text{d}}x} ,$$
(19)

where \(\rho\) is the mass density of the bulk material, and \(A\) is the area of the nanobeam cross section.

2.3 Equations of Motion

In this section, the differential equations of motion governing the behavior of the NEMS system are derived by the means of the extended Hamilton’s principle.

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T_{\text{B}} + \delta T_{\text{S}} - \left( {\delta U_{\text{B}} + \delta U_{\text{S}} } \right) + \delta W_{\text{B}} + \delta W_{\text{S}} + \delta W_{\text{ext}}^{(1)} + \delta W_{\text{ext}}^{(2)} } \right)} \,{\text{d}}t = 0$$
(20)

The external work done by the electrostatic and Casimir forces is equal to:

$$\delta W_{\text{ext}}^{(1)} = \int_{0}^{L} {\left( {F_{\text{elec}} + F_{\text{cas}} } \right)} \,\delta w{\text{d}}x$$
(21)

Considering visco-Pasternak medium between the two VPNBs, the external force can be written as follows (Arani et al. 2015b)

$$F_{\text{vP}} = C\left( {\dot{w}_{1} - \dot{w}_{2} } \right) + k_{\text{w}} \left( {w_{1} - w_{2} } \right) - k_{\text{g}} \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {w_{1} - w_{2} } \right)$$
(22)

And, the corresponding external work done by visco-Pasternak components is given by

$$\delta W_{\text{ext}}^{(2)} = \int_{0}^{L} {\left( { - F_{\text{vP}} \delta w_{1} + F_{\text{vP}} \delta w_{2} } \right){\text{d}}x}$$
(23)

For convenience, the following non-dimensional quantities are introduced:

$$\tilde{w}_{1} = \frac{{w_{1} }}{{g_{0} }},\;\tilde{w}_{2} = \frac{{w_{2} }}{{g_{0} }}\;\tilde{x} = \frac{x}{L}\;\tilde{t} = \frac{t}{{t^{*} }},\;\tilde{\eta } = \frac{\eta }{{t^{*} }},\;\tilde{\varOmega } = \varOmega t^{*} ,$$
(24)

where \(t^{*}\) is a characteristic time (timescale) defined as follows:

$$t^{*} = \sqrt {\frac{{\left( {\rho A} \right)_{\text{eq}} L^{4} }}{{\left( {EI} \right)_{\text{eq}} }}}$$
(25)

After some straightforward mathematical manipulations, and dropping the tildes for the sake of simplicity, one can derive the non-dimensional differential equations of motion for the transverse vibration of the NEMS device, as follows:

Nanobeam 1

$$\begin{aligned} & \frac{{\partial^{2} w_{1} \left( {x,t} \right)}}{{\partial t^{2} }} + \left( {1 + \beta_{1} + \beta_{2} } \right)\frac{{\partial^{4} w_{1} \left( {x,t} \right)}}{{\partial x^{4} }} + \left( {1 + \beta_{1} } \right)\eta \frac{{\partial^{5} w_{1} \left( {x,t} \right)}}{{\partial t\partial x^{4} }} + \beta_{6} \frac{{\partial^{4} w_{1} \left( {x,t} \right)}}{{\partial t^{2} \partial x^{2} }} \\ & \quad - \left[ {\beta_{3} + \beta_{4} + \beta_{5} \varGamma \left( {w_{1} ,w_{1} } \right) + 2\beta_{5} \eta \varGamma \left( {\dot{w}_{1} ,w_{1} } \right)} \right]\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + K_{\text{w}} \left( {w_{1} - w_{2} } \right) + C_{\text{D}} \left( {\frac{{\partial w_{1} }}{\partial t} - \frac{{\partial w_{2} }}{\partial t}} \right) \\ & \quad - K_{\text{G}} \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {w_{1} - w_{2} } \right) = \frac{{\beta_{7} \left( {V_{\text{DC}} + V_{\text{AC}} \cos \left( {\varOmega t} \right)} \right)^{2} }}{{\left( {1 - w_{1} } \right)^{2} }}\left( {1 + b_{0} \left( {1 - w_{1} } \right)} \right) + \beta_{8} \frac{1}{{\left( {1 - w_{1} } \right)^{4} }} \\ \end{aligned}$$
(26)

Nanobeam 2

$$\begin{aligned} & \frac{{\partial^{2} w_{2} \left( {x,t} \right)}}{{\partial t^{2} }} + \left( {1 + \beta_{1} + \beta_{2} } \right)\frac{{\partial^{4} w_{2} \left( {x,t} \right)}}{{\partial x^{4} }} + \left( {1 + \beta_{1} } \right)\eta \frac{{\partial^{5} w_{2} \left( {x,t} \right)}}{{\partial t\partial x^{4} }} + \beta_{6} \frac{{\partial^{4} w_{2} \left( {x,t} \right)}}{{\partial t^{2} \partial x^{2} }} - \left[ {\beta_{3} + \beta_{4} + \beta_{5} \varGamma \left( {w_{2} ,w_{2} } \right)} \right. \\ & \quad + \left. {2\beta_{5} \eta \varGamma \left( {\dot{w}_{2} ,w_{2} } \right)} \right]\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} - K_{\text{w}} \left( {w_{1} - w_{2} } \right) - C_{\text{D}} \left( {\frac{{\partial w_{1} }}{\partial t} - \frac{{\partial w_{2} }}{\partial t}} \right) + K_{\text{G}} \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {w_{1} - w_{2} } \right) = 0 \\ \end{aligned}$$
(27)

Subject to the following boundary conditions:

$$w_{i} \left( {0,t} \right) = w_{i} \left( {1,t} \right) = 0,\,\,\,\,\,\,w^{\prime}_{i} \left( {0,t} \right) = w^{\prime}_{i} \left( {1,t} \right) = 0;\,\,i = 1,2$$
(28)

where

$$\begin{aligned} & \varGamma \left( {\varphi_{1} \left( {x,t} \right),\varphi_{2} \left( {x,t} \right)} \right) = \int_{0}^{1} {\frac{{\partial \varphi_{1} }}{\partial x} \cdot \frac{{\partial \varphi_{2} }}{\partial x}} \,{\text{d}}x,\;\beta_{1} = \frac{{Al^{2} C_{66} }}{{\left( {\text{EI}} \right)_{\text{eq}} }},\;\beta_{2} = - \frac{{2\upsilon \tau_{0} I}}{{h\left( {\text{EI}} \right)_{\text{eq}} }},\;\beta_{3} = \frac{{F_{\text{s}} L^{2} }}{{\left( {\text{EI}} \right)_{\text{eq}} }} \\ & \beta_{4} = - \frac{{2V_{\text{p}} A\bar{e}_{31} L^{2} }}{{h\left( {\text{EI}} \right)_{\text{eq}} }},\;\beta_{5} = \frac{{\left( {\text{EA}} \right)_{\text{eq}} g_{0}^{2} }}{{2\left( {\text{EI}} \right)_{\text{eq}} }},\;\beta_{6} = \frac{{\left( {\rho I} \right)_{\text{eq}} }}{{L^{2} \left( {\rho A} \right)_{\text{eq}} }},\;\beta_{7} = \frac{{\varepsilon_{0} bL^{4} }}{{2g_{0}^{3} \left( {\text{EI}} \right)_{\text{eq}} }},\;\beta_{8} = \frac{{\pi^{2} \hbar cbL^{4} }}{{240g_{0}^{5} \left( {\text{EI}} \right)_{\text{eq}} }} \\ & K_{\text{w}} = \frac{{k_{\text{w}} L^{4} }}{{\left( {\text{EI}} \right)_{\text{eq}} }},\;C_{\text{D}} = \frac{{CL^{4} }}{{\left( {\text{EI}} \right)_{\text{eq}} t^{*} }},K_{\text{G}} = \frac{{k_{\text{g}} L^{4} }}{{\left( {\text{EI}} \right)_{\text{eq}} }},b_{0} = \frac{0.65}{b}g_{0} \;\left( {\text{EI}} \right)_{\text{eq}} = \bar{C}_{11} I + E^{\text{s}} I^{\text{s}} , \\ & \left( {\text{EA}} \right)_{\text{eq}} = \bar{C}_{11} A + E^{\text{s}} A^{\text{s}} ,\;\left( {\rho A} \right)_{\text{eq}} = \rho A + \rho^{\text{s}} A^{\text{s}} ,\;F_{\text{s}} = 2\tau_{0} \left( {2b + h} \right),\;\left( {\rho I} \right)_{\text{eq}} = \frac{{2\upsilon \rho^{s} I}}{h} \\ \end{aligned}$$
(29)

The integral term in Eqs. (26) and (27) stands for the midplane stretching of the nanobeam due to the immovable edges.

3 Reduced-Order Model of VPNBs

In this section, to generate the reduced-order model (ROM) of the system, Galerkin discretization method is applied to the coupled partial differential equations, Eqs. (26) and (27). Therefore, the following finite series are assumed as the solution for the motions of the NEMS resonator.

$$\begin{aligned} & w_{1} \left( {x,t} \right) = \sum\limits_{i = 1,3,5, \ldots }^{{N_{1} }} {q_{i} \left( t \right)\varphi_{i} \left( x \right)} \\ & w_{2} \left( {x,t} \right) = \sum\limits_{i = 1,3,5, \ldots }^{{N_{2} }} {p_{i} \left( t \right)\varphi_{i} \left( x \right)} \\ \end{aligned}$$
(30)

where \(\varphi_{i} \left( x \right)\) is the eigenfunction of doubly clamped linear undamped nanobeam under piezoelectric actuation, considering the effects of size and surface energy. \(q_{i} \left( t \right)\) and \(p_{i} \left( t \right)\) indicate the \(i\)’th time-dependent generalized coordinates for \(w_{1}\) and \(w_{2}\) motions, respectively. Note, that here only the symmetric eigenfunctions are considered because of the symmetry in the configuration of the NEMS device and the electrostatic and dispersion Casimir forces. In addition, \(\varphi_{i}\) s are normalized such that \(\int_{0}^{1} {\varphi_{i} \cdot \varphi_{j} } \,{\text{d}}x = \delta_{ij}\) and satisfying the following eigenvalue problem:

$$\left( {1 + \beta_{1} + \beta_{2} } \right)\varphi_{i}^{\text{IV}} = \left( {\beta_{3} + \beta_{4} + \beta_{6} \omega_{i}^{2} } \right)\varphi^{\prime\prime}_{i} + \omega_{i}^{2} \varphi_{i} ,\;\varphi_{i} \left( x \right) = 0,\,\varphi^{\prime}_{i} \left( x \right) = 0\,\,\,\,\,\,{\text{at}}\,\,\,x = 0,1$$
(31)

where \(\omega_{i}\) is the \(i'\)th dimensionless natural frequency of the corresponding linear system. Substituting Eq. (30) into Eqs. (26) and (27) and using Eq. (31) to eliminate \(\varphi_{i}^{\text{IV}}\), then based on Galerkin technique multiplying both sides by \(\varphi_{n}\), and integrating the resultant over the length of the nanobeam reduces to a set of nonlinear differential equations in terms of generalized coordinates, \(q_{i}\) and \(p_{i}\).

$$\begin{aligned} & \ddot{q}_{n} + \sum\limits_{i = 1}^{N} {\left( {\beta_{3} + \beta_{4} + \beta_{6} \omega_{i}^{2} } \right)k_{ni} q_{i} } + \omega_{n}^{2} q_{n} + \frac{{\left( {1 + \beta_{1} } \right)\eta }}{{\left( {1 + \beta_{1} + \beta_{2} } \right)}}\left( {\sum\limits_{i = 1}^{N} {\left( {\beta_{3} + \beta_{4} + \beta_{6} \omega_{i}^{2} } \right)k_{ni} \dot{q}_{i} } + \omega_{n}^{2} \dot{q}_{n} } \right) \\ & \quad - \left( {\beta_{3} + \beta_{4} } \right)\sum\limits_{i = 1}^{N} {k_{ni} q_{i} } - \beta_{5} \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\sum\limits_{l = 1}^{N} {q_{i} q_{j} q_{l} k_{nl} \int_{0}^{1} {\varphi^{\prime}_{i} \varphi^{\prime}_{j} {\text{d}}x} } } } - 2\beta_{5} \eta \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\sum\limits_{l = 1}^{N} {\dot{q}_{i} q_{j} q_{l} k_{nl} \int_{0}^{1} {\varphi^{\prime}_{i} \varphi^{\prime}_{j} {\text{d}}x} } } } + \beta_{6} \sum\limits_{i = 1}^{N} {k_{ni} \ddot{q}_{i} } \\ & \quad + \sum\limits_{i = 1}^{N} {\left( {K_{\text{w}} \delta_{ni} - K_{\text{G}} k_{ni} } \right)\left( {q_{i} - p_{i} } \right)} + C_{\text{D}} \sum\limits_{i = 1}^{N} {k_{ni} \left( {\dot{q}_{i} - \dot{p}_{i} } \right)} = \beta_{7} \left( {V_{\text{DC}} + V_{\text{AC}} \cos \left( {\varOmega t} \right)} \right)^{2} \\ & \quad \times \int_{0}^{1} {\left( {\frac{{\varphi_{n} }}{{\left( {1 - \sum\limits_{i = 1}^{N} {k_{ni} q_{i} } } \right)^{2} }}\left( {1 + b_{0} \left( {1 - \sum\limits_{i = 1}^{N} {k_{ni} q_{i} } } \right)} \right)} \right){\text{d}}x} + \beta_{8} \int_{0}^{1} {\frac{{\varphi_{n} {\text{d}}x}}{{\left( {1 - \sum\limits_{i = 1}^{N} {k_{ni} q_{i} } } \right)^{4} }}} ,\,\,\,\,\,\,\,\,\,\,n = 1,2, \ldots ,N \\ \end{aligned}$$
(32)
$$\begin{aligned} & \ddot{p}_{n} + \sum\limits_{i = 1}^{N} {\left( {\beta_{3} + \beta_{4} + \beta_{6} \omega_{i}^{2} } \right)k_{ni} p_{i} } + \omega_{n}^{2} p_{n} + \frac{{\left( {1 + \beta_{1} } \right)\eta }}{{\left( {1 + \beta_{1} + \beta_{2} } \right)}}\left( {\sum\limits_{i = 1}^{N} {\left( {\beta_{3} + \beta_{4} + \beta_{6} \omega_{i}^{2} } \right)k_{ni} \dot{p}_{i} } + \omega_{n}^{2} \dot{p}_{n} } \right) \\ & \quad - \left( {\beta_{3} + \beta_{4} } \right)\sum\limits_{i = 1}^{N} {k_{ni} p_{i} } - \beta_{5} \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\sum\limits_{l = 1}^{N} {p_{i} p_{j} p_{l} k_{nl} \int_{0}^{1} {\varphi^{\prime}_{i} \varphi^{\prime}_{j} {\text{d}}x} } } } - 2\beta_{5} \eta \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {\sum\limits_{l = 1}^{N} {\dot{p}_{i} p_{j} p_{l} k_{nl} \int_{0}^{1} {\varphi^{\prime}_{i} \varphi^{\prime}_{j} {\text{d}}x} } } } + \beta_{6} \sum\limits_{i = 1}^{N} {k_{ni} \ddot{p}_{i} } \\ & \quad - \sum\limits_{i = 1}^{N} {\left( {K_{\text{w}} \delta_{ni} - K_{\text{G}} k_{ni} } \right)\left( {q_{i} - p_{i} } \right)} - C_{\text{D}} \sum\limits_{i = 1}^{N} {k_{ni} \left( {\dot{q}_{i} - \dot{p}_{i} } \right)} = 0,\,\,\,\,\,\,\,\,\,\,n = 1,2, \ldots ,N \\ \end{aligned}$$
(33)

where

$$k_{ni} = \int_{0}^{1} {\varphi^{\prime\prime}_{i} \left( x \right)\varphi_{n} \left( x \right){\text{d}}x}$$
(34)

In this work, it is assumed that \(N_{1} = N_{2} = N\). In Eqs. (32) and (33), overdot indicates \({\raise0.7ex\hbox{$\partial $} \!\mathord{\left/ {\vphantom {\partial {\partial t}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial t}$}}\) and prime stands for \({\raise0.7ex\hbox{$\partial $} \!\mathord{\left/ {\vphantom {\partial {\partial x}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial x}$}}\), and \(\delta_{ni}\) symbols the kronecker delta.

The two terms in the right hand side of Eq. (32) represent the electrostatic and Casimir dispersion forces, respectively, which consist of complex displacement-dependent nonlinearities in the denominator. A combined arclength continuation-shooting method is schemed to capture the frequency–response curves of the system. Although this method causes large computational cost, it is very reliable. In the rest of the paper, the influences of the length-scale parameter, surface energy, interatomic dispersion force, and piezoelectric voltage on the frequency–response behavior of the double-layered VPNBs system near superharmonic (Ω = 3ω0) resonance are investigated. To this aim, the complicated set of nonlinear ODEs is numerically solved employing a combined shooting–arclength continuation scheme with direct-time integration. The Floquet theory is used to perform stability analysis.

4 Results and Discussion

The geometrical parameters of the PZT-5H nanobeams and the values related to the mechanical properties of the bulk, and surface layer are listed in Table 1 (mechanical properties of the surface layer were adopted from (Zhang et al. 2014)).

Table 1 Geometrical and material properties of the PZT-5H nanobeams
Full size table

In the rest of the paper, the numerical simulations are performed for \(K_{\text{w}} = 2\) and \(K_{\text{G}} = 1\) unless indicated in the text. The non-dimensional damping coefficient of the elastic medium, \(C_{\text{D}}\), is set to be 0.1 throughout the simulations. Two-mode approximation is considered for each nanobeam displacement to analyze the nonlinear dynamic response of the double-layer VPNBs. In fact, the system of equations of motion consists of four second-order nonlinear differential equations which are converted to an 8-degree-of-freedom system in state space. The blue and black dots represent the stable solution while the red and violet dots denote the unstable one for the lower and upper nanobeams, respectively.

The influence of the length-scale parameter on the amplitude of the steady-state response of the NEMS system, W1max and W2max, is depicted in Fig. 2. The AC frequency-displacement plots are obtained for three values of length-scale parameter. As observed, the nanoresonator exhibits mixed hardening–softening-type behavior with four saddle-node bifurcation points, \(S_{1}\), \(S_{2}\), \(S_{3}\) and \(S_{4}\). Increasing the amount of length-scale parameter causes the frequency–response branches and consequently the bifurcation points’ loci almost rigidly shift to the right. In other words, the slope of the solution manifolds is not remarkably affected by the impact of the couple-stress parameter. It is also seen that the response amplitude level of the upper nanobeam is smaller than that of the lower one. Moreover, the upper nanobeam shows more extreme softening behavior in comparison with the lower one, which is inferred by the intense bending of the high-amplitude solution manifolds to the left, Fig. 2b.

Fig. 2
figure 2

Influence of the small-scale parameter on AC frequency–response curves of the NEMS resonator near superharmonic resonance; a lower nanobeam, b upper nanobeam. VDC = 1 V and VAC = 2 V

Full size image

For larger impact of viscoelasticity, the effect of the couple-stress parameter on the superharmonic resonance characteristics corresponding to the lower nanobeam is illustrated in Fig. 3. In Fig. 3a, the parameter η is assumed to be 0.0001, and it is seen that for classical continuum theory (CCT), the frequency–response curve consists of both hardening and softening behaviors; containing three stable and three unstable solution manifolds. While the effect of small-scale parameter is considered (for MCST), the amplitude level of the system response is remarkably reduced so that the large-amplitude unstable branches are disappeared. For η = 0.00012, the nanobeam dynamics undergoes only hardening-type behavior for both CCT and MCST; however, similar to the previous case, the maximum amplitude of the periodic orbit decreases and the slope of the solution manifolds remains unchanged while the influence of size is considered, Fig. 3b.

Fig. 3
figure 3

Influence of the small-scale parameter on AC frequency–response behavior of the lower nanobeam near superharmonic resonance; for aη = 0.0001 and bη = 0.00012. VDC = 1 V and VAC = 2 V

Full size image

Figure 4 illustrates the effect of surface energy on dynamic response of the double-layered NEMS system in the vicinity of superharmonic resonance. Similar to the previous case, the frequency–response plots consist of three stable and three unstable solution manifolds which intersect at four saddle-node bifurcation points. According to Fig. 4a, the response amplitude level far from the resonance region significantly increases, while the effect of surface energy is not included in the model. Furthermore, the horizontal distance between the stable and unstable branches corresponding to the hardening motion is reduced in the presence of the surface energy effect. It is also observed that, the softening behavior of the lower nanobeam is slightly weakened while the system dynamics is affected by the surface parameters; whereas the upper nanobeam shows a little more softening-type behavior in the presence of the surface effect.

Fig. 4
figure 4

Influence of the surface energy on AC frequency–response curves of the NEMS resonator near superharmonic resonance; a lower nanobeam, b upper nanobeam. VDC = 1 V and VAC = 2 V

Full size image

Figure 5 shows the influence of the interatomic Casimir regime on the nonlinear dynamic response of the double-layered NEMS device. As observed in the figure, the system displays a combined hardening and softening-type behavior whether or not the effect of Casimir force is considered. As seen, in the absence of the dispersion force, the maximum level of the system’s response amplitude is extremely larger than those obtained in the presence of the Casimir force. As observed in Fig. 5a, the bending of the solution manifolds increases in both hardening and softening parts of the frequency–response curve while the effect of the Casimir force is not taken into account in the system dynamics. However, for the upper nanobeam (Fig. 5b), the slope of the both stable and unstable solution branches remains almost unchanged, and thus, the order of nonlinearity is not affected by the Casimir regime. Furthermore, for both nanobeams, the bifurcation points’ locus is shifted to the left while considering the influence of the Casimir force.

Fig. 5
figure 5

Influence of the Casimir force on AC frequency–response curves of the NEMS resonator near superharmonic resonance; a lower nanobeam, b upper nanobeam. VDC = 1 V and VAC = 2 V

Full size image

The effect of piezoelectric voltage value and its polarization is shown in Fig. 6. The amplitude of the steady-state response of the lower and upper nanobeams are obtained for three different levels of piezoelectric voltage, Vp = − 100 mV, Vp = 0 and Vp = 100 mV. As observed in the figure, for zero piezoelectric actuation, the resonance occurs in the system while the excitation frequency approaches Ω ≈ 7.4. For the case of positive polarization, a tensile axial force is induced in the nanobeams which results in an enhancement in the bending stiffness of the structure. Therefore, the resonance region shifts to the higher frequencies (Ω ≈ 8.2). In contrast, when a negative piezoelectric voltage is applied in direction of the nanobeams’ thickness, a compressive axial force is induced in the VPNBs. This reduces the nanobeam bending stiffness, and consequently the system undergoes resonant at lower frequencies (Ω ≈ 6.6).

Fig. 6
figure 6

Influence of the piezoelectric voltage on AC frequency–response curves of the NEMS resonator near superharmonic resonance; a lower nanobeam, b upper nanobeam. VDC = 1 V and VAC = 2 V

Full size image

In the following, we aim to study the influences of the direct and alternative- current voltage values on the dynamic pull-in behavior of the proposed NEMS device. For these cases, the effects of couple-stress parameter, surface strain energy, and the dispersion force are all included in dynamical model. The impact of viscoelasticity is considered as previous, and the system is actuated by a certain piezoelectric voltage value; Vp = 100 mV. Figure 7 illustrates the frequency–response behavior of the lower nanobeam in the neighborhood of the superharmonic resonance of one-third of the fundamental natural frequency, for VDC = 1 V and VAC = 3.5 V. As seen in the figure, there are two frequency regions named A = [10.17, 10.2] and B = [10.57, 10.61], in which there exist two stable solutions; one low-amplitude and one large-amplitude motion. In the middle region, there is no stable solution manifold and, therefore, the system undergoes dynamic pull-in instabilities for the frequencies in the interval of 10.49, 10.52]. There is only one stable solution branch in the other frequency ranges. Figure 8 depicts the nonlinear dynamic response of the system for the electrostatic voltages of VDC = 2 V and VAC = 3.5 V. It can be seen that, the resonance region shifts to the left, and the distance between the solution manifolds enhances as the level of DC load is increased. Furthermore, the pull-in band width increases while increasing the DC voltage load, and the system becomes unstable in the frequency interval of [10.3, 10.41].

Fig. 7
figure 7

Frequency–response behavior of the lower nanobeam near superharmonic resonance, considering the effects of size-dependency (l = h/6), surface energy, and the Casimir forces. VDC = 1 V and VAC = 3.5 V; Vp = 100 mV

Full size image
Fig. 8
figure 8

Frequency–response behavior of the lower nanobeam near superharmonic resonance, considering the effects of size-dependency (l = h/6), surface energy, and the Casimir forces. VDC = 2 V and VAC = 3.5 V; Vp = 100 mV

Full size image

Similar to the previous case, there are two regions, A and B, one before and one after the pull-in band; consisting of two stable solutions and one unstable solution amplitude. In this case, the frequency interval B becomes narrower than that obtained in Fig. 7. This is based on the fact, that for the larger values of DC voltage load, the softening behavior due to electrostatic force dominates the hardening behavior rising from midplane stretching; thus, the slope of the lower solution manifolds increases up to that of a vertical line, Fig. 8.

The frequency-displacement behavior of the NEMS system for the electrostatic loads of VDC = 1 V and VAC = 4 V is drawn in Fig. 9. Comparing Figs. 7 and 9, it is observed that, the resonance frequency shifts to the left as the level of AC voltage load increases; however, the slope of the lower solution branches remains constant. Moreover, the width of the frequency interval in which the system undergoes dynamic pull-in instabilities increases as the alternative-current voltage grows. In this case, the pull-in range is approximated in the interval of [10.36, 10.47]. Unlike the previous case, in which the region A shifted to the right by increasing the amount of DC load, here, the region shifts to the lower frequencies while the AC load increases.

Fig. 9
figure 9

Frequency–response behavior of the lower nanobeam near superharmonic resonance, considering the effects of size-dependency (l = h/6), surface energy, and the Casimir forces. VDC = 1 V and VAC = 4 V; Vp = 100 mV

Full size image

5 Conclusion

The impetus of this paper was to investigate the nonlinear characteristics of a double-layered viscoelastic NEMS device near superharmonic resonance. Two nanobeams are made of piezoelectric material and coupled through a visco-Pasternak medium in between. Taking into account the effects of size and surface strain energy for the nanosized structure, the modified couple-stress theory together with Gurtin–Murdoch surface elasticity theory were utilized. Kelvin–Voigt model is also employed to consider the impact of viscoelasticity.

For a certain value of the viscoelasticity parameter, η = 0.00001, the influences of the length-scale parameter, surface energy and Casimir force on the nonlinear characteristics of the system are studied. The results revealed that the nanoresonator exhibits a combined hardening–softening-type behavior with four saddle-node bifurcation points, so that increasing the amount of couple-stress parameter results in a right-shift to the frequency–response branches. In addition, the upper nanobeam shows more extreme softening behavior in comparison with the lower one. It has been observed that, both the response amplitude level of the horizontal solution manifolds and the horizontal distance between the stable and unstable branches is remarkably reduced while the effect of surface energy is considered. This study also revealed that, ignoring the influence of Casimir force leads to enhancement in the maximum vibration amplitude of the system as well as the bending degree of the solution branches in both hardening and softening part of the frequency–response curve, Fig. 5a. Furthermore, the results indicate that application of MCST, and the presence of the surface energy effects and Casimir force shift the saddle-node bifurcation point’s loci and affect the jump phenomenon.

In this work, the effects of the DC and AC voltage values on the dynamic pull-in behavior of the proposed NEMS device are also studied. The results showed that the resonance region shifts to the left; the distance between the solution manifolds and the pull-in band width increases as the level of both DC and AC loads enhances. The obtained results can be useful in designing and analyzing the novel nanoelectromechanical devices which are made of viscoelastic piezoelectric materials, so that they can be modeled by two nanobeams and a third medium in between.