1 Introduction

The field of nonlinear dynamics in MEMS is very extensive. The behavior of the most MEMS is strongly nonlinear. There are various sources of nonlinearities in MEMS including electrostatic excitation, nonlinear damping mechanisms, and nonlinear geometries [1, 2]. The most common way of actuation in MEMS is electrostatic actuation, which is inherently a nonlinear position dependant force. The electrostatic actuation is usually a combination of a tuning DC voltage [3–5] and a harmonic AC voltage [6–13], which prompts the system to oscillate about its equilibrium position due to the tuning voltage. Another important source of nonlinearity in MEMS is the geometric nonlinearity. In clamped-clamped microbeams due to the immovable boundary conditions, the stretching of the mid-plane of the microbeam imposes an axial deflection dependant stress, which affects the bending stiffness in such a way that resembles a cubic type of nonlinearity [2]. The presence of these two sources of nonlinearities leads to the appearance of various interesting dynamic behaviors including softening [11, 12, 14, 15], hardening [8, 11, 12], hysteresis [2], jump phenomenon [2], chaotic response [13, 16, 17], multivalued responses [2], and generation of secondary sub and superharmonic resonances in the microbeam response [9, 15]. The very initial studies on the nonlinear dynamics of the MEMS refers back to the investigation of the static and dynamic pull-in instabilities under the effect of DC electrostatic force, which arises in the analysis of the microswitches and microsensors [5, 10, 18–25]. To reduce the energy consumption and to use the MEMS in resonance conditions especially in RF MEMS filters, application of simultaneous AC harmonic electrostatic excitation is proposed in numerous papers in the literature [2, 10, 13]. From 2003, many papers have been published on the nonlinear dynamics of the clamped-clamped microbeams exposed to a combination of a tuning DC and harmonic electrostatic actuations [7, 10–12, 14, 26]. In most of the papers, the multiple time scales method is applied to obtain the frequency response curves [7, 14]. To apply the perturbation technique to the governing differential equation of the motion, two conditions need to be satisfied, small enough amplitude of AC voltage and high enough quality factor, which implies a small damping coefficient [27]. Nayfeh et al. [10] in 2007 used the shooting method [2, 28] as an outcome to the shortage of the perturbation technique and reported the frequency response curves regarding the primary resonance. The results show that as the applied DC tuning voltage increases the softening effect of the electrostatic nonlinearity dominates the hardening effect of the cubic nonlinearity leading in the softening type frequency response curve. Corresponding to a DC tuning voltage, increasing the amplitude of the AC harmonic excitation leads in the appearance of both hardening and softening effects in the frequency response curves. They obtained the pull-in band and discussed on the bifurcation types. In 2009, Alsaleem et al. [26] studied the nonlinear resonances and pull-in instability of MEMS resonators. They verified their theoretical results by experiments. They presented basins of attraction for the limit cycles corresponding to some actuation frequencies. Some papers have focused on the discretization methods of the governing equation to reduce it to finite degree of freedom consisting of ordinary differential equations in time [29]. They multiplied both sides of the governing partial differential equation of the motion in the denominator of the electrostatic force so that they could use the Galerkin method; they showed that the Tailor expansion of the electrostatic force fails to correctly represent the electrostatic force as the deflection increases. In this paper, a clamped-clamped piezoelectrically sandwiched resonator is considered; the piezoelectric layers are deposited throughout the entire length of the microbeam. Through the lower piezoelectric layer, the resonator is exposed to a combination of a DC and a harmonic AC electrostatic voltage. In the presented model, the piezoelectric layers are used to shift the primary resonances of the structure. The DC voltage in the MEMS is apparently used for two main purposes: the first one is to lower the resonance frequency (backward shifting) and the other one is to prevent the doubling of the harmonic excitation frequency [2] (in the case of very small amplitudes of AC voltage in comparison with the DC tuning voltage). Based on the axial force (tensile/compressive) induced in the microbeam, due to the piezoelectric excitation, the proposed model has the potential of two-side shifting (forward/backward shifting) the primary resonances. The shooting method is applied to capture the periodic solutions corresponding to each excitation frequency. The bifurcation types in the frequency response curves are discussed and the pull-in bands redetermined. The results of this study can be used in the design of flexible band-pass RF MEMS filters or flexible resonance band resonators.

2 Modeling

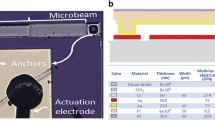
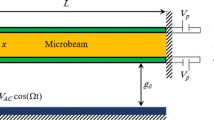
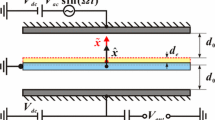
The proposed model is a clamped-clamped microbeam sandwiched with two piezoelectric layers throughout the entire length (Fig. 1). The piezoelectric layers are deposited on pure silicon through the length of the microbeam. The piezoelectric layers are actuated by a DC voltage denoted by V p ; this voltage is applied along the height direction of the piezoelectric layers. Through the lower piezoelectric layer, the microbeam is subjected to a combination of a DC and an AC voltage with amplitude V AC and frequency Ω. Length thickness and the width of the microbeam are respectively denoted by, l,h, and a; E and ρ correspond to the Young’s modulus and the density of the silicon, respectively. Symbols with subscript “p” represent the geometrical or material properties corresponding to the piezoelectric layer. The equivalent piezoelectric coefficient is denoted by \(\bar{e}_{31}\). The coordinate system as illustrated in Fig. 1, and is attached to the mid-plane of the left clamped end of the microbeam where x and z refer to the horizontal and vertical coordinates, respectively. The deflection of the microbeam along the z axis is denoted by w(x,t).

Fig. 1
figure 1

Schematics of the clamped-clamped piezoelectrically sandwiched microbeam and the electrodes

Full size image

The total potential strain energy of the microbeam is due to bending (U b ), axial force due to piezoelectric actuation denoted by (U p ), axial force due to the mid-plane stretching represented by (U a ), and electrical coenergy stored between the substrate and the lower piezoelectric layer (\(U_{e}^{*}\)) [30].

The strain energy due to mechanical bending is expressed as

$$\begin{aligned} U_{b} &= \int\frac{\varepsilon_{b}\sigma_{b}}{2}\,dv \\ &= \int\frac{E}{2} \biggl( - z\frac{\partial^{2}w}{\partial x^{2}} \biggr) \biggl( - z \frac{\partial^{2}w}{\partial x^{2}} \biggr) dv \end{aligned}$$
(1)

where ε b and σ b are the strain and stress fields due to the bending and dv is the volume of infinite small element; considering the geometry of the microbeam and simplifying, Eq. (1), reduces to

$$ U_{b} = \frac{(EI)_{\mathrm{eq}}}{2}\int\biggl(\frac{\partial^{2}w}{\partial x^{2}} \biggr)^{2}dx $$
(2)

where

$$ ( EI)_{\mathrm{eq}} = EI + E_{P}hah_{P}\biggl( \frac{h}{2} + h_{p}\biggr) $$
(3)

Due to the immovable edges, the extended length of the beam (l′) becomes more than the initial length l and this leads to the introduction of an axial stress and accordingly an axial force denoted as [13]:

$$ F_{a} = \frac{(EA)_{\mathrm{eq}}}{l}\bigl(l' - l\bigr) \approx \frac{(EA)_{\mathrm{eq}}}{2l}\int_{0}^{l}\biggl( \frac{\partial w}{\partial x} \biggr)^{2}\,dx $$
(4)

where

$$ (EA)_{\mathrm{eq}} = Eah + 2E_{p}ah_{p} $$
(5)

Integration of the arc length “ds” gives the stretched length (l′) as

$$\begin{aligned} l' &= \int_{0}^{l}ds \approx \int_{0}^{l}\sqrt{1 + \biggl( \frac{\partial w}{\partial x} \biggr)^{2}} \,dx = l \\ &\quad {} + \frac{1}{2}\int_{0}^{l} \biggl( \frac{\partial w}{\partial x} \biggr)^{2}\,dx \end{aligned}$$
(6)

The strain energy stored due to the mid-plane stretching is as follows:

$$ U_{a} = \frac{1}{2}F_{a}\bigl(l' - l \bigr) $$
(7)

substituting Eqs. (4) and (6) into Eq. (7), the strain energy due to the mid-plane stretching reduces to

$$ U_{a} = \frac{(EA)_{\mathrm{eq}}}{8l} \biggl( \int_{0}^{l} \biggl( \frac {\partial w}{\partial x} \biggr)^{2} \biggr)^{2} $$
(8)

Piezoelectric actuation due to immovable boundary conditions leads to the introduction of another axial force; based on the constitutive equation of piezoelectricity, [31, 32] and considering the direction of the applied electrical field (E 3) the axial stress due to the piezoelectric actuation reduce to:

$$ \sigma_{1} = - e_{31}E_{3} $$
(9)

where e 31 is the corresponding piezoelectric voltage constant (Coulomb/m2); Considering E 3=V p /h p , the axial force due to the piezoelectric actuation reduces to

$$\begin{aligned} F_{p} &= \int_{A_{p}} \sigma_{1}\, dA_{p} = 2 \int_{0}^{h_{p}} ( - e_{31}E_{3})a\,dh \\ &= - 2e_{31}V_{p}ah_{p} \end{aligned}$$
(10)

The strain potential energy due to the axial piezoelectric force is expressed as

$$ U_{p} = F_{p}\bigl(l' - l\bigr) = \frac{F_{p}}{2}\int_{0}^{l} \biggl( \frac{\partial w}{\partial x} \biggr)^{2}\,dx $$
(11)

The total potential energy of the system reduces to

$$ U = U_{b} + U_{a} + U_{p} + U_{e} $$
(12)

The kinetic energy of the microbeam is represented as

$$ T = \frac{(\rho ah)_{\mathrm{eq}}}{2}\int_{x = 0}^{x = l} \biggl( \frac{\partial w}{\partial t}\biggr)^{2}\, dx $$
(13)

where

$$ (\rho ah)_{\mathrm{eq}} = (\rho A)_{\mathrm{eq}} = \rho ah + 2 \rho_{p}ah $$
(14)

The work of the electrostatic force from zero deflection to w(x), is expressed as follows:

$$\begin{aligned} w_{el} &= \int_{0}^{l} \biggl( \int _{0}^{w} \frac{\varepsilon_{0}aV_{es}^{2}}{2(g_{0} - \zeta)^{2}} \, d\zeta \biggr) \,dx \\ &= \frac{\varepsilon_{0}aV_{es}^{2}}{2} \int_{0}^{l} \biggl( \frac {1}{g_{0} - w} - \frac{1}{g_{0}} \biggr) \, dx \end{aligned}$$
(15)

where g 0 is the initial gap between the microbeam and the substrate and ε 0 is the dielectric constant of the gap medium and ζ is a dummy parameter. The governing partial differential equation of the motion is obtained by the minimization of the Hamiltonian using variational principle as

$$ \delta\int_{0}^{t} H \,dt = \delta\int _{0}^{t} (T - U + w_{el})\, dt = 0 $$
(16)

Introducing Eqs. (12), (13), and (15) into Eq. (16), the Hamiltonian reduces to:

$$\begin{aligned} \delta\int_{0}^{t} H\,dt &= \int_{0}^{t} \left\{ \begin{array}{l} - ( EI )_{\mathrm{eq}}w''\delta w' \bigl\vert _{0}^{l} + ( EI )_{\mathrm{eq}}w'''\delta w \bigr\vert _{0}^{l} - ( EI )_{\mathrm{eq}}\int_{0}^{l} w^{IV}\delta w\,dx \\ - F_{p}w'\delta w \bigl\vert _{0}^{l} + F_{p}\int_{0}^{l} w''\delta w\,dx - \frac{ ( EA )_{\mathrm{eq}}}{2}\int_{0}^{l} w^{\prime 2}\, dx w'\delta w \bigr\vert _{0}^{l} \\ + \frac{ ( EA )_{\mathrm{eq}}}{2}\int_{0}^{l} w^{\prime 2}\,dx \int_{0}^{l} w''\delta w\,dx + \frac{\varepsilon_{0}aV_{es}^{2}}{2}\int_{0}^{l} \frac{\delta w}{(g_{0} - w)^{2}}\,dx \end{array} \right\}\,dt \\ &\quad {}+ \int_{0}^{t} \biggl\{ ( \rho A )_{\mathrm{eq}} \int_{0}^{l} \dot{w}\delta w \vert _{0}^{l} - ( \rho A )_{\mathrm{eq}}\int _{0}^{t} \ddot{w}\delta w\,dt \biggr\} \, dx = 0 \end{aligned}$$
(17)

The governing equation and the corresponding boundary conditions reduce to

$$\begin{aligned} & (EI)_{\mathrm{eq}}\frac{\partial^{4}w(x,t)}{\partial x^{4}} + (\rho A)_{\mathrm{eq}}\frac{\partial^{2}w(x,t)}{\partial t^{2}} \\ &\qquad {}- \biggl(F_{P} + \frac{(EA)_{\mathrm{eq}}}{2l}\int_{0}^{l} \biggl(\frac{\partial w(x,t)}{\partial x} \biggr)^{2}\,dx\biggr) \\ &\qquad {}\times \frac{\partial^{2}w(x,t)}{\partial x^{2}} \\ &\quad {} = \frac{\varepsilon_{0}a(V_{\mathrm{DC}} + V_{\mathrm{AC}}\sin(\varOmega t))^{2}}{2(g_{0} - w(x,t))^{2}} \end{aligned}$$
(18)

Subjected to the following boundary conditions:

$$ w ( 0,t ) = w ( l,t ) = 0,\qquad \frac{\partial w(0,t)}{\partial x} = \frac{\partial w(l,t)}{\partial x} = 0 $$
(19)

The following nondimensional parameters are used to obtain the equation of the motion in nondimensional form.

$$ \hat{w} = \frac{w}{g_{0}}, \qquad \hat{x} = \frac{x}{l},\qquad \hat{t} = \frac{t}{\tilde{t}},\qquad \stackrel{\frown}{\varOmega} = \varOmega\tilde{t} $$
(20)

where

$$ \tilde{t} = \sqrt{\frac{(\rho A)_{\mathrm{eq}}l^{4}}{(EI)_{\mathrm{eq}}}} $$
(21)

Substituting Eq. (20) in Eq. (18), and considering viscous damping effect due to the squeeze film damping [4] and dropping the hats the differential equation of the motion in nondimensional form is obtained as

$$\begin{aligned} & \frac{\partial^{4}w(x,t)}{\partial x^{4}} + \frac{\partial^{2}w(x,t)}{\partial t^{2}} - \bigl[\alpha_{1} + \alpha _{2}\varGamma (w,w)\bigr] \\ &\qquad {}\times \frac{\partial^{2}w(x,t)}{\partial x^{2}} + \alpha_{3} \frac {\partial w(x,t)}{\partial t} \\ &\quad {}= \frac{\alpha_{4}[V_{\mathrm{DC}} + V_{\mathrm{AC}}\sin(\varOmega t)]^{2}}{(1 - w)^{^{2}}} \end{aligned}$$
(22)

Subject to the following boundary conditions in nondimensional form:

$$ w ( 0,t ) = w ( 1,t ) = 0,\qquad \frac{\partial w(0,t)}{\partial x} = \frac{\partial w(1,t)}{\partial x} = 0 $$
(23)

For simplicity in Eq. (22), the function Γ and the coefficients α i are defined as

$$ \begin{aligned} & \varGamma\bigl(f_{1}(x,t),f_{2}(x,t)\bigr) = \int_{0}^{1} \frac{\partial f_{1}}{\partial x}\frac{\partial f_{2}}{\partial x}\,dx \\ & \alpha_{1} = \frac{F_{P}l^{2}}{(EI)_{\mathrm{eq}}}, \qquad \alpha_{2} = \frac{(EA)_{\mathrm{eq}}g_{0}^{2}}{2(EI)_{\mathrm{eq}}},\\ & \alpha_{3} = \frac{\stackrel{\frown}{c} l^{2}}{\sqrt{(\rho A)_{\mathrm{eq}}(EI)_{\mathrm{eq}}}},\qquad \alpha_{4} = \frac{\varepsilon_{0}al^{4}}{2g_{0}^{3}(EI)_{\mathrm{eq}}} \end{aligned} $$
(24)

3 Numerical solution

The approximate solution of Eq. (22) is supposed to be in the following form:

$$ w(x,t) = \sum_{i = 1}^{M} u_{i}(t)\varphi_{i}(x) $$
(25)

where u i (t) is the generalized coordinate and φ i (x) is the ith undamped mode shape function, which is normalized such that \(\int_{0}^{1} \varphi_{i}\varphi_{j}\, dx = \delta_{ij} \) and governed by

$$ \begin{aligned} & \varphi_{i}^{iv} = \alpha_{1}\varphi_{i} '' + \omega_{i}^{2} \varphi_{i} \\ & \varphi_{i} = 0\qquad \varphi_{i}' = 0\quad \mbox{at}\ x = 0\ \mbox{and}\ x = 1\end{aligned} $$
(26)

here, ω i is the ith natural frequency of the clamped-clamped microbeam. Both sides of Eq. (22) are multiplied by φ n (x)(1−w)2, and Eq. (26) is substituted in the resulting equation. Considering Eq. (26) and integrating the outcome from x=0 to x=1 reduce to:

$$\begin{aligned} & \omega_{n}^{2}u_{n} + \sum _{i = 1}^{M} \sum_{j = 1}^{M} \sum_{k = 1}^{M} \omega_{i}^{2}u_{i}u_{j}u_{k} \int_{0}^{1} \varphi_{n}\varphi_{i} \varphi_{j}\varphi_{k}\,dx \\ &\qquad {} - 2\sum_{i = 1}^{M} \sum _{j = 1}^{M} \omega_{i}^{2}u_{i}u_{j} \int_{0}^{1} \varphi_{n}\varphi_{i} \varphi_{j}\, dx + \ddot{u}_{n} \\ &\qquad {} + \sum_{i = 1}^{M} \sum _{j = 1}^{M} \sum_{k = 1}^{M} u_{i}u_{j}\ddot{u}_{k}\int_{0}^{1} \varphi_{n}\varphi_{i}\varphi_{j}\varphi_{k}\,dx \\ &\qquad {}- 2\sum_{i = 1}^{M} \sum _{j = 1}^{M} u_{i}\ddot{u}_{j}\int _{0}^{1} \varphi_{n}\varphi_{i} \varphi_{j}\,dx + \alpha_{3}\dot{u}_{n} + \alpha_{3} \\ &\qquad {}\times \sum_{i = 1}^{M} \sum _{j = 1}^{M} \sum_{k = 1}^{M} u_{i}u_{j}\dot{u}_{k}\int_{0}^{1} \varphi_{n}\varphi_{i}\varphi_{j}\varphi_{k}\,dx \\ &\qquad {} - 2\alpha_{3}\sum_{i = 1}^{M} \sum_{j = 1}^{M} u_{i} \dot{u}_{j}\int_{0}^{1} \varphi_{n}\varphi_{i}\varphi_{j}\,dx - \alpha_{2} \\ &\qquad {}\times \sum_{i = 1}^{M} \sum _{j = 1}^{M} \sum_{k = 1}^{M} u_{i}u_{j}u_{k}\varGamma(\varphi_{i}, \varphi_{j})\int_{0}^{1} \varphi_{n} \varphi_{k}''\,dx \\ &\qquad {} - \alpha_{2}\sum_{i = 1}^{M} \sum_{j = 1}^{M} \sum _{k = 1}^{M} \sum_{l = 1}^{M} \sum_{m = 1}^{M} u_{i}u_{j}u_{k}u_{l}u_{m} \varGamma (\varphi_{i},\varphi_{j}) \\ &\qquad {}\times \int_{0}^{1} \varphi_{n} \varphi_{m}\varphi_{l}\varphi_{k}'' \,dx \\ & \qquad {}+ 2\alpha_{2}\sum_{i = 1}^{M} \sum_{j = 1}^{M} \sum _{k = 1}^{M} \sum_{l = 1}^{M} u_{i}u_{j}u_{k}u_{l} \varGamma( \varphi_{i},\varphi_{j}) \\ &\qquad {}\times \int_{0}^{1} \varphi_{n} \varphi_{l}\varphi_{k}''\,dx \\ &\quad {} = \alpha_{4}\bigl[V_{\mathrm{DC}} + V_{\mathrm{AC}}\cos( \varOmega t)\bigr]^{2}\int_{0}^{1} \varphi_{n}\,dx \\ &\quad {}\mbox{for}\ n = 1,2,\ldots, M \end{aligned}$$
(27)

Equation (27), is the discretized form of the equation of the motion; to catch the periodic solutions and accordingly plot the frequency response curves using shooting method, the single degree of freedom model is considered and the equations of the motion are integrated numerically to get the components of the so-called monodromy matrix at time T; and the stability of the periodic solutions are examined using the Floquet theory [2].

4 Perturbation analysis

To validate the frequency responses obtained by the shooting technique, we have applied multiple time scales of perturbation technique to Eq. (22). As mentioned, to apply the perturbation method to the equation of the motion and analyze the response in the vicinity of the primary resonance, the amplitude of the motion needs to be sufficiently small; to satisfy this condition, it is assumed that the deflection of the microbeam u is a combination of static component w s due to V DC, V P and dynamic component w d due to the harmonic excitation V AC; and study the motion governing the w d .

$$ w(x,t) = w_{s}(x) + w_{d}(x,t) $$
(28)

To calculate the static deflection w s , we set the time derivatives and the harmonic excitation in Eq. (22) equal to zero and get

$$ w_{s}^{IV}(x) - \bigl[ \alpha_{1} + \alpha_{2}\varGamma(w_{s},w_{s}) \bigr]w_{s}'' = \alpha_{4}\frac{V_{es}^{2}}{(1 - w_{s})^{2}} $$
(29)

Subject to the following boundary conditions:

$$ w_{s}(x = 0,1) = 0,\qquad \frac{dw_{s}}{dx} = 0 $$
(30)

Substituting Eq. (28) in Eq. (22), considering Eq. (29) and expanding the electrostatic force in Tailor expansion about the static equilibrium position, the problem governing the dynamic behavior is generated as

$$ \begin{aligned} &\ddot{w}_{d} + \alpha_{3} \dot{w}_{d} + w_{d}^{IV} - \bigl[ \alpha_{1} + \alpha_{2}\varGamma(w_{s},w_{s}) \bigr]w_{d}'' \\ &\quad {} - 2\alpha_{2}\varGamma(w_{s},w_{d})w_{d}'' - 2\alpha_{2}\varGamma (w_{s},w_{d})w_{s}''\\ &\quad {}- \alpha_{2}\varGamma(w_{d},w_{d})w_{s}'' - \alpha_{2}\varGamma(w_{d},w_{d})w_{d}'' = \alpha_{4} \\ & \biggl[ \frac{2V_{\mathrm{DC}}^{2}}{(1 - w_{s})^{3}}w_{d} + \frac{3V_{\mathrm{DC}}^{2}}{(1 - w_{s})^{4}}w_{_{d}}^{2}\\ &\quad {}+ \frac{4V_{\mathrm{DC}}^{2}}{(1 - w_{s})^{5}}w_{_{d}}^{3} + \frac{2V_{\mathrm{DC}}V_{\mathrm{AC}}\cos(\varOmega t)}{(1 - w_{s})^{2}}\\ &\quad {} + \frac{4V_{\mathrm{DC}}V_{\mathrm{AC}}\cos(\varOmega t)}{(1 - w_{s})^{3}}w_{d} +\cdots \biggr] \end{aligned} $$
(31)

\(w_{d}(x,t) = \sum_{i = 1}^{n} q_{i}(t)\varphi_{i}(x)\) is substituted in Eq. (31) where q i (t) is the generalized coordinate corresponding to the dynamic component of the deflection. Using Galerkin method and considering the first mode in the governing ordinary differential equations gives:

$$\begin{aligned} &\ddot{q}(t) + C\dot{q}(t) + Kq(t) + K_{nq}q^{2}(t) + K_{nc}q^{3}(t) \\ &\quad {} = F_{1}V_{\mathrm{AC}}\cos( \varOmega t) + F_{2}q(t)V_{\mathrm{AC}}\cos(\varOmega t) \end{aligned}$$
(32)

where

$$\begin{aligned} & C = \alpha_{3} \\ &K = \int_{x = 0}^{x = 1} \varphi_{1}(x) \varphi_{1}^{IV}(x)\, dx - \bigl[ \alpha_{1} + \alpha_{2}\varGamma(w_{s},w_{s}) \bigr] \\ &\hphantom{K =} {}\times \int _{x = 0}^{x = 1} \varphi_{1}(x)\varphi_{1}''(x) \,dx \\ &\hphantom{K =}{} - 2\alpha_{2}\varGamma \bigl[ w_{s}, \varphi_{i}(x) \bigr]\int_{x = 0}^{x = 1} \varphi_{1}(x)w_{s}''\,dx \\ &\hphantom{K =}{} - 2 \alpha_{4}V_{\mathrm{DC}}^{2}\int_{x = 0}^{x = 1} \frac{\varphi_{1}(x)\varphi_{1}(x)}{(1 - w_{s})^{3}}\,dx \\ &K_{nq} = - 2\alpha_{2}\varGamma \bigl[ w_{s}, \varphi_{k}(x) \bigr]\int_{x = 0}^{x = 1} \varphi_{1}(x)\varphi_{1}''(x)\, dx \\ &\hphantom{K_{nq} =}{} - \alpha_{2}\varGamma \bigl[ \varphi_{1}(x),\varphi_{1}(x) \bigr]\int_{x = 0}^{x = 1} \varphi_{1}(x)w_{s}'' \,dx \\ &\hphantom{K_{nq} =}{}- 3\alpha_{4}V_{\mathrm{DC}}^{2}\int _{x = 0}^{x = 1} \frac{\varphi_{1}(x)\varphi_{1}(x)\varphi_{1}(x)}{(1 - w_{s})^{4}}\,dx \\ & K_{nc} = - \alpha_{2}\varGamma \bigl[ \varphi_{1}(x),\varphi_{1}(x) \bigr]\int_{x = 0}^{x = 1} \varphi_{1}(x)\varphi_{1}''(x)\, dx \\ & \hphantom{K_{nc} =}{}- 4 \alpha_{4}V_{\mathrm{DC}}^{2}\int_{x = 0}^{x = 1} \frac{\varphi_{1}(x)\varphi_{1}(x)\varphi_{1}(x)\varphi_{1}(x)}{(1 - w_{s})^{5}}\,dx \\ & F_{1} = 2\alpha_{4}V_{\mathrm{DC}}\int _{x = 0}^{x = 1} \frac{\varphi_{1}(x)}{(1 - w_{s})^{2}}\,dx \\ & F_{2} = 4\alpha_{4}V_{\mathrm{DC}}\int _{x = 0}^{x = 1} \frac{\varphi_{1}(x)\varphi_{1}(x)}{(1 - w_{s})^{3}}\,dx \end{aligned}$$
(33)

We consider a uniform asymptotic solution of Eq. (32) in the following form:

$$\begin{aligned} q(t) &= \varepsilon q_{1}(T_{0},T_{1},T_{2}) + \varepsilon^{2}q_{2}(T_{0},T_{1},T_{2}) \\ &\quad {}+ \varepsilon^{3}q_{3}(T_{0},T_{1},T_{2}) +\cdots \end{aligned}$$
(34)

Here, ε is a nondimensional book keeping parameter. T 0=t, T 1=εt, and T 2=ε 2 t are time scales, respectively. In order that the nonlinearity balances the effects of damping and excitation, they are scaled so that they appear together in the modulation equation; hence in Eq. (32) we consider V AC=ε 3 V AC,C ij =ε 2 C ij . Considering the operator \(D_{n} = \frac{\partial}{\partial t_{n}}\), substituting Eq. (34) in Eq. (32) and equating coefficients of like powers of ε.

$$\begin{aligned} & \varepsilon D_{0}^{2}q_{1} + \omega^{2}q_{1} = 0,\quad \omega^{2} = K \\ & \varepsilon^{2} D_{0}^{2}q_{2} + \omega^{2}q_{2} = - 2D_{0}D_{1}q_{1} - K_{nq}q_{1}^{2} \\ & \varepsilon^{3} D_{0}^{2}q_{3} + \omega^{2}q_{3} \\ &\quad {} = - 2D_{0}D_{1}q_{2} - 2D_{0}D_{2}q_{1} - D_{1}^{2}q_{1} - CD_{0}q_{1} \\ &\qquad {} - 2K_{nq}q_{1}q_{2} - K_{nc}q_{1}^{3} + F_{1}V_{\mathrm{AC}} \cos(\varOmega T_{0}) \end{aligned}$$
(35)

The solution of the first ordinary differential equation is expressed as

$$ q_{1} = A(T_{1},T_{2})e^{i\omega T_{0}} + \bar{A}(T_{1},T_{2})e^{ - i\omega T_{0}} $$
(36)

Substituting Eq. (36) in the ordinary differential equation corresponding to ε 2 and considering the solvability condition, it can is concluded that the A is a complex valued function of the slow time scale A=A(T 2) that is determined by imposing the solvability condition at third order. The solution of the second-order equation is expressed as

$$ q_{2} = \frac{K_{nq}}{3\omega^{2}} \bigl( A^{2}e^{2i\omega T_{0}} + \bar{A}^{2}e^{ - 2i\omega T_{0}} \bigr) - \frac{2K_{nq}}{\omega^{2}}A\bar{A} $$
(37)

In order to describe the closeness of the excitation frequency Ω to the fundamental frequency ω, the detuning parameter σ is defined as

$$ \varOmega= \omega+ \varepsilon^{2}\sigma $$
(38)

Substituting Eqs. (36), (37), and (38) into the equation of ε 3, the secular terms need to vanish for uniform expansion as

$$\begin{aligned} & \left \{ \begin{array} {l} - Ci\omega A(T_{2}) - 2 \dfrac{dA(T_{2})}{\partial T_{2}}i\omega+ 4\dfrac{K_{nq}^{2}}{\omega^{2}}A^{2}(T_{2})\bar {A}(T_{2}) \\ \quad {}- \dfrac{2}{3}\frac{K_{nq}^{2}}{\omega^{2}}A^{2}(T_{2}) \bar{A}(T_{2}) - 3K_{nc}A^{2}(T_{2}) \bar{A}(T_{2})\\ \quad {} + F_{1}\dfrac{V_{\mathrm{AC}}}{2}e^{i\sigma T_{2}} \end{array} \right \} \\ &\quad {}\times e^{i\omega T_{0}} = 0 \end{aligned}$$
(39)

To determine a second-order approximation of the solution we need only three time scales (T 0, T 1 and T 2); hence there is no need to solve the equation of the third order ε 3 for q 3 but only to solve the corresponding solvability condition Eq. (39) to determine A as a function of T 2 [33].

$$ A(T_{2}) = \frac{1}{2}ae^{i\beta},\quad a = a(T_{2}),\ \beta= \beta(T_{2}) $$
(40)

Here, a and β are real functions of T 2. Substituting Eq. (40) in Eq. (39) and multiplying both sides in e −iβ, Eq. (39) reduces to

$$ \begin{aligned} & a' = \frac{1}{\omega} \biggl( - C\omega \frac{1}{2}a + F_{1}\frac{V_{\mathrm{AC}}}{2}\sin(\gamma) \biggr) \\ & \gamma' = \frac{1}{\omega a} \biggl( \omega a\sigma+ a^{3}\biggl(\frac{5}{12}\frac{K_{nq}^{2}}{\omega^{2}} - \frac{3}{8}K_{nc} \biggr)\\ &\hphantom{\gamma' =}{} + F_{1}\frac{V_{\mathrm{AC}}}{2}\cos ( \gamma ) \biggr) \end{aligned} $$
(41)

where σT 2−β=γ and prime denotes the differentiation with respect to T 2. To determine the steady state responses, there is no need to integrate Eq. (41) for long time; instead, we use the fact that a and γ are constants, and obtain the fixed points of Eq. (41) (a 0,γ 0); By setting a′=γ′=0 and eliminating γ 0 from Eq. (41), the frequency response curve is obtained as

$$\begin{aligned} & 4 \biggl( \omega a\sigma+ a^{3}\biggl(\frac{5}{12} \frac{K_{nq}^{2}}{\omega ^{2}} - \frac{3}{8}K_{nc}\biggr) \biggr)^{2} + ( C\omega a )^{2} \\ &\quad {} = ( F_{1}V_{\mathrm{AC}} )^{2} \end{aligned}$$
(42)

Equation (42) is an implicit function of the amplitude a of the periodic solution, as a function of the detuning parameter σ as a representative of the excitation frequency, the quadratic K nq and cubic stiffness K nc terms, the damping coefficient C, and the amplitude of the harmonic excitation V AC. The stability of the periodic orbits are is determined by determining the eigenvalues of the Jacobian matrix of Eq. (41) evaluated at the fixed points (a 0,γ 0).

5 Results and discussions

The geometrical and mechanical properties of the case study are represented in Table 1 as follows.

Table 1 Geometrical and material properties of the microbeam and piezoelectric layers
Full size table

Figure 2 depicts the static equilibria of the center of the microbeam versus V DC, for three different levels of the piezoelectric actuation voltages (0 mV, 20 mV, and −20 mV). Corresponding to each V DC, there are two equilibria including one stable and one unstable (the unstable one is nearer to the substrate). As V DC increases, these two equilibria approach each other and their distance decreases; the stable equilibrium point meets the unstable one in the saddle node bifurcation point where stable and unstable manifolds destroy each other; this type of bifurcation in MEMS is classified as a dangerous bifurcation since the system is forced to escape to the substrate, so-called pull-in. Beyond the saddle node bifurcation point, there are neither stable nor unstable equilibria. Piezoelectric actuation with negative polarity decreases the bending stiffness of the microbeam due to the generation of compressive axial force; this is why the microbeam undergoes saddle node bifurcation in a lower V DC in comparison with positive piezoelectric polarity.

Fig. 2
figure 2

Maximum static deflection versus V DC, for three different levels of piezoelectric voltage

Full size image

As mentioned in the previous section, in order that the perturbation technique to be applicable to the governing equation, the damping coefficient and the amplitude of the excitation frequency need to be of the orders V AC=ε 3 V AC,C ij =ε 2 C ij ; this means that for low quality factors and high amplitudes of the harmonic excitation the perturbation technique is not a good candidate; hence, in the following case with V DC=2.0 v, V AC=10.0 mV, and V P =0.0 V, we validate the results of the shooting technique with those of perturbation method and in the rest of the paper regardless of the amounts of the quality factor and the amplitude of the excitation frequency we report the results based on the shooting technique. As Fig. 3 exhibits, the amplitude of the periodic solutions predicted by the perturbation technique and shooting method are in good agreement. The difference between the amplitudes of the periodic attractors, predicted by the multiple times scale and shooting method increases as the orbit amplitude increases. This can be due to the Tailor expansion of the electrostatic force; Tailor series expansion is used to avoid strong nonlinearities and to apply the perturbation method.

Fig. 3
figure 3

Frequency response curve obtained by the perturbation technique (solid lines represent stable manifold) and shooting method (filled squares represent the stable manifold) for V DC=2 V, V AC=10 mV and V P =0.0 mV

Full size image

For dynamic analysis, we have adopted two levels of V DC (2 and 4 volt). Figure 4 illustrates the frequency response curve near the primary resonance with different piezoelectric voltages; here, we assume quality factor Q=1000, which is related to the damping coefficient and the fundamental natural frequency as c=ω 1/Q; the more the quality factor, the more the resonator efficiency; however, it is worth noting that the amount of the quality factor does not qualitatively affect the frequency response curve, but changes the amplitude of the periodic solutions; In the present study, the quality factor is supposed to be constant. The shooting technique is utilized to capture the periodic solutions [10, 28] and the stability of the periodic solutions are investigated via the Floquet theory [1, 3]. The filled and unfilled squares, respectively, represent the stable and unstable branches of periodic solutions.

Fig. 4
figure 4

Frequency response curve representing the hardening effect near primary resonance (filled squares represent the stable periodic solutions) V DC=2 V, V AC=10 mV (a) V P =0.0 mV, (b) V P =−20.0 mV, (c) V P =20.0 mV

Full size image

According to Fig. 4, there are no pull-in bands regardless of the polarity of the piezoelectric actuation; this means that at least one stable periodic solution corresponding to each excitation frequency exists. In some regions in the vicinity of the primary resonance, there are even up to three periodic solutions including two stable and one unstable. There are no basins of attraction for the unstable periodic solution. The trajectory in the phase space is attracted to a particular periodic solution; this depends on the location of the initial conditions. As mentioned, two different sources of nonlinearity in this study have two different effects on the frequency response curves. The electrostatic actuation has a softening effect whereas the cubic nonlinear stiffness (so-called nonlinear geometric stiffness) has a hardening effect. In Fig. 4, the hardening effect of nonlinear stiffness overweighs the softening effect of electrostatic actuation; this is due to the low amplitudes of the periodic orbits. Figure 5 shows the frequency response curves for the same V DC and V P as of Fig. 4, but different V AC=200 mV. Unlike the frequency response curves represented in Fig. 4, the frequency response curves here do not close within the figure and three cyclic fold bifurcations occur (A, B, and C in Fig. 5(c)); one of the Floquet multipliers appertaining to the cyclic fold bifurcation points approaches unity while the slope of the curve approaches infinity. Higher amplitudes of V AC imply the existence of periodic orbits about the static equilibrium position with higher amplitudes; this causes the softening effect of electrostatic actuation to dominate the hardening effect of the geometric nonlinearity for periodic orbits with higher amplitudes. The frequency response curves for V AC=200 mV, for small amplitudes of the periodic orbits are of hardening nature, this is due to the hardening effect of the geometric nonlinearity. As Fig. 5 exhibits, the resonance region strongly depends on both the amount and the polarity of the piezoelectric actuation. Application of piezoelectric voltage with positive and negative polarities shifts the resonance frequency to the right and left on the frequency axis, in comparison to the zero piezoelectric voltage, respectively.

Fig. 5
figure 5

Frequency response curve representing the hardening-softening effect near primary resonance (filled squares represent the stable periodic solutions) V DC=2 V, V AC=200 mV, (a) V P =0.0 mV, (b) V P =−20.0 mV, (c) V P =20.0 mV

Full size image

Figure 6 illustrates the three periodic attractors corresponding to the parameters of Fig. 5(a) and Ω=25.85 (These periodic attractors are indicated by P 1, P 2, and P 3 in Fig. 5a). The initial conditions obtained by the shooting method are on the periodic orbits; hence, there is no transient dynamics on the temporal response.

Fig. 6
figure 6

Periodic attractors corresponding to V DC=2 V AC=200 mV, Ω=25.85 (a) temporal response, (b) phase plane

Full size image

Figure 7 represents the basins of attraction corresponding to the periodic attractors 1, 2, and 3 represented in Fig. 6.

Fig. 7
figure 7

The basins of attraction corresponding to the (a) Periodic attractor 1, (b) Periodic attractor 2, (c) Periodic attractor 3 (the filled areas are the basins of attraction)

Full size image

It is worth mentioning that the periodic attractors with lower amplitudes have larger basins of attraction in comparison with high amplitude attractors; this means a that a randomly chosen initial condition will most probably be attracted to a periodic solution with lower amplitude provided that the chosen initial condition is out of the pull-in band.

Figure 8 represents the frequency response curves for the resonator exhibiting softening type behavior where V DC=4.0 V and V AC=10 mV.

Fig. 8
figure 8

Frequency response curve representing the softening effect near primary resonance (filled squares represent the stable periodic solutions) V DC=4 V, V AC=10 mV (a) V P =0.0 mV, (b) V P =−20.0 mV, (c) V P =20.0 mV

Full size image

Figure 9 represents the frequency response curves for the resonator with V DC=4.0 V and V AC=200 mV. Some frequency bands in these figures are denoted as pull-in bands; in these frequency bands, there are no stable periodic attractors; however, there are some unstable periodic orbits. An unstable periodic orbit has no basins of attraction; hence, no trajectory is attracted to an unstable orbit unless the initial conditions are exactly located on the corresponding orbit, which can solely be a mathematical point of interest rather than a physical problem. In a pull-in band, although some unstable periodic orbits exist, practically no trajectory in phase space is attracted to these orbits and the resonator collapse to the substrate leading to pull-in. This band for V p=−20.0 mV is larger than that for V p=0.0 mV; this is because of the reduction of bending stiffness of the resonator due to the compressive piezoelectric axial load. Since the piezoelectric actuation with positive polarity imposes tensile force leading to the increase of the bending stiffness, the pull-in band vanishes for V p=20.0 mV.

Fig. 9
figure 9

Frequency response curve representing the softening effect near primary resonance (filled squares represent the stable periodic solutions) V DC=4 V, V AC=200 mV (a) V P =0.0 mV, (b) V P =−20.0 mV, (c) V P =20.0 mV

Full size image

Figure 10 illustrates the frequency response curves for the same V DC as that of Fig. 9, but with a higher V AC=500 mV. The frequency response curves for V P =−20.0 mV is not represented here because the unstable periodic solutions in the pull-in band are highly unstable; hence, one is likely to deviate from an unstable periodic solution even if the initial conditions are precisely determined.

Fig. 10
figure 10

Frequency response curve representing the softening effect near primary resonance (filled squares represent the stable periodic solutions) V DC=4 V, V AC=500 mV (a) V P =0.0 mV (b) V P =20.0 mV

Full size image

6 Conclusion

The nonlinear dynamics of a piezoelectrically sandwiched clamped-clamped microbeam exposed to electrostatic actuation was studied. The differential equation of the motion was derived using the Hamiltonian principle and extended to dissipative viscous systems. The static equilibria of the microbeam for pure V DC with different piezoelectric voltages were investigated; then the bifurcation types considering V DC as the control parameter were clarified. It was shown that the polarity of the piezoelectric actuation directly affects the bending stiffness of the microbeam, and accordingly the locus of saddle node bifurcation point shifts on the bifurcation diagram. It was shown that the positive polarity of the piezoelectric actuation adds to the bending stiffness of the microbeam; however, negative polarity reduces the bending stiffness. This phenomenon was used as a tool for tuning the primary resonance of the structure. Furthermore, we used the benefit of this event to cancel the pull-in band from the frequency response curves, which is the most famous failure in MEMS structures. We studied the dynamics of the model with two different levels of DC electrostatic voltage (V DC=2, 4 V), three levels of AC harmonic excitation (10, 200, and 500 mV), and three different piezoelectric excitations (V P =−20, 0, and 20 mV). The frequency response curves with different levels of actuation were determined; the shooting method was applied to capture the periodic attractors. The stability of the periodic orbits was studied by determining the eigenvalues of the so-called monodromy matrix. There were two dominant sources of nonlinearities in the dynamics of the problem including electrostatic actuation and nonlinear geometric stiffness due to the mid-plane stretching resembling cubic type of nonlinearity. It was revealed that the electrostatic voltage has a softening effect, whereas the geometric nonlinearity has a hardening effect on the frequency response curves. For V DC=2.0 V and V AC=10 mV, the frequency response curves were all of the hardening type and they closed themselves within the figure. Increasing the amplitude of the harmonic excitation resulted in the appearance of three cyclic fold bifurcation points on the frequency response curve and also the appearance of both softening and hardening behaviors. Increasing the amplitude of V DC led to the disappearance of hardening behaviors on the frequency response curves due to the domination of the electrostatic nonlinearity. The pull-in bands were also determined on the frequency response curves; in these regions, there were no stable periodic attractors; hence, any trajectory evolution regardless of the locus of the initial conditions on the phase plane led to pull-in, and accordingly the collapse of the microbeam to the substrate. As one of the interesting results of the present study, we could cancel the pull-in band in the frequency response curves by applying piezoelectric voltage with an appropriate polarity and amplitude. One of the challenging dilemmas in the design process of MEMS RF resonators is the tuning of the resonance frequency; unlike the traditional tunings, the proposed model enables both forward and backward tuning of the resonance frequency. This is due to the introduction of a compressive/tensile axial force due to the different polarities of the piezoelectric actuation. In the case of small amplitudes of harmonic excitation and high enough quality factors, the frequency response curves were validated with those of multiple time scales of the perturbation technique. The results of present study can be used in the design of novel MEMS resonators.