1 Introduction

Reliable rainfall data with an appropriate spatial and temporal coverage are required for wise management of our water resources system projects and their optimal design. These projects include but are not limited to watershed management, analysis of wet and dry periods, water budget studies, reservoir operation, storm water drainage design, flood forecasting and control, determination of probable groundwater recharge, design of hydraulic and river training structures, etc. The higher the spatial and temporal variability of the attribute under consideration, the denser the resulting components of the network will become. Among various processes within the hydrological cycle, rainfall is considered to be a prerequisite for occurring of other processes. Thus, to achieve economical design of these projects, an appropriate rain gauge network with maximum information content is required.

Traditionally, various efforts assume three scenarios in evaluating a rain gauge network design (Chacon-Hurtado et al. 2017), namely relocation (i.e., prioritizing or ranking the existing rain gauge network in terms of its contribution to estimation accuracy), augmentation (i.e., adding new gauges or relocating the existing gauges to yield better estimation accuracy) and reduction {i.e., choosing a number of gauges n from an existing rain gauge network N [i.e., \(C\left( {N,n} \right) = \left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right) = \frac{N!}{{n!\left( {N - n} \right)!}}\)] to reduce cost indirectly with due consideration on acceptable accuracy}.

Generally speaking, design of rain gauge network for various scenarios depends on numerous interrelated factors documented in more detail in Shaghaghian and Abedini (2013). Inclusion of these factors in optimal rain gauge network design is the subject of operational hydrology for the last four decades or so. These numerous interrelated factors imply the complexity involved in designing a given rain gauge network with new method usually emerging with new advances in computer software and hardware.

Optimal delineation of number and spatial locations of rain gauges considers a variety of procedures in reference to the objective function used. These procedures are classified as variance-based methods (Bastin et al. 1984; Kassim and Kottegoda 1991; Cheng et al. 2008; Shafiei et al. 2014; Adhikary et al. 2015; Haggag et al. 2016; Feki et al. 2017, Attar et al. 2019; Shahidi and Abedini 2018), entropy-based techniques (Krstanovic and Singh 1992; Al-Zahrani and Husain 1998; Yoo et al., 2008; Karimi-Hosseini et al. 2011; Vivekanandan et al. 2012; Xu et al. 2015), fractal-based approaches (Mazzarella and Tranfaglia 2000; Capecchi et al. 2012), distance-based styles (Van Groenigen et al. 2000) and a combination of cost with one of these approaches (Pardo-Igúzquiza 1998). For more details on various approaches, advantages and disadvantages of sensor placement design, interested readers may want to consult with Chacon-Hurtado et al. (2017). All in all, most studies conducted to design a given rain gauge network consider either variance-based or entropy-based formulation in casting the governing objective function.

Rain gauge network design based on variance approach receives scholars’ attention in totally two different avenues. Studies such as Bastin et al. (1984), Kassim and Kottegoda (1991) and Attar et al. (2019) consider BOK for casting the objective function prioritization. Needless to say, in the aforementioned studies or Add One In (AOI) procedure, the exponentially decaying function is reproduced from left to right in a forward manner, while in Kassim and Kottegoda’s simplified scheme or Leave One Out (LOO) approach, the same curve is reproduced from right to left in a backward manner. Attar et al. (2019) also investigated the impact of incorporated simplifications on rain gauge network design by coupling a random search optimization with BOK. However, Cheng et al. (2008), Shafiei et al. (2014) and Haggag et al. (2016) cast their objective function based on POK for variance computation. They introduced a measure so-called the percentage of area with acceptable accuracy to go around the distributed objective function. In their study, they implemented an AOI to obtain the goodness of fit criterion (i.e., ascending function) to redesign a given rain gauge network. It is worth noting that in all of the studies cited above, no efforts were made to independently verify the measure of accuracy with reference to point versus block estimation.

In all entropy-based network design, investigators attempted to base their optimization problem on point maximization of information content. In almost all such studies, the investigators assume some simplifications in designing a given network. In particular, they surmounted the curse of dimensionality issue by making some explicit or implicit assumptions (Krstanovic and Singh 1992, Al-Zahrani and Husain 1998; Chen et al. 2008; Yeh et al. 2011, Yoo et al. 2008; Vivekanandan et al. 2012; Mahmoudi-Meimand et al. 2016). Obviously, these simplifications would not necessarily lead to similar results particularly for intermediate values of n compared to all scenarios for \(C\left( {N,n} \right)\) with no simplification considered. Needless to say, one could delineate a few studies with kriging and entropy in the title. However, in such studies, kriging, as a stochastic interpolant, is implemented to fill the gap in data and then entropy, as a measure of information content, is used to design the network emerging from the resulting database (Chen et al. 2008; Yeh et al. 2011, Awadallah 2012; Chiang et al. 2014, Mahmoudi-Meimand et al. 2016; Xu et al. 2018). Inter-comparison of optimal network resulting from various approaches is missing from the existing literature. Even it is not quite clear if network design based on entropy measure would give rise to the same results as variance-based procedure. In subsequent paragraphs, the relevant literature will be provided to see how researchers consider independent validation of goodness of fit criterion developed and try to avoid such simplifications incorporated.

A number of investigators alluded to the cited simplification and tried to surmount it while they coupled geostatistical approach or entropy techniques with random search algorithms for rain gauge network design (Pardo-Igúzquiza 1998; Barca et al. 2008; Karimi-Hosseini et al. 2011; Chebbi et al. 2013; Aziz 2014, Aziz et al. 2016; Adib and Moslemzadeh 2016). In the meanwhile, a comparative study can be delineated in the recent literature to compare and contrast exhaustive search versus simplified approaches for rain gauge network design (Attar et al. 2019). Nevertheless, the approaches adopted on point versus block estimation by various investigators were not verified by independent party and even they themselves did not compare their results with benchmark solutions. Even in the entropy-based procedure, almost all studies revolve around point as opposed to block to optimally design the corresponding network.

In a nutshell, critical review of the relevant literature on rain gauge network design confirms the fact that almost all approaches adapted to go for network design suffer from two shortcomings. First, the independent verification of incorporated assumptions is missing. Second, the impact of simplifications in surmounting the curse of dimensionality was not investigated. The current study intends to address the first shortcoming in the current literature and the second issue had already been addressed by Attar et al. (2019) while comparing and contrasting exhaustive versus simplified approaches. As such the main focus of the current paper is to compare and contrast point and block ordinary kriging in rain gauge network design. For this purpose, appropriate casting of objective function and its wise coupling with a random search algorithm so-called ABC optimization will be pursued in the current paper. In addition, the recent paradigm on point measure proposed by Cheng et al. (2008) and subsequently used by Shafiei et al. (2014) and Haggag et al. (2016) is submitted to rigorous experimentation for independent verification. The proposed approach [i.e., POK coupled with a random search optimization algorithm so-called Discrete Artificial Bee Colony (DisABC)] is compared and contrasted with block kriging-based network design coupled with DisABC to evaluate the performance of the proposed scheme.

The paper is organized as follows: At first, a brief account of theoretical background will be offered in the next section. Then, materials and methods are provided followed by the proposed methodology. In subsequent sections, the results of different methodologies on rain gauge network design will be compared and contrasted. Finally, conclusions which can be drawn from this study are summarized in the last section.

2 Theoretical Background

In this paper, the network design is implemented using variance-based approach whereby the objective function is the percentage of area with acceptable accuracy over the study area. For the sake of paper integrity, it is essential to have a brief account of geostatistical jargons (Isaaks and Srivastava 1998) and ABC optimization procedures which will be provided in the following subsections.

2.1 Point and Block Ordinary Kriging (POK-BOK)

Ordinary kriging is known as the best linear unbiased estimator (BLUE). While in POK, the support size for both the observation and estimation is a point, in BOK, it should be acknowledged that the support size for observation is point-wise while that of estimation is block-wise. Denoting the surface coordinate \(\left( {x,y} \right)_{ }\) by the vector \(\left( {{\mathbf{s}}_{ } } \right)\), the annual rainfall depth at sampled points \(P\left( {{\mathbf{s}}_{i} } \right)\) is considered to be a partial, single realization of a random function. In any flavor of kriging approach including point and block ordinary kriging, residuals (i.e., estimation error) can be written as follow:

$$R\left( {{\mathbf{s}}_{0} } \right) = \hat{P}\left( {{\mathbf{s}}_{0} } \right) - P\left( {{\mathbf{s}}_{0} } \right)$$
(1)
$$R_{V} \left( {{\mathbf{s}}_{0} } \right) = \hat{P}_{V} \left( {{\mathbf{s}}_{0} } \right) - P_{V} \left( {{\mathbf{s}}_{0} } \right)$$
(2)

where \(R_{ } \left( {{\mathbf{s}}_{0} } \right),\) \(R_{V} \left( {{\mathbf{s}}_{0} } \right)\) are residuals corresponding to point and block ordinary kriging, respectively. \(\hat{P}\left( {{\mathbf{s}}_{0} } \right)\) and \(P_{ }\) (\({\mathbf{s}}_{0}\)) are the estimated and the true value of annual rainfall at spatial location \({\mathbf{s}}_{0} ,\) \(\hat{P}_{V}^{ } \left( {{\mathbf{s}}_{0} } \right)\) and \(P_{V}\)(\({\mathbf{s}}_{0}\)) are the estimated and the true value of the mean annual rainfall over block V index at \({\mathbf{s}}_{0} ,\) respectively. Thus, in point and block ordinary kriging, two fundamental criteria (i.e., unbiasedness and minimum variance conditions) should be imposed on residuals. As a result, point and block ordinary kriging system in terms of variogram can be written as:

$$\left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1}^{N} \lambda_{j}^{ } \left( {{\mathbf{s}}_{0} } \right)\gamma \left( {{\mathbf{s}}_{i} ,{\mathbf{s}}_{j} } \right) - \mu \left( {{\mathbf{s}}_{0} } \right) = \gamma \left( {{\mathbf{s}}_{i} ,{\mathbf{s}}_{0} } \right)} \hfill & { i = 1,2, \ldots ,N} \hfill & {(3)} \hfill \\ {\mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{ } \left( {{\mathbf{s}}_{0} } \right) = 1} \hfill & {} \hfill & {(4)} \hfill \\ \end{array} } \right.$$
$$\left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{j = 1}^{N} \lambda_{j}^{\text{BK}} \left( {{\mathbf{s}}_{0} } \right)\gamma \left( {{\mathbf{s}}_{i} ,{\mathbf{s}}_{j} } \right) - \mu_{ }^{\text{BK}} \left( {{\mathbf{s}}_{0} } \right) = \frac{1}{M}\mathop \sum \limits_{k = 1}^{M} \gamma \left( {{\mathbf{s}}_{i} ,{\mathbf{s}}_{k}^{\prime } } \right)} \hfill & { i = 1,2, \ldots ,N} \hfill & {(5)} \hfill \\ {\mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{\text{BK}} \left( {{\mathbf{s}}_{0} } \right) = 1} \hfill & {} \hfill & {(6)} \hfill \\ \end{array} } \right.$$

where N is the total number of rain gauge stations,\(\mu \left( {{\mathbf{s}}_{0} } \right)\) and \(\mu_{ }^{\text{BK}}\) \(({\mathbf{s}}_{0} )\) are the Lagrange multiplier for point and block ordinary kriging, \(\lambda_{j}^{ }\) and \(\lambda_{j}^{\text{BK}}\) are the weighting coefficients corresponding to observed value of rainfall depth at (\({\mathbf{s}}_{0}\)). Thus, in BOK, (‘) and M represent discretized points (s′) and the number of points inside a typical block, respectively. The variance of residuals at point \(\varvec{s}_{0}\) and over block V centered at \(\varvec{s}_{0}\) is given by the following relationship:

$${\text{Var}}\left[ {R\left( {{\mathbf{s}}_{0} } \right)} \right] = - \mu \left( {{\mathbf{s}}_{0} } \right) + \mathop \sum \limits_{i = 1}^{N} \lambda_{i}^{ } \left( {{\mathbf{s}}_{0} } \right)\gamma \left( {{\mathbf{s}}_{i} ,{\mathbf{s}}_{0}^{ } } \right)$$
(7)
$${\text{Var}}\left[ {R_{V} \left( {{\mathbf{s}}_{0} } \right)} \right] = - \mu_{ }^{\text{BK}} \left( {{\mathbf{s}}_{0} } \right) + \frac{1}{M}\mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{k = 1}^{M} \lambda_{i}^{\text{BK}} \left( {{\mathbf{s}}_{0} } \right)\gamma \left( {{\mathbf{s}}_{i} ,{\mathbf{s}}_{k}^{\prime } } \right) - \frac{1}{{M^{2} }}\mathop \sum \limits_{k = 1}^{M} \mathop \sum \limits_{j = 1}^{M} \gamma \left( {{\mathbf{s}}_{j}^{\prime } ,{\mathbf{s}}_{k}^{\prime } } \right)$$
(8)

Equations (7) and (8) have been extensively utilized to delineate optimum rain gauge network over the study area after coupling it with an appropriate optimization algorithm such as ABC to be described in the next subsection.

2.2 Artificial Bee Colony Algorithm (ABC Algorithm)

In recent years, stochastic optimization based on activities of a set of particles (i.e., swarm intelligence) who behave in a certain systematic way attracts researchers’ attention to address optimization problems in higher dimensions. Implementation of such algorithms to address real-life problems proves to be quite efficient due to their parsimonious structure, flexibility, robustness and high convergence speed. Components of a typical rain gauge network (e.g., rain gauges, their numbers and spatial locations) can be easily simulated using behavior of a swarm of bees. In particular, maximization of information content corresponds to maximization of nectar amount of food sources in a typical hive. Spatial location of rain gauges can be considered to be very similar to the nectar of food sources surrounding the hive. Obviously, as the nectar amount of various food sources regarding their spatial location has a direct impact on amount of nectar produced in a hive, various rain gauges influence the information content of the entire network very similarly. Initially, ABC was introduced by Karaboga (2005) to solve continuous optimization problems. In a sense, ABC attempts to simulate the behavior of honey bees in food foraging. Foraging task consists of exploration and exploitation processes. Traditionally, ABC consists of three types of bees:

2.2.1 Employed Bees

Employed bees are sent to the food sources to bring the nectar. They share the information of food sources with onlooker bees by waggle dance. Clearly, all the bees associated with the food sources which are exploited fully, abandon it and will become scouts or onlookers.

2.2.2 Onlooker Bees

Onlooker bees are waiting on the dance area and choosing a food source with probability related to its nectar amount (fitness) using roulette wheel selection. In fact, by using this approach, good and bad food sources are selected randomly while the good food sources attract more attention compared to bad ones.

2.2.3 Scout Bees

To yield the global optimization [i.e., maximizing the nectar amount of possible food sources], scout bees try to explore the environment surrounding the nest for the new food sources to escape from local optimum.

Specifically, the position of a food source represents a potential solution, while the nectar amount of a food source corresponds to the quality (fitness) of related solution. For more details on ABC algorithm, interested readers can refer to papers written on the subject elsewhere (Karaboga and Akay 2009; Karaboga et al. 2014).

3 Materials and Methods

3.1 Description of the Study Area

The proposed study is intended to be implemented on an area consisting of 34 non-recording rain gauge stations. The study area is located in the flat region of Kohkiloyeh-Bouyerahmad and Khouzestan provinces in Southwest of Iran covering an area of approximately 25,000 km2. It is located between longitude 49° 17′ and 51° 22′ east, and between latitude 30° 2′ and 31° 56′ north. The monthly rainfall depths, for at least a 10-year period, are used in this study. UTM coordinates, terrain elevations from mean sea level and the average annual rainfall depth of each rain gauge station (in mm) are collected and summarized in Table 1 (Attar et al. 2019). The location of the current study area along with rain gauge locations is shown in Fig. 1. The subsequent analysis will be conducted on these averaged annual rainfall data.

Table 1 Rainfall data used for interpolation
Full size table
Fig. 1
figure 1

Location of study area and rain gauge stations

Full size image

3.2 Definition of the Acceptable Accuracy

While a majority of papers written on rain gauge network design considered variance of residuals over the entire study area for network optimization, in recent years, a few investigators tried to refine the point rainfall estimation and introduced a measure to convert point estimation to block as large as the study area (Cheng et al. 2008; Shafiei et al. 2014; Haggag et al. 2016; Shahidi and Abedini 2018). These investigators proposed a measure so-called the percentage of area with acceptable accuracy to prioritize the rain gauge stations. As Cheng et al. (2008) pointed out, a reliable rain gauge network is the one for which most of the points inside the study area should have an acceptable accuracy satisfying a threshold.

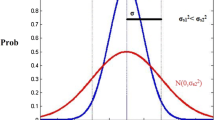
Generally speaking, one can assign probability of occurrence to estimated rainfall at each point. The higher the probability of occurrence, the closer the estimated value is to the true value. Fortunately, the network density is highly related to the probability of occurrence. The higher the network density, the higher the probability level. Hence, one can search for a network density whereby the probability level at each point honors a threshold. In this way, one can count the number of points satisfying the threshold and see which network density, for a particular n, would correspond to the percentage of area that the probability of the error variance at each point will fall in the range (− σ, σ).

On the other hand, the estimation of rainfall at un-gauge spatial location \((\varvec{s}_{0} )\) is considered to be acceptable only if its value falls within a given range (r) of the true value (Cheng et al. 2008).

$$\left| {R\left( {\varvec{s}_{0} } \right)} \right| = \left| {\hat{P}\left( {\varvec{s}_{0} } \right) - P\left( {\varvec{s}_{0} } \right)} \right| < r ,$$
(9)

where r > 0 and \(R\left( {\varvec{s}_{0} } \right)\) refers to estimation error (residuals). As mentioned earlier, in any watershed, numerous interrelated factors influence the amount of rainfall from one event to another. Therefore, standard deviation of the rainfall field (\(\sigma )\), as an arguable criterion, can be implemented to express the acceptable range for the estimation error which means:

$$\text{Prob}\left[ {\left| {\hat{P}\left( {\varvec{s}_{0} } \right) - P\left( {\varvec{s}_{0} } \right)} \right| < k\sigma } \right] \ge \alpha ,$$
(10)

where “Prob” means the probability, k is a multiplier and α is the minimum acceptable probability as a threshold. In light of this, the probability of residuals at any point in the network falls in the range \(\left( { - k\sigma ,k\sigma } \right)\). It means the probability of residuals is acceptable only if their value be more than α. Parameters k and α will be chosen based on available budget for rain gauge installation, operation, maintenance level, repair and the required estimation accuracy.

As a rule, residuals [\(R\left( {\varvec{s}_{0} } \right)]\) has normal distribution with zero mean and variance equal to \(\sigma_{R}^{2} \left( {\varvec{s}_{0} } \right)\) \(\{ {\text{i}}.{\text{e}}.,R\left( {\varvec{s}_{0} } \right) = N\left[ {0,\sigma_{R}^{2} \left( {\varvec{s}_{0} } \right)} \right]\}\). Therefore, the probability of estimation error can be calculated by dividing \(R\left( {\varvec{s}_{0} } \right)\) to residual’s standard deviation at point \(\varvec{s}_{0}\) [i.e., \(\sigma_{R} \left( {\varvec{s}_{0} } \right)\)]. As a result, standardized estimation error can be found as:

$$\text{Prob}\left[ {\left| {R\left( {\varvec{s}_{0} } \right)} \right| < \sigma } \right] = \text{Prob}\left[ {\frac{{\left| {R\left( {\varvec{s}_{0} } \right)} \right|}}{{\sigma_{R} \left( {\varvec{s}_{0} } \right)}} < \frac{\sigma }{{\sigma_{R} \left( {\varvec{s}_{0} } \right)}}} \right] = \text{Prob}\left[ {\left| {R^{ *} \left( {\varvec{s}_{0} } \right)} \right| < \frac{\sigma }{{\sigma_{R} \left( {\varvec{s}_{0} } \right)}}} \right] = A_{\text{point}} \left( {\varvec{s}_{0} } \right)$$
(11)

where \(R^{ *} \left( {\varvec{s}_{0} } \right)\) is the standardized estimation error and has normal standard distribution [i.e., N(0,1)]. \(A_{\text{point}} \left( {\varvec{s}_{0} } \right)\) is the “acceptable probability” at an un-gauged spatial location \((\varvec{s}_{0} )\). This point-based goodness of fit criterion of accuracy \(\left[ {A_{\text{point}} \left( {\varvec{s}_{0} } \right)} \right]\) can be accepted only if the associated “acceptable probability” is greater than α [\(A_{\text{point}} \left( {\varvec{s}_{0} } \right) > \alpha\)]. Finally, in order to convert point-based to block-based goodness of fit criterion, a new parameter so-called the percentage of area with acceptable accuracy (hereafter denoted by \(A_{\text{Areal}}\)) is introduced. It is the percentage of area that their acceptance probability [i.e., \(A_{\text{point}} \left( {\varvec{s}_{0} } \right)\)] is greater than α. Interested readers may want to consult Cheng et al. (2008) for further detailed information.

3.3 Application of ABC Algorithm for Binary Optimization (DisABC)

As mentioned earlier, the original version of the ABC algorithm can only manage continuous optimization problems, whereas in the current study, all different decision variables (rain gauge spatial locations) have a binary option (i.e., 0 for exclusion and 1 for inclusion). Therefore, the conventional continuous ABC which employs the continuous differential expression is not appropriate for this binary optimization problem. To fulfill this gap, DisABC which is introduced by Husseinzadeh Kashan et al. (2012) will be applied to solve the discrete optimization problem. In DisABC, a new differential expression is used to maintain the major characteristics of the original version. This new operator employs a measure of similarity/dissimilarity between binary vectors which is compatible with discrete structures. For this purpose, the dissimilarity between two binary vectors must be quantified. After its quantification, one has to generate a new binary solution to be used in subsequent calculations. For more detail on practical implementation of this algorithm in discrete mode, interested readers can refer to the relevant literature (Husseinzadeh Kashan et al. 2012; Attar et al. 2019).

4 Results and Discussion

4.1 Variogram Modeling

As mentioned earlier, point and block ordinary kriging are the most wildly used stochastic interpolation methods in recent years. Stochastic interpolation methods depend strongly on the variogram model used, which somehow defines the spatial variability in data. Generally speaking, hydrologists assume three scenarios in defining a variogram model (Oliver and Webster 2014), namely experimental variogram (i.e., which can be drawn from finite data as half of the average squared difference between the attribute values of every pair of data), regional variogram (i.e., which can be constructed if the attribute under consideration is monitored at every point in space calling for a computer with infinite capacity) and theoretical variogram (i.e., which should honor the experimental variogram). These functions have to be withdrawn from all competing functions with positive definite property.

The experimental semi-variogram \(\hat{\gamma }\left( {h_{ij} } \right)\) ordinate can be computed via the following relation:

$$\hat{\gamma }\left( {s_{i} ,s_{j} } \right) = \hat{\gamma }\left( {h_{ij} } \right) = \frac{1}{{2N\left( {h_{ij} } \right)}}\sum [P\left( {s_{i} } \right) - P\left( {s_{j} } \right)]^{2}$$
(12)

where N(\(h_{ij}\)) is the number of data pairs whose separation vector or distance is \(h_{ij }\).

$$h_{ij } = s_{i } {-}s_{j}$$
(13)

In general, the variogram is a function of both distance and direction, but due to uneven spatial distribution of rain gauges and lack of sufficient data points in different directions, directional variogram is not considered. Experimental omnidirectional variogram is constructed with annual rainfall data tabulated in Table 1. The selected theoretical model consisting of an exponential structure with a sill of \(\sigma^{2} = 37511 \,{\text{mm}}^{2}\) (i.e., global variance) and a range of 206,991 m (206.991 km, radius of influence) is shown in Fig. 2. As the focus of the current paper is to compare and contrast point versus block ordinary kriging on rain gauge network design, the impact of variogram parameters was not pursued here. Interested readers may want to refer to numerous references cited in the literature for more detail on variogram modeling (Oliver and Webster 2014; Adhikary et al. 2016).

Fig. 2
figure 2

Graphical representation of theoretical versus experimental variograms

Full size image

4.2 The Adopted Approaches and Summary of Results

As mentioned before, the adopted approach consists of two parts. In the first part, BOK will be coupled with DisABC optimizer to obtain optimum network density for various values of n (Attar et al. 2019). This part can be effectively used as an appropriate yardstick to check the validity of the proposed approach for all values of n to be discussed in the second part. Subsequently, DisABC optimizer can be efficiently utilized to obtain optimum network density upon maximizing the acceptable accuracy criterion over the entire study area for all values of n.

To be more specific, initially, a well-known paradigm so-called BOK in rain gauge network design is offered and then coupled with DisABC as an optimizer to bypass the curse of dimensionality and develop the exponentially decaying function in the current case study. Then, as the attribute under consideration at every point in space is assumed to be a random variable which has distribution of its own, to each point estimation, a probability can be attributed whereby the estimated value falls in the certain interval of true value. Aggregation of these point probabilities which will honor a threshold can be compared for various combinations of rain gauge stations in order to delineate an optimum combination with maximum percentage of area with acceptable accuracy \([A_{\text{Areal}} ]\) (Cheng et al. 2008).

One basic advantage of the cited technique is to propose a methodology which will use POK in a distributed fashion and then aggregation of point estimation into a spatial scale as large as the study area can be compared and contrasted with its counterpart BOK’s results for independent validation. Once again, the literature is found to be quite silent for the cited independent verification.

In other words, according to one school of thought, the variance of residuals over the entire study area has to be minimized, while according to the second school of thought, the percentage of area with acceptable accuracy over the entire study area is supposed to be maximized. This seemingly different goodness of fit criteria might be a good cause to observe that this independent validation did not attract the attention of spatial analysts in linking the two approaches.

In subsequent paragraphs, a summary of the step-by-step procedure to prioritize rain gauge stations, based on BOK, and the proposed methodology will be provided. Finally, the two approaches are compared and contrasted to bring up and emphasize the advantages of the new proposal.

4.3 Block Ordinary Kriging (BOK)

For the past six decades or so, investigators have applied BOK to design a rain gauge network. Bastin et al. (1984) and Kassim and Kottegoda (1991) considered BOK as the interpolant to design a rain gauge network and developed the exponentially decaying function without coupling it with any optimization algorithm. In fact, they used Bellman’s principle of optimality in a totally different context to surmount the curse of dimensionality cited before. The major characteristic of the BOK is the uniqueness of goodness of fit criterion. Due to this capability, in the current paper, DisABC is coupled with BOK to design a rain gauge network with no simplification involved.

The step-by-step procedure in BOK is very similar to the procedure which will be introduced in the next section. It means while the objective function in the proposed approach is the percentage of area with acceptable accuracy, in BOK, the objective function is variance of residuals. Figure 3 illustrates the exponentially decaying function resulting from coupling BOK with DisABC. In this figure, the numbers assigned to each data points correspond to station number documented in Table 1. As an example, 18–27 implies a two-station scenario which will lead to minimum variance of residuals compared to other scenarios. In addition, Fig. 4 shows the spatial location and arrangement of the best eight-stations scenario while coupling BOK with DisABC.

Fig. 3
figure 3

Minimum possible variance of residuals in a block versus the number of rain gauge stations (n)—BOK approach

Full size image
Fig. 4
figure 4

The location of the selection stations—BOK approach

Full size image

4.4 Point Ordinary Kriging (POK)—The Proposed Approach

As mentioned earlier, in the proposed approach, one is inclined to estimate the attribute under consideration at every grid point over the study area using POK. One basic advantage of kriging of any flavor is that the framework for estimation is stochastic implying possibility of assigning error to each estimation. This stochastic framework can be effectively utilized to compute probability of occurrence at each point in space. Aggregating these probabilities would give rise to a unique measure for subsequent maximization of information content. Cheng et al. (2008), Shafiei et al. (2014) and Haggag et al. (2016) had already implemented this viewpoint for rain gauge network design without verifying its validity. In addition, they assumed very similar simplification trying to bypass the curse of dimensionality. In the current study, the proposed methodology is used to obtain optimum network configuration via coupling it with DisABC without incorporating any assumptions and simplifications. Due to the random nature of search strategy in this optimization algorithm, no explicit or implicit simplification is required. It means the proposed algorithm will take care of small, intermediate and large values of n simultaneously. The step-by-step procedure to implement the cited scheme is documented in the following paragraphs:

Step 1. Exploratory spatial data analysis to understand and clean the data for further processing.

Step 2. Structural modeling or variography.

Step 3. Discretization of the study area to obtain the percentage of area with acceptable accuracy over a block as large as the study area.

Step 4. Development of a MATLAB code to couple POK with DisABC to generate various generations of rain gauge combinations for a particular value of n.

Step 5. Definition of a measure of dissimilarity between two binary vectors to construct new binary vectors of subsequent generation. The construction of binary vectors in each generation will continue until no further improvement in goodness of fit criterion can be achieved.

Step 6. Development of variation in \(A_{\text{Areal}}\) versus number of rain gauges and graphical representation of this variation (see Fig. 5).

Fig. 5
figure 5

Comparison between different values of α

Full size image

Step 7. Conversion of results obtained from previous step into results to be compared with conventional approach as demonstrated in Fig. 6 and finally Fig. 7 shows the location of the selection stations using the proposed approach.

Fig. 6
figure 6

Graphical representation of equivalent variance of residuals versus the number of rain gauge stations (n)—the proposed approach

Full size image
Fig. 7
figure 7

The location of the selection stations—the proposed approach

Full size image

5 Discussion of Results

In reference to the results obtained in previous parts, a possible rationalization of results and their implications at large will be pursued in this section. As a general rule, a typical rain gauge network can be evaluated in terms of network information content and the associated cost. Even though, no specific and direct accommodation of cost is considered in this study, the flexibility of the proposed approach implicitly if not explicitly takes care of this factor as well. Obviously, the network accuracy and the associated cost of operation, maintenance and repair depend on the number and spatial location of the existing rain gauges in the area under study. As such, rain gauge network design concerns with searching for a combination of rain gauges which either maximizes the accuracy (i.e., information content) and/or minimizes the errors corresponding to the estimator. Obviously, augmentation, reduction and/or relocation of the existing rain gauges would have a major influence on the numerical values of the goodness of fit criterion. To choose the best combination of rain gauge stations for the study area under consideration, two rain gauge network paradigms with similar parameters (mesh characteristics, i.e., size and number of grid nodes, variogram model and the associated parameters) are implemented on the study area as mentioned before. For the implementation of both point and block ordinary kriging, the study area is decomposed into a 13 km \(\times\) 13 km square grid. Graphical representation of minimum variance of residuals and the percentage of area with acceptable accuracy versus the number of rain gauge stations over the study area emerging from these implemented paradigms are demonstrated in Figs. 3 and 5. Both approaches provide areal accuracy corresponding to the block as large as the study area. For the sake of comparison and contrast, the converted results from this approach into the variance of residuals versus the number of rain gauge stations are computed and depicted in Fig. 6. Finally, the location of the selected stations using these approaches is depicted in Figs. 4 and 7.

Logical explanation and justification of results in reference to the above figures are summarized as follows:

  1. 1.

    For the sake of completeness, different values of α (0.80, 0.85 and 0.90) are tested. As Fig. 5 clearly illustrates, as the threshold value (α) increases, the network will reach the asymptotic level at a lower value. Upon increasing α, two important observations can be made. First, it can be seen that the percentage of area with acceptable accuracy for higher values of α is reduced. It means, for say eight rain gauge stations, \(A_{\text{Areal}}\) values are considerably high at α = 0.8 and will be reduced significantly at α = 0.9 (from 99 to 41%). Second, the goodness of fit criterion will stabilize at a lower number of rain gauges associated with lower values of α. This will be explained in more detail in the next item. All in all, the decision makers are advised to select a realistic choice for α parameter.

  2. 2.

    As shown in Fig. 5 for α = 0.8, only eight rain gauge stations are required to stabilize \(A_{\rm Areal}\) compared to the original network. It means, almost 26 redundant rain gauge stations have little or no contribution to the existing rain gauge network accuracy as used in the base network. When α = 0.9, almost 21 rain gauge stations are required to stabilize \(A_{\rm Areal}\) compared to the base network. However, in BOK as shown in Fig. 3, readers cannot see this trend due to the shape and nature of the associated decaying function. Practically speaking, in this approach, the variance of residuals will decrease even further upon addition of new rain gauge stations. However, the rate of variance reduction does not diminish considerably.

  3. 3.

    The proposed approach is recommended for augmentation and/or relocation of rain gauge stations due to the flexibility of choosing the parameters associated with this approach such as k, α and \(A_{\text{Areal}}\). On the contrary, BOK suffers from introducing any parameters and/or degrees of freedom to offer alternative choice to the decision makers.

  4. 4.

    The flexibility incorporated in DisABC algorithm provides the potential users with numerous various combinations when n, the number of rain gauge stations, is large. It means, this feature offers decision makers to look for a scenario which will best honor the constraints set forth over the ground (e.g., accessibility issue). In other words, when n equals 8, variance of residuals in the BOK over the entire study area is 1102 corresponding to rain gauge station combination as 7, 11, 15, 17, 21, 24, 30, 31, while DisABC coupled with the proposed approach suggests 13 cases similar to each other with acceptable and comparable percentage of area. The percentage of area with acceptable accuracy for α = 0.8 is calculated and tabulated in Table 2 using DisABC algorithm with due consideration on possibilities of incorporating additional constraints (e.g., accessibility, ease of maintenance, etc.) regarding selecting optimum combination.

    Table 2 Maximum percentage of area with acceptable accuracy for \(\left( {\begin{array}{*{20}c} {34} \\ 8 \\ \end{array} } \right)\) scenario (DisABC approach)
    Full size table
  5. 5.

    In the proposed approach, the percentage of area with acceptable accuracy for α = 0.90 when n varies from 21 to 34 is 77%. It means when n, number of rain gauge stations, reaches a certain level, the network accuracy would not change any longer. However, the operation, maintenance and repair (OMR) costs will increase. In other words, to look for a best rain gauge network configuration, implementation costs along with precision must be considered.

  6. 6.

    For the two approaches implemented in the current study, the spatial distribution of rain gauges is very similar as illustrated in Fig. 1. As an example, when n equals two for α = 0.80, the best stations corresponding to the maximum percentage of area with acceptable accuracy are 7, 22 while in BOK, the best stations are 18, 27. Looking in more detail into Fig. 1 confirms the fact that the selected stations function very similarly when it comes to computation of variance of residuals. Upon increasing n, the study area will be eventually filled with rain gauges in a uniform manner.

  7. 7.

    The original rain gauge network in K and B province consists of 48 non-recording rain gauges. The trend of topographic variation in the province is more or less mountainous and this fluctuating topography calls for a denser network. However, for hypothesis testing purposes and feasibility of comparing and contrasting the results with earlier research conducted on the same data (Shaghaghian and Abedini 2013), the study area and the corresponding network chosen, coincides with the flatter region of the province, mainly near the Behbahan border. The number of optimal rain gauges found in the study area can be justified by resorting to the flat topography involved in that region.

6 Concluding Remarks

Delineation of optimum number and spatial location of monitoring rain gauge stations has received remarkable attention in recent years and undergone gradual improvement in various aspects. Recent advances in computer hardware and software created a situation to eliminate the incorporated simplifications and also conduct independent verification of various assumptions introduced in network design paradigm. The current study intended to compare the results obtained from the recent viewpoint on acceptable accuracy with conventional, long lasting paradigm in rain gauge network design (i.e., variance minimization) for its independent validation.

In the current paper, a methodology is introduced to design a real-world rain gauge network via coupling ABC as an algorithm of minimization or maximization of objective functions to make the estimation of annual and long-term average rainfall more accurate. Here, the so-called notion regarding the percentage of area with acceptable accuracy is submitted to rigorous experimentation for possible independent verification. For this purpose, the proposed approach suggested by Cheng et al. (2008) are coupled with DisABC to design the network and then the results obtained from the proposed methodology is compared and contrasted with BOK to touch on advantages of the proposed methodology. After implementing the proposed approach on an existing network in Southwestern part of Iran, the similar results obtained from this comparison confirm seemingly different assumptions incorporated into the cited formulation. In particular, the flexibility in choosing the parameters associated with the proposed scheme along with unique and distributed nature of the proposed methodology gives decision makers and stakeholders enough freedom to consider various limitations and constraints available in practice. As kriging-based approaches utilize extensive amount of CPU time due to numerous matrix inversion, research is underway to consider deterministic estimator (i.e., inverse distance weighting scheme) for rain gauge network design to resolve the lack of time efficiency of the proposed scheme. This would in turn address the CPU time issue in rain gauge network design which is quite important while using kriging-based approaches.