1 Introduction

The distribution of a geophysical network is a multi-stage decision process which mainly relies on economic and demographic interests and on access problems in remote areas. Although an ideal network of stations should be spatially homogeneous and sufficiently dense to discriminate the minimum wave-length of the investigated geophysical phenomena, the irregularity and sparsity of observation points imply interpolation errors when reporting data on a regular grid. The areal clustering of point-sets can be measured by statistical indices as pointed out by Ouchi and Uekawa (1986) or, when the inter-station distances are scale-invariant, it can be well characterized thanks to a fractal analysis (Mandelbrot 1982).

If the point-set is self-similar, i.e. any small part of it is the magnified version of the whole set, the set is a fractal and it can be characterized by its fractal dimension D H , which is a real number with D H  < D E , where D E is the standard euclidean dimension of the embedding space (in our case, D E  = 2). In literature several works (Korvin et al. 1990; Lovejoy et al. 1986; Mazzarella and Tranfaglia 2000; Olsson and Niemczynowicz 1996; Tessier et al. 1994) deal with the fractal characterization of a single-point observation network and sometimes this analysis is used as a method to drive an optimal enlargement of the network (Mazzarella and Tranfaglia 2000). Lovejoy et al. (1986) state that any sufficiently sparsely distributed phenomena having a fractal dimension smaller than the dimensional deficit δ = 2 − D H of the observing network cannot be detected by the network itself. Since the sparse precipitating phenomena are the most intense and potentially severe, they are of prominent interest, particularly when the network of measuring stations are constantly used for civil protection purposes. The aim of this study was to compute the fractal dimension D H of the rain-gauge network belonging to the Centro Funzionale Regionale in Tuscany (Central Italy) and to compare D H with the fractal dimension d of daily rainfall events occurring in the same area, using an independent network for rainfall, for the month of July 2010. We find that D H  ≃ 1.85, therefore giving a dimensional deficit δ ≃ 0.15. On the other hand, all rain patterns give a fractal dimension d > 0.6, well above δ. A rough extrapolation of data for d as a function of 24-h rain thresholds suggests that our rain-gauge networks might fail to record precipitation events whose intensity is about 75 mm/day or more.

The paper is organized as follows. In Section 2 we detail the data used in this study and the methodology adopted to evaluate D H . In Section 3 the computation of the fractal dimension of the rain-gauge network is presented and compared to those obtained for rainy days. Finally in Section 4 results are discussed with reference to the potentiality and limits of the applied methodology.

2 Data sources and methods

2.1 Data sources

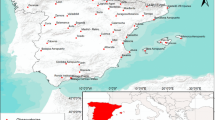
The location of the rain-gauges belonging to the Centro Funzionale Regionale (CFR) in Tuscany (Central Italy) is shown in Fig. 1. Its establishment has been a long-term decision process involving several local institutions over more than 20 years. The network comprises 377 stations and encloses several basins over an area of about 23,000 km2 (yielding a density of about one station every 60 km2). More than 90% of the stations are located below 810 m. The biggest inter-station distance (in other words the size or diameter of the point-set) is about 250 km. These data make the geography of our network similar to that studied by Mazzarella and Tranfaglia (2000).

Fig. 1
figure 1

Location of rain gauges (right side of the picture)—belonging to the Centro Funzionale Regionale network in Tuscany (Central Italy, on left side of the picture)

Full size image

Satellite imagery acquired by the Meteosat Second Generation (MSG-2) satellite in the infrared (IR) channel centered at 10.8 μm was used in this study as a proxy to detect and monitor cold clouds systems. The study period is July 2010 while the spatial and temporal data resolutions are 4.5 × 4.5 km2 and 15 min, respectively. A brightness temperature (T B ) threshold was used to identify cold cloud systems that are most likely to be associated with convective activity. Kolios and Feidas (2007, 2010) used a T B of 228 K to best identify convective systems in the Mediterranean area based on a set of lighting data. The same temperature threshold of 228 K was used by Morel and Senesi (2002) for assessing the climatology of the European MCSs, this value being very close to that of 221 K used by Garcia-Herera et al. (2005) for Spain. This low-temperature threshold allows to investigate mostly anvil regions and embedded areas of active deep convection (Johnson et al. 1990). In this study, a 228 K T B threshold value was chosen for identifying very deep convective events over Tuscany. Furthermore, discrimination between precipitating and non-precipitating cold cloud systems, previously subjected to T B threshold test, was performed using RADAR data provided by the DPCN (National Civil Protection Department) radar network. The data consist of a mosaic of instantaneous surface rainfall intensities (SRI) with a spatial and temporal resolution of 1 km and 15 min, respectively. Several daily precipitation amounts were tested; thresholds values of 1, 2, 5, 10, 15, 20, 25, 30, 35 mm per day were used to analyze the different phenomenology linked to precipitation, from weak to moderate regimes.

2.2 Methodology

While euclidean geometry deals with ideal geometric forms and assigns dimension 0 to points, 1 to lines and so on, fractal geometry deals with non-integer dimensions. The fractal, or Hausdorff, dimension D H has been the most common used measure of the strangeness of attractors of dissipative dynamical systems that exhibit chaotic behavior (Grassberger and Procaccia 1983b). Since for experimental data the value of D H is difficult to determine using the box-counting algorithm (Strogatz 1994), we computed the fractal dimension D 2 of point-set using the method proposed in Grassberger and Procaccia (1983a, b), as also found in the literature (Korvin et al. 1990; Lovejoy et al. 1986; Mazzarella and Tranfaglia 2000; Olsson and Niemczynowicz 1996). In the case under examination we choose to use D 2 as a good approximation of D H , since as stated in Grassberger and Procaccia (1983b), D 2 ≤ D H and inequalities are rather tight in most cases.

In the present study we compute the correlation dimension in a 2-dimensional space but in general, to obtain D 2 given a point-set \(\{{\bf{X}}_i\}_{i=1}^{N}\) with \({\bf{X}}_i\in{\bf{R}}^n\), we have to consider the correlation integral C(R) that counts the number of pairs \(\left\{{\bf{X}}_i,{\bf{X}}_j\right\}\) such that ∥ X i  − X j  ∥ is smaller than a given threshold R > 0, with ∥ · ∥ being the standard euclidean distance in R n. In formulas:

$$ C(R) = \frac{2}{N(N-1)}\sum\limits_{i=1}^N \sum\limits^N_{\substack{j=1 \\ j \ne i}} \Theta(R - \parallel{\bf{X}}_i- {\bf{X}}_j\parallel), $$
(1)

where Θ is the Heaviside function and where \(\frac{2}{N(N-1)}\) is the normalization factor so that C(R) tends to 1 for R tending to infinite.

If the rain-gauge network is a fractal then C(R) grows like a power:

$$ C(R) \varpropto R^{D_2}, $$
(2)

that is

$$\log(C(R)) \varpropto D_2\log(R). $$
(3)

Therefore, one can derive D 2 from the regression coefficient of relationship (3).

In order to determine the correlation dimension D 2 of the rain-gauge network described previously, we computed the correlation function defined in Eq. 1, as described in Lovejoy et al. (1986), i.e. we determined the cumulative frequency distribution of the inter-station distances for the total number of 377 stations. The distances were determined by spherical trigonometry, using geographic coordinates and ignoring elevations owing to the smallness of the elevation with respect to the two horizontal dimensions.

For what concerns the values of the parameter R, as done in Mazzarella and Tranfaglia (2000), we started in computing the inter-station distances defined in Eq. 1 from 1 km. This value was gradually increased by a factor of 1.1 up to 250 km since, as expected by definition of C(R) given in Eq. 1, for all \(R\ge\text{size (area of interest)}\) the correlation integral C(R) saturates to 1 and log(C(R)) saturates to 0.

For experimental data the linear behavior of log(C(R)) on log(R) is limited to a scaling region S R , i.e. only for R belonging to the interval S R  = [R min, R max] (Strogatz 1994). This happens because C(R) is underestimated from those points near the edge of the set so that the criteria to determine the bounds of S R need to be analyzed in each singular case (Liebovitch and Toth 1989). According to the literature (Forrest and Witten 1979; Grassberger and Procaccia 1983a; Korvin et al. 1990), the upper limit R max is chosen equal to one third of the diameter of the area (about 80 km). In order to choose the lower limit R min, we didn’t perform any statistical significance computation, since in our case the correlation coefficients are statistically significant at 99% confident level for all R ≥ 1 km. Rather, for each station we computed the distance of the nearest neighbor and took the average of this distribution as the meaningful index of the points separation.

In Fig. 2 we plot this distribution; the average of nearest neighbor’s distances is about 4.2 km and this value is considered as the lower limit R min meaningful for the regression.

Fig. 2
figure 2

Distribution of nearest neighbor’s distances for each station in the point-set. Average value is 4.2 km which is taken as R min, the lower limit for the regression of log(C(R)) on log(R)

Full size image

3 Results

The linear fitting between log(C(R)) and log(R) within the scaling region S R bounded by R min = 4.2 km and R max = 80.2 km yields a slope, and thus a correlation dimension value D 2 of 1.85. Figure 3 shows the results of this regression. The dimensional deficit δ of the network, defined as the difference between the dimension of the embedded space and D 2, is (2 − D 2) = 0.15.

Fig. 3
figure 3

Log-log plot of correlation integral C(R) on R with scaling region delimited by R min = 4.2 km and R max = 80.2 km. The corresponding slope of the regression line which determines the correlation dimension D 2 is equal to 1.85

Full size image

The value of δ should be related to the dimension d of rainfall phenomena. From a climatological point of view, the area of interest (central Italy) is mainly affected by convective storms or frontal systems, depending on the seasonality. Convective storms are of uppermost interest for our analysis since they are smaller, more or less separate rainfall areas displaying a considerable spatial variability and thus suitable for fractal analysis. They are typical of the warm season (from June to September roughly). The frontal storms are characterized by continuous rainfall areas of large spatial extensions and are typical in autumn and winter seasons.

Using remote sensing and ground instruments described in Section 2 we collect data for every day in July 2010. First step is to select all the pixel in the MSG-2 15-min dataset having a brightness temperature below 228 K so that we can obtain a point-set (i.e. pixel-set) of potential precipitation cells (Kolios and Feidas 2010; Morel and Senesi 2002). Secondly, to assign a rain amount to the selected pixels we use the radar data. For each selected pixel in the MSG 15-min dataset we retrieve the surface rainfall intensities (SRI) as estimated by the RADAR data provided by the DPCN (National Civil Protection Department). Finally for each day of July 2010 we add all the 96 daily images (for each day we have one image every 15 min) and obtain a daily estimate of precipitation amount. Rain estimates were processed in order to compute the correlation dimension using the method detailed in Section 2. In Fig. 4 we plot the correlation dimensions of rainfall events registered in the month of July 2010 in Tuscany. Daily rainfall events were divided on the basis of prescribed thresholds, chosen equal to 1, 2, 5, 10, 15, 20, 30, and 35 mm. For each threshold, Fig. 4 shows the average and standard deviation values of correlation dimension of the rainy pixel-set for those days having a significant number of points that registered an amount of precipitation above the threshold.

Fig. 4
figure 4

Correlation dimensions of rainfall events (average values and standard deviations) registered in Tuscany in the month of July 2010 for different thresholds. Horizontal gray line is δ, the dimensional deficit of rain-gauge network

Full size image

4 Discussion

The present study achieved the issue to estimate the areal sparseness of the monitoring rain-gauge network belonging to the CFR owned by Tuscany Administration by means of the fractal (correlation) dimension D 2. In Table 1, we compare this value with dimension D 2 found in other, similar studies in the literature. Except the cases of Australia and Canada, where the dominance of inhabited areas along the coast lowers the value of the fractal dimension, our D 2 value is in good agreement with the others.

Table 1 Comparison of D 2 computed in the present study with other correlation dimensions found in literature
Full size table

However, we have to point out that the computed correlation dimension D 2 must be handled with care because, according to the Tsonis criterion (Tsonis et al. 1994), the minimum number N min of points required to produce a correlation integral with no more than an error Err (normally Err = 0.05D E ) is approximately

$$ N_{\rm min}\varpropto 10^{2+0.4D_2} $$

which, in our case, means N min ≃ 600 whereas we have 377 stations.

In order to analyze the dimensional deficit δ = 0.15, we need to compare it with the fractal dimension of rainfall events, as done in the previous section. As for the precipitations fallen in July 2010, even the more intense ones were characterized by a fractal dimension d > 0.6, much greater than the dimensional deficit δ = 0.15. We stress that the used rain data (see Fig. 4) are independent from the rain-gauge network used to determine the fractal dimension D H  = 1.85. Therefore, these preliminary results allow us to state with a good confidence that our rain-gauge network was precise enough to record all precipitation events occurred in July 2010. Empirically we can suppose that the fractal dimension goes to zero as the threshold increases; this because intense precipitation events (at least thermo-convective ones) are more scattered. On the other hand light rains are more homogeneous and then associated to a (decreasing) linear trend for small thresholds. We then choose to fit the values plotted in Fig. 4 with an exponential model which is almost linear for small values of x and decreases to zero as x tends to infinity. We can then suppose that

$$ y=Ae^{-x/x_0} $$

where the independent variable x on the x-axis represents the daily amount of rain, y represents the fractal dimensions and the parameters are A = 1.657 and x 0 = 31.133. The model is calibrated using the first values of x (thresholds from 1 mm/day up to 15 mm/day, continuous line in Fig. 4), since above we don’t have any significant statistics (just two days registering at least 20 pixels with a precipitation above 20 mm and one day registering at least 20 pixels with a precipitation above 25 mm).

The exponential regression intersects δ = 0.15 for

$$ x_\delta=-x_0\ln\left(\frac{\delta}{A}\right) $$

that is x 0.15 ≃ 75 mm/day. In other words our data suggests that rainfalls with daily amount equal or above 75 mm/day might correspond to a fractal dimension d < δ, so that these events could not be detected. This value is based, by construction, on the remote sensed data and ground instruments and on the phenomenology of rainfall events. Ongoing efforts are directed toward the improvements of the accuracy of instruments and toward the calibration of the algorithms.

Further studies are required to investigate the relationship between correlation dimension D 2 of the observing network (but we are rather interested in the dimensional deficit δ) and the dimensions d of rainfall events. Firstly the most important improvement of the research is to expand the statistics of precipitating events considering several months for, at least, a couple of years. Moreover it would be interesting to take into consideration the fall/winter precipitations, which are mainly associated with cold and warm fronts, to evaluate the different behavior of dimension d and check if, for some thresholds, it drops below δ.